2016-03-02 收稿,
2016-04-18 录用,
2016-04-24 网络版发表
基金项目:国家自然科学基金(10972200)和河南省国际合作基金(144300510008)资助项目.
引言
由于胶黏剂使用简单,粘接结构重量轻,有较好的抗腐蚀和抗疲劳等优点,粘接结构被广泛地应用在汽车、航空、建筑和微电子等工业领域[1-3]. 为了使粘接结构能得到更广泛、更可靠的应用,其断裂过程和断裂特征需要更准确的研究和预测.
内聚力模型(cohesive zone models,
CZMs)被用在模拟和预测粘接结构的开裂和裂纹扩展过程,此模型首先由Barenblatt[4]和Dugdale[5]提出,当拉伸力达到临界值时,裂纹开始萌生,然后拉伸力下降,裂纹向前扩展直至完全断开.内聚力模型也被广泛应用于分析金属、陶瓷、高分子材料和复合材料的断裂失效,它可以准确分析裂纹尖端的塑性区、龟裂现象和蠕变行为等[6-10].
随后,Needleman[11]提出了二次多项式和指数形式的非线性内聚力模型(即抛物线型),用来分析金属的晶粒的开裂,以及有气泡的晶粒裂纹动态扩展过程;Tvergaard和Hutchinson[12]提出了弹性和理想塑性的三线型内聚力模型;Camacho和Oritiz[13]提出脆性断裂的双线型内聚力模型,并利用此聚力模型模拟了双臂梁试件在冲击载荷下裂纹扩展过程;Geubelle和Baylor[14]使用双线型内聚力模型模拟了复合纤维板在低速冲击载荷下的裂纹萌生、扩展和分层过程.以上计算结果与实验结果作比较,都能很好地反应实际的断裂特性.不同形状的内聚力模型对应着不同的拉伸-分离的本构关系,其主要的断裂参数是临界应力和断裂能,而形状参数确定了内聚力模型的形状(抛物线型、双线型和三线型)及其力学性质[15-17].通过理论计算与实验对比的方法获得内聚力模型的断裂和裂纹萌生的力学性能参数,用于分析实际工况下的不同粘接材料和粘接结构的可靠性[18-23].虽然,Blackman等[24]认为双臂梁的断裂过程中,内聚力模型的形状参数与断裂曲线无关;而Yan和Shang[25]的计算结果得到内聚力模型的形状参数在其分析过程中是起作用的.最近研究学者[26-28]开始重视研究内聚力模型形状和重要参数对其模拟不同胶黏剂和粘接结构的影响;Campilho
等[29-30]的研究表明内聚力模型的形状对延展性胶黏剂粘接的搭接结构有很大,对脆性胶黏剂影响不大.然而,粘接结构的裂纹萌生、扩展与粘接材料的性质关系如何,以及如何选用恰当的内聚力模型进行粘接结构的断裂分析,这些是目前使用内聚力模型比较模糊的问题,此类研究文献在国内外也不多见. 所以,对以上问题本文做出更深入的研究.
本研究采用两种不同性能的胶黏剂,一种为脆性的环氧树脂胶,一种为延展性的VHB(very high bond)胶.分别对其对接试件进行拉伸、剪切实验和双臂梁试件的断裂实验,通过与实验对比得到两种胶黏剂的拉伸-分离的关系曲线,并获得其临界应力、断裂能和形状参数.采用抛物线型,三线型和双线型3种类型内聚力模型,对以上两种粘接结构的拉伸、剪切和断裂过程进行数值模拟.通过计算结果与实验结果的对比分析,确定出更适合的内聚力模型可以模拟不同的胶黏剂与不同的粘接结构的断裂过程.
1 实验过程
1.1 粘接试件制作
脆性胶黏剂采用商用环氧树脂强度结构胶,型号为LORD 320/322,由美国LORD(洛德)公司生产.延展性胶黏剂采用带状的G16F VHB$^{\rm TM}$,一种建筑用压敏胶,由美国3M公司生产. 其宽度为25.4 mm,厚度为1 mm.
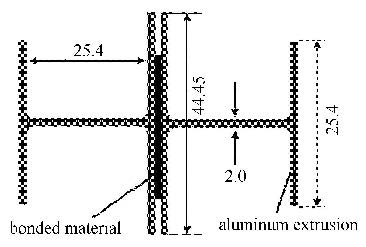
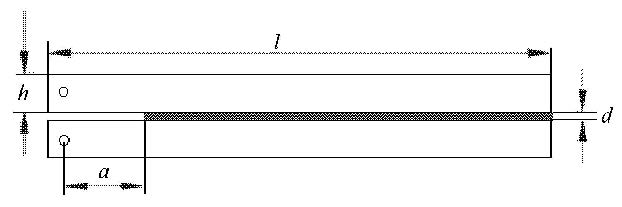
对接试件的被粘物采用工字型铝合金,型号6061-T6,长度50 mm,试件的粘接形式和结构尺寸如图 1所示.采用这种形式的被粘物,可以减少实验过程中试件边缘的应力集中.这种工字型铝合金的强度经过测试,能够达到本实验要求.铝型材的粘接面用100号砂纸打磨,确保表面有统一的粗糙度,粘接面使用丙酮进行表面清洗,清除表面的灰尘、油泥等污染物,并在烘干箱内烘干30 min 后进行粘接. 双臂梁试件按照ASTM(美国材料与试验协会)标准制作,如图 2所示.图中$a=50$ mm,$l=250$ mm,$h=12.75$ mm,$d=1$ mm,试件宽度为25.4 mm. 被粘物采用T6061
铝合金,粘接面采用220号砂纸打磨. 同样,粘接面使用丙酮进行表面清洗,并在烘干箱内烘干30 min后进行粘接.制作对接试件和双臂梁试件时,采用1 mm厚的聚四氟乙烯膜(teflon film),夹在被粘物之间,保证粘接后的胶体厚度都控制在1 mm. 每组试件在室内保持24 h之后进行实验.
1.2 实验方案
拉伸和剪切实验采用一种带有平衡调节的Arcan固定装置,此装置可以实现拉伸、剪切和其他角度的强度实验[31-32],Arcan固定装置如图 3(a)所示.为实现试件与固定装置更好结合,设计了一种特制的夹持结构,夹具如图 3(b)所示,夹具与固定装置Arcan用销钉连接,夹具与试件用螺栓顶紧,它可以保证试件固定,实验时没有附加的滑移. 实验采用Instron
5800力学试验机,分别采用5 kN和30 kN的力传感器,用于两种胶体粘接的试件进行实验;脆性胶黏剂粘接的试件进行拉伸和剪切实验,采用引伸计测量位移,引伸计固定在如图 4(a)和图 4(b)所示的位置,记录拉伸和剪切的应变.其他实验用试验机自身元件测量位移. 本实验采用位移控制,位移速度控制为0.5 mm/min. 每组实验重复5次.
2 内聚力模型
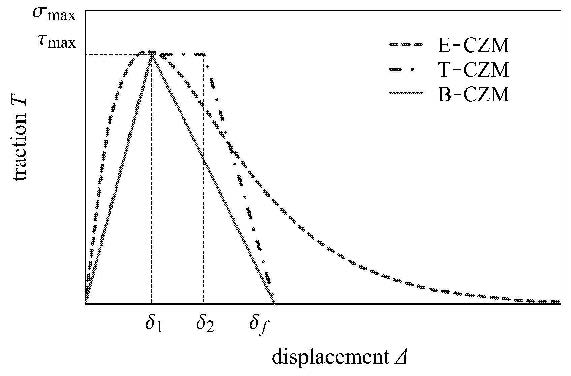
目前,被广泛采用的内聚力模型有:指数形式的抛物线模型(E-CZM)[6],弹性-理想塑性的三线型模型(T-CZM)[7]和弹性的双线型模型(B-CZM)[8]. 3种内聚力模型的拉伸-分离关系如图 5所示.
2.1 抛物线型内聚力模型
指数形式的内聚力模型的拉伸力与分离位移之间的关系式为
|
$T_n = - \dfrac{\phi _n }{\delta _{n1} }\exp \Bigg ( - \dfrac{\varDelta _n }{\delta _n }
\Bigg) \Bigg\{ \dfrac{\varDelta _n }{\delta _n }\exp \left( { - \dfrac{\varDelta _\tau^2 }{\delta _{\tau
1}^2 }} \right) + $
$ \dfrac{1 - q}{r - 1}\left[{1 - \exp \left( { - \dfrac{\varDelta _\tau ^2 }{\delta
_{\tau 1}^2 }} \right)} \right]\left( {r - \dfrac{\Delta _n }{\delta _{n1} }} \right) \Bigg \} $
|
(1) |
|
$T_\tau = - \dfrac{\phi _n }{\delta _{n1} } 2\dfrac{\delta _{n1} }{\delta _{\tau 1} }
\dfrac{\varDelta _\tau }{\delta _{\tau 1} }\left[{q + \left( {\dfrac{r - q}{r - 1}} \right)\dfrac{\varDelta
_n }{\delta _{n1} }} \right]\cdot $
$ \exp \left( { - \dfrac{\varDelta _n }{\delta _{n1} }} \right)\exp \left( { -
\dfrac{\varDelta _\tau ^2 }{\delta _{\tau 1}^2 }} \right) $
|
(2) |
拉伸和剪切的断裂能与临界应力相关联,分别表示为
|
$\phi _{\rm n} = \sigma _{\max } \delta _{n1} {\rm e}$
|
(3) |
|
$\phi _{\tau} = \sqrt {{\rm e}/ 2} \tau _{\max } \delta _{\tau 1} $
|
(4) |
式中,$T_{ n} $和$T_{\tau} $是拉伸和剪切力; $\phi _n$ 和$\phi _\tau$
分别是拉伸和剪切的分离功; $\varDelta _n $和$\varDelta _\tau $分别为拉伸和剪切的分离位移; $\sigma _{\max }
$和$\tau _{\max } $为拉伸和剪切断裂的临界应力;$\delta _{n1} $和$\delta _{\tau 1} $分别为拉伸和剪切应力达到临界应力时的位移;$q = \phi _\tau / \phi _n $,$r = \varDelta _n^\ast / \delta
_{n1}$,如图 5所示.
2.2 双线型内聚力模型
双线型内聚力模型的拉伸力与分离位移之间的关系式为
|
$T_n = \left\{ \!\! \begin{array}{ll}
\dfrac{\sigma _{\max } }{\sigma _{n1} }\varDelta _n &
\left( {\varDelta _n ≤ \delta _{n1} } \right) \\
\sigma _{\max } \dfrac{\delta _n^{\rm f} - \varDelta _n }{\delta _n^{\rm f} - \delta _{n1} } & \left(
{\varDelta _n > \delta _{n1} } \right)\end{array} \right.$
|
(5) |
|
$T_\tau = \left\{ \!\! \begin{array}{ll} \dfrac{\tau _{\max } }{\delta _{\tau 1}
}\varDelta _\tau & \left( {\varDelta _\tau \leq \delta _{\tau 1} } \right) \\
\tau _{\max } \dfrac{\delta _\tau ^{\rm f} - \varDelta _\tau }{\delta _\tau ^{\rm f} -
\delta _{\tau 1} } & \left( {\Delta _\tau > \delta _{\tau 1} } \right) \end{array} \right. $
|
(6) |
拉伸和剪切的断裂能为
|
$\phi _n = \dfrac{1}{2}\sigma _{\max } \delta _n^{\rm f} $
|
(7) |
|
$\phi _\tau = \dfrac{1}{2}\tau _{\max } \delta _\tau ^{\rm f} $
|
(8) |
式中,$\delta _n^{\rm f}$ 和$\delta _\tau ^{\rm f}$ 为界面分离的临界位移,也是双线型模型的形状参数,如图 5所示.
2.3 三线型内聚力模型
三线型内聚力模型的拉伸力与分离位移之间的关系式为
|
$T_n = \left\{ \!\!\begin{array}{ll} \dfrac{\sigma _{\max } }{\sigma _{n1} }\varDelta _n & \left(
{\varDelta _n ≤ \delta _{n1} } \right) \\
\sigma _{\max }
& \left( {\delta _{n1} ≤ \varDelta _n ≤ \delta _{n2} } \right) \\
\dfrac{\sigma _{\max } }{\delta _n^{\rm f} - \delta _{n2} }\;(\delta _n^{\rm f} -
\varDelta _n ) & \left( {\delta _{n2} ≤ \varDelta _n ≤ \delta _n^{\rm f} } \right) \\
0 & \left( {\varDelta _n>\delta _n^{\rm f} } \right)\end{array} \right. $
|
(9) |
|
$T_\tau = \left\{ \begin{array}{ll}
\dfrac{\tau _{\max } }{\sigma _{\tau 1} }\varDelta _\tau
& \left( {\varDelta _\tau ≤ \delta _{\tau 1} } \right) \\
\tau _{\max }
& \left( {\delta _{\tau 1} ≤ \varDelta _\tau ≤ \delta _{\tau 2} } \right) \\
\dfrac{\tau _{\max } }{\delta _\tau ^{\rm f} - \delta _{\tau 2} }\;(\delta _\tau^{\rm f} - \varDelta _\tau ) &
\left( {\delta _{\tau 2}
≤ \varDelta _\tau ≤ \delta _\tau^{\rm f} } \right)\\
0 & \left( {\varDelta _\tau>\delta _\tau^{\rm f} } \right)\end{array} \right. $
|
(10) |
此内聚力模型的拉伸和剪切的断裂能为
|
$\phi _n = \dfrac{1}{2}\sigma _{\max } \left( {\delta _{n2} - \delta _{n1} +
\delta _n^{\rm f} } \right) $
|
(11) |
|
$\phi _\tau = \dfrac{1}{2}\tau _{\max } \left( {\delta _{\tau 2} - \delta
_{\tau 1} + \delta _\tau ^{\rm f} } \right) $
|
(12) |
式中,$\delta _{n1}$,$\delta _{n2}$,$\delta _n^{\rm f}$,$\delta _{\tau 1}$,$\delta _{\tau 2}$ 和$\delta _\tau ^{\rm f} $分别是内聚力模型不同应力对应的分离位移,是三线型内聚力模型的形状参数. 其他参数含义同上,如图 5所示.
3 模型建立和模拟方法
应用商用ABAQUS软件,通过有限元法对两种胶体粘接试件的拉伸剪切和双臂梁的断裂过程进行模拟. 粘接材料的本构关系分别采用3种内聚力模型的拉伸(剪切)-$\!$分离关系,本研究通过建立用户材料子程序方法,赋予粘接层不同的内聚力关系,计算过程使用显性积分计算. 被粘物的力学性质为弹性材料,弹性模量和泊松比分别为,$E =69$ GPa,$\mu =0.3$. 根据试件的几何特点和加载情况,采用二维结构模型和平面应变状体模拟. 被粘物采用四节点平面应变单元CEP4,对接结构网格数为1 200个,双臂梁的网格为1 500个;粘接层采用4节点二维的单层粘接单元COH2D4,对接结构网格数为50个,双臂梁的网格数为200个,几何模型与试件结构一致.
4 结果与分析
4.1 脆性胶黏剂拉伸和剪切实验及数值计算
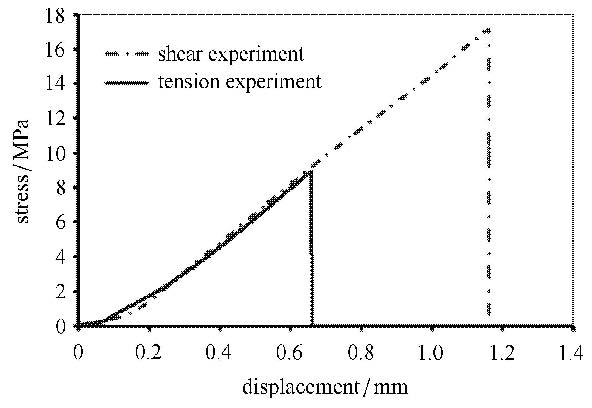
脆性胶黏剂粘接的对接试件,其拉伸和剪切实验结果,如图 6所示,拉伸和剪切的应力-位移呈线性关系.
实验中发现,剪切的断裂强度高于拉伸强度,即临界剪切应力大于临界拉伸应力;断裂时,裂纹一旦出现,会迅速扩展到全部断开. 粘接界面的失效表现为脆性断裂,没有发现黏性和塑性现象的发生.而且,从断裂面上分析,断裂一般都发生在胶体层上.从与实验结果的对比中可以得到内聚力模型需要的主要参数,通过调节内聚参数使得模拟实验的加载曲线与真实的加载曲线吻合,从而确定内聚参数. 为了能更好地模拟实验结果,对比内聚力模型和拉伸与剪切实验曲线获得其形状参数比例.3个内聚力模型的主要参数如表 1所示.
在模拟的过程中,几何模型的建立、材料性能、边界条件和加载情况都与实验过程相同,但粘接层采用不同内聚力拉伸-分离关系的用户材料子程序. 而且,计算时3个模型采用相同的临界应力和断裂能.拉伸和剪切实验的模拟结果与实验对比结果,如图 7和图 8所示.结果对比可以发现,使用内聚力模型模拟对接结构的拉伸和剪切断裂过程中,临界应力和断裂能是重要的参数,而且形状参数起到非常重要,决定了断裂的主要特征.对于脆性粘接材料的断裂,无论是拉伸和剪切情况,只有双线型内聚力模型才能准确模拟出对接结构断裂的脆性特征,其他两个模型不适于模拟脆性胶黏剂粘接的对接结构断裂过程.
表 1(Table 1)

表 1 脆性胶接试件断裂实验得到的内聚力模型参数
Table 1 Cohesive zone parameter from the brittle adhesive experiment
results
|
表 1 脆性胶接试件断裂实验得到的内聚力模型参数
Table 1 Cohesive zone parameter from the brittle adhesive experiment
results
|
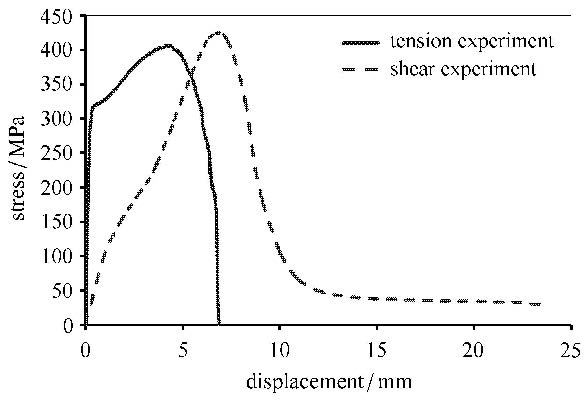
4.2 延展性胶黏剂拉伸和剪切实验及数值计算
延展性胶黏剂粘接的对接试件拉伸和剪切实验的结果,如图 9所示. 实验过程观察到开裂路径是在胶层与粘接界面之间交替出现.可以看到拉伸和剪切情况下,应力-位移曲线上升阶段和下降阶段都呈现出非线性,剪切临界应力略高出拉伸临界应力;此粘接结构断裂失效表现为延展材料特性,此粘接材料的拉伸应变达到600%,剪切应变为1000%.胶黏剂粘接的临界应力和断裂能也是通过实验结果的对比中获得的.内聚力模型计算所需的形状参数比例也需要从实验结果比较中得到.计算延展性胶黏剂断裂过程的3个内聚力模型主要参数,如表 2所示.
表 2(Table 2)

表 2 延展性胶接试件断裂实验得到的内聚力模型参数
Table 2 Cohesive zone parameter from the ductile adhesive experiment results
|
表 2 延展性胶接试件断裂实验得到的内聚力模型参数
Table 2 Cohesive zone parameter from the ductile adhesive experiment results
|
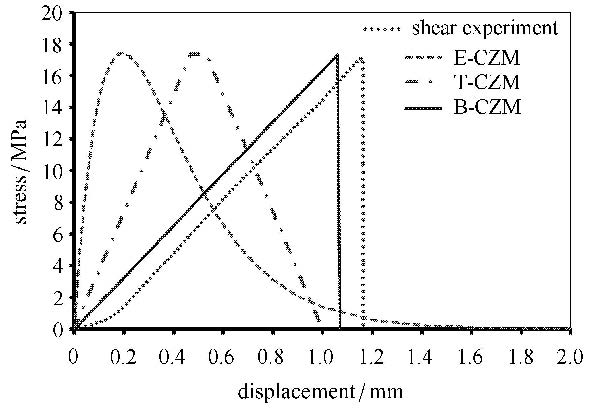
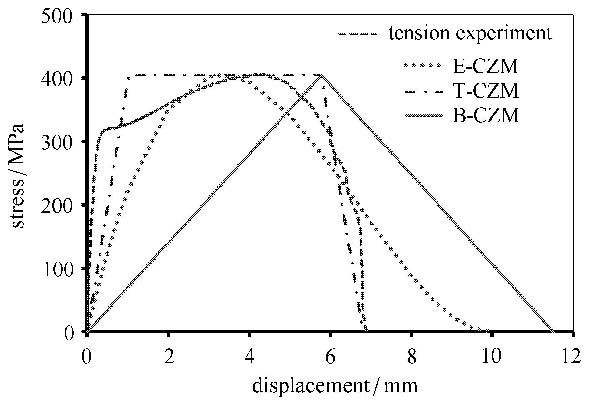
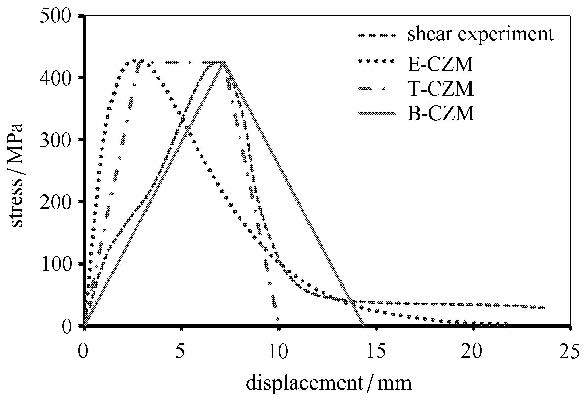
采用3种内聚力模型,分别计算延展性胶黏剂粘接的对接试件的断裂过程.同样,3个模型采用实验获得相同的临界应力和断裂能. 拉伸和剪切实验的模拟结果与实验结果对比,如图 10和图 11所示.结果发现,在使用内聚力模型模拟延展性胶黏剂粘接的对接结构拉伸和剪切断裂过程中,形状参数起到很重要作用.从3种内聚力模型模拟的拉伸和剪切断裂曲线与实验结果对比可以发现,虽然模拟拉伸断裂过程中,抛物线型模拟的曲线在断裂尾部与实验曲线相差很多,三线型的模拟曲线在中间部分与实验曲线重合度不好;而模拟剪切断裂时,断裂曲线上升阶段,双线型模拟曲线与实验曲线重合比较好,而断裂曲线下降阶段,三线型模拟的结果与实验曲线比较接近.但综合曲线的形状分析,延展性粘接材料粘接的对接试件断裂过程,抛物线型的内聚力模型相对比较适合,而双线型和三线型的内聚力模型只能适合分析某一段的对接结构拉伸和剪切断裂过程.
4.3 双臂梁试件的断裂实验及数值计算
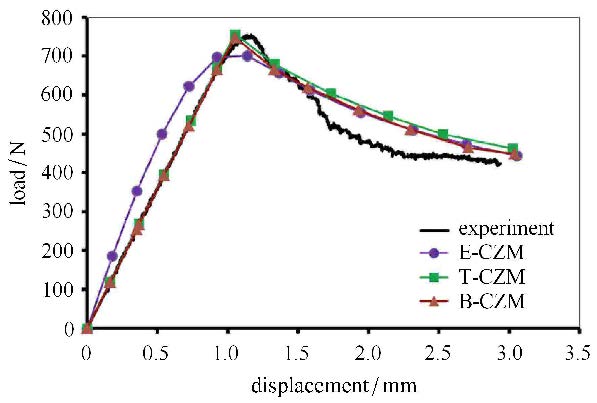
双臂梁断裂实验是对双臂梁两端夹持进行力和位移的测量,并得到拉力-位移实验曲线.实验发现,实验的断裂曲线开始阶段为线性上升,断裂后粘接强度逐渐下降,下降阶段表现为非线性,直至全部开裂,如图 12所示.为了体现不同内聚力模型数值模拟双臂梁的断裂过程适应性,采用3种内聚力模型分别计算脆性胶黏剂粘接的双臂梁试件断裂过程.在计算过程中,几何模型、材料性能、边界条件和加载情况都与实验过程相同,但粘接层采用不同内聚力拉伸-分离关系用户材料子程序,采用前面实验获得的参数,如表 1所示,3种内聚力模型采用相同的临界应力和断裂能.计算结果发现,双线型和三线型内聚力模型,在曲线的开始阶段与实验曲线有相同的线性上升趋势,重合度很好,并同时达到最大值,比实验值小7 N;在下降过程中双线型模型能更接近实验曲线.而抛物线型内聚力模型在上升阶段表现为非线性,与实验曲线不符,峰值力低于实验值45 N,下降趋势与其他模型接近.文献[26, 29]中都使用ABAQUS自带模型(线性上升和非线性下降的内聚力模型)代替抛物线模型,这样无法体现抛物线型内聚力模型非线性上升的特点.本文采用的抛物线内聚力模型的数值计算方法可以更准确地比较模型的整体模拟效果.通过3种模型模拟结果与实验曲线比较,双线型内聚力模型的模拟结果更接近实验曲线.由于在双臂梁的断裂过程中,粘接层在拉伸和剪切组合力的作用下断裂,不能确定哪个应力贡献更多.同时,被粘物的弯曲变形力也对拉力有作用. 所以,在双臂梁断裂过程中,内聚力模型中的形状参数的作用被淡化,不如对接结构的拉伸和剪切,内聚力模型形状起到绝对作用,但形状参数与材料力学性质相关,对断裂过程的曲线有一定的影响.
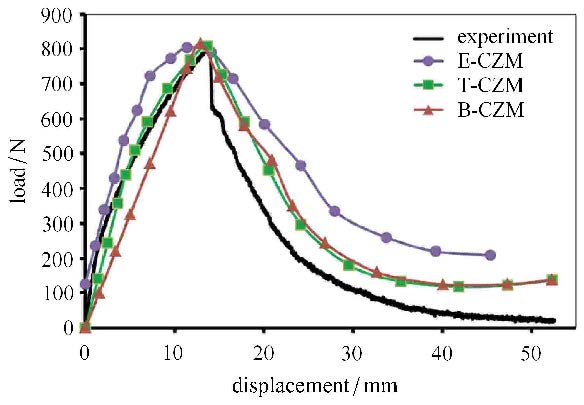
延展性胶黏剂粘接的双臂梁试件的断裂实验结果,如图 13所示.这种胶黏剂粘接的双臂梁断裂初始阶段,载荷表现为非线性上升,期间经历很长的位移;达到断裂的峰值后,然后快速下降,断裂载荷有很大延展性.模拟双臂梁断裂实验过程中,3个模型都采用与前面拉伸和剪切实验相同的临界应力、断裂能和形状参数,计算结果与实验对比如图 13所示.结果发现,对于数值模拟延展性胶黏剂粘接的双臂梁试件断裂过程,抛物线型和三线型内聚力模型能模拟出断裂上升阶段的非线性,双线型内聚力模型模拟的上升阶段只是线性.其中,三线型模拟结果与实验曲线出重合度很好,3个模型都能达到最大拉力;断裂的下降阶段,虽然双线型和三线型模拟曲线与实验曲线比高出95 N,但这两个曲线与实验曲线的趋势很接近.比较3种内聚力模型结果,三线型内聚力模型模拟曲线和实验曲线最接近,文献[29]中,作者虽然采用搭接粘接结构来研究内聚力模型的形状对两种胶黏剂的模拟结果影响,与本文的双臂梁粘接结构的研究结果也是相同的,三线型内聚力模型更适合计算延展性胶黏剂粘接的双臂梁断裂过程.说明数值模拟延展性胶黏剂粘接结构断裂时,更依靠内聚力模型的形状选择,用ABAQUS自带简单的双线型无法准确数值模拟其断裂过程.实验和计算结果也表明双臂梁粘接结构的裂纹萌生、扩展与粘接材料的性质关系很大,而内聚力模型的形状参数与材料力学性质相关,所以,形状参数对不同粘接材料的结构断裂过程起一定作用.
5 结论
本文采用两种类型的胶黏剂,对其粘接的对接试件进行了拉伸、剪切实验,以及对双臂梁试件进行断裂实验,并通过对接试件的拉伸和剪切实验对比获取了临界应力、断裂能和相应形状参数比值.采用3种类型的内聚力模型(抛物线型、双线型和三线型)分别计算了以上粘接结构的断裂过程,并与实验结果进行对比.结果发现,双线型内聚力模型更适用分析脆性胶黏剂的拉伸与剪切的断裂;抛物线型内聚力模型适用于计算延展性胶黏剂的拉伸和剪切的断裂;临界应力、断裂能和模型的形状参数是分析拉伸和剪切的重要参数;然而,由于拉伸、剪切和被粘物体变形同时起作用的双臂梁试件的断裂过程,内聚力模型的形状参数起到的作用被相对减小,双线型内聚力模型更适合脆性胶黏剂粘接的双臂梁断裂过程的计算,三线型内聚力模型更适合计算延展性胶黏剂粘接的双臂梁断裂过程.结果表明双臂梁粘接结构的裂纹萌生、扩展与粘接材料的性质有关,而内聚力模型的形状与材料力学性质相关,所以它对不同的粘接结构和粘接材料都起作用. 此研究结果对于内聚力模型的使用和粘接结构的断裂预测有重要意义.
参考文献
| 1 |
He X. A review of finite element analysis of adhesively bonded joints.
International Journal of Adhesion & Adhesives,2011, 31 : 248-264.
( 0) 0)
|
| 2 |
郑锐, 林建平, 吴倩倩, 等. 结构胶胶接汽车车身金属接头抗环境腐蚀性能研究进展.
材料工程,2015, 43 (3) : 98-105.
( Zheng Rui, Lin Jianping, Wu Qianqian, et al. Progress in research on environmental corrosion-resistance of structural adhesive bonding automotive-body metal joint.
Journal of Materials Engineering,2015, 43 (3) : 98-105.
(in Chinese) ) ( 0) 0)
|
| 3 |
叶斐, 杨世文. 碳纤维复合材料胶接单搭接接头的力学研究.
汽车实用技术,2015, 2 : 68-70.
( Ye Fei, Yang Shiwen. The mechanics study of carbon fiber composite single lap adhesive joints.
Automobile Applied Technology,2015, 2 : 68-70.
(in Chinese) ) ( 0) 0)
|
| 4 |
Barenblatt GI. The formation of equilibrium cracks during brittle fracture:general ideas and hypotheses, axially symmetric crack.
Applied Mathematics and Mechanics,1959, 23 : 622-636.
DOI: 10.1016/0021-8928(59)90157-1. ( 0) 0)
|
| 5 |
Dugdale DS. Yielding of steel sheets containing slits.
Journal of the Mechanics and Physics of Solids,1960, 8 : 100-104.
DOI: 10.1016/0022-5096(60)90013-2. ( 0) 0)
|
| 6 |
刘湘云, 陈普会, 马维, 等. 复合材料-金属毛化接头的失效预测模型.
固体力学学报,2015, 36 (1) : 55-62.
( Liu Xiangyun, Chen Puhui, Ma Wei, et al. A model for a composite-metal-weld joint.
Journal of Solid Mechanics,2015, 36 (1) : 55-62.
(in Chinese) ) ( 0) 0)
|
| 7 |
Feraren P, Jensen HM. Cohesive zone modelling of interface fracture near flaws in adhesive joints.
Engineering Fracture Mechanics,2004, 71 : 2125-2142.
DOI: 10.1016/j.engfracmech.2003.12.003. ( 0) 0)
|
| 8 |
Park K, Paulino GH, Roesler JR. Determination of the kink point in the bilinear softening model for concrete.
Engineering Fracture Mechanics,2008, 75 : 3806-3818.
DOI: 10.1016/j.engfracmech.2008.02.002. ( 0) 0)
|
| 9 |
张军, 张永祥, 杨军. 环氧树脂胶湿热与室温环境下的蠕变行为研究.
机械强度,2015, 37 (6) : 237-242.
( Zhang Jun, Zhang Yongxiang, Yang Jun. Investigation on Epoxy Creep Behavior at Ambient and Hydrothermal Environment.
Journal of Mechanical Strength,2015, 37 (6) : 237-242.
(in Chinese) ) ( 0) 0)
|
| 10 |
张军, 王增威, 杨军, 等. 环氧树脂胶对接结构的疲劳试验与理论研究.
中国胶粘剂,2014, 23 (9) : 17-21.
( Zhang Jun, Wang Zengwei, Yang Jun, et al. Fatigue experiment and theoretical investigation on epoxy resin adhesive butt joint.
China Adhesives,2014, 23 (9) : 17-21.
(in Chinese) ) ( 0) 0)
|
| 11 |
Needleman A. A continuum model for void nucleation by inclusion debonding.
Journal of Applied Mechanics,1987, 54 : 525-531.
DOI: 10.1115/1.3173064. ( 0) 0)
|
| 12 |
Tvergaard V, Hutchinson JW. The relation between crack growth resistance and fracture process parameters in elastic-plastic solids.
Journal of Mechanics and Physics of Solids,1992, 40 : 1377-1397.
DOI: 10.1016/0022-5096(92)90020-3. ( 0) 0)
|
| 13 |
Camacho GT, Ortiz M. Computational modeling of impact damage in brittle materials.
International Journal of Solids and Structures,1996, 33 : 2899-2938.
DOI: 10.1016/0020-7683(95)00255-3. ( 0) 0)
|
| 14 |
Geubelle PH, Baylor J. Impact-induced delamination of laminated composites:a 2D simulation.
Composites Part B:Engineering,1998, 29 : 589-602.
DOI: 10.1016/S1359-8368(98)00013-4. ( 0) 0)
|
| 15 |
Alfano M, Furgiuele F, Leonardi A, et al. Mode I fracture of adhesive joints using tailored cohesive zone models.
International Journal of Fracture,2009, 157 : 193-204.
DOI: 10.1007/s10704-008-9293-4. ( 0) 0)
|
| 16 |
Martiny PH, Lani F, Kinloch AJ, et al. A maximum stress at a distance criterion for the prediction of crack propagation in adhesivelybonded joints.
Engineering Fracture Mechanics,2013, 97 : 105-135.
DOI: 10.1016/j.engfracmech.2012.10.025. ( 0) 0)
|
| 17 |
Jhin G, Azari S, Ameli A, et al. Crack growth rate and crack path in adhesively bonded joints:Comparison of creep fatigue and fracture.
International Journal of Adhesion and Adhesives,2013, 46 : 74-84.
DOI: 10.1016/j.ijadhadh.2013.05.009. ( 0) 0)
|
| 18 |
张军.
界面应力及内聚力模型在界面力学的应用. 郑州: 郑州大学出版社, 2011 .
( Zhang Jun.
Application of Interface Stress and Cohesive Zone Model in Interface Mechanics. Zhengzhou: Zhengzhou University Press, 2011 .
(in Chinese) ) ( 0) 0)
|
| 19 |
Liljedhal CDM, Crocombe AD, Wahab MA. Damage modeling of adhesively bonded joints.
International Journal of Fracture,2006, 141 : 147-161.
DOI: 10.1007/s10704-006-0072-9. ( 0) 0)
|
| 20 |
Chen CC, Linzell DG. Modeling end notched flexure tests to establish cohesive element mode Ⅱ fracture parameters.
Engineering Fracture Mechanics,2010, 77 : 1338-1347.
DOI: 10.1016/j.engfracmech.2010.03.017. ( 0) 0)
|
| 21 |
李伟东, 吴坤岳, 胡平. 周期激励下单搭接接头强度与振动特性研究.
计算力学学报,2014, 31 (4) : 446-452.
( LiWeidong, Wu Kunyue, Hu Ping. Study on strength and fatigue behavior of single lap joint under periodic excitation.
Chinese Journal of Computational Mechanics,2014, 31 (4) : 446-452.
(in Chinese) ) ( 0) 0)
|
| 22 |
张盼, 许英杰, 汪海滨, 等. 基于粘弹性本构模型的双搭接胶结接头应力分析.
应用数学和力学,2015, 36 (2) : 160-166.
( Zhang Pan, Xu Yingjie, Wang Haibin, et al. Stress analyses of double lap bonding joint using viscoelastic constitutive model.
Applied Mathematics and Mechanics,2015, 36 (2) : 160-166.
(in Chinese) ) ( 0) 0)
|
| 23 |
X uW, Wei Y. Strength analysis of metallic bonded joints containing Defects.
Computational Materials Science,2012, 53 : 444-450.
DOI: 10.1016/j.commatsci.2011.09.008. ( 0) 0)
|
| 24 |
Blackman BRK, Hadavinia H, Kinloch AJ, et al. The use of a cohesive zone model to study the fracture of fibre composites and adhesively-bonded joints.
International Journal of Fracture,2003, 119 : 25-46.
DOI: 10.1023/A:1023998013255. ( 0) 0)
|
| 25 |
Yan Y, Shang F. Cohesive zone modeling of interfacial delamination in PZT thin films.
International Journal of Solids and Structures,2009, 46 : 2739-2749.
DOI: 10.1016/j.ijsolstr.2009.03.002. ( 0) 0)
|
| 26 |
Lorena M, Fern C, Sonia S. Influence of the cohesive law shape on the composite adhesively-bonded patch repair behavior.
Composites Part B,2016, 91 : 414-421.
DOI: 10.1016/j.compositesb.2016.01.056. ( 0) 0)
|
| 27 |
Cui H. Simulation of ductile adhesive failure with experimentally determined cohesive law. Composites Part B, 2016, Accepted Manuscript
( 0) 0)
|
| 28 |
Jousset P, Rachik M. Comparison and evaluation of two types of cohesive zone models for the finite element analysis of fracture propagation in industrial bonded structures.
Engineering Fracture Mechanics,2014, 132 : 48-69.
DOI: 10.1016/j.engfracmech.2014.10.018. ( 0) 0)
|
| 29 |
Campilho RDSG, Banea MD, Neto JABP, et al. Modelling adhesive joints with cohesive zone models:effect of the cohesive law shape of the adhesive layer.
International Journal of Adhesion & Adhesives,2013, 44 : 48-56.
( 0) 0)
|
| 30 |
Campilho RDSG, Fernandes TAB. Comparative evaluation of single-lap joints bonded with different adhesives by cohesive zone modellin.
Procedia Engineering,2015, 114 : 102-109.
DOI: 10.1016/j.proeng.2015.08.047. ( 0) 0)
|
| 31 |
Arcan L, Arcan M, Daniel L. SEM fractography of pure and mixed mode Interlaminar fracture in graphite/epoxy composites. In:Masters JE and Au JJ eds. Fractography of Modern Engineering Materials:Composites and Metals, ASTM Technology Publish, Philadelphia, 1987
( 0) 0)
|
| 32 |
Arnaud N, Créacohcadec R, Cognard JY. A tension/compressiontorsion test suited to analyze the mechanical behavior of adhesives under non-proportional loadings.
International Journal of Adhesion & Adhesives,2014, 53 : 3-14.
( 0) 0)
|
INFLUENCE OF COHESIVE ZONE MODELS SHAPE ON ADHESIVELY BONDED JOINTS
Zhang Jun

,
Jia Hong
School of Chemical Engineering and Energy, Zhengzhou University, Zhengzhou 450001, China
Abstract:
Cohesive zone models have been increasingly used to simulate fracture of adhesively bonded joint. In order to understand the relation between the delamination of the different types of adhesives and the shape of cohesive zone models (CZMs), the uniaxial tension and shear experiments were conducted using two distinct adhesives, an epoxy-based adhesive in a brittle manner and VHBTM tape adhesive in a ductile manner. Three types of CZMs shapes are adopted, including exponential, bilinear, and trapezoidal models. The results demonstrate that the bilinear CZM more suitably simulate the tension and shear failure of the brittle adhesive, while the exponential CZM suitably describes the ductile adhesive. The cohesive strength, work of separation and the shape parameters are the significant effect factors on the simulation results of the uniaxial tension and shear debonding procedures. Nevertheless, the shape of CZM has certain influences on the simulation of the double cantilever beam fracture. The comparison between the numerical and the experiment results demonstrate that the bilinear CZM more suitably simulate the double cantilever beam fracture of the brittle adhesive, while the trapezoidal CZM suitably describes the ductile adhesive. The investigation results are significant to use CZMs to precisely analyze adhesively bonded joints fracture.
Key words: cohesive zone models adhesive adhesively bonded joints fracture



 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 2016, Vol. 48
2016, Vol. 48


