石墨烯作为目前最薄也最坚韧的纳米材料,被誉为最具战略意义的新型材料之一[1-3].作为一种新型高性能纳米材料,石墨烯的加工和掺杂是其工程应用和性能开发的重要手段,也是实际应用中必须解决的问题.离子辐照技术[4]是实现上述目的的有效途径,但是,在利用离子辐照技术对石墨烯进行加工时,由于辐照粒子入射的随机性,在辐照过程中不可避免地会给石墨烯带来损伤缺陷[5-6].完美石墨烯具有优异的抗拉能力,其拉伸破坏机理已得到较为系统的研究[7-12],但对于辐照损伤后的石墨烯,其力学性能和破坏机理有待进一步的研究分析.
石墨烯辐照后的力学、光学、电学、化学性能,已经引起许多学者的注意,并从各个角度对其进行了研究[13].Compagnini等[14]分析了单层石墨烯离子辐照缺陷形成的过程,以及辐照前后石墨烯的性能变化.Tapaszto等[15]研究了离子辐照对石墨烯电子结构的调整,结果表明粒子辐照可以改变其电子杂化方式.Marks等[16]建立了入射离子和稳态应力之间的关系. Terdalkar 等[17]通过分子动力学研究了离子辐照对石墨烯变形的影响,研究表明辐照能量和辐照角度对形成缺陷类型和数量有着重要影响.Lehtinen等[18]利用分子动力学模拟方法建立了一种在辐照过程中石墨烯形态变化的动力学蒙特卡罗方法,研究了不同入射角度、不同类型粒子入射以及不同入射能量等因素对石墨烯裁剪的影响.梁力等[5]利用分子动力学方法研究了石墨烯碳离子辐照后的力学性能,并对辐照后的石墨烯进行了拉伸模拟,结果表明损伤后的石墨烯薄膜弹性模量及拉伸强度会随着入射离子数目的增加而降低.Wu等[19]通过对速度的控制使得入射粒子停留在石墨烯薄膜层与层之间,并形成键的作用,实现了石墨烯薄膜层的连接.Zeng等[20]研究了快重离子及高电荷态离子辐照单层石墨烯,通过石墨烯与块体石墨辐照损伤的理论与实验研究,获得石墨烯与块体石墨辐照损伤程度的变化规律,首次得到辐照损伤差异的成因.
本文建立了硅离子辐照石墨烯以及辐照后的拉伸变形分子动力学模型,对不同辐照条件下石墨烯的缺陷进行分析,研究了不同辐照剂量影响下的辐照后石墨烯的拉伸性能,并探讨了其破坏机理.
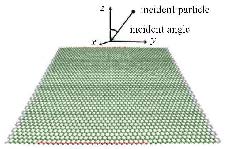
1 辐照模型 1.1 Si离子辐照石墨烯模型本文利用分子动力学方法[21-22]对硅离子辐照石墨烯进行数值模拟,所建辐照模型如图 1所示,大小为 8.05 nm×7.95 nm,包含2 508个碳原子.辐照时,入射粒子初始位于石墨烯模型上方一定高度,以一定角度和速度随机入射到模型上,入射粒子与石墨烯靶原子发生碰撞作用.模拟中采用AIREBO势函数[23]描述石墨烯内碳原子间的相互作用,Tersoff/ZBL作用势描述入射粒子硅离子与石墨烯靶原子之间的相互作用. Tersoff/ZBL势函数是通过将多体势Tersoff函数[24]与Ziegler-Biersack-Littmark (ZBL)普适屏蔽函数[25]平滑地衔接在一起形成的一种作用势,能很好地描述入射粒子与靶原子的碰撞过程.
|
图 1 石墨烯模型硅离子入射示意图 Figure 1 Sketch map of Si ions irradiating graphene |
模拟过程中,首先在NPT (number-pressure-temperature)系综下对石墨烯模型进行充分的弛豫[26],使其达到稳定平衡状态. 弛豫后,将石墨烯模型左右两端各一列碳环固定,控制$x$和$y$方向为自由边界条件,$z$方向为周期性边界条件. 辐照过程在NVT (number-volume-temperature)系综下进行,选取能量为1 keV的硅离子[5],给定离子入射初始位置,即确定第一个粒子入射位置为距离模型中心4 nm高度处,而其他粒子入射位置由计算机随机产生并入射到石墨烯表面.每入射完一个粒子后,将模型弛豫10 ps使其温度恢复至初始设定温度300 K,然后再进行下一个粒子的入射,直到完成所设定的辐照剂量,辐照停止.
1.2 辐照后石墨烯拉伸模型离子辐照后石墨烯会产生各类缺陷,为研究此时其拉伸力学性能和变形破坏机理,需对辐照损伤后的石墨烯继续进行拉伸模拟,如图 2所示.

|
图 2 辐照后石墨烯拉伸模型示意图 Figure 2 Tensile test simulation model for irradiated graphene |
模拟中,选用Tersoff势函数[27]模拟Si-C键的作用,研究表明,用它来描述Si-C键的相互作用,所得的结果与实验能符合得很好[7]. C原子的质量为12.01原子质量单位(1原子质量单位为1.660 540 2×10$^{ - 27}$ kg), 时间步长取1 fs. 控制$x$和$ y$方向为自由边界条件,$z$方向为周期性边界条件[5], 为了避免原子热激活引起的干扰,采用Nose-Hoover等温调节法[28-30],温度控制在0.01 K.拉伸过程中,首先对辐照后的原子构型在NPT系综下进行充分的弛豫,使系统处于能量最低的平衡状态,然后将模型上下两端各一列碳环固定,在NVT系综下以0.001 ps$^{-1}$的应变率拉伸[31].在接近准静态情况下,应变率对结果并无明显影响,只是计算效率会有所不同.但如果速率过大,比如0.005 ps$^{-1}$,则会对结果产生较大的影响.根据韩同伟等[32]的研究,0.005 ps$^{-1}$是石墨烯拉伸力学性能的一个临界应变率,如果速率大于0.005 ps$^{-1}$,在拉伸模拟中,石墨烯不再是沿主断裂带断裂破坏,而是形成了缺陷簇,具有非晶化特征.每次拉伸后,模型弛豫10 ps,重复此拉伸、弛豫过程,直至石墨烯被拉断.
2 不同辐照条件下的石墨烯缺陷分析在辐照过程中,入射粒子会与材料发生碰撞,当入射粒子在撞击过程中传递给石墨烯靶原子的能量达到靶原子的离位阈能,靶原子就会离开在晶体中的位置,当入射粒子不能传递给靶原子足够的能量时,入射原子会吸附在靶原子晶体中.在辐照过程中形成的缺陷主要有吸附缺陷、空位缺陷和复杂缺陷这几种,其中空位缺陷又分为单空位缺陷和双空位缺陷[33].在本文中,将单空位缺陷、双空位缺陷和复杂缺陷纳入缺陷统计中,吸附原子个数则单独统计[5].不同条件下的辐照效果各不相同[34-36],影响辐照效果的因素有很多,如:辐照剂量、辐照粒子能量、辐照角度等,这里就这3个主要因素影响下的辐照情况进行了分析.
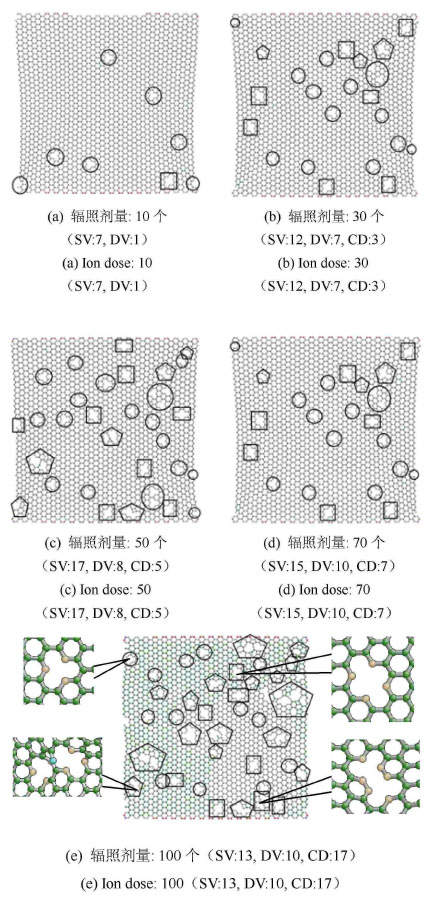
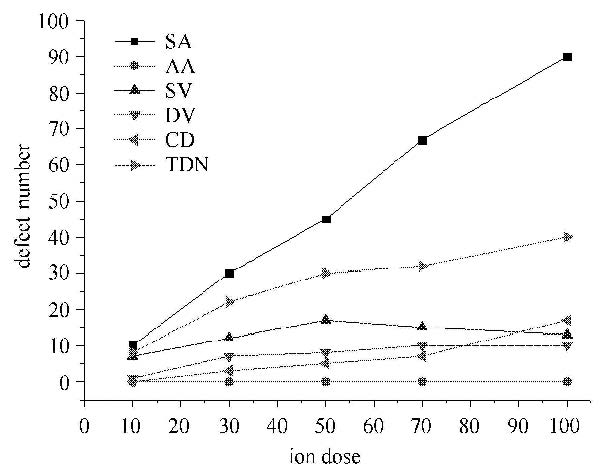
2.1 不同剂量下的辐照本文构建硅离子辐照石墨烯数值模型,离子辐照能量1 keV,入射高度4 nm,这是由于当入射粒子距离靶原子大于4 nm时,靶原子与入射粒子之间无任何相互作用[37].不同剂量的硅粒子随机垂直入射到石墨烯薄膜上表面,所得缺陷图如图 3所示,图 3(a) $\sim$图 3(e)分别为辐照剂量10个、30个、50个、70个和100个时辐照后石墨烯的原子构型图,并用粗线将缺陷位置标示出来,其中圆形表示单原子空位缺陷(single vacancy,SV),矩形表示双原子空位缺陷(double vacancy,DV),五边形代表复杂型缺陷(complex defects,CD). 产生的各类缺陷数目如图 4所示,其中SA是sputtered atom的简称,表示溅射原子;AA是adsorbed atom的简称,表示吸附原子;TDN是total defect number的简称,表示缺陷总数.
|
图 3 不同剂量硅离子辐照后的石墨烯原子构型(圆形表示单原子空位缺陷(SV),矩形表示双原子空位缺陷(DV),五边形代表复杂缺陷(CD) Figure 3 Configuration of graphene irradiated by different number of incident Si ions (circular represents single vacancy (SV),rectangle represents double vacancy (DV),pentagon repre-sents complex defects (CD)) |
|
图 4 不同剂量硅离子入射下石墨烯缺陷统计 Figure 4 Statistics of defects in graphene introduced by Si ions with different doses |
观察辐照后石墨烯薄膜的原子构型图,并对其缺陷数量进行统计,例如当入射Si离子剂量为10个时,溅射原子数目为9个,有7个单空位缺陷和1个双空位缺陷.图 4中统计了不同剂量辐照后石墨烯的吸附原子数、溅射原子数、不同类型缺陷数和缺陷总数,可以看出,随着入射剂量的增大,溅射原子数增大,缺陷总数也增大,并以单空位缺陷类型为主.这是由于辐照剂量的增大增加了入射粒子与靶原子碰撞的机率,使得溅射原子数量增多,石墨烯样品产生更多的空位,形成缺陷.在整个过程中,吸附原子数目都为0,这是由于原子吸附数目主要取决于入射粒子的能量.
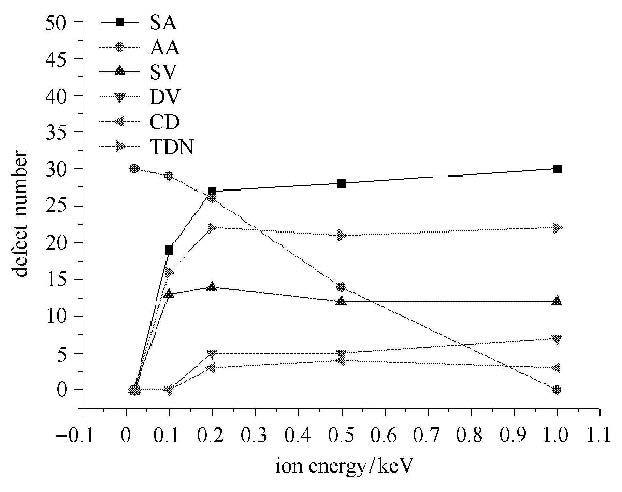
2.2 不同能量下的辐照为了研究入射粒子能量对辐照效果的影响,本文选取辐照剂量30个,辐照高度4 nm,取不同能量的硅离子随机垂直入射到石墨烯薄膜上表面,模拟结果如图 5所示.由图 5可以看出,随着入射粒子能量的增加,吸附原子数量明显减少,溅射原子数和缺陷总数都增加,以空位缺陷为主要缺陷类型.当辐照能量为0.02 keV时,无粒子溅射;当辐照能量为0.1 keV$\sim$0.5 keV时,出现空位缺陷、复杂缺陷和吸附原子共存的状态;当辐照能量为1 keV时,无粒子吸附.这是由于当辐照能量较小时,入射粒子在碰撞石墨烯时没有足够的能量传递给靶原子,靶原子无法达到离位阈能,同时由于范德华力的作用,使得入射粒子与石墨烯靶原子相互吸引,从而形成物理吸附现象,随着辐照能量的增大,辐照粒子撞击靶原子并穿透石墨烯,靶原子溅射出石墨烯表面,形成缺陷,这与文献[16]结论相一致.
|
图 5 不同能量硅离子入射下石墨烯缺陷统计 Figure 5 Statistics of defects in graphene introduced by Si ions with different energies |
为研究辐照角度对辐照效果的影响,选取辐照剂量30个,辐照高度4 nm,入射粒子能量均为1 keV的硅离子,以不同角度(0°,30°,45°,60°和 90°)随机入射到石墨烯薄膜上表面,模拟结果如图 6所示. 由图 6可以看出在其他条件一定的情况下,随着角度的增加,吸附原子数目增多,溅射原子数目与缺陷总数随着辐照角度的变化趋势类似. 当辐照角度在0°$\sim $30°时,溅射原子数量和缺陷数目均稍有减少,此后开始增加,当辐照角度达到45°时,二者均达到最大值,此后随着辐照角度的增加,二者又呈减小趋势. 在整个过程中,单空位缺陷为主要缺陷类型. 辐照角度对石墨烯缺陷的影响是通过对辐照剂量和辐照能量这两个因素的影响来实现的,随着辐照角度的增加,辐照过程中$z$向,即硅离子入射方向的能量就越小,同时,辐照角度的变化,也影响随机辐照到石墨烯薄膜模型上表面的硅离子剂量.

|
图 6 不同角度硅离子入射下石墨烯缺陷统计 Figure 6 Statistics of defects in graphene introduced by Si ions with different angle |
以辐照能量1 keV,辐照高度4 nm,硅粒子垂直入射,不同辐照剂量为条件,分析辐照产生的不同缺陷数目对石墨烯拉伸力学性能的影响和其拉伸破坏机理.
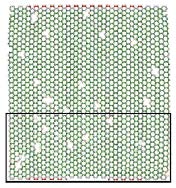
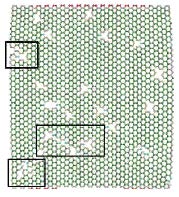
3.1 含缺陷石墨烯的拉伸破坏分析以辐照剂量30个为例,分析含缺陷石墨烯拉伸破坏机理. 图 7是辐照后石墨烯原子构型图,图 8是对其拉伸后的原子构型图,可以观察到缺陷扩大,由原来的单空位缺陷衍生为双空位缺陷或更复杂的缺陷形式,如图 8中黑框所示,双空位缺陷和复杂缺陷衍生为更复杂的缺陷,这主要是由于缺陷处C原子成键不完全,使得点阵束缚能较低,在拉伸过程中容易发生进一步的破坏,其中多空位复杂缺陷最容易形成起裂缺陷带.
|
图 7 辐照后石墨烯原子图 Figure 7 Sketch map of irradiated graphene |
|
图 8 缺陷扩展图 Figure 8 The extension of defects |
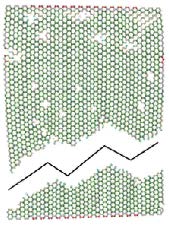
随着拉伸应变的增加,会发生多个缺陷贯通.由于单个缺陷的不断扩展,缺陷区域逐渐扩大,相近缺陷区域或缺陷密集区域连接形成较大的缺陷并进一步形成缺陷簇,以后成片的缺陷簇会进一步贯通成与拉伸方向呈一定角度的缺陷带,如图 9中黑线所示,以石墨烯缺陷带为起始位置发生破坏,如图 10中黑线所示,随着拉伸应变的继续增加,破坏沿着缺陷带分布迅速向石墨烯内部延伸,直至石墨烯完全破坏,如图 11中黑线所示.

|
图 9 缺陷扩展形成缺陷簇 Figure 9 The clusters of defects |

|
图 10 破坏起始 Figure 10 The initial destory |
|
图 11 含缺陷石墨烯的断裂走向 Figure 11 The fracture directions of irradiated grapheme |
根据数值模拟结果,辐照后的石墨烯在拉伸荷载作用下,变形破坏过程可分为缺陷扩展、缺陷贯通、石墨烯断裂3个过程.辐照后石墨烯的起裂位置和断裂走向与缺陷带的位置以及缺陷带上原子点阵空位情况密切相关,因此,辐照后的石墨烯断裂走向并不像完美石墨烯那样,从边缘开始断裂并沿45°直线方向向内部延伸[6].
3.2 缺陷对石墨烯力学性能的影响以不同剂量硅粒子辐照后的缺陷石墨烯为例,对其进行拉伸模拟,所得的拉伸应力-应变曲线如图 12所示,可以看出,辐照后的石墨烯在拉伸过程中经历了弹性变形、屈服、强化和断裂4个阶段,但与完美石墨烯相比[38],强化阶段缩短,且随着缺陷数目的增多,缩短趋势愈加明显. 一方面这是由于辐照后石墨烯含有缺陷,缺陷处原子成键不完全,或新粒子的加入,能量分布不平衡,使缺陷处更容易起裂.

|
图 12 不同剂量辐照后含缺陷石墨烯的拉伸应力-应变图 Figure 12 Stress-strain curve of graphene irradiated by Si ions with different doses |
另一方面缺陷的存在使材料的微观原子的熵值和微观结构不稳定性增加,影响材料的性能,在拉伸过程中更加容易破坏.
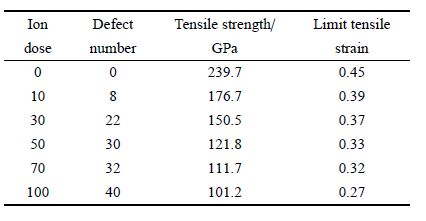
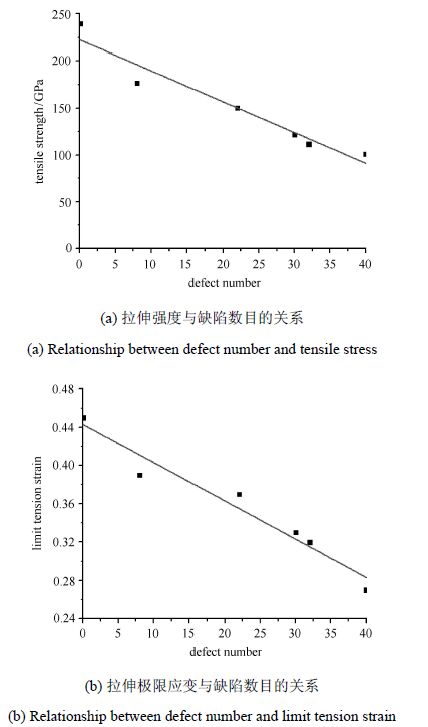
分析缺陷对石墨烯力学性能的影响,并将所得拉伸力学性能总结如表 1所示. 辐照剂量为0即完美石墨烯,拉伸强度最大为239.7 GPa,拉伸极限应变为0.45.随着辐照剂量的增加缺陷数目增多,石墨烯的拉伸力学性能明显降低,这与文献[5]中的结论相一致.图 13展示了拉伸强度和拉伸极限应变随模型中缺陷数目的变化,并对其进行线性拟合,如图中实线所示.可以看出拉伸强度和拉伸极限应变与缺陷数目近似成线性关系,随着缺陷数目的增加,拉伸强度由239.7 GPa降到101.2 GPa,降幅达到了57.7%;拉伸极限应变由0.45降到了0.27,降幅达到了40.0%.由此可见,缺陷对石墨烯力学性能有着重要影响.
| 表 1 石墨烯样品被不同剂量硅离子辐照后,缺陷数目、拉伸强度与拉伸极限应变的变化 Table 1 Tensile stress and limit tensile strain of graphene irradiated by Si ions with different doses |
|
图 13 辐照后石墨烯,拉伸强度和拉伸极限应变与缺陷数的关系 Figure 13 Tensile strength and limit strain of defective grapheme |
离子入射对完美石墨烯造成缺陷,会影响石墨烯的拉伸力学性能.本文对不同影响因素下的石墨烯缺陷进行了分析,并研究了缺陷对石墨烯拉伸力学性能的影响和含缺陷石墨烯的拉伸破坏机理,得出以下结论:
(1) 在其他条件一定的情况下,随着辐照剂量的增加,溅射原子数增多,缺陷数目增多,且缺陷类型以空位缺陷为主.辐照能量的大小,直接影响入射离子碰撞中传递给靶原子能量的大小,当辐照能量较小($ ≤$0.02 keV)时,靶原子无法达到离位阈能,从而产生吸附现象,随着辐照能量的增大,吸附原子数目减少,溅射原子数量和缺陷数量增多,并以空位缺陷为主. 当辐照能量到达一定值($ ≥ $1 keV)时,再无吸附原子.随着角度的增大,吸附原子数目增多.当辐照角度为0°$\sim$30°时,溅射原子数目和缺陷数量随着辐照角度的增大而稍有减少,随后又增大,当辐照角度为45°时,二者均达到最大值,其后又呈减小趋势.
(2) 含缺陷石墨烯的拉伸过程与完美石墨烯的相似,经历了弹性阶段、屈服阶段、强化阶段和断裂阶段,不同的是含缺陷石墨烯的强化阶段明显缩短.通过数据拟合可以发现拉伸强度和拉伸极限应变与缺陷数目近似成线性关系,二者均随着缺陷数目的增多而线性降低.
(3) 完美石墨烯的拉伸破坏是从一侧开始,沿45°直线方向向石墨烯内部延伸,随着C-C键的断裂,石墨烯最终被拉断[6].对于辐照损伤后的石墨烯,在拉伸荷载作用下,其起裂位置及断裂走向具有较大的不确定性.其断裂是从缺陷带最不稳定处开始,并沿着缺陷带延伸,最终断裂,因此,缺陷带是决定其起裂位置和断裂走向的重要因素.
| 1 |
郭俊贤, 王波, 杨振宇. 石墨烯/Cu复合材料力学性能的分子动力学模拟.
复合材料学报,2014, 31 (1) : 152-157.
( Guo Junxian, Wang Bo, Yang Zhenyu. Molecular dynamics simulation on the mechanical properties of graphene/Cu composites.
Acta Materiae Compositae Sinica,2014, 31 (1) : 152-157.
(in Chinese) ) ( 0) 0)
|
| 2 |
白树林, 赵云红. 石墨烯热学性能及表征技术.
力学进展,2014, 44 : 201406.
( Bai Shulin, Zhao Yunhong. Thermal properties and characterization techniques of graphene.
Advances in Mechanics,2014, 44 : 201406.
(in Chinese) ) ( 0) 0)
|
| 3 |
Rafiee MA, Rafiee J, Wang Z, et al. Enhanced mechanical properties of nanocomposites at low graphene content.
ACS Nano,2009, 3 (12) : 3884-3890.
DOI: 10.1021/nn9010472. ( 0) 0)
|
| 4 |
Gao A, Zoethout E, Sturm JM, et al. Defect formation in single layer graphene under extreme ultraviolet irradiation.
Applied Surface Science,2014, 317 : 745-751.
DOI: 10.1016/j.apsusc.2014.08.177. ( 0) 0)
|
| 5 |
梁力, 赵仕俊, 王宇钢, 等. 重粒子辐照下石墨烯力学性能的分子动力学研究.
北京大学学报(自然科学版),2013, 49 (3) : 365-370.
( Liang Li, Zhao Shijun, Wang Yugang, et al. Molecular dynamics simulation of graphene under mechanical properties irradiated by heavy particles.
Acta Scientiarum Naturalium Universitatis Pekinensis,2013, 49 (3) : 365-370.
(in Chinese) ) ( 0) 0)
|
| 6 |
袁小亚. 石墨烯的制备研究进展.
无机材料学报,2011, 26 (6) : 561-570.
DOI: 10.3724/SP.J.1077.2011.00561. ( Yuan Xiaoya. Progress in preparation of graphene.
Journal of Inorganic Materials,2011, 26 (6) : 561-570.
(in Chinese) DOI: 10.3724/SP.J.1077.2011.00561. ) ( 0) 0)
|
| 7 |
韩同伟. 石墨烯力学性能的分子动力学研究.[博士论文]. 上海:同济大学,2009
( Han Tongwei. Molecular dynamics simulation of graphene under mechanical properties.[PhD Thesis]. Shanghai:Tongji University, 2009(in Chinese)
) ( 0) 0)
|
| 8 |
Jiang JW, Wang JS, Li BW. Young's modulus of graphene:A molecular dynamics study.
Physical Review B Condensed Matter,2009, 80 (11) : 113405.
DOI: 10.1103/PhysRevB.80.113405. ( 0) 0)
|
| 9 |
Wang MC, Yan C, Ma L, et al. Effect of defects on fracture strength of graphene sheets.
Computational Materials Science,2012, 54 : 236-239.
DOI: 10.1016/j.commatsci.2011.10.032. ( 0) 0)
|
| 10 |
Cho JH, Yang SJ, Lee K, et al. Si-doping effect on the enhanced hydrogen storage of single walled carbon nanotubes and graphene.
International Journal of Hydrogen Energy,2011, 36 (19) : 12286-12295.
DOI: 10.1016/j.ijhydene.2011.06.110. ( 0) 0)
|
| 11 |
Hua J, Li DB, Zhao D, et al. Reaserch on the mechanics performance of graphene based on the modified molecular mechanics method.
Journal of Wuhan University of Technology-Materials Science Edition,2015 : 1172-1178.
( 0) 0)
|
| 12 |
殷常乐, 温绍国, 王继虎, 等. 石墨烯/聚氨酯复合材料的研究进展.
高分子通报,2016, 2 : 40-55.
( Yin Changle, Wen Shaoguo, Wang Jihu, et al. Advances research on graphene/polyurethane composites.
Chin Polym Bull,2016, 2 : 40-55.
(in Chinese) ) ( 0) 0)
|
| 13 |
华军, 武霞霞, 李东波, 等. 基于神经网络的石墨烯弹性参量识别方法研究.
西安建筑科技大学学报(自然科学版) 2,2015, 47 (5) : 871-877.
( Hua Jun, Wu Xiaxia, Li Dongbo, et al. Idenfication of elastic parameters method for graphene based on neural network.
Xi'an Univ. of Arch. & Tech,2015, 47 (5) : 871-877.
(in Chinese) ) ( 0) 0)
|
| 14 |
Compagnini G, Giannazzo F, Sonde S, et al. Ion irradiation and defect formation in single layer graphene.
Carbon,2009, 47 (14) : 3201-3207.
DOI: 10.1016/j.carbon.2009.07.033. ( 0) 0)
|
| 15 |
Tapaszt DL, Dobrik G, Nemes-Incze P, et al. Tuning the electronic structure of graphene by ion irradiation.
Physical Review B Condensed Matter,2009, 78 (23) : 1879-1882.
( 0) 0)
|
| 16 |
Marks NA, Mckenzie DR, Pailthorpe BA. Molecular-dynamics study of compressive stress generation.
Physical Review B Condensed Matter,1996, 53 (7) : 4117-4124.
DOI: 10.1103/PhysRevB.53.4117. ( 0) 0)
|
| 17 |
Terdalkar SS, Zhang SL, Rencis JJ, et al. Molecular dynamics simulations of ion-irradiation induced deflection of 2D graphene films.
International Journal of Solids & Structures,2008, 45 (13) : 3908-3917.
( 0) 0)
|
| 18 |
Lehtinen O, Kotakoski J, Krasheninnikov AV, et al. Cutting and controlled modification of graphene with ion beams.
Nanotechnology,2011, 22 (17) : 175306.
DOI: 10.1088/0957-4484/22/17/175306. ( 0) 0)
|
| 19 |
Wu X, Zhao HY, Zhong ML, et al. Molecular dynamics simulations of graphene sheets joining under ion beam irradiation.
Carbon,2014, 66 (1) : 31-38.
( 0) 0)
|
| 20 |
Zeng J, Liu J, Yao HJ, et al. Comparative study of irradiation effects in graphite and graphene induced by swift heavy ions and highly charged ions.
Carbon,2016, 100 : 16-26.
DOI: 10.1016/j.carbon.2015.12.101. ( 0) 0)
|
| 21 |
常旭. 多层石墨烯的表面起伏的分子动力学模拟.
物理学报,2014, 63 (8) : 086102.
( Chang Xu. Ripples of multilayer graphenes:a molecular dynamics study.
Acta Phys Sin,2014, 63 (8) : 086102.
(in Chinese) ) ( 0) 0)
|
| 22 |
姚曼, 崔薇, 王旭东, 等. W辐照损伤初期的分子动力学研究.
金属学报,2015, 51 (6) : 724-732.
( Yao Man, CuiWei, Wang Xudong, et al. Molecular dynamics simulation of initial radiation damage in tungsten.
Acta Metallurgica Sinica,2015, 51 (6) : 724-732.
(in Chinese) ) ( 0) 0)
|
| 23 |
Stuart SJ, Tutein AB, Harrison JA. A reactive potential for hydrocarbons with intermolecular interactions.
Journal of Chemical Physics,2000, 112 (14) : 6472-6486.
DOI: 10.1063/1.481208. ( 0) 0)
|
| 24 |
Terso J. New empirical approach for the structure and energy of covalent systems.
Phys Rev B,1988, 37 : 6991.
DOI: 10.1103/PhysRevB.37.6991. ( 0) 0)
|
| 25 |
Ziegler JF, Biersack JP, Littmark U, et al. The stopping and ranges of ions in matter.
Treatise on Heavy-Ion Science,1977, 268 (11-12) : 93-129.
( 0) 0)
|
| 26 |
韩强, 韩凌燕. 石墨烯薄膜拉伸性能的分子动力学模拟.
华南理工大学学报,2012, 40 (2) : 29-33.
( Han Qiang, Han Lingyan. Molecular dynamics simulation of a graphene sheet under tensile properties.
Journal of South China University of Technology,2012, 40 (2) : 29-33.
(in Chinese) ) ( 0) 0)
|
| 27 |
赵晓西, 李永池. 手性石墨烯薄膜拉伸力学性能分子动力学研究.
华南理工大学学报,2014, 38 (5) : 691-700.
( Zhao Xiaoxi, Li Yongchi. Molecular dynamic simulation of tensile mechanical properties of chiral graphene sheet.
Journal of South China University of Technology,2014, 38 (5) : 691-700.
(in Chinese) ) ( 0) 0)
|
| 28 |
Nosé S. A molecular dynamics method for simulations in the canonical ensemble.
Molecular Physics,2006, 52 (2) : 255-268.
( 0) 0)
|
| 29 |
Hoover W G. Canonical dynamics:equilibrium phase-space distribution.
Physical Review A,1985, 31 (3) : 1695-1697.
DOI: 10.1103/PhysRevA.31.1695. ( 0) 0)
|
| 30 |
韩同伟, 贺鹏飞, 王健, 等. 单层石墨烯薄膜拉伸变形的分子动力学模拟.
新型炭材料,2010, 25 (4) : 261-266.
( Han Tongwei, He Pengfei, Wang Jian, et al. Molecular dynamic simulation of a single graphene sheet under tension.
New Carbon Materials,2010, 25 (4) : 261-266.
(in Chinese) ) ( 0) 0)
|
| 31 |
韩同伟, 贺鹏飞, 王健, 等. 空位缺陷对单层石墨烯薄膜拉伸力学性能的影响.
同济大学学报(自然科学版),2010, 38 (8) : 1210-1214.
( Han Tongwei, He Pengfei, Wang Jian, et al. Effect of vacancy defects on tensile mechanical properties of single graphene sheets.
Journal of Tongji University (Natural Science),2010, 38 (8) : 1210-1214.
(in Chinese) ) ( 0) 0)
|
| 32 |
韩同伟, 贺鹏飞, 王健, 等. 单层石墨烯薄膜拉伸应变率相关性的分子动力学模拟.
中国科学G辑:物理学力学天文学,2009, 9 : 146-153.
( Han Tongwei, He Pengfei, Wang Jian, et al. Strain rate dependences of tensile failure process for single graphene sheet:a molecular dynamics study.
Science in China (Series G:Physics, Mechanics & Astronomy),2009, 9 : 146-153.
(in Chinese) ) ( 0) 0)
|
| 33 |
Liu LL, Qing MQ, Wang YB, et al. Defects in graphene:generation, healing, and their effects on the properties of graphene:a review.
Journal of Materials Science & Technology,2015, 31 (6) : 599-606.
( 0) 0)
|
| 34 |
Lehtinen O, Kotakoski J, Krasheninnikov AV, et al. Effects of ion bombardment on a two-dimensional target:atomistic simulations of graphene irradiation.
Physical Review B Condensed Matter,2010, 81 (15) : 2149-2149.
( 0) 0)
|
| 35 |
Li WS, Liang L, Zhao SJ, et al. Fabrication of nanopores in a graphene sheet with heavy ions:a molecular dynamics study.
Journal of Applied Physics,2013, 114 (23) : 234304.
DOI: 10.1063/1.4837657. ( 0) 0)
|
| 36 |
Wang H, Wang Q, Cheng Y, et al. Doping monolayer graphene with single atom substitutions.
Nano Letters,2012, 12 (1) : 141-144.
DOI: 10.1021/nl2031629. ( 0) 0)
|
| 37 |
Wu X, Zhao HY, Zhong ML, et al. Molecular dynamics simulation of graphene sheets joining under ion beam irradiation.
Carbon,2014, 66 (3) : 31-38.
( 0) 0)
|
| 38 |
戴宪起, 孙永灿, 赵建华, 等. 空位和Si参杂对In在石墨烯上吸附的影响.
新型炭材料,2011, 26 (1) : 46-51.
( Dai Xianqi, Sun Yongcan, Zhao Jianhua, et al. Space and Si mixed a ect In adsorption on graphene.
New Carbon Materials,2011, 26 (1) : 46-51.
(in Chinese) ) ( 0) 0)
|
 2016, Vol. 48
2016, Vol. 48