颗粒材料在剪切流动中可表现为类似固体或类似液体的力学行为,并会在一定条件下发生相互转化,即类固液转化现象.该现象广泛地存在于雪崩、冰塞、沙丘演化以及山体滑坡等自然现象,以及矿物传输、化工原料混合等工业过程中.在颗粒材料的类固液转化过程中,细观尺度下的颗粒接触模式及其力链结构是宏观尺度本构模型和流动状态的内在因素[1-3].由于颗粒材料在类固液转化过程中的强非线性,以及宏观流动形态和细观结构的复杂性,对其力学机理的揭示和转化条件的建立是近年来颗粒材料在物理力学领域的重要研究方向.
颗粒材料呈现不同流动状态的一个典型试验是斜面流动试验,其由下向上分别呈现为类固态、液态,甚至是气态的运动状态[4].王光谦等[1]通过颗粒间的持续接触、半持续接触、瞬时接触和无接触4种接触模式来阐释颗粒材料的准静态、极慢、慢速和快速流动状态.此外,通过斜槽中的颗粒流动试验可确定颗粒材料由稀疏流到密集流、甚至是阻塞的转变过程[5-7].在颗粒材料类固液转变的离散元数值模拟中,单剪流动是广泛采用的剪切运动形式[8-11].Babic等[8]最早系统地分析了在不同剪切率和体积分数下颗粒材料由快速向慢速、准静态转变的过程,讨论了颗粒流在转变区的力链结构特征和应力变化规律. 在颗粒材料的类固液转化过程中,也可将其划分为弹性准静态、弹性惯性、惯性非碰撞和惯性碰撞等几种状态[9, 12].此外,颗粒材料的阻塞现象是当前颗粒材料流动状态转化的一个研究热点[13-15].
在颗粒材料的类固液相变研究中,Liu等[16]最早给出了颗粒材料的相变图;Zhang等[17]则进一步讨论了在颗粒温度$T =0$时发生相变的$J$点.季顺迎等[18]在离散元模拟的基础上建立了不同流动状态间相互转化的相变图,并讨论了配位数、接触时间数、有效摩擦系数等参数的分布规律. 此外,由于颗粒材料在类固液转变过程中,宏观应力与剪切速率有不同的对应关系[19-21],因此,全面地考虑颗粒形态、材料性质和约束条件等因素,如何合理地建立颗粒材料在不同运动状态下的本构方程仍是目前颗粒材料力学研究的难点[11, 22-23].
为描述颗粒材料的宏观流动特性,引入了无量纲参量惯性数$I$,其与有效摩擦系数 $I$有密切关系,记作$\mu_{\rm eff}(I)$[24-26]. 由于$I$表征的是颗粒材料在垂直和平行于剪切方向移动一定距离所需时间的比值,其可写作剪切速率、法向应力、粒径和颗粒密度的函数[24].此外,$I$还可视为颗粒材料在细观尺度上的重组时间与宏观尺度上的变形时间的比值[27].由于有效摩擦系数又与剪切流动状态密切相关[9, 11, 28],因此从$\mu_{\rm eff}(I)$的分布形式上就可以判断颗粒材料所处的流动状态[24-25, 29]. da Cruz等[25]基于平面剪切流动的离散元模拟系统地分析了$I$的影响因素,以及$I$与有效摩擦系数、配位数、体积分数的对应关系.最近,Baker等[27]进一步讨论了$\mu_{\rm eff}(I)$在描述颗粒材料不同流动状态下的适用性. 目前,$\mu_{\rm eff}-I $ 对应关系是判别颗粒材料流动状态的一个重要依据.
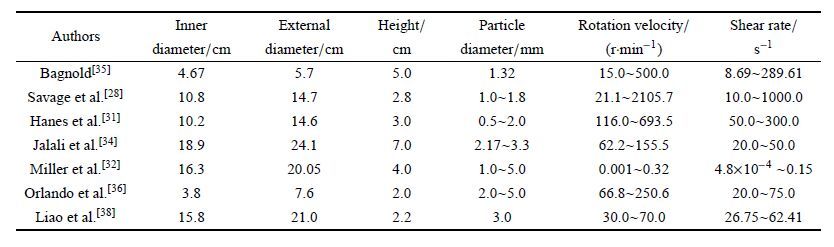
对颗粒材料类固液转化规律的试验研究是从20世纪80年代系统地开展的,并从最初的环剪试验发展到后来的平面剪切、斜面流动、堆积流动、滚筒等试验[4, 24, 30].目前,环剪仪广泛地用于颗粒材料的剪切流动试验以研究其在不同剪切速率、法向应力下的流动状态[28, 31-34].Bagnold[35]最早通过同轴剪切流变仪测量颗粒材料的应力-应变率关系,得到了颗粒材料流动时其宏观应力与剪切速率平方成正比的关系,该关系称为Bagnold效应.该试验主要研究了颗粒材料在快速剪切条件下的流动行为.在颗粒材料的环剪试验研究中,最早关注的是颗粒材料在不同剪切速率、体积分数下宏观应力与剪切速率的对应关系[28, 31].Savage等[28]通过环剪试验讨论了剪切速率和体积分数对有效摩擦系数的影响.在环剪试验中,粒径、黏性、含水量和边界条件等因素对颗粒材料的流动状态也有很大的影响[35-38].此外,颗粒材料的环剪试验还可用于对离散元计算模型的验证[39-41].通过颗粒材料环剪流动的离散元分析可研究其由准静态向惯性流动转化过程,并可确定惯性数与有效摩擦系数的对应关系[3, 35, 40, 42].在以往颗粒材料的环剪流动试验中,大多针对颗粒材料在快速流动状态下进行宏观应力、剪切速率和体积分数的测试分析.表 1给出了典型及近年颗粒环剪仪试验中环剪盒尺寸、颗粒粒径、转速及剪切速率等参数.从中可以发现,在颗粒材料的环剪试验中,剪切速率一般在10~10$^{3}$s$^{-1}$之间,此时颗粒材料呈现为快速流动状态[28, 31, 34, 37].虽然,Miller等[32]在慢速剪切速率下进行了环剪试验,但其关注的是颗粒材料宏观应力的脉动特性,而对颗粒材料的流动状态未开展深入研究.近年来,颗粒材料在不同流动状态下转化机理的研究引起了人们的极大关注,并成为揭示滑坡、泥石流、雪崩等自然灾害发生、演化机理的有效途径[4, 18, 20].针对颗粒材料在不同流动状态下的转化特性,人们开展了斜面流、平面剪切等试验研究[5-6, 24].但采用环剪试验可获得颗粒材料更加持续稳定的流动特性.然而,目前对颗粒材料由慢速向快速流动的转化过程的环剪试验研究还未开展.通过设置环剪试验中转速、法向应力等试验条件可改变剪切速率、体积分数等参数,可获得颗粒材料的慢速、快速流动状态及其相互转化过程,从而确定不同流动状态下的力学特性.
| 表 1 颗粒材料环剪试验的基本参数统计 Table 1 Review of major parameters in annular shear cell tests of granular materials |
为研究颗粒材料在不同流动状态下的力学性质,本文通过研发中尺度环剪仪对颗粒材料在受剪流动下的剪切应力和体积膨胀率进行试验,并探讨颗粒材料从慢速流向快速流转化的基本规律,并进一步分析法向应力对流动状态的影响.
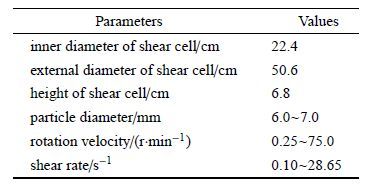
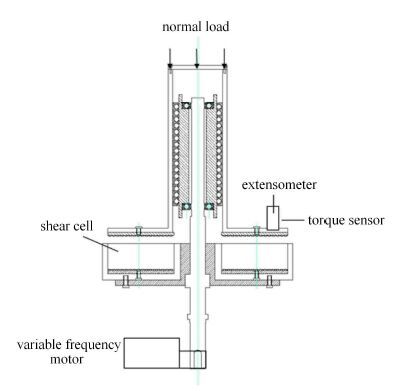
1 颗粒剪切流动的环剪试验系统 1.1 环剪试验装置为测试颗粒材料在不同剪切速率下的流动特性,本文研制了中尺度环剪仪,结构如图 1所示. 主要参数见表 2.为实现慢速转动,该环剪仪安装了变频电机.在剪切盒上安装了扭矩传感器和电子引伸计,可测量试验过程中环剪仪上剪切面与颗粒材料之间的剪切力以及颗粒材料的体积变化.此外,该剪切盒可提供0~350 N的竖向压力以对颗粒材料施加不同的法向应力.剪切盒内径$r=22.4$ cm,外径$R=50.6$ cm,深度$h=6.8$ cm.该环剪仪的剪切盒尺寸要明显大于土体材料的环剪仪[43-44],同时也大于传统的颗粒材料环剪仪[28, 31, 45]. 由此,它对颗粒材料的粒径范围有更强的适用性.此外,由于它可提供[0.5~75] r/min范围内低速转动,其可使剪切盒内颗粒材料的剪切速率在[0.10 ~28.65] r/min范围内变化,从而可获得颗粒材料的慢速和快速流动状态.
|
图 1 颗粒材料环剪盒的试验装置 Figure 1 Sketch of shear cell apparatus of granular materials |
| 表 2 本文研制环剪仪的主要参数 Table 2 Major parameters in shear cell of this paper |
该环剪仪将变频电机的输出轴与剪切盒的中间竖向轴相连. 剪切盒侧壁选用光滑钢化玻璃材料以减小摩擦.剪切盒的上、下边界为粗糙面以对颗粒材料提供有效的摩擦作用,如图 2所示.考虑颗粒材料初始排列状态对试验结果有一定的影响,因此在试验中采取相同的颗粒填充方式.将装料漏斗置于剪切盒上方,给剪切盒一个固定的转速,在剪切盒开始旋转后将颗粒材料均匀地填充在剪切盒内.

|
图 2 环剪仪的上、下剪切面结构图 Figure 2 The top and bottom shear plates of shear cell |
在试验过程中,下剪切盒及下剪切面随竖向轴按设定转速转动,上剪切面则通过力传感器固定并同时测量相应的扭矩.颗粒材料在剪切盒内通过上下剪切面之间的摩擦发生剪切流动.通过激光测速仪、电子引伸计与扭矩传感器同时测量试验过程中的转速、颗粒材料高度变化以及相应的剪力.在环剪试验中,通过调整电机转速以及剪切盒的上部压力来设定颗粒材料的剪切速率与法向应力.
1.2 环剪试验中的参数确定在颗粒材料的环剪试验中,通过对环剪盒转速、竖向载荷、环剪盒体积、上剪切盒扭矩等参数的测量,可确定颗粒材料在环剪流动中所承受的法向应力$\sigma$、剪切速率$\dot\gamma$和体积膨胀率$v$等参数.
剪切盒上剪切面颗粒材料的法向应力为
| $ \sigma_{\rm top} =\dfrac{W}{\pi(R^2-r^2)} $ | (1) |
式中,$\sigma_{\rm top}$为剪切盒上表面的法向应力,$W$ 为剪切盒上的法向力.对于下剪切面,则应考虑剪切室内颗粒重量对法向应力的影响. 由此,剪切室内的有效法向应力取为上、下剪切面的均值,即
| $ \sigma=\dfrac{W+0.5M_{\rm s}g}{\pi(R^2-r^2)} $ | (2) |
式中,$M_{\rm s}$为剪切盒内的颗粒质量,$R$为剪切盒外径,$r$为剪切盒内径,$g$为重力加速度.
颗粒材料上表面的剪切应力为
| $ \tau=\dfrac{3T}{2\pi(R^3-r^3)} $ | (3) |
式中,$\tau$为剪切应力,$T$为颗粒材料对上剪切面的扭矩,其可写作
| $ T=\int^R_r 2\pi r^2\tau d \tau $ | (4) |
若进一步考虑剪切盒侧壁摩擦对扭矩的影响,则式(3)改进为[46]
| $ \tau=\dfrac{3T}{2\pi(R^3-r^3)}-\dfrac{2\mu_{\rm f}\sigma h}{2\pi(R-r)} $ | (5) |
式中,$h$为环剪盒内颗粒试样的有效厚度;$\mu_{\rm f}$为颗粒材料与剪切盒侧壁的摩擦系数,这里取$\mu_{\rm f}=0.2$.
颗粒材料的剪切速率$\dot\gamma$为
| $ \dot\gamma=\dfrac{2\pi}{60}\dfrac{\omega(R+r)}{2h} $ | (6) |
式中,$\dot\gamma $为剪切速率(s$^{ - 1})$,$\omega$为转动角速度(r/min).
环剪室内颗粒材料的体积分数为
| $ \phi=\dfrac{V_{\rm s}}{V}=\dfrac{M_{\rm s}/\rho_{\rm s}}{h\pi(R^2-r^2)} $ | (7) |
式中,$V_{\rm s}$为环剪盒内的颗粒体积,$V$为剪切流动中剪切室内的体积,$\rho_{\rm s}$为颗粒密度.
颗粒材料在剪切流动中的体积膨胀率为
| $ v=\dfrac{V-V_0}{V_0}=\dfrac{h-h_0}{h_0} $ | (8) |
式中,$v$为颗粒材料在剪切流动中的体积膨胀率,$V_0$为剪切室内的初始体积,$h_0$为剪切室内颗粒试样的初始有效高度.
在本文环剪试验中选用粒径范围$D=6.0\sim 7.0$ mm 的球形玻璃颗粒,粒径均值$D_{\rm mean}=6.5$ mm,密度$\rho_{\rm s}=2.45\times 10^{3}$ kg/m$^{3}$.在试验中采用了同一批次的玻璃颗粒进行测试,从而保证了试验结果的一致性.
2 剪切速率对颗粒材料流动状态的影响为研究颗粒材料由低速剪切到高速剪切过程中剪切应力的变化规律,这里对不同剪切速率下的颗粒材料所承受的扭矩和试样高度进行了测量,由此确定相应的剪切应力和体积膨胀率.
2.1 剪切应力表征的临界剪切速率为研究颗粒材料在环剪流动中剪切应力的变化特性,下面对不同剪切速率下的流动状态进行测试. 这里颗粒质量$M_{\rm s}=1.50$ kg,法向应力$\sigma=2.0$ kPa. 在试验过程中,颗粒材料有一个由静态向剪切流动的启动过程.当颗粒材料进入稳定流动状态后,测试其剪切应力和体积变化情况.
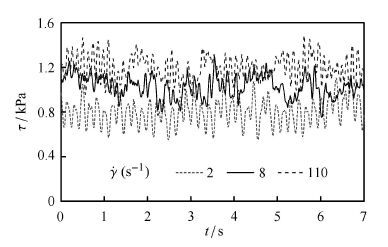
当剪切速率$\dot\gamma=2$ s$^{-1}$,8 s$^{-1}$和110 s$^{-1}$时,颗粒材料进入稳态流动后的剪切应力$\tau$如图 3所示. 可以看出,剪切应力在不同剪切速率下均呈现出显著的脉动特性.这主要是由于颗粒材料在剪切过程中具有很强的滞滑效应,从而导致颗粒间相对运动的脉动现象.颗粒材料在剪切流动中的滞滑效应和剪切应力的脉动现象已得到广泛的试验验证[47-49],并在环剪试验中也测试到了相似的试验现象[32, 48, 50].从图 3中还可以发现,剪切应力在脉动过程中有一个相对稳定的均值$\tau_{\rm m}$. 当$\dot\gamma=2$ s$^{-1}$, 8 s$^{-1}$和110 s$^{ - 1}$时,剪切应力均值分别是$\tau_{\rm m}=0.80$ MPa,1.03 MPa和1.20 MPa.由此表明,剪切应力均值$\tau_{\rm m}$随剪切速率$\dot\gamma$的增加而增大.
|
图 3 不同剪切速度下剪切应力随时间的脉动特性 Figure 3 Fluctuations of shear stress versus time under various shear rates |
为研究剪切应力与剪切速率之间的对应关系,下面对以上颗粒材料在法向应力 $\sigma=0.60$ kPa条件下进行不同剪切速率下的环剪流动试验.在颗粒材料的剪切流动状态研究中,一般建立宏观应力$\tau $与剪切速率$\dot\gamma^2$的对应关系,即$\tau=f(\dot\gamma^2)$,以识别颗粒材料处于准静态、慢速流或快速流动状态[3, 8-9, 11, 40].为此,这里将不同剪切速率下测得的平均剪切应力$\tau_{\rm m}$与$\dot\gamma^2$的对应关系绘于图 4中,其中横坐标采用了对数坐标. 从中可以发现,在$\tau_{\rm m}$随$\dot\gamma^2$的增加而增大过程中存在一个明显的转折点$\dot\gamma_{\rm c}$. 这里$\dot\gamma^2=19.86$ s$^{-2}$,即$\dot\gamma_{\rm c}=4.46$ s$^{-1}$.

|
图 4 剪切应力$\tau $与剪切速率平方$\dot\gamma^2$的对应关系 Figure 4 The relationship between shearstress and the square of \shell rate $\dot\gamma^2$ |
无论是$\dot\gamma < \dot\gamma_{\rm c}$,还是$\dot\gamma > \dot\gamma_{\rm c}$ 时,剪切应力$\tau_{\rm m}$与$\dot\gamma^2$ 在对数坐标下均呈现明显的线性关系,但其斜率有很大的差异.这表明颗粒材料在该临界剪切速率两侧呈现出不同的流动状态,从而使宏观应力与剪切速率具有不同的对应关系.在Bagnold的颗粒材料同轴剪切试验中,得到了在不同剪切速率下颗粒材料可呈现准静态流和惯性流两个不同的流动状态,并定义了无量纲参数$N_{\rm Bag}$ 来描述宏观应力与剪切速率的对应关系[35].Hunt等[51]进一步分析Bagnold的测量结果,发现其宏观应力与剪切速率呈分段线性关系.从图 4所示试验结果与Bagnold的同轴剪切流变试验来看,颗粒材料剪切应力均随剪切速率的增加而呈分段线性增加.Bagnold采用的无量纲参数$N_{\rm Bag}$是剪切速率的线性函数.然而,从剪切应力与剪切速率的分段线性关系来看,Hunt等[51]得到的斜率在临界剪切速率$\dot\gamma_{\rm c}$后增大,而本文所得斜率则是减小. 以上差异的原因主要是本文与Bagnold试验在试验条件上的不同. 这主要体现为:(1)Bagnold采用的是同轴剪切流变仪,颗粒材料在一个圆筒内进行剪切流动,颗粒流动随离轴心的距离增大而增强,且处于轴心处的颗粒流动较慢;而本文采用的是环剪试验,颗粒材料在一个圆环内剪切流动,全部颗粒材料均发生剪切流动,从而呈现出更强的剪切流动状态.(2)Bagnold试验中的颗粒材料处于牛顿流体中,流体对颗粒的浮力作用在一定程度上克服了重力的影响,从而可更容易地呈现出不同流动状态的转变;本文试验则是在干环境下,颗粒流动状态受重力的影响较大.(3) Bagnold试验中的剪切速率在8.69~289.61 s$^{-1}$范围内,如表 1所示;而在本文试验中,剪切速率则相对较低,在0.1~28.65 s$^{-1}$范围内,此时颗粒材料未达到快速流动状态.受以上因素影响,本文试验中颗粒在慢速流动状态下,颗粒间的动量传递很难贯穿整个颗粒层,而颗粒呈现局部流动状态.此外,在快速流动状态下,本文的剪切速率明显相对较低且又受重力影响,颗粒尚未达到理想的惯性流动状态.因此,本文所获得的颗粒材料在慢速和快速流动状态间的转变特性与Bagnold的结果存在一定的差异.
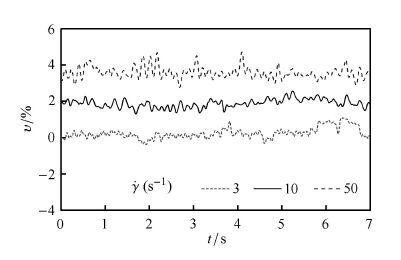
2.2 体积膨胀率表征的临界剪切速率颗粒材料在剪切流动过程中,其体积分数随剪切速率也有明显的变化,并表现出相应的剪胀现象.这里采用体积膨胀率来表征颗粒材料的剪胀程度. 这里取用以上相同的颗粒系统,即平均粒径$D_{\rm mean}=6.5$ mm,颗粒质量$M_s=1.50$ kg.当法向应力$\sigma=1.0$ kPa,颗粒系统在稳定剪切流动时的体积膨胀率随时间变化如图 5所示.类似于图 3所示的剪切应力,颗粒材料的体积膨胀率$v$在剪切流动中也具有显著的脉动特性,且其均值随剪切速率的增加而增大. 当 $\dot\gamma=3$ s$^{-1}$,10 s$^{-1}$和50 s$^{-1}$时,体积膨胀率分别为$\nu=1.07%$,2.73%和3.58%.
|
图 5 不同剪切速度下颗粒材料体积膨胀率随时间变化的脉动特性 Figure 5 Fluctuations of volume dilation rate of granular materials versus time under various shear rates |
为分析不同剪切速率下颗粒材料的体积膨胀率,对以上颗粒材料在法向应力 $\sigma=0.60$ kPa时进行环剪流动试验. 这里将不同剪切速率下测得的体积膨胀率 $\nu$与$\dot\gamma^2$的对应关系绘于图 6中,其中横坐标采用对数坐标. 从中可以发现,$\nu$随$\dot\gamma^2$的增大而增大,且在$\dot\gamma^2=19.86$ s$^{ - 2}$处有一个明显的突变.由此,颗粒材料的体积膨胀率也表征出一个临界剪切速率,其与剪切应力所确定的临界剪切速率相一致,即$\dot\gamma_{\rm c}=4.46$ s$^{ - 1}$.无论是$\dot\gamma < \dot\gamma_{\rm c}$,还是$\dot\gamma >\dot\gamma_{\rm c}$时,体积膨胀率$\nu$与$\dot\gamma^2$在对数坐标下均呈现良好的线性关系,但其斜率有很大的差异.该体积膨胀率的斜率变化规律与剪切应力的变化规律正好相反. $\tau_{\rm m}$与$\dot\gamma^2$的线性斜率在$\dot\gamma < \dot\gamma_{\rm c}$时要高于$\dot\gamma >\dot\gamma_{\rm c}$时的斜率,而$v$与$\dot\gamma^2$的斜率在$\dot\gamma < \dot\gamma_{\rm c}$ 时要低于$\dot\gamma > \dot\gamma_{\rm c}$时的斜率.也就是说,在低剪切速率下颗粒材料的剪切应力对剪切速率更敏感,而在高剪切速率下体积膨胀率对剪切速率则比较敏感.

|
图 6 体积膨胀率$\upsilon $与剪切速率平方$\dot\gamma^2$的对应关系 Figure 6 Relationship between the volume dilation rate and the square of shell rate $\dot\gamma^2$ |
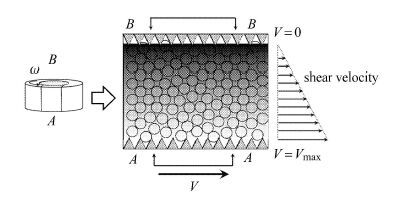
颗粒材料在环剪流动过程中,受法向应力和剪切速率的影响,会呈现出不同的流动状态.在本文试验中,环剪盒的顶板固定不动,通过 底板的转动来实现环剪盒内颗粒材料的速度梯度和剪切流动,如图 7所示.颗粒材料在环剪盒内通过颗粒间的随机碰撞和摩擦实现能量传递,而颗粒间的力链结构则是颗粒材料内作用力的主要传递途径.在不同的流动状态下,颗粒间作用力的传递方式会有很大的差异.颗粒材料在不同的剪切速率下会呈现出类似于固体或液体的力学特性,并在一定条件下发生相互转化[2, 11, 52-53].在不同流动相态下,颗粒材料的宏观应力与剪切速率的对应关系与其细观尺度下颗粒间力链的持续时间、空间长度和作用力大小等因素密切相关[9, 24, 54-55].在类液态下,颗粒分布相对稀疏,碰撞接触以瞬时二体碰撞为主,颗粒间的随机碰撞导致有效摩擦系数较大;在类固态下,颗粒的体积分数较高,颗粒紧密接触从而形成相对稳定的力链,颗粒在相互作用过程中因不断滑动而使有效摩擦系数较低[1, 8, 11, 55].有效摩擦系数与惯性数的密切关系亦可作为判别颗粒系统类固液转化的依据[4, 18, 24-25, 56].为分析环剪试验中颗粒材料的流动状态,下面对不同剪切速率下的有效摩擦系数和惯性指数进行分析.
|
图 7 剪切盒内颗粒材料剪切流动时环向速度分布示意图 Figure 7 Distribution of annular velocity of granular materials in shear cell |
在颗粒系统的不同流动状态下,有效摩擦系数$\mu_{\rm eff}$ 也存在很大差异.Savage等[28]最早通过环剪试验发现,$\mu_{\rm eff}$ 随剪切速率的增大而增大.在类液态的快速流动中,颗粒间碰撞剧烈,$\mu_{\rm eff}$较高,并与剪切速率成正比;而在类固态的准静态下,颗粒间接触紧密,$\mu_{\rm eff}$基本保持为一个定值,与剪切速率无关. 该关系也得到了一系列的物理试验和数值计算的验证[9, 11, 24].目前$\mu_{\rm eff}$已成为表征颗粒系统固液相变特性的一个重要参量.
在颗粒材料的流动状态研究中,有人提出了惯性数的概念[20, 24, 57],即
| $ I=\dfrac{\dot\gamma D}{\sqrt{\sigma/\rho_{\rm s}} }$ | (9) |
式中,$\rho_{\rm s}$是颗粒材料密度,$I$为惯性数.
由于颗粒系统的惯性数$I$能够合理地表征其运动状态,可将不同流动状态下的$\mu_{\rm eff}$设为$I$的函数[4, 22, 24-25, 29],即
| $ \mu_{\rm eff}(I)=\mu_{\rm s}+\dfrac{\mu_2-\mu_s}{I_0/I+1} $ | (10) |
式中,$\mu_{\rm s},\mu_2$和$I_0$均为颗粒材料常数. 对于准静态,即当$I=0$时,$\mu_{\rm eff}=\mu_{\rm s}$;随着$\dot\gamma$的增大,惯性数$I$亦相应增大,此时 $\mu_{\rm eff}$趋向于其最大值$\mu_2$[4, 20, 24, 56-58].
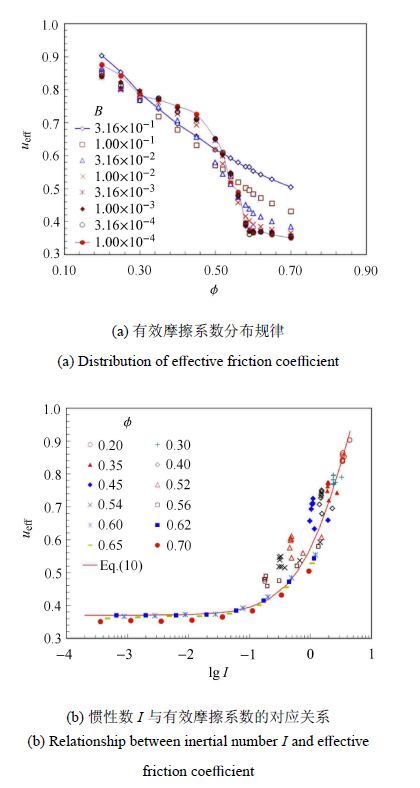
基于对单剪流动的离散元模拟,季顺迎等[18]研究了颗粒材料不同体积分数和剪切速率下发生类固液转化过程,并确定了相应的$\mu_{\rm eff}-\phi$ 关系,如图 8(a)所示. 从中可以发现,颗粒材料的类固液转化点发生在体积分数$\phi=0.62$时,此时$\mu_{\rm eff}=0.61$. 该图中$B$ 为无量级剪切速率,其定义为$B=\dot\gamma\sqrt{\rho_{\rm s}D^3/K_n}$,式中$K_n$为颗粒间的法向刚度系数. 此外,还进一步得到了$\mu_{\rm eff}\sim I$对应关系,如图 8(b)所示. 由此可确定式(10)中的参数,即 $\mu_{\rm s}={\rm tan} (20.3^\circ)=0.37$,$\mu_2={\rm tan}(56.2^\circ)=1.49$,$I_0=4.5$.
|
图 8 颗粒材料在单剪流动状态下发生类固液转化过程[18] Figure 8 Quasi-solid-liquid phase transition of granular material under simple shear flow state[18] |
基于以上分析,可以发现颗粒材料的有效摩擦系数$\mu_{\rm eff}$和惯性数$I$可表征颗粒材料的流动状态. 为此将本文环剪试验图 4的结果转为由$\mu_{\rm eff}$和$I$表示,如图 9所示. 从图 9(a)可发现,$\mu_{\rm eff}$在$\dot\gamma^2=19.86$ s$^{-2}$处有一个明显的转化点,其所对应的有效摩擦系数$\mu_{\rm eff}^*=0.45$. 当$\mu_{\rm eff} < \mu_{\rm eff}^*$时,颗粒之间以持续接触为主,颗粒摩擦作用占主导;当$\mu_{\rm eff}>\mu_{\rm eff}^*$时,颗粒之间主要以碰撞为主,其惯性作用显著.

|
图 9 颗粒材料在不同剪切速率下的有效摩擦系数 Figure 9 Effective friction coefficient of granular material under various shear rates |
从图 9(b)所示$\mu_{\rm eff}$-$I$对应关系可以发现,$\mu_{\rm eff}$ 随$I$的增大而增大,且在$\mu_{\rm eff}^*=0.45$处$I$ 也存在一个特征值$I^*=0.059$. 一般地,当$I<10^{-3}$时为类固态流动,即准静态;当 $I>10^{ -1}$时为类液态流动,即快速流动;当10$^{ - 3}< I<10^{ -1}$时为密集流,此时颗粒系统发生类固液转化[18, 24-25]. 从图 9(b)中可以发现,当惯性数$I<I^*$时,颗粒材料在剪切流动中更多地呈现为准静态的特征,而当$I>I^*$时,则呈现为快速流动.
由此可见,图 4和图 6中宏观应力与体积膨胀率在特征剪切速率$\dot\gamma_{\rm c}=4.46$ s$^{ -1}$处的突变主要是由于颗粒材料的流动状态发生了很大的变化. 在$\dot\gamma=\dot\gamma_{\rm c}$处,同时存在特征有效摩擦系数$\mu_{\rm eff}^*=0.45$和特征惯性数$I^*=0.059$.当$\dot\gamma <\gamma_{\rm c}$时,颗粒之间以弹性持续接触为主,颗粒材料呈现为慢速流动状态;当$\dot\gamma>\dot\gamma_{\rm c}$时,颗粒之间以弹性碰撞为主,颗粒材料则呈现为快速流动状态.
从图 9(a)和图 9(b)所示颗粒材料有效摩擦系数$\mu_{\rm eff}$的随$\dot\gamma^2$ 和$I$的变化规律来看,$\mu_{\rm eff}$随$\dot\gamma^2$和$I$ 的增大而增大.这个变化趋势在以往颗粒材料的流动试验和数值模拟中均得到了相关证实[9, 11, 24, 28]. 然而,在不同的试验条件下,试验结果也会存在一定的差别. 在 MiDi[24]的颗粒材料平面剪切流动中,所得到的$\mu_{\rm eff}$-$I$关系与图 9(b)是一致的,即:$\mu_{\rm eff}$随$I$的增大而增大,其增大幅度随$I$的增大而更加显著.这主要是本文及MiDi试验均是在有重力的干颗粒条件下进行的,颗粒材料受重力的影响很难实现低密集度下的高速流动.Forterre等[4]在颗粒平面剪切流动也得到了类似的结果. 这均与无重力影响下的数值结果存在一定的差异.此外,对比图 8(b)和图 9(b)可以发现,本文试验所得$I$在[0.25,0.56]范围内,而数值计算中的$I$在[10$^{-4}$,10$^{1}$]之间,其有更大的变化范围,从而使颗粒材料可完全实现由慢速流向快速流的转化,并当$I<10^{ -1}$时,$\mu_{\rm eff}$趋于恒定.因此,在颗粒环剪试验中应采用更小的剪切速率,从而获得不同流动状态发生完全转化时$\mu_{\rm eff}$的变化规律.
3 法向应力对颗粒材料流动状态的影响以上临界剪切速率$\gamma_{\rm c}$是在法向应力$\sigma=0.60$ kPa条件下试验确定的. 为分析法向应力对临界剪切速率以及快速流动状态的影响,下面在不同的法向应力下进行颗粒材料的环剪试验.
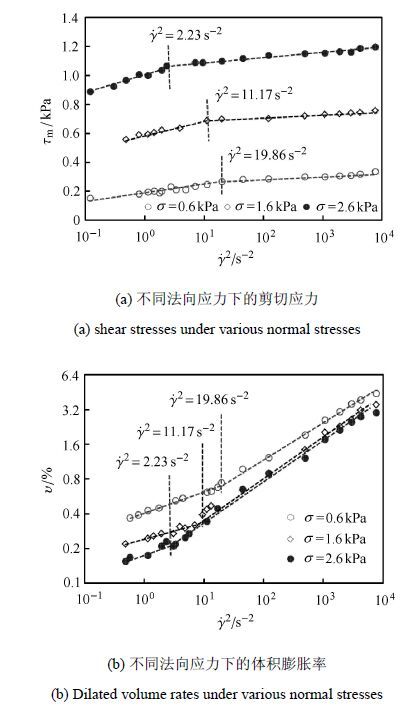
3.1 法向应力对临界剪切速率的影响将质量$M_{\rm s}=1.50$ kg的玻璃颗粒置于环剪盒内,分别在法向应力$\sigma=0.6$ kPa,1.6 kPa和2.6 kPa时进行不同剪切速率的环剪试验.当颗粒材料进入稳态流动时,测得相应的剪切应力和体积膨胀率如图 10所示,其中横坐标取$\dot\gamma^2$ 的对数值.可以发现,法向应力越大,剪切应力就越大,体积膨胀率就越低.
|
图 10 不同法向应力下的剪切应力及体积膨胀率 Figure 10 The shear stress and dilated volume rate under various ormal stresses |
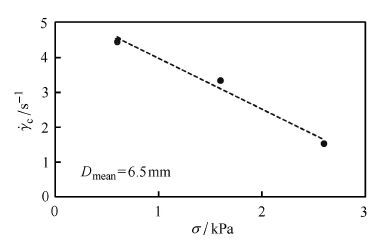
此外,可以发现在不同的法向应力下,剪切应力$\tau_{\rm m}$ 和体积膨胀率$\nu$均与剪切速率$\dot\gamma^2$呈现明显的分段线性关系. 也就是说,在相应的转折点处颗粒材料的流动状态发生了明显的转化,即由低速率下的慢速流向高速率下的快速流转化. 从图 10(a)中可以确定在法向应力 $\sigma=0.6$ kPa,1.6 kPa和2.6 kPa时所对应的剪切速率$\dot\gamma^2=19.86$ s$^{-2}$,11.17 s$^{-2}$和2.33 s$^{-2}$.同样,从图 10(b)也可以清楚发现体积膨胀率$\nu$随$\dot\gamma^2$呈分段线性关系.由此可确定相应的临界剪切速率$\gamma_{\rm c}=4.46$ s$^{-1}$,3.34 s$^{-1}$和1.53 s$^{-1}$,如图 11所示.从中可以发现,临界剪切速率随法向应力的增大而线性降低. 也就是说,法向应力可有效地促进颗粒材料由慢速流动状态向快速流动状态的转化.
|
图 11 不同法向应力下颗粒材料的临界剪切速率 Figure 11 Critical shear rate of granular matter under various ormal stresses |
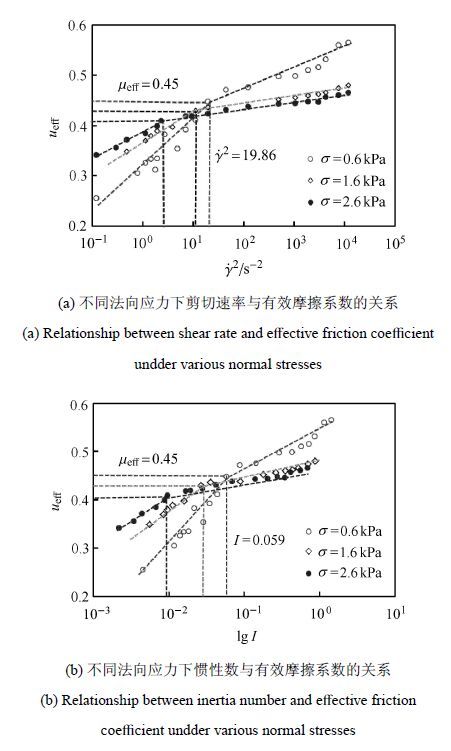
不同法向应力下有效摩擦系数与剪切速率、惯性数的对应关系如图 12所示,其中标出了 $\sigma=0.6$ kPa时的临界剪切速率和惯性数. 图 12(a)中临界剪切速率与图 10(a)相一致,而图 12(b)中的临界惯性数则与相应的有效摩擦系数相对应. 可以发现,在临界剪切速率和惯性数处,颗粒材料的有效摩擦系数在对数坐标下均具有很好的分段线性,从而显示了颗粒材料流动状态的差异. 当$\sigma=0.6$ kPa,1.6 kPa和2.6 kPa时,相应的临界有效摩擦系数$\mu_{\rm eff}=0.45$,0.42和0.41. 这表明法向应力越大,颗粒材料发生慢速-快速流动状态转化时的临界有效摩擦系数越小.
|
图 12 不同法向应力下剪切速率和惯性数对有效摩擦系数的影响 Figure 12 Influence of shear rate and inertia number on effective friction coefficient under various normal stresses |
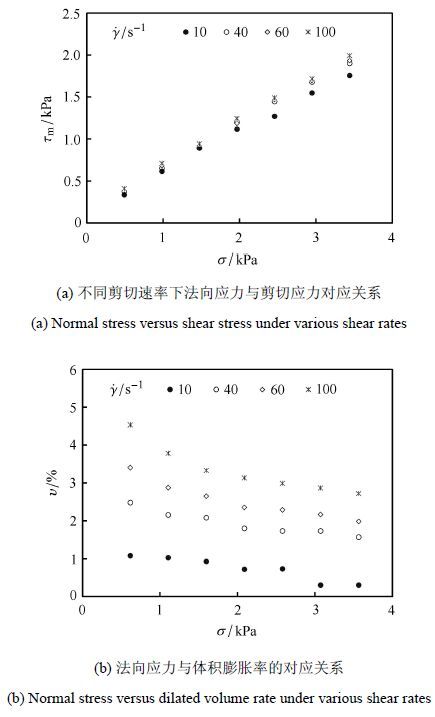
颗粒材料进入快速流动状态后,在不同剪切速率和法向应力下的剪切应力如图 13(a)所示.可以发现,法向应力对剪切应力的影响不明显,且剪切应力与法向应力有很强的线性关系,其斜率即为有效摩擦系数.当剪切速率$\dot\gamma=10$ s$^{ - 1}$和100 s$^{ - 1}$时,有效摩擦系数$\mu_{\rm eff}$分别为0.47和0.53.也就是说,在快速流动状态下,颗粒之间以快速碰撞为主,其剪切运动主要通过颗粒间的瞬时碰撞进行驱动.剪切速率越快,颗粒之前的瞬时碰撞效应也就越明显. 这有效地增强了颗粒间的能量传递和切向作用,从而增大了有效摩擦系数. 在采用离散元方法模拟的颗粒材料单剪流动中,也得到了相似的变化规律[3, 9, 12, 18].
|
图 13 快速流动下法向应力对剪切应力、体积膨胀率的影响 Figure 13 Influences of normal stress on shear stress and volume dilation rate under rapid flow state |
此外,颗粒材料在不同剪切速率下的体积膨胀率如图 13(b)所示. 可以看出,剪切速率越快或法向应力越小,体积膨胀率也就越大. 这也说明在快速剪切流动中,剪切速率的增加可促进颗粒间的瞬时碰撞作用,使颗粒材料的体积分数降低;而法向应力的增加则有效地约束了颗粒材料的剪切膨胀作用.
4 结论为研究颗粒材料的剪切流动特性,本文研制了中尺度环剪仪并测试不同剪切速率和法向应力下的剪切应力和体积膨胀率.试验结果表明,剪切应力$\tau$和体积膨胀率$\nu$均随剪切速率$\dot{\varepsilon }$的增加而增加,并存在一个临界值$\dot\gamma_{\rm c}$,使$\tau$和$\nu$ 均与$\dot\gamma^2$呈分段线性关系.颗粒材料在$\dot\gamma <\dot\gamma_{\rm c}$ 时呈慢速流动状态,而在$\dot\gamma >\dot\gamma_{\rm c}$时呈快速流动状态. $\tau$-$\dot\gamma^2$在慢速流动状态下的斜率要小于快速流动状态下的斜率,而$\nu$-$\dot\gamma^2$的斜率变化正好相反. 通过对颗粒材料流动状态转化过程中有效摩擦系数$\mu_{\rm eff}$和惯性数$I$变化规律的研究,确定了相应的临界值$\mu_{\rm eff}$和$I$,并进一步讨论了环剪试验中慢速流动向快速流动转化的内在机理.
通过对不同法向应力下的环剪试验,确定了法向应力$\sigma$ 对临界剪切速率$\dot\gamma_{\rm c}$的影响.试验结果表明,$\dot\gamma_{\rm c}$随$\sigma$的增大而降低,即法向约束应力可促进颗粒材料由慢速流动向快速流动状态的转化.此外,不同法向应力下快速流动状态的环剪试验结果表明,剪切速率对剪切应力的影响不显著,即在快速流动状态下,有效摩擦系数相对稳定,但体积膨胀率对法向应力的变化则非常敏感.
在本文环剪试验中,由于受重力因素的影响,颗粒材料很难呈现理想的低密集度快速剪切流动.尽管本文研制的环剪仪可实现剪切速率达10$^{ - 1}$s$^{ - 1}$的慢速剪切流动,但仍不能呈现出理想的准静态流动.为此,在颗粒材料的环剪流动试验中,还需要设计转速更慢的剪切仪,从而获得颗粒材料从慢速向快速流动的完全转化过程.
| 1 |
王光谦, 熊刚, 方红卫. 颗粒流动的一般本构关系.
中国科学(E辑),, 28 (3) : 282-288.
( Wang Guangqian, Xiong Gang, Fang Hongwei. The normal constitutive law of granular.
Science in China (Series E),, 28 (3) : 282-288.
(in Chinese) ) ( 0) 0)
|
| 2 |
吴清松, 胡茂彬. 颗粒流的动力学模型和实验研究进展.
力学进展,2002, 32 (2) : 250-258.
( Wu Qingsong, Hu Maobin. Advances on dynamic modeling and experimental studies for granular flow.
Advances in Mechanics,2002, 32 (2) : 250-258.
(in Chinese) ) ( 0) 0)
|
| 3 |
Wang X, Zhu HP, Luding S, et al. Regime transitions of granular flow in a shear cell:A micromechanical study.
Physical Review E,2013, 88 : 032203.
DOI: 10.1103/PhysRevE.88.032203. ( 0) 0)
|
| 4 |
Forterre Y, Pouliquen O. Flows of dense granular media.
Annual Review of Fluid Mechanics,2008, 40 : 1-24.
DOI: 10.1146/annurev.fluid.40.111406.102142. ( 0) 0)
|
| 5 |
厚美瑛, 陈唯, 张彤, 等. 颗粒物质从稀疏流到密集流转变的普适规律.
物理,2004, 33 (7) : 473-476.
( Hou Meiying, Chen Wei, Zhang Tong, et al. Global property of the dilute-to-dense transition of granular flows in a 2D channel.
Physics,2004, 33 (7) : 473-476.
(in Chinese) ) ( 0) 0)
|
| 6 |
钟杰, 彭政, 吴耀宇, 等. 二维颗粒流从稀疏态到密集态的临界转变.
物理学报,2006, 55 (12) : 6691-6696.
( Zhong Jie, Peng Zheng, Wu Yaoyu, et al. The critical phenomena of the dilute-to-dense transition in two-dimensional granular flow.
Acta Physica Sinica,2006, 55 (12) : 6691-6696.
(in Chinese) ) ( 0) 0)
|
| 7 |
Hu MB, Liu QY, Jiang R, et al. Phase transition and flow-rate behavior of merging granular lows.
Physical Review E,2015, 91 : 022206.
DOI: 10.1103/PhysRevE.91.022206. ( 0) 0)
|
| 8 |
Babic M, Shen HH, Shen HT. The stress tensor in granular shear flows of uniform, deformable disks at high solids concentrations.
Journal of Fluid Mechanics,1990, 219 : 81-118.
DOI: 10.1017/S0022112090002877. ( 0) 0)
|
| 9 |
Campbell CS. Granular shear flows at the elastic limit.
Journal of Fluid Mechanics,2002, 465 : 261-291.
( 0) 0)
|
| 10 |
季顺迎, ShenHH. 颗粒介质在类固液相变过程中的时空参数特性.
科学通报,2006, 51 (3) : 255-262.
( Ji Shunying, Shen H Hayley. Characteristics of temporal-spatial parameters in quasi-solidfluid phase transition of granular materials.
Chinese Science Bulletin,2006, 51 (3) : 255-262.
(in Chinese) ) ( 0) 0)
|
| 11 |
季顺迎. 非均匀颗粒介质的类固液相变行为及其本构方程.
力学学报,2007, 39 (2) : 223-237.
( Ji Shunying. The quasi-solid-liquid phase transition of non-uniform granular materials and their constitutive equation.
Chinese Journal of Theoretical and Applied Mechanics,2007, 39 (2) : 223-237.
(in Chinese) ) ( 0) 0)
|
| 12 |
Campbell CS. Granular material flows-an overview.
Powder Technology,2006, 162 : 208-229.
DOI: 10.1016/j.powtec.2005.12.008. ( 0) 0)
|
| 13 |
Utter B, Behringer RP. Experimental measures of affine and nonaffine deformation in granular shear.
Physical Review Letters,2008, 100 : 208302.
DOI: 10.1103/PhysRevLett.100.208302. ( 0) 0)
|
| 14 |
Chaudhuri P, Berthier L, Kob W. Universal nature of particle displacements close to glass and jamming transitions.
Physical Review Letters,2007, 99 : 060604.
DOI: 10.1103/PhysRevLett.99.060604. ( 0) 0)
|
| 15 |
Ashwin SS, Yamchi MZ, Bowles RK. Inherent structure landscape connection between liquids, granular materials, and the jamming phase diagram.
Physical Review Letters,2013, 110 : 145701.
DOI: 10.1103/PhysRevLett.110.145701. ( 0) 0)
|
| 16 |
Liu AJ, Nagel SR. Jamming is not just cool any more.
Nature,1998, 396 : 21.
DOI: 10.1038/23819. ( 0) 0)
|
| 17 |
Zhang Z, Xu N, Chen DTN, et al. Thermal vestige of the zerotemperature jamming transition.
Nature,2009, 459 : 230-233.
DOI: 10.1038/nature07998. ( 0) 0)
|
| 18 |
季顺迎, 孙其诚, 严颖. 颗粒物质剪切流动的类固-液转化特性及相变图的建立.
中国科学:物理学力学天文学,2011, 41 (9) : 1112-1125.
( Ji Shunying, Sun Qicheng, Yan Ying. Characteristics in quasi-solid-liquid phase transition of granular shear flow and its phase diagram.
Scientia Sinica-Phys, Mech & Astron,2011, 41 (9) : 1112-1125.
(in Chinese) ) ( 0) 0)
|
| 19 |
Nemat-Nasser S, Zhang J. Constitutive relations for cohesionless frictional granular materials.
International Journal of Plasticity,2002, 18 : 531-547.
DOI: 10.1016/S0749-6419(01)00008-0. ( 0) 0)
|
| 20 |
Lois G, Lemaitre A, Carlson J. Numerical tests of constitutive laws for dense granular flows.
Physical Review E,2005, 72 : 051303.
DOI: 10.1103/PhysRevE.72.051303. ( 0) 0)
|
| 21 |
孙其诚, 王光谦. 颗粒流动力学及其离散模型评述.
力学进展,2008, 38 (1) : 87-100.
( Sun Qicheng, Wang Guangqian. Review on granular flow dynamics and its discrete element method.
Advances in Mechanics,2008, 38 (1) : 87-100.
(in Chinese) ) ( 0) 0)
|
| 22 |
张国华, 孙其诚, 黄芳芳, 等. 摩擦颗粒体系各向同性压缩过程中的堵塞行为.
物理学报,2011, 60 (12) : 124502.
( Zhang Guohua, Sun Qicheng, Huang Fangfang, et al. Jamming phenomena of a two-dimensional frictional granular system under isotropic confining.
Acta Physica Sinica,2011, 60 (12) : 124502.
(in Chinese) ) ( 0) 0)
|
| 23 |
Jop P, Forterre Y, Pouliquen O. A constitutive law for dense granular flows.
Nature,2006, 441 (8) : 727-730.
( 0) 0)
|
| 24 |
MiDi GDR. On dense granular flows.
The European Physical Journal E,2004, 14 : 341-365.
DOI: 10.1140/epje/i2003-10153-0. ( 0) 0)
|
| 25 |
da Cruz F, Emam S, Prochnow M, et al. Rheophysics of dense granular materials:discrete simulation of plane shear flows.
Physical Review E,2005, 72 : 021309.
DOI: 10.1103/PhysRevE.72.021309. ( 0) 0)
|
| 26 |
Jop P, Forterre Y, Pouliquen O. Crucial role of sidewalls in granular surface flows:consequences for the rheology.
Journal of Fluid Mechanics,2005, 541 : 167-192.
DOI: 10.1017/S0022112005005987. ( 0) 0)
|
| 27 |
Baker JL, Barker T, Gray JMNT. A two-dimensional depth-averaged (I)-rheology for dense granular avalanches.
Journal of Fluid Mechanics,2016, 787 : 367-395.
DOI: 10.1017/jfm.2015.684. ( 0) 0)
|
| 28 |
Savage SB, Sayed M. Stresses developed by dry cohesionless granular materials sheared in an annular shear cell.
Journal of Fluid Mechanics,1984, 142 : 391-430.
DOI: 10.1017/S0022112084001166. ( 0) 0)
|
| 29 |
Pouliquen O, Cassar C, Jop P, et al. Flow of dense granular material:towards simple constitutive laws.
Journal of Statistical Mechanicstheory and Experiment,2006 : P07020.
( 0) 0)
|
| 30 |
Tardos GI, Khan MI, Schae er DG. Forces on a slowly rotating, rough cylinder in a Couette device containing a dry, frictional powder.
Physics of Fluids,1998, 10 (2) : 335-341.
DOI: 10.1063/1.869525. ( 0) 0)
|
| 31 |
Hanes DM, Inman DL. Observations of rapidly flowing granularfluid materials.
Journal of Fluid Mechanics,1985, 150 : 357-380.
DOI: 10.1017/S0022112085000167. ( 0) 0)
|
| 32 |
Miller B, O'Hern C, Behringer RP. Stress fluctuations for continuously sheared granular materials.
Physical Review Letters,1996, 77 (15) : 3110-3113.
DOI: 10.1103/PhysRevLett.77.3110. ( 0) 0)
|
| 33 |
Wildman RD, Martin TW, Huntley JM, et al. Experimental investigation and kinetic-theory-based model of a rapid granular shear flow.
Journal of Fluid Mechanics,2008, 602 : 63-79.
( 0) 0)
|
| 34 |
Jalali P, Ritvanen J, Sarkomaa P. Transient and steady state behaviors of rapid granular shear flows.
Experiments in Fluids,2005, 39 : 552-561.
( 0) 0)
|
| 35 |
Bagnold RA. Experiments on a gravity free dispersion of large solid spheres in a Newtonian fluid under shear.
Proc Roy Soc London A,1954, 225 : 49-63.
DOI: 10.1098/rspa.1954.0186. ( 0) 0)
|
| 36 |
Orlando AD, Shen HH. Effect of particle size and boundary conditions on the shear stress in an annular shear cell.
Granular Matter,2012, 14 (3) : 423-431.
DOI: 10.1007/s10035-012-0313-8. ( 0) 0)
|
| 37 |
Koval G, Roux JN, Corfdir A, et al. Annular shear of cohesionless granular materials:From the inertial to quasistatic regime.
Physical Review E,2009, 79 : 021306.
DOI: 10.1103/PhysRevE.79.021306. ( 0) 0)
|
| 38 |
Liao CC, Hsiau SS, Chang PS. Bottom wall friction coefficis on the dynamic properties of sheared granular flows.
Powder Technology,2015, 270 : 348-357.
DOI: 10.1016/j.powtec.2014.10.043. ( 0) 0)
|
| 39 |
Alenzi A, Marinack M, Higgs CF, et al. DEM validation using an annular shear cell.
Powder Technology,2013, 248 : 131-142.
DOI: 10.1016/j.powtec.2013.05.003. ( 0) 0)
|
| 40 |
Ji S, Hanes DM, Shen HH. Comparisons of physical experiment and discrete element simulations of sheared granular materials in an annular shear cell.
Mechanics of Materials,2008, 41 : 764-776.
( 0) 0)
|
| 41 |
McCarthy JJ, Jasti V, Marinack M, et al. Quantitative validation of the discrete element method using an annular shear cell.
Powder Technology,2010, 203 : 70-77.
DOI: 10.1016/j.powtec.2010.04.011. ( 0) 0)
|
| 42 |
Lu K, Brodsky EE, Kavehpour HP. A thermodynamic unification of jamming.
Nature Physics,2008, 4 : 404-407.
DOI: 10.1038/nphys934. ( 0) 0)
|
| 43 |
杨有莲, 朱俊高, 余挺, 等. 土与结构接触面力学特性环剪试验研究.
岩土力学,2009, 30 (11) : 3256-3260.
( Yang Youlian, Zhu Jungao, Yu Ting, et al. Experimental study of mechanical behaviour of soil-structureinterface by ring shear test.
Rock and Soil Mechanics,2009, 30 (11) : 3256-3260.
(in Chinese) ) ( 0) 0)
|
| 44 |
张明, 胡瑞林, 殷跃平, 等. 滑坡型泥石流转化机制环剪试验研究.
岩石力学与工程学报,2010, 29 (4) : 822-832.
( Zhang Ming, Hu Ruilin, Yin Yueping, et al. Study of transform mechanism of landslide-debris flow with ring shear test.
Chinese Journal of Rock Mechanics and Engineering,2010, 29 (4) : 822-832.
(in Chinese) ) ( 0) 0)
|
| 45 |
Hsiau SS, Yang WL. Stresses and transport phenomena in sheared granular flowswith different wall conditions.
Physics of Fluids,2002, 14 (2) : 612-621.
DOI: 10.1063/1.1428324. ( 0) 0)
|
| 46 |
Qin H. Flow behavior of granular materials:quasi-static to inertial transition.[Master Thesis]. Florida:University of Florida, 2000
( 0) 0)
|
| 47 |
Liu CH, Nagel SR, Schecter DA, et al. Force fluctuations in bead packs.
Science,1995, 269 : 513-515.
DOI: 10.1126/science.269.5223.513. ( 0) 0)
|
| 48 |
Hsiau SS, Shieh YM. Fluctuations and self-diffusion of sheared granular material flows.
Journal of Rheology,2002, 43 (5) : 1049-1066.
( 0) 0)
|
| 49 |
Castillo G, Mujica N, Soto R. Fluctuations and criticality of a granular solid-liquid-like phase transition.
Physical Review Letters,2012, 109 : 095701.
DOI: 10.1103/PhysRevLett.109.095701. ( 0) 0)
|
| 50 |
Howell DW, Behringer RP, Veje CT. Stress fluctuations in a 2D granular Couette experiment:a continuous transition.
Physical Review Letters,1999, 26 : 5241-5244.
( 0) 0)
|
| 51 |
Hunt ML, Zenit R, Campbell CS, et al. Revisiting the 1954 suspension experiments of R. A. Bagnold.
Journal of Fluid Mechanics,2002, 452 : 1-24.
( 0) 0)
|
| 52 |
Jaeger HM, Nagel SR. Physics of the granular state.
Science,1992, 255 : 1523-1531.
DOI: 10.1126/science.255.5051.1523. ( 0) 0)
|
| 53 |
Wang D, Zhou Y. Particle dynamics in dense shear granular flow.
Acta Mechanica Sinica,2010, 26 : 91-100.
DOI: 10.1007/s10409-009-0322-y. ( 0) 0)
|
| 54 |
Keys AS, Abate AR, Glotzer SC, et al. Measurement of growing dynamical length scales and prediction of the jamming transition in a granular material.
Nature Physics,2007, 3 : 260-264.
DOI: 10.1038/nphys572. ( 0) 0)
|
| 55 |
Jaeger HM, Nagel SR, Behringer RP. Granular solids, liquids, and gases.
Reviews of Modern Physics,1996, 68 : 1259-1273.
DOI: 10.1103/RevModPhys.68.1259. ( 0) 0)
|
| 56 |
Renouf M, Bonamy D, Dubois F, et al. Numerical simulation of two-dimensional steady granular flows in rotating drum:on surface flow rheology.
Physics of Fluids,2005, 17 : 103303.
DOI: 10.1063/1.2063347. ( 0) 0)
|
| 57 |
Baran O, Ertas D, Halsey TC, et al. Velocity correlations in dense gravity-driven granular chute flow.
Physical Review E,2006, 74 : 051302.
DOI: 10.1103/PhysRevE.74.051302. ( 0) 0)
|
| 58 |
Yan Y, Ji S. Energy conservation in a granular shear flow and its quasi-solid-liquid transition.
Particulate Science and Technology,2009, 27 (2) : 126-138.
DOI: 10.1080/02726350902775970. ( 0) 0)
|
 2016, Vol. 48
2016, Vol. 48