商用航空发动机喷流通常呈高亚声速流动状态,伴随产生的强声辐射构成飞机起飞过程中主要噪声源. 为指导发动机降噪设计适应航空噪声管制规定,喷流噪声形成机制受到长期关注.
基于Lighthill声比拟理论[1-2],早期人们认为喷流噪声由给定平均流内随机分布小尺度湍流涡构成的系统产生,然而该理论结合Doppler频移原理得到飞行状态下喷流下游噪声主导频率应高于上游的推论与实际观测不符.20世纪80年代初,Kibens[3]和Laufer等[4]发现不稳定频率激励下高速喷流的自然宽频噪声被抑制,最显著噪声成分具有特征频率,且对应的声源空间位置固定在剪切层涡对并处.Chu等[5]指出高亚声速喷流主要声源在紧邻势流核下游,Juvé等[6]通过实验研究了势流核末端受湍流间歇性影响的声形成特征.
Tam等[7-8]通过大量实验归纳亚声速喷流噪声谱包含两部分,一部分源于大尺度结构,向下游辐射;另一部分源于小尺度湍流,向侧向辐射. 但该观点与湍流谱连续多尺度的本质特性不符,且没有实验证据显示大尺度拟序结构和小尺度随机结构之间存在尺度间断.
随着近年计算机技术的发展,采用数值方法直接模拟喷流噪声产生及辐射过程变得可行,为喷流噪声机制提供了新研究途径.Freund[9]较早采用直接数值模拟(direct numerical simulation,DNS)方法计算马赫数0.9,雷诺数3 600的圆喷流声辐射,获得了可与实验[10]声场定量对比的结果.Freund[9]还通过Lighthill声源滤波方法,分析确定喷流中具有呈简单谐波形态的可辐射声源,且其声辐射明显指向下游,印证了喷流主导声源和不稳定波之间的相关性. Bogey等[11]通过大涡模拟(large eddy simulation, LES)分析认为亚声速喷流中拟序结构间歇侵入势流核是产生大振幅声波的机制.之后,Bogey等[12]的LES结果也显示了亚声速喷流噪声由失稳波和小尺度湍流两类声源机制产生.同时,Viswanathan等[13]通过数值模拟发现临近势流核末端的下游处存在空间位置固定且具有指向性的强声源.
近年来,一种广受关注的气动噪声理论认为喷流慢变非平行平均流内的不稳定波在演化过程中形成了波包结构,其中可向外传播的波包构成主导声辐射,据此揭示大尺度湍流结构产生声辐射的机制[14-15].Obrist[16]基于近似的Lighthill声比拟理论,在频率-波数空间构造Gauss包络形状波包声源模型,并可通过设置波包构型参量控制声辐射的指向性,证实波包在声辐射中的支配地位.但目前仍无法从真实流场中提取合适波动信息验证波包是喷流主导声波形成的直接机制,湍流喷流混合噪声的本质物理机制建模还待完善.
本文采用LES方法对高亚声速喷流数值分析,并耦合可穿透面FW-H方法外推其声远场,以确定喷流和声辐射间的关系,进一步揭示喷流声源发声机制.第1节介绍喷流模型及数值方法;第2节详细校核并分析了亚声速喷流湍流场特性;第3节外推了喷流声辐射远场,并分离主导声模态分析拟序结构或波包在声源辐射中的作用;第4节为总结.
1 数值方法 1.1 控制方程及离散考虑无量纲化三维可压缩Favre滤波Navier--Stokes方程
| $ \dfrac{\partial \bar {\rho }}{\partial t} + \dfrac{\partial \bar {\rho }\tilde {u}_i }{\partial x_i } = 0 $ | (1) |
| $\dfrac{\partial \bar {\rho }\tilde {u}_i }{\partial t} + \dfrac{\partial \bar {\rho }\tilde {u}_i \tilde {u}_j }{\partial x_j } + \dfrac{\partial \bar {p}}{\partial x_i } - \dfrac{\partial }{\partial x_i }(\tilde {\tau }_{ij} - \tau _{ij}^{\rm SGS} + D_{ij}^{\rm SGS} ) = 0 $ | (2) |
| $\begin{align} & \frac{\partial \bar{e}}{\partial t}+\frac{\partial \left[ (\bar{e}+\bar{p}){{{\tilde{u}}}_{i}} \right]}{\partial {{x}_{i}}}-\frac{\partial }{\partial {{x}_{i}}}({{{\tilde{u}}}_{j}}{{{\tilde{\tau }}}_{ij}}-{{{\tilde{u}}}_{j}}\tau _{ij}^{\text{SGS}}+\sigma _{i}^{\text{SGS}}- \\ & {{{\tilde{q}}}_{i}}-Q_{i}^{\text{SGS}}-H_{i}^{\text{SGS}})=0\text{ } \\ \end{align}$ | (3) |
其中$\bar {\rho }$,$\tilde {u}_i $,$\bar {p}$,$\bar {e}$,$\tilde {q}_i $和$\tilde {\tau }_{ij} $分别为Favre滤波密度、速度、压力、总能、热通量和黏性应力张量. 以喷流喷口参量,即喷口半径$r_{0}^{\ast }$、声速$a_{j}^{\ast }$、密度$\rho _j^\ast $、温度$T_j^\ast $等作为特征参量对方程(1)$\sim$(3)无量纲化,方程(1)$\sim$(3)中亚网格尺度(subgrid-scale,SGS)项通过经典Smagorinsky模型进行建模. 其中SGS黏性应力张量为
| $\begin{align} & \tau _{ij}^{\text{SGS}}=-2{{C}_{S}}\bar{\rho }{{\Delta }^{2}}{{{\tilde{S}}}_{M}}\left( {{{\tilde{S}}}_{ij}}-\frac{1}{3}{{{\tilde{S}}}_{kk}}{{\delta }_{ij}} \right)+ \\ & \frac{2}{3}{{C}_{I}}\bar{\rho }{{\Delta }^{2}}\tilde{S}_{M}^{2}{{\delta }_{ij}} \\ \end{align}$ | (4) |
上式$\tilde {S}_{ij} $为Favre滤波应变率张量,$\tilde {S}_M = \left( {2\tilde {S}_{ij} \tilde {S}_{ij} } \right)^{1/2}$. $\varDelta $是LES的滤波尺度,本文取当地网格宽度. $\delta_{ij} $ 为Kronecker符号. SGS热通量为
| $ Q_i^{\rm SGS} = \dfrac{ - C_S \bar {\rho }\Delta ^2\tilde {S}_M }{\Pr _t }\dfrac{\partial \tilde {T}}{\partial x_i } $ | (5) |
其中,Smagorinsky模型及其可压缩修正系数为$C_S = 0.012$,$C_I = 0.006 6$,湍流Prandtl数$ Pr _{\rm t} = 0.9$.另外SGS黏性扩散项$\sigma ^{\rm SGS}_i$及由SGS黏性应力和SGS热通量引起的$D^{\rm SGS}_i$和$H^{\rm SGS}_i$在喷流计算中相比式(4)和式(5)的SGS项作用较小而被忽略.
为使方程(1)$\sim$(3)封闭,补充状态方程
| $ \bar {p} = {\bar {\rho }\tilde {T}} / \gamma $ | (6) |
其中比热比$\gamma = 1.4$.
采用低色散、低耗散的DRP(dispersion-relation-preserving)格式[17-18]离散方程(1)$\sim$(3)中无黏通量项,黏性项采用二阶中心差分格式离散,时间推进使用低存储6步4阶优化Runge-Kutta格式[19]. 由于DRP格式无法抑制高波数短波导致的Gibbs数值振荡,引入人工选择性阻尼[17-18]. 使用Bogey等[20]提出的自适应滤波方法抑制强湍流脉动导致的数值振荡,该滤波方法由邻近网格点变量提供的两个阻尼通量构成
| $ f_l^{\rm sc} = f_l - \left( {\sigma _{l + 1 /2}^{\rm sc} D_{l + 1 / 2}^{\rm sc} - \sigma _{l -1/2}^{\rm sc} D_{l - 1/ 2}^{\rm sc} } \right) $ | (7) |
其中$f_l $和$f_l^{\rm sc} $分别为点$l$处滤波前、后的流场变量. 滤波强度$0\text{ }\le {{\sigma }^{\text{sc}}}\le 1$,需配合激波探测函数动态确定. 阻尼函数$D_{l + 1/2}^{\rm sc} $和$D_{l - 1 /2}^{\rm sc} $由变量$f$插值确定
| $D_{l+1/2}^{\text{sc}}=\sum\limits_{j=1-n}^{n}{{{c}_{j}}{{f}_{l+j}}},D_{l-1/2}^{\text{sc}}=\sum\limits_{j=1-n}^{n}{{{c}_{j}}{{f}_{l+j-1}}}$ | (8) |
上述处理可有效维持数值计算稳健性,且对物理流场求解的影响较小.
针对守恒变量,在方程求解的最后一个Runge-Kutta时间子步中引入黏性项、SGS项、选择性阻尼项及自适应滤波项运算.
1.2 可穿透面FW-H方法可穿透面FW-H方法是原始FW-H方法的修正积分形式,具体形式为[21]
| $ {p}'(x,y,z,t) = {p}'_{\rm T} (x,y,z,t) + {p}'_{\rm L} (x,y,z,t) + {p}'_{\rm Q} (x,y,z,t) $ | (9) |
其中,($x,y,z$)为FW-H声源控制面上坐标,${p}'_{\rm T} $为类单极子的厚度噪声,${p}'_{\rm L}$为类偶极子的载荷噪声. ${p}'_{\rm Q } $为四极子噪声. 可穿透面FW-H方法中,${p}'_{\rm Q }$对应于声源控制面以外,由于其所占比重小且体积积分求解花费高,因此计算中一般被忽略.
式(9)中${p}'_{\rm T} $和${p}'_{\rm L} $形式为
| $\left. \begin{array}{*{35}{l}} {{{{p}'}}_{\text{T}}}(x,y,z,t)=\frac{1}{4\pi }\int_{S}{{{\left[ \frac{{{\rho }_{\infty }}{{{\dot{U}}}_{n}}}{r} \right]}_{\text{ret}}}dS} \\ {{{{p}'}}_{\text{L}}}(x,y,z,t)=\frac{1}{4\pi {{a}_{\infty }}}\int_{S}{{{\left[ \frac{{{{\dot{L}}}_{r}}}{r} \right]}_{\text{ret}}}dS+\int_{S}{{{\left[ \frac{{{L}_{r}}}{{{r}^{2}}} \right]}_{\text{ret}}}dS}} \\ \end{array} \right\}$ | (10) |
其中,$S$表示声源控制面,通常设置在包含所有声源的空间位置处. 下标 ret表示延迟时间,即声源与观察点之间的$t_r =t - \left| { { x}-{ x}' } \right| / a_\infty $,$t$为观察坐标时间,其中也使用${ x}$和 ${x}'$表示观察点和控制面的坐标. 顶标"."表示对声源时间导数,下标$r$和$n$表示与辐射方向单位向量$\hat{r}$或控制面外法向单位向量${ n}_i $点乘,${ r}$是从声源(控制面)到观察点的有向距离. 下标$\infty$表示环境变量,上标" $'$ "表示脉动量. 变量$U_i $和$L_i $具体形式
| $\begin{array}{*{35}{l}} {{U}_{i}}=\frac{\rho {{u}_{i}}}{{{\rho }_{\infty }}} \\ {{L}_{i}}={{P}_{ij}}{{{\hat{n}}}_{j}}+\rho {{u}_{i}}{{u}_{n}} \\ \end{array}$ | (11) |
其中,$u_i $是速度向量,$P_{ij} $是可压缩应力张量减去常值$p_\infty \delta_{ij} $.
式(10)的频域形式为
| $\begin{array}{*{35}{l}} {{{\hat{{p}'}}}_{\text{T}}}(x,y,z,\omega )=-\frac{\text{i}\omega }{4\pi }\int_{S}{{{\text{e}}^{\text{i}\omega r/{{a}_{\infty }}}}\frac{{{\rho }_{\infty }}{{{\hat{U}}}_{n}}}{r}dS} \\ {{{\hat{{p}'}}}_{\text{L}}}(x,y,z,\omega )=-\frac{\text{i}\omega }{4\pi {{a}_{\infty }}}\int_{S}{{{\text{e}}^{\text{i}\omega r/{{a}_{\infty }}}}\frac{{{{\hat{L}}}_{r}}}{r}dS+\int_{S}{\frac{{{{\hat{L}}}_{r}}}{{{r}^{2}}}dS}} \\ \end{array}$ | (12) |
其中,$\hat {p}$,$\hat {U}_n $和$\hat {L}_r $分别由${p}'$,$U_n $和$L_r $做Fourier变换获得,如${p}'\left[{(x,y,z),t} \right] = R\left\{ {\left[ {\hat {p}(x,y,z)} \right] {\rm e}^{-{\rm i}\omega t}} \right\}$,$\omega $ 是圆频率.
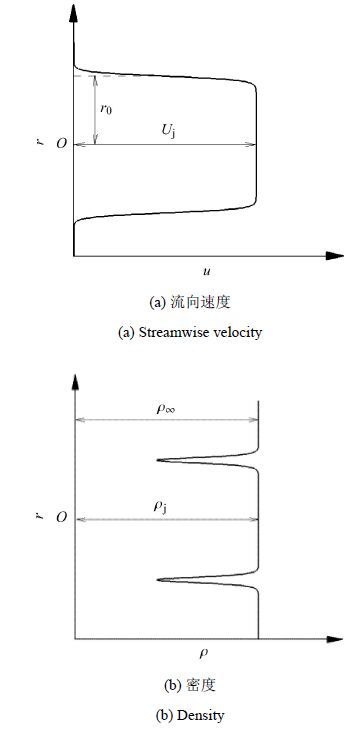
1.3 喷流模型数值模拟中未包含喷管几何模型,如图 1(a)所示,在计算域$x=0$位置,采用双曲正切函数分布的流向速度剖面近似模仿圆喷口流动
| $ u\left( r \right) = \dfrac{U_{\rm j} }{2} + \dfrac{U_{\rm j} }{2}\tanh \left( {\dfrac{1 - r}{2\delta _\theta }} \right) $ | (13) |
其中,喷口剪切层初始动量厚度$\delta_{\theta }=0.03$,$r$为喷流径向坐标,喷口中心速度(马赫数) $U_j =0.9$,喷口径向速度和周向速度均为0. 以喷口直径为特征长度定义喷流雷诺数$Re=3 600$.如图 1(b),等压圆喷流来流密度剖面由Crocco-Busemann关系式给定
| $ \rho \left( r \right) = \left[{1 + \dfrac{\gamma - 1}{2}u\left( r \right)\left({U_{\rm j} - u\left( r \right)} \right)} \right]^{ - 1} $ | (14) |
其中比热比$\gamma =1.4$,另外喷流中心温度与周围环境温度一致.
|
图 1 喷口来流剖面 Figure 1 Jet inflow profile |
为迫使喷流层流剪切层快速向湍流转捩,在喷口下游$x =1$位置处,使用Bogey等[11]提出的涡环扰动进行人工激励
| $\left. \begin{array}{*{35}{l}} {{U}_{x}}=2\frac{{{r}_{0}}}{r}\frac{r-{{r}_{0}}}{{{\Delta }_{0}}}\exp \left( -\ln (2){{\left( \frac{\Delta (x,r)}{{{\Delta }_{0}}} \right)}^{2}} \right) \\ {{U}_{r}}=-2\frac{{{r}_{0}}}{r}\frac{x-{{x}_{0}}}{{{\Delta }_{0}}}\exp \left( -\ln (2){{\left( \frac{\Delta (x,r)}{{{\Delta }_{0}}} \right)}^{2}} \right) \\ \end{array} \right\}$ | (15) |
其中,$r=\sqrt{{{y}^{2}}+{{z}^{2}}}\ne 0\Delta {{(x,r)}^{2}}={{(x-{{x}_{0}})}^{2}}+{{(r-{{r}_{0}})}^{2}}$,设置参数$x_{0}=r_{0}=1$以确定涡环扰动空间位置. 涡环扰动与周向角 $\theta $的函数结合形成周向扰动,扰动叠加形式如下
| $ \left. \!\!\begin{array}{l} u_x = u_x + \sum_{n = 0}^{15} {\alpha \varepsilon _n \cos (n\theta + \varphi _n )U_x U_{\rm j} } \\ u_r = u_r + \sum_{n = 0}^{15} {\alpha \varepsilon _n \cos (n\theta + \varphi _n )U_r U_{\rm j} } \\ \end{array}\!\!\right\} $ | (16) |
式中,$n$为周向模态数,选取$n =0,1,\cdots,15$,共16个周向模态. $\varepsilon _n $和$\varphi _n $分别为随机的扰动振幅和相位,范围:$ - 1 ≤ \varepsilon _n ≤ 1$,$ - 1 ≤ \varphi _n ≤ 1$. $\alpha $是扰动振幅,取$\alpha =0.005$,以确保剪切层较快转捩且不影响物理流场求解.
使用由线化Euler方程的远场渐近解构造的辐射无反射边界条件[17, 22]处理喷流计算域所有边界,且在计算域下游的出口区域进一步设置声吸收区(sponge zone)[11, 22]以避免非线性湍流脉动与出口边界相互干扰产生强伪声反射.
1.4 网格设置参考文献[9, 11-12],如图 2所示,采用了正交Descartes网格,网格数255 × 193 × 193 (x × y × z),约900万量级. $x$正方向为喷流流向,沿流向计算域被分为物理区和声吸收区.物理区内流向网格均匀分布,间距为 $\Delta x =0.09$,至$x =20$物理区终止,共215个网格点.声吸收区网格沿流向逐渐拉伸,拉伸比为0.43%,吸收区流向沿伸至$x =30$,使用40个网格点,最大网格间距 $\Delta x_{\max}=0.5$. 计算域的展向和法向区间为$y=z =-9 \sim 9$,网格分布相同,均沿喷流轴的水平面和垂直面对称. 喷流核心流域附近进行网格加密以精确识别小尺度湍流结构,加密区采用均匀分布网格 $\Delta y = \Delta z =0.04$,共100个网格点. 当$y$,$z >2$后网格沿展向和法向拉伸,拉伸比为0.5%,最大网格间距 $\Delta y_{\max}=\Delta z_{\max}=0.5$.
值得注意的是,LES计算结果显示,在具有湍流自相似特征的喷流中心线下游$x=16.0$位置,统计得到流动Kolmogorov尺度[11] $\eta =0.012$,Taylor尺度[11]$\lambda _{g}=0.185$.表明本文网格尺度可捕捉大于Taylor尺度的湍流结构,且滤除了Kolmogorov尺度以下的湍流结构,符合LES网格尺度要求.

|
图 2 超声速喷流计算网格(每3点显示) Figure 2 The computational grid of the supersonic jet (every 3rd grid point is shown) |
根据网格尺度及喷流状态,并数值验证确定无量纲化时间步长设置为$\Delta t =0.04$,可满足高频湍流脉动捕捉需求.每网格点每次迭代需0.63 μs,共迭代50 000步,第10 000步后进行湍流及噪声统计.
由于圆喷流数值计算建立于正交坐标系下,为方便与相关文献中柱坐标系数据对比,将数据统计分析集中在$x$-$y$($z =0$)对称面内,该对称面内Descartes坐标($x$,$y$,$z$)与柱坐标($x$,$r$,$\theta $)一致.
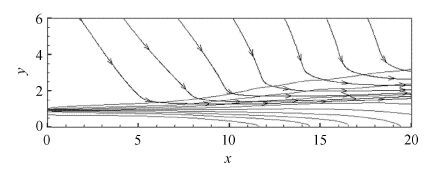
2 喷流流场 2.1 湍流统计图 3给出喷流时均统计后流向速度等值线分布. 以平均流速度降至0.95 $U_{\rm j} $确定势流核区,由图可判断势流核在流向$x =11.8$处结束. 雷诺数较小时,势流核长度一般较长,相同来流条件下Stromberg等[10]的实验测得势流核长度$L =14 r_{0}$,而Freund[9]的DNS结果显示该长度$L$约为$ 16 r_{0}$.图 3中流线显示环境流体受喷流卷吸、夹带机制进入喷流区,亦表明辐射边界条件允许流体进入计算域并补充喷流带走的流体质量,保证了数值模拟获得与实验相符的喷流特征.
|
图 3 平均流向速度等值线[0.05$U_{\rm j}$,0.95$U_{\rm j}$]及流线 Figure 3 Streamwise velocity of meanflow [0.05$U_{\rm j}$,0.95$U_{\rm j}$] \with streamlines |
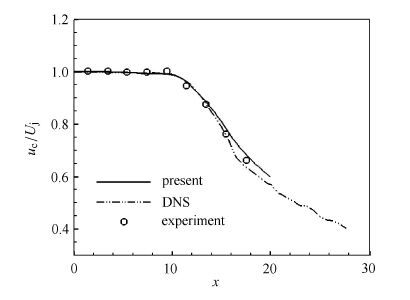
针对喷流轴线上的平均速度,如图 4所示,将LES结果与实验[10]及DNS[9]结果进行对比.在同实验比较时,由于DNS[9]获得了较长的势流核,其将喷口坐标向下游移动至$x=2$位置,而本文LES得到的势流核较短,故将喷口坐标向上移至$x =-2$位置.这是由于受网格分辨率限制,数值模拟采用的喷口剪切层初始动量厚度比实验大两个量级,且使用了人工扰动激励,剪切层失稳进程差异导致了不同的势流核长度.在统一坐标后,图 4显示LES和DNS结果与实验吻合很好,表明数值方法能够正确地模拟喷流下游流动特性.
|
图 4 喷流中心线平均速度对比 Figure 4 Mean velocity in jet center line |
为确认LES对湍流脉动求解的准确性,图 5所示为湍流脉动水平定量对比. 值得注意的是由于可压缩喷流湍流强度测量困难,这里利用湍流自相似特征,与不可压缩喷流湍流强度$\sqrt {\overline {{u}'{u}'} } / U_{\rm c} $,$\sqrt {\overline{{v}'{v}'} } / U_{\rm c} $,$\sqrt {\overline {{w}'{w}'} } / U_{\rm c} $及$\sqrt {\overline {{u}'{v}'} } /U_{\rm c} $等统计对比,其中湍流强度均以当地喷流轴心速度$U_{ \rm c }$进行归一化.选取对应于湍流转捩及充分发展区3个站位$x =16.0$,17.5,19.0,对比显示LES结果与实验结果吻合很好,数据均落在实验数据[23-24]之间,表明获得了可靠的湍流脉动数值结果.

|
图 5 湍流强度对比 Figure 5 Comparison of turbulence intensity |
图 6为喷流中心线上流向湍流强度对比,显示本文LES结果湍流强度与文献[25-26]的计算结果吻合很好.由于未对流向坐标进行平移,和实验数据[27-28]流向坐标出现一定差异,但湍流强度水平一致.

|
图 6 中心线流向湍流强度比较 Figure 6 Comparison of turbulence intensity in jet center line |
根据喷流流动特征,分别在剪切层内(4.0,1,0),(8.0,1,0),(12.0,1,0),(16.0,1,0)四点、喷流中心线上(11.0,0,0),(16.0,0,0)两点等典型位置采样,进一步分析喷流湍流脉动能谱.
针对剪切层内4个采样位置径向脉动速度$v'$信号进行频谱分析,以揭示剪切层内扰动波发展特征. 如图 7所示,在剪切层发展初期(4.0,1,0),流动具有明显的占优模态,对应的无量纲频率$St_{\rm D}=fD/U_{\rm j}=0.54$,可知LES的喷流剪切层内存在不稳定扰动波诱导的大尺度拟序结构. 在剪切层(8.0,1,0)位置,已展现出一定宽频谱特征,但仍具有占优模态,其无量纲频率$St_{\rm D}$下降至0.4左右. 在(12.0,1,0)和(16.0,1,0)位置,两条能谱曲线几乎重合,表明主导扰动波消失,高、低频谱的各种扰动均发展饱和,流动转捩结束,呈现为湍流状态.

|
图 7 径向脉动速度$v'$功率谱密度 Figure 7 Power spectral density of radial fluctuation velocity $ v'$ |
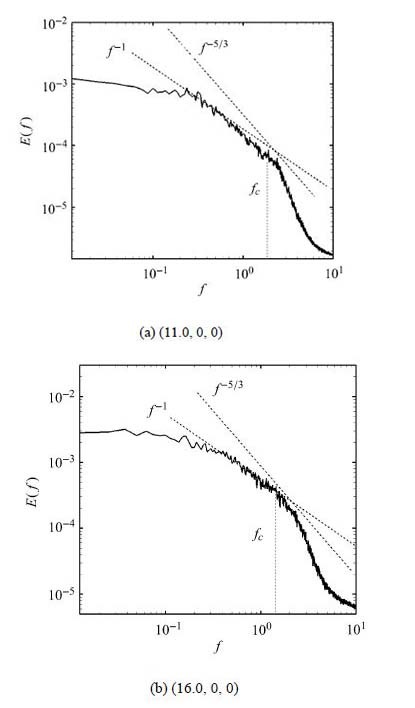
根据Taylor冻结湍流假设,可由时间能谱$E(f)$估算空间能谱$E_{k}(k_{1})$,并据此分析湍流标度律区间.图 8分析了喷流中心线上两个典型位置湍动能能谱,为识别物理谱,图中均标出了截断频率$f_{\rm c}$,同时给出了$-5/3$次律参考线,且为方便辨识能谱规律,图中给出了$-1$次的辅助线.如图 8(a),在势流核结束位置前,喷流还未完全形成宽频谱区,低频和高频扰动均未发展起来,在势流核终止后,如图 8(b),湍动能谱呈现宽频特性,但中心线上未能找到$-5/3$次律的标度律区间.
|
图 8 喷流中心线湍动能谱 Figure 8 Turbulent kinetic energy spectrum of flow in jet center line |
由于喷流雷诺数$Re=3 600$过小,湍动能谱的平衡区被黏性耗散子区占据,因此未能形成惯性子区. 但湍动能仍涵盖了大范围的频域空间,流动具有多尺度特性,可被认为形成了湍流流动. 针对低雷诺数喷流,文献[9]也得到相同结论.另外,截断频率$f_{\rm c}$显示LES计算已捕获了主要的湍动能谱段,达到亚网格尺度建模高波数流动.
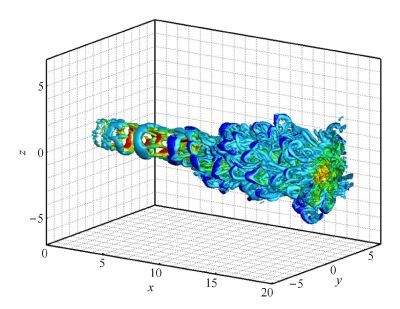
2.3 流场演化图 9采用$Q$等值面展示了LES计算获得的瞬时涡量场.受Kelvin-Helmholtz不稳定性主导,在强迫扰动下剪切层内的占优扰动快速发展饱和,促使初始喷流剪切层约在$x$=5的位置发生涡卷起形成大尺度涡环结构.涡环在向下游对流时,在$x$=11附近形成涡对并现象.同时涡环演化过程中,伴随螺旋扭曲且由于高频波的增长形成大量涡辫等小尺度结构,加速涡结构对并及破碎.大尺度涡结构不断发展增强,最终导致上下层涡在势流核下游相遇融合,并导致势流核终止.在三维效应下,融合后的大尺度涡结构快速破碎成大量小尺度涡,并向下游对流形成湍流尾迹.
|
图 9 瞬时$Q$等值面:$Q=0.01$,以流向速度$u$着色 Figure 9 Instantaneous $Q$ isosurface: $Q =0.01$,colored by streamwise velocity $u$ |
为观察湍流涡结构沿流向的三维演化特征,图 10展示了图 9中不同流向站位上的涡量值等值线. 在剪切层起始位置$x =5$,流动保持层流状态,涡量沿周向呈圆形涡环,但三维扰动已得到一定发展,涡环内部的三维周向不对称性逐渐呈现.进一步向下游发展至$x =8$,剪切层周向失稳导致涡环外部形成涡辫结构. 在$x=10$位置,涡辫结构进一步增强,涡环开始扭曲破碎. 至$x =12$处,涡辫与小尺度涡区逐渐融合,直至下游$x=15$处势流核及环形涡结构消失,喷流与周围环境流体完全混合. 在$x=18$处,大量小尺度涡结构出现,喷流进入湍流自相似区.

|
图 10 喷流不同流向站位的涡量演化;涡量值:[0.2,4] Figure 10 Vorticity evolution along the jet streamwise,vorticity magnitude: [0.2,4] |
由于喷流径向9倍喷口半径计算域过小,无法描述远场声辐射特征,采用可穿透面FW-H声外推方法,将积分面设置于展向及法向$y$,$z=\pm 7.0$处,以此外推获取声远场.
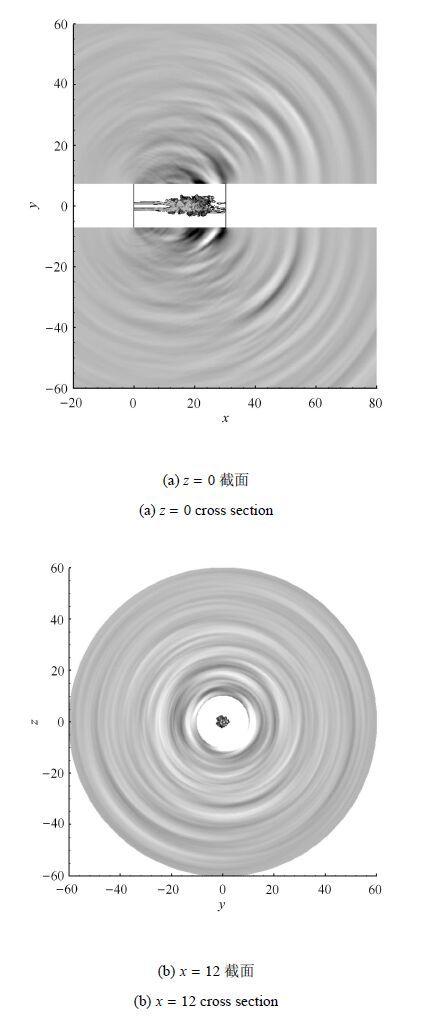
图 11展示了由FW-H声外推方法推导的喷流瞬时声场,其中远场采用声压显示,近场为涡量值. 由图 11(a)可见喷流产生了具有清晰波阵面的声辐射,且对应声源区在喷流势流核末端.以势流核末端为中心,在与喷流轴呈约30°的方位噪声强度达到峰值,展现出明显的喷流声辐射指向性特征,而喷流前向远场区域占优的声模态辐射强度减弱. 图 11(b)为喷流流向截面($x=12$)内瞬时声场,图中显示声波以喷流轴为圆心呈圆形向外辐射,呈现为三维球面波特征.
以Stromberg等[10]、Mollo-Christensen等[29]及Lush[30]的实验结果,Freund[9]的DNS结果和Bogey等[11]的LES结果为参考,图 12比较了距离喷口60倍喷口半径的圆弧上远场整体声压级(OASPL).由图可见,本文LES预测的噪声整体声压级略高于实验测量的结果,也略高于Bogey等[11]LES预测中等雷诺数喷流远场噪声,而与Freund的DNS预测噪声水平相同.对于最强声压级的方位角的预测略大于实验以及DNS的预测结果,而与Bogey等[11]的结果接近.对比Mollo-Christensen等[29]和Lush[30]高雷诺数以及Bogey等[11]LES中等雷诺数喷流数据,显示出低雷诺数喷流噪声具有更强的指向性. 最强声压级方位角预测与文献一致,均在 $\alpha=30^{\circ}$附近,再次印证喷流噪声LES的准确性.
|
图 11 瞬时喷流声场 Figure 11 Instantaneous acoustic field of the jet |

|
图 12 整体声压级随方位角$\alpha$分布 Figure 12 Overall sound pressure level (OASPL) distribution with the azimuth angle $\alpha $ |
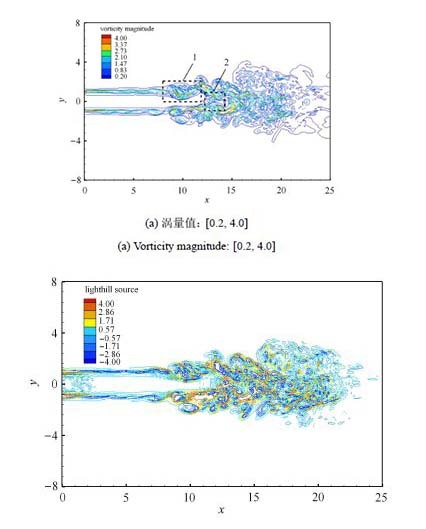
图 13展示了喷流瞬时涡量场及Lighthill声源分布.对比可见声源分布与涡量具有一致性,表明涡量在声源中扮演重要的作用.对应于涡量,声源也主要分布在喷流剪切层内及下游湍流混合区,其中在10<x<20区间为声源集中区,来自于势流核结束后强湍流脉动.该声源与图 11(a)展现的远场声辐射分布规律一致,尤其是对应于远场低方位角 $\alpha =30^{\circ}$附近的周期性辐射声波.
|
图 13 涡量及Lighthill声源的瞬时分布 Figure 13 Distribution of instantaneous vorticity magnitude and Lighthill acoustic source |
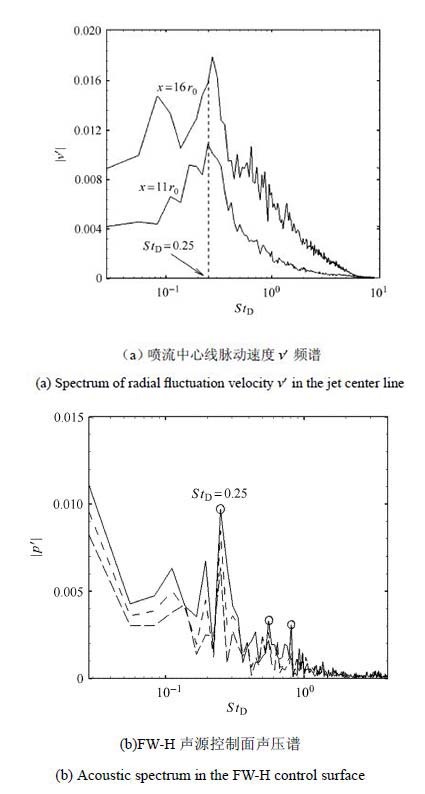
为建立远场声辐射与喷流近场声源联系,图 14给出喷流中心线上$x =11$和$x =16$两点的径向脉动速度$v'$频谱以分析流场脉动. 图中显示在势流核即将结束位置(11,0,0)处具有主导频率$St_{D}=0.25$,如图 13(a)虚线框1,该频率对应流向$x =9 \sim 15$区域内剪切层涡并现象. 主涡对并后剪切层内涡量累积,如13(b)虚线框2,导致涡结构在剪切层下游径向融合,并使得势流核终止. 图 14显示中下游(16,0,0)位置的主导频率较(11,0,0)处稍高,但占优特性仍较明显,这是由于该位置处不同频段扰动波增长趋向饱和,流动呈湍流化状态. 图 14(b)对FW-H声源控制面上距离势流核末端较近的 3个位置(10,7,0),(11.2,7,0),(12,7,0)进行声压频谱分析,获得的主导声辐射频率与势流核末端径向脉动速度频率一致,均为$St_{D}=0.25$. 这表明该占优声模态产生于势流核末端附近.
|
图 14 喷流流动和声辐射频谱 Figure 14 Spectrums of jet flow and its acoustic field |
利用频域FW-H声外推方法提取该主导声辐射模态,如图 15所示,清晰地展现了主导声波形成于势流核末端附近,最强辐射方位角在 $\alpha =30^{\circ}$附近.结合流场和声场特征频率相同,可确定剪切层涡并及涡量累积后大尺度拟序结构的径向融合形成了低频模态占优可辐射行波或波包,其对外辐射产生喷流中低方位角占优的主导声模态,且该声模态是高亚声速喷流超级指向性声辐射特征的主要原因. 此外,图 15(b)还展示了主导声模态在$x=16$流向站位的辐射情形,显示其在周向上具有分段指向性特征,表明对应的喷流声源波包具有三维结构特性.

|
图 15 喷流主导声模态($St_{\rm D}=0.25$) Figure 15 Dominate acoustic mode of the jet ($St_{\rm D}=0.25$) |
以高亚声速喷流为研究对象,利用高精度LES方法对其流场演化及噪声辐射特性进行了计算分析,主要获得以下结论:
(1) 仔细验证了喷流平均流和湍流脉动统计数据,确定了LES结果准确性;利用LES喷流声源数据结合可穿透面FW-H方法求解了喷流声远场,通过与文献中实验及计算结果对比,确认声远场计算精确,并再次证明LES求解获得喷流声源可靠.
(2) 对于低雷诺数高亚声速喷流,由于剪切层Kelvin-Helmhotz不稳定性特征,在强迫扰动下剪切层内的占优扰动快速发展饱和,促使剪切层形成大尺度涡环结构,涡环在向下游对流时螺旋扭曲并伴随涡辫等小尺度结构产生,加速涡结构对并及破碎.在势流核末端,涡环对并形成的大尺度拟序结构在喷流中心线沿径向融合,导致势流核终止并进入充分发展湍流区.
(3) 建立了喷流流场中大尺度拟序结构和远场主导声模态间的联系,并对主导声波的形成机制进行解释. 认为在势流核末端附近,剪切层主涡对并及在径向融合等演化形成了可辐射的低波数声源波包,产生的主导声模态在远场低方位角占优,构成强指向性声场,噪声峰值方位角约为$ 30^{\circ}$.
| 1 |
Lighthill MJ. On sound generated aerodynamically I. General theory.
Proc R Soc London A,1952, 211 (1107) : 564-587.
DOI: 10.1098/rspa.1952.0060. ( 0) 0)
|
| 2 |
Lighthill MJ. On sound generated aerodynamically II. Turbulence as a source of sound.
Proc R Soc London A,1954, 222 (1148) : 1-32.
DOI: 10.1098/rspa.1954.0049. ( 0) 0)
|
| 3 |
Kibens V. Discrete noise spectrum generated by an acoustically excited jet.
AIAA J,1980, 18 (4) : 434-441.
DOI: 10.2514/3.50776. ( 0) 0)
|
| 4 |
Laufer J, Yen T. Noise generation by a low-Mach-number jet.
J Fluid Mech,1983, 134 : 1-31.
DOI: 10.1017/S0022112083003195. ( 0) 0)
|
| 5 |
Chu WT, Kaplan RE. Use of a spherical concave reflector for jetnoise-source distribution diagnosis.
J Acoust Soc Am,1976, 59 (6) : 1268-1277.
DOI: 10.1121/1.381014. ( 0) 0)
|
| 6 |
Juvé D, Sunyach M, Comte-Bellot G. Intermittency of the noise emission in subsonic cold jets.
J Sound Vib,1980, 71 (3) : 319-332.
DOI: 10.1016/0022-460X(80)90416-2. ( 0) 0)
|
| 7 |
Tam CKW. Jet noise:Since 1952.
Theor Comp Fluid Dyn,1998, 10 : 393-405.
DOI: 10.1007/s001620050072. ( 0) 0)
|
| 8 |
Tam CKW, Golebiowski M, Seiner JM. On the two components of turbulent mixing noise from supersonic jets. AIAA Paper 1996-1716, 1996
( 0) 0)
|
| 9 |
Freund JB. Noise sources in a low-Reynold-number turbulent jet at Mach 0.9.
J Fluid Mech,2001, 439 : 277-305.
( 0) 0)
|
| 10 |
Stromberg JL, McLaughlin DK, Troutt TR. Flow field and acoustic properties of a Mach number 0.9 jet at a low Reynold number.
J Sound Vib,1980, 72 (2) : 159-176.
DOI: 10.1016/0022-460X(80)90650-1. ( 0) 0)
|
| 11 |
Bogey C, Bailly C, Juvé D. Noise investigation of a high subsonic, moderate Reynold number jet using a compressible LES.
Theor Comp Fluid Dyn,2003, 16 (4) : 273-297.
DOI: 10.1007/s00162-002-0079-4. ( 0) 0)
|
| 12 |
Bogey C, Bailly C. Investigation of subsonic jet noise using LES:Mach and Reynold number effects. AIAA Paper 2004-3023, 2004
( 0) 0)
|
| 13 |
Viswanathan K, Shur ML, Spalart PR, et al. Computation of the flow and noise of round and beveled nozzles. AIAA Paper 2006-2445, 2006
( 0) 0)
|
| 14 |
Goldstein ME. On identifying the true sources of aerodynamic sound.
J Fluid Mech,2005, 526 : 337-347.
DOI: 10.1017/S0022112004002885. ( 0) 0)
|
| 15 |
Jordan P, Colonius T. Wave packets and turbulent jet noise.
Annu Rev Fluid Mech,2013, 45 : 173-195.
DOI: 10.1146/annurev-fluid-011212-140756. ( 0) 0)
|
| 16 |
Obrist D. Directivity of acoustic emissions from wave packets to the far field.
J Fluid Mech,2009, 640 : 165-186.
DOI: 10.1017/S0022112009991297. ( 0) 0)
|
| 17 |
Tam CKW, Webb JC. Dispersion-relation-preserving finite difference schemes for computational acoustics.
J Comput Phys,1993, 107 (2) : 262-281.
DOI: 10.1006/jcph.1993.1142. ( 0) 0)
|
| 18 |
Tam CKW. Computational aeroacoustics:issues and methods.
AIAA J,1995, 33 (10) : 1788-1796.
DOI: 10.2514/3.12728. ( 0) 0)
|
| 19 |
Berland J, Bogey C, Bailly C. Optimized explicit schemes:matching and boundary schemes and 4 th-order Runge-Kutta algorithm. AIAA Paper 2004-2814, 2004
( 0) 0)
|
| 20 |
Bogey C, de Cacqueray N, Bailly C. A shock-capturing methodology based on adaptative spatial filtering for high-order non-linear computations.
J Comput Phys,2009, 228 (5) : 1447-1465.
DOI: 10.1016/j.jcp.2008.10.042. ( 0) 0)
|
| 21 |
Lyrintzis AS, Uzun A. Integral techniques for jet aeroacoustics calculations. AIAA Paper 2001-2253, 2001
( 0) 0)
|
| 22 |
Bogey C, Bailly C. Three-dimensional non-reflective boundary conditions for acoustic simulations:far field formulation and validation test cases.
Acta Acustica,2002, 88 (4) : 463-471.
( 0) 0)
|
| 23 |
Panchapakesan NR, Lumley JL. Turbulence measurements in axisymmetric jets of air and helium. Part I. Air jet.
J Fluid Mech,1993, 246 : 197-223.
DOI: 10.1017/S0022112093000096. ( 0) 0)
|
| 24 |
Hussein HJ, Capp SP, George WK. Velocity measurements in a high-Reynold-number, momentum-conserving, axisymmetric, turbulent jet.
J Fluid Mech,1994, 258 : 31-75.
DOI: 10.1017/S002211209400323X. ( 0) 0)
|
| 25 |
Bodony DJ, Lele SK. On using large-eddy simulation for the prediction of noise from cold and heated turbulent jets.
Phys. Fluids,2005, 17 (8) : 85-103.
( 0) 0)
|
| 26 |
Bogey C, Bailly C. LES of high Reynold, high subsonic jet:effects of the inflow conditions on flow and noise. AIAA Paper 2003-3170, 2003
( 0) 0)
|
| 27 |
Arakeri VH, Krothapalli A, Siddavaram V, et al. On the use of microjets to suppress turbulence in a Mach 0.9 axisymmetric jet.
J Fluid Mech,2003, 490 : 75-98.
DOI: 10.1017/S0022112003005202. ( 0) 0)
|
| 28 |
Lau JC, Morris PJ, Fisher MJ. Measurements in subsonic and supersonic free jets using a laser velocimeter.
J Fluid Mech,1979, 93 (1) : 1-27.
DOI: 10.1017/S0022112079001750. ( 0) 0)
|
| 29 |
Mollo-Christensen E, Kolpin MA, Martucelli JR. Experiments on jet flows and jet noise far-field spectra and directivity patterns.
J Fluid Mech,1964, 18 (2) : 285-301.
DOI: 10.1017/S0022112064000209. ( 0) 0)
|
| 30 |
Lush PA. Measurements of subsonic jet noise and comparison with theory.
J Fluid Mech,1971, 46 (3) : 477-500.
DOI: 10.1017/S002211207100065X. ( 0) 0)
|
 2016, Vol. 48
2016, Vol. 48
