2. 天津市现代工程力学重点实验室, 天津 300350
超疏水壁面(SH)是指液滴表观接触角大于150°且滚动角小于10°的固壁表面[1],由于表面微纳二级结构引起的超疏水特性,具有减阻和自清洁的功能,因而获得了很多领域研究者的广泛关注[2-3].自然界中有很多动植物表面都具有疏水性,例如荷叶表面[4],蝴蝶、蝉的翅膀表面等[5]. Neinhuis等[6]通过观察植物叶表面的微观结构发现,这种疏水性是由一定粗糙度表面上微米级突起以及纳米级蜡状物共同作用引起的.Cassie等[7]在研究物质表面时,提出了"空气垫模型",指出液滴与物质表面接触时并不是完全与物质表面直接接触,还有一部分是与表面微结构内部驻留气体形成的空气垫接触,使实际固液接触面积减小,导致表面摩擦阻力降低.Min等[8]对超疏水壁面湍流减阻的直接数值模拟结果表明,超疏水壁面可产生滑移,其中流向滑移有益于减阻,展向滑移不利于减阻. Aljallis等[9]通过对喷涂了疏水纳米颗粒的铝板和机翼模型进行外流减阻研究发现,超疏水壁面减阻除了依赖于表面的速度滑移之外还与其表面的结构特征和气膜稳定性相关.现在研究者多从超疏水微纳米二重结构[10-11]以及其壁面表观滑移[12-15]等方面认识超疏水壁面减阻机理,而容易忽视湍流中相干结构[16]对壁面阻力的影响.
相干结构对近壁区湍流和壁面摩擦阻力可产生重要影响[17],Kang等[18]和Kim等[19]分别从正反两方面证明壁面摩擦力有很大部分由发卡涡产生. 实验研究表明,湍流边界层中流-法向平面内除存在大量涡量为负的发卡涡展向涡头(顺向涡),还从一定的法向位置开始检测到涡量为正的逆向涡存在,其迁移速度与顺向涡相同,旋转方向相反[20].逆向涡的发现对发卡涡理论模型提出了挑战,Hambleton 等[21]通过立体粒子图像测速技术对平板湍流边界层中两种涡的相对位置关系进行了研究,发现顺向涡始终处于逆向涡的下游和上方,因此他们推断逆向涡可能是涡环结构或者
本文针对微纳米二级结构超疏水壁面,利用高时间分辨率粒子图像测速技术(time-resovled partical image velocimetry, TRPIV) 获得速度场,比较超疏水与亲水壁面(PH)的平均速度剖面,计算超疏水壁面减阻率.采用空间多尺度局部平均涡量的概念提取壁湍流中流-法向涡结构,研究两种壁面湍流边界层中顺向涡和逆向涡相对位置的差异以及逆向涡对顺向涡的影响,最后通过两种壁面湍流边界层中顺向涡和逆向涡数量对比结果来进一步验证逆向涡与超疏水壁面减阻的关系.
1 实验设备与参数实验在天津大学流体力学实验室低速循环式水槽中进行,调节水流的流速主要通过调节变频器控制的步进电机供水泵来实现,在0~50 Hz的频率范围内连续可调,实验段尺寸为530 cm × 25 cm × 38 cm.实验模型包括一块尺寸为240 cm × 38 cm × 1.5 cm的有机玻璃大平板,以及两块可镶嵌到大平板方槽中的亲水平板和超疏水平板(28 cm × 28 cm × 1.5 cm),方槽距大平板前缘190 cm.平板与水槽底面平行放置并固定于水槽中心线,前端为8:1半椭圆修形,在距前缘8 cm位置加拌线以获得充分发展的湍流边界层.实验中用到的微纳二重结构超疏水板由清华大学姚朝晖课题组[23]制作,其接触角为161°,滚动角为0.9°.
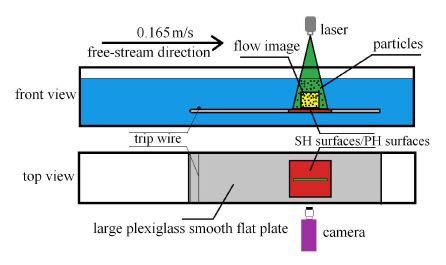
TRPIV 系统是基于PIV原理的高时间分辨率粒子图像测速技术,它拥有高速CCD相机以及高频脉冲激光器.实验中激光片光源、 高速CCD相机及平板的相对布置情况如图 1所示. 示踪粒子为直径20 μm的空心玻璃微珠,粒子密度为1.03 g/cm3.水槽中自由来流速度保持在0.165 m/s,经测量水温为21℃,此时水的密度和动力黏度分别为998 kg/m3,1.003 × 10-3 kg/(m·s),水槽来流的背景湍流度小于0.7%.所用相机的采样频率为500 Hz,脉冲时间间隔2 000 μs,单帧曝光时间1 500 μs,每种壁面结果记录6 547张图像(像素为1 280×1 024).对原始图像采用互相关算法进行处理,图像视野实际大小56.6 mm × 45.1 mm(流向×法向),查询窗口像素设置为32×32,窗口重叠率为75%,得到的瞬时速度场中具有157×125(流向×法向)个速度矢量,对应流向和法向相邻矢量之间的实际距离为0.36 mm.
|
图 1 实验装置图 Figure 1 Experimental facility diagram |
对实验结果进行处理得到湍流边界层的平均壁面摩擦速度
|
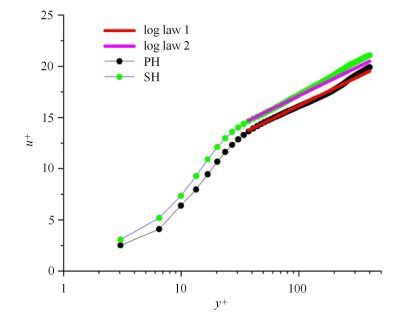
图 2 平均速度剖面 Figure 2 Average velocity distribution profile |
|
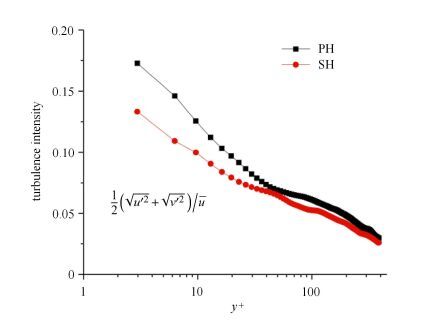
图 3 湍流度对比 Figure 3 Comparison of turbulence intensity |
为了研究超疏水壁面对湍流边界层中相干结构的影响,需要从瞬时速度场中识别提取大尺度展向涡结构[24],因此,准确识别涡心和排除小尺度涡的干扰是需首要解决的问题.本文利用空间多尺度局部平均涡量[25]的概念来提取完整的展向涡结构. 流场中xy平面中一点的展向涡量为
| $\begin{align} & \overline{\omega \left( {{x}_{0}},{{y}_{0}},{{l}_{x}},{{l}_{y}} \right)}=\delta {{v}_{x}}\left( {{x}_{0}},{{y}_{0}},{{l}_{x}} \right)- \\ & \delta {{u}_{x}}\left( {{x}_{0}},{{y}_{0}},{{l}_{y}} \right) \\ \end{align}$ | (1) |
其中
| $ \delta v_x \left( {x_0 ,y_0 ,l_x } \right) = \overline {{ v}\left( {x_0 + x,y_0 } \right)} _{x \in \left[{0,l_x } \right]} - \overline {{ v}\left( {x_0 - x,y_0 } \right)} _{x \in \left[{0,l_x } \right]} $ | (2) |
| $\delta u_y \left( {x_0 ,y_0 ,l_y } \right) = \overline {{ u}\left( {x_0 ,y_0 + y} \right)} _{y \in \left[{0,l_y } \right]} - \overline {{ u}\left( {x_0 ,y_0 -y} \right)} _{y \in \left[{0,l_y } \right]} $ | (3) |
式中,u ,v分别表示流向法向的脉动速度矢量,
湍流边界层中存在大量发卡涡以及发卡涡包,因此可在xy平面检测出大量发卡涡展向涡头,本文检测了流场中发卡涡展向涡头的中心,即
| $\begin{align} & {{D}_{1}}\left( x,y \right)= \\ & \left\{ \begin{array}{*{35}{l}} 1,\left\{ \begin{array}{*{35}{l}} \overline{\omega \left( x,y \right)}<0 \\ \overline{\omega \left( x-1,y \right)}>\overline{\omega \left( x,y \right)}\And \overline{\omega \left( x+1,y \right)}>\overline{\omega \left( x,y \right)} \\ \overline{\omega \left( x,y-1 \right)}>\overline{\omega \left( x,y \right)}\And \overline{\omega \left( x,y+1 \right)}>\overline{\omega \left( x,y \right)} \\ \end{array} \right. \\ 0,\text{otherwise} \\ \end{array} \right. \\ \end{align}$ | (4) |
| $\begin{align} & {{D}_{2}}\left( x,y \right)= \\ & \left\{ \begin{array}{*{35}{l}} 1,\left\{ \begin{array}{*{35}{l}} \overline{\omega \left( x,y \right)}>0 \\ \overline{\omega \left( x-1,y \right)}<\overline{\omega \left( x,y \right)}\And \overline{\omega \left( x+1,y \right)}\text{ }<\overline{\omega \left( x,y \right)}\text{ } \\ \overline{\omega \left( x,y-1 \right)}<\overline{\omega \left( x,y \right)}\And \overline{\omega \left( x,y+1 \right)}<\overline{\omega \left( x,y \right)} \\ \end{array} \right. \\ 0,\text{otherwise} \\ \end{array} \right. \\ \end{align}$ | (5) |
其中,
| $f\left( {{x}_{L}},{{y}_{L}} \right)=\frac{1}{N}\sum\limits_{m=1}^{N}{f}\left( {{x}^{*}}\left( m \right)+{{x}_{L}},{{y}^{*}}\left( m \right)+{{y}_{L}} \right)$ | (6) |
式中,
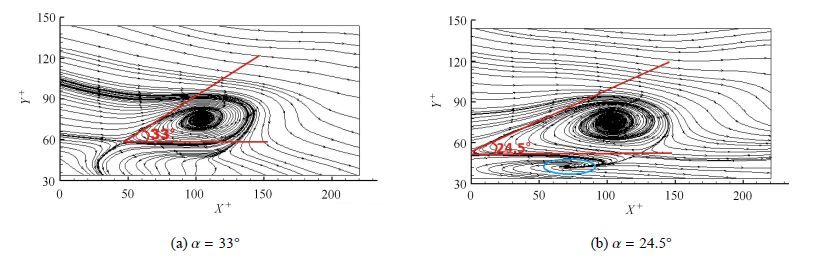
图 4(a)和图 4(b)分别为亲水壁面与超疏水壁面发卡涡在$x y$ 平面检测到的展向涡头结构[27].速度滞止点在流线场中呈现鞍点结构,处于展向涡头上游剪切层上,涡核表现为焦点结构,流线呈螺旋线结构顺时针旋转.由Elsinga等[28]的观点可知,展向涡头的法向尺度随着壁面法向距离的增加而变大,展向涡头由椭圆形涡逐渐发展为圆形涡,发展的更为完整.因此,用过鞍点的剪切线(与上方剪切层相切)与水平方向的夹角表示发卡涡展向涡头发展的充分性,用α角来表示.Tian等[29]同样通过TRPIV实验方法得到结论:在两种壁面中,α角随着法向位置的增高而增大,在相同法向高度,超疏水壁面α角均小于对应亲水壁面,说明了超疏水壁面发卡涡的发展受到抑制. 图 4为在Y+=75.0处顺向涡涡心的检测结果,图中显示,超疏水壁面α角为24.5°,而在同一法向位置亲水壁面为 33°,明显大于超疏水壁面. 仔细观察图 4(b)可以发现,在超疏水壁面展向涡的左下方有一个相对较小的逆向涡(由蓝色椭圆标志,逆时针旋转),正是逆向涡的上剪切层与顺向涡的下剪切层相互作用,使顺向涡的流向尺度拉伸,抑制法向尺度的成长,使超疏水壁面α角明显小于亲水壁面,证明逆向涡的出现可阻碍发卡涡的进一步增强.逆向涡与展向涡的这种相互作用使逆向涡具有进一步研究的意义.
|
图 4 展向涡周围流线分布图(左:亲水壁面,右:超疏水壁面) Figure 4 Distributions of streamline around spanwise vortex (left:PH,right:SH) |
逆向涡是由低速条带与其下方较为快速的流体相互剪切所产生,必须在顺向发卡涡头离开壁面一定远的距离下才会产生.
3.2.1 亲水和超疏水两种壁面顺向涡和逆向涡相对位置的对比本节针对一对顺向涡和逆向涡位置关系在亲水和超疏水两种壁面相同法向高度进行对比研究,观察涡结构的内部特征.图 5为亲水、超疏水壁面在不同法向位置提取到的逆向涡结果(逆向涡涡心的检测位置依次为Y+=58.0,Y+=61.5,Y+=65.0).与提取顺向涡(图 4)相比,顺向涡和逆向涡相对位置更加明显,这是由于顺向涡数量远大于逆向涡所致. 图 5中,提取的逆向涡右上方始终存在一个顺向涡,但是因为检测区域是以逆向涡涡心为中心叠加而获得,而顺向涡相对逆向涡位置会有一定的变化,所以同时提取到的顺向涡会表现出不完整性.

|
图 5 顺向涡和逆向涡相对位置(左:亲水壁面,右:超疏水壁面) Figure 5 Clockwise and retrograde vortex relative position (left:PH,right:SH) |
虽然提取到的顺向涡不完整,但是获得的顺向涡涡心仍然含有其位置统计量信息,可用来研究顺向涡和逆向涡相对位置关系.图 5中逆向涡始终处于顺向涡的左下方,再次验证了逆向涡是涡环结构或者
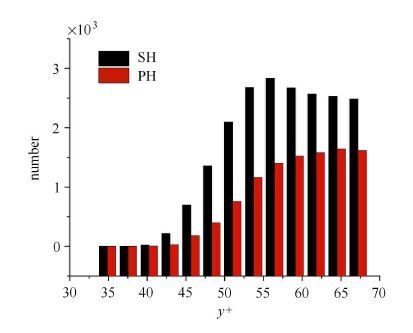
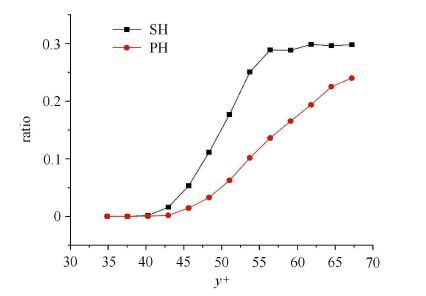
图 6为检测到的亲水和超疏水两种壁面上逆向涡数目沿法向分布规律,由图 6可知,在对数区的内边界以下(y+<40),没有逆向涡的存在,但在边界层外区(y+>50),逆向涡的数量逐渐增加并趋于稳定.图 7表示两种壁面上的逆向涡和顺向涡数目比沿法向分布规律,由图可知,亲水和超疏水两种壁面逆向涡与顺向涡数目比都在随着法向距离的增加而增大,分别达到了0.30 (SH)和0.24 (PH),但是超疏水壁面二者的比值始终大于亲水壁面,这表明,阻力小的超疏水壁面逆向涡出现概率更大. 结合上文中逆向涡对顺向涡抑制的结论可知:更多逆向涡的出现有助于减阻的发生.
|
图 6 逆向涡数目沿法向分布规律 Figure 6 Distributions of the number of retrograde vortex along normal-wall positions |
|
图 7 逆向涡和顺向涡数目比沿法向分布规律 Figure 7 Distributions of the ratio of retrograde vortex along ormal-wall positions |
本文利用高时间分辨率粒子图像测速技术分别对超疏水和亲水壁面的平板湍流边界层瞬时速度场进行测量,得到超疏水壁面在雷诺数
| 1 |
Bhushan B, Yong CJ, Koch K. Micro-, nano-and hierarchical structures for superhydrophobicity, self-cleaning and low adhesion.
Philosophical Transactions,2009, 367 (1894) : 1631-1672.
DOI: 10.1098/rsta.2009.0014. ( 0) 0)
|
| 2 |
胡海豹, 黄苏和, 宋保维, 等. 疏水微形貌表面水下减阻研究进展.
船舶力学,2015, 19 (8) : 1011-1022.
( Hu Haibao, Huang Suhe, Song Baowei, et al. Recent development about drag reduction on hydrophobic micro-structured surfaces.
Journal of Ship Mechanics,2015, 19 (8) : 1011-1022.
(in Chinese) ) ( 0) 0)
|
| 3 |
Waqner P, Furstner R, Barthlott W, et al. Quantitative assessment to the structural basis of water repellency in natural and technical surfaces.
Exp Bot,2003, 54 : 1295-1303.
DOI: 10.1093/jxb/erg127. ( 0) 0)
|
| 4 |
Barthlott W, Neinhuis C. Purity of the sacred lotus, or escape from contamination in biological surfaces.
Planta,1997, 202 (1) : 1-8.
DOI: 10.1007/s004250050096. ( 0) 0)
|
| 5 |
Feng L, Li SH, Li YS, et al. Super-hydrophobic surfaces:from natural to artificial.
Advanced Materials,2002, 14 (24) : 1857-1860.
DOI: 10.1002/adma.200290020. ( 0) 0)
|
| 6 |
Neinhuis C, Barthlott W. Characterization and distribution of waterrepellent, self-cleaning plant surfaces.
Annals of Botany,1997, 79 (6) : 667-677.
DOI: 10.1006/anbo.1997.0400. ( 0) 0)
|
| 7 |
Cassie ABD, Baxter S. Wettability of porous surfaces.
Transactions of the Faraday Society,1944, 40 : 546-551.
DOI: 10.1039/tf9444000546. ( 0) 0)
|
| 8 |
Min T, Kim J. Effects of hydrophobic surface on skin-friction drag.
Physics of Fluids,2004, 16 (7) : L55-L58.
DOI: 10.1063/1.1755723. ( 0) 0)
|
| 9 |
Aljallis E, Sarshar MA, Datla R, et al. Experimental study of skin friction drag reduction on superhydrophobic flat plates in high Reynolds number boundary layer flow.
Physics of Fluids,2013, 25 (2) : 025103-025114.
DOI: 10.1063/1.4791602. ( 0) 0)
|
| 10 |
张静娴, 姚朝晖, 郝鹏飞, 等. 复合超疏水表面制备及其上液滴运动特性研究.
应用数学和力学,2014, 35 (3) : 322-330.
( Zhang Jingxian, Yao Zhaohui, Hao Pengfei, et al. Study of preparation and dynamic hydrophobicity of superhydrophobic surfaces with micronano textures.
Applied Mathematics & Mechanics,2014, 35 (3) : 322-330.
(in Chinese) ) ( 0) 0)
|
| 11 |
Bhushan B, Jung YC, Koch K. Micro-, nano-and hierarchical structures for superhydrophobicity, self-cleaning and low adhesion.
Philosophical Transactions of the Royal Society of London A:Mathematical, Physical and Engineering Sciences,2009, 367 (1894) : 1631-1672.
DOI: 10.1098/rsta.2009.0014. ( 0) 0)
|
| 12 |
张雪花, 胡钧. 固液界面纳米气泡的研究进展.
化学进展,2004, 16 (5) : 673-681.
( Zhang Xuehua, Hu Jun. Nanobubbles at the solid/water interface.
Progress in Chemistry,2004, 16 (5) : 673-681.
(in Chinese) ) ( 0) 0)
|
| 13 |
Lum K, Chandler D, Weeks J D. Hydrophobicity at small and large length Scales.
The Journal of Physical Chemistry B,1999, 103 (22) : 4570-4577.
DOI: 10.1021/jp984327m. ( 0) 0)
|
| 14 |
Martell MB, Rothstein JP, Perot JB. An analysis of superhydrophobic turbulent drag reduction mechanisms using direct numerical simulation.
Physics of Fluids,2010, 22 (6) : 065102-065113.
DOI: 10.1063/1.3432514. ( 0) 0)
|
| 15 |
王新亮, 狄勤丰, 张任良, 等. 超疏水表面滑移理论及其减阻应用研究进展.
力学进展,2010, 40 (3) : 241-249.
( Wang Xinliang, Di Qinfeng, Zhang Renliang, et al. Progress in theories of superhydrophobic surface slip effect and its application to drag reduction technology.
Advances in Mechanics,2010, 40 (3) : 241-249.
(in Chinese) ) ( 0) 0)
|
| 16 |
Yang SQ, Jiang N. Tomographic TR-PIV measurement of coherent structure spatial topology utilizing an improved quadrant splitting method.
Science China Physics Mechanics & Astronomy,2012, 55 (10) : 1863-1872.
( 0) 0)
|
| 17 |
许春晓. 壁湍流相干结构和减阻控制机理.
力学进展,2015, 45 (1) : 111-140.
( Xu Chunxiao. Coherent structures and drag-reduction mechanism in wall turbulence.
Advances in Mechanics,2015, 45 (1) : 111-140.
(in Chinese) ) ( 0) 0)
|
| 18 |
Kang YD, Choi KS, Chun HH. Direct intervention of hairpin structures for turbulent boundary-layer control.
Physics of Fluids,2008, 20 (10) : 561-570.
( 0) 0)
|
| 19 |
Kim K, Adrian RJ, Balachandar S, et al. Dynamics of hairpin vortices and polymer-induced turbulent drag reduction.
Physical Review Letters,2008, 100 (13) : 3182-3186.
( 0) 0)
|
| 20 |
刘璐璐, 张军, 姚志崇等. 湍流边界层反向涡结构的数值分析研究.//吴有生, 唐洪武, 王超编. 第二十七届全国水动力学研讨会文集,南京,2015-11-06. 上海:海洋出版社,2015. 40-46
( Liu Lulu, Zhang Jun, Yao Zhichong, et al. Numerical analysis of retrograde spanwise vortices in turbulent boundary layer.//Wu Yousheng, Tang Hongwu, Wang Chao. In:Proceedings of the 27th National conference on Hydrodynamics. Nanjing, 2015-11-06. Shanghai:China Ocean Press, 2015. 40-46(in Chinese)
) ( 0) 0)
|
| 21 |
Hambleton WT, Hutchins N, Marusic I. Simultaneous orthogonalplane particle image velocimetry measurements in a turbulent boundary layer.
Journal of Fluid Mechanics,2006, 560 : 53-64.
DOI: 10.1017/S0022112006000292. ( 0) 0)
|
| 22 |
Yang W, Meng H, Sheng J. Dynamics of hairpin vortices generated by a mixing tab in a channel flow.
Experiments in Fluids,2001, 30 (6) : 705-722.
DOI: 10.1007/s003480000252. ( 0) 0)
|
| 23 |
郝鹏飞, 汪幸愉, 姚朝晖, 等. 疏水微槽道内层流减阻的实验研究.
实验流体力学,2009, 23 (3) : 7-11.
( Hao Pengfei, Wang Xingyu, Yao Chaohui, et al. Experimental study on laminar drag reduction in micro-channels with Superhydrophobic surfaces.
Journal of Experiments in Fluid Mechanics,2009, 23 (3) : 7-11.
(in Chinese) ) ( 0) 0)
|
| 24 |
Wu Y, Christensen KT. Population trends of spanwise vortices in wall turbulence.
Journal of Fluid Mechanics,2006, 568 (10) : 55-76.
( 0) 0)
|
| 25 |
姜楠, 管新蕾, 于培宁. 雷诺应力各向异性涡黏模型的层析TRPIV测量.
力学学报,2012, 44 (2) : 213-221.
( Jiang Nan, Guan Xinlei, Yu Peining. Tomographic TRPIV measurement of anisotropic eddy-viscosity model for coherent structure Reynolds stress.
Chinese Journal of Theoretical and Applied Mechanics,2012, 44 (2) : 213-221.
(in Chinese) ) ( 0) 0)
|
| 26 |
姜楠, 于培宁, 管新蕾. 湍流边界层相干结构空间拓扑形态的层析TRPIV测量.
航空动力学报,2012, 27 (5) : 1113-1121.
( Jiang Nan, Yu Peining, Guan Xinlei. Tomo-TRPIV measurement of coherent structure spatial topology in turbulent boundary layer.
Journal of Aerospace Power,2012, 27 (5) : 1113-1121.
(in Chinese) ) ( 0) 0)
|
| 27 |
Adrian RJ, Meinhart CD, Tomkins CD. Vortex organization in the outer region of the turbulent boundary layer.
Journal of Fluid Mechanics,2000, 422 (13) : 1-54.
( 0) 0)
|
| 28 |
Elsinga GE, Marusic I. Evolution and lifetimes of flow topology in a turbulent boundary layer.
Physics of Fluids,2009, 22 (1) : 96-102.
( 0) 0)
|
| 29 |
Tian HP, Zhang JX, Jiang N, et al. Effect of hierarchical structured superhydrophobic surfaces on coherent structures in turbulent channel flow.
Experimental Thermal and Fluid Science,2015, 69 : 27-37.
DOI: 10.1016/j.expthermflusci.2015.07.018. ( 0) 0)
|
| 30 |
Kim HT, Kline SJ, Reynolds WC. The production of turbulence near a smooth wall in a turbulent boundary layer.
Journal of Fluid Mechanics,1971, 50 (1) : 133-160.
DOI: 10.1017/S0022112071002490. ( 0) 0)
|
| 31 |
Adrian RJ, Meinhart CD, Tomkins CD. Vortex organization in the outer region of the turbulent boundary layer.
Journal of Fluid Mechanics,2000, 422 (13) : 1-54.
( 0) 0)
|
2. Tianjin Key Laboratory of Modern Engineering Mechanics, Tianjin 300350, China
 2016, Vol. 48
2016, Vol. 48
