2. 中国飞行试验研究院飞机所, 西安 710089
灵敏度分析主要研究的是:模型的输出不确定性是如何分配到输入不确定性的[1].灵敏度主要分为:局部灵敏度[2-3]和全局灵敏度[4].局部灵敏度定义为:输入变量取名义值时功能函数的偏导数,其无法提供输入变量在整个取值范围内的综合灵敏度信息.全局灵敏度以其能够反映输入变量在其整个分布范围的不确定性对输出响应不确定性的影响而被广为应用.目前,全局灵敏度的分析模型主要分为3类:非参模型(相关系数模型)[5-6]、基于方差的模型[7-10]和矩独立模型[11-14].非参模型无法解决非线性模型,并且对于输入变量的高阶交叉影响项也无法提供充足的灵敏度信息,因此不具有"模型独立性".基于方差的灵敏度指标从输入输出函数关系的角度直接给出了输入变量对功能函数输出方差的贡献,其满足"全局性、可量化性及模型独立性".然而,方差仅是输出不确定性的一部分信息,其不能从整个分布的角度衡量输入变量的重要性信息.基于此,Borgonovo和Apostolakis[2]提出了矩独立全局灵敏度指标,其从输出整个分布的角度考虑了输入变量的重要性,该指标在满足基于方差的灵敏度指标所具有的"全局性、可量化性及模型独立性"的基础上同时也满足"矩独立性".在Borgonovo和Apostolakis[2] 提出的矩独立全局灵敏度的基础上,Cui等[15]提出了基于失效概率的矩独立全局灵敏度指标,其主要衡量的是输入变量的不确定性对结构系统失效概率影响的大小.Li等[16]随后建立了失效概率矩独立全局灵敏度指标与方差全局灵敏度指标的关系.然而,如何高效准确地计算该指标,仍亟待解决.
目前计算该指标的方法分为两类:基于代理模型的方法[16-17]和基于数字模拟的方法[18].本文主要致力于研究高效准确的数字模拟法. 在基于数字模拟的方法中,Wei等[18]提出了单层Monte Carlo 模拟法(MCS)、重要抽样法及截断重要抽样法3种计算该指标的方法,虽然重要抽样法及截断重要抽样法的计算效率远高于MCS,但是其计算量依然与维数呈线性相关.本文为了解决失效概率矩独立全局灵敏度指标计算中的维数相关性,将空间分割[19-20]及重要抽样的思想相结合,选择密度中心在设计点处的密度函数作为重要抽样密度函数,通过重要抽样使得样本落入失效域的概率增加,以此来获得高的抽样效率和快的收敛速度;再通过对重要抽样得到的样本空间进行不同的划分从而近似估计各个输入变量的失效概率矩独立全局灵敏度指标值.本文所提方法大大提高了样本的利用率,并且计算量与输入变量的维数无关.通过工程算例的计算结果,可以看出本文所提方法在计算精度及收敛速度方面都远高于Wei等[9]提出的单层MCS以及重要抽样法.
1 基于失效概率的矩独立全局灵敏度指标的
对于可靠性模型
| ${I_F}(X) = \left\{ {\matrix{ {1,X \in F} \cr {0,X \notin F} \cr } } \right.$ | (1) |
式中,
| ${P_{{f_Y}}} = \int_{{R^n}} {{I_F}} (x){f_X}(x){\rm{d}}x = \int_F {{f_X}} (x){\rm{d}}x$ | (2) |
其中
为更好地分析输入变量在其分布范围内变化时对结构系统失效概率的影响程度,Cui等[15]定义了基于失效概率的矩独立全局灵敏度指标
| $ \delta _i^P = E_{X_i } \left( {P_{f_Y } - P_{f_{Y | X_i } } } \right)^2 =\\ \int_{ - \infty }^{ + \infty } {\left( {P_{f_Y } - P_{f_{Y| X_i } } } \right)^2f_{X_i } (x_i ) d x_i } $ | (3) |
其中
Li等[16]证明了
| $ \delta _i^P = V_{X_i } (E_{{ X}_{ - i} } (I_{ F} | X_i )) $ | (4) |
Wei等[18]通过添加
| $ S_i = \dfrac{V_{X_i } (E_{{ X}_{ - i} } (I_{ F} | X_i )}{V(I_{ F} )} $ | (5) |
通过求解式(5)所示的指标,可以确定影响失效概率的重要变量,从而控制重要变量的不确定性,以达到最大程度地降低结构或系统失效概率的目的.
2 基于空间分割和重要抽样的Si计算新方法 2.1 基于空间分割的Si近似计算公式
本节首先利用文献[20]中的方法,给出失效概率矩独立全局灵敏度指标的近似计算公式;然后证明在有限连续不重叠区间划分基础上的全期望和全方差公式;在该全方差公式的基础上将
| $ { E}_{X_i } (V_{{ X}_{ - i} } (I_{ F} | X_i )) =\\ \sum_{k = 1}^s {p_k (V(I_{ F} | X_i \in A_k ) - V_{X_i } (E(I_{ F} | X_i } ) | X_i \in A_k )) =\\ E_{A_k } (V(I_{ F} | X_i \in A_k )) - \sum_{k = 1}^s {p_k } V_{X_i } (E(I_{ F} | X_i ) | X_i \in A_k ) $ | (6) |
其中,
| $ S_i = \dfrac{V_{X_i } (E_{{ X}_{ - i} } (I_{ F} | X_i ))}{V(I_{ F} )} =\\ 1 - \dfrac{E_{X_i } (V_{{ X}_{ - i} } (I_{ F} | X_i ))}{V(I_{ F} )} \approx 1 - \dfrac{E_{A_k } (V(I_{ F} | X_i \in A_k ))}{V(I_{ F} )} $ | (7) |
式(7)虽然使得求解所有变量的
在输入变量相互独立时将
| $\eqalign{ & E({I_F}|{X_i} \in {A_k}) = \cr & \int_{ - \infty }^{ + \infty } {\int_{ - \infty }^{ + \infty } \cdots } \int_{{a_{k - 1}}}^{{a_k}} {{I_F}} (x)f_X^ * (x)d{x_i}\prod\limits_{j = 1,jei}^n d {x_j} \cr} $ | (8) |
其中,
| $ f_{ X}^\ast ({ x}) = \left\{ \begin{array}{cl} \dfrac{f_{ X} ({ x})}{\int_{a_{k - 1} }^{a_k } f_{X_i } (x_i ) d x_i } ,& x_i \in [a_{k - 1} ,a_k] \\ 0 ,& x_i otin [a_{k - 1} ,a_k] \end{array} \right. $ | (9) |
因此,将式(9)代入到式(8)中得
| $\eqalign{ & E({I_F}|{X_i} \in {A_k}) = {1 \over {\int_{{a_{k - 1}}}^{{a_k}} {{f_{{X_i}}}} ({x_i})d{x_i}}} \cdot \cr & \int_{ - \infty }^{ + \infty } {\int_{ - \infty }^{ + \infty } \cdots } \int_{{a_{k - 1}}}^{{a_k}} {{I_F}} (x){f_X}(x)d{x_i}\prod\limits_{j = 1,jei}^n d {x_j} \cr} $ | (10) |
由于
| $\eqalign{ & {E_{{A_k}}}(E({I_F}|{X_i} \in {A_k})) = \cr & \sum\limits_{k = 1}^s {P\{ {X_i} \in {A_k}\} \cdot E({I_F}|{X_i} \in {A_k})} = \cr & \sum\limits_{k = 1}^s {\int_{{a_{k - 1}}}^{{a_k}} {{f_{{X_i}}}({x_i})d{x_i} \cdot {1 \over {\int_{{a_{k - 1}}}^{{a_k}} {{f_{{X_i}}}} ({x_i})d{x_i}}}} } \cdot \cr & \int_{ - \infty }^{ + \infty } {\int_{ - \infty }^{ + \infty } { \cdots \int_{{a_{k - 1}}}^{{a_k}} {{I_F}(x){f_X}(x)d{x_i}} \prod\limits_{j = 1,jei}^n {d{x_j}} } } = \cr & \sum\limits_{k = 1}^s {\int_{ - \infty }^{ + \infty } {\int_{ - \infty }^{ + \infty } { \cdots \int_{{a_{k - 1}}}^{{a_k}} {{I_F}(x){f_X}(x)d{x_i}} } } } \prod\limits_{j = 1,jei}^n {d{x_j}} = \cr & \int_{ - \infty }^{ + \infty } {\int_{ - \infty }^{ + \infty } { \cdots \int_{{b_1}}^{{b_2}} {{I_F}(x){f_X}(x)} } } dx = E({I_F}) \cr} $ | (11) |
式(11)证明了在连续区间上的全期望公式,即
| $ V_{A_k } (E(I_{ F} | X_i \in A_k )) =\\ E_{A_k } (E^2(I_{ F} | X_i \in A_k )) - E_{A_k }^2 (E(I_{ F} | X_i \in A_k ))= \\ E_{A_k } (E^2(I_{ F} | X_i \in A_k )) - E^2(I_{ F} ) $ | (12) |
| $ E_{A_k } (V(I_{ F} | X_i \in A_k )) =\\ E_{A_k } (E(I_{ F}^2 | X_i \in A_k ) - E^2(I_{ F} | X_i \in A_k )) =\\ E(I_{ F} ^2) - E_{A_k } (E^2(I_{ F} | X_i \in A_k )) $ | (13) |
将式(12)与式(13)相加得
| $ E_{A_k } (V(I_{ F} | X_i \in A_k ) + V_{A_k } (E(I_{ F} | X_i \in A_k )) = V(I_{ F} ) $ | (14) |
基于式(14)的连续区间上的全方差公式,对式(7)的近似式进行等价变形如下
| $ S_i \approx 1 - \dfrac{E_{A_k } (V(I_{ F} | X_i \in A_k ))}{V(I_{ F} )} =\\ 1 - \dfrac{V(I_{ F} ) - V_{A_k } (E(I_{ F} | X_i \in A_k ))}{V(I_{ F} )} =\\ \dfrac{V_{A_k } (E(I_{ F} | X_i \in A_k ))}{V(I_{ F} )} $ | (15) |
由式(15)可知原始近似计算式中的二阶条件矩
失效概率矩独立全局灵敏度指标的空间分割方法计算中的抽样与方差灵敏度指标的空间分割方法中的抽样要求是不同的,前者要求尽可能多的样本点落入到失效域中,然而,一般的简单随机抽样,低偏差抽样是难以满足的. 因此,本文将重要抽样与空间分割结合,利用重要抽样[22-26]将抽样中心平移到设计点处,使得抽取出的样本以较大的概率落入失效域而加快计算的收敛速度,再通过空间分割,重复利用重要抽样所产生的样本,计算得到所有变量的灵敏度指标. 重要抽样结合空间分割计算失效概率矩独立全局灵敏度指标的推导如下
| $\eqalign{ & E({I_F}|{X_i} \in {A_k}) = \int_{{A_k}} {{I_F}} (x){{{f_X}(x)} \over {\int_{{A_k}} {{f_{{X_i}}}} ({x_i})d{x_i}}}dx = \cr & \int_{{A_k}} {{I_F}} (x) \cdot {{{f_X}(x)} \over {\int_{{A_k}} {{f_{{X_i}}}} ({x_i})d{x_i}}} \cdot \cr & {{\int_{{A_k}} {{H_{{X_i}}}} ({x_i})d{x_i}} \over {{H_X}(x)}} \cdot {{{H_X}(x)} \over {\int_{{A_k}} {{H_{{X_i}}}} ({x_i})d{x_i}}}dx = \cr & {{\int_{{A_k}} {{H_{{X_i}}}} ({x_i})d{x_i}} \over {\int_{{A_k}} {{f_{{X_i}}}} ({x_i})d{x_i}}} \cdot \int_{{A_k}} {{I_F}} (x){{{f_X}(x)} \over {{H_X}(x)}} \cdot \cr & {{{H_X}(x)} \over {\int_{{A_k}} {{H_{{X_i}}}} ({x_i})d{x_i}}}dx = \cr & {{\int_{{A_k}} {{H_{{X_i}}}} ({x_i})d{x_i}} \over {\int_{{A_k}} {{f_{{X_i}}}} ({x_i})d{x_i}}} \cdot {E_{{A_k}|H_X^*(x)}}[{I_F}(x){{{f_X}(x)} \over {{H_X}(x)}}] \cr} $ | (16) |
其中
| $\eqalign{ & H_X^ * (x) = \left\{ {\matrix{ {{{{H_X}(x)} \over {\int_{{A_k}} {{H_{{X_i}}}} ({x_i})d{x_i}}},} \hfill & {{x_i} \in {A_k}} \hfill \cr {0,} \hfill & {{x_i}otin{A_k}} \hfill \cr } } \right. \cr & {E_{{A_k}}}(E({I_F}|{X_i} \in {A_k})) = \cr & \sum\limits_{k = 1}^s {P\{ {X_i} \in {A_k}} \} \cdot E({I_F}|{X_i} \in {A_k}) = \cr & \sum\limits_{k = 1}^s {\int_{{A_k}} {{f_{{X_i}}}({x_i})d{x_i}} } \cdot {{\int_{{A_k}} {{H_{{X_i}}}({x_i})d{x_i}} } \over {\int_{{A_k}} {{f_{{X_i}}}({x_i})d{x_i}} }} \cdot \cr & {E_{{A_k}|H_X^ * (x)}}\left[ {{I_F}(x){{{f_X}(x)} \over {{H_X}(x)}}} \right] = \cr & \sum\limits_{k = 1}^s {\int_{{A_k}} {{H_{{X_i}}}({x_i})d{x_i}} } \cdot {E_{{A_k}|H_X^ * (x)}}\left[ {{I_F}(x){{{f_X}(x)} \over {{H_X}(x)}}} \right] \cr} $ | (17) |
| $\eqalign{ & {V_{{A_k}}}(E({I_F}|{X_i} \in {A_k})) = \sum\limits_{k = 1}^s {\int_{{A_k}} {{f_{{X_i}}}({x_i})d{x_i}} } \cdot \cr & {\left( {E({I_F}|{X_i} \in {A_k}) - {E_{{A_k}}}(E({I_F}|{X_i} \in {A_k}))} \right)^2} \cr} $ | (18) |
通过式(16)
第一步:采用改进的一次二阶矩方法计算出最可能失效点(设计点)
| $ { A} = \left[\!\!\begin{array}{cccc} {x_1^{(1)} } & {x_2^{(1)} } & \cdots & {x_n^{(1)} } \\ {x_1^{(2)} } & {x_2^{(2)} } & \cdots & {x_n^{(2)} } \\ \vdots & \vdots & \ddots & \vdots \\ {x_1^{(N)} } & {x_2^{(N)} } & \cdots & {x_n^{(N)} } \end{array} \!\! \right]$ | (19) |
第二步:依据失效域指示函数
第三步:等样本数连续地将
| $ P_{X_i }^H (A_k ) = \int_{a_{k - 1} }^{a_k } {H_{X_i } (x_i )d x_i } $ | (20) |
| $P_{{X_i}}^f({A_k}) = \int_{{a_{k - 1}}}^{{a_k}} {{f_{{X_i}}}({x_i})d{x_i}} $ | (21) |
根据
| $ B_k = \{I_{ F} | X_i \in A_k \} ,1 ≤ k ≤ s$ | (22) |
那么
| $ E_{A_k | H_{ X}^\ast ({ x})} \left[{I_{ F} ({ x})\dfrac{f_{ X} ({ x})}{H_{ X} ({ x})}} \right] = E\left( {B_k \cdot \dfrac{f_{ X} ({ x}) | x_i \in A_k }{H_{ X} ({ x}) | x_i \in A_k } } \right)$ | (23) |
| $ E(I_{ F} | X_i \in A_k ) = E(B_k )$ | (24) |
第四步:条件期望的方差项
| $ \widehat{V_{X_i } }(E_{{ X}_{ - i} } (I_{ F} | X_i )) = \sum_{k = 1}^s P_{X_i }^f (A_k ) \cdot \\ \left( {E(B_k ) - \sum_{k = 1}^s P_{X_i }^H (A_k )E\left( {B_k \cdot \dfrac{f_{ X} ({ x}) | x_i \in A_k }{H_{ X} ({ x}) | x_i \in A_k }} \right) } \right)^2$ | (25) |
因此,
| $ \widehat{S}_i = \dfrac{\widehat{V_{X_i } }(E_{{ X}_{ - i} } (I_{ F} | X_i ))}{\widehat{V}(I_{ F} )}$ | (26) |
本文所提重要抽样结合空间分割的思想,在计算
式(15)的估计值趋于真实值的前提条件是
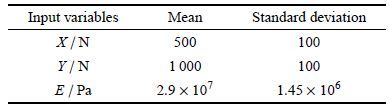
矩形截面悬臂梁受到水平和竖直方向的载荷
| $ g = D_0 - D(E,X,Y,w,t,L)$ | (27) |
其中,
| 表 1 矩形截面悬臂梁结构随机输入变量的分布特征 Table 1 The distribution parameters of inputs for the rectangular cross-section cantilever beam |
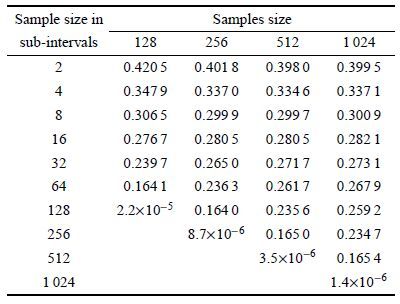
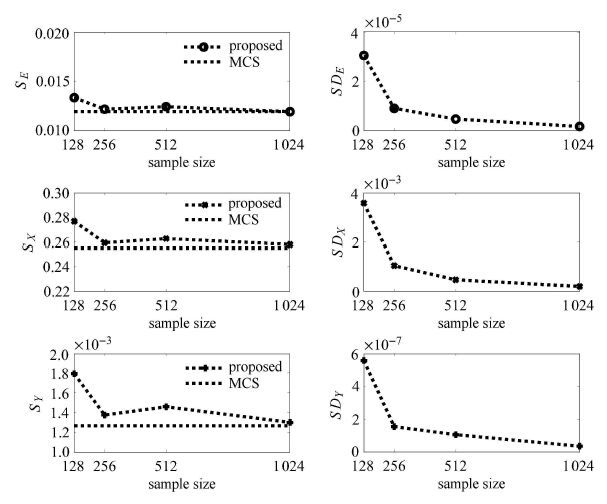
通过表 2对不同样本及不同区间划分情况下
|
表 2 |
|
图 1 矩形截面悬臂梁结构计算结果及计算结果的标准差随样本增加变化图( |
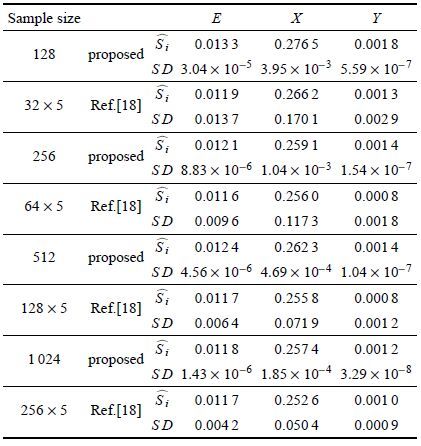
| 表 3 本文所提方法与文献[18]计算结果对比 Table 3 The results estimated by our proposed method and the method in Ref.[18] |
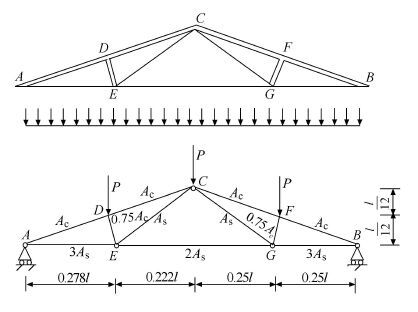
如图 2所示是一屋架结构的示意图,屋架的上弦杆和其他压杆采用钢筋混凝土杆,下弦杆和其他拉杆采用钢杆. 设屋架承受均布载荷
|
图 2 屋架结构 Fig. 2 Roof truss structure model |
| $ g = 0.025 - \varDelta _c$ | (28) |
随机输入变量
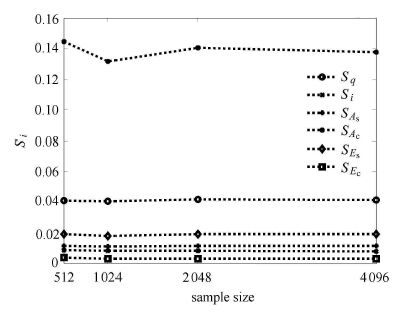
|
图 3 屋架结构计算结果随样本变化图 Fig. 3 Results of the proposed method varying with the increase of sample size for roof truss |
| 表 4 屋架结构随机输入变量的分布参数 Table 4 The distribution parameters of inputs for roof truss |
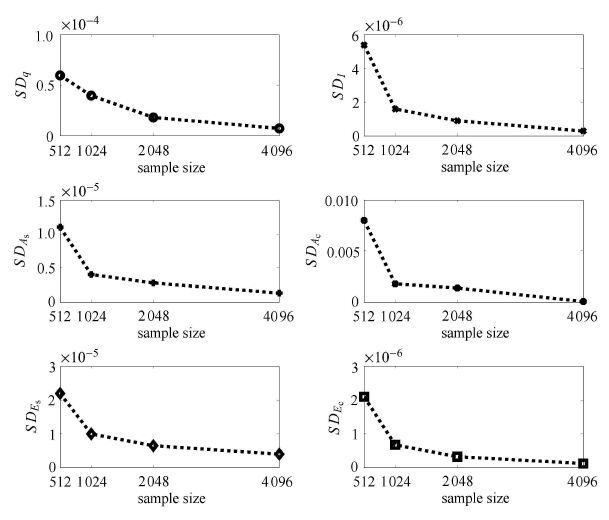
|
图 4 屋架结构100次重复计算结果标准差随样本变化图 Fig. 4 Standard derivation of the proposed method by 100 iterations varying with increase of sample size |
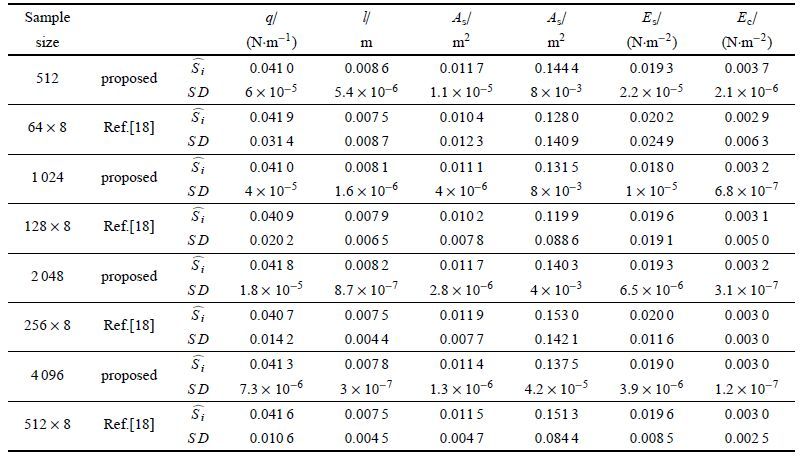
| 表 6 本文所提方法与重要抽样法[18]计算结果对比 Table 6 The results estimated by our proposed method and the method in Ref.[18] |
本文将连续区间上的全方差公式、空间分割及重要抽样法相结合,提出了一种高效准确计算失效概率矩独立全局灵敏度指标的方法,该方法通过重要抽样密度高效地抽取到失效的样本点,再通过空间分割的思想重复利用这一组样本即可得到所有随机输入变量的灵敏度指标,该方法的计算量与输入变量的维数无关,大大提高了样本的利用率和计算效率. 通过与文献[18]提出的单层MCS结合重要抽样方法对比,说明了本文所提方法有较高的准确性、高效性及稳健性. 由于本文采用的是改进的一次二阶矩方法寻找设计点,因此,对于非线性程度较高的功能函数及多设计点的情况,该方法的使用将受到限制.
| [1] |
Saltelli A. Sensitivity analysis for importance assessment[J].
Risk Analysis,2002, 22 (3) : 579-590.
DOI: 10.1111/risk.2002.22.issue-3. ( 0) 0)
|
| [2] |
Borgonovo E, Apostolakis GE. A new importance measure for risk-informed decision-making[J].
Reliability Engineering and System Safety,2001, 72 (2) : 193-212.
DOI: 10.1016/S0951-8320(00)00108-3. ( 0) 0)
|
| [3] |
Borgonovo E, Apostolakis GE, Tarantola S, et al. Comparison of local and global sensitivity analysis techniques in probability safety assessment[J].
Reliability Engineering and System Safety,2003, 79 : 175-185.
DOI: 10.1016/S0951-8320(02)00228-4. ( 0) 0)
|
| [4] |
Saltelli A, Ratto M, Andreffs T, et al. Global Sensitivity Analysis. The Primer. John Wiley & Sons, 2008
( 0) 0)
|
| [5] |
Saltelli A, Marivoet J. Non-parametric statistics in sensitivity analysis for model output: a comparison of selected techniques[J].
Reliability Engineering and System Safety,1990, 28 (2) : 229-253.
DOI: 10.1016/0951-8320(90)90065-U. ( 0) 0)
|
| [6] |
Iman RL, Johnson ME, Watson Jr CC. Sensitivity analysis for computer model projections of hurricane losses[J].
Risk analysis,2005, 25 (5) : 1277-1297.
DOI: 10.1111/risk.2005.25.issue-5. ( 0) 0)
|
| [7] |
Zhang XF, Pandey MD. An effective approximation for variancebased global sensitivity analysis[J].
Reliability Engineering and System Safety,2014, 121 : 164-174.
DOI: 10.1016/j.ress.2013.07.010. ( 0) 0)
|
| [8] |
郝文锐, 吕震宙, 魏鹏飞. 多项式输出中相关变量的重要性测度分析[J].
力学学报,2012, 44 (1) : 167-173.
( HaoWenrui, Lü Zhenzhou, Wei Pengfei. Importance measure of correlated variables in polynomial output[J].
Chinese Journal of Theoretical and Applied Mechanics,2012, 44 (1) : 167-173.
(in Chinese) ) ( 0) 0)
|
| [9] |
Wei P, Lu ZZ, Song JW. A new variance-based global sensitivity analysis technique[J].
Computation Physics Communication,2013, 184 (10) : 2540-2551.
( 0) 0)
|
| [10] |
Deman G, Konakli K, Sudret B, et al. Using sparse polynomial chaos expansions for the global sensitivity analysis of groundwater lifetime expectancy in mult-layered hydrogeological model[J].
Reliability Engineering and System Safety,2016, 147 : 156-169.
DOI: 10.1016/j.ress.2015.11.005. ( 0) 0)
|
| [11] |
Pianosi F, Wagener T. A simple and efficient method for global sensitivity analysis based on cumulative distribution functions[J].
Environmental Modelling & Software,2015, 67 : 1-11.
( 0) 0)
|
| [12] |
Borgonovo E. A new uncertainty importance measure[J].
Reliability Engineering and System Safety,2007, 92 (6) : 771-784.
DOI: 10.1016/j.ress.2006.04.015. ( 0) 0)
|
| [13] |
Zhou CC, Lu ZZ, Zhang LG, et al. Moment independent sensitivity analysis with correlations[J].
Applied Mathematical Modelling,2014, 38 (19) : 4885-4896.
( 0) 0)
|
| [14] |
Camboa F, Klein T, Lagnoux A. Sensitivity analysis based on Cramer von Mises Distance[J].
arXiv,1506, 04133 (math.PR) : 1-20.
( 0) 0)
|
| [15] |
Cui LJ, Lu ZZ, Zhao XP. Moment-independent importance measure of basic random variable and its probability density evolution solution[J].
Science China Technological Sciences,2010, 53 (4) : 1138-1145.
DOI: 10.1007/s11431-009-0386-8. ( 0) 0)
|
| [16] |
Li LY, Lu ZZ, Feng J, et al. Moment-independent importance measure of basic variable and its state dependent parameter solution[J].
Structural Safety,2012, 38 : 40-47.
DOI: 10.1016/j.strusafe.2012.04.001. ( 0) 0)
|
| [17] |
张磊刚, 吕震宙, 陈军. 基于失效概率的矩独立重要性测度的高效算法[J].
航空学报,2014, 35 (8) : 2199-2206.
( Zhang Leigang, Lü Zhenzhou, Chen Jun. An efficient method of failure probabilitybased moment-independent importance measure[J].
Acta Aeronautica et Astronautica Sinica,2014, 35 (8) : 2199-2206.
(in Chinese) ) ( 0) 0)
|
| [18] |
Wei PF, Lu ZZ, Hao WR, et al. Efficient sampling methods for global reliability sensitivity analysis[J].
Computation Physics Communication,2012, 183 (8) : 1728-1743.
DOI: 10.1016/j.cpc.2012.03.014. ( 0) 0)
|
| [19] |
Plischke E, Borgonovo E, Smith CL. Global sensitivity measures from given data[J].
European Journal of Operational Research,2013, 226 (3) : 536-550.
DOI: 10.1016/j.ejor.2012.11.047. ( 0) 0)
|
| [20] |
Zhai QQ, Yang J, Zhao Y. Space-partition method for the variancebased sensitivity analysis: Optimal partition scheme and comparative study[J].
Reliability Engineering and System Safety,2014, 131 : 66-82.
DOI: 10.1016/j.ress.2014.06.013. ( 0) 0)
|
| [21] |
Mood AM, Graybill FA, Boes DC. Introduction to the Theory of Statistics. 3rd edn. McGraw-Hill, 1974
( 0) 0)
|
| [22] |
Harbitz A. An efficient sampling method for probability of failure calculation[J].
Structural Safety,1986, 3 (2) : 109-115.
DOI: 10.1016/0167-4730(86)90012-3. ( 0) 0)
|
| [23] |
Melchers RE. Importance sampling in structural system[J].
Structural Safety,1989, 6 (1) : 3-10.
DOI: 10.1016/0167-4730(89)90003-9. ( 0) 0)
|
| [24] |
Au SK, Beck JL. A new adaptive importance sampling scheme[J].
Structural Safety,1999, 21 (2) : 135-158.
DOI: 10.1016/S0167-4730(99)00014-4. ( 0) 0)
|
| [25] |
Au SK, Beck JL. Importance sampling in high dimensions[J].
Structural Safety,2003, 25 (2) : 139-163.
DOI: 10.1016/S0167-4730(02)00047-4. ( 0) 0)
|
| [26] |
戴鸿哲, 薛国锋, 王伟. 基于小波阈值密度的自适应重要抽样方法[J].
力学学报,2014, 46 (3) : 480-484.
( Dai Hongzhe, Xue Guofeng, Wang Wei. A wavelet thresholding density-based adaptive importance sampling method[J].
Chinese Journal of Theoretical and Applied Mechanics,2014, 46 (3) : 480-484.
(in Chinese) ) ( 0) 0)
|
| [27] |
Hasfer AM, Lind NC. Exact and invariant second moment code format[J].
Journal of Engineering Mechanics, ASCE,1974, 100 (1) : 111-121.
( 0) 0)
|
| [28] |
Dai HZ, WangW. Application of low-discrepancy sampling method in structural reliability analysis[J].
Structural Safety,2009, 31 (1) : 55-64.
DOI: 10.1016/j.strusafe.2008.03.001. ( 0) 0)
|
| [29] |
Sobol IM. Uniformly distributed sequences with additional uniformity properties[J].
USSR Computational Mathematics and Mathematical Physics,1976, 16 : 236-242.
( 0) 0)
|
| [30] |
Sobol IM. On quasi-Monte Carlo integrations[J].
Mathematics and Computers in Simulation,1998, 47 (2) : 103-112.
( 0) 0)
|
2. Aircraft Flight Test Technology Institute, Chinese Flight Test Establishment, Xi'an 710089, China
 2016, Vol. 48
2016, Vol. 48