2. 赣州有色冶金研究所, 江西赣州 341000 ;
3. 江西理工大学理学院, 江西赣州 341000 ;
4. 江西理工大学资源与环境工程学院, 江西赣州 341000
采场结构的稳定性受多种因素影响,其稳定性的判据目前还没有统一的认识[1-2]. 从单一的应力、位移角度很难综合评价采场结构的稳定性,冯夏庭等[3]提出地下工程稳定性的综合集成智能分析与动态设计优化的新思路,并获得了成功应用. 能量法由于可以避免研究工程结构失稳破坏的中间复杂受力、应变过程,因而受到国内外一些学者的青睐,他们通过能量原理研究和探索了地下工程结构失稳破坏的相关问题,并取得了一定的成果[4-9].
人工矿柱作为地下矿山开采中一种重要的采场结构,一方面可充分回收矿产资源,另一方面可人为改变采空区围岩应力环境[10-11],支撑上覆岩体和控制围岩变形.针对原生矿柱(残留矿柱)稳定性方面的研究,已经取得了一定的研究成果:唐春安等[12]运用自主研发的岩石破裂过程分析程序(RFPA),对矿柱的变形与破坏过程及其声发射模式进行了研究;潘岳等[13]研究了非对称开采时矿柱受偏压时的失稳破坏特征;赵奎[14]分析了矿柱纵波速度与所受压力之间的定量关系以及矿柱破裂区分布特点,建立了基于声波测试的矿柱稳定性模糊推理系统,能够更加全面地反映矿柱稳定状态和损伤情况;周科平等[15]对采场矿柱进行强度折减,采用矿柱塑性破坏区贯通作为相邻采场整体失稳的判据,利用矿柱强度折减的ANN-GA模型在某铜矿取得了满意效果;杨永杰等[16]从蠕变试验的角度研究了石膏矿柱长期的稳定性问题;杨宇江和李元辉[17]将加卸载响应比(LURR)理论引入矿柱动力稳定性研究中,对非均质矿柱模型在动力载荷循环作用下的破坏过程进行全时程动力分析. 刘洪强等[18]、Zhou等[19]、徐文彬等[20]一些学者在原生矿柱稳定性方面也取得了非常有益的研究成果.
目前对人工矿柱在金属矿山地下开采支护的研究成果相对较少[21-24],且大多为人工矿柱的施工工艺、现场应用及定性分析方面研究. 近来,曹帅等[25]基于弹性力学平面应变基本假设,建立阶段嗣后胶结充填体矿柱力学模型并进行理论求解;陈庆发等[26]基于突变理论建立了金属矿山人工矿柱突发失稳的尖点突变模型,得出了满意的结果.因此,本文根据金属矿山人工矿柱尺寸和自身材料特性,从力学和能量守恒的角度研究其稳定性问题.
1 人工矿柱破坏模式及力学模型由于金属矿山人工矿柱受多种因素的影响,其强度往往很难达到设计的要求,易发生失稳破坏. 在覆岩的载荷作用下,人工矿柱破坏模式与压杆失稳破坏模式相似,但由于覆岩、人工矿柱及载荷作用,其失稳机理比压杆更复杂. 在很多试验中,纵向劈裂破坏模式较多[27].
由于人工矿柱与上覆岩体之间有较大的摩擦力 (图 1(a)),导致在垂直压力作用下人工矿柱顶面发生相对水平位移较小,很少产生较大的膨胀变形,而人工矿柱中部则因周围无约束力而发生"鼓形"(泊松)劈裂膨胀破坏. 继续加载时,人工矿柱中部对称位置上将产生竖向裂纹,并随载荷增大而发生贯通,使矿柱胀裂分开,并单独承受上覆岩体重力. 但此时,由于之前人工矿柱已产生横向变形而不再单纯是轴心受力,而是产生了初始偏心距的偏心受压的若干小矿柱体. 本文将人工矿柱视为压杆失稳破坏的模式,以"鼓形"(泊松)形式研究其稳定性.
取破坏后的某个小矿柱进行能量突变分析,为便于分析,假设人工矿柱长度

|
图 1 人工矿柱破坏模式示意图 Fig. 1 Artificial pillar failure modes sketch map |
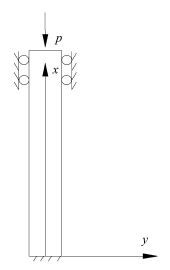
|
图 2 人工矿柱简化力学模型 Fig. 2 Artificial pillars simplified mechanical model |
根据前述破坏模式及力学模型分析,人工矿柱的边界条件为
| $x(0) = 0 ,\quad x(h) = 0 $ | (1) |
| ${x}'(0) = 0 ,\quad {x}'(h) = 0 $ | (2) |
由以上二式满足位移边界条件[28],可设矿柱的挠度曲线方程为
| $ y = a_1 \Big (1 - \cos \dfrac{2\pi x}{h} \Big) + b_1 \Big (1 - \cos \dfrac{6\pi x}{h} \Big) $ | (3) |
式中,
由能量原理知[30],人工矿柱总能量
| $ \varPi = - W_P - W_G + U $ | (4) |
式中,
作为小变形体的人工矿柱,由于在尺寸上,矿柱的高度大于矿柱宽度,在承受单轴压缩时,常规的破坏是"鼓形"(泊松)破坏,这里仅考虑其弯曲应变能
| $U = {1 \over 2}\int_0^{{\varphi _{\max }}} M (x){\rm{ }}\varphi = {1 \over 2}\int_0^h M (x) \cdot {{M(x)} \over {EI}}ds = {{EI} \over 2}\int_0^h {{{(y'')}^2}} ds$ | (5) |
式中,
将
| $ \sqrt {1 + ({y}')^2} \approx 1 + \dfrac{1}{2}({y}')^2 $ |
则
| $ d s = \left[{1 + \dfrac{1}{2}({y}')^2} \right] d x $ | (6) |
将式(6)代入式(5)得
| $ U = \dfrac{EI}{2}\int_0^h ({y}")^2\left[{1 + \dfrac{1}{2}({y}')^2} \right] d x $ | (7) |
由于实际问题中,
| $ U = \dfrac{EI}{2}\int_0^h ({y}")^2 d x $ | (8) |
将式(3)分别进行一阶求导与二阶求导得
| $ \left. {y}' = \dfrac{2\pi a_1 }{h}\sin \dfrac{2\pi x}{h} + \dfrac{6\pi b_1 }{h}\sin \dfrac{6\pi x}{h} \\ {y}" = \dfrac{4\pi ^2a_1 }{h^2}\cos \dfrac{2\pi x}{h} + \dfrac{36\pi ^2b_1 }{h^2}\cos \dfrac{6\pi x}{h} \!\!\right\} $ | (9) |
将式(9)代入式(8)得
| $\eqalign{ & U = {{EI} \over 2}\int_0^h ( {{4{\pi ^2}{a_1}} \over {{h^2}}}\cos {{2\pi x} \over h} + {{36{\pi ^2}{b_1}} \over {{h^2}}}\cos {{6\pi x} \over h}{)^2}dx = \cr & {{4EI{\pi ^4}} \over {{h^3}}}(a_1^2 + 81b_1^2) \cr} $ | (10) |
令
| $\eqalign{ & \lambda = {1 \over 2}\int_0^h ( {{2\pi {a_1}} \over h}\sin {{2\pi x} \over h} + {{6\pi {b_1}} \over h}\sin {{6\pi x} \over h}{)^2}dx = \cr & {{{\pi ^2}} \over h}(a_1^2 + 9b_1^2) \cr} $ |
式中,
则外载荷
| $ W_P = P\lambda = \dfrac{P\pi ^2}{h}(a_1^2 + 9b_1^2 ) $ | (11) |
矿柱自重势能为
| $ W_G = \dfrac{1}{2}mgh = 0.5\rho gsh^2 $ | (12) |
式中,
将式(10)
| $ \varPi = - W_P - W_G + U=\\ \dfrac{4EI\pi ^4}{h^3}(a^2_1 + 81b_1^2 ) - \\ \dfrac{P\pi ^2}{h}(a_1^2 + 9b_1^2 ) - 0.5\rho gsh^2 $ | (13) |
此式即为结构功能(势能)函数的数学表达式. 由突变理论的相关知识可知[31-32],用势函数$\varPi (x)$的空间曲面图形来表示如图 3.
图 3(a)所示的是一个具有光滑折痕的曲面,其上一点代表所研究系统的一种平衡状态. 在该曲面上叶和下叶上,满足
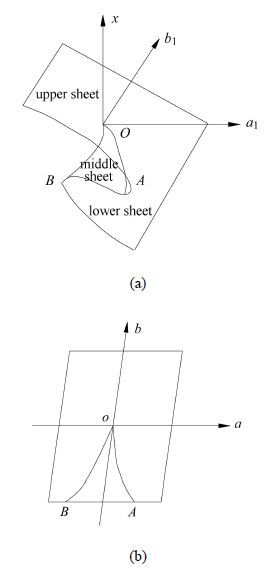
|
图 3 势函数 |
在曲面上叶和下叶与中叶的交界,即图 3(b)所示的光滑折痕
如前所述,当
令
| $ P = \dfrac{4EI\pi ^2}{h^2}\cdot \dfrac{a_1^2 + 81b_1^2 }{a_1^2 + 9b_1^2 } - \dfrac{\rho gsh^3}{2\pi ^2}\cdot \\ \dfrac{1}{(a_1^2 + 9b_1^2 )} $ | (14) |
从上式中可看出,
外载荷
| $ P_{\rm cr} = \dfrac{4EI\pi ^2}{h^2} - \dfrac{\rho gsh^3}{2\pi ^2a_1^2 } $ | (15) |
式中,
相应的,临界应力
| $ \sigma _{\rm cr} = \dfrac{p_{\rm cr} }{A} = \dfrac{ 4EI\pi ^2}{h^2bl} - \dfrac{\rho gh^3}{2\pi ^2a_1 ^2} $ | (16) |
根据非线性科学的理论[33],该系统的定态方程为
| $ \left.\begin{array}{l} {\dfrac{\partial \varPi }{\partial a_1 } = 0} \\ {\dfrac{\partial \varPi }{\partial b_1 } = 0} \end{array} \right \} $ | (17) |
将式(13)代入得
| $ \left.\begin{array}{l} {a_1 \Big(\dfrac{8EI\pi ^4}{h^3} - \dfrac{2\pi ^2}{h}P \Big) = 0} \\ {b_1 \Big(\dfrac{36EI\pi ^4}{h^3} - \dfrac{\pi ^2}{h}P \Big) = 0} \end{array} \!\! \right \} $ | (18) |
解此方程组可得
| $①\left\{ {\matrix{ {{a_1} = 0} \cr {{b_1} = 0} \cr } } \right.②\left\{ {\matrix{ {{a_1} = 0} \cr {P = {{36EI{\pi ^2}} \over {{h^2}}}} \cr } } \right.③\left\{ {\matrix{ {P = {{4EI{\pi ^2}} \over {{h^2}}}} \cr {{b_1} = 0} \cr } } \right.$ |
当第①组解代入式(3)有
再由式(14)讨论外载荷
稳定性的影响,即
可用其偏导数来研究外载荷
| $ \left. \dfrac{\partial P}{\partial a_1 } = - \dfrac{a_1 (576\pi ^4EIb_1^2 - \rho gsh^5)}{\pi ^2h^2(a_1^2 + 9b_1^2 )^2} \\ \dfrac{\partial P}{\partial b_1 } = \dfrac{9b_1 (64EI\pi ^4a_1^2 + \rho gsh^5)}{h^2\pi ^2(a_1^2 + 9b_1^2 )^2} \!\!\right\} $ | (19) |
根据式(19)可得载荷力(压力)
当
同理,当
由材料力学可知,矿柱产生突变时,必须满足
考虑式(13)及式(18) 可知:
当
在外载荷(压力)
综上可知,欲使人工矿柱系统处于稳定平衡状态,则作用在人工矿柱上的外载荷小于临界载荷,即
根据上述针对人工矿柱承受外载荷的稳定性分析,为了能将该理论研究应用到矿山工程实践中,作者所在课题组对焦冲金矿[22]采用人工混凝土矿柱代替原生矿柱的尺寸参数进行了优化设计,并对支护效果进行了研究.
该矿

|
图 4 |
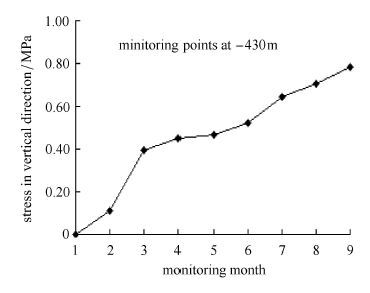
|
图 5 |
根据矿柱和矿房的布置,每个矿柱承载左右相邻每个矿房一半面积的上覆岩层载荷,一个矿柱应该承载的顶板面积
| $ s_1 = \dfrac{b}{2} \left( {b + w} \right) $ | (20) |
式中,
将上述参数代入式(15),可得人工矿柱的临界载荷
| $ P_{\rm cr} = 3.90 \times 10^5 {\rm kN} $ | (21) |
从上述现场实测数据可知,课题组优化设计的人工矿柱所承受覆岩载荷为464 MN,根据前述所建立的人工矿柱临界应力函数关系式所计算出的人工矿柱临界载荷为390 MN,实测人工矿柱承受载荷约为理论设计临界载荷的十分之一,远小于其临界载荷的支撑力,课题组所设计的人工矿柱是稳定的,符合工程安全规范要求,能够满足矿山安全生产的需要.为了进一步优化人工矿柱尺寸,减少充填成本,将该中段其他剩余人工矿柱的宽度又适当减小后进行施工.截止到2014年12月底,通过5年多的矿山生产实践,
通过现场实验和多年的矿山生产实践,表明上述所建立的能量极限状态方程可以作为金属矿山人工矿柱设计的力学依据.
5 结论(1) 将人工矿柱受力环境进行分析简化,根据能量守恒原理得出考虑外载荷做功、自重势能和应变能条件下的人工矿柱总能量方程,推导出了结构功能(势能)函数的表达式. 根据突变理论的相关知识,建立了在考虑弹性模量、高宽比等参数条件下的能量极限状态方程,根据势函数的稳定判据得出了外载荷的临界应力函数关系式.
(2) 根据临界载荷关系,从力学角度定量评判了人工矿柱在外载荷变化过程对其稳定性的影响. 当外力
(3) 根据理论研究结果,对优化设计后的焦冲金矿人工矿柱承受载荷现场实测,其实测结果约为理论设计临界载荷的十分之一,远小于其临界载荷的支撑力. 通过5年多的矿山生产实践,人工矿柱及覆岩都较稳定,能够满足矿山安全生产的需要. 表明所建立的人工矿柱能量极限状态方程,可为地下金属矿山人工矿柱设计提供一定的力学参考依据和理论指导.
| [1] |
王金安, 李大钟, 尚新春. 采空区坚硬顶板流变破断力学分析[J].
北京科技大学学报,2011, 33 (2) : 142-148.
( Wang Jin'an, Li Dazhong, Shang Xinchun. Mechanics analysis on creep fracture of strong roof strata above mined-out area[J].
Journal of University of Science and Technology Beijing,2011, 33 (2) : 142-148.
(in Chinese) ) ( 0) 0)
|
| [2] |
周维垣. 岩体工程结构的稳定性[J].
岩石力学与工程学报,2010, 29 (9) : 1729-1753.
( Zhou Weiyuan. Structure stability of rock mass engineering[J].
Chinese Journal of Rock Mechanics and Engineering,2010, 29 (9) : 1729-1753.
(in Chinese) ) ( 0) 0)
|
| [3] |
冯夏庭, 江权, 苏国韶. 高应力下硬岩地下工程的稳定性智能分析与动态优化[J].
岩石力学与工程学报,2008, 27 (7) : 1341-1352.
( Feng Xiating, Jiang Quan, Su Guoshao. Integrated intelligent stability analysis and dynamic optimization of underground engineering in hard rock with high geostress[J].
Chinese Journal of Rock Mechanics and Engineering,2008, 27 (7) : 1341-1352.
(in Chinese) ) ( 0) 0)
|
| [4] |
Deshpande VS, Evans AG. Inelastic deformation and energy dissipation in ceramics:A mechanism-based constitutive model[J].
Journal of the Mechanics and Physics of Solids,2008, 56 (10) : 3077-3100.
DOI: 10.1016/j.jmps.2008.05.002. ( 0) 0)
|
| [5] |
谢和平, 鞠杨, 黎立云. 基于能量耗散与释放原理的岩石强度与整体破坏准则[J].
岩石力学与工程学报,2005, 24 (17) : 3003-3010.
( Xie Heping, Ju Yang, Li Liyun. Criteria for strength and structural failure of rocks based on energy dissipation and energy release principles[J].
Chinese Journal of Rock Mechanics and Engineering,2005, 24 (17) : 3003-3010.
(in Chinese) ) ( 0) 0)
|
| [6] |
左建平, 黄亚明, 熊国军, 等. 脆性岩石破坏的能量跌落系数研究[J].
岩土力学,2014, 35 (2) : 321-327.
( Zuo Jianping, Huang Yaming, Xiong Guojun, et al. Study of energy-drop coefficient of brittle rock failure[J].
Rock and Soil Mechanics,2014, 35 (2) : 321-327.
(in Chinese) ) ( 0) 0)
|
| [7] |
陈昀, 金衍, 陈勉. 基于能量耗散的岩石脆性评价方法[J].
力学学报,2015, 47 (6) : 984-993.
( Chen Yun, Jin Yan, Chen Mian. A rock brittleness evaluation method based on energy dissipation[J].
Chinese Journal of Theoretical and Applied Mechanics,2015, 47 (6) : 984-993.
(in Chinese) ) ( 0) 0)
|
| [8] |
杨官涛, 李夕兵, 王其胜, 等. 地下采场失稳的能量突变判断准则及其应用[J].
采矿与安全工程学报,2008, 25 (3) : 268-271.
( Yang Guantao, Li Xibing, Wang Qisheng, et al. Criterion for judging energy mutation in destabilized stope and its application[J].
Journal of Mining & Safety Engineering,2008, 25 (3) : 268-271.
(in Chinese) ) ( 0) 0)
|
| [9] |
潘岳, 王志强. 岩体动力失稳的功、能增量-突变理论研究方法[J].
岩石力学与工程学报,2004, 23 (9) : 1433-1438.
( Pan Yue, Wang Zhiqiang. Research approach on increment of work and energycatastrophe theory of rock dynamic destabilization[J].
Chinese Journal of Rock Mechanics and Engineering,2004, 23 (9) : 1433-1438.
(in Chinese) ) ( 0) 0)
|
| [10] |
古德生, 李夕兵.
现代金属矿床开采科学技术[M]. 北京: 冶金工业出版社, 2006 .
( Gu Desheng, Li Xibing.
Modern Mining Science and Technology for Metal Mineral Resources[M]. Beijing: Metallurgical Industry Press, 2006 .
(in Chinese) ) ( 0) 0)
|
| [11] |
Xu S, Liu JP, Xu SD, et al. Experimental studies on pillar failure characteristics based on acoustic emission location technique[J].
Transactions of Nonferrous Metals Society of China,2012, 22 : 2792-2798.
DOI: 10.1016/S1003-6326(11)61534-3. ( 0) 0)
|
| [12] |
唐春安, 乔河, 徐小荷, 等. 矿柱破坏过程及其声发射规律的数值模拟[J].
煤炭学报,1999, 24 (3) : 266-269.
( Tang Chun'an, Qiao He, Xu Xiaohe, et al. Numerical simulation on pillar failure and associated acoustic emissions[J].
Journal of China Coal Society,1999, 24 (3) : 266-269.
(in Chinese) ) ( 0) 0)
|
| [13] |
潘岳, 张勇, 吴敏应, 等. 非对称开采矿柱失稳的突变理论分析[J].
岩石力学与工程学报,2006, 25 (Supp2) : 3694-3702.
( Supp2):3694-3702 (Pan Yue, Zhang Yong, Wu Minying, et al. Analysis of catastrophe theory for pillar destabilization in dissymmetric mining[J].
Chinese Journal of Rock Mechanics and Engineering,2006, 25 (Supp2) : 3694-3702.
(in Chinese) ) ( 0) 0)
|
| [14] |
赵奎. 岩金矿山采空区及残留矿柱回采稳定性研究[J].
岩石力学与工程学报,2003, 22 (8) : 1404.
( Zhao Kui. Stability study on minedout areas and recovery of residual pillars in rocky gold mine[J].
Chinese Journal of Rock Mechanics and Engineering,2003, 22 (8) : 1404.
(in Chinese) ) ( 0) 0)
|
| [15] |
周科平, 王星星, 高峰. 基于强度折减与ANN-GA 模型的采场结构参数优化[J].
中南大学学报(自然科学版),2013, 44 (7) : 2848-2854.
( Zhou Keping, Wang Xingxing, Gao Feng. Stope structural parameters optimization based on strength reduction and ANN-GA model[J].
Journal of Central South University (Science and Technology),2013, 44 (7) : 2848-2854.
(in Chinese) ) ( 0) 0)
|
| [16] |
杨永杰, 邢鲁义, 张仰强, 等. 基于蠕变试验的石膏矿柱长期稳定性研究[J].
岩石力学与工程学报,2015, 34 (10) : 2106-2113.
( Yang Yongjie, Xing Luyi, Zhang Yangqiang, et al. Analysis of long-term stability of gypsum pillars based on creep tests[J].
Chinese Journal of Rock Mechanics and Engineering,2015, 34 (10) : 2106-2113.
(in Chinese) ) ( 0) 0)
|
| [17] |
杨宇江, 李元辉. 基于加卸载响应比理论的矿柱动力稳定性分析[J].
岩土力学,2013, 34 (S1) : 324-330.
( Yang Yujiang, Li Yuanhui. Dynamic stability analysis of pillar based on loading-unloading response ratio theory[J].
Rock and Soil Mechanics,2013, 34 (S1) : 324-330.
(in Chinese) ) ( 0) 0)
|
| [18] |
刘洪强, 张钦礼, 潘常甲, 等. 空场法矿柱破坏规律及稳定性分析[J].
采矿与安全工程学报,2011, 28 (1) : 138-143.
( Liu Hongqiang, Zhang Qinli, Pan Changjia, et al. Analysis of the failure law and stability of the pillar in open stope mining[J].
Journal of Mining & Safety Engineering,2011, 28 (1) : 138-143.
(in Chinese) ) ( 0) 0)
|
| [19] |
Zhou J, Li XB, Shi XZ, et al. Predicting pillar stability for underground mine using Fisher discriminant analysis and SVM methods[J].
Transactions of Nonferrous Metals Society of China,2011, 12 : 2734-2743.
( 0) 0)
|
| [20] |
徐文彬, 宋卫东, 曹帅, 等. 地下矿山采场群稳定性分析及其控制技术[J].
采矿与安全工程学报,2015, 32 (4) : 658-664.
( Xu Wenbin, Song Weidong, Cao Shuai, et al. Stopes stability in underground mine and its control technique[J].
Journal of Mining and Safety Engineering,2015, 32 (4) : 658-664.
(in Chinese) ) ( 0) 0)
|
| [21] |
赵康. 焦冲金矿覆岩移动机理及防治研究. [博士论文]. 北京: 北京科技大学, 2012
( Zhao Kang. Study of overburden movement mechanism and prevention in jiaochong gold mine. [PhD Thesis]. Beijing: University of Science and Technology Beijing, 2012 (in Chinese)
) ( 0) 0)
|
| [22] |
王晓军, 冯萧, 杨涛波, 等. 深部回采人工矿柱合理宽度计算及关键影响因素分析[J].
采矿与安全工程学报,2012, 29 (1) : 54-59.
( Wang Xiaojun, Feng Xiao, Yang Taobo, et al. Reasonable width calculation and analysis of artificial pillar in deep mining[J].
Journal of Mining and Safety Engineering,2012, 29 (1) : 54-59.
(in Chinese) ) ( 0) 0)
|
| [23] |
陈庆发, 周科平. 低标号充填体对采矿环境结构稳定性作用机制研究[J].
岩土力学,2010, 31 (9) : 2811-2816.
( Chen Qingfa, Zhou Keping. Action mechanism of low-grade backfill on stability of mining environment structure[J].
Rock and Soil Mechanics,2010, 31 (9) : 2811-2816.
(in Chinese) ) ( 0) 0)
|
| [24] |
张雯, 郭进平, 张卫斌, 等. 大型残留矿柱回采时采空区处理方案研究[J].
金属矿山,2012, 1 : 10-13.
( Zhang Wen, Guo Jinping, Zhang Weibin, et al. Study on the stoped-out area treatment when recovering large and residual pillars[J].
Metal Mine,2012, 1 : 10-13.
(in Chinese) ) ( 0) 0)
|
| [25] |
曹帅, 杜翠凤, 谭玉叶, 等. 金属矿山阶段嗣后充填胶结充填体矿柱力学模型分析[J].
岩土力学,2015, 36 (8) : 2370-2376.
( Cao Shuai, Du Cuifeng, Tan Yuye, et al. Mechanical model analysis of consolidated filling pillar using stage-delayed backfill in metal mines[J].
Rock and Soil Mechanics,2015, 36 (8) : 2370-2376.
(in Chinese) ) ( 0) 0)
|
| [26] |
陈庆发, 古德生, 周科平, 等. 对称协同开采人工矿柱失稳的突变理论分析[J].
中南大学学报(自然科学版),2012, 43 (6) : 2338-2342.
( Chen Qingfa, Gu Desheng, Zhou Keping, et al. Analysis of catastrophe theory for artificial pillar instability in symmetric synergistic mining[J].
Journal of Central South University (Science and Technology),2012, 43 (6) : 2338-2342.
(in Chinese) ) ( 0) 0)
|
| [27] |
Li C, Richard P, Erling N. The stress strain behaviour of rock material related to fracture under compression[J].
Engineering Geology,1998, 49 (2) : 293-302.
( 0) 0)
|
| [28] |
李廉锟.
结构力学(第5 版)(下册)[M]. 北京: 高等教育出版社, 2010 .
( Li Liankun.
Structural Mechanics (5th ed) (Part II)[M]. Beijing: Higher Education Press, 2010 .
(in Chinese) ) ( 0) 0)
|
| [29] |
孙训方, 方孝淑, 关来泰.
材料力学(第2 版)(上册)[M]. 北京: 人民教育出版社, 1979 .
( Sun Xunfang, Fang Xiaoshu, Guan Laitai.
Mechanics of Materials (2nd edn)(Part I)[M]. Beijing: People's Education Press, 1979 .
(in Chinese) ) ( 0) 0)
|
| [30] |
梁炳文, 胡世光.
弹塑性稳定理论[M]. 北京: 国防工业出版社, 1983 .
( Liang Bingwen, Hu Shiguang.
Elastoplastic Stability Theory[M]. Beijing: National Defense Industry Press, 1983 .
(in Chinese) ) ( 0) 0)
|
| [31] |
唐春安, 徐小荷. 岩石破裂过程失稳的尖点灾变模型[J].
岩石力学与工程学报,1990, 9 (2) : 100-107.
( Tang Chun'an, Xu Xiaohe. A cusp catastrophic model of rock unstable failure[J].
Chinese Journal of Rock Mechanics and Engineering,1990, 9 (2) : 100-107.
(in Chinese) ) ( 0) 0)
|
| [32] |
殷有泉.
岩石力学与岩石工程的稳定性[M]. 北京: 北京大学出版社, 2011 .
( Yin Youquan.
Stability of Rock Mechanics and Rock Engineering[M]. Beijing: Peking University Press, 2011 .
(in Chinese) ) ( 0) 0)
|
| [33] |
Qin S, Jiao JJ, Wang S. A cusp catasrophe model of instability of slip buckling slope[J].
Rock Mechanics and Rock Engineering,2001, 34 (2) : 119-134.
DOI: 10.1007/s006030170018. ( 0) 0)
|
2. Ganzhou Nonferrous Metallurgy Research Institute, Ganzhou 341000, Jiangxi, China ;
3. School of Science, Jiangxi University of Science and Technology, Ganzhou 341000, Jiangxi, China ;
4. School of Resources and Environment Engineering, Jiangxi University of Science and Technology, Ganzhou 341000, Jiangxi, China
 2016, Vol. 48
2016, Vol. 48
