柔性旋转梁是空间机械臂、涡轮叶片、直升机旋翼及卫星天线等诸多工程结构的理论模型,其动力学特性对系统精度、性能与安全可靠性具有重要影响[1-4].相关问题一直是国内外学者的研究热点,在动力学模型和建模理论方法方面,发展出了动力刚化模型[5]、一次近似耦合模型[6-8]、一次精确耦合模型[9-11]、高次耦合模型[12]、几何精确模型[13]、浮动坐标法[14-15]、绝对节点坐标法[16]、随转坐标法[17]、有限段方法[18]、一致线性化方法[19]等;在变形场离散与插值方法方面发展了Bezier插值法[20-21]、B样条插值法[22]及无网格插值法[23-24]等;动力学方程分析求解方面,发展了假设模态法[25]、有限差分法[26]、有限元法等方法[27];取得了诸多研究成果.
为了准确进行旋转结构的设计,需要正确估计旋转系统结构及状态参数对其固有振动特性的影响. 在以旋转叶片、旋翼为背景的平面内柔性旋转梁问题研究中, 有学者发现系统频率、模态振型随旋转速度变化出现频率转向与振型转换现象[28].在以含梁式柔性附件的航天器为背景的中心刚体-柔性旋转梁系统动力学特性研究中,蒋丽忠和洪嘉振[29]指出大范围运动转速对频率和模态均有影响,杨辉等[30-31]通过理论分析和实验验证发现定边界的模态与动边界的模态存在较大差异,指出刚柔耦合系统模态频率与刚体-柔性梁转动惯量比值有一定关系,方建士等[32]发现随着转速的增加,旋转悬臂梁将出现频率转向与振型转换现象,Zhao等[33]也同样发现刚柔耦合系统动力学特性会随着中心刚体转动惯量及转速的变化而变化.但上述研究在动力学建模时多认为旋转梁根部与中心刚体为刚性固接,而实际工程中由于连接件弹性变形[34]、根部裂纹[35-37]等因素,根部边界处不是理想的刚性连接,而应视为具有一定扭转刚度的铰接.此外,现有研究在动力学特性分析时多集中于旋转速度对系统固有频率与振型的影响,而对系统径长比、梁的长细比等因素的影响分析较少. 最后,现有离散方法往往需要根据不同的边界条件构造不同的形函数,处理过程复杂[38].Chebyshev谱方法作为具有指数收敛特性的高精度数值方法,能够很好地解决各类线性、非线性梁动力学问题,结合投影矩阵法能够"一致"地处理固支、铰支及弹性支撑等不同边界问题,为解决上述问题提供了一种新的途径[38-39].
本文基于Gauss-Lobattoe节点与Chebyshev多项式插值对柔性梁变形场进行离散,在此基础上考虑根部连接弹性,对平面内旋转柔性梁动力学特性进行研究,通过投影矩阵法施加固定及弹性连接边界条件,利用Chebyshev谱方法获得系统固有频率及模态振型的数值解,将仿真结果与有限元法、加权残余法等方法进行对比,验证方法的有效性;并对弹性连接刚度、角速度比率、系统径长比及梁的长细比等参数对系统固有频率及模态振型的影响进行分析.
1 旋转柔性梁动力学模型 1.1 系统动力学方程
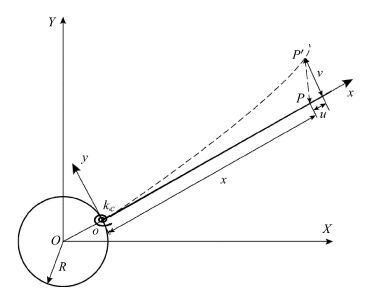
考虑图 1所示平面内旋转柔性梁系统,中心刚体半径为
|
图 1 弹性连接旋转柔性梁 Fig. 1 Rotating flexible beam with elastically restrain |
基于von-Kavman非线性应变理论,采用Euler-Bernoulli梁模型,平面内旋转柔性梁系统自由振动动力学方程可表示为[28, 40]
| $\left. {\matrix{ {\rho A\left( {\ddot u - 2\Omega \dot v - {\Omega ^2}u - \dot \Omega v} \right) - EAu'' = } \cr {\rho A{\Omega ^2}\left( {R + x} \right)} \cr {\rho A\left( {\ddot v + 2\Omega \dot u + \dot \Omega u - {\Omega ^2}v} \right) - EA{{\left( {u'v'} \right)}^\prime } + EIv'''' = } \cr { - \rho A\dot \Omega \left( {R + x} \right)} \cr } } \right\}$ | (1) |
式中,
| $ \left. \!\! u\left( {0,t} \right) = 0 ,v\left( {0,t} \right) = 0 ,\ {v}'\left( {0,t} \right) = 0 \\ {u}'\left( {L,t} \right) = 0 ,{v}"\left( {L,t} \right) = 0 ,\ {v}"'\left( {L,t} \right) = 0 \!\!\right\} $ | (2) |
对于弹性连接,有边界条件
| $ \left. \!\! u\left( {0,t} \right) = 0 ,v\left( {0,t} \right) = 0 ,\ \left. {EI{v}" - k_{\rm c} {v}'} \right|_{x = 0} = 0 \\ {u}'\left( {L,t} \right) = 0 ,\ {v}"\left( {L,t} \right) = 0 ,\ {v}"'\left( {L,t} \right) = 0 \!\!\right\}$ | (3) |
考虑大范围匀速运动情况,此时
| $ u = u_0 + \Delta u $ | (4) |
平衡状态变形量
| $ u_0 = \dfrac{R\beta \cos \left[{\beta \left( {L - x} \right)} \right] + \sin \left( {\beta x} \right)}{\beta \cos \left( {\beta L} \right)} - \left( {R + x} \right) $ | (5) |
式中
| $ \left. \begin{array}{l} \ddot {u} - 2\Omega \dot {v} - \Omega ^2u - \chi {u}" = 0 \\ \ddot {v} + 2\Omega \dot {u} - \Omega ^2v - \chi \left( {{u}"_0 {v}' + {u}'_0 {v}"} \right) + \tau {{v}"}" = 0 \end{array} \right\}$ | (6) |
式中
Chebyshev谱方法以Chebyshev多项式插值为基础的方法.本文采用第一类Chebyshev多项式,它是一类递归正交多项式,其第
| $ T_k (x) = \cos (k\arccos x) ,\quad k = 1,2,3,\cdots$ | (7) |
且满足递推关系
| $ T_k (x) = 2xT_{k - 1} (x) - T_{k - 2} (x)$ | (8) |
式中
| $ y_N (x) = \sum_{k = 0}^{N - 1} a_k T_k (x)$ | (9) |
若采用 Gauss-Lobatto 节点
| ${ y} = { \Gamma }_{\rm B} { a}$ | (10) |
| $ { \Gamma }_{\rm B} = \left[\!\! \begin{array}{cccc} {T_0 (x_0 )} & {T_1 (x_0 )} & \cdots & {T_{N - 1} (x_0 )} \\ {T_0 (x_1 )} & {T_1 (x_1 )} & \cdots & {T_{N - 1} (x_1 )} \\ \vdots & \vdots & \ddots & \vdots \\ {T_0 (x_{N - 1} )} & {T_0 (x_{N - 1} )} & \cdots &{T_0 (x_{N - 1} )} \end{array}\!\! \right]$ | (11) |
并可得函数
| $ {y}'_N (x) = \sum_{k = 0}^{N - 1} a_k {T}'_k (x) = \sum_{k = 0}^{N - 1} b_k T_k (x) $ | (12) |
多项式系数
| $ { b} = { D a}$ | (13) |
式中
| $ { y }^{(n)} = { \Gamma }_{\rm B} { D }^n{ \Gamma }_{\rm B}^{ - 1} { y } = { Q }_n { y }$ | (14) |
| $ \int_{l_1 }^{l_2 } {y_N (x)} d x = \sum_{k = 0}^N {a_k } \int_{l_1 }^{l_2 } {T_k (x)} d x = { v }^{\rm T}{ a }_N$ | (15) |
式中
| $ \int_{l_1 }^{l_2 } {f(x)g(x)d x = { f}^{\rm T}} { V g}$ | (16) |
| $ \int_{l_1 }^{l_2 } {f\left( x \right)} g\left( x \right)h\left( x \right)d x = { f }^{\rm T}{ V }_h { g }$ | (17) |
式中
由Chebyshev多项式理论可知,在已知函数
采用Chebyshev多项式对变形场进行逼近,则变形量
| $u\left( {x,t} \right) \approx \sum\limits_{k = 0}^{N - 1} {{a_{uk}}\left( t \right)} {T_k}\left( x \right)$ | (18) |
| $ v\left( {x,t} \right) \approx \sum_{k = 0}^{N - 1} {a_{vk} \left( t \right)} T_k (x) $ | (19) |
由于采用有限项多项式逼近,将式(18)和式(19)代入式(6)后,等式右端并不为0,将存在残差,根据伽辽金方法,选择可用Chebyshev多项式表示的函数
| ${\matrix{ {\int_0^L {{\theta _u}\left( {\ddot u - 2\Omega \dot v - {\Omega ^2}u - \chi u''} \right)} dx = 0} \cr {\int_0^L {{\theta _v}\left[ {\ddot v + 2\Omega \dot u - {\Omega ^2}v - \chi \left( {{{u''}_0}v' + {{u'}_0}v''} \right) + \tau v''''} \right]dx} } \cr } }$ | (20) |
采用Gauss-Lobatto节点,节点值构成
| $\left. {\matrix{ {\theta _u^{\rm{T}}V\left( {\ddot u - 2\Omega \dot v - {\Omega ^2}u - \chi {Q_2}u} \right) = {\bf{0}}} \cr {\theta _v^{\rm{T}}\left[ {V\left( {\ddot v + 2\Omega \dot u - {\Omega ^2}v + \tau {Q_4}v} \right) - } \right.} \cr {\left. {\chi \left( {{V_{\matrix{ {u''} \cr {_0} \cr } }}{Q_1}v + {V_{{{u'}_0}}}{Q_2}v} \right)} \right] = {\bf{0}}} \cr } } \right\}$ | (21) |
表示为矩阵形式为
| $ { \theta }^{\rm T}\left( {{ M}\ddot{ q } + { G}\dot { q} + { K}{ q} } \right) = {\bf 0}$ | (22) |
式中
| ${ q } = \left\{ \!\! \begin{array}{c} { u } \\ { v } \end{array} \!\! \right\} , \quad { \theta } = \left[\!\! \begin{array}{c} {{ \theta }_u } \\ {{ \theta }_v } \end{array} \!\! \right]$ | (23) |
| ${ M } = \left[\!\! \begin{array}{cc} { V } & {\bf 0} \\ { 0 } & { V} \end{array} \!\! \right] , \quad { G } = \left[\!\! \begin{array}{cc} {\bf 0 } & { - 2\Omega { V }} \\ {2\Omega { V }} & {\bf 0} \end{array} \!\! \right]$ | (24) |
| $\eqalign{ & K = \cr & \left[ {\matrix{ { - {\Omega ^2}V - \chi V{Q_2}} & {\bf{0}} \cr {\bf{0}} & { - {\Omega ^2}V + \tau V{Q_4} - \chi \left( {{V_{{{u''}_0}}}{Q_1} + {V_{{{u'}_0}}}{Q_2}} \right)} \cr } } \right] \cr} $ | (25) |
离散后,式(2)中刚性连接边界条件可表示为
| ${ B q } = { b}$ | (26) |
| ${ B } = \left[\!\! \begin{array}{cc} { e }_1 & {\bf 0} \\ {\bf 0 } & { e }_1 \\ {\bf 0 } & { e }_1 { Q }_1 \\ { e }_N { Q }_1 & {\bf 0 } \\ {\bf 0} & { e }_N { Q }_2 \\ {\bf 0} & { e }_N { Q }_3 \end{array} \!\! \right] , \quad { b } = \left[\!\! \begin{array}{c} { 0} \\ { 0} \\ { 0} \\ { 0} \\ { 0} \\ { 0} \end{array} \!\! \right]$ | (27) |
对于式(3) 中弹性边界条件,上式中
| $ { B } = \left[\!\! \begin{array}{cc} { e }_1 & {\bf 0} \\ {\bf 0} & { e }_1 \\ {\bf 0} & EI{ e }_1 { Q }_2 - k_c { E }_1 { Q }_1 \\ { e }_N { Q }_1 & {\bf 0} \\ {\bf 0} & { e }_N { Q }_2 \\ {\bf 0} & { e }_N { Q }_3 \end{array} \!\! \right]$ | (28) |
上述两式中
| $ { q} = { P}\tilde { q} + { R b}$ | (29) |
其中
| $ { \theta } = { P}\tilde {\theta } + { R b}$ | (30) |
将式(29)和式 (30)代入式(22),并考虑到
| $ \tilde{ \theta }^{\rm T}{ P }^{\rm T}\left( {{ M}{ P}\ddot {\tilde { q}} + { G P}\dot {\tilde { q}} + { K P}\tilde { q}} \right) = {\bf 0}$ | (31) |
由于试函数
| $\tilde{ M}\ddot {\tilde { q}} + \tilde{ G}\dot {\tilde { q} } + \tilde { K}\tilde{ q} = {\bf 0}$ | (32) |
| $ \tilde{ M} = { P }^{\rm T}{ M P } ,\quad \tilde{ G} = { P }^{\rm T}{ G P } ,\quad \tilde{ K } = { P }^{\rm T}{ K P }$ | (33) |
根据式(32)采用状态空间法可得到系统模态频率与振型,令
| $ { z } = \left[ \tilde{ q }^{\rm T} \dot {\tilde { q} }^{\rm T} \right]^{\rm T}$ | (34) |
式(32)转换为状态方程
| $ { C}\dot { z} + { D z} = {\bf 0}$ | (35) |
式中
| $ { C} = \left[\!\! \begin{array}{cc} \tilde{ G} & \tilde{ M} \\ \tilde{ M} & {\bf 0} \end{array}\!\! \right] , \quad { D} = \left[\!\! \begin{array}{cc} \tilde{ K} & {\bf 0} \\ {\bf 0} & -\tilde{ M} \\ \end{array} \!\! \right]$ | (36) |
设方程的解为
| $ \left( {s{ C} + { D} } \right){ Z} = {\bf 0}$ | (37) |
式中,
引入以下无量纲变量
| $\eqalign{ & \cr & \left. {\matrix{ {\delta = {R \over L},\quad \alpha = \sqrt {{{A{L^2}} \over I}} ,\quad \gamma = \Omega {L^2}\sqrt {{{\rho A} \over {EI}}} } \cr {f = \omega {L^2}\sqrt {{{\rho A} \over {EI}}} ,\quad \kappa = {{{k_{\rm{c}}}L} \over {EI}}} \cr } } \right\} \cr} $ | (38) |
式中,
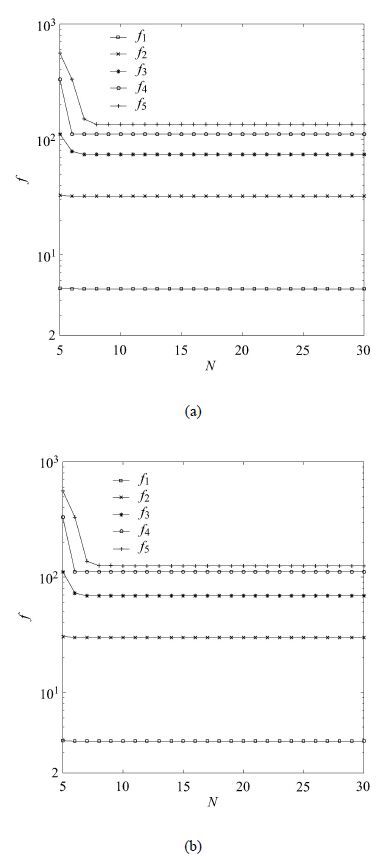
为验证Chebyshev谱方法的有效性,考虑刚性连接边界条件下
|
图 2 无量纲固有频率计算结果收敛性 Fig. 2 The convergence of dimensionless natural frequencies |
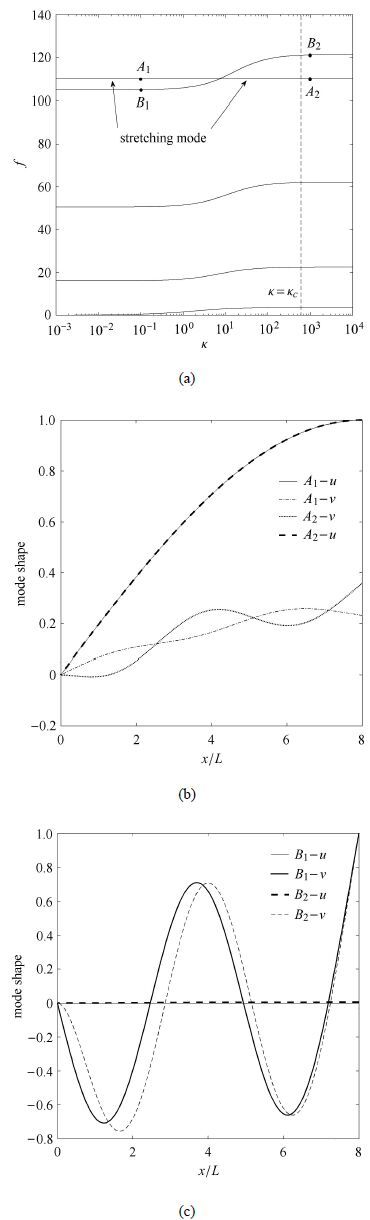
图 3为
|
图 3 弹性连接刚度对系统固有频率与振型的影响 Fig. 3 Variation of dimensionless frequencies and mode shapes with dimensionless connection stiffness |
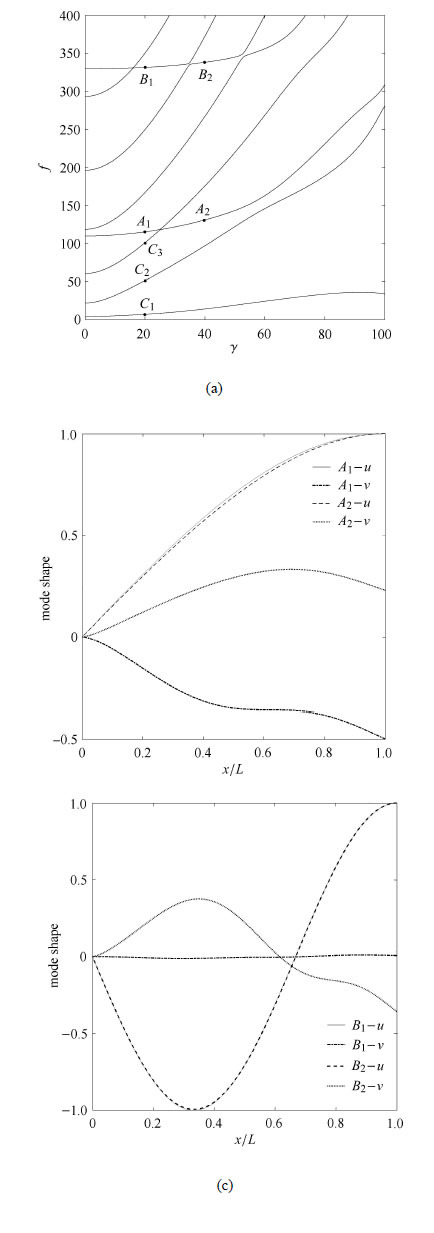
图 4为
|
图 4 角速度比率对模态频率与振型的影响 Fig. 4 Variation of dimensionless frequencies and mode shapes with dimensionless rotating speed |
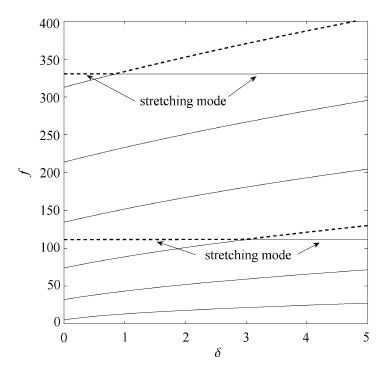
图 5为
|
图 5 系统径长比对无量纲固有频率的影响 Fig. 5 Variation of dimensionless frequencies with ratio of hub's radius and length of beam |
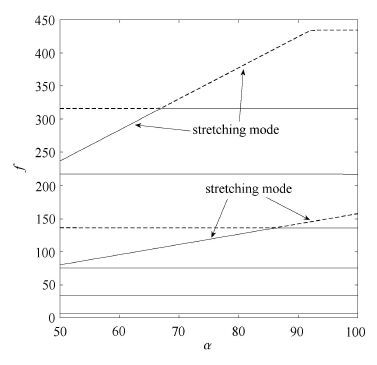
图 6为
|
图 6 梁的长细比对无量纲固有频率影响 Fig. 6 Variation of dimensionless frequencies with slenderness ratio of beam |
(1) Chebyshev谱方法应用于柔性旋转梁动力学分析结果与有限元及加权残余法结果基本一致,采用较少的多项式阶数即可获得与有限元方法相当的精度,采用投影矩阵方法可以方便地用同样形式处理固定及弹性边界条件.
(2) 出现频率转向与振型转换的原因是系统弯曲模态、拉伸模态随系统参数变化规律不一致,变化快的低价模态频率增大并超过原高阶模态频率.
(3) 系统弯曲模态频率随连接刚度呈阶梯状变化,拉伸模态频率不随连接刚度变化而变化,二者频率变化曲线交叉,出现频率转向与振型转换现象,为保证系统动力学特性稳定,连接刚度应大于关键刚度
(4) 系统弯曲模态频率随系统径长比增大而增大,拉伸模态频率不随径长比变化而变化,二者频率变化曲线交叉,出现频率转向与振型转换现象.
(5) 拉伸模态频率随梁的长细比的增大而增大,弯曲模态频率保持不变,二者频率变化曲线交叉,出现频率转向与振型转换现象.
| [1] |
蔡国平, 洪嘉振. 旋转运动柔性梁的假设模态方法研究[J].
力学学报,2005, 37 (1) : 48-56.
( Cai Guoping, Hong Jiazhen. Assumed mode method of a rotating flexible beam[J].
Acta Mechanica Sinica,2005, 37 (1) : 48-56.
(in Chinese) ) ( 0) 0)
|
| [2] |
赵婕, 于开平, 学忠. 末端带有刚体的旋转梁运动稳定性分析[J].
力学学报,2013, 45 (4) : 606-613.
( Zhao Jie, Yu Kaiping, Xue Zhong. The motion stability analysis of a rotating beam with a rigid body on its end[J].
Chinese Journal of Theoretical and Applied Mechanics,2013, 45 (4) : 606-613.
(in Chinese) ) ( 0) 0)
|
| [3] |
赵迪, 尚新春. 含裂纹旋转叶片结构的振动特征分析[J].
武汉大学学报(工学版),2011, 44 (4) : 487-491.
( Zhao Di, Shang Xinchun. Analysis of vibration characteristic of rotating blade with cracks[J].
Engineering Journal of Wuhan University,2011, 44 (4) : 487-491.
(in Chinese) ) ( 0) 0)
|
| [4] |
董兴建, 孟光, 蔡国平, 等. 旋转柔性梁的动力学建模及分析[J].
振动工程学报,2006, 19 (4) : 488-493.
( Dong Xingjian, Meng Guang, Cai Guoping, et al. Dynamic modeling and analysis of a rotating flexible beam[J].
Journal of Vibration Engineering,2006, 19 (4) : 488-493.
(in Chinese) ) ( 0) 0)
|
| [5] |
Kane TR, Ryan R, Banerjee AK. Dynamics of a cantilever beam attached to a moving base[J].
Journal of Guidance Control & Dynamics,1987, 10 (2) : 139-151.
( 0) 0)
|
| [6] |
蔡国平, 洪嘉振. 中心刚体-柔性悬臂梁系统的动力特性研究[J].
航空学报,2004, 25 (3) : 248-253.
( Cai Guoping, Hong Jiazhen. Dynamic analysis of a flexible hub-beam system[J].
Acta Aeronautica et Astronautica Sinica,2004, 25 (3) : 248-253.
(in Chinese) ) ( 0) 0)
|
| [7] |
刘锦阳, 李彬, 洪嘉振. 作大范围空间运动柔性梁的刚-柔耦合动力学[J].
力学学报,2006, 38 (2) : 276-282.
( Liu Jinyang, Li Bin, Hong Jiazhen. Rigid-flexible coupling dynamics of a flexible beam with three-dimensional large overall motion[J].
Chinese Journal of Theoretical and Applied Mechanics,2006, 38 (2) : 276-282.
(in Chinese) ) ( 0) 0)
|
| [8] |
杨辉, 洪嘉振, 余征跃. 动力刚化问题的实验研究[J].
力学学报,2004, 36 (1) : 118-124.
( Yang Hui, Hong Jiazhen, Yu Zhengyue. Experimental investigation on dynamic stiffening phenomenon[J].
Acta Mechanica Sinica,2004, 36 (1) : 118-124.
(in Chinese) ) ( 0) 0)
|
| [9] |
和兴锁, 邓峰岩, 王睿. 具有大范围运动和非线性变形的空间柔性梁的精确动力学建模[J].
物理学报,2010, 59 (3) : 1428-1436.
( He Xingsuo, Deng Fengyan, Wang Rui. Exact dynamic modeling of a spatial flexible beam with large overall motion and nonlinear deformation[J].
Acta Physica Sinica,2010, 59 (3) : 1428-1436.
(in Chinese) ) ( 0) 0)
|
| [10] |
赵国威, 吴志刚. 应变能中耦合项对旋转悬臂梁振动频率的影响[J].
力学学报,2015, 47 (2) : 362-366.
( Zhao Guowei, Wu Zhigang. Effect of coupling terms in strain energy on frequency of a rotating cantilever beam[J].
Chinese Journal of Theoretical and Applied Mechanics,2015, 47 (2) : 362-366.
(in Chinese) ) ( 0) 0)
|
| [11] |
Li L, Zhu WD, Zhang DG, et al. A new dynamic model of a planar rotating hub-beam system based on a description using the slope angle and stretch strain of the beam[J].
Journal of Sound & Vibration,2015, 345 : 214-232.
( 0) 0)
|
| [12] |
陈思佳, 章定国, 洪嘉振. 大变形旋转柔性梁的一种高次刚柔耦合动力学模型[J].
力学学报,2013, 45 (2) : 251-256.
( Chen Sijia, Zhang Dingguo, Hong Jiazhen. A high-order rigid-flexible coupling model of a rotating flexible beam under larger deformation[J].
Chinese Journal of Theoretical and Applied Mechanics,2013, 45 (2) : 251-256.
(in Chinese) ) ( 0) 0)
|
| [13] |
Davide I, Lorenzo D. A fully consistent linearized model for vibration analysis of rotating beams in the framework of geometrically exact theory[J].
Journal of Sound and Vibration,2016, 370 : 351-371.
DOI: 10.1016/j.jsv.2016.01.049. ( 0) 0)
|
| [14] |
李彬, 刘锦阳, 洪嘉振. 计及剪切变形的Timoshenko 梁的刚-柔耦合动力学[J].
计算力学学报,2006, 23 (4) : 419-422.
( Li Bin, Liu Jinyang, Hong Jiazhen. Coupling dynamics of Timoshenko beam with shear deformation[J].
Chinese Journal of Computational Mechanics,2006, 23 (4) : 419-422.
(in Chinese) ) ( 0) 0)
|
| [15] |
李莉, 刘铸永, 洪嘉振. 中心刚体-柔性梁刚柔耦合动力学模型降阶研究[J].
动力学与控制学报,2015, 13 (1) : 6-10.
( Li Li, Liu Zhuyong, Hong Jiazhen. Model reduction of rigid-flexible coupling dynamics of hub-beam system[J].
Journal of Dynamics and Control,2015, 13 (1) : 6-10.
(in Chinese) ) ( 0) 0)
|
| [16] |
章孝顺, 章定国, 陈思佳, 等. 基于绝对节点坐标法的大变形柔性梁几种动力学模型[J].
物理学报,2016, 65 (9) : 0945001.
( Zhang Xiaoshun, Zhang Dingguo, Chen Sijia, et al. Several dynamic models of a large deformation flexible beam based on the absolute nodal coordinate formulation[J].
Acta Physica Sinica,2016, 65 (9) : 0945001.
(in Chinese) ) ( 0) 0)
|
| [17] |
洪嘉振, 刘铸永. 刚柔耦合动力学的建模方法[J].
上海交通大学学报,2008 (11) : 1922-1926.
( Hong Jiazhen, Liu Zhuyong. Modeling methods of rigid-flexible coupling dynamics[J].
Journal of Shanghai Jiaotong University,2008 (11) : 1922-1926.
(in Chinese) ) ( 0) 0)
|
| [18] |
刘又午, 阎绍泽, 张大钧. 计及动力刚化的柔体动力学[J].
中国机械工程,1997 (4) : 81-84.
( Liu Youwe, Yan Shaoze, Zhang Dajun. Dynamics of flexible bodies considering the dynamic stiffening term[J].
China Mechanical Engineering,1997 (4) : 81-84.
(in Chinese) ) ( 0) 0)
|
| [19] |
阎绍泽, 季林红, 范晋伟, 等. 柔性机械系统动力学的变形耦合方法[J].
机械工程学报,2001, 37 (8) : 1-4.
DOI: 10.3901/JME.2001.08.001. ( Yan Shaoze, Ji Linhong. Deformation-coupling modeling method for dynamics of flexible mechanical systems[J].
Chinese Journal of Mechanical Engineering,2001, 37 (8) : 1-4.
(in Chinese) DOI: 10.3901/JME.2001.08.001. ) ( 0) 0)
|
| [20] |
范纪华, 章定国, 洪嘉振. 基于Bezier 插值方法的作大范围旋转运动锥形悬臂梁动力学研究[J].
动力学与控制学报,2012, 10 (4) : 347-354.
( Fan Jihua, Zhang Dingguo, Hong Jiazhen. Dynamic analysis of a rotating tapered cantilever beam based on Bezier curve interpolation[J].
Journal of Dynamics and Control,2012, 10 (4) : 347-354.
(in Chinese) ) ( 0) 0)
|
| [21] |
范纪华, 章定国. 旋转柔性悬臂梁动力学的Bezier 插值离散方法研究[J].
物理学报,2014, 63 (15) : 154501.
( Fan Jihua, Zhang Dingguo. Bezier interpolation method for the dynamics of rotating flexible cantilever beam[J].
Acta Physica Sinica,2014, 63 (15) : 154501.
(in Chinese) ) ( 0) 0)
|
| [22] |
范纪华, 章定国. 旋转悬臂梁动力学的B 样条插值方法[J].
机械工程学报,2012, 48 (23) : 59-64.
DOI: 10.3901/JME.2012.23.059. ( Fan Jihua, Zhang Dingguo. B-spline interpolation method for the dynamics of rotating cantilever beam[J].
Journal of Mechanical Engineering,2012, 48 (23) : 59-64.
(in Chinese) DOI: 10.3901/JME.2012.23.059. ) ( 0) 0)
|
| [23] |
杜超凡, 章定国, 洪嘉振. 径向基点插值法在旋转柔性梁动力学中的应用[J].
力学学报,2015, 47 (2) : 279-288.
( Du Chaofan, Zhang Dingguo, Hong Jiazhen. A meshfree method based on radial point interpolation method for the dynamic analysis of rotating flexible beams[J].
Chinese Journal of Theoretical and Applied Mechanics,2015, 47 (2) : 279-288.
(in Chinese) ) ( 0) 0)
|
| [24] |
杜超凡, 章定国. 基于无网格点插值法的旋转悬臂梁的动力学分析[J].
物理学报,2015, 64 (3) : 34501.
( Du Chaofan, Zhang Dingguo. A meshfree method based on point interpolation for dynamic analysis of rotating cantilever beams[J].
Acta Physica Sinica,2015, 64 (3) : 34501.
(in Chinese) ) ( 0) 0)
|
| [25] |
Cheng JL, Xu H, Yan AZ. Frequency analysis of a rotating cantilever beam using assumed mode method with coupling effect[J].
Mechanics Based Design of Structures & Machines,2006, 34 (1) : 25-47.
( 0) 0)
|
| [26] |
朱由锋, 任勇生. 基于有限差分法的水平旋转梁自由振动解析[J].
振动与冲击,2012, 31 (14) : 43-46.
( Zhu Youfeng, Ren Yongsheng. Free vibration analysis of horizontal spinning beams by using finite difference method[J].
Journal of Vibration and Shock,2012, 31 (14) : 43-46.
(in Chinese) ) ( 0) 0)
|
| [27] |
Kee YJ, Shin SJ. Structural dynamic modeling for rotating blades using three dimensional finite elements[J].
Journal of Mechanical Science and Technology,2015, 29 (4) : 1607-1618.
DOI: 10.1007/s12206-015-0332-6. ( 0) 0)
|
| [28] |
Kim H, Hong HY, Chung J. Dynamic model for free vibration and response analysis of rotating beams[J].
Journal of Sound & Vibration,2013, 332 (22) : 5917-5928.
( 0) 0)
|
| [29] |
蒋丽忠, 洪嘉振. 大范围运动对弹性梁振动频率及模态的影响[J].
振动与冲击,1999, 18 (2) : 12-16.
( Jiang Lizhong, Hong Jiazhen. The frequency and mode of elastic beams in large overall motion[J].
Journal of Vibration and Shock,1999, 18 (2) : 12-16.
(in Chinese) ) ( 0) 0)
|
| [30] |
杨辉, 洪嘉振, 余征跃. 一类刚-柔耦合系统的模态特性与实验研究[J].
宇航学报,2002, 23 (2) : 67-72.
( Yang Hui, Hong Jiazhen, Yu Zhengyue. Vibration analysis and experiment investigation for a typical rigid-flexible coupling system[J].
Journal of Astronautics,2002, 23 (2) : 67-72.
(in Chinese) ) ( 0) 0)
|
| [31] |
杨辉, 洪嘉振, 余征跃. 柔性多体系统动力学实验研究综述[J].
力学进展,2004, 34 (2) : 171-181.
( Yang Hui, Hong Jiazhen, Yu Zhengyue. Survey of experiments for dynamics of flexible multibody system[J].
Advances in Mechanics,2004, 34 (2) : 171-181.
(in Chinese) ) ( 0) 0)
|
| [32] |
方建士, 黎亮, 章定国, 等. 基于刚柔耦合动力学的旋转悬臂梁的频率转向与振型转换特性[J].
机械工程学报,2015, 51 (17) : 59-65.
DOI: 10.3901/JME.2015.17.059. ( Fang Jianshi, Li Liang, Zhang Dingguo, et al. Frequency veering and mode shape interaction properties of a rotating cantilever beam based on rigid-flexible coupling dynamics[J].
Journal of Mechanical Engineering,2015, 51 (17) : 59-65.
(in Chinese) DOI: 10.3901/JME.2015.17.059. ) ( 0) 0)
|
| [33] |
Zhao Z, Liu C, Ma W. Characteristics of steady vibration in a rotating hub–beam system[J].
Journal of Sound & Vibration,2016, 363 : 571-583.
( 0) 0)
|
| [34] |
宋春明, 王明洋, 王德荣. 柔性动边界梁的弹塑性动力响应分析[J].
工程力学,2008, 25 (12) : 42-47.
( Song Chun-ming, Wang Mingyang, Wang Derong. Analysis of elastic-plastic dynamic responses of beams with flexible supports[J].
Engineering Mechanics,2008, 25 (12) : 42-47.
(in Chinese) ) ( 0) 0)
|
| [35] |
Sarvestan V, Mirdamadi HR, Ghayour M, et al. Spectral finite element for vibration analysis of cracked viscoelastic Euler–Bernoulli beam subjected to moving load[J].
Acta Mechanica,2015, 226 (12) : 1-22.
( 0) 0)
|
| [36] |
Cheng Y, Yu Z, Wu X, et al. Vibration analysis of a cracked rotating tapered beam using the p-version finite element method[J].
Finite Elements in Analysis & Design,2011, 47 (7) : 825-834.
( 0) 0)
|
| [37] |
江凡, 薛冬新, 宋希庚. 裂纹悬臂梁的扭转弹簧模型及其实验验证[J].
振动、测试与诊断,2004, 24 (2) : 143-162.
( Jiang Fan, Xue Dongxin, Song Xigeng. Analysis and experiments of cracked cantilever beam using torsional spring model[J].
Journal of Vibration, Measurement & Diagnosis,2004, 24 (2) : 143-162.
(in Chinese) ) ( 0) 0)
|
| [38] |
Yagci B, Filiz S, Romero LL, et al. A spectral-Tchebychev technique for solving linear and nonlinear beam equations[J].
Journal of Sound & Vibration,2007, 321 (s1-2) : 375-404.
( 0) 0)
|
| [39] |
Romero L, Filiz S, Ozdoganlar OB. An analytical model for microendmill Dynamics[J].
Journal of Control & Vibration,2008, 14 (8) : 1125-1150.
( 0) 0)
|
| [40] |
Huang CL, Lin WY, Hsiao KM. Free vibration analysis of rotating Euler beams at high angular velocity[J].
Computers & Structures,2010, 88 (17) : 991-1001.
( 0) 0)
|
| [41] |
Chung J, Yoo HH. Dynamic analysis of a rotating cantilever beam by using the finite element method[J].
Journal of Sound & Vibration,2002, 249 (1) : 147-164.
( 0) 0)
|
 2016, Vol. 48
2016, Vol. 48
