非线性切换系统具有广泛的工程背景,其复杂动力学行为及其机理研究是当前国内外动力学与控制领域的热点课题之一[1-7],如电路系统中继电、饱和、滞环等环节以及发电机组或大型设备进出电网[8],汽车行驶过程中的换档[9]等都有非线性切换系统的应用.目前关于非线线性切换系统的工作大都都局限于系统的稳定性及稳定条件分析,如Zhang等[10]给出了一类非线性切换系统的稳定性条件,Xiang等[11]基于状态更新探讨了一类不确定非线性切换系统的鲁棒性,Jin等[12]提出了一种控制非线性切换序列稳定性的新方法.但是,上述相关工作包括其他一些相关类型的研究[13-17]基本上都是围绕平衡点的稳定性开展的,即使对于控制,其目标也是尽快实现平衡点的稳定[18-24],而实际系统存在着各种各样的平衡态,可能是周期振荡、概周期振荡、有时甚至是混沌振荡.同时,不同参数的变化会影响切换系统的特性,因此需要深入探讨切换系统的动力学演化过程,进而揭示其复杂性本质.
非线性切换系统有不同的切换模式,主要有时间切换、状态切换和混合切换等模式.对于时间切换模式如周期切换等非线性切换系统,国内外学者开展了研究工作,取得了一定成果[25-28].而切换模式依赖于状态变量的非线性切换系统的研究相对较少,如Kousaka等[29]介绍了一种二维非线性切换系统在状态切换模式下的动力学特性,给出了一种切换系统分岔的一种验证方法,并且发现切分岔和全局分岔是产生各种周期解和混沌的主要原因;另外张春等[30]在Duffing振子和vanderPol振子之间引入混合切换条件,给出了相关Lyapunov指数的算法,并研究了其动力学特性.但是Kousaka给出的系统维数较低,而张春所做的混合切换没有具体的物理模型进行验证,还存在可优化之处,因此相关工作尚处在初步阶段,许多问题尤其是各种状态切换下的振荡行为及机理分析还有待进一步深入.
本文为了分析双状态切换面导致的各种复杂行为及其演化过程,引入典型的广义BVP振子[31],构建双状态切换下的非线性系统模型,以期揭示其复杂本质.这对于深入理解非线性状态切换系统的各种新的复杂现象,进而发展非线性理论具有一定的科学意义,同时对于实际切换系统中的新现象解释、参数识别、模型论证以及控制技术等等也具有一定的实际应用价值.
1 切换系统的数学模型
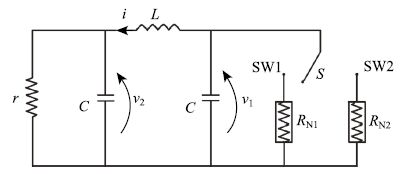
考察引入双向开关切换的广义BVP振子,如图 1所示.该系统由一个线性电阻
|
图 1 广义BVP切换电路 Fig. 1 The extended BVP switching circuit |
| $\begin{equation}\label{eq1} \left. {\begin{array}{l} C\dfrac{{\rm d}v_1 }{{\rm d}t} =-i_1-g_\sigma (v_1 ),\\ C\dfrac{{\rm d}v_2 }{{\rm d}t} = i_1-\dfrac{v_2 }{r},\\ L\dfrac{{\rm d}i_1 }{{\rm d}t} = v_1-v_2 . \\ \end{array}}~~\sigma = 1,2\right\}\end{equation}$ | (1) |
其中
引入
| $\begin{equation}\label{eq2} \left. {\begin{array}{l} \dot x=-z + A_\sigma x + \tanh B_\sigma x \\ \dot y = z-\delta y \\ \dot z= x-y \\ \end{array}},~~~ \sigma = 1,2\right\}\end{equation}$ | (2) |
切换系统方程(2)可简写为
| $\begin{equation}\label{eq3} \dot { X}= { F}_\sigma ({ X}),\quad\sigma =1,2\end{equation}$ | (3) |
其中
| $\sigma = \left\{ {\matrix{ {1,\quad \sigma = 2} \hfill \cr {2,\quad \sigma = 1} \hfill \cr } {\rm{and}}\matrix{ {x = {x_{01}}} \cr {x = {x_{02}}} \cr } } \right.$ |
其相应的无量纲数学模型以一定的规律在两个子系统之间切换,显然该切换系统存在两个不同的状态切换面,即
由于切换系统(3)涉及到两个向量场,其动力学行为与两个向量场的动力学特性密切相关.为揭示该切换系统的复杂行为,首先讨论两子系统的分岔特性.
为方便起见,在此假设参数
从图 2可以看出,随着参数

|
图 2 子系统随参数变化的分岔图 Fig. 2 The bifurcation diagram of the subsystem |
数值仿真可以发现与上述平衡点分岔特性相吻合的动力学演化过程,即在
由于切换系统是一个非光滑系统,其诸如周期运动和混沌运动的动力学行为必须通过一定的统计规律加以验证,本文用Lyapunov指数加以验证.
对于平衡点和周期运动,很多学者常用系统在平衡点的Jacobi矩阵特征值实部以及周期运动扰动方程的特征指数实部来判断其稳定性.Lyapunov指数是对上述特征值和特征指数的一种推广,给出了对系统任意相邻相轨线平均发散程度或平均收敛程度的一种度量.因此,它可以度量系统吸引子的稳定性,还可以判定吸引子的类型,如平衡点、周期运动、概周期运动及混沌运动等,是目前判断各种动力学行为的一种可靠定量方法.但对于非光滑系统(尤其是状态切换系统),李雅普诺夫指数的计算不能直接使用光滑系统的方法,需要采用复合系统的微分包含理论和Poincaré映射的数学方法,对于切换部分需要使用复合映射及复合映射的链式法则进行计算,并进行必要的处理. 下面分2节介绍其具体计算原理.
3.1 Lyapunov指数
在计算非线性切换动力系统Lyapunov指数时,采用Poincaré映射的数学方法,即应用Poincaré映射
| $\begin{equation}\label{eq4} { X}_{(k)} = P({ X}_{(k-1)} ),{ X} \in R^3,k = 1,2,\cdots ,N\end{equation}$ | (4) |
注意到在
| $\delta { X}_{^{(k-1)}} = {X}_{^{(k-1)}} ({ X}_{^0} + \delta { X}_{^0} )-{X}_{^{(k-1)}} ({ X}_{^0} )$ |
充分小,式(4)在
| $\delta { X}_{^{(k)}} = DP({ X}_{^{(k-1)}} )\delta {X}_{^{(k-1)}}$ |
由上式递推得到
| $\delta { X}_{^{(k)}} = DP_{^k} ({ X}_{^{(0)}} )\delta {X}_{^{(0)}} ,\quad {{ X} \in R^3},$k = 1,2,\cdots ,N$ |
式中
| $\begin{equation}\label{eq5}\begin{array}{c} DP_k ({ X}_{(0)} ) = DP({ X}_{(k-1)} \times \\ DP({ X}_{(k-2)} )\times \cdots \times DP({ X}_{(0)} ) \\ \end{array}\end{equation}$ | (5) |
由此离散系统可得整个切换系统的Lyapunov指数
| $\begin{equation}\label{eq6} \lambda = \mathop {\lim }\limits_{N \to \infty }\frac{1}{N}\sum\limits_{k = 0}^{N-1} {\ln \left| {DP_{^k} ({X}_{^{(0)}} )} \right|}\end{equation}$ | (6) |
对于非光滑系统如切换系统必须使用复合映射及复合映射求导的链式法则求出对应的Poincaré映射
设
| $\varSigma{}_1=\{({ X},t) = (x,y,z,t) \in R^3\times R^+|x =x_{01}\}$ |
其中,
| $\varSigma{}_2 { = \left\{ {({ X},t) = (x,y,z,t) \in R^3\times R^ + \left| {x = x_{02} } \right.} \right\}}$ |
其中,
| $\varSigma{} { = \left\{ {{ X} = (x,y,z) \in R^3\left| {x =x_{\rm ref} } \right.} \right\}}$ |
这样在
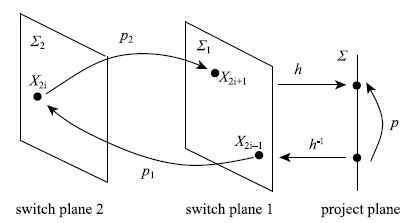
| $\varSigma \buildrel {h^{-1}} \over \longrightarrow \varSigma{}_1\buildrel {P_1 } \over \longrightarrow \varSigma{}_2 \buildrel {P_2 } \over \longrightarrow \varSigma{}_1 \buildrel h \over \longrightarrow \varSigma $ |
其中
| $\begin{array}{lll}P_1:\varSigma _1 \to \varSigma _2 \\{ X}_{2i-1} \mapsto { X}_{2i} = \varphi _1 (T_1 ,{X}_{2i-1} )\\ P_2 : \varSigma _2 \to \varSigma _1\\ { X}_{2i + 1} \mapsto \varphi _2 (T_2 ,{ X}_{2i} ) = \varphi _2 (T_2 ,\varphi (T_1 ,{ X}_{2i-1} ))=\\ \quad~~ \varphi _2 \circ \varphi _1 (T_1 + T_2 ,{ X}_{2i-1} )\\ h:\varSigma _1 \to \varSigma ,~~(x,y,z) \mapsto (y,z)~~\mbox{即}\\ h_1 (x,y,z) = y,~~ h_2 (x,y,z) = z\\ h^{-1}:\varSigma \to \varSigma _1,~~(y,z) \mapsto (x,y,z)~~\mbox{即}\\ h_1^{-1} (y,z) = x,~~h_2^{-1} (y,z) = y\\ h_3^{-1} (y,z) = z\end{array}$ |
|
图 3 Poincaré截面和Poincaré映射示意图 Fig. 3 Poincaré section and Poincaré mapping |
于是
| $\begin{equation}\label{eq7} { D}P = \nabla h \circ { D}P_2 \circ { D}P_1\circ \nabla h^{-1}\end{equation}$ |
设映射
| $\frac{{\rm d}{ X}}{{\rm d}t} = { F}_\sigma ({ X}),\quad \sigma = 1,2$ | (7) |
由于
| ${ D}P_1 = \left( {{ I}-\frac{{ F}_1 ({ X}_{2i})\times \nabla q_1 }{\nabla q_1 \cdot { F}_1 ({ X}_{2i} )}}\right)\times \left( {\frac{\partial \varphi _1 }{\partial { X}_{2i-1} }} \right)$ |
同理
| ${ D}P_2 = \left( {{ I}-\frac{{ F}_2 ({ X}_{2i + 1})\times \nabla q_2 }{\nabla q_2 \cdot { F}_2 ({ X}_{2i + 1})}} \right)\times \left( {\frac{\partial \varphi _2 }{\partial { X}_{2i} }} \right)$ |
其中,
| $\left. {\begin{array}{ll} \dfrac{{\rm d}}{{\rm d}t}\left[{\dfrac{\partial \varphi _\sigma }{\partial { u}}} \right] =\dfrac{\partial { F}_\sigma }{\partial x}\dfrac{\partial x}{\partial { u}} \\ \dfrac{\partial { X}}{\partial { u}} = { I} \\ \end{array}},\quad \sigma = 1,2\right\}$ |
方程组求出,这里
| $\nabla h = \left( {{\begin{array}{*{20}c} {\dfrac{\partial h_1 }{\partial x}} & {\dfrac{\partial h_1 }{\partial y}} & {\dfrac{\partial h_1 }{\partial z}} \\ {\dfrac{\partial h_2 }{\partial x}} & {\dfrac{\partial h_2 }{\partial y}} & {\dfrac{\partial h_2 }{\partial z}} \\ \end{array} }} \right) =\left[{{\begin{array}{*{20}c} 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array} }} \right] $ |
| $\nabla h^{-1} = \left( {{\begin{array}{*{20}c} {\dfrac{\partial h_1^{-1} }{\partial y}} & {\dfrac{\partial h_1^{-1} }{\partial z}} \\ {\dfrac{\partial h_2^{-1} }{\partial y}} & {\dfrac{\partial h_2^{-1} }{\partial z}} \\ {\dfrac{\partial h_3^{-1} }{\partial y}} & {\dfrac{\partial h_3^{-1} }{\partial z}} \\ \end{array} }} \right) =\left[{{\begin{array}{*{20}c} 0 & 0 \\ 1 & 0 \\ 0 & 1 \\ \end{array} }} \right]~~~~~~~~~~~$ |
注意到,由于此处切换面均与
由于状态切换条件的引入,整个系统轨迹会依次受到不同向量场的控制,从而引起复杂的动力学行为. 首先考察两子系统的运动特征.
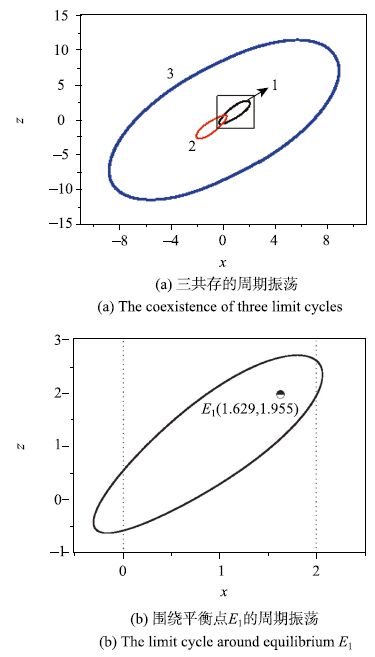
在子系统1中选取参数为
|
图 4 系统的稳定吸引子( |
在子系统二中固定参数
| $\eqalign{ & \sum {_1} = \left\{ {(X,t) = (x,y,z,t) \in {R^3} \times {R^ + }\left| {x = 0.0} \right.} \right\} \cr & \sum {_2} = \left\{ {(X,t) = (x,y,z,t) \in {R^3} \times {R^ + }\left| {x = 2.0} \right.} \right\} \cr} $ |
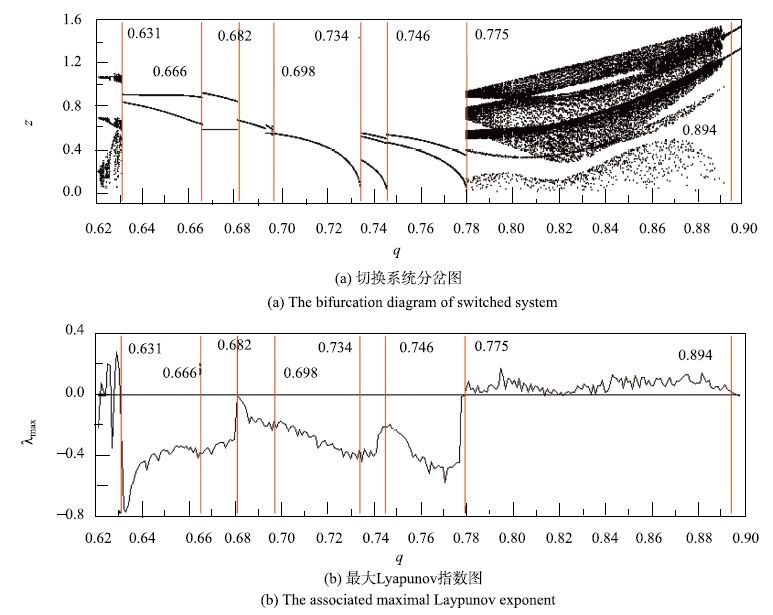
确定两子系统参数及切换面之后,利用数值仿真画出切换系统随参数
|
图 5 切换系统的分岔图和最大Lyapunov指数图 Fig. 5 The bifurcation characteristic of switched system |
稳定的周期振荡在
值得注意的是,当参数
图 6分别给出了
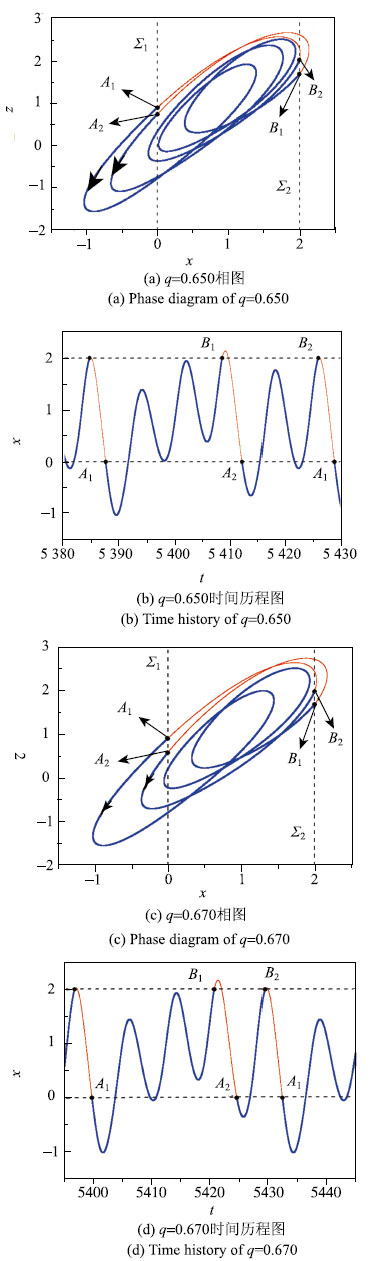
|
图 6 突变点 |
从图 6可以看出,两周期振荡的轨迹存在着很大的差异,导致这种差异的原因在于参数
同样在突变点
依然从相同的
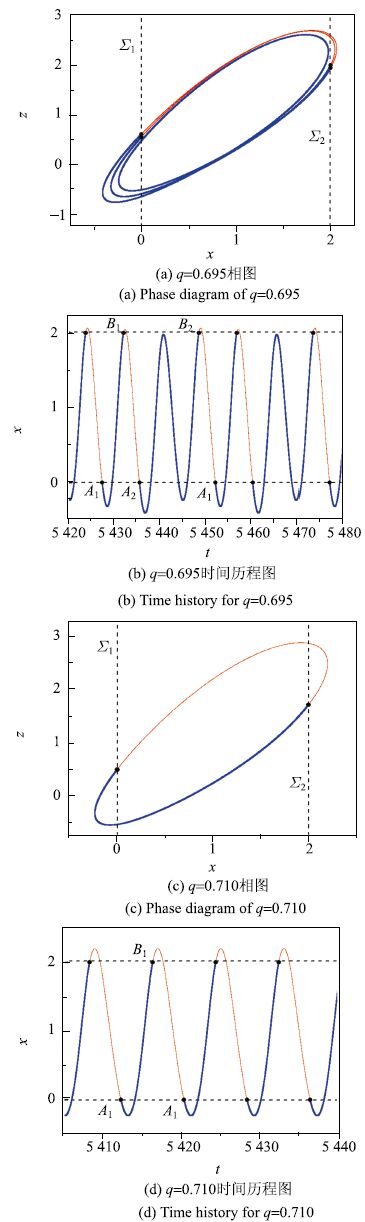
|
图 7 突变点 |
稳定的周期振荡在
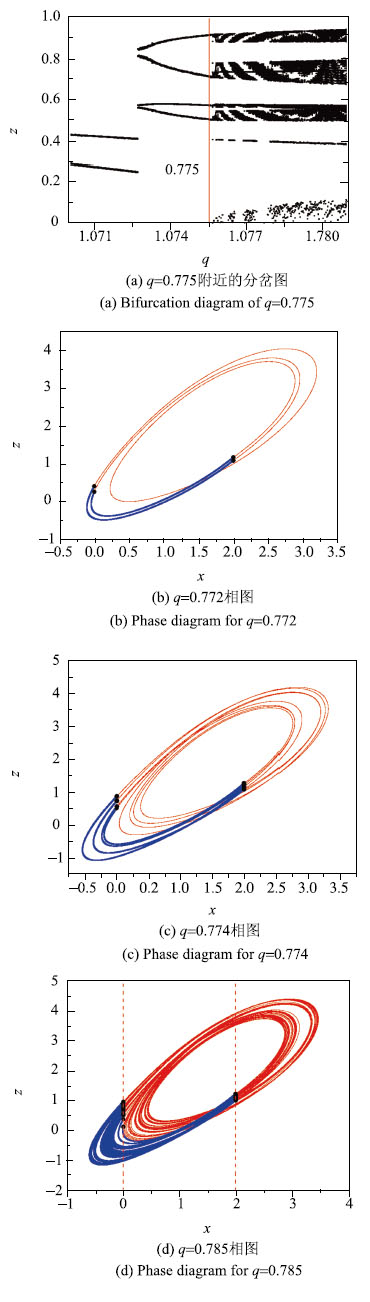
|
图 8 周期直接分岔为混沌 Fig. 8 Period-doubling bifurcation to chaos |
必须指出的是,切换系统的倍周期分岔序列与光滑系统中的倍周期分岔序列不同,因为在光滑系统中只存在单个系统,而在切换系统中,轨迹的运动涉及到两个不同的子系统,而且,其中的一个子系统随参数
与固定时间切换和单状态切换系统不同,双临界状态切换系统存在着更为复杂的非线性现象,如周期突变现象,即在突变点参数的两侧,虽然同样是周期运动,但其运动模式和相应的周期均会存在很大的差异,导致这一现象的主要原因在于切换点的位置及相应的子系统的吸引子存在明显的区别.同时,系统也存在着倍周期分岔序列导致混沌的道路,然而,与光滑系统中的倍周期分岔序列不同,切换系统的倍周期分岔序列只对应于切换点数目的成倍增加,而其相应的周期一般不对应于严格的周期倍化过程.
| [1] |
Pérez C, Bensítez F. Switched convergence of second-order switch nonlinear systems[J].
Journal of Control, Automation, and Systems,2012, 10 (5) : 920-930.
DOI: 10.1007/s12555-012-0508-0. ( 0) 0)
|
| [2] |
王仁明, 关治洪, 刘新芝. 一类非线性切换系统的稳定性分析[J].
系统工程与电子技术,2004, 26 (1) : 68-71.
( Wang Renming, Guan Zhihong, Liu Xinzhi. Stability analysis for a class of nonlinear switched systems[J].
Systems Engineering and Electronics,2004, 26 (1) : 68-71.
(in Chinese) ) ( 0) 0)
|
| [3] |
Davila J, Pisano A, Usai E. Continuous and discrete state reconstruction for nonlinear switched system via high-order sliding-mode observers[J].
International Journal of System Science,2011, 42 (5) : 725-735.
DOI: 10.1080/00207721.2010.518254. ( 0) 0)
|
| [4] |
刘正凡, 蔡晨晓, 段文勇, 等. 不确定切换时滞非线性系统状态切换的指数稳定性[J].
控制与决策,2014, 29 (12) : 2247-2252.
( Liu Zhengfan, Cai Chenxiao, Duan Wenyong, et al. Exponential stability of uncertain switched nonlinear time-delay systems with statedependent switching[J].
Control and Decision,2014, 29 (12) : 2247-2252.
(in Chinese) ) ( 0) 0)
|
| [5] |
Oishi M, Mitchell I, Bayen AM, et al. Hybrid verification of an interface for an automatic landing[J].
Proceeding of the IEEE Conference on Decision and Control,2002, 2 : 1607-1613.
DOI: 10.1109/CDC.2002.1184749. ( 0) 0)
|
| [6] |
Bishop BE, Spong MW. Control of redundant manipulators using logic-based switching[J].
Proceedings of the 36th IEEE Conference on Decision and Control,1998, 2 : 16-18.
( 0) 0)
|
| [7] |
Horowitz R, Varaiya P. Control design of an automated highway system[J].
Proceedings of IEEE,2000, 88 (7) : 913-925.
DOI: 10.1109/5.871301. ( 0) 0)
|
| [8] |
方志明. 切换系统稳定性分析与优化控制若干问题研究. [博士论文]. 南京: 南京理工大学, 2012
( Fang Zhiming. Study on several problems of stability and optimal control of switched systems. [PhD Thesis]. Nanjing: Nanjing University of Science & Technology, 2012 (in Chinese)
) ( 0) 0)
|
| [9] |
Goncalves JM. Constructive global analysis of hybrid systems. [PhD thesis]. MA, USA:Massachusetts Institute of Technology, 2000
( 0) 0)
|
| [10] |
Zhang JF, Han ZZ, Zhu FB, et al. Absolute exponential stability and stabilization of switched nonlinear systems[J].
Systems & Control Letters,2014, 66 (1) : 51-57.
( 0) 0)
|
| [11] |
Xiang WM, Xiao J, Iqba MN. Robust fault detection for a class of uncertain switched nonlinear systems via the state updating approach[J].
Nonlinear Analysis: Hybrid Systems,2014, 12 (2) : 132-146.
( 0) 0)
|
| [12] |
Jin Y, Fu J, Zhang YM, et al. Reliable control of a class of switched cascade nonlinear systems with its application to flight control[J].
Nonlinear Analysis: Hybrid Systems,2014, 11 (1) : 11-21.
( 0) 0)
|
| [13] |
Yu Aleksandrov A, Chen Y, Platonov AV, et al. Stability analysis for a class of switched nonlinear systems[J].
Automatica,2011, 47 (10) : 2286-2291.
DOI: 10.1016/j.automatica.2011.08.016. ( 0) 0)
|
| [14] |
Moulay E, Bourdais R, Perruquetti W. Stabilization of nonlinear switched systems using control Lyapunov functions[J].
Nonlinear Analysis: Hybrid Systems,2007, 1 (4) : 482-490.
DOI: 10.1016/j.nahs.2005.12.001. ( 0) 0)
|
| [15] |
Liu YY, Zhao J. Stabilization of switched nonlinear systems with passive and non-passive subsystems[J].
Nonlinear Dyn,2012, 67 (3) : 1709-1716.
DOI: 10.1007/s11071-011-0098-z. ( 0) 0)
|
| [16] |
Colaneria P, Geromelb JC, Astolfic A. Stabilization of continuoustime switched nonlinear systems[J].
Systems & Control,2008, 57 (1) : 95-103.
( 0) 0)
|
| [17] |
Alessandria A, Sanguineti M. Connections between Lp stability and asymptotic stability of nonlinear switched systems[J].
Nonlinear Analysis: Hybrid Systems,2007, 1 (1) : 501-509.
( 0) 0)
|
| [18] |
Hajiahmadi M, De Schutter B, Hellendoorn H. Stabilization and robust H1 control for sector-bounded switched nonlinear systems[J].
Automatica,2014, 50 (10) : 2726-2731.
DOI: 10.1016/j.automatica.2014.08.015. ( 0) 0)
|
| [19] |
Han TT, Ge SS, Lee TH. Adaptive neural control for a class of switched nonlinear systems[J].
Systems & Control Letters,2009, 58 (2) : 109-118.
( 0) 0)
|
| [20] |
Elfarra NH, Mhaskar P, Christofider PD. Output feedback control of switched nonlinear systems using multiple Lyapunov functions[J].
Systems & Control Letters,2005, 54 (12) : 1163-1182.
( 0) 0)
|
| [21] |
Chiang ML, Fu LC. Rubust output feedback stabilization of switched nonlinear systems with average dwell time[J].
Asian Journal of Control,2014, 16 (1) : 264-276.
DOI: 10.1002/asjc.2014.16.issue-1. ( 0) 0)
|
| [22] |
Jouili K, Braiek NB. Stabilization of non-minimum phase switched nonlinear systems with the concept of multi-diffeomorphism[J].
Commun Nonlinear Sci Numer Simulat,2015, 23 (1-3) : 282-293.
DOI: 10.1016/j.cnsns.2014.11.018. ( 0) 0)
|
| [23] |
Mojica-Nava E, Quijano N, Rakoto-Ravalontsalama N. A polynomial approach for optimal control of switched nonlinear systems[J].
Robust Nonlinear Control,2014, 24 (12) : 1797-1808.
DOI: 10.1002/rnc.v24.12. ( 0) 0)
|
| [24] |
Lin Q, Loxton R, Teo KL. Optimal control of nonlinear switched systems: computational methods and applications[J].
Journal of the Operations Research Society of China,2013, 1 (3) : 275-311.
DOI: 10.1007/s40305-013-0021-z. ( 0) 0)
|
| [25] |
陈章耀, 雪增红, 张春, 等. 周期切换下Rayleigh 振子的振荡行为及机理[J].
物理学报,2014, 63 (1) : 1-8.
( Chen Zhangyao, Xue Zenghong, Zhang Chun, et al. Oscillation behaviors and mechanism of Rayleigh oscillator with periodic switches[J].
Acta Phys. Sin,2014, 63 (1) : 1-8.
(in Chinese) ) ( 0) 0)
|
| [26] |
Jerome JW. Time dependent closed quantum systems: nonlinear Kohn–Sham potential operators and weak solutions[J].
Journal of Mathematical Analysis and Applications,2015, 429 (2) : 995-1006.
DOI: 10.1016/j.jmaa.2015.04.047. ( 0) 0)
|
| [27] |
Yang JQ, Chen YT, Zhu FL, et al. Synchronous switching observer for nonlinear switched systems with minimum dwell time constraint[J].
Journal of the Franklin Institute,2015, 352 (11) : 4665-4681.
DOI: 10.1016/j.jfranklin.2015.07.010. ( 0) 0)
|
| [28] |
Ma RC, Zhao SZ, Wang M. Global robust stabilisation of a class of uncertain switched nonlinear systems with dwell time specifications[J].
International Journal of Control,2014, 87 (3) : 589-599.
DOI: 10.1080/00207179.2013.852247. ( 0) 0)
|
| [29] |
Kousaka T, Ueta T, Kawakami H. Bifurcation of switched nonlinear dynamical systems[J].
IEEE Trans. Circuits Syst,1999, 46 (7) : 878-885.
DOI: 10.1109/82.775383. ( 0) 0)
|
| [30] |
Zhang C, Bi QS, Han XJ, et al. On two-parameter bifurcation analysis of switched system composed of Duffing and van der Pol oscillators[J].
Communications in Nonlinear Science and Numerical Simulation,2014, 19 (3) : 750-757.
DOI: 10.1016/j.cnsns.2013.06.028. ( 0) 0)
|
| [31] |
Nishiuchi Y, Ueta T, Kawakami H. Stable torus and its bifurcation phenomena in a simple three-dimensional autonomous circuit[J].
Chaos, Solitons and Fractals,2006, 27 (4) : 941-951.
DOI: 10.1016/j.chaos.2005.04.092. ( 0) 0)
|
 2016, Vol. 48
2016, Vol. 48
