工程结构在服役过程中往往承受着复杂的多轴非比例循环载荷.试验结果表明:相比于单轴或比例加载条件,多轴非比例加载条件下的结构构件有更快的损伤累积和更短的疲劳寿命[1-11].对多轴非比例疲劳而言,由于研究初期受试验条件等的限制,研究者们难以解释多轴非比例疲劳损伤破坏的机理;在确定多轴非比例疲劳损伤控制参量时,通常采用一个等效应变量,然后将单轴加载条件下的Manson-Coffin疲劳寿命预测公式推广应用于多轴非比例疲劳寿命的预测.尽管等效应变法对多轴比例疲劳寿命的预测结果相对满意,但基于等效应变法进行多轴非比例疲劳寿命预测时,寿命预测结果与试验结果相比误差较大[1-2, 11]. 因此,需要发展新的疲劳损伤控制参量进行多轴非比例疲劳寿命的预测和评估.目前,疲劳损伤临界面法因具有较为明确的物理意义而被广泛讨论和研究.
临界破坏平面概念基于疲劳裂纹萌生及扩展断裂机理,该机理认为疲劳失效发生在某一特定材料平面上,疲劳损伤的累积、疲劳寿命的估算都在该平面上进行. Brown和Miller[3]较早研究了基于应变参量的多轴疲劳损伤临界面法.他们认为:疲劳寿命可表示为疲劳损伤临界面上应变状态的函数,通过将最大剪应变幅平面定义为疲劳临界面,提出了适用于多轴低周疲劳寿命预测的临界面模型.之后,疲劳研究者们针对基于应变参量的多轴非比例低周疲劳临界面法进行了大量的研究,提出了诸多临界面损伤控制准则,如Kandil-Brown-Miller (KBM)准则[1]、Socie准则[4]、Lohr-Ellison准则[5]、Fatemi-Socie (FS)准则[6]、Wang-Yao准则[7]、Shang-Wang准则[8]、MKBM准则[9]等.Karolczuk等[10]和You等[11]综述了不同学者提出的多轴非比例低周疲劳临界面法,指出:不同学者在构建多轴非比例低周疲劳临界面准则时,一般将最大剪切应变幅平面定义为疲劳损伤临界面,通过将疲劳临界面上的最大剪切应变幅和该平面上的法向正应变或法向正应力进行(非)线性组合来建立临界面疲劳损伤控制参量,并结合Manson-Coffin公式进行多轴非比例低周疲劳寿命的预测.虽然多轴疲劳寿命临界面法具有明确的物理意义,但是不同学者提出的各类疲劳寿命预测临界面模型并不能适用于所有的材料类型,建立统一适用的多轴非比例疲劳临界面损伤控制参量仍需要大量的研究[8, 11].
本文基于5种材料的圆管薄壁试件在拉-扭复合加载情况下的多轴疲劳试验结果,对比分析了多轴非比例低周疲劳临界面法中广泛讨论的KBM模型和FS模型,指出了FS模型的不足;通过分析非比例加载条件引起多轴疲劳寿命降低的原因,提出了一个能考虑非比例加载路径变化和材料附加强化效应双重作用的非比例影响因子,参照FS准则提出了一种新的多轴非比例低周疲劳寿命预测临界面模型;利用5种材料的多轴疲劳试验数据,将本文提出的临界面模型对多轴非比例疲劳寿命的预测精度与FS模型的预测精度进行了对比分析.
1 临界面法 1.1 临界面模型
Brown和Miller[3]根据疲劳裂纹的物理解释提出基于应变参量的多轴疲劳寿命预测临界面法后,疲劳研究学者们主要是基于不同材料的圆管薄壁试件在拉-扭复合加载条件下的多轴疲劳试验结果,提出了不同形式的多轴低周疲劳临界面准则[12-13],其中最广泛讨论的两种临界面准则是KBM准则和FS准则. Kandil, Brown和Miller[1]的研究认为,材料的疲劳损伤起始于最大剪切应变幅平面;他们通过分析临界面上剪切应变和法向正应变对裂纹发展过程的共同贡献,将临界面疲劳损伤控制参量表示为最大剪切应变幅
| $\eqalign{ & {{\Delta {\gamma _{\max }}} \over 2} + {S^ * }\Delta {\varepsilon _n} = \left[ {1 + {\upsilon _{\rm{e}}} + \left( {1 - {\upsilon _{\rm{e}}}} \right){S^ * }} \right]{{{{\sigma '}_{\rm{f}}}} \over E}{\left( {2{N_{\rm{f}}}} \right)^b} + \cr & \left[ {1 + {\upsilon _{\rm{p}}} + \left( {1 - {\upsilon _{\rm{p}}}} \right){S^ * }} \right]{{\varepsilon '}_f}{\left( {2{N_{\rm{f}}}} \right)^c} \cr} $ | (1) |
式中,
Fatemi 和Socie[6]研究指出,在建立临界面疲劳损伤控制参量时,仅采用应变参量(如KBM模型中的
| $\eqalign{ & {{\Delta {\gamma _{\max }}} \over 2}\left( {1 + k{{{\sigma _{n,\max }}} \over {{\sigma _{\rm{y}}}}}} \right) = \cr & [\left( {1 + {\upsilon _{\rm{e}}}} \right){{{{\sigma '}_{\rm{f}}}} \over E}{\left( {2{N_{\rm{f}}}} \right)^b} + \left( {1 + {\upsilon _{\rm{p}}}} \right){{\varepsilon '}_{\rm{f}}}{\left( {2{N_{\rm{f}}}} \right)^c}] \cr & \left[ {1 + k{{{{\sigma '}_{\rm{f}}}} \over {2{\sigma _{\rm{y}}}}}{{\left( {2{N_{\rm{f}}}} \right)}^b}} \right] \cr} $ | (2) |
式中,
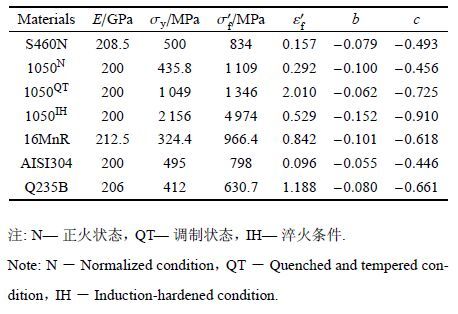
为了验证KBM模型和FS模型对多轴疲劳寿命的预测能力,本文采用5种材料(4种钢材和1种铝合金材料)在45°拉扭比例、45°椭圆非比例和90°圆形非比例3种加载路径下的多轴疲劳试验结果进行模型验证.多轴疲劳试验数据分别取自文献[14-18]. 多轴疲劳试验均采用圆管薄壁试件,多轴加载方式采用正弦波拉-扭复合加载. 材料的基本力学参数及疲劳性能参数见表 1.
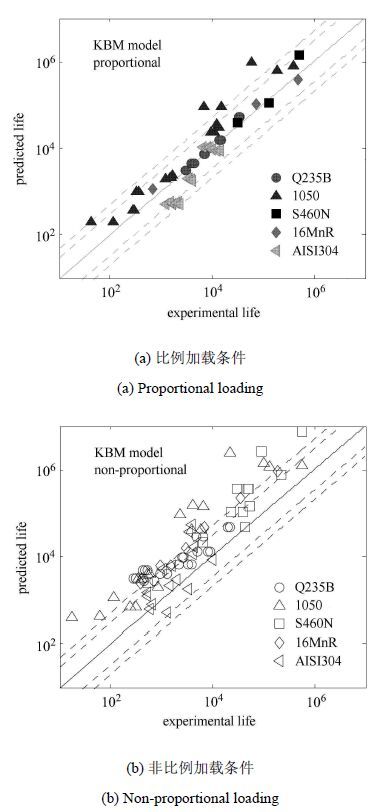
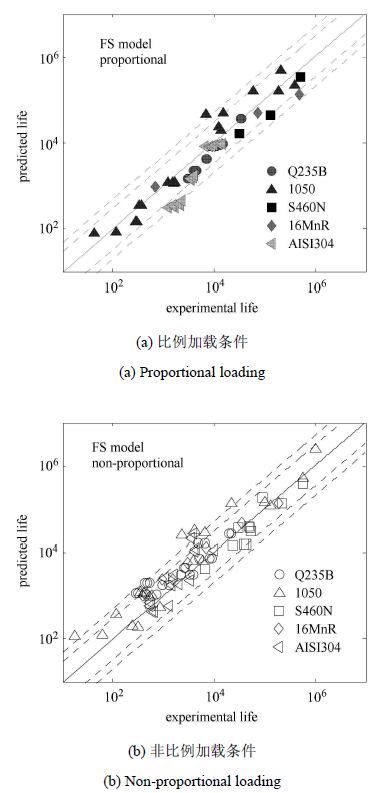
图 1 和图 2分别给出了双对数坐标下KBM模型和FS模型在比例和非比例加载条件下的多轴疲劳寿命预测结果.图中由内向外分别给出了3倍和5倍的误差因子范围.
从图 1和图 2中可以看出:在比例加载条件下,KBM模型和FS模型的疲劳寿命预测结果与试验结果均符合较好,大部分预测结果能维持在3倍的误差因子范围之内;但在非比例加载条件下,KBM模型的预测能力远不如FS模型,且大部分的预测结果偏于危险估计. 为了评价不同多轴疲劳寿命预测模型的预测效果,定义如下误差评价指标[19-20]
| 表 1 材料基本力学参数和疲劳性能参数 Table 1 The mechanical parameters and fatigue properties of investigated materials |
|
图 1 KBM模型疲劳寿命预测结果 Fig. 1 Fatigue life prediction based on KBM parameter |
|
图 2 FS模型疲劳寿命预测结果 Fig. 2 Fatigue life prediction based on FS parameter |
| $ EC ( S )=\dfrac{\hbox{误差因子} S \hbox{内的试验数据量},N \Big( \dfrac{1}{S} \!≤ \!\dfrac{N_{\rm p} }{N_{\rm t} } \!≤\! S \Big)}{\hbox{总的试验数据量},N_{\rm total} } $ | (3) |
式中,
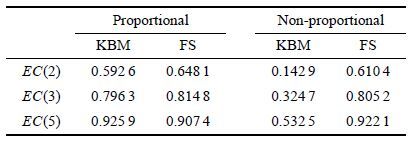
从表 2可以看出:对文中5种材料的多轴疲劳寿命预测而言,FS模型的多轴疲劳寿命预测精度总体上要高于KBM模型.在3倍和5倍的误差因子范围内,比例加载条件下KBM模型和FS模型的预测效果相对均较为理想;但非比例加载条件下,KBM模型总体上的预测精度仅为32.5%和53.3%,预测结果不理想;FS模型预测精度则分别达到了80.5%和92.2%,预测结果与试验符合较好.
| 表 2 不同多轴疲劳寿命预测模型的评价指标 Table 2 The error criterion of life prediction models |
从总体的模型验证结果看,FS模型在非比例加载条件下的多轴疲劳预测效果相对较好.这主要是由于FS模型引入了一个规格化的应力项以考虑材料非比例附加强化对多轴疲劳损伤的影响,从而提高了其寿命预测能力.但值得注意的是,在非比例条件下并非所有的金属材料都存在明显的循环附加强化特征.
对于存在明显非比例附加强化效应的材料,Wang
等[21]研究指出,可以通过修正比例加载条件下的循环应力-应变关系得到非比例循环应力-应变关系,他们通过修正Ramberg-Osgood方程中材料的循环强度系数
| $ \dfrac{\varepsilon _{\rm eq} }{2} = \dfrac{\sigma _{\rm eq} }{2E} + \left[{\dfrac{\sigma _{\rm eq} }{2{K}'\left( {1 + L \cdot \Phi } \right)}} \right]^{\tfrac{1}{n'}}$ | (4) |
式中,
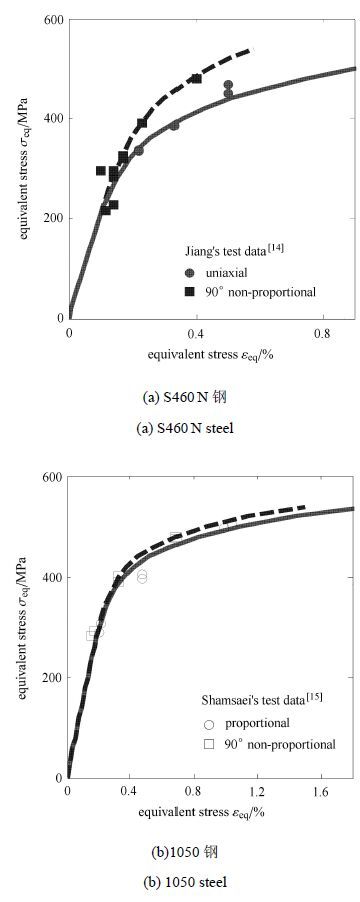
从图 3可以看出,非比例加载条件下S460N钢的循环应力-应变曲线明显高于单轴加载条件下的应力-应变曲线,表现出明显的非比例附加强化特征;相比而言,1050钢的非比例附加强化效应不明显.为了验证FS模型对这两类材料的预测能力,表 3给出了FS模型对文中五种材料的圆管薄壁试件在拉扭复合加载下的多轴非比例疲劳寿命预测能力的评价指标.
|
图 3 S460N钢和1050钢的循环应力-应变拟合曲线 Fig. 3 Fitted cyclic stress-strain curves of S460N and 1050 steel |
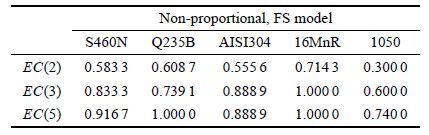
| 表 3 FS模型对5种材料的寿命预测评价指标 Table 3 The error criterion of FS model for five materials |
从表 3可以看出,FS模型对存在非比例附加强化的材料(S460N、Q235B、16MnR钢和AISI304铝合金)的预测能力,整体上高于不存在非比例附加强化的材料(1050钢);从图 2(b)可知,FS模型对1050钢的多轴非比例疲劳寿命预测值主要偏高于试验结果.这主要是因为:在等应变前提下,对存在非比例附加强化的材料,FS模型中的应力项在非比例加载条件下要大于比例加载条件,由此可计算得到较大的FS损伤控制参量值,从而给出相对于比例加载条件较低的疲劳寿命预测,符合多轴非比例疲劳寿命低于比例加载条件下疲劳寿命的预期;但对不存在附加强化的材料,FS模型中的应力项在非比例和比例加载条件下几乎没有差别,因此,在两种不同加载条件下FS模型会给出相同的疲劳寿命预测结果,从而得到较差的多轴非比例疲劳寿命预测.
FS模型的研究思路是[6, 23-24]:非比例加载条件引起材料附加强化,进而导致多轴非比例疲劳寿命的降低;但是这一思路不能解释"对不存在非比例附加强化的材料,在非比例加载条件下同样存在较低的疲劳寿命"这一试验结论.因此,本文从这个角度出发研究FS模型改进方法,以解决FS模型对不存在非比例附加强化的材料适用性不足的问题.
2.2 非比例路径因子已有的多轴非比例疲劳研究表明[25-28]:非比例加载条件除了引起材料的附加强化效应之外,不同的非比例路径会导致材料一点处应力应变主轴发生不同程度的旋转.这样,非比例加载条件导致材料抗疲劳性能降低的原因就可归纳为以下两个方面:(1) 材料相关性,即非比例加载条件引起的材料附加强化效应;(2) 路径相关性,即非比例加载条件引起应力应变主轴的旋转变化特征.
对不存在非比例附加强化效应的材料,材料相关性因素不影响其非比例多轴疲劳性能;但非比例加载路径的变化仍会引起材料一点处应变主轴在循环加载过程中发生不同程度的旋转,导致材料内部开动更多滑移系,使得金属材料晶体层次难以形成稳定的位错结构,从而降低了多轴非比例加载条件下材料的抗疲劳性能[28].这种影响仅依赖于非比例加载路径的变化,而与材料的循环强化特征无关.
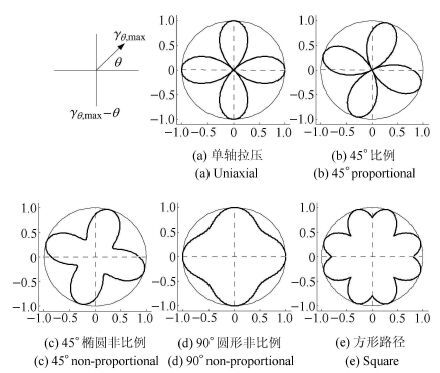
以简谐波拉-扭复合加载条件下的圆管薄壁试件为例,考察不同加载路径下圆管薄壁试件表面危险点处主应变轴的旋转变化特征. 对于承受拉-扭复合简谐波加载的圆管薄壁试件,材料表面一点处任一平面角度
|
图 4 不同应变路径下的 |
从图 4可以看出:在不同的应变加载路径下
| $\Phi = 2{{{A_{\theta ,\max }}} \over {{A_{\max }}}} - 1{\rm{ }}$ | (5) |
式中:
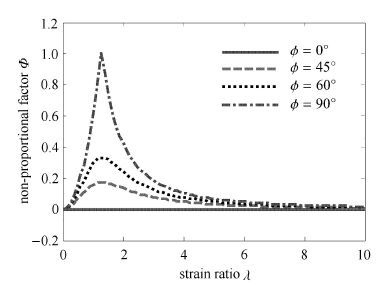
从图 5可以看出: 在比例加载条件下(
|
图 5 非比例路径因子 Fig. 5 Non-proportional path factor |
FS模型的核心思想是引入了最大剪切应变幅平面上规格化的最大法向正应力来反映材料的非比例附加强化,这样FS临界面损伤控制参量保持了最大剪切应变幅的量纲,可以认为是通过引入一个最大剪切应变幅的修正系数
为了能反映非比例加载条件下路径变化和不同类型材料非比例循环附加强化特征对多轴疲劳性能的双重影响,本文建议一个非比例影响因子
| ${\kappa ^ * } = 1 + \sqrt {{\Phi ^2} + {{(L \cdot {\rm{ \backslash varPhi}})}^2}} = 1 + {\rm{ \backslash varPhi}}\sqrt {1 + {L^2}} $ | (6) |
式中,
| $ L = \dfrac{\bar {\sigma }_{\rm OP} }{\bar {\sigma }_{\rm IP} } -1 $ | (7) |
式中,
可以看出: 式(6)提出的非比例影响因子
| $ \dfrac{\Delta \gamma _{\max } }{2}\left( {1 + \kappa ^\ast \dfrac{\bar {\sigma }_{ {n},\max } }{\sigma _{\rm y} }} \right) = f\left( {N_{\rm f} } \right)$ | (8) |
在该临界面疲劳损伤准则中,采用
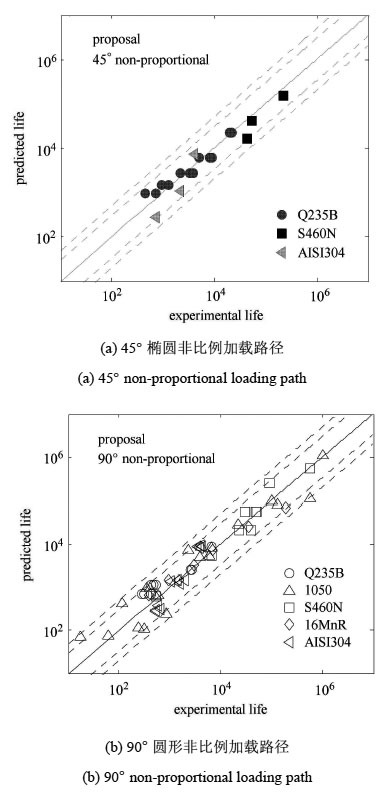
采用本文提出的修正FS临界面准则,对3种材料在45°椭圆非比例路径下的多轴疲劳寿命(其他两种材料疲劳数据文献中未给出)和5种材料在90°圆形非比例路径下的多轴疲劳寿命进行预测,预测结果与试验结果的对比分析如图 6所示.图中由内向外分别给出了3倍和5倍的误差因子范围.
|
图 6 修正FS模型疲劳寿命预测结果 Fig. 6 Fatigue life prediction based on modified FS model |
根据式(3)定义的评价指标,计算本文修正FS模型对文中5种材料的圆管薄壁试件在拉-扭复合非比例加载条件下的误差评价指标,如表 4所示.
| 表 4 修正FS模型误差评价指标 Table 4 The error criterion of modified FS model |
对比表 3和表 4可以看出,相比较于FS模型,在相同的误差因子范围内,本文提出的修正临界面模型对5种材料的多轴非比例疲劳寿命预测精度均有不同程度的提高.对不存在附加强化效应的材料1050钢而言,在2倍、3倍和5倍的误差因子内,FS模型的预测精度仅为30%,60%, 74%,而本文修正模型的预测精度为50%,75%, 100%,预测精度明显提高;同样,对4种存在非比例附加强化效应的材料S460N,Q235B, AISI304和16MnR,多轴非比例疲劳寿命预测结果能全部保持在3倍的误差因子范围之内,预测精度均有明显提高.
需要指出的是,目前的多轴疲劳寿命预测模型均是基于对疲劳试验结果的统计分析而提出的经验模型,建立一种统一适用的临界面疲劳寿命预测模型尚较为困难[33-34].本文通过分析非比例加载对多轴疲劳损伤的双重影响,改进了FS模型,改进模型的预测精度有明显提高,但仍属于经验分析模型范畴.总体而言,多轴疲劳理论发展的不成熟以及疲劳试验结果的分散性仍然是导致多轴疲劳预测寿命与试验寿命存在一定误差的主要原因.
3 结论(1) 采用5种材料的圆管薄壁试件在拉-扭复合加载条件下的多轴疲劳试验结果验证了KBM模型和FS模型对多轴疲劳寿命的预测能力.结果表明:KBM模型对多轴非比例低周疲劳的预测结果不理想,而FS模型对存在非比例附加强化效应的材料的疲劳寿命预测结果与试验符合较好.
(2) 分析了非比例加载条件对多轴疲劳损伤的影响,提出了一个能考虑非比例路径变化和材料附加强化效应双重作用的非比例影响因子,参照FS准则提出一种新的多轴非比例低周疲劳寿命预测临界面模型.模型验证结果表明:文中修正FS临界面模型对多轴非比例疲劳寿命预测结果与试验结果符合较好,预测精度优于FS模型,且该模型能较好地适用于具有不同附加强化特征材料的多轴疲劳寿命预测.
| [1] |
Socie DF, Marquis GB. Multiaxial fatigue. Warrendale, PA: SAE, 2000
( 0) 0)
|
| [2] |
Gladskyi M, Shukaev S. A new model for low cycle fatigue of metal alloys under non-proportional loading[J].
International Journal of Fatigue,2010, 32 (10) : 1568-1572.
DOI: 10.1016/j.ijfatigue.2010.02.016. ( 0) 0)
|
| [3] |
Brown MW, Miller KJ. A theory for fatigue failure under multiaxial stress-strain conditions[J].
Proceedings of the Institution of Mechanical Engineers,1973, 187 (1) : 745-755.
( 0) 0)
|
| [4] |
Socie DF, Shield TW. Mean stress effects in biaxial fatigue of inconel 718[J].
Journal of Engineering Materials & Technology,1984, 106 (3) : 227-232.
( 0) 0)
|
| [5] |
Lohr RD, Ellison EG. A simple theory for low cycle multiaxial fatigue[J].
Fatigue & Fracture of Engineering Materials & Structures,1980, 3 (1) : 1-17.
( 0) 0)
|
| [6] |
Fatemi A, Socie DF. A critical plane approach to multiaxial fatigue damage including out-of-phase loading[J].
Fatigue & Fracture of Engineering Materials & Structures,1988, 11 (3) : 149-165.
( 0) 0)
|
| [7] |
Wang YY, Yao WX. A multiaxial fatigue criterion for various metallic materials under proportional and nonproportional loading[J].
International Journal of Fatigue,2006, 28 (4) : 401-408.
DOI: 10.1016/j.ijfatigue.2005.07.007. ( 0) 0)
|
| [8] |
Shang DG, Sun GQ, Deng J, et al. Multiaxial fatigue damage parameter and life prediction for medium-carbon steel based on the critical plane approach[J].
International Journal of Fatigue,2007, 29 (12) : 2200-2207.
DOI: 10.1016/j.ijfatigue.2006.12.005. ( 0) 0)
|
| [9] |
Li J, Zhang Z, Sun Q, et al. Multiaxial fatigue life prediction for various metallic materials based on the critical plane approach[J].
International Journal of Fatigue,2011, 33 (2) : 90-101.
DOI: 10.1016/j.ijfatigue.2010.07.003. ( 0) 0)
|
| [10] |
Karolczuk A, Macha E. A review of critical plane orientations in multiaxial fatigue failure criteria of metallic materials[J].
International Journal of Fracture,2005, 134 (3-4) : 267-304.
DOI: 10.1007/s10704-005-1088-2. ( 0) 0)
|
| [11] |
You BR, Lee SB. A critical review on multiaxial fatigue assessments of metals[J].
International Journal of Fatigue,1996, 18 (4) : 235-244.
DOI: 10.1016/0142-1123(96)00002-3. ( 0) 0)
|
| [12] |
尚德广, 王德俊.
多轴疲劳强度[M]. 北京: 科学出版社, 2007 .
( Shang Deguang, Wang Dejun.
Multiaxial Fatigue Strength[M]. Beijing: Science Press, 2007 .
(in Chinese) ) ( 0) 0)
|
| [13] |
Shang DG, Sun GQ, Deng J, et al. Multiaxial fatigue damage parameter and life prediction for medium-carbon steel based on the critical plane approach[J].
International Journal of Fatigue,2007, 29 (12) : 2200-2207.
DOI: 10.1016/j.ijfatigue.2006.12.005. ( 0) 0)
|
| [14] |
Jiang Y, Hertel O, Vormwald M. An experimental evaluation of three critical plane multiaxial fatigue criteria[J].
International Journal of Fatigue,2007, 29 (8) : 1490-1502.
DOI: 10.1016/j.ijfatigue.2006.10.028. ( 0) 0)
|
| [15] |
Shamsaei N, Fatemi A. Effect of hardness on multiaxial fatigue behaviour and some simple approximations for steels[J].
Fatigue & Fracture of Engineering Materials & Structures,2009, 32 (8) : 631-646.
( 0) 0)
|
| [16] |
张小元. Q235 钢多轴低周疲劳寿命及评估方法研究. [硕士论文]. 南宁:广西大学, 2013
( Zhang Xiaoyuan. Research on multiaxial low-cycle fatigue and life evaluation for Q235 steel. [Master Thesis]. Nanning: Guangxi University, 2013 (in Chinese)
) ( 0) 0)
|
| [17] |
Nitta A, Ogata T, Kuwabara K. Fracture mechanisms and life assessment under high-strain biaxial cyclic loading of type 304 stainless steel[J].
Fatigue & Fracture of Engineering Materials & Structures,1989, 12 (2) : 77-92.
( 0) 0)
|
| [18] |
Gao Z, Zhao T, Wang X. Multiaxial fatigue of 16MnR steel[J].
Journal of Pressure Vessel Technology,2009, 131 (2) : 73-80.
( 0) 0)
|
| [19] |
Li J, Zhang Z, Sun Q, et al. Low-cycle fatigue life prediction of various metallic materials under multiaxial loading[J].
Fatigue & Fracture of Engineering Materials & Structures,2011, 34 (4) : 280-290.
( 0) 0)
|
| [20] |
Lee KS, Song JH. Estimation methods for strain-life fatigue properties from hardness[J].
International Journal of Fatigue,2006, 28 (4) : 386-400.
DOI: 10.1016/j.ijfatigue.2005.07.037. ( 0) 0)
|
| [21] |
Wang CH, Brown MW. A path-independent parameter for fatigue under proportional and non ‐ proportional loading[J].
Fatigue & Fracture of Engineering Materials & Structures,1993, 16 (12) : 1285-1297.
( 0) 0)
|
| [22] |
赵社戌, 匡震邦. 考虑路径相关性的非比例循环塑性本构模型[J].
力学学报,1999, 4 (4) : 484-492.
( Zhao Shexu, Kuang Zhenbang. A constitutive model for non-proportional cyclic plasticity with loading path dependence[J].
Acta Mechanica Sinica,1999, 4 (4) : 484-492.
(in Chinese) ) ( 0) 0)
|
| [23] |
Reis L, Li B, Freitas MD. Crack initiation and growth path under multiaxial fatigue loading in structural steels[J].
International Journal of Fatigue,2009, 31 (s11-12) : 1660-1668.
( 0) 0)
|
| [24] |
Itoh T, Sakane M, Ohsuga K. Multiaxial low cycle fatigue life under non-proportional loading[J].
International Journal of Pressure Vessels & Piping,2013, 110 : 50-56.
( 0) 0)
|
| [25] |
张成成, 姚卫星. 一种新的多轴高周疲劳寿命预测模型[J].
力学学报,2010, 42 (6) : 1225-1230.
( Zhang Chengcheng, Yao Weixing. A new model for life prediction of multiaxial high-cycle fatigue[J].
Chinese Journal of Theoretical and Applied Mechanics,2010, 42 (6) : 1225-1230.
(in Chinese) ) ( 0) 0)
|
| [26] |
Shamsaei N, Fatemi A. Effect of microstructure and hardness on non-proportional cyclic hardening coefficient and predictions[J].
Materials Science & Engineering A,2010, 527 (12) : 3015-3024.
( 0) 0)
|
| [27] |
Mcclaflin D, Fatemi A. Torsional deformation and fatigue of hardened steel including mean stress and stress gradient effects[J].
International Journal of Fatigue,2004, 26 (7) : 773-784.
DOI: 10.1016/j.ijfatigue.2003.10.019. ( 0) 0)
|
| [28] |
李静, 孙强, 李春旺, 等. 一种新的多轴疲劳寿命预测方法[J].
机械工程学报,2009, 45 (9) : 285-290.
DOI: 10.3901/JME.2009.09.285. ( Li Jing, Sun Qiang, Li Chunwang, et al. New prediction method for multiaxial fatigue life[J].
Journal of Mechanical Engineering,2009, 45 (9) : 285-290.
(in Chinese) DOI: 10.3901/JME.2009.09.285. ) ( 0) 0)
|
| [29] |
Chen X, Gao Q, Sun XF. Low-cycle fatigue under non-proportional loading[J].
Fatigue & Fracture of Engineering Materials & Structures,1996, 19 (7) : 839-854.
( 0) 0)
|
| [30] |
Shamsaei N, Fatemi A, Socie DF. Multiaxial fatigue evaluation using discriminating strain paths[J].
International Journal of Fatigue,2011, 33 (4) : 597-609.
DOI: 10.1016/j.ijfatigue.2010.11.002. ( 0) 0)
|
| [31] |
Shamsaei N, Mckelvey SA. Multiaxial life predictions in absence of any fatigue properties[J].
International Journal of Fatigue,2014, 67 (10) : 62-72.
( 0) 0)
|
| [32] |
Borodii MV, Shukaev SM. Additional cyclic strain hardening and its relation to material structure, mechanical characteristics, and lifetime[J].
International Journal of Fatigue,2007, 29 (6) : 1184-1191.
DOI: 10.1016/j.ijfatigue.2006.06.014. ( 0) 0)
|
| [33] |
刘嘉, 李静, 张忠平. 基于临界面法的剪切式多轴疲劳寿命预测模型[J].
固体力学学报,2012, 33 (1) : 58-62.
( Liu Jia, Li Jing, Zhang Zhongping. A multiaxial fatigue life prediction model with shear form based on the critical plane approach[J].
Chinese Journal of Solid Mechanics,2012, 33 (1) : 58-62.
(in Chinese) ) ( 0) 0)
|
| [34] |
Gómez C, Canales M, Calvo S, et al. High and low cycle fatigue life estimation of welding steel under constant amplitude loading: Analysis of different multiaxial damage models and in-phase and out-ofphase loading effects[J].
International Journal of Fatigue,2011, 33 (4) : 578-587.
DOI: 10.1016/j.ijfatigue.2010.10.015. ( 0) 0)
|
 2016, Vol. 48
2016, Vol. 48