2. 沈阳建筑大学土木工程学院, 沈阳 110168
在爆破设计和理论研究中一般将岩石视为均质体,而实际天然岩体作为地质作用的产物,通常都含有不同尺度的裂隙、节理等不连续面,使得岩体具有典型的非连续性和各向异性,由此对爆破载荷分布规律和最终的破碎效果有着重要的影响[1].Gnirk[2]的试验表明,节理等结构面对爆破效果的影响超过了岩体其它物理力学性质的影响.Ash[3]认为节理面的存在使应力波能量急剧衰减,并指出不连续面能为径向和弯曲破裂提供有利的发展方向,爆生裂纹不仅能沿不连续面发展,而且还向自由面方向发展.陆文[4]对歌乐山石灰石矿进行的爆破试验结果也表明,节理的存在严重阻隔了爆炸应力波的传播,使炸药对岩体的破坏程度减弱.高文学和刘清荣[5]在研究层状岩体的预裂爆破时发现,与炮孔连线有一定交角的结构面的存在,将形成炮孔间的"之"字形断裂.肖同社等[6]的试验结果表明,当爆炸初始裂纹与节理面夹角小于或等于30°时,爆生裂纹很难穿过节理面继续扩展,当夹角接近或等于90°时,裂纹最容易穿过节理面继续扩展.丁黄平[7]的研究结果也表明,为形成光面爆破轮廓线,节理和炮孔连线夹角需大于某一数值,这一数值的大小主要取决于节理面抗剪强度及其泊松比,一般为70°左右. 胡荣等[8-10]基于AUTODYN、UDEC和LS-DYNA3D等数值软件开展的含节理岩体爆破模拟也得到了和试验结果相一致的结论.
另一方面,岩体是地质体,赋存于一定的地质环境中,存在由自重应力和构造应力等引起的初始地应力,爆破作用力与初始应力场相叠加,对爆破效果具有加强或减弱作用[11-15]. 戴俊和钱七虎[16]针对高地应力条件下巷道崩落爆破参数的计算结果表明,地应力越高,崩落爆破的最小抵抗线和炮孔间距减小越多,单位耗药量和循环炮孔数量增加越多. 肖正学等[17]通过对室内试验和现场实例的分析发现初始应力场的存在改变了应力波的传播规律,同时对爆破地震波的传播和裂纹发展起着导向作用. 赵宝友和王海东[18]针对含瓦斯煤层的深孔爆破数值模拟结果也表明裂隙区半径随地应力的增大而近线性地减小,煤层地应力的主应力方向在一定程度上影响着爆生裂隙的扩展方向.
综上所述,针对含节理岩体爆破机理已有大量研究成果,但主要侧重于试验研究. 在力学模型中主要侧重于爆炸应力波的研究,对爆生气体准静态压力和地应力的考虑不足[19]. 为此,本文基于已有爆破损伤模型,把爆破过程视为爆炸应力波和爆生气体压力共同作用的结果,同时考虑不同的地应力条件,针对含节理岩体爆破过程开展数值模拟,研究地应力条件和节理角度(节理面与炮孔连线之间的夹角)对爆生裂纹萌生、扩展过程的影响机理.
1 控制方程岩石爆破破岩理论主要包含两部分内容:一是爆炸应力波的动态作用,二是爆生气体的准静态作用,目前普遍认为岩石的爆破破坏是两者共同作用的结果.该理论认为,岩体内最初裂纹的形成是由爆炸应力波造成的,随后爆生气体楔入裂纹,在准静态压力作用下使裂纹进一步扩展[7, 20].
1.1 动量守恒方程假设岩体是理想弹性体,在爆炸应力波作用下的岩体满足如下运动微分方程(动量守恒方程)
| $G{u_{1i,jj}} + {G \over {1 - 2\nu }}{u_{1j,ji}} + {F_{1i}} = {\rho _s}{{{\partial ^2}{u_{1i}}} \over {\partial {t^2}}}$ | (1) |
式中,G为剪切模量(Pa);v为泊松比;u1i (i =x,y,z)为位移(m);t为时间(s);F1i为i方向体力分量(N/m3); ρs为岩体密度(kg/m3).
1.2 静力平衡方程岩体在爆生气体准静态压力作用下的变形满足如下静力平衡方程
| $G{u_{2i,jj}} + {G \over {1 - 2\nu }}{u_{2j,ji}} + \alpha {p_{,i}} + {F_{2i}} = 0$ | (2) |
式中,u2i (i =x,y,z)表示位移(m);F2i表示i方向体力分量(N/m3);p为爆生气体压力(Pa),α为有效压力系数(Biot系数).
本文采用方程(2)描述岩体在爆生气体准静态压力作用下的变形和受力状态. 同时,在爆炸应力波动态作用和爆生气体准静态作用过程中,岩体本身可能还会受到围压(地应力)的静态作用,同样满足方程(2)所示的静力平衡方程.
1.3 爆生气体渗流方程岩石爆破过程中,炸药爆炸瞬间产生高温高压高速的气体,可简称为爆生气体.爆生气体瞬间充满炮孔,并在压力作用下由炮孔向围岩裂隙中传播,其运移过程是非常复杂的.本文旨在研究爆破载荷作用下岩石的损伤演化过程,关注的重点是爆生气体压力锲入已有裂纹后对裂纹尖端附近区域的受力状态.因此本文将爆生气体的运移过程简化为渗流过程,仍然基于连续介质力学理论和损伤力学理论,对损伤区域(爆生裂纹区域)赋予极大的渗透率,模拟爆生气体在裂纹中的运动过程,得到爆生气体压力在裂纹中的分布情况,进而基于方程(2)得到裂纹尖端应力场分布.
基于质量守恒定律,爆生气体渗流的连续性方程(质量守恒方程)可表示为
| ${{\partial \left( {\phi p} \right)} \over {\partial t}} - \nabla \cdot \left( {{k \over \mu }p\nabla p} \right) = {{{p_a}} \over {{\rho _{{\rm{ga}}}}}}{Q_s}$ | (3) |
其中,φ 为爆生裂纹的孔隙率(或裂隙率);k为爆生裂纹的渗透率(m2);μ 为爆生气体的动力黏性系数(Pa⋅s); pa和ρ ga为标准条件下的气体压力(Pa)和密度(kg/m3);Qs为汇源项(kg/(m3⋅ s)).
本文采用方程(3)描述爆生气体在爆生裂纹中的运移过程,在损伤分析时会根据不同位置的损伤情况对其孔隙率和渗透率进行调整.
1.4 爆炸载荷加载过程本文的损伤分析理论详见文献[21-24],限于篇幅,本文不再细述.
基于爆炸应力波和爆生气体压力共同作用理论,同时为了便于在数值模拟中分析二者对岩石爆破的不同作用机理与效果,本文将其简化为两个独立的先后作用过程[21- 24].
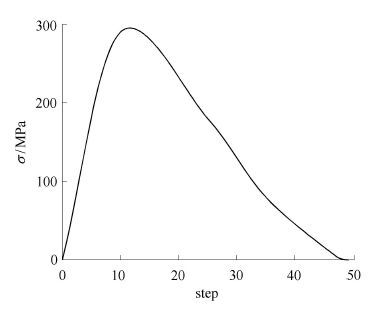
第1∼50步是爆炸应力波作用阶段[25-28],视为动态过程,每步计算时长为10 μs,共500 μs,爆炸应力波加载曲线见图 1. 具体加载过程为:在岩体中开挖爆破孔,爆炸应力波施加于孔壁.
|
图 1 爆炸应力波加载曲线 Fig. 1 Load curve of blasting stress wave |
第51∼100步是爆生气体压力作用阶段,视为准静态过程[29-31].在爆破过程中,由于孔周压碎区和裂纹区的存在,爆生气体会迅速楔入孔壁围岩中,导致炮孔中气体压力迅速降低.本文对这一过程作一简化处理,具体加载过程为:岩体中的炮孔区域不开挖,以初始条件的形式在炮孔区域施加初始气体压力,进而基于方程(3)求解其渗流过程.
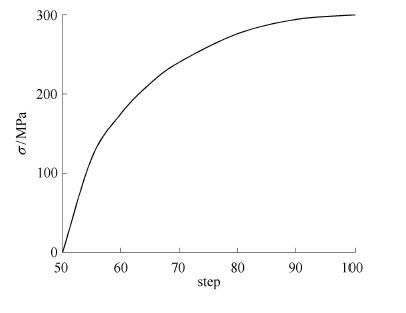
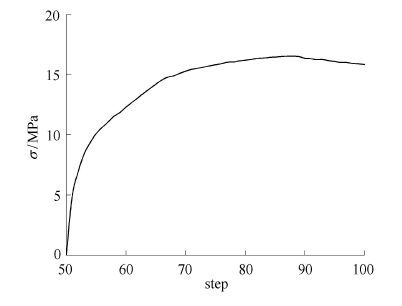
图 2所示为施加于炮孔中的爆生气体初始压力曲线,图 3所示为无地应力、无节理条件下(见后文图 6(a))得到的爆生气体压力,可以看出:爆生气体在第85步达到峰值,峰值压力也由300 MPa降低至16 MPa左右.针对不同工况条件,爆炸应力波作用阶段形成的孔周压碎区和裂纹区分布不同,后续的爆生气体压力曲线也不同.
|
图 2 爆生气体初始压力曲线 Fig. 2 Pressure curve of initial exploitation gas |
|
图 3 炮孔实测得到的爆生气体压力曲线 Fig. 3 The actual pressure curve of exploitation gas measured in blasting hole |
本文作者已在其他文献[21-24]中对所建爆破损伤模型及其求解的正确性进行了验证,图 4所示为针对Cho等[28]PMMA爆破试验的数值模拟,可以看出数值模拟完整再现了爆破作用下PMMA试样孔周压碎区、径向微裂纹区和径向主裂纹区的分布形态,与试验结果具有较好的一致性.

|
图 4 PMMA爆破数值模拟结果与试验结果的比较 Fig. 4 Comparison of numerical and experimental result for PMMA blasting |
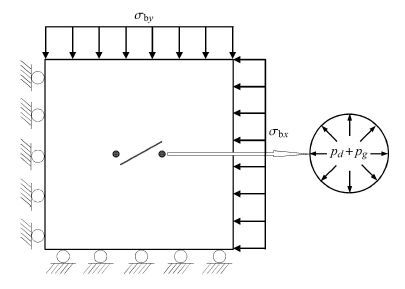
本文所建数值模型见图 5,模型尺寸为12 m × 12 m,在其中开挖两个直径为0.1 m的圆形炮孔,孔间距3 m.两炮孔间存在一张开型(空)节理,节理长度为3 m,节理角度分别设置为0°,30°,45°,60° 和90°.岩石试样的密度为2 650 kg/m3,均质度取为6,细观单元静态弹性模量均值为70 GPa,单轴抗压强度均值为157 MPa,抗拉强度为14 MPa,泊松比为0.2.
对于动力学分析,模型四周为透射边界,孔壁施加爆炸应力波pd,爆炸应力波加载曲线见图 1.
对于静力学分析,模型底部及左侧采用位移约束,上部施加竖直方向地应力σby=7.5 MPa(对应埋深约600 m),右侧施加水平地应力σbx=λσ by (λ定义为侧压力系数,分别取值为0.5,1和2),炮孔区域施加爆生气体准静态压力pg,爆生气体初始压力曲线见图 2.
|
图 5 数值模型 Fig. 5 Numerical model |
图 6所示为不考虑地应力作用(σbx=σ by=0)时,孔壁周边裂纹在爆炸应力波及爆生气体压力作用下的完整演化过程. 第1∼50步是爆炸应力波作用阶段,第51∼100步是爆生气体压力作用阶段.
由图 6(a)可以看出,无节理时,在爆炸应力波作用阶段,两炮孔壁附近形成很小范围的压碎区,压碎区以外则是随机分布的径向微裂纹区(step 25). 之后随着应力波向孔壁围岩深处的不断传播,径向微裂纹区逐渐扩大(step 50),形成几条不是很明显的径向主裂纹.分析其机理,压碎区是由于径向压应力超过了岩石的抗压强度,径向微裂纹区是由于环向拉应力超过了岩石的抗拉强度.同时由于岩石的非均匀性,裂纹会在围岩中的软弱区域优先发展,形成几条主裂纹.由于应力波在传播过程中能量不断衰减,作用强度逐渐降低,其致裂效果也逐渐减弱,最终的致裂区只限于爆破近区.之后在爆生气体压力作用阶段,爆生气体楔入已形成的压碎区和径向裂纹区,并在裂纹尖端引起较大的拉应力,促使径向主裂纹进一步扩展(step 60,step 80),最终两孔间爆生裂纹实现贯通(step 100).可以看出,数值模拟完整再现了爆破载荷作用下岩石试样孔周压碎区、径向微裂纹区和径向主裂纹区的演化过程.
由图 6(b)可以看出,当两爆破孔间存在一水平节理且节理没有与两孔连通时,在爆炸应力波作用阶段与图 6(a)类似,形成小范围的压碎区和径向微裂纹区. 在爆生气体压力作用阶段,已有径向微裂纹沿原方向进一步扩展,其中水平方向的微裂纹与水平节理连通(step 60). 之后,水平方向的微裂纹向节理方向以及节理反方向迅速扩展(step 80),最终到达试样外边界(step 100),而其他方向的主裂纹则扩展不明显. 显然,爆生裂纹与水平节理贯通后,对后续裂纹的扩展具有明显的导向作用.
由图 6(c)可以看出,当两炮孔间存在一30°角的节理时,在爆炸应力波作用阶段,在孔壁周边形成几条径向主裂纹(step 25),同时在节理端部位置萌生局部损伤(step 50). 分析其机理,这是由于应力波传至此处时发生反射,形成拉伸应力所致. 在爆生气体压力作用阶段,由于节理端部的应力集中效应,导致靠近节理端部的爆生裂纹在扩展过程中向节理端部方向偏斜(step 60,step 80),最终两炮孔间爆生裂纹也并未连通(step 100).
由图 6(d)和图 6(e)可以看出,当两炮孔间存在一45°或 60°角的节理时,在爆炸应力波作用阶段,节理对爆生裂纹形成与演化的影响较弱,最终在孔壁周边形成压碎区和径向微裂纹区,而在节理端部位置并未萌生局部损伤(step 50). 在爆生气体压力作用阶段,原有主裂纹进一步扩展(step 60),其中背离节理面一侧的裂纹沿原方向进一步扩展,靠近节理面一侧的裂纹在扩展过程中向节理端部方向偏斜(step 80),而节理面的阻隔作用限制了该方向原有主裂纹沿原方向的进一步延伸,形成许多"次分支"裂纹,导致该局部区域损伤严重(step 100). 显然,当节理角度与炮孔连线夹角为45°或 60°时,对爆生裂纹具有明显的促进作用,爆破效果良好.
由图 6(f)可以看出,当两炮孔间存在一90°角的节理时,在爆炸应力波作用阶段与图 6(e)类似,节理对爆生裂纹没有影响,最终在孔壁周边形成压碎区和径向微裂纹区(step 50). 在爆生气体压力作用阶段,已有主裂纹沿原方向进一步扩展(step 60),节理面对裂纹的阻隔作用不明显,最终水平方向爆生裂纹实现贯通(step 80).而节理端部对其附近区域的裂纹扩展具有一定的导向作用,爆生裂纹在沿原方向扩展过程中有向节理端部延伸(或偏斜)的趋势,最终在节理端部位置实现贯通(step 100).对比图 6(f)与图 6(a)可以看出,当节理角度与炮孔连线夹角为90°时,节理不会阻隔炮孔间裂纹的贯通,且对爆生裂纹的发展具有一定的促进作用,爆生裂纹分布更加均匀,爆破效果更好.

|
图 6 无地应力时含节理岩体爆生裂纹演化过程 Fig. 6 Blasting induced crack evolution for jointed rock without in-situ stress |
进一步对比不同节理角度时爆生裂纹的演化过程和贯通情况,可以看出:节理角度为30°时效果最差,炮孔间形成典型的"之"字形断裂.吴立和陶鲜[32]针对光面爆破开展的试验结果也表明,岩体结构面与爆破断裂面的夹角在30°左右时爆破效果最差,本文模拟结果与该试验结果吻合.
3.2 不同地应力条件下含节理岩体爆破效果分析图 7所示为不同地应力条件下爆生裂纹的最终分布形态,限于篇幅,此处没有给出爆生裂纹的完整演化过程.
由图可以看出:当两炮孔间无节理(见图 7(a))或存在一水平节理且节理没有与两孔贯通时(见图 7(b)),爆生裂纹的扩展规模完全受控于地应力条件, λ=0.5,1和2时最终形成的裂纹长度明显小于无地应力时,且 λ=0.5时竖直方向裂纹长度大于水平方向,λ =2时水平方向裂纹长度大于竖直方向,即裂纹扩展主方向趋于最大地应力方向.分析其机理,爆生裂纹主要是由环向拉伸应力引起的径向裂纹,侧压力系数 λ =0.5,1和2时,炮孔壁周边围岩在各方向所受地应力均为压应力作用,不利于裂纹的萌生与扩展.该结果与戴俊和钱七虎[16]针对高地应力条件下巷道崩落爆破参数的计算结果一致.

|
图 7 各计算工况条件下最终形成的爆生裂纹分布图 Fig. 7 Blasting induced crack distribution under different cases |
当节理角度为30°时(见图 7(c)),爆生裂纹在扩展过程中向节理端部位置延伸,而炮孔另一侧与节理面平行方向的主裂纹也得到显著扩展,其余方向主裂纹则扩展不明显.显然,存在初始地应力且节理角度为30°时,节理对爆生裂纹具有明显的导向和促进作用,裂纹扩展形态主要受控于节理而非地应力条件.
当两炮孔间存在一45°,60°或90°角的节理时(见图 7(d)∼图 7(f)),裂纹分布形态与30°时相似,裂纹扩展过程中向节理端部方向延伸,节理对爆生裂纹具有明显的导向作用.
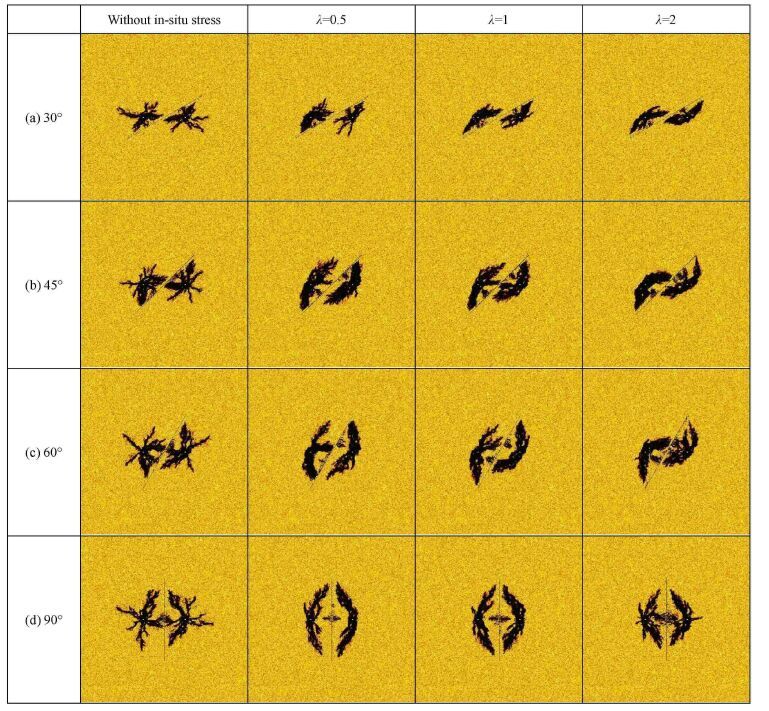
3.3 节理长度6 m时爆破效果分析前文图 6和图 7中节理角度为30°,45°,60°和90°时对应的节理长度为3 m,与两炮孔间距相等. 图 7进一步给出节理长度为6 m,节理角度为30°,45°,60°和90°,岩石试样力学参数、爆破载荷、边界条件都不变的情况下,最终得到的爆生裂纹分布. 对比图 8与图 7,可以看出:由于节理端部对爆生裂纹的导向作用,最终形成的爆生裂纹长度和裂纹区面积均随节理长度增加而增大,节理对裂纹扩展的促进作用更加显著.
|
图 8 节理长度6 m时最终形成的爆生裂纹分布图 Fig. 8 Blasting induced crack distribution for joint length of 6 m |
本文主要开展了不同节理角度和地应力条件下岩石双孔爆破的数值试验,得到的主要结论有:
(1) 无地应力时,节理角度30°时两孔间爆生裂纹贯通效果最差;节理角度45°和60°时对两孔间裂纹贯通具有一定的阻隔作用;节理角度90°时对裂纹的阻隔作用不明显,最终水平方向爆生裂纹实现贯通.
(2) 有地应力时,初始地应力场的压应力作用不利于爆生裂纹的萌生与扩展,但节理的存在对裂纹的扩展具有明显的导向和促进作用,裂纹扩展形态主要受控于节理而非地应力条件.
(3) 由于节理端部对爆生裂纹的导向作用,最终形成的爆生裂纹长度和裂纹区面积均随节理长度增加而增大.
| [1] |
季荣生. 含不连续面岩体爆炸加载试验研究. [博士论文]. 北京: 中国地质大学, 2008
( Ji Rongsheng. Experimental analysis of blasting loads on rock mass containing discontinuity planes. [PhD Thesis]. Beijing: China University of Geoscience, 2008 (in Chinese)
) ( 0) 0)
|
| [2] |
Gnirk PF. On the correlation between explosive crater formation and rock properties. The 9th U.S. Symposium on Rock Mechanics, USA, Colorado, 1967: 321-345
( 0) 0)
|
| [3] |
Ash RL. The influence of geological discontinuities on rock blasting. [PhD Thesis]. Minnesota State: University of Minnesota, 1973
( 0) 0)
|
| [4] |
陆文. 岩体节理裂隙对爆炸应力波阻隔作用的试验研究[J].
四川冶金,2004, 1 : 6-9.
( LuWen. Resistance function of rock joints to stress wave propagation[J].
Sichuan Metallurgy,2004, 1 : 6-9.
(in Chinese) ) ( 0) 0)
|
| [5] |
高文学, 刘清荣. 含结构面岩体预裂爆破研究. 第二届全国岩石动力学学术会议, 宜昌市, 1990: 150-159
( Gao Wenxue, Liu Qingrong. Study of the pre-splitting blasting in rock block. In: Proceeding of the 2nd National Conference on Rock Dynamics, Yichang, 1990: 150-159 (in Chinese)
) ( 0) 0)
|
| [6] |
肖同社, 杨仁树, 庄金钊, 等. 节理岩体爆生裂纹扩展动态焦散线模型实验研究[J].
爆炸与冲击,2007, 27 (2) : 159-164.
( Xiao Tongshe, Yang Renshu, Zhuang Jinzhao, et al. Dynamic caustics model experiment of blasting crack developing on sandwich rock[J].
Explosion and Shock Waves,2007, 27 (2) : 159-164.
(in Chinese) ) ( 0) 0)
|
| [7] |
丁黄平. 节理裂隙岩体隧道爆破成型效果研究. [博士论文]. 长春: 吉林大学, 2009
( Ding Huangping. Study on the shaping effect jointed rock mass under blasting in tunnel. [PhD Thesis]. Changchun: Jilin University, 2009 (in Chinese)
) ( 0) 0)
|
| [8] |
胡荣, 朱哲明, 张晓燕, 等. 节理方位对岩石爆破的影响规律[J].
四川大学学报(工程科学版),2012, 44 (s2) : 41-44.
( Hu Rong, Zhu Zheming, Zhang Xiaoyan, et al. Effect of joint orientation on rock blasting[J].
Journal of Sichuan University (Engineering Science Edition),2012, 44 (s2) : 41-44.
(in Chinese) ) ( 0) 0)
|
| [9] |
谢冰, 李海波, 王长柏, 等. 节理几何特征对预裂爆破效果影响的数值模拟[J].
岩土力学,2011, 32 (12) : 3812-3820.
( Xie Bing, Li Haibo, Wang Changbai, et al. Numerical simulation of presplit blasting influenced by geometrical characteristics of joints[J].
Rock and Soil Mechanics,2011, 32 (12) : 3812-3820.
(in Chinese) ) ( 0) 0)
|
| [10] |
璩世杰, 刘际飞. 节理角度对预裂爆破成缝效果的影响研究[J].
岩土力学,2015, 36 (1) : 189-195.
( Qu Shijie, Liu Jifei. Numerical analysis of joint angle effect on cracking with presplit blasting[J].
Rock and Soil Mechanics,2015, 36 (1) : 189-195.
(in Chinese) ) ( 0) 0)
|
| [11] |
Yang Liyun. Experimental study on rock-type materials dynamic fracture and blasting crack propagation under confining pressure. [PhD Thesis]. Beijing: China University of Mining and Technology, 2011 (in Chinese)
( 0) 0)
|
| [12] |
Bäckblom G, Martin CD. Recent experiments in hard rocks to study the excavation response: implications for the performance of a nuclear waste geological repository[J].
Tunnelling and Underground Space Technology,1999, 14 (3) : 377-394.
DOI: 10.1016/S0886-7798(99)00053-X. ( 0) 0)
|
| [13] |
Ma GW, An XM. Numerical simulation of blasting-induced rock fractures[J].
International Journal of Rock Mechanics & Mining Sciences,2008, 45 (6) : 966-975.
( 0) 0)
|
| [14] |
杨栋, 李海波, 夏祥, 等. 高地应力条件下爆破开挖诱发围岩损伤的特性研究[J].
岩土力学,2014, 35 (4) : 1110-1117.
( Yang Dong, Li Haibo, Xia Xiang, et al. Study of blasting-induced dynamic damage of tunnel surrounding rocks under high in-situ stress[J].
Rock and Soil Mechanics,2014, 35 (4) : 1110-1117.
(in Chinese) ) ( 0) 0)
|
| [15] |
朱俊, 杨建华, 卢文波, 等. 地应力影响下隧洞边墙的爆破振动安全[J].
爆炸与冲击,2014, 34 (2) : 153-160.
( Zhu Jun, Yang Jianhua, Lu Wenbo, et al. Influence of blasting vibration on the sidewall of underground tunnel[J].
Explosion and Shock Waves,2014, 34 (2) : 153-160.
(in Chinese) ) ( 0) 0)
|
| [16] |
戴俊, 钱七虎. 高地应力条件下的巷道崩落爆破参数[J].
爆炸与冲击,2007, 27 (3) : 272-277.
( Dai Jun, Qian Qihu. Break blasting parameters for driving a roadway in rock with high residual stress[J].
Explosion and Shock Waves,2007, 27 (3) : 272-277.
(in Chinese) ) ( 0) 0)
|
| [17] |
肖正学, 张志呈, 李端明. 初始应力场对爆破效果的影响[J].
煤炭学报,1996, 21 (5) : 497-501.
( Xiao Zhengxue, Zhang Zhicheng, Li Duanming. The influence of initial stress field on blasting[J].
Journal of China Coal Society,1996, 21 (5) : 497-501.
(in Chinese) ) ( 0) 0)
|
| [18] |
赵宝友, 王海东. 深孔爆破技术在高地应力低透气性高瓦斯煤层增透防突中的适用性[J].
爆炸与冲击,2014, 34 (2) : 145-152.
( Zhao Baoyou, Wang Haidong. Feasibility of deep-hole blasting technology for outburst prevention and permeability enhancement in highgas-content coal seams with low-permeability subjected to high geostresses[J].
Explosion and Shock Waves,2014, 34 (2) : 145-152.
(in Chinese) ) ( 0) 0)
|
| [19] |
李清. 爆炸致裂的岩石动态力学行为与断裂控制试验研究. [博士论文]. 北京: 中国矿业大学(北京), 2009
( Li Qing. Experiment of fracture behaviors and control for crack propagation under blasting load. [PhD Thesis]. Beijing: China University of Mining & Technology, Beijing, 2009 (in Chinese)
) ( 0) 0)
|
| [20] |
戴俊.
爆破工程[M]. 北京: 机械工业出版社, 2005 .
( Dai Jun.
Blasting Engineering[M]. Beijing: China Machine Press, 2005 .
(in Chinese) ) ( 0) 0)
|
| [21] |
Zhu WC, Wei CH, Li S, et al. Numerical modeling on destress blasting in coal seam for enhancing gas drainage[J].
International Journal of Rock Mechanics and Mining Sciences,2013, 59 : 179-190.
DOI: 10.1016/j.ijrmms.2012.11.004. ( 0) 0)
|
| [22] |
魏炯, 朱万成, 魏晨慧, 等. 导向孔对两爆破孔间成缝过程影响的数值模拟[J].
工程力学,2013, 30 (5) : 335-339.
( Wei Jiong, Zhu Wancheng, Wei Chenhui, et al. Numerical simulation on contribution of guide-hole to crack coalescence of two boreholes[J].
Engineering Mechanics,2013, 30 (5) : 335-339.
(in Chinese) ) ( 0) 0)
|
| [23] |
白羽, 朱万成, 魏晨慧, 等. 不同地应力条件下双孔爆破的数值模拟[J].
岩土力学,2013, 34 (s1) : 466-471.
( Bai Yu, Zhu Wancheng, Wei Chenhui, et al. Numerical simulation on two-hole blasting under different in-situ stress conditions[J].
Rock and Soil Mechanics,2013, 34 (s1) : 466-471.
(in Chinese) ) ( 0) 0)
|
| [24] |
白羽. 地应力影响下岩石爆破损伤模型及其数值试验. [博士论文]. 沈阳: 东北大学, 2014
( Bai Yu. Blasting damage model and numerical test of rock under effect of in Situ stress. [PhD Thesis]. Shenyang, China Northeastern University, 2014 (in Chinese)
) ( 0) 0)
|
| [25] |
Donze FV, Bouchez J, Magnier SA. Modeling fractures in rock blasting[J].
International Journal of Rock Mechanics and Mining Sciences,1997, 34 (8) : 1152-1163.
( 0) 0)
|
| [26] |
Yang RS, Wang YB, Xue HJ, et al. Dynamic behavior analysis of perforated crack propagation in two-hole blasting[J].
Procedia Earth and Planetary Science,2012 (5) : 254-261.
( 0) 0)
|
| [27] |
Zhu ZM, Xie HP, Mohanty B. Numerical investigation of blastinginduced damage in cylindrical rocks[J].
International Journal of Rock Mechanics and Mining Sciences,2008, 45 : 111-121.
DOI: 10.1016/j.ijrmms.2007.04.012. ( 0) 0)
|
| [28] |
Cho SH, Nakamura Y, Mohanty B, et al. Numerical study of fracture plane control in laboratory-scale blasting[J].
Engineering Fracture Mechanics,2008, 75 (13) : 3966-3984.
DOI: 10.1016/j.engfracmech.2008.02.007. ( 0) 0)
|
| [29] |
Kutter HK, Fairhurst C. On the fracture process in blasting[J].
International Journal of Rock Mechanics and Mining Sciences,1971, 8 (5) : 181-202.
( 0) 0)
|
| [30] |
Hagan TN. Rock breakage by explosives[J].
Acta Astronautica,1979, 6 (3-4) : 329-340.
DOI: 10.1016/0094-5765(79)90102-4. ( 0) 0)
|
| [31] |
Mohammadi S, Pooladi A. A two-mesh coupled gas flow-solid interaction model for 2D blast analysis in fractured media[J].
Finite Elements in Analysis and Design,2012, 50 : 48-69.
DOI: 10.1016/j.finel.2011.08.016. ( 0) 0)
|
| [32] |
吴立, 陶鲜. 岩体结构面影响爆破效果的理论分析与试验研究[J].
矿业研究与开发,1999, 19 (1) : 40-43.
( Wu Li, Tao Xian. Theoretical analysis and experimental study of the influence of rock structural planes on blasting effect[J].
Mining Research and Development,1999, 19 (1) : 40-43.
(in Chinese) ) ( 0) 0)
|
2. School of Civil Engineering, Shenyang Jianzhu University, Shenyang 110168, China
 2016, Vol. 48
2016, Vol. 48
