石墨烯是由单层碳原子通过共价键连接构成的蜂窝状晶体结构,是目前发现的唯一存在的二维自由态原子晶体[1].石墨烯具有块体材料无法比拟的优良力学性质,一般块体材料的力学性能随着厚度的减小而变差,而石墨烯薄膜只有一层碳原子却具有超高的强度、刚度和超强导电性能等特性,可望在高性能纳电子器件、场发射材料、生物医药及能量存储等领域获得广泛应用,具有非常广阔的应用前景[2-3].然而,由于环境和制造工艺的限制,现有技术条件制备出的石墨烯含有各式各样的缺陷,例如空位缺陷、Stone-Thrower-Wales(STW)拓扑缺陷和其他非拓扑结构缺陷等.缺陷的存在虽然会降低石墨烯的力学性能以及限制其工业化应用,但是同时也能够提高石墨烯某些其他的性质.相较于完美石墨烯严苛的制备工艺和过高的性价比,缺陷石墨烯亦具有很大的应用潜质与可行性.如果能够研究和掌握缺陷对石墨烯性能影响,将其合理利用,就能以目前的生产技术开展石墨烯量产应用,将会对其工业化应用产生巨大的推动作用[4-5].
当材料的尺寸达到纳米尺度时,由于尺寸效应、量子效应和表面效应的影响,材料的力学特性发生明显变化,从而呈现出与宏观材料不同的性质.此时,经典连续介质力学理论和传统实验手段已经不再适合用于研究纳米材料的特性[4].纳米压痕技术,可以在纳米尺度上测量材料的许多力学特性,如断裂韧性、黏弹性、硬度和蠕变行为等.纳米压痕技术已经应用于材料学中的测量及微纳米尺度的机械性能表征,在表面科学、纳米科学和微电子等领域有着越来越广泛的应用[6-11].关于石墨烯基础性能的研究是纳米材料的研究热点之一.杨晓东等[12]基于分子动力学方法建立了石墨烯纳米压痕实验模型,测得石墨烯弹性模量为1 TPa,强度为240 GPa. 张霖等[13]利用纳米压痕分析了单层石墨烯的力学性能,得到石墨烯薄膜的弹性模量不随材料半径的变化而发生变化. Lee等[14- 15]运用原子力显微镜对石墨烯的弹性性能进行了研究,得出双层石墨烯的弹性模量和破坏强度.Frank等[16]利用纳米压痕法测得石墨烯片(小于5层)的有效刚度常数.谭新君[17]采用分子动力学方法利用圆膜弹性理论对独立式悬置圆膜石墨烯进行模拟计算获得石墨烯的杨氏模量.得出石墨烯的杨氏模量值对石墨烯的厚度具有一定的依赖作用.近年来石墨烯的电学和化学性能以及结构的理论计算等方面都得到了深入的研究.但是,其力学性能方向尚有许多问题有待于进一步研究,因此,有必要对单层以及多层石墨烯的力学特性深入研究.
本文应用分子动力学模拟含缺陷双层石墨烯在球形金刚石压头作用下的变形和破坏机制,分析其杨氏模量和强度,重点探讨STW拓扑缺陷,单、双空位以及圆孔缺陷对石墨烯力学性能的影响.
1 力学模型及模拟方法 1.1 模型建立空位缺陷是点缺陷的一种,可分为单空位缺陷和双空位缺陷.双空位缺陷是石墨烯制备过程中存在的一种重要拓扑缺陷,这种缺陷会影响其结构和性能,它包括邻空位缺陷、间空位缺陷和对空位缺陷.STW拓扑缺陷,也称五七环缺陷,是石墨烯中一种典型的拓扑缺陷[18-27].各种缺陷的形貌如图 1所示.
一般认为多层石墨烯结构为AB堆垛结构,也就是两层并不重合而是相差(1.23,0.71,-0.34)个坐标[17, 28].本文建立了由金刚石压头和双层石墨烯薄膜组成的纳米压痕模拟体系,如图 2所示.圆形双层石墨烯薄膜直径为22 nm,厚度为0.68 nm.为了方便模拟纳米压痕过程,把石墨烯碳原子分为内部的牛顿层和最外圈的固定层.牛顿层直径为20 nm,其中的原子遵循经典牛顿运动定律,在压痕模拟中保持自由,通过计算原子间的作用力确定每个时刻原子的位置和速度.固定层原子在模拟中位置固定不动,以保证体系的稳定.球形金刚石压头采用正四面体空间结构,并做刚体处理,即在压痕过程中不考虑压头的变形.压头半径为2 nm,位于圆形石墨烯薄膜中心正上方1 nm处.
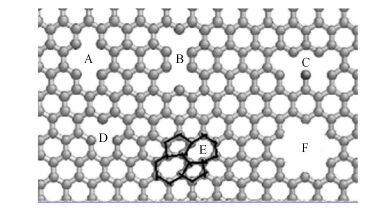
|
图 1 缺陷示意图 (A、B、C、D分别为邻、对、间、单空位缺陷,E和F分别为STW、圆孔缺陷) Fig. 1 Sketch of defect (A,B,C and D are the adjacent,registration,interval,single vacancy defect,E and F are the STW, hole defect,respectively) |

|
图 2 双层石墨烯薄膜的纳米压痕模型图 Fig. 2 Atomic configuration of bilayer graphene model |
系统中各粒子之间的相互作用是通过势函数来控制的,势函数的选取是分子动力学模拟的关键.本文模型中共有两种原子类型:石墨烯原子和金刚石压头原子,根据原子结构和外层电子分布特点,选用不同的势函数来描述它们之间的相互作用.由于Tersoff势函数是一种三体势函数,它可以很好地模拟C---C共价键的各种特性,包括键长、键角、键能、晶格常数和键的断裂重组等动态行为,能够较真实的反映碳元素所构成的固态材料的物理性质[28-38].因此,本文采用Tersoff势来模拟双层石墨烯和金刚石内部原子的相互作用,采用Lernnard-Jones势函数来模拟双层石墨烯不同层非成键碳原子之间、金刚石与石墨烯碳原子之间的相互作用力.
Lenard-Jones (L-J)势函数
| ${\Phi _{ij}}\left( {{r_{ij}}} \right) = 4\varepsilon \left[ {{{\left( {{{{r_{ij}}} \over \sigma }} \right)}^{ - m}} - {{\left( {{{{r_{ij}}} \over \sigma }} \right)}^{ - n}}} \right]$ | (1) |
其中 σ 是相互作用的势能正好为零时的两体距离,ε为最小势能处的能量,r为两原子之间的距离.双层石墨烯层间作用采用参数[17, 32]:
分子动力学模拟过程如下:首先采用共轭梯度法对系统结构进行能量最小化,以消除材料的表面效应得到初始构型.然后在常温常压下对双层石墨烯弛豫30 ps使得系统处于能量最低的平衡态,为下一步压痕模拟提供一个结构以及能量稳定的构型.此时,边界原子z向的位移需要被固定,以模拟石墨烯放在纳米缺口上的情形,牛顿层石墨烯原子可以在平面内自由运动.最后进行纳米压痕模拟,系综采用NVT,施加周期性边界条件,将边界原子3个方向的位移全部固定,以防止石墨烯发生滑动.采用Verlet有限差分算法进行计算,计算步长为1 fs,沿石墨烯表面法向进行加载,加载速度为0.05 nm/ps.
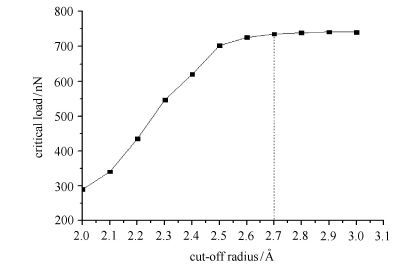
2 结果分析及讨论为了确定LJ势函数的截断半径,取若干大小在2.0∼3.0Å之间的截断半径,得到图 3所示曲线.由图可见LJ势函数的截断半径对纳米压痕有重要的影响,当截断半径取值从2.0到2.6Å 变化时,临界载荷基本成线性比例增加.通过对球形压头在z方向的受力分量分析,发现载荷并不是随着压深的增加而增加,而是上下波动.截断半径越小,这种波动度越大,这使得石墨烯薄膜的载荷-位移曲线越不光滑.当截断半径取值在2.7Å 以及以上时,临界载荷以及压深基本趋于稳定.因此本文中LJ势函数的截断半径选取为2.7Å .
|
图 3 LJ势函数的截断半径与临界载荷关系曲线 Fig. 3 The relationship between critical load and LJ potential's cut-off radius |
根据图 1缺陷构型,本文模拟了当缺陷位于石墨烯薄膜中心时的压痕过程,其中双层石墨烯的缺陷基本在上下层同一位置.势函数求导可获得原子间的相互作用力,压头所有原子相互作用力之和在z方向的分量就是压头所受的载荷.模拟时动态输出球形压头在z方向的受力分量以及压头底端原子的z向坐标值,得出石墨烯的载荷-位移曲线如图 4所示.可以看出,除圆孔外其它缺陷石墨烯的载荷-位移曲线的曲率与完美石墨烯相同,唯一不同的是临界载荷和相应的压深都有不同程度的减小,即临界载荷和压深都随着相邻原子数目缺失的增多而减小.双空位缺陷的3种类型对不同层数石墨烯的影响也不一样,其中对空位缺陷对单层石墨烯影响最大,临界载荷为267.1 nN,相应的压深为4.75 nm,与单层完美石墨烯相比分别下降了44.1%和20.6%.间空位缺陷对于双层石墨烯影响最大,临界载荷为392.5 nN,相应的压深为4.36 nm,与完美双层石墨烯相比分别下降了47.1 %和21.8%.圆孔半径越大,曲线曲率越小,临界载荷随着圆孔半径的增大而显著减小.

|
图 4 缺陷石墨烯载荷-位移曲线 Fig. 4 Load-depth curves of defective graphene films |
双层圆形石墨烯的纳米压痕模型可以简化为一个中心加载、圆周固定的弹性薄膜.该薄膜载荷-位移关系式为[4, 17, 32]
| $F = \sigma _0^{{\rm{2D}}}\left( {\pi Rd} \right)\left( {{h \over R}} \right){\left( {{r \over R}} \right)^{{\textstyle{3 \over 4}}}} + {E^{2D}}\left( {{q^3}Rd} \right){\left( {{h \over R}} \right)^3}{\left( {{r \over R}} \right)^{{\textstyle{1 \over 4}}}}$ | (2) |
其中,F为压头所受的力,σ02D为薄膜预张力,h为压头的位移,E2D二维杨氏模量,R和r分别为薄膜和压头的半径.ν = 0.165 为石墨烯的泊松比[2, 15],q = 1/(1.049 - 0.15ν - 0.16ν 2) = 0.980 5为无量纲常数.由于石墨烯是二维材料,其应变能密度可用单位面积的能量来表征,相应的应力和弹性模量表示为σ02D和E2D.将二维应力和模量除以双层石墨烯有效厚度0.68 nm,可以得到三维应力和模量.根据文献[4, 12, 17],当r/R > 0.1时,压头半径对荷载位移有较大影响.本文采用球形加载方式,表达式中为此添加了校正因子( {r/ R)3/4和(r / R)1/4以修正压头对薄膜形变的影响.
对于本简化模型,其薄膜最大应力可表示为
| $\sigma _{{\rm{MAX}}}^{{\rm{2D}}} = \sqrt {{{{F_{{\rm{cr}}}}{E^{{\rm{2D}}}}} \over {4\pi r}}} $ | (3) |
其中,σMAX2D为薄膜最大应力,Fcr为双层石墨烯破坏时的压头受力.将压头半径以及二维弹性模量带入式(3)可求得双层石墨烯的破坏强度.
本文计算所得的双层石墨烯弹性模量和强度见表 1.由表可见,双层完美石墨烯薄膜的弹性模量和强度分别约为0.897 TPa 和197.3 GPa.本文获得的杨氏模量与文献[12-17]中通过试验与数值模拟方法获
| 表 1 双层石墨烯弹性模量和强度 Table 1 Young's modulus and strength of bilayer graphene |
得的值有较好的一致性.石墨烯缺陷的具体结构与破坏强度有很大关系:除圆孔缺陷外,间空位缺陷对双层石墨烯的力学性能影响最大,其三维弹性模量和强度与完美相比分别减少了3.1 %和28.4 %,可见空位缺陷虽然使得石墨烯薄膜的弹性模量有所降低,但影响较小,而破坏强度下降幅度特别明显,该结果与文献[33-35]中的相关结论有较好的一致性.对于圆孔缺陷,其力学性能随着圆孔半径的增大而显著降低.
2.2 缺陷在不同位置时的影响分析改变缺陷到石墨烯薄膜中心的距离,研究同等条件下单空位、双空位、圆孔缺陷距薄膜中心d=0 ,1,2,4,6, 8 nm的纳米压痕过程,得到图 5所示的缺陷到薄膜中心的距离与临界载荷关系曲线.
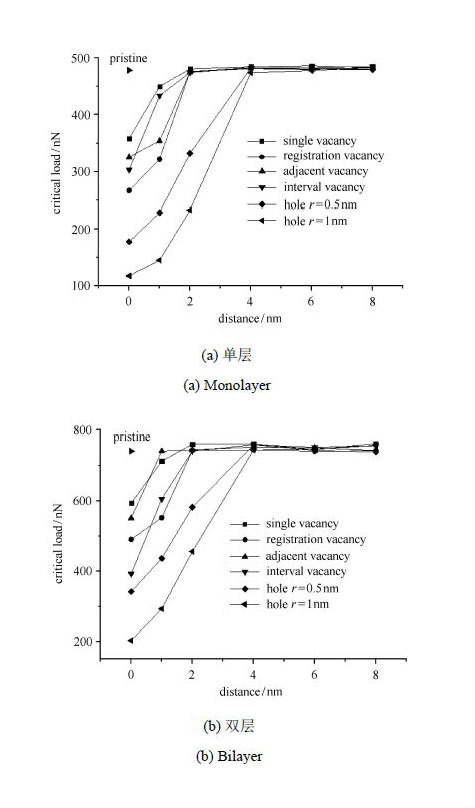
从图 5可以看出,曲线走向基本相同,随着距离的增大临界载荷先增大最后趋于水平稳定.进一步分析得出以下结论:第一,与完美石墨烯相比,缺陷在薄膜中心时临界载荷最小,对模拟的结果影响最大.第二,单空位缺陷对临界载荷影响最小,对石墨烯的结构影响小于双空位缺陷.与完美石墨烯相比,薄膜中心存在缺陷的单、双层临界载荷分别下降了25.1%和19.9%.第三,在压头半径范围内存在单个空位缺陷时,临界载荷与缺陷到薄膜中心的距离近似呈线性增长比例关系.石墨烯的破坏强度随着缺陷到薄膜中心的距离的减小而降低,超出这个范围后载荷-位移曲线基本都与完美石墨烯重合.值得一提的是,这时临界载荷比完美石墨烯稍微偏大一点,主要原因是缺陷的存在局部破坏了石墨烯结构的稳定,减弱了C---C共价键之间的相互作用,故而使其延展性表现出增强的现象.这说明石墨烯结构非常稳定,韧性好,对单个空位缺陷敏感度小. 第四,根据图 5,随着相邻原子缺失数目的增多,圆孔缺陷对石墨烯薄膜纳米压痕结果的影响范围开始扩大.与空位缺陷相比,当圆孔半径为0.5 nm时其对薄膜的影响区域扩大了一倍,即在0 <d <4 nm范围内,临界载荷随着圆孔中心到石墨烯薄膜中心距离d的增大基本呈线性增加.从模拟结果还可看出,圆孔半径从0.5 nm增大到1 nm,只是相应的临界载荷有一定程度降低,但影响范围基本没变.
|
图 5 缺陷到薄膜圆心的距离与临界载荷关系曲线 Fig. 5 The relationship between critical load and distance (from defect to the film's center) |
(1) 空位缺陷数目的影响
由2.2得出结论,当在压头半径范围内存在空位缺陷时对石墨烯力学性能有很大影响,超出这个范围后几乎没有影响.为了验证缺陷的数目是否遵循这一性质,以不同数目单空位和圆孔缺陷为例,构建了4种带缺陷的计算模型.第1种:带2个缺陷,位于图 6(a)中的D,E处;第2种:带4个缺陷,位于位于图 6(a)中的B,D,E,G处;第3种:带6个缺陷,位于位于图 6(a)中的A,B,D,E,G,H处;第4种:带8个缺陷,位于位于图 6(a)中的A,B,C,D,E,F,G处.双空位缺陷模型与单空位建立方法类似.
首先计算缺陷正好均匀分布在以薄膜中心为基点边长为8 nm的正方形边上,图 7只列出了不同数目的单空位缺陷石墨烯薄膜载荷-压深曲线,可以看出,当缺陷均匀分布时,载荷-位移曲线基本都与完美石墨烯重合.这种现象说明了当在压头半径范围外存在多个缺陷时,对石墨烯的力学性质几乎没有

|
图 6 缺陷石墨烯初始构型图 Fig. 6 Model of single vacancy defect |

|
图 7 多个单空位缺陷下的石墨烯薄膜载荷-位移曲线 Fig. 7 Load-depth curves of graphene with multiple single vacancy defects |
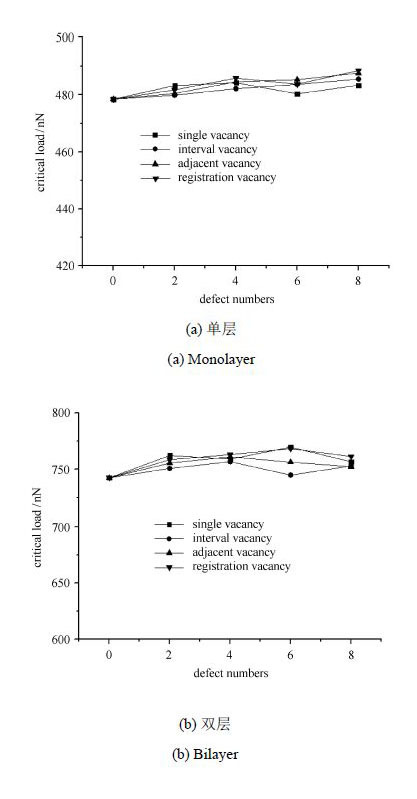
造成影响.此结果与文献[35-37]中的结论一致.图 8为不同数目缺陷与临界载荷关系曲线,从图中得出结论,临界载荷与缺陷数目并不是呈比例增加,而是围绕某一值上下波动.双层石墨烯的波动幅度相比单层情况明显变大,可见层数的增加使得石墨烯延展性由于缺陷的存在表现出增强这一性质得到提高,验证了石墨烯结构稳定,韧性好,对空位缺陷敏感度小.
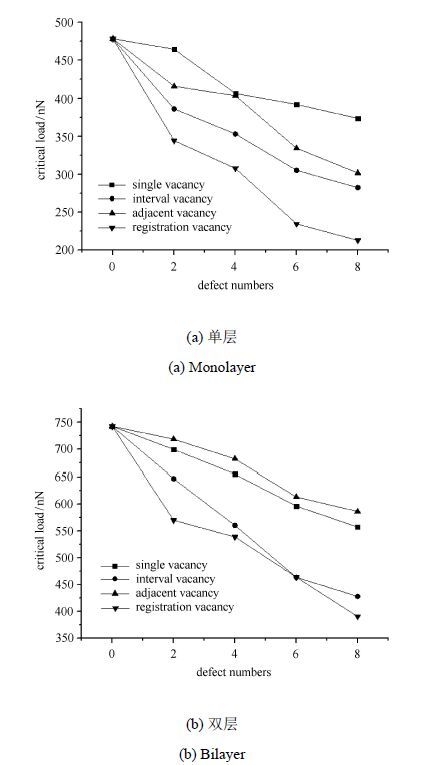
类似的,本文建立了不同数目空位缺陷均匀分布在以薄膜中心为基点边长为2 nm的正方形边上的计算模型.图 9为不同数目空位缺陷与临界载荷的变化曲线,可以看出,曲线走向基本相同,即随着缺陷数目的增多临界载荷都开始显著减小.进一步分析得出以下几点结论:第一,缺陷对不同层数的石墨烯力学性质影响不一致.对单层石墨烯来说,单空位缺陷的影响最小,对空位影响最大,且相同数目的两种缺陷临界载荷最大相差33.6%.对双层石墨烯来说,邻空位缺陷影响最小,对空位影响最大,相同数目的两种缺陷的临界载荷最大相差26.3%.说明缺陷的数目对单层石墨烯的影响大于双层,且随着缺陷数目的增多,这种差距将会出现越来越大的趋势.第二,当缺陷在压头半径范围内时,缺陷数目越多,石墨烯的力学性能就会降低的越快.
|
图 8 不同数目空位缺陷与临界载荷关系曲线 Fig. 8 The relationship between the critical loads and multiple vacancy defects |
|
图 9 空位缺陷位于压头下方时缺陷数目与临界载荷关系曲线 Fig. 9 The relationship between the critical loads and multiple vacancy defects located in the region covered by the indenter |
(2) 圆孔缺陷数目的影响分析
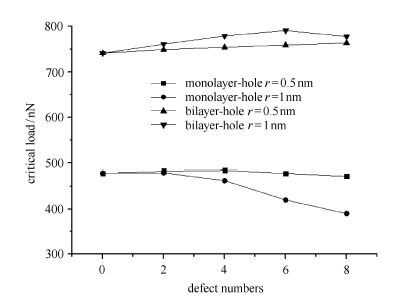
当在距离薄膜中心4 nm处存在圆孔缺陷且其半径小于1 nm时,对石墨烯力学性能几乎不产生影响.为了研究圆孔缺陷数目对压痕结果产生的影响,本文对半径为0.5 nm和1 nm的圆孔缺陷分别构建了4种带缺陷的计算模型,如图 6(b),建立方法与图 6(a)类似.图 10为不同数目圆孔缺陷与临界载荷的变化曲线,对于单层石墨烯,当圆孔半径为0.5 nm时,临界载荷随着圆孔缺陷数目基本不变;当半径为1 nm时,临界载荷随着圆孔缺陷数目的增多开始大幅度降低,可见在影响范围外存在缺陷数目较多且半径大于一定值后将会对石墨烯薄膜造成很大的影响.对于双层,曲线都呈上升趋势,双层石墨烯由于缺陷的存在表现出的延展性明显高于单层.
|
图 10 不同数目圆孔缺陷与临界载荷关系曲线 Fig. 10 The relationship between the critical loads with multiple hole defects |
本文讨论了LJ势函数的截断半径,并确定了其截断半径最佳值为2.7Å.通过利用分子动力学方法对含有缺陷双层石墨烯薄膜进行了纳米压痕模拟,并把计算结果与完美石墨烯的力学性能进行了对比分析,得出以下结论:双层完美石墨烯薄膜弹性模量和强度分别约为0.897 TPa和197.3 GPa.薄膜中心存在空位缺陷时,载荷-位移曲线的曲率基本与完美石墨烯相同,唯一不同的是临界载荷和相应的压深都有一定程度的减小.这导致石墨烯的弹性模量略有降低,而破坏强度下降幅度特别明显.通过调整空位缺陷与石墨烯薄膜中心的距离d,分析发现,空位缺陷只有在压头半径范围内时,临界载荷随着缺陷到薄膜中心距离增大而增大,即对石墨烯力学性质的影响越来越小;空位缺陷数目越多,其杨氏模量、破坏强度等就越低.当超出这个范围后,临界载荷不再随d以及空位缺陷数目而变化,载荷-位移曲线基本都与完美石墨烯重合,说明石墨烯结构非常稳定,韧性好,对空位缺陷敏感度小.当薄膜中心存在圆孔缺陷时,随着半径的增大,圆孔缺陷对石墨烯薄膜纳米压痕结果的影响范围开始扩大.调整圆孔缺陷与石墨烯薄膜中心的距离,与空位缺陷相比,圆孔半径为0.5 nm时缺陷对薄膜的影响区域扩大了一倍,即在0 <d<4 nm范围内,临界载荷随着圆孔中心到石墨烯薄膜中心距离d的增大基本呈线性增加.在压头范围外存在圆孔缺陷的数目多或半径达到一定尺度后,将会使石墨烯的力学性质大幅度降低,也就是在此范围外的缺陷影响与其尺寸有关.本文结论也说明石墨烯结构稳定,对小缺陷不敏感,缺陷石墨烯仍具有较好的性能和使用价值.
| [1] |
尚福林, 郭显聪, 北村隆行, 等. 纳米材料力学行为的原子尺度模拟研究[J].
力学进展,2010, 40 (4) : 263-283.
( Shang Fulin, Guo Xiancong, Kitamura T, et al. A review on atomistic simulation studies on mechanical behaviors of nano-materials[J].
Advances in Mechanics,2010, 40 (4) : 263-283.
(in Chinese) ) ( 0) 0)
|
| [2] |
Novoselov KS, Geim AK, Morozov SV, et al. Electric field effect in atomically thin carbon films[J].
Science,2004, 306 (22) : 666-669.
( 0) 0)
|
| [3] |
Sakhaee-Pour A. Elastic properties of single-layered graphene sheet[J].
Come Mater Sci,2009, 45 (2) : 266-270.
DOI: 10.1016/j.commatsci.2008.09.024. ( 0) 0)
|
| [4] |
Wang WD, Li S, Min JJ, et al. Nanoindentation experiments for single-layer rectangular graphene films: a molecular dynamics study[J].
Nanoscale Research Letters,2014, 9 (1) : 41-49.
DOI: 10.1186/1556-276X-9-41. ( 0) 0)
|
| [5] |
Oliver WC, Pharr GM. An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments[J].
J Mater Res,1992, 7 (6) : 1564-1583.
DOI: 10.1557/JMR.1992.1564. ( 0) 0)
|
| [6] |
Kim SY, Cho SY, Kang JW, et al. Molecular dynamics simulation study on mechanical responses of nanoindented monolayergraphene-nanoribbon[J].
Physica E,2013, 54 : 118-124.
DOI: 10.1016/j.physe.2013.06.016. ( 0) 0)
|
| [7] |
Alzebdeh KI. An atomistic-based continuum approach for calculation of elastic properties of single-layered graphene sheet[J].
Solid State Communications,2014, 177 : 28-25.
( 0) 0)
|
| [8] |
Hemmasizadeh A, Mahzoon M, Hadi E, et al. A method for developing the equivalent continuum model of a single layer graphene sheet[J].
Thin Solid Films,2008, 516 : 7636-7640.
DOI: 10.1016/j.tsf.2008.05.040. ( 0) 0)
|
| [9] |
Sha ZD, Wan Q, Pei QX, et al. On the failure load and mechanism of polycrystalline graphene by nanoindentation[J].
Scientific Reports,2014, 4 : 7437-7443.
DOI: 10.1038/srep07437. ( 0) 0)
|
| [10] |
Song ZG, Artyukhov VI, Wu J, et al. Defect-detriment to graphene strength is concealed by local probe: the topological and geometrical effects[J].
ACS Nano,2015, 9 (1) : 401-408.
DOI: 10.1021/nn505510r. ( 0) 0)
|
| [11] |
Song ZG, Xu ZP. Geometrical effect ‘stiffens' graphene membrane at finite vacancy concentrations[J].
Extreme Mechanics Letters,2016, 6 : 82-87.
DOI: 10.1016/j.eml.2015.12.010. ( 0) 0)
|
| [12] |
杨晓东, 贺鹏飞, 吴艾辉, 等. 石墨烯纳米压痕实验的分子动力学模拟[J].
中国科学,2010, 40 (3) : 353-360.
( Yang Xiaodong, He Pengfei, Wu Aihui, et al. Molecular dynamics simulation of nanoindentation for graphene[J].
Science China,2010, 40 (3) : 353-360.
(in Chinese) ) ( 0) 0)
|
| [13] |
张森, 赵宏伟, 杨倚寒, 等. 单层石墨烯薄膜材料纳米压痕过程的分子动力学解析[J].
吉林大学学报,2013, 43 (6) : 1558-1565.
( Zhang Sen, Zhao Hongwei, Yang Yihan, et al. Molecular mechanics simulations of nanoindentation of single-layer graphene sheet[J].
Journal of Jilin University,2013, 43 (6) : 1558-1565.
(in Chinese) ) ( 0) 0)
|
| [14] |
Lee C, Wei X, Kysar J. Measurement of the elastic properties and intrinsic strength of monolayer graphene[J].
Science,2008, 321 (5887) : 385-388.
DOI: 10.1126/science.1157996. ( 0) 0)
|
| [15] |
Lee CG, Wei XD, Li QY, et al. Elastic and frictional properties of graphene[J].
Phys Status Solidi B,2009, 246 (11) : 2562-2567.
( 0) 0)
|
| [16] |
Frank I, Tanenbaum D, Van der Zande A, et al. Mechanical properties of suspended graphene sheets[J].
J Vac Sci Technol B,2007, 16 (26) : 2558-2561.
( 0) 0)
|
| [17] |
谭新君. 石墨烯薄膜杨氏模量的分子动力学研究. [硕士论文]. 湖南:湘潭大学, 2011
( Tan Xinjun. Molecular dynamics study of the Young's modulus of graphene sheet. [Master's thesis]. Hunan: Xiangtan University, 2011 (in Chinese)
) ( 0) 0)
|
| [18] |
Zhang B, Yang G. A micromorphic model for monolayer hexagonal boron nitride with determined constitutive constants by phonon dispersions[J].
Physica B Condensed Matter,2014, 451 : 48-52.
DOI: 10.1016/j.physb.2014.06.020. ( 0) 0)
|
| [19] |
Xiao JR, Staniszewski J, Gillespie JW Jr. Fracture and progressive failure of defective graphene sheets and carbon nanotubes[J].
Composite Structures,2009, 88 (4) : 602-609.
DOI: 10.1016/j.compstruct.2008.06.008. ( 0) 0)
|
| [20] |
Gao YW, Hao P. Mechanical properties of monolayer grapheme under tensile and compressive loading[J].
Physica E,2009, 41 (8) : 1561-1566.
DOI: 10.1016/j.physe.2009.04.033. ( 0) 0)
|
| [21] |
徐巍, 王立峰, 蒋经农. 基于应变梯度中厚板单元的石墨烯振动研究[J].
力学学报,2015, 47 (5) : 751-761.
( Xu Wei, Wang Lifeng, Jiang Jingnong. Finite element analysis of strain gradient middle thick plate model on the vibration of graphene sheets[J].
Chinese Journal of Theoretical and Applied Mechanics,2015, 47 (5) : 751-761.
(in Chinese) ) ( 0) 0)
|
| [22] |
徐巍, 王立峰, 蒋经农. 基于应变梯度有限元的单层石墨稀振动研究[J].
固体力学学报,2014, 35 (5) : 441-450.
( Xu Wei, Wang Lifeng, Jiang Jingnong. Finite element analysis of strain gradient on the vibration of solid mechanics[J].
Chinese Journal of Solid Mechanics,2014, 35 (5) : 441-450.
(in Chinese) ) ( 0) 0)
|
| [23] |
Ouyang F, Huang B, Li Z, et al. Chemical functionalization of graphene nanoribbons by carboxyl groups on Stone-Wales defects[J].
J Phys Chem C,2008, 112 (31) : 12003-12007.
DOI: 10.1021/jp710547x. ( 0) 0)
|
| [24] |
Hashimoto A, Suenaga K, Gloter A, et al. Direct evidence for atomic defects in graphene layers[J].
Nature,2004, 430 (7002) : 870-873.
DOI: 10.1038/nature02817. ( 0) 0)
|
| [25] |
Tserpes KI, Papanikos P. The effect of Stone-Wales defect on the tensile behavior and fracture of single-walled carbon nanotubes[J].
Composite Structures,2007, 79 (4) : 581-589.
DOI: 10.1016/j.compstruct.2006.02.020. ( 0) 0)
|
| [26] |
黄坤, 殷雅俊, 屈本宁, 等. 基于Lenosky 原子作用势单层石墨烯片的力学模型[J].
力学学报,2014, 46 (6) : 905-910.
( Huang Kun, Yin Yajun, Qu Benning, et al. A mechanics model of a monolayer graphene based on the lenosky interatomic potential energy[J].
Chinese Journal of Theoretical and Applied Mechanics,2014, 46 (6) : 905-910.
(in Chinese) ) ( 0) 0)
|
| [27] |
杨刚, 张斌. 类石墨烯二维原子晶体的微态理论模型[J].
力学学报,2015, 47 (3) : 451-457.
( Yang Gang, Zhang Bin. Micromorphic model of graphene-like two-dimensional atomic crystals[J].
Chinese Journal of Theoretical and Applied Mechanics,2015, 47 (3) : 451-457.
(in Chinese) ) ( 0) 0)
|
| [28] |
李婷. 缺陷对双层石墨烯电子结构与力学性能的影响. [硕士论文]. 湖南: 湘潭大学, 2011
( Li Ting. Effect of defects on electronic structure and mechanical properties of bilayer grapheme. [Master's thesis]. Hunan: Xiangtan University, 2011 (in Chinese)
) ( 0) 0)
|
| [29] |
Kwon S, Ko JH. Enhanced nanoscale friction on fluorinated graphene[J].
American Chemical Society,2012, 12 (12) : 6043-6048.
( 0) 0)
|
| [30] |
Tersoffff J. Modeling solid-state chemistry: Interatomic potentials for multicomponent systems[J].
Phys Rev B,1990, 41 (5) : 3248-3248.
( 0) 0)
|
| [31] |
Miro P, Audiffred M, Heine T. An atlas of two-dimensional material[J].
Chemical Society Reviews,2014, 43 : 6537-6554.
DOI: 10.1039/C4CS00102H. ( 0) 0)
|
| [32] |
Neek Amal M, Peeters FM. Nanoindentation of acircular sheet of bilayer graphene[J].
Phys Rev B,2011, 81 (23) : 235421.
( 0) 0)
|
| [33] |
华军, 武霞霞, 李东波, 等. 基于神经网络的石墨烯弹性参量识别方法研究[J].
西安建筑科技大学学报,2015, 47 (5) : 760-765.
( Hua Jun, Wu Xiaxia, Li Dongbo, et al. Idenfication of elastic parameters method for graphene based on neural network[J].
J Xi'an Univ of Arch & Tech,2015, 47 (5) : 760-765.
(in Chinese) ) ( 0) 0)
|
| [34] |
Tserpes KI, Papanikos P. Finite element modeling of single-walled carbon nanotubes[J].
Composite part B: Engineering,2005, 36 (5) : 468-477.
DOI: 10.1016/j.compositesb.2004.10.003. ( 0) 0)
|
| [35] |
Ansari R, Ajori S, Motevalli B. Mechanical properties of defective single-layered graphene sheets via molecular dynamics simulation[J].
Superlattices and Microstructures,2012, 51 (2) : 274-289.
DOI: 10.1016/j.spmi.2011.11.019. ( 0) 0)
|
| [36] |
Xin H, Han Q, Yao X. Buckling of defective single-walled and double-walled carbon nanotubes under axial compression by molecular dynamics simulation[J].
Compos Sci Technol,2008, 68 (7) : 1809-1814.
( 0) 0)
|
| [37] |
Tang Xianqiong, Deng Xuhui, Ding Yanhuai, et al. Molecular dynamics simulation of nanoindentation for granphene sheets[J].
China mechanical Assembly and Qian Xuesen's 100th Anniversary Meeting,2011, 1 .
( 0) 0)
|
| [38] |
白树林, 赵云红. 石墨烯热学性能及表征技术[J].
力学进展,2014, 44 : 201406.
( Bai Shulin, Zhao Yunhong. Thermal properties and characterization techniques of graphene[J].
Advances in Mechanics,2014, 44 : 201406.
(in Chinese) ) ( 0) 0)
|
 2016, Vol. 48
2016, Vol. 48

