2. 西安交通大学航天航空学院, 机械结构强度与振动国家重点实验室, 西安 710049
微机电系统(MEMS)泛指尺寸在厘米级别甚至更小的小型装置,或主要由传感器、执行器和微电源三个部分组成的独立的智能系统.一般认为,微机电系统是以微电子、微机械和材料科学为基础,研究、设计、开发并加工制造具有特定功能的微型机械,包括微传感器和微系统等.
在MEMS的力学范畴内,研究主要针对微平板[1-4]和微悬臂梁[5-7]模型,或基于二者的穿孔[8-9]、开槽[10-11]模型,考察其在微尺度下的力学特性,选取不同参数时的频谱特征,以及不同材料的功能和适用性分析等.
例如,Zhang等[12]采用连续弹性理论对微梁结构的振动器进行了力学分析,Craighead[13]则对扭转结构振动器中的微平板和微梁结构进行了分析.Mehner等[14]对微悬臂梁的理论研究从Reynolds方程入手,分析了孔径、孔深等参数对带孔微悬臂梁力学性能的影响;随后,他们加大了模型的复杂程度,由单个微悬臂梁过渡到对称的"L"型双悬臂梁模型,并考虑了两个悬臂梁之间的相互作用.
当研究对象的尺度进一步缩小时,经典的连续弹性理论不再适用.有鉴于此,近年来,基于Cosserat理论的微尺度下振动力学特性研究渐被学者接受.例如,康新和席占稳[15]研究了微梁结构在尺度效应下的振动特性,分析了本征长度对微梁固有频率的影响;王晓明等[16]研究了四边简支微平板在尺度效应下的振动特性,同时分析了本征长度对微平板固有频率的影响.
此外,研究MEMS中微结构的振动特性,还应考虑压膜阻尼(气膜力)的影响.Bao和Yang[17]利用Langlois[18]的摄动方法,给出了气膜力的表达形式,该形式采用无穷级数的表示方法,考虑了垂直方向的弹性阻尼力以及切向的黏性阻尼力,在此基础上可分析挤压数、频率等对气膜力大小的影响,同时可研究带孔、槽的微平板的力学特性.Bao和Yang[17]的研究结果与Griffin等[19]以及Blech[20]的理论结果完全吻合,证明了其理论分析的准确性和正确性.
在微尺度条件下,由于研究对象的尺度接近于气体分子的平均自由程,还需考虑气体的尺度效应.衡量所研究对象气体尺度因素的一个重要参数就是Knudsen数[21-23],它表征了流体分子平均自由程和研究对象特征尺寸之间的比值,直接反映了该系统中气体的稀薄程度.Knudsen数越大,系统中的气体稀薄性越强,气体的连续性假设越得不到满足;反之,Knudsen数越小,系统中的气体稀薄性越弱.Knudsen数较大时,流体的黏性系数发生明显变化,需要引入有效黏性系数[24]的概念,这部分内容将在后文的模型建立和参数讨论部分中详细说明.Veijola等[25]的研究归纳综合了前人关于定量计算有效黏性系数的理论,根据Fukui和Kaneko[26-27]的研究成果,采用拟合的方法,得到了有效黏性系数的表达式,其误差小于5%.该表达式表明,尺度效应对微尺度下力学模型的影响不可忽略,且在Knudsen数很大的情况下,其影响极其巨大[25].
在不考虑板和气体两种尺度效应的情况下,Carneal等[28]分析了双板结构的声学效应,指出双板之间的相互辐射作用会导致更大的传声损失,并作出了相应的频谱分析.任树伟等[29]开展了更为深入的研究,不仅考虑了本征长度对微平板固有频率的影响,还采用无穷级数的相关理论,给出了声压激励下微平板传声损失的叠加解,分析了传声损失受板厚和本征长度影响的频谱图:这些结果具有较大的实际意义和参考价值.
目前,国内外学者针对MEMS微结构的研究很少涉及的声学和力学的耦合领域.有鉴于此,在同时考虑板和气体的尺度效应的情况下,本文重点研究声学激励下微平板结构的声学特性和阻尼效应的耦合.首先,在考虑阻尼效应的基础上,从传声控制方程入手,通过多重级数的展开理论,获得了阻尼和声压激励下的耦合解.其次,在中低频振动条件下,数值求解了声压与阻尼耦合效应下的静态传声损失.最后,考虑微尺度效应,系统分析了不同振动条件下阻尼对传声损失的影响.
1 考虑阻尼效应的微平板声振耦合理论模型在很多情况下,在微机电系统中的微结构中存在压膜阻尼作用.压膜阻尼是由于两平行板相对运动挤压其中的薄膜气体而产生的,一般分为阻尼和刚度两种形式.Bao和Yang[17]给出了这种压膜阻尼的数学表现形式.
1.1 声振耦合模型的建立本文所研究模型如1所示.考虑两个边长为L、厚度为h的正方形微平板,其中上部平板(top plate)为四边简支,底部平板(bottom plate)相对上部平板做上下往复简谐振动. 振动位移大小为δh0,其中δ是振动位移和两个微平板之间初始间距之比.由于相同大小的振动位移对不同尺寸微平板的力学性能的影响不尽相同,故考虑振动的绝对大小意义不大,而考虑振动位移和其他宏观尺寸(如板间距)的关系更有价值.有鉴于此,本文关于振动位移的讨论对象为δ.
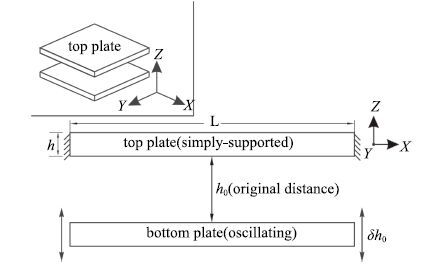
|
图 1 双板模型 Fig. 1 Double-micro-plates model |
由于微平板之间的相对运动,图 1所示运动微平板和简支微平板之间的气体对两个微平板产生阻尼效应.两板相对靠近彼此时,板间隙中的气体压强增大,同时板边缘的气体被挤出;两板相对远离彼此时,板间的气体压强减小,外部气体被吸入间隙,流动的气体产生的黏滞拉力作用于两板,并根据压缩程度呈现阻尼和刚度两种形式[30].这种阻尼效应的强度可表示为压膜(squeeze film)阻尼强度psf.
因此,本文所研究的简支微平板受到入射声压pi、反射声压pr、透射声压pt和压膜阻尼强度psf的共同作用,如2所示.
对简支微平板而言,考虑其长度远大于其厚度
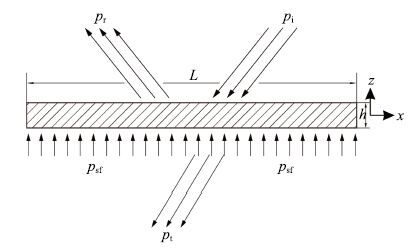
|
图 2 声压、气膜力耦合模型 Fig. 2 Acoustic pressure and squeeze film coupling model |
对Cosserat理论进行线性化处理,可得约束转动Cosserat理论,该理论假定粒子的转动等同于物质转动,即
| $ \omega_1 = \frac{\partial w}{\partial y},~~\omega_2 = \frac{\partial w}{\partial x} $ | (1) |
鉴于曲率张量
| $\left. \begin{matrix} {{\chi }_{11}}=\frac{{{\partial }^{2}}\omega }{\partial y\partial x},~~{{\chi }_{12}}=\frac{{{\partial }^{2}}\omega }{\partial {{y}^{2}}} \\ {{\chi }_{21}}=-\frac{{{\partial }^{2}}\omega }{\partial {{x}^{2}}},~~{{\chi }_{22}}=-\frac{{{\partial }^{2}}\omega }{\partial x\partial y} \\ \end{matrix} \right\}$ | (2) |
采用旋转约束Cosserat理论,应变能密度仅为应变和曲率的函数[31],故可将应变能表示为
| $ U = \int\left[{\mu _{\rm L} \left( {\varepsilon _{ij} \varepsilon _{ij} + l^2\chi _{ij} \chi _{ij} } \right) + \frac{\lambda _{\rm L} \varepsilon _{ii} \varepsilon _{jj} }{2}} \right]{\rm d}V $ | (3) |
其中,ij表示应变张量,μ L和λ L为拉梅系数,l为材料的本征长度.
微平板的动能T和外界激励做功W满足下式
| $\left. \begin{array}{*{35}{l}} T=\frac{1}{2}\int{\rho }h{{\left( \frac{\partial w}{\partial t} \right)}^{2}}\text{d}A \\ W=\int{\left( {{p}_{\text{i}}}+{{p}_{\text{r}}}-{{p}_{\text{t}}}+{{p}_{\text{sf}}} \right)}w\text{d}A \\ \end{array} \right\}$ | (4) |
其中,ρ为微平板的材料密度,A为微平板的面积,h为微平板的板厚.
根据Hamilton变分原理
| $ \delta H = \int_{t_1 }^{t_2 } \left( {\delta U - \delta T - \delta W} \right){\rm d}t = 0 $ | (5) |
将式(3)和式(4)代入上式,可得
| $\begin{align} & \int_{{{t}_{1}}}^{{{t}_{2}}}{\int{\{}}\left[ \frac{E\left( 1+\text{j}\eta \right){{h}^{3}}\left( 1-\nu \right)}{12\left( 1+\nu \right)\left( 1-2\nu \right)}+\frac{E\left( 1+\text{j}\eta \right){{l}^{2}}h}{2\left( 1+\nu \right)} \right]{{\nabla }^{4}}w+ \\ & \rho h\frac{{{\partial }^{2}}w}{\partial {{t}^{2}}}-\left( {{p}_{\text{i}}}+{{p}_{\text{r}}}-{{p}_{\text{t}}}+{{p}_{\text{sf}}} \right)\}\delta w\text{d}A\text{d}t=0 \\ \end{align}$ | (6) |
其中,η表示材料的阻尼系数;ν为材料的泊松比,取0.278;E为材料的弹性模量,取50 GPa;
综合上述,可得声激励和阻尼效应共同作用下的振动控制方程
| $ D\nabla ^2\nabla ^2w + \rho h\frac{\partial ^2w}{\partial t^2} = p_{\rm i} + p_{\rm r} - p_{\rm t} + p_{\rm sf} $ | (7) |
其中,D表示考虑尺度效应时微平板的等效弯曲刚度,即
| $ D = \frac{E\left( {1 + {\rm j}\eta } \right)h^3\left( {1 - \nu } \right)}{12\left( {1 + \nu } \right)\left( {1 - 2\nu } \right)} + \frac{E\left( {1 + {\rm j}\eta } \right)l^2h}{2\left( {1 + \nu } \right)} $ | (8) |
在空气和简支微平板下表面的交界面上,气体质点和与之相邻的微平板质点在垂直于交界面方向上的速度分量相等,即满足速度连续性条件
上表面
| $-\frac{\partial {{\Phi }_{1}}}{\partial \text{z}}=\text{j}{{\omega }_{\text{s}}}w$ | (9) |
下表面
| $-\frac{\partial {{\Phi }_{2}}}{\partial z}=\text{j}{{\omega }_{\text{s}}}w$ | (10) |
其中,Φ1 和Φ2分别代表上、下表面声场的速度势函数,ωs是声波的圆频率.
定义入射声波声场的速度势函数为[32]
| ${{\Phi }_{\text{1},\text{i}}}\left( x,y,z;t \right)={{I}_{\text{i}}}{{\text{e}}^{\text{j}\left( {{\omega }_{\text{s}}}t-{{k}_{x}}x-{{k}_{y}}y-{{k}_{z}}z \right)}}$ | (11) |
其中,Ii是相应的幅值,kx,ky和kz分别是波数k0在x,y和z方向的分量,满足
| $ \left.\begin{array}{l} k_0 = {\omega _{\rm s} }/ c \\ k_x = k_0 \sin \varphi \cos \theta \\ k_y = k_0 \sin \varphi \sin \theta \\ k_z = k_0 \cos \varphi \\ \end{array}\right\} $ | (12) |
其中,φ是入射俯仰角,即入射声压与z轴夹角;θ是入射方向角,即入射声压与x轴夹角;c为声速,取340 m/s.
同理,定义反射声波声场的速度势函数和透射声波声场的速度势函数为
| $ \varPhi _{\rm 1,r} \left( {x,y,z;t} \right) = \beta _{\rm r} {\rm e}^{{\rm j}\left( {\omega _{\rm s} t - k_x x - k_y y + k_z z} \right)} $ | (13) |
| $ \varPhi _{\rm 2,t} \left( {x,y,z;t} \right) = \varepsilon _{\rm t} {\rm e}^{{\rm j}\left( {\omega _{\rm s} t - k_x x - k_y y - k_z z} \right)} $ | (14) |
其中,βr 和εt是相应的幅值.
因此,微平板上表面的声场速度势函数为Φ1 =Φ1,i+ Φ1,r,即
| $ \varPhi _1 \left( {x,y,z;t} \right) = I_{\rm i} {\rm e}^{{\rm j}\left( {\omega _{\rm s} t - k_x x - k_y y - k_z z} \right)} + \beta _{\rm r} {\rm e}^{{\rm j}\left( {\omega _{\rm s} t - k_x x - k_y y + k_z z} \right)} $ | (15) |
声压与声压速度势有如下关系
| $ p_{\rm r} + p_{\rm i} = {\rm j}\omega _{\rm s} \rho _0 \varPhi _1 $ | (16) |
其中,ρ0为空气密度,取ρ0= 1.293 kg/m3.联合式(16)和式(9),可得速度连续性条件的另一种形式
上表面
| $\frac{\partial \left( {{p}_{\text{i}}}+{{p}_{\text{r}}} \right)}{\partial \text{z}}={{\rho }_{0}}\omega _{\text{s}}^{2}w$ | (17) |
在简支微平板的下表面,由于气膜压仅与底部微平板的振动有关,而与简支微平板的振动无关,故将式(12)带入Φ2 = Φ2,t中可得
| $ \varPhi _2 \left( {x,y,z;t} \right) = \varepsilon {\rm e}^{{\rm j}\left( {\omega _{\rm s} t - k_x x - k_y y - k_z z} \right)} $ | (18) |
同理,可得速度连续性条件(10)的另一种形式
下表面
| $\frac{\partial {{p}_{\text{t}}}}{\partial \text{z}}={{\rho }_{0}}\omega _{\text{s}}^{2}w$ | (19) |
综合式(17)和式(19),可得速度连续性条件为
上表面
| $\frac{\partial \left( {{p}_{\text{i}}}+{{p}_{\text{r}}} \right)}{\partial \text{z}}={{\rho }_{0}}\omega _{\text{s}}^{2}w$ | (20a) |
下表面
| $\frac{\partial {{p}_{\text{t}}}}{\partial \text{z}}={{\rho }_{0}}\omega _{\text{s}}^{2}w$ | (20b) |
简支边界条件下,微平板的挠度可表示为\vspace{-1mm}
| $w=\sum\limits_{m=1}^{\infty }{\sum\limits_{n=1}^{\infty }{{{A}_{mn}}}}{{\varphi }_{mn}}{{\text{e}}^{\text{j}{{\omega }_{\text{s}}}t}}$ | (21) |
其中,
同时,将入射声压、反射声压和透射声压分别表示为简支态级数的形式
| $ p_{\rm i} \left( {x,y,t} \right) = \mathop \sum \limits_{m = 1}^\infty \mathop \sum \limits_{n = 1}^\infty I_{mn} \varphi _{mn} {\rm e}^{{\rm j}\left( {\omega _{\rm s} t - k_z z} \right)} $ | (22) |
| ${{p}_{\text{r}}}\left( x,y,t \right)=\sum\limits_{m=1}^{\infty }{\sum\limits_{n=1}^{\infty }{{{\beta }_{mn}}}}{{\varphi }_{mn}}{{\text{e}}^{\text{j}\left( {{\omega }_{\text{s}}}t+{{k}_{z}}z \right)}}$ | (23) |
| ${{p}_{\text{t}}}\left( x,y,t \right)=\sum\limits_{m=1}^{\infty }{\sum\limits_{n=1}^{\infty }{{{\varepsilon }_{mn}}}}{{\varphi }_{mn}}{{\text{e}}^{\text{j}\left( {{\omega }_{\text{s}}}t-{{k}_{z}}z \right)}}$ | (24) |
其中,βmn,εmn和Imn分别为第mn阶反射声压、透射声压和入射声压的幅值.由于入射声压可表示为
| $ p_{\rm i} \left( {x,y,t} \right) = I{\rm e}^{{\rm j}\left( {\omega _{\rm s} t - k_x x - k_y y - k_z z} \right)} $ | (25) |
则由上两式得
| ${{I}_{mn}}=\frac{4mn{{\pi }^{2}}\left( {{\text{e}}^{-\text{j}{{k}_{x}}L}}\cos m\pi -1 \right)\left( {{\text{e}}^{-\text{j}{{k}_{y}}L}}\cos n\pi -1 \right)I}{\left[ {{\left( {{k}_{x}}L \right)}^{2}}-{{\left( m\pi \right)}^{2}} \right]\left[ {{\left( {{k}_{y}}L \right)}^{2}}-{{\left( n\pi \right)}^{2}} \right]}$ | (26) |
将式(17)∼式(20)代入式(20),可得
| $ \beta _{mn} = \frac{ - {\rm j}\rho _0 \omega _{\rm s}^2 A_{mn} {\rm e}^{{\rm j}\frac{k_z h}{2}} + I_{mn} k_z {\rm e}^{{\rm j}k_z h}}{k_z } $ | (27) |
| ${{\varepsilon }_{mn}}=\frac{\text{j}{{\rho }_{0}}\omega _{\text{s}}^{2}{{\text{e}}^{\text{j}\frac{{{k}_{z}}h}{2}}}}{{{k}_{z}}}{{A}_{mn}}$ | (28) |
Bao和Yang[17]的研究表明,可将气膜力表示为
| $ F = - \frac{P_{\rm a} A}{h_0 }f_{\rm e} \left( \sigma \right)z - \frac{P_{\rm a} A}{h_0 \omega _{\rm sf} }f_{\rm d} \left( \sigma \right)\dot {z} $ | (29) |
其中,ωsf为底部微平板的振动频率,σ为挤压数且
| $ \sigma = \frac{12\eta _{\rm eff} \omega _{\rm sf} L^2}{P_{\rm a} h_0^2 } $ | (30) |
其中,ηeff为有效黏性系数,与Knudsen数有关,二者关系为[26]
| $ \eta _{\rm eff} = \frac{\eta }{1 + 9.638K_n^{1.159} } $ | (31) |
Knudsen数定义为
| $ K_n = \frac{\lambda }{h_0 } $ | (32) |
其中,λ表示环境空气分子的平均自由程.
挤压数σ决定了空气薄膜的可压缩性:挤压数较高时,空气薄膜的可压缩性较好,空气薄膜力可近似看作弹性力;挤压数较低时,空气薄膜的可压缩性较差,空气薄膜力主要以阻尼力形式表现[17].因此,空气薄膜力可视为由弹性力和阻尼力两部分组成.
令
| $ F = - k_{\rm e} z - c_{\rm d} \dot {z} $ | (33) |
ke和cd可被视为空气薄膜力的弹性系数和阻尼系数,其值共同决定了空气薄膜力的大小.Blech[20]给出了空气薄膜力的弹性系数和阻尼系数,即
| ${{k}_{\text{e}}}=\frac{64{{\sigma }^{2}}{{P}_{\text{a}}}A}{{{\pi }^{8}}{{h}_{0}}}\sum\limits_{m,n=\text{odd}}{\frac{1}{{{\left( mn \right)}^{2}}\left\{ {{\left[ {{m}^{2}}+{{\left( n{{\varepsilon }_{0}} \right)}^{2}} \right]}^{2}}+\frac{{{\sigma }^{2}}}{{{\pi }^{4}}} \right\}}}$ | (34) |
| ${{c}_{\text{d}}}=\frac{64\sigma {{P}_{\text{a}}}A}{{{\pi }^{6}}{{h}_{0}}}\sum\limits_{m,n=\text{odd}}{\frac{{{m}^{2}}+{{\left( n{{\varepsilon }_{0}} \right)}^{2}}}{{{\left( mn \right)}^{2}}\left\{ {{\left[ {{m}^{2}}+{{\left( n{{\varepsilon }_{0}} \right)}^{2}} \right]}^{2}}+\frac{{{\sigma }^{2}}}{{{\pi }^{4}}} \right\}}}$ | (35) |
其中,ε0为微平板的长宽比,鉴于本文假设微平板为正方形,故ε0=1.
由于振动形式为频率ωsf、振幅δh0的简谐振动,故振动微平板的位移z和速度
| $ \left.\begin{array}{ll} z = \delta h_0 \cos (\omega _{\rm sf} t) \\ \dot {z} = - \omega _{\rm sf} \delta h_0 \sin (\omega _{\rm sf} t )\\ \end{array}\right\} $ | (36) |
将式(34)∼式(36)代入式(33),并除以微平板的面积A,得psf(t)的表达式如下
| $\begin{array}{*{35}{l}} {{p}_{\text{sf}}}\left( t \right)=\frac{F}{A}=-\frac{64{{\sigma }^{2}}{{P}_{\text{a}}}\delta {{h}_{0}}\cos ({{\omega }_{\text{sf}}}t)}{{{\pi }^{8}}{{h}_{0}}}\cdot \\ ~\sum\limits_{m,n=\text{odd}}^{\infty }{\frac{1}{{{\left( mn \right)}^{2}}\left\{ {{\left[ {{m}^{2}}+{{\left( n\varepsilon \right)}^{2}} \right]}^{2}}+\frac{{{\sigma }^{2}}}{{{\pi }^{4}}} \right\}}}+ \\ \begin{align} & ~~~~~\frac{64\sigma {{P}_{\text{a}}}{{\omega }_{\text{sf}}}\delta {{h}_{0}}\sin ({{\omega }_{\text{sf}}}t)}{{{\pi }^{6}}{{h}_{0}}}\cdot \\ & \sum\limits_{m,n=\text{odd}}^{\infty }{\frac{{{m}^{2}}+{{\left( n\varepsilon \right)}^{2}}}{{{\left( mn \right)}^{2}}\left\{ {{\left[ {{m}^{2}}+{{\left( n\varepsilon \right)}^{2}} \right]}^{2}}+\frac{{{\sigma }^{2}}}{{{\pi }^{4}}} \right\}}} \\ \end{align} \\ \end{array}~$ | (37) |
可将上式进行形式上的简化,即
| $ p_{\rm sf} \left( t \right) = a\cos (\omega _{\rm sf} t) + b\sin (\omega _{\rm sf} t)$ | (38) |
其中,a和b满足下式
| $\begin{array}{*{35}{l}} a=-\frac{64{{\sigma }^{2}}{{P}_{\text{a}}}\delta }{{{\pi }^{8}}}\cdot \\ \sum\limits_{m=1,\text{odd}}^{\infty }{\sum\limits_{n=1,\text{odd}}^{\infty }{\frac{1}{{{\left( mn \right)}^{2}}\left\{ {{\left[ {{m}^{2}}+{{\left( n\varepsilon \right)}^{2}} \right]}^{2}}+\frac{{{\sigma }^{2}}}{{{\pi }^{4}}} \right\}}}} \\ \end{array}$ | (39) |
| $\begin{align} & b=\frac{64\sigma {{P}_{\text{a}}}\delta {{\omega }_{\text{sf}}}}{{{\pi }^{6}}}\cdot \\ & \sum\limits_{m=1,\text{odd}}^{\infty }{\sum\limits_{n=1,\text{odd}}^{\infty }{\frac{{{m}^{2}}+{{\left( n\varepsilon \right)}^{2}}}{{{\left( mn \right)}^{2}}\left\{ {{\left[ {{m}^{2}}+{{\left( n\varepsilon \right)}^{2}} \right]}^{2}}+\frac{{{\sigma }^{2}}}{{{\pi }^{4}}} \right\}}}} \\ \end{align}$ | (40) |
将acos(ω sf t)和bsin(ω sf t)分别展开为如下无穷级数
| $\begin{align} & a\cos ({{\omega }_{\text{sf}}}t)=\sum\limits_{m=1}^{\infty }{\sum\limits_{n=1}^{\infty }{{{a}_{mn}}}}{{\phi }_{mn}}{{\text{e}}^{\text{j}{{\omega }_{\text{s}}}t}} \\ & b\sin ({{\omega }_{\text{sf}}}t)=\sum\limits_{m=1}^{\infty }{\sum\limits_{n=1}^{\infty }{{{b}_{mn}}}}{{\phi }_{mn}}{{\text{e}}^{\text{j}{{\omega }_{\text{s}}}t}} \\ \end{align}$ |
然后将两式变换为以下形式
| $ \frac{a\cos ({{\omega }_{\text{sf}}}t)}{{{\text{e}}^{\text{j}{{\omega }_{\text{s}}}t}}}=\sum\limits_{m=1}^{\infty }{\sum\limits_{n=1}^{\infty }{{{a}_{mn}}}}\sin \frac{m\pi x}{L}\sin \frac{n\pi y}{L}$ | (41) |
| $\frac{b\sin ({{\omega }_{\text{sf}}}t)}{{{\text{e}}^{\text{j}{{\omega }_{\text{s}}}t}}}=\sum\limits_{m=1}^{\infty }{\sum\limits_{n=1}^{\infty }{{{b}_{mn}}}}\sin \frac{m\pi x}{L}\sin \frac{n\pi y}{L}$ | (42) |
苏联数学家菲赫金哥尔茨[33]提出了多重Fourier级数的展开方式.当函数
| $f\left( x,y \right)\tilde{\ }\sum\limits_{n,m=0}^{\infty }{{{\lambda }_{n,m}}}{{a}_{n,m}}\sin \frac{m\pi x}{L}\sin \frac{n\pi y}{L} $ | (43) |
其中λn,m满足
| ${{\lambda }_{n,m}}=\left\{ \begin{array}{*{35}{l}} 0.25, & m=0,n=0 \\ 0.5, & m=0,n\ne 0,n=0 \\ 0, & m\ne 0,n\ne 0 \\ \end{array} \right.$ |
当m或n最少一个为零时,
| $f\left( x,y \right)\tilde{\ }\sum\limits_{n,m=1}^{\infty }{{{a}_{mn}}}\sin \frac{m\pi x}{L}\sin \frac{n\pi y}{L}$ | (44) |
其中,系数amn 满足
| ${{a}_{mn}}=\frac{4}{mn{{\pi }^{2}}}\left( 1-\cos n\pi \right)\left( 1-\cos m\pi \right)a\cos {{\omega }_{\text{sf}}}t\cdot {{\text{e}}^{-\text{j}{{\omega }_{\text{s}}}t}}$ | (45) |
同理,可得
| ${{b}_{mn}}=\frac{4}{mn{{\pi }^{2}}}\left( 1-\cos n\pi \right)\left( 1-\cos m\pi \right)b\sin {{\omega }_{\text{sf}}}t\cdot {{\text{e}}^{-\text{j}{{\omega }_{\text{s}}}t}}$ | (46) |
将式(21)~式(24)以及式(27)和式(28)代入式(7),并考虑上述对psf( t )的推导,可得
| ${{A}_{mn}}=\frac{2{{\text{e}}^{\frac{\text{j}{{k}_{z}}h}{2}}}{{I}_{mn}}+\left( {{a}_{mn}}+{{b}_{mn}} \right)}{D{{\left[ {{\left( \frac{m\pi }{L} \right)}^{2}}+{{\left( \frac{n\pi }{L} \right)}^{2}} \right]}^{2}}-\left( \rho h-2j\frac{{{\rho }_{0}}}{{{k}_{z}}} \right)\omega _{\text{s}}^{2}}$ | (47) |
将上式代入式(28),可得
| ${{\varepsilon }_{mn}}=\frac{\text{j}{{\rho }_{0}}\omega _{\text{s}}^{2}{{\text{e}}^{\text{j}\frac{{{k}_{z}}h}{2}}}\left[ 2{{\text{e}}^{\frac{\text{j}{{k}_{z}}h}{2}}}{{I}_{mn}}+{{a}_{mn}}+{{b}_{mn}} \right]}{{{k}_{z}}\left\{ D{{\left[ {{\left( \frac{m\pi }{L} \right)}^{2}}+{{\left( \frac{n\pi }{L} \right)}^{2}} \right]}^{2}}-\left( \rho h-2\text{j}\frac{{{\rho }_{0}}}{{{k}_{z}}} \right)\omega _{\text{s}}^{2} \right\}}$ | (48) |
入射声功率Wi和透射声功率Wt可以无穷级数形式[29]表示为
| $ W_{\rm i} = \frac{L^2}{8\rho _0 c}\mathop \sum \limits_{m = 1}^\infty \mathop \sum \limits_{n = 1}^\infty I_{mn}^2 $ | (49) |
| $ W_{\rm t} = \frac{L^2}{8\rho _0 c}\mathop \sum \limits_{m = 1}^\infty \mathop \sum \limits_{n = 1}^\infty \varepsilon _{mn}^2 $ | (50) |
定义传声损失STL(sound transmission loss,STL)为
| $ S_{\rm TL} = 10\lg\left( {\frac{W_{\rm i} }{W_{\rm t} }} \right)$ | (51) |
综合式(49)~式(51),可得
| ${{S}_{\text{TL}}}=10\lg \frac{\left| \sum\limits_{m=1}^{\infty }{\sum\limits_{n=1}^{\infty }{I_{mn}^{2}}} \right|}{\left| \text{ }\sum\limits_{m=1}^{\infty }{\sum\limits_{n=1}^{\infty }{\varepsilon _{mn}^{2}}} \right|}$ | (52) |
一般而言,针对传声效应的分析多集中于其频谱特性.利用频谱特性,可得一定参量条件下所研究对象的最佳吸声效果、最佳隔声效果或最小传声损失与声波频率的关系,进而针对工程实际中具体传声的需求设计相关参数.
下文我们系统分析简支微平板的本征长度、Knudsen数、振动微平板的振动频率和振动幅度,以及两微平板的间距对简支微平板传声损失特性的影响.针对各种参数的讨论,如无特殊说明,相关变量的取值如表 1所示.
| 表 1 变量表 Table 1 Variables |
其他常数参量的选取如表 2所示.
| 表 2 常量表 Table 2 Constants |
考虑阻尼效应后,由于本文模型的传声损失与时间相关(见式(45)和式(46)),欲考察传声损失的频谱特性,必须排除时间因素.我们选择在一定时间内,分散选取若干传声损失并取其平均值作为该频率段的传声损失.实际上,由于微平板在低频振动时传声损失的稳定性,在任意时间取点均不会有太大误差;但是,为了结果的精确性和取值的广泛性,我们采取了在大范围时间段取点求平均的方法,以获取更为可靠的结果.
2.1 收敛性分析式(52)以级数形式给出,故在数值计算时需考察其收敛性.一般而言,若级数求和在给定的声压频率处收敛,则该级数求和结果在低于此给定频率的任意频率处均收敛[32].由于本文数值求解的最高振动频率ωsf为200~kHz,最高声波频率ω s为50~MHz,故选择此振动频率和声波频率用于检验STL 的收敛性.图 3结果表明,当级数项数m和n取值40或更大时,传声损失是收敛的.
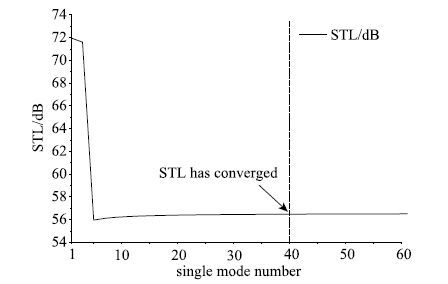
|
图 3 传声损失的收敛性分析 Fig. 3 Convergence of STL |
本文模型考察的微尺度效应包括两个方面,即本征长度l和Knudsen数Kn,它们分别影响简支微平板的等效刚度和压膜力的大小.
首先分析Knudsen数对传声损失的影响.作为分子平均自由程和系统尺度的比值,Knudsen数表征了气体的稀薄程度.Knudsen数越大,气体稀薄性越强;Knudsen数越小,气体的稀薄性越弱.在给定微平板间距h0的条件下,研究Knudsen数对传声损失的影响,实际是研究气体稀薄程度对传声的影响.
图 4显示了声压斜入射(φ =45°)时,不同Knudsen数对传声损失的影响.随着Knudsen数的增大,即随着系统微观程度的增加,传声损失曲线出现更为明显的波峰,且在靠近波峰所处的频段,传声损失随Knudsen数增大而增大的现象越明显.例如,在 35~MHz,41~MHz,44~MHz等附近的波峰处,考虑微尺度效应比不考虑微尺度效应对传声损失的影响大数个数量级.
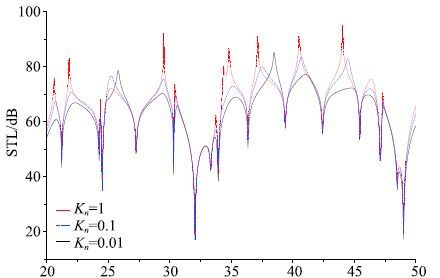
|
图 4 Knudsen数对传声损失的影响 Fig. 4 Influence of Knudsen number on STL |
图 4中Knudsen数从0.01变化到1,表示气体物理模型从滑移区到过渡区,一方面连续流体假设的适用性逐渐降低,另一方面有效黏性系数显著变化.实际上,通过式(30)和(31)可知,随着Knudsen数的增大,有效黏性系数ηeff减小.这是因为当Knudsen数远小于1时,系统的黏性耗能主要由气体分子之间的相互碰撞导致,因此随着气体的稀薄性越来越强,气体分子之间的碰撞逐渐减少,黏性系数相应会越来越小;当Knudsen数逐渐增大,系统尺度和气体分子平均自由程处在同一个数量级上时,气体分子与微平板之间的碰撞逐渐占到主导地位,但此时随着气体的稀薄性越来越强,气体分子与微平板之间的碰撞也会逐渐减少,黏性系数相应越来越小[24]. 有效黏性系数的减小导致挤压数σ减小,即减小了阻尼力,从而使得传声损失增大.因此,随着系统微尺度效应的加大,传声损失随之增加.
本征长度l是Cosserat理论中的一个重要参数,它与材料内部微结构的尺度相关,并影响简支微平板的等效刚度.声压垂直入射(φ =0°)时,图 5给出了不同本征长度对传声损失的影响曲线.由于不同本征长度对传声损失影响曲线在斜入射条件下图线密集,且受到周期性波谷的影响,规律不够显著,故采用垂直入射条件.

|
图 5 本征长度对传声损失的影响 Fig. 5 Influence of characteristic length on STL |
由图 5可知,本征长度(l=0.5~µm)相较于系统尺寸(微平板边长L=80~µm)较小时,其频谱图与不考虑本征长度(l=0~µm)时的传声损失曲线较为吻合.而且,声压频率相对较低(小于30~MHz)时,两者基本重合;在高频段,两者间也仅仅是相位有略微的差别.本征长度较大(l=1 µm)时,相较于不考虑本征长度时的传声损失曲线,频谱图的波峰和波谷变化明显,且整条曲线出现了明显的右移.
本征长度对传声损失的影响实际上是考虑具有不同内部微结构的材料对传声性能的影响.材料内部微结构的非均匀性将使材料的力学性能出现不同于经典弹性理论的结果.因此在本文考虑尺度效应的理论中,材料的本征长度会对材料的传声性能产生较大影响.激励声压的频率和微平板的固有频率相同时,微平板产生共振,加剧了微平板下表面附近的空气质点振动,导致声波的透射显著增强,从而明显降低了传声损失.这就是在传声损失的频谱图中出现波谷的物理机制.因此,传声损失的波谷所对应的频率一般与简支微平板的某些固有频率相等.
微平板的固有振动频率为
| ${{f}_{mn}}=\frac{\pi }{2}\left( \frac{{{m}^{2}}}{{{L}^{2}}}+\frac{{{n}^{2}}}{{{L}^{2}}} \right)\sqrt{\frac{D}{\rho h}}$ | (53) |
在相同模态(相同m和n)条件下,波谷的频率和微平板的弯曲刚度D呈正相关关系,随着D的增大而增大.由式(8)可知,弯曲刚度D又随着本征长度l的增大而增大.因此,由式(53)和式(8)可知,随着本征长度l的增大,传声损失的波谷向高频移动,进而导致频谱图的右移.
2.3 振动微平板振动频率的影响振动微平板的振动频率直接影响压膜阻尼效应,进而对传声损失产生影响.此外,振动频率是影响阻尼效应的关键因素.
在声压垂直入射(φ=0°)条件下,图 6给出了不同振动频率对传声损失的影响曲线.随着振动频率的增加,传声损失曲线在中低频段整体下降. 从100~kHz开始,阻尼效应对传声损失的影响逐渐加大,且呈现频率越高,传声损失衰减越大的现象.例如,200~kHz对应的实线明显不同于不考虑阻尼效应的点线.
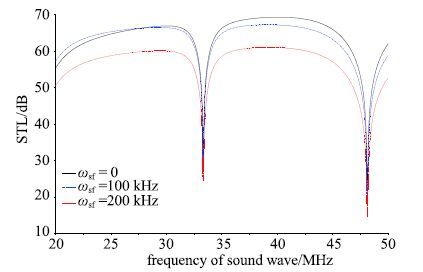
|
图 6 不同振动频率对传声损失的影响 Fig. 6 Influence of oscillation frequency on STL |
由式(37)可知,阻尼力随着振动频率的增大而增大.也就是说,随着振动频率的增大,阻尼效应加剧,从而使传声损失发生衰减.
2.4 振动微平板振动幅度和板间距的影响由式(39)和(40)可知,振动微平板的振动幅度δ的增大会导致参量a和b的增大,进而使得阻尼效应的影响加剧.
在声压斜入射(φ=45°)条件下,图 7给出了不同振动幅度δ对传声损失的影响曲线.其中,实线表示不考虑阻尼效应的传声损失频谱曲线,虚线和点线分别表示振动幅值为0.1倍板间距(0.1h0)和0.3倍板间距(0.3h0 )时传声损失的频谱曲线.一般而言,振动幅度越大,传声损失的衰减越大.具体而言,未考虑阻尼效应时的波峰在考虑阻尼效应之后变得更加平滑,传声损失随着振动幅度的增大而衰减;在一些频段,如27~MHz和39~MHz处,传声损失除了随振动频率增大而衰减之外,还随着振动幅度的增大而右移.
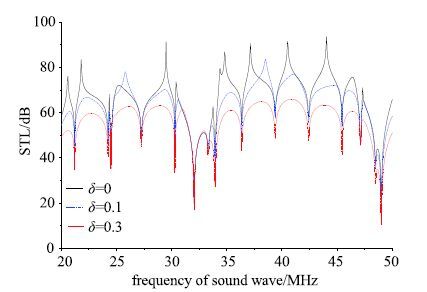
|
图 7 振动幅度对传声损失的影响 Fig. 7 Influence of oscillation amplitude on STL |
振动幅度δ直接影响气膜力是产生以上变化的原因:随着振动幅度δ的增大,气膜力增大;而气膜力越大,传声损失衰减越明显.因此,振动幅度通过影响气膜力的大小影响传声损失,且随着振动幅度δ的增大,传声损失减小.
在声压斜入射(φ=45°)条件下,图 8给出了不同微平板间距对传声损失的影响曲线.一般而言,频谱中传声损失的波峰随着微平板间距的增大而发生上移,波峰的峰值更加尖锐;此外,在25~MHz∼27~MHz以及38~MHz∼40~MHz处,不仅传声损失随间距的增大而增大,波峰也相应左移.但是,对波谷而言,波谷段几乎不随微平板间距的变化而变化.
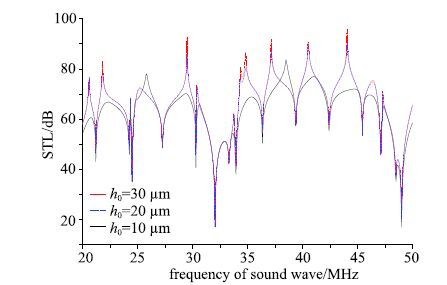
|
图 8 微平板间距对传声损失的影响 Fig. 8 Influence of gap distance on STL |
微平板的间距越大,气膜力越小,且二者间呈二次曲线关系.同时,不考虑阻尼效应时,微平板的间距对传声损失无影响.由此可知,考虑阻尼效应后,随着微平板间距的增大,传声损失会出现增大现象.但是,由于微平板间距对气膜力大小的影响无法达到跨数量级的程度,故其对传声损失的影响有限.
与图 7结果类似,不同的间距仅对传声损失的量值有较小的影响,但整个曲线的形式几乎无变化.这主要是因为,由于采用了线性板模型,微平板系统的固有振动频率不随振动幅度δ和微平板间距h0的变化而变化.
3 结论本文针对MEMS中的典型微平板结构,采用Cosserat理论得到简支微平板的等效刚度,通过考虑振动微平板引入了气膜力,建立了声压和气膜力共同激励下的微平板的声振耦合控制方程,然后利用多重Fourier变换求得结构传声损失的数值解,在此基础上系统分析了不同尺度效应以及不同参数条件下,微结构中气体薄膜所产生的阻尼力对微平板结构传声特性的影响.结论如下:
(1) 本征长度的增大导致频谱曲线向高频移动,且本征长度越大,移动越明显;增大Knudsen数会使频谱曲线的波峰变陡,峰值变大;
(2) 控制并减小振动幅度可提高微平板的隔声性能,增大微平板间距也可提高微平板的隔声性能;
(3) 振动幅度越大,或板间距越小,传声损失曲线极大值所在的峰值越平坦.
本文结果为MEMS典型微结构的设计提供了一定的理论依据,并完善了相关微结构声学的理论研究.
| [1] |
张文明, 孟光, 魏克湘. 参数激励下静电驱动微机电系统动力特性研究[J].
力学学报,2009, 41 (2) : 282-288.
( Zhang Wenming, Meng Guang, Wei Kexiang. Dynamic characteristics of electrostatically actuated MEMS under parametric excitations[J].
Chinese Journal of Theoretical and Applied Mechanics,2009, 41 (2) : 282-288.
(in Chinese) ) ( 0) 0)
|
| [2] |
Xu L, Sun L. Electromechanical coupled non-linear vibration of the micro plate[J].
Journal of Mechanical Engineering Science,2010, 224 (C6) : 1383-1396.
( 0) 0)
|
| [3] |
孙丽波, 许立忠, 刘庆玲. 静电激励微板动力学特性研究[J].
振动工程学报,2015, 24 (4) : 525-530.
( Sun Libo, Xu Lizhong, Liu Qingling. Research on dynamics of electrostatically actuated microplate[J].
Journal of Vibration Engineering,2015, 24 (4) : 525-530.
(in Chinese) ) ( 0) 0)
|
| [4] |
Xu LZ, Sun LB. Muti-field coupled dynamics for micro plate[J].
International Journal of Applied Electromagnetics and Mechanics,2011, 35 : 201-229.
( 0) 0)
|
| [5] |
董天宝, 宋亚勤. 光热激励下微悬臂梁在流体中的振动研究[J].
力学学报,2014, 46 (5) : 703-709.
( Dong Tianbao, Song Yaqin. Study on the vibration of microcantilevers immersed in fluids under photothermal excitation[J].
Chinese Journal of Theoretical and Applied Mechanics,2014, 46 (5) : 703-709.
(in Chinese) ) ( 0) 0)
|
| [6] |
吕劲楠, 唐洁影. MEMS 微悬臂梁在冲击环境下的可靠性[J].
功能材料与器件学报,2008, 14 (1) : 103-106.
( Lü Jinnan, Tang Jieying. Reliability for MEMS micro-cantilevers under shock load[J].
Journal of Functional Materials and Devices,2008, 14 (1) : 103-106.
(in Chinese) ) ( 0) 0)
|
| [7] |
热合曼·艾比布力, 胡英杰, 王同东, 等. 微悬臂梁结构的谐振式 MEMS 黏度传感器[J].
仪表技术与传感器,2015, 5 : 8-27.
( Rahman Hebibul, Hu Yingjie, Wang Tongdong, et al. Resonant MEMS viscosity sensor of micro cantilever beam structure[J].
Instrument Technique and Sensor,2015, 5 : 8-27.
(in Chinese) ) ( 0) 0)
|
| [8] |
董林玺, 刘国华, 钱忺. 孔的形状和排列方式对厚孔板微结构压膜空气阻尼的影响分析[J].
传感技术学报,2007, 20 (6) : 1262-1266.
( Dong Linxi, Liu Guohua, Qian Xian. The effects of hole shapes and array forms on the squeeze film air damping of thick perforated microstructures[J].
Chinese Journal of Sensors and Actuators,2007, 20 (6) : 1262-1266.
(in Chinese) ) ( 0) 0)
|
| [9] |
Vijay C, Mark S, Louis C. Experimental study of acoustic impedance of MEMS-based micro-perforated liners//27th AIAA Aeroacoustics Conference. 2006.
( 0) 0)
|
| [10] |
邵宝东, 孙兆伟. 基于MEMS 的微槽冷却系统在微纳卫星热控中的应用[J].
上海航天,2006, 4 : 34-38.
( Shao Baodong, Sun Zhaowei. Application of MEMS-based microchannel cooling systems in micro/ nano satellite thermal control[J].
Aerospace Shanghai,2006, 4 : 34-38.
(in Chinese) ) ( 0) 0)
|
| [11] |
Agache V, Blanco-Gomez G, Baleras F, et al. An embedded microchannel in a MEMS plate resonator for ultrasensitive mass sensing in liquid[J].
Lab on a Chip,2011, 11 : 2598-2603.
DOI: 10.1039/c1lc20011a. ( 0) 0)
|
| [12] |
Zhang CL, Xu GH, Jiang Q. Analysis of the air-damping effect on a micromachined beam resonator[J].
Mathematics and Mechanics of Solids,2003, 8 (3) : 315-325.
DOI: 10.1177/1081286503008003006. ( 0) 0)
|
| [13] |
Craighead HG. Nanoelectromechanical systems[J].
Science,2000, 290 (5496) : 1532-1535.
DOI: 10.1126/science.290.5496.1532. ( 0) 0)
|
| [14] |
Mehner JE, Doetzel W, Schauwecker B. Reduced order modeling of fluid structural interactions in MEMS based on model projection techniques//IEEE ed. Transducers 2003, 12th International Conference on Solid-State Sensors, Actuators and Microsystems, Boston, 2003. Danvers: Institute of Electrical and Electronics Engineers, 2003. Vol. 2, pp. 1840-1843
( 0) 0)
|
| [15] |
康新, 席占稳. 基于Cosserat 理论的微梁振动特性的尺度效应[J].
机械强度,2007, 29 (1) : 1-4.
( Kang Xin, Xi Zhanwen. Size effect on the dynamic characteristic of a micro beam based on cosserat theory[J].
Journal of Mechanical Strength,2007, 29 (1) : 1-4.
(in Chinese) ) ( 0) 0)
|
| [16] |
王晓明, 王飞, 赵学增, 等. 基于Cosserat 理论的四边简支自由振动微平板尺度效应研究[J].
固体力学学报,2012, 33 (1) : 63-68.
( Wang Xiaoming, Wang Fei, Zhao Xuezeng, et al. On the size effect in a freely-vibrating micro-plate with the four edges simply-supported based on the cosserat theory[J].
Chinese Journal of Solid Mechanics,2012, 33 (1) : 63-68.
(in Chinese) ) ( 0) 0)
|
| [17] |
Bao MH, Yang H. Squeeze film air damping in MEMS[J].
Sensors and Actuators A: Physical,2007, 136 (1) : 3-27.
DOI: 10.1016/j.sna.2007.01.008. ( 0) 0)
|
| [18] |
Langlois WE. Isothermal squeeze films[J].
Quart Appl Math,1962, XX (2) : 131-150.
( 0) 0)
|
| [19] |
Griffin WS, Richarson HH, Yamanami S. A study of fluid squeezefilm damping[J].
Journal of Basic Engineering,1966, 88 (2) : 451-456.
DOI: 10.1115/1.3645878. ( 0) 0)
|
| [20] |
Blech J. On isothermal squeeze films[J].
Journal of Lubrication Technology,1983, 105 (4) : 615-620.
DOI: 10.1115/1.3254692. ( 0) 0)
|
| [21] |
Cussler EL.
Diffusion: Mass Transfer in Fluid Systems. Cambridge University Press[M]. 1997 .
( 0) 0)
|
| [22] |
Tison SA. Experimental data and theoretical modeling of gas flows through metal capillary leaks[J].
Vacuum,1993, 44 : 1171-1175.
DOI: 10.1016/0042-207X(93)90342-8. ( 0) 0)
|
| [23] |
Coronell DG, Jensen K F. Analysis of transition regime flows in low pressure CVD reactors using the direct simulation monte carlo method[J].
Journal of Electrochemical Society,1992, 139 : 2264-2273.
DOI: 10.1149/1.2221213. ( 0) 0)
|
| [24] |
Beskok A, Karniadakis GE. Report: a model for flows in channels, pipes, and ducts at micro and nano scales[J].
Microscale Thermophysical Engineering,1999, 3 : 43-77.
DOI: 10.1080/108939599199864. ( 0) 0)
|
| [25] |
Veijola T, Kuisma H, Lahdenperä J, et al. Equivalent-circuit model of the squeezed gas film in a silicon accelerometer[J].
Sensors and Actuators A: Physical,1995, 48 (3) : 239-248.
DOI: 10.1016/0924-4247(95)00995-7. ( 0) 0)
|
| [26] |
Fukui S, Kaneko R. Analysis of ultra-thin gas film lubrication based on linearized Boltzmann equation: first report—derivation of a generalized lubrication equation including thermal creep flow[J].
Journal of Tribology,1988, 110 (2) : 253-261.
DOI: 10.1115/1.3261594. ( 0) 0)
|
| [27] |
Fukui S, Kaneko R. A database for interpolation of Poiseuille flow rates for high Knudsen number lubrication problems[J].
Journal of Tribology,1990, 112 (1) : 78-83.
DOI: 10.1115/1.2920234. ( 0) 0)
|
| [28] |
Carneal JP, Fuller CR. An analytical and experimental investigation of active structural acoustic control of noise transmission through double panel systems[J].
Journal of Sound and Vibration,2004, 272 (3) : 749-771.
( 0) 0)
|
| [29] |
任树伟, 辛锋先, 卢天健. 考虑尺度效应的微平板声振耦合特性研究[J].
中国科学: 技术科学,2014, 44 : 201-208.
( Ren Shuwei, Xin Fengxian, Lu Tianjian. Scale effect analysis for the vibro-acoustic performance of a simply-supported micro-plate[J].
Sci Sin Tech,2014, 44 : 201-208.
(in Chinese) ) ( 0) 0)
|
| [30] |
武洁. 微悬臂梁机电系统的动力学特性研究. [硕士论文]. 上海: 上海交通大学. 2012
( Wu Jie. Investigation of microcantilever electromechanical system dynamic. [Master Thesis]. Shanghai: Shanghai Jiao Tong University. 2012 (in Chinese)
) ( 0) 0)
|
| [31] |
Chong ACM, Yang F, Lam DCC, et al. Torsion and bending of micron-scaled structures[J].
Journal of Materials Research,2001, 16 (4) : 1052-1058.
DOI: 10.1557/JMR.2001.0146. ( 0) 0)
|
| [32] |
辛锋先, 卢天健.
轻质板壳结构设计的振动和声学基础[M]. 北京: 科学出版社, 2012 .
( 0) 0)
|
| [33] |
菲赫金哥尔茨. 微积分学教程, 第三卷, 第十九章. 路可见, 等译. 高等教育出版社, 2006
( 0) 0)
|
2. State Key Laboratory for Strength and Vibration of Mechanical Structures, Xi'an Jiaotong University, Xi'an 710049, China
 2016, Vol. 48
2016, Vol. 48


