2. 中国航空研究院, 北京 100012
非线性动力学系统的数学模型一般是一组偏微分方程,例如雷诺平均Navier--Stokes方程、结构动力学方程等,都可以采用时间推进方法进行求解.但是,随着问题规模爆炸式的增加,时间推进方法需要耗费大量的计算资源和计算时间,根本无法应用到工程实际应用中.在这种背景下,降阶模型方法应运而生,成为研究热点.目前最具发展前景的方法主要有Volterra级数[1-2]、本征正交分解(proper orthogonal decomposition)降阶方法[3]、谐波平衡(harmonic balance,HB)方法[4]等.Lucia等[5]对以上3种方法进行了大量的对比研究,认为在这3个方法中,HB是最成熟的方法,已成功应用到三维构型的非定常流场分析中,并正在向复杂构型扩展.
HB方法的完整阐述和表达最早由Kryloff和Bogoliuboff 给出[6].该方法将方程的解用Fourier级数展开,就可以消去其中的时间导数项,最终得到一个以自变量的Fourier系数为求解目标的方程组[7].然后采用Newton-Raphson迭代求解方程组,得到最终的频域结果,也可以转化为时域结果.但是,原始谐波平衡方法在非线性项的处理上存在重大缺陷,使之在复杂问题中的应用变得非常困难[8].Lau和Cheung[9]提出的增量谐波平衡(incremental harmonic balance, IHB)方法,通过引入增量项,大幅简化降阶方程的处理难度,已成功应用于非线性振子方程[10]和非线性气弹系统[11]中.此外,Hall等[12]提出的高阶谐波平衡方法(high-order harmonic balance,HOHB)通过离散傅里叶变换将求解目标由非定常时域解的Fourier系数转换为一个周期内各等分时间层上方程的解.再加上Hall等提出 "伪时间步τ"的概念,就能够将非线性方程转换为"定常"形式,对已有的定常求解器进行一定的修改即可得到HOHB求解器[5],在强迫运动[13-14]、动导数计算[15 - 16]、极限环分析[4, 17-18]、伴随优化[19-20]和涡轮机械流场分析[21-22]等方面得到广泛应用,其计算消耗远比非定常计算低得多.目前HOHB方法已成功应用到OVERFLOW2[23],ELSA[24],PMB[15],COSA[15]等成熟的CFD软件中,应用前景十分广阔.McMullen等[25 - 26]和Dai等[27]分别提出的非线性频域方法和时间配置法从另外的角度对偏微分方程降阶处理,从本质上与HOHB方法是等价的.
为了研究HB和HOHB方法的差别,Liu等[7]采用这两种方法对达芬振子方程, 范德波尔振子方程[8]以及二阶延迟微分方程[28]等进行对比分析,主要得出以下两点结论:(1)HOHB方法可能产生非物理解,原因在于迭代计算过程中Fourier系数的不收敛[7];(2)当方程的非线性较强时,HOHB方法所需的谐波数是HB方法的两倍以上[7-8, 28].
本文通过对HOHB中迭代方法和非线性项的分析,进一步探索非物理解的来源.本文选择Newton下山法,减小迭代方法对初值选取的敏感性.然后,从HOHB方程的推导出发,探明非物理解产生的根本原因.再次,根据非线性项的特点提出HOHB方法中处理非线性项的改进方法,最后则通过达芬振子和立方刚度非线性气动弹性系统的模拟结果验证改进方法的可行性.
1 高阶谐波平衡方法下面以达芬振子方程为例阐述HOHB方法的处理过程[7]
| $\ddot x + 2\xi \dot x + x + {x^3} = F\sin (\omega t)$ | (1) |
将自变量x(t)用Fourier级数展开至NH阶如下所示
| $x(t) = {{\hat x}_0} + \sum\limits_{n = 1}^{{N_{\rm{H}}}} {\left[ {{{\hat x}_{2n - 1}}\cos (n\omega t) + {{\hat x}_{2n}}\sin (n\omega t)} \right]} $ | (2) |
将上式写成向量乘积的形式如下
| $x(t) = {\varphi ^{\rm{T}}}\widehat x$ | (3) |
其中
| $\matrix{ {\varphi = {{\left[ {1 \cos \omega t \sin \omega t \cdots \cos {N_{\rm{H}}}\omega t \sin {N_{\rm{H}}}\omega t} \right]}^{\rm{T}}}} \hfill \cr {\widehat x = {{\left[ {{{\hat x}_0} {{\hat x}_1} {{\hat x}_2} \cdots {{\hat x}_{2{N_{\rm{H}}} - 1}}{{\hat x}_{2{N_{\rm{H}}}}}} \right]}^{\rm{T}}}} \hfill \cr } $ |
自变量x(t)的一阶和二阶导数可表示如下
| $\begin{equation} \label{eq4} \dot {x}(t) = {{ \varphi }}^{\rm T}{{{ D}\hat { x}}},\quad \ddot {x}(t) = {{ \varphi }}^{\rm T}{{ D}}^2{{\hat { x}}} \end{equation}$ | (4) |
其中
| $ {{ D}} = \left[{{\begin{array}{*{20}c} 0 & & & \\ & {{{ J}}_1 } & & \\ & & \ddots & \\ & & & {{{ J}}_{N_{\rm H} } } \\ \end{array} }} \right], \quad {{ J}}_n = \left[{{\begin{array}{*{20}c} 0 & { - n\omega } \\ {n\omega } & 0 \\ \end{array} }} \right] $ |
达芬振子中的非线性刚度项r(t)=x3(t)和外力项也可以写成向量形式
| $\begin{equation} \label{eq5} \left.\begin{array}{ll} r(t) = {{ \varphi }}^{\rm T}{{\hat { r}}} \\ F\sin \omega t = {{\varphi }}^{\rm T}{{\hat { f}}} \end{array}\right\} \end{equation}$ | (5) |
其中
| $ \begin{array}{l} {{\hat { r}}} = \left[{{\begin{array}{*{20}c} {\hat {r}_0 } & {\hat {r}_1 } & {\hat {r}_2 } & \cdots & {\hat {r}_{2N_{\rm H} - 1} } & {\hat {r}_{2N_{\rm H} } } \\ \end{array} }} \right]^{\rm T} \\ {{\hat { f}}} = \left[{{\begin{array}{*{20}c} 0 & 0 & F & \cdots & 0 & 0 \\ \end{array} }} \right]^{\rm T} \\ \end{array} $ |
然后将式(3)∼式(5)代入式(1)中,将式(1)写成向量形式如下
| $\begin{equation} \label{eq6} {{\varphi }}^{\rm T}{{ D}}^2{{\hat { x}}} + 2\xi {{ \varphi }}^{\rm T}{{{ D}\hat { x}}} + {{\varphi }}^{\rm T}{{\hat { x}}} + {{ \varphi }}^{\rm T}{{\hat { r}}} = {{\varphi }}^{\rm T}{{\hat { f}}} \end{equation}$ | (6) |
由于上式对任意时间t都成立,所以各阶谐波系数完全相等,可以得到如下非线性代数方程组
| $\begin{equation} \label{eq7} \left( {{{ D}}^2 + 2\xi {{ D}} + {{ I}}} \right){{\hat { x}}} + {{\hat { r}}} = {{\hat { f}}} \end{equation}$ | (7) |
这样就将非线性微分方程的求解问题转化为非线性代数方程组的求解问题,上式就是HB方法的求解公式,共有2NH+1个方程,待求目标为
| $\left. {\matrix{ {{{\hat r}_0} = {1 \over {2\pi }}\int_0^{2\pi } {{{\left[ {{{\hat x}_0} + \sum\limits_{n = 1}^{{N_{\rm{H}}}} {\left( {{{\hat x}_{2n - 1}}\cos nt + {{\hat x}_{2n}}\sin nt} \right)} } \right]}^3}} {\rm{d}}t} \hfill \cr {{{\hat r}_{2n - 1}} = {1 \over {2\pi }}\int_0^{2\pi } {\left[ {{{\hat x}_0}} \right. + } } \hfill \cr {{{\left. {\sum\limits_{n = 1}^{{N_{\rm{H}}}} {\left( {{{\hat x}_{2n - 1}}\cos nt + {{\hat x}_{2n}}\sin nt} \right)} } \right]}^3}\cos nt{\rm{d}}t{\rm{ }}} \hfill \cr {{{\hat r}_{2n}} = {1 \over {2\pi }}\int_0^{2\pi } {\left[ {{{\hat x}_0}} \right.} + } \hfill \cr {{{\left. {\sum\limits_{n = 1}^{{N_{\rm{H}}}} {\left( {{{\hat x}_{2n - 1}}\cos nt + {{\hat x}_{2n}}\sin nt} \right)} } \right]}^3}\sin nt{\rm{d}}t} \hfill \cr } } \right\}$ | (8) |
通过理论推导或数值求解都可以得到上式的结果,但是处理过程非常复杂.针对这个问题,HOHB方法以一个周期内各子时间层的自变量值为待求目标,如下所示
| $\begin{equation} \label{eq9} {{\tilde { x}}} = \left[{{\begin{array}{*{20}c} {x(t_0 )} & {x(t_1 )} & \cdots & {x(t_{2N_{\rm H} } )} \end{array} }} \right]^{\rm T} \end{equation}$ | (9) |
其中,
| $\begin{equation} \label{eq10} {{\hat { x}}} = {{{ E}\tilde { x}}},\quad {{\tilde { x}}} = {{ E}}^{ - 1}{{\hat { x}}} \end{equation}$ | (10) |
其中
| $\eqalign{ & E = {2 \over {2{N_{\rm{H}}} + 1}}\left[ {\matrix{ {1/2} & {1/2} & {1/2} & \cdots & {1/2} & {1/2} \cr {\cos {t_0}} & {\cos {t_1}} & {\cos {t_2}} & \cdots & {\cos {t_{2{N_{\rm{H}}} - 1}}} & {\cos {t_{2{N_{\rm{H}}}}}} \cr {\sin {t_0}} & {\sin {t_1}} & {\sin {t_2}} & \cdots & {\sin {t_{2{N_{\rm{H}}} - 1}}} & {\sin {t_{2{N_{\rm{H}}}}}} \cr \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \cr {\cos {N_{\rm{H}}}{t_0}} & {\cos {N_{\rm{H}}}{t_1}} & {\cos {N_{\rm{H}}}{t_2}} & \cdots & {\cos {N_{\rm{H}}}{t_{2{N_{\rm{H}}} - 1}}} & {\cos {N_{\rm{H}}}{t_{2{N_{\rm{H}}}}}} \cr {\sin {N_{\rm{H}}}{t_0}} & {\sin {N_{\rm{H}}}{t_1}} & {\sin {N_{\rm{H}}}{t_2}} & \cdots & {\sin {N_{\rm{H}}}{t_{2{N_{\rm{H}}} - 1}}} & {\sin {N_{\rm{H}}}{t_{2{N_{\rm{H}}}}}} \cr } } \right] \cr & {E^{ - 1}} = \left[ {\matrix{ 1 & {\cos {t_0}} & {\sin {t_0}} & \cdots & {\cos {N_{\rm{H}}}{t_0}} & {\sin {N_{\rm{H}}}{t_0}} \cr 1 & {\cos {t_1}} & {\sin {t_1}} & \cdots & {\cos {N_{\rm{H}}}{t_1}} & {\sin {N_{\rm{H}}}{t_1}} \cr 1 & {\cos {t_2}} & {\sin {t_2}} & \cdots & {\cos {N_{\rm{H}}}{t_2}} & {\sin {N_{\rm{H}}}{t_2}} \cr \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \cr 1 & {\cos {t_{2{N_{\rm{H}}} - 1}}} & {\sin {t_{2{N_{\rm{H}}} - 1}}} & \cdots & {\cos {N_{\rm{H}}}{t_{2{N_{\rm{H}}} - 1}}} & {\sin {N_{\rm{H}}}{t_{2{N_{\rm{H}}} - 1}}} \cr 1 & {\cos {t_{2{N_{\rm{H}}}}}} & {\sin {t_{2{N_{\rm{H}}}}}} & \cdots & {\cos {N_{\rm{H}}}{t_{2{N_{\rm{H}}}}}} & {\sin {N_{\rm{H}}}{t_{2{N_{\rm{H}}}}}} \cr } } \right] \cr} $ |
类似的,非线性项和外力项也可转换如下
| $\begin{equation} \label{eq11} {{\hat { r}}} = {{ E}}^{ - 1}{{\tilde { r}}},\quad {{\hat { f}}} = {{ E}}^{ - 1}{{\tilde { f}}} \end{equation}$ | (11) |
其中
| $ \begin{array}{ll} {{\tilde { r}}} = \left[{{\begin{array}{*{20}c} {x^3(t_0 )} & {x^3(t_1 )} & \cdots & {x^3(t_{2N_{\rm H} } )} \end{array} }} \right]^{\rm T} \\ {{\tilde { f}}} = \left[{{\begin{array}{*{20}c} {F\sin t_0 } & {F\sin t_1 } & \cdots & {F\sin t_{2N_{\rm H} } } \end{array} }} \right]^{\rm T} \\ \end{array} $ |
将式(10)和式(11)代入式(7)中,即可得到如下非线性方程组
| $\begin{equation} \label{eq12} \left( {{{ A}}^2 + 2\xi {{ A}} + {{ I}}} \right){{\tilde { x}}} + {{\tilde { r}}} = {{\tilde { f}}} \end{equation}$ | (12) |
其中
| $\begin{equation}\label{eq13} {{\tilde { x}}}^{k + 1} = {{\tilde { x}}}^k -{{ J}}^{ - 1}{{ R}}^k\end{equation}$ | (13) |
其中
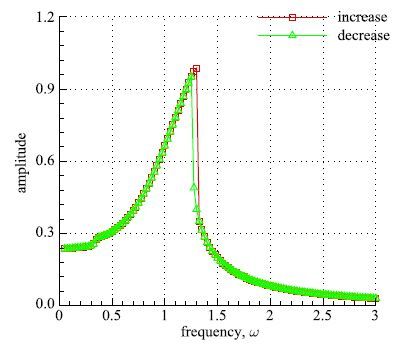
以达芬振子方程为例,阻尼系数ξ=0.1,外部激励模值F=0.25,采用四阶Runge-Kutta时间推进方法进行求解,频率由0.05增加至3.0和3.0减小至0.05,变化量分别为0.025和-0.025,前一个频率的最终结果作为后一个频率的初值,图 1为时域响应振幅随外部激励频率的变化趋势,ω=1.25至1.325范围内频率增加和频率减小的时域响应振幅差别较大,出现典型的滞后现象.
|
图 1 F=0.25时杜芬振子方程的时间推进解 Fig. 1 Time marching results of Duffing oscillator when F=0.25 |
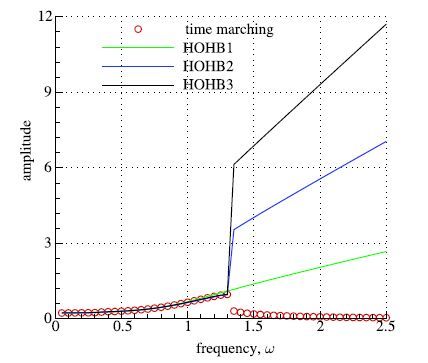
当采用Newton-Raphson迭代求解HOHB降阶方程时,在增加频率计算过程中,当频率超过1.35时,振幅并不会下降,而是会进一步增大,如图 2所示.
|
图 2 F=0.25时HOHB方法频率逐渐增大情况下振幅随频率变化趋势 Fig. 2 Variation of amplitude as the frequency decreases in HOHB when F=0.25 |
Liu等[7]认为出现图 1中非物理解的原因是计算过程中Fourier系数没有收敛.本文则利用同样的算例进一步分析非物理解的来源.
初值选取的苛刻性是Newton-Raphson迭代方法的主要缺陷.为了放宽初值的选择范围,选择Newton下山法,即将Newton-Raphson的计算结果与本步的结果做加权平均后得到的结果作为下一步的结果
| $\eqalign{ & {{\tilde x}^{k + 1}} = \left( {1 - \lambda } \right){{\tilde x}^k} + \lambda \left( {{{\tilde x}^k} - {J^{ - 1}}{R^k}} \right) = \cr & {{\tilde x}^k} - \lambda {J^{ - 1}}{R^k} \cr} $ | (14) |
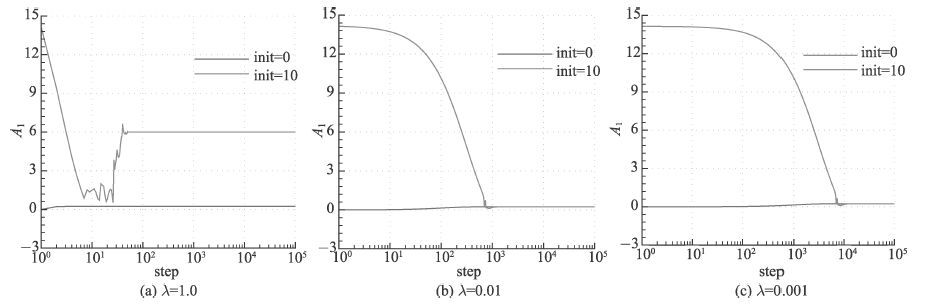
仍然以达芬振子方程为例,F=0.25,ω=1.4作为验证状态,谐波数NH=4,初值分别选择0和10,以不同的λ值进行迭代求解,一阶谐波振幅
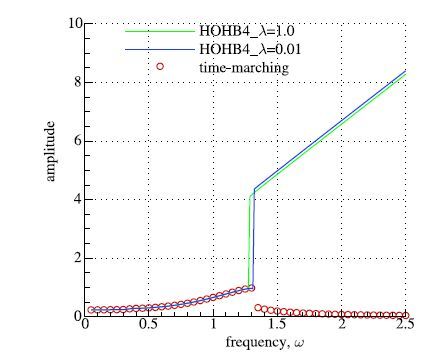
由图 3可见,不同的λ值对计算过程和结果有明显影响.但是当λ选得足够小时,均能保证问题的收敛性.这就说明文献[7]中Fourier系数没有收敛的原因是Newton-Raphson迭代的缺陷.图 4是不同的λ值情况下HOHB4方法和时间推进方法得到的结果.由图可见当采用Newton下山法克服对初值敏感这个缺陷之后,计算结果仍出现非物理解.这就说明Fourier系数不收敛并不是出现非物理解的原因.
|
图 3 不同λ值情况下一阶谐波振幅的收敛情况 Fig. 3 The convergence of amplitude of first-order harmonic under different λ value |
|
图 4 HOHB和时间推进得到的振幅随频率变化情况对比 Fig. 4 Comparison of relations between amplitude and frequency obtained by HOHB and time-marching |
为了探究非物理解出现的原因,以一阶HOHB方法为例,x(t)的展开形式如下
| $\begin{equation} \label{eq15} x(t) = \hat {x}_0 + \hat {x}_1 \cos \omega t + \hat {x}_2 \sin \omega t \end{equation}$ | (15) |
通过上式,可以得到非线性刚度项
| $\begin{align} & \begin{array}{*{35}{l}} r(t)={{\left( {{{\hat{x}}}_{0}}+{{{\hat{x}}}_{1}}\cos \omega t+{{{\hat{x}}}_{2}}\sin \omega t \right)}^{3}}= \\ ~~~~~{{{\hat{r}}}_{0}}+{{{\hat{r}}}_{1}}\cos \omega t+{{{\hat{r}}}_{2}}\sin \omega t+{{{\hat{r}}}_{3}}\cos 2\omega t+ \\ \end{array} \\ & {{{\hat{r}}}_{4}}\sin 2\omega t+{{{\hat{r}}}_{5}}\cos 3\omega t+{{{\hat{r}}}_{6}}\sin 3\omega t \\ \end{align}$ | (16) |
将式(15)和(16)代入原始达芬振子方程如下
| $\begin{align} & \begin{array}{*{35}{l}} {{{\hat{x}}}_{0}}+{{{\hat{r}}}_{0}}+\left( -{{\omega }^{2}}{{{\hat{x}}}_{1}}+\omega {{{\hat{x}}}_{2}}+{{{\hat{x}}}_{1}}+{{{\hat{r}}}_{1}} \right)\cos \omega t+ \\ ~~~~~\left( -{{\omega }^{2}}{{{\hat{x}}}_{2}}-\omega {{{\hat{x}}}_{1}}+{{{\hat{x}}}_{2}}+{{{\hat{r}}}_{2}} \right)\sin \omega t+{{{\hat{r}}}_{3}}\cos 2\omega t+ \\ \end{array} \\ & ~{{{\hat{r}}}_{4}}\sin 2\omega t+{{{\hat{r}}}_{5}}\cos 3\omega t+{{{\hat{r}}}_{6}}\sin 3\omega t=F\sin \omega t \\ \end{align}$ | (17) |
根据同阶谐波项相等的原则,忽略高阶谐波项,则HB方法得到的非线性方程组如下
| $\begin{equation} \label{eq18} \left. {\begin{array}{ll} \hat {x}_0 + \hat {r}_0 = 0 \\ - \omega ^2\hat {x}_1 + \omega \hat {x}_2 + \hat {x}_1 + \hat {r}_1 = 0 \\ - \omega ^2\hat {x}_2 - \omega \hat {x}_1 + \hat {x}_2 + \hat {r}_2 = F \\ \end{array}} \right\} \end{equation}$ | (18) |
而HOHB方法则是按照子时间层对非线性刚度项进行简化处理,各个子时间层上的非线性刚度项如下
| $\left. \begin{array}{*{35}{l}} r({{t}_{0}})={{{\hat{r}}}_{0}}+{{{\hat{r}}}_{1}}+{{{\hat{r}}}_{3}}+{{{\hat{r}}}_{5}}\text{ } \\ r({{t}_{1}})={{{\hat{r}}}_{0}}-\frac{1}{2}{{{\hat{r}}}_{1}}+\frac{\sqrt{3}}{2}{{{\hat{r}}}_{2}}-\frac{1}{2}{{{\hat{r}}}_{3}}-\frac{\sqrt{3}}{2}{{{\hat{r}}}_{4}}+{{{\hat{r}}}_{5}}\text{ } \\ r({{t}_{2}})={{{\hat{r}}}_{0}}-\frac{1}{2}{{{\hat{r}}}_{1}}-\frac{\sqrt{3}}{2}{{{\hat{r}}}_{2}}-\frac{1}{2}{{{\hat{r}}}_{3}}+\frac{\sqrt{3}}{2}{{{\hat{r}}}_{4}}+{{{\hat{r}}}_{5}} \\ \end{array} \right\}$ | (19) |
将上式变换到频域为
| $\begin{equation} \label{eq20} {{\hat { r}}'} = {{ E}}^{ - 1}{{\tilde { r}}} = \left[{{\begin{array}{lll} {\hat {r}_0 + \hat {r}_5 } \\ {\hat {r}_1 + \hat {r}_3 } \\ {\hat {r}_2 - \hat {r}_4 } \\ \end{array} }} \right] \end{equation}$ | (20) |
HOHB方法中非线性项的零阶谐波项系数
| $\begin{equation} \label{eq21} \left. {\begin{array}{ll} \hat {x}_0 + \hat {r}_0 + \hat {r}_5 = 0 \\ - \omega ^2\hat {x}_1 + \omega \hat {x}_2 + \hat {x}_1 + \hat {r}_1 + \hat {r}_3 = 0 \\ - \omega ^2\hat {x}_2 - \omega \hat {x}_1 + \hat {x}_2 + \hat {r}_2 + \hat {r}_4 = F \\ \end{array}} \right\} \end{equation}$ | (21) |
这就会导致上式左右两边并不是严格相等的,本文认为这才是非物理解产生的根本原因.
3 改进方法由式(16)可知,三次非线性项会产生更高阶的谐波项,具体的说,对于NH阶HOHB方法,会产生NH+1至3×NH阶谐波.为了改进式(21)左右两边不相等的缺点,需要对非线性项进行额外的处理.通过Fourier变换和逆变换,将一个周期由2NH+1改为6NH+1个时间层
| $\left. \begin{array}{*{35}{l}} \hat{x}=E\tilde{x} \\ {{{\tilde{x}}}_{2}}=E_{2}^{-1}\hat{x} \\ \end{array} \right\}\Rightarrow {{\tilde{x}}_{2}}=E_{2}^{-1}E\tilde{x}$ | (22) |
其中
| $\begin{align} & {{{\tilde{x}}}_{2}}={{\left[ x({{{{t}'}}_{0}})~~x({{{{t}'}}_{1}})~~x({{{{t}'}}_{2}})~~\cdots ~~x({{{{t}'}}_{6{{N}_{\text{H}}}-1}})~~x({{{{t}'}}_{6{{N}_{\text{H}}}}}) \right]}^{\text{T}}}~~{{{{t}'}}_{n}}=\frac{2n\pi }{6{{N}_{\text{H}}}+1} \\ & {{E}_{2}}=\frac{2}{2{{N}_{\text{H}}}+1}\left[ \begin{matrix} 1/2 & 1/2 & 1/2 & \cdots & 1/2 & 1/2 \\ \cos {{t}_{0}} & \cos {{t}_{1}} & \cos {{t}_{2}} & \cdots & \cos {{t}_{6{{N}_{\text{H}}}-1}} & \cos {{t}_{6{{N}_{\text{H}}}}} \\ \sin {{t}_{0}} & \sin {{t}_{1}} & \sin {{t}_{2}} & \cdots & \sin {{t}_{6{{N}_{\text{H}}}-1}} & \sin {{t}_{6{{N}_{\text{H}}}}} \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ \cos 3{{N}_{\text{H}}}{{t}_{0}} & \cos 3{{N}_{\text{H}}}{{t}_{1}} & \cos 3{{N}_{\text{H}}}{{t}_{2}} & \cdots & \cos 3{{N}_{\text{H}}}{{t}_{6{{N}_{\text{H}}}-1}} & \cos 3{{N}_{\text{H}}}{{t}_{6{{N}_{\text{H}}}}} \\ \sin 3{{N}_{\text{H}}}{{t}_{0}} & \sin 3{{N}_{\text{H}}}{{t}_{1}} & \sin 3{{N}_{\text{H}}}{{t}_{2}} & \cdots & \sin 3{{N}_{\text{H}}}{{t}_{6{{N}_{\text{H}}}-1}} & \sin 3{{N}_{\text{H}}}{{t}_{6{{N}_{\text{H}}}}} \\ \end{matrix} \right] \\ & E_{2}^{-1}=\left[ \begin{matrix} 1 & \cos {{t}_{0}} & \sin {{t}_{0}} & \cdots & \cos 3{{N}_{\text{H}}}{{t}_{0}} & \sin 3{{N}_{\text{H}}}{{t}_{0}}\text{ } \\ 1 & \cos {{t}_{1}} & \sin {{t}_{1}} & \cdots & \cos 3{{N}_{\text{H}}}{{t}_{1}} & \sin 3{{N}_{\text{H}}}{{t}_{1}}\text{ } \\ 1 & \cos {{t}_{2}} & \sin {{t}_{2}} & \cdots & \cos 3{{N}_{\text{H}}}{{t}_{2}} & \sin 3{{N}_{\text{H}}}{{t}_{2}} \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 1 & \cos {{t}_{6{{N}_{\text{H}}}-1}} & \sin {{t}_{6{{N}_{\text{H}}}-1}} & \cdots & \cos 3{{N}_{\text{H}}}{{t}_{6{{N}_{\text{H}}}-1}} & \sin 3{{N}_{\text{H}}}{{t}_{6{{N}_{\text{H}}}-1}} \\ 1 & \cos {{t}_{6{{N}_{\text{H}}}}} & \sin {{t}_{6{{N}_{\text{H}}}}} & \cdots & \cos 3{{N}_{\text{H}}}{{t}_{6{{N}_{\text{H}}}}} & \sin 3{{N}_{\text{H}}}{{t}_{6{{N}_{\text{H}}}}} \\ \end{matrix} \right] \\ \end{align}$ |
然后得到非线性项在6NH+1个时间层上的结果
| ${{\tilde{r}}_{2}}={{\left[ {{x}^{3}}({{{{t}'}}_{0}})~{{x}^{3}}({{{{t}'}}_{1}})~{{x}^{3}}({{{{t}'}}_{2}})~\cdots ~{{x}^{3}}({{{{t}'}}_{6{{N}_{\text{H}}}-1}})~{{x}^{3}}({{{{t}'}}_{6{{N}_{\text{H}}}}}) \right]}^{\text{T}}}$ | (23) |
再将
| $\hat{r}={{E}_{2}}{{\tilde{r}}_{2}}$ | (24) |
其中
| ${{{\tilde{r}}}_{3}}=E{{{{\hat{r}}'}}_{2}}$ | (25) |
其中
| $ \begin{array}{ll} {{\hat { r}}'}_2 = \left[{{\begin{array}{*{20}c} {\hat {r}_0 } & {\hat {r}_1 } & {\hat {r}_2 } & \cdots & {\hat {r}_{2N_{\rm H} - 1} } & {\hat {r}_{2N_{\rm H} } } \\ \end{array} }} \right]^{\rm T} \\ {{\tilde { r}}}_3 = \left[{\tilde {r}_3 (t_0 )~~\tilde {r}_3 (t_1 )~~\tilde {r}_3 (t_2 )~~\cdots ~~\tilde {r}_3 (t_{2N_{\rm H} - 1} )~~\tilde {r}_3 (t_{2N_{\rm H} } )} \right]^{\rm T} \\ \end{array} $ |
以达芬振子方程和立方非线性气弹系统为例验证改进方法的可行性.
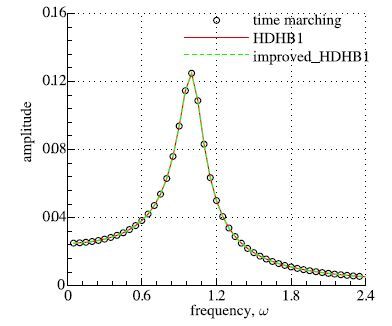
4.1 达芬振子方程\vspace{2mm} 图 5为F=0.025时振幅随频率变化情况,频率从范围为0.05至2.5,间隔0.05.由于此时系统并没有表现出任何迟滞效应,不论从0.05增加至2.5还是从2.5减小至0.05,曲线完全重合.采用时间推进、一阶HOHB及改进方法得到的结果完全一致.
|
图 5 F=0.025时振幅随频率变化情况 Fig. 5 Variation of amplitude by frequency when F=0.025 |
图 6为F=0.25时振幅随频率变化情况,(a)是一阶HOHB方法计算结果,increase是频率从0.05增加至2.5,decrease是频率从2.5减小至0.05,间隔0.05.由图可见,不论是HOHB方法还是改进方法,仅采用一阶谐波时都没有捕捉到ω=0.3处振幅的跳跃情况;然而,当采用三阶谐波方法时,除了HOHB方法中的非物理解,两种方法和时间推进结果吻合都较好.

|
图 6 F=0.25时振幅随频率变化情况 Fig. 6 Variation of amplitude by frequency when F=0.25 |
图 7是F=1.25时振幅随频率变化情况.HOHB方法仍然出现非物理解,改进方法则消除了非物理解,当采用五阶谐波时,精度高于HOHB5,略低于HOHB8.

|
图 7 F=1.25时振幅随频率变化情况 Fig. 7 Variation of amplitude by frequency when F=1.25 |
Liu等[29-30]和Dai等[31]分别采用高阶谐波平衡方法和时间配置方法对立方刚度非线性二维翼型气弹系统进行研究,结构运动方程为无量纲的两自由度沉浮/俯仰运动方程
| $\left. \begin{array}{*{35}{l}} \ddot{\xi }+{{x}_{\alpha }}\ddot{\alpha }+2{{\zeta }_{\xi }}\frac{{\bar{\omega }}}{{{U}^{*}}}\dot{\xi }+{{\left( \frac{{\bar{\omega }}}{{{U}^{*}}} \right)}^{2}}G\left( \xi \right)=-\frac{1}{\pi \mu }{{C}_{L}}\left( \tau \right) \\ \frac{{{x}_{\alpha }}}{r_{\alpha }^{2}}\ddot{\xi }+\ddot{\alpha }+2{{\zeta }_{\alpha }}\frac{1}{{{U}^{*}}}\dot{\alpha }+{{\left( \frac{1}{{{U}^{*}}} \right)}^{2}}M\left( \alpha \right)=\frac{2}{\pi \mu r_{\alpha }^{2}}{{C}_{M}}\left( \tau \right) \\ \end{array} \right\}$ | (26) |
式中,ξ=h/b为无量纲沉浮位移,α为俯仰角.(⋅)为相对于无量纲时间τ的导数,τ=Ut/b.U*为无量纲速度,U*=Ubωα. ω为沉浮自然频率ωξ和俯仰自然频率ωα的比值. ζξ和ξα分别为沉浮和俯仰阻尼系数,rα为相对弹性轴的旋转半径.G(ξ)和M(α)则为非线性沉浮和俯仰刚度
| $M\left( \alpha \right)=\alpha +80{{\alpha }^{3}},\quad G\left( \xi \right)=\xi $ | (27) |
结构参数的具体值为:ω=0.2,xα=0.25, μ=100,rα=0.5,ah=-0.5,ζξ=ξα=0.其中立方非线性刚度用于研究俯仰自由度硬化弹簧的行为.气动力采用基于Jones近似的Wagner函数,此处不再赘述,具体可以参考文献[32].整个系统的时域推进求解方程为
| $\left. \begin{array}{*{35}{l}} {{c}_{0}}\ddot{\xi }+{{c}_{1}}\ddot{\alpha }+{{c}_{2}}\dot{\xi }+{{c}_{3}}\dot{\alpha }+{{c}_{4}}\xi +{{c}_{5}}\alpha + \\ \quad {{c}_{6}}{{w}_{1}}+{{c}_{7}}{{w}_{2}}+{{c}_{8}}{{w}_{3}}+{{c}_{9}}{{w}_{4}}+{{c}_{10}}M\left( \xi \right)=0 \\ {{d}_{0}}\ddot{\xi }+{{d}_{1}}\ddot{\alpha }+{{d}_{2}}\dot{\xi }+{{d}_{3}}\dot{\alpha }+{{d}_{4}}\xi +{{d}_{5}}\alpha + \\ \quad {{d}_{6}}{{w}_{1}}+{{d}_{7}}{{w}_{2}}+{{d}_{8}}{{w}_{3}}+{{d}_{9}}{{w}_{4}}+{{d}_{10}}G\left( \alpha \right)=0 \\ {{{\dot{w}}}_{1}}=\alpha -{{\varepsilon }_{1}}{{w}_{1}} \\ {{{\dot{w}}}_{2}}=\alpha -{{\varepsilon }_{2}}{{w}_{2}} \\ {{{\dot{w}}}_{3}}=\xi -{{\varepsilon }_{1}}{{w}_{3}} \\ {{{\dot{w}}}_{4}}=\xi -{{\varepsilon }_{2}}{{w}_{4}} \\ \end{array} \right\}$ | (28) |
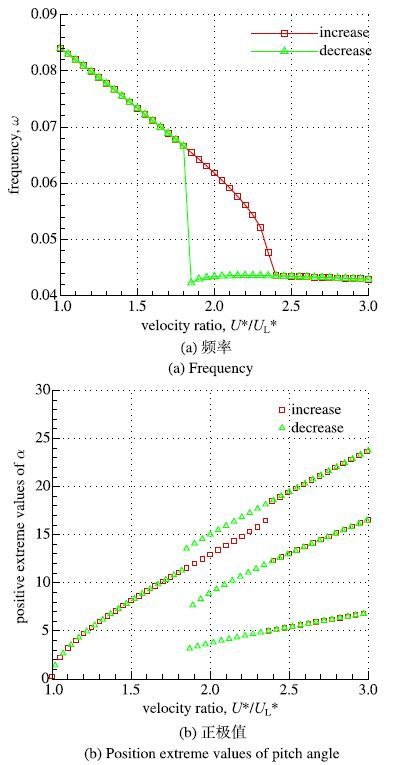
其中c0∼ c10和d0∼d10是与结构参数和来流速度有关的系数.上式可以重组为一阶常微分方程组的形式,通过四阶Runge-Kutta方法进行求解,无量纲颤振速度UL*约为6.295 45,速度范围U*/UL*=1.0至3.0时,系统的振荡频率和俯仰位移的正极值如图 8所示,increase为速度由1.0增加至3.0,decrease为速度由3.0减小至1.0,变化量分别为0.01和-0.01,将前一个速度的最终结果作为当前速度的初值.由图可见,系统首先出现Hopf分岔,然后在U*/UL*=2.0附近出现二次分岔,频率和极值都发生跳跃,且在U*/UL*=1.85至2.35出现迟滞现象.
|
图 8 时间推进结果 Fig. 8 Time-marching results |
采用HOHB方法对式(21)进行处理,得到如下降阶方程
| $\left. \begin{array}{*{35}{l}} \left( {{c}_{0}}{{\omega }^{2}}{{D}^{2}}+{{c}_{2}}\omega D+{{c}_{4}}I+{{c}_{10}}I \right)\tilde{\xi }+ \\ \quad \left( {{c}_{1}}{{\omega }^{2}}{{D}^{2}}+{{c}_{3}}\omega D+{{c}_{5}}I \right)\tilde{\alpha }+ \\ \quad {{c}_{6}}{{{\tilde{w}}}_{1}}+{{c}_{7}}{{{\tilde{w}}}_{2}}+{{c}_{8}}{{{\tilde{w}}}_{3}}+{{c}_{9}}{{{\tilde{w}}}_{4}}=0 \\ \left( {{d}_{0}}{{\omega }^{2}}{{D}^{2}}+{{d}_{2}}\omega D+{{d}_{4}}I \right)\tilde{\xi }+ \\ \quad \left( {{d}_{1}}{{\omega }^{2}}{{D}^{2}}+{{d}_{3}}\omega D+{{d}_{5}}I \right)\tilde{\alpha }+ \\ \quad {{d}_{6}}{{{\tilde{w}}}_{1}}+{{d}_{7}}{{{\tilde{w}}}_{2}}+{{d}_{8}}{{{\tilde{w}}}_{3}}+{{d}_{9}}{{{\tilde{w}}}_{4}}+{{d}_{10}}\tilde{G}=\mathbf{0} \\ \left( \omega D+{{\varepsilon }_{1}}I \right){{{\tilde{w}}}_{1}}=\tilde{\alpha } \\ \left( \omega D+{{\varepsilon }_{2}}I \right){{{\tilde{w}}}_{2}}=\tilde{\alpha } \\ \left( \omega D+{{\varepsilon }_{1}}I \right){{{\tilde{w}}}_{3}}=\tilde{\xi } \\ \left( \omega D+{{\varepsilon }_{2}}I \right){{{\tilde{w}}}_{4}}=\tilde{\xi } \\ \end{array} \right\}$ | (29) |
oindent 上式中关于
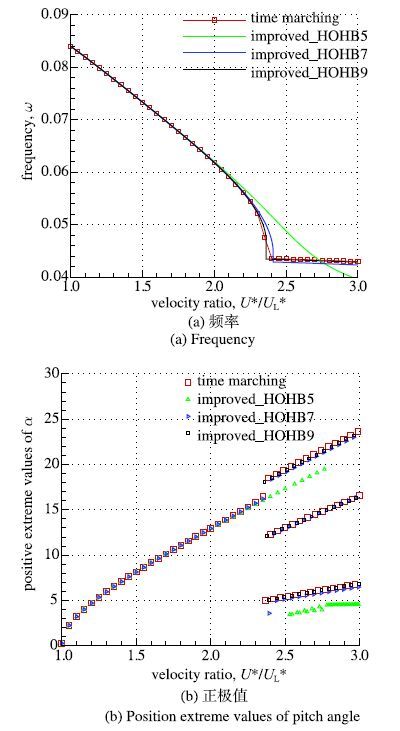
对立方刚度项进行处理,得到改进后的HOHB方法,其结果与时间推进结果对比如图 9所示.改进后的方法仅采用7阶谐波项就能预测二次分岔,9阶方法得到的极值精度与HOHB15基本接近,大幅减小了强非线性情况时所需的谐波项数目.

|
图 9 时间推进和HOHB结果对比 Fig. 9 Comparison between time-marching and HOHB results |
|
图 10 时间推进和改进HOHB结果对比 Fig. 10 Comparison between time-marching and improved HOHB results |
本文对非线性系统的高阶谐波平衡方法中出现非物理解的原因进行探讨并对其进行改进,得到结论如下: (1) 非物理解出现的原因是非线性导致高阶谐波平衡方程左右两边不严格相等,并不是参考文献[7]中认为的Fourier级数未收敛; (2) 在非线性项的处理过程中,扩充子时间层上的时域解,并将非线性项的更高阶谐波截断,可以使方程左右两边严格相等; (3) 相比高阶谐波平衡方法,改进方法不仅消除了非物理解,还大幅减少了强非线性问题所需的谐波数; (4) 改进方法和参考文献[7-8, 16, 29]中的原始谐波平衡方法精度相似,结果也较为吻合,验证了本方法的有效性和可行性,而且改进方法还避免了原始谐波平衡方法通过积分得到非线性项的Fourier系数这个复杂的过程;改进方法在非线性项处理过程中需要将时域解扩充,会在一定程度上增加的计算消耗,如果方程中非线性项较多时,本方法的计算消耗会有所增加.
| [1] |
Silva WA. Reduced-order models based on linear and nonlinear aerodynamic impulse responses. AIAA-99-1262
( 0) 0)
|
| [2] |
Raveh DE. Reduced-order models for nonlinear unsteady aerodynamics[J].
AIAA Journal,2001, 39 (8) : 1417-1429.
DOI: 10.2514/2.1473. ( 0) 0)
|
| [3] |
Thomas JP, Dowell EH, Hall KC. Three-dimensional transonic aeroelasticity using proper orthogonal decomposition based reduced order models[J].
AIAA,2001 : 1526.
( 0) 0)
|
| [4] |
Thomas JP, Dowell EH, Hall KC. Modeling viscous transonic limitcycle oscillation behavior using a harmonic balance approach[J].
Journal of Aircraft,2004, 41 (6) : 1266-1274.
DOI: 10.2514/1.9839. ( 0) 0)
|
| [5] |
Lucia DJ, Beran PS, Silva WA. Reduced-order modeling: new approaches for computational physics[J].
Progress in Aerospace Sciences,2004, 40 : 51-117.
DOI: 10.1016/j.paerosci.2003.12.001. ( 0) 0)
|
| [6] |
Krylo N, Bogoliubo N.
Introduction to Nonlinear Mechanics. Princeton University Press, Princeton, NJ[M]. 1947 .
( 0) 0)
|
| [7] |
Liu L, Thomas JP, Dowell EH, et al. A comparison of classical and high dimensional harmonic balance approaches for a Duffing oscillator[J].
Journal of Computational Physics,2006, 215 : 298-320.
DOI: 10.1016/j.jcp.2005.10.026. ( 0) 0)
|
| [8] |
Liu L, Dowell EH, Hall KC. A novel harmonic balance analysis for the Van Der Pol oscillator[J].
International Journal of Non-Linear Mechanics,2007, 42 : 2-12.
DOI: 10.1016/j.ijnonlinmec.2006.09.004. ( 0) 0)
|
| [9] |
Lau SL, Cheung YK. Amplitude incremental variational principle for nonlinear vibration of elastic systems[J].
ASME Journal of Applied Mechanics,1981, 48 : 959-964.
DOI: 10.1115/1.3157762. ( 0) 0)
|
| [10] |
Shen JH, Lin KC, Chen SH, et al. Bifurcation and route-to-chaos analyses for Mathieu-Duffing oscillator by the incremental harmonic balance method[J].
Nonlinear Dynamics,2008, 52 : 403-414.
DOI: 10.1007/s11071-007-9289-z. ( 0) 0)
|
| [11] |
Liu JK, Chen FX, Chen YM. Bifurcation analysis of aeroelastic systems with hysteresis by incremental harmonic balance method[J].
Applied Mathematics and Computation,2012, 219 : 2398-2411.
DOI: 10.1016/j.amc.2012.08.034. ( 0) 0)
|
| [12] |
Hall KC, Thomas JP, Clark WS. Computation of unsteady nonlinear flows in cascades using a harmonic balance technique[J].
International Symposium on Unsteady Aerodynamics, Aeroacoustics and Aeroelasiticity of Turbomachines,2000 .
( 0) 0)
|
| [13] |
陈琦, 陈坚强, 谢昱飞, 等. 谐波平衡法在非定常流场中的应用[J].
航空学报,2014, 35 (3) : 736-743.
( Chen Qi, Chen Jianqiang, Xie Yufei, et al. Application of harmonic balance method to unsteady flow field[J].
Acta Aeronautica et Astronautica Sinica,2014, 35 (3) : 736-743.
(in Chinese) ) ( 0) 0)
|
| [14] |
Woodgate MA, Badcock KJ. Implicit harmonic balance solver for transonic flow with forced motions[J].
AIAA Journal,2009, 47 (4) : 893-901.
DOI: 10.2514/1.36311. ( 0) 0)
|
| [15] |
Rouch AD, McCracken AJ, Badcock KJ, et al. Linear frequency domain and harmonic balance predictions of dynamic derivatives[J].
Journal of Aircraft,2013, 50 (3) : 694-707.
DOI: 10.2514/1.C031674. ( 0) 0)
|
| [16] |
陈琦, 陈坚强, 袁先旭, 等. 谐波平衡法在动导数快速预测中的应用研究[J].
力学学报,2014, 46 (2) : 183-190.
( Chen Qi, Chen Jianqiang, Yuan Xianxu, et al. Application of a harmonic balance method in rapid predictions of dynamic stability derivatives[J].
Chinese Journal of Theoretical and Applied Mechanics,2014, 46 (2) : 183-190.
(in Chinese) ) ( 0) 0)
|
| [17] |
Thomas JP, Dowell EH, Hall KC. Nonlinear inviscid aerodynamic effects on transonic divergence, flutter, and limit-cycle oscillations[J].
AIAA Journal,2002, 40 (4) : 638-646.
DOI: 10.2514/2.1720. ( 0) 0)
|
| [18] |
( 0) 0)
|
| [19] |
Ekici K, Beran PS. Adjoint sensitivity analysis of low-speed flows using an efficient harmonic balance technique[J].
AIAA Journal,2014, 52 (6) : 1330-1336.
( 0) 0)
|
| [20] |
Huang H, Ekici K. A discrete adjoint harmonic balance method for turbomachinery shape optimization[J].
Aerospace Science and Technology,2014, 39 : 481-490.
DOI: 10.1016/j.ast.2014.05.015. ( 0) 0)
|
| [21] |
Sicot F, Gomar A, Dufour G, et al. Time-domain harmonic balance method for turbomachinery aeroelasticity[J].
AIAA Journal,2014, 52 (1) : 62-71.
DOI: 10.2514/1.J051848. ( 0) 0)
|
| [22] |
Weiss JM, Subramanian V, Hall KC. Simulation of unsteady turbomachinery flows using an implicitly coupled nonlinear harmonic balance method[J].
GT,2011 : 46367.
( 0) 0)
|
| [23] |
Thomas JP, Custer CH, Dowell EH, et al. Unsteady flow computation using a harmonic balance approach implemented about the OVERFLOW 2 flow solver[J].
AIAA,2009 : 4270.
( 0) 0)
|
| [24] |
Blanc F, Roux F, Jouhaud J. Harmonic-balance-based code-coupling algorithm for aeroelastic systems subjected to forced excitation[J].
AIAA Journal,2010, 48 (11) : 2472-2481.
DOI: 10.2514/1.45444. ( 0) 0)
|
| [25] |
McMullen M, Jameson A, Alonso J. Demonstration of nonlinear frequency domain methods[J].
AIAA Journal,2006, 44 (7) : 1428-1435.
DOI: 10.2514/1.15127. ( 0) 0)
|
| [26] |
McMullen M, Jameson A. The computational efficiency of nonlinear frequency domain methods[J].
Journal of Computational Physics,2006, 212 : 637-661.
DOI: 10.1016/j.jcp.2005.07.021. ( 0) 0)
|
| [27] |
Dai H, Schnoor M, Atluri SN. A simple collocation scheme for obtaining the periodic solutions of the Duffing equation, and its equivalence to the high dimensional harmonic balance method: subharmonic oscillations[J].
CMES,2012, 84 (5) : 459-497.
( 0) 0)
|
| [28] |
Liu L, Kalmar-Nagy T, Dowell EH. The high dimensional harmonic balance analysis for second-order delay-differential equations[J].
DETC,2007 : 34396.
( 0) 0)
|
| [29] |
Liu L, Dowell EH. The secondary bifurcation of an aeroelastic airfoil motion: effect of high harmonics[J].
Nonlinear Dynamics,2004, 37 : 31-49.
DOI: 10.1023/B:NODY.0000040033.85421.4d. ( 0) 0)
|
| [30] |
Liu L, Dowell EH, Thomas JP. A high dimensional harmonic balance approach for an aeroelastic airfoil with cubic restoring forces[J].
Journal of Fluids and Structures,2007, 23 : 351-363.
DOI: 10.1016/j.jfluidstructs.2006.09.005. ( 0) 0)
|
| [31] |
Dai H, Yue X, Yuan J, et al. A time domain collocation method for studying the aeroelasticity of a two dimensional airfoil with a structural nonlinearity[J].
Journal of Computational Physics,2014, 270 : 214-237.
DOI: 10.1016/j.jcp.2014.03.063. ( 0) 0)
|
| [32] |
Jones RT. The unsteady lift of a wing of finite aspect ratio. NACA Report 681, 1940
( 0) 0)
|
2. Chinese Aeronautic Establishment, Beijing 100012, China
 2016, Vol. 48
2016, Vol. 48
