尾桨是常规直升机不可或缺的关键气动部件之一[1]. 尾桨的气动性能对直升机整体性能有重要影响.剪刀式尾桨作为一种非常规构型尾桨已经在一些机型上得到了应用,例如美国AH-64和我国Z-10攻击直升机均采用了不同构型参数的剪刀式尾桨.从公开发表的国内外文献来看,对剪刀式尾桨的研究远比常规构型尾桨少.剪刀式尾桨与常规尾桨相比,主要区别在于桨叶非等间距分布以及非零的轴间距,因此剪刀式尾桨的流场特性比常规尾桨更加复杂,直接导致剪刀式尾桨的气动特性和常规尾桨之间存在很大不同.通过深入研究剪刀式尾桨复杂的涡干扰流场特性,可以更好地掌握剪刀式尾桨气动特性的参数影响规律,为设计高性能的直升机提供理论基础.
剪刀式尾桨研究的主要难点在于准确、高效地模拟上下两幅旋翼桨叶产生的涡-桨和涡-涡干扰的流动细节特征,为剪刀式尾桨气动性能的理论分析提供可靠基础.国内外对剪刀式尾桨开展了一些理论和试验研究工作. 在试验方面,Sonneborn等[2]较早进行了非等间距剪刀式旋翼的试验研究,结果表明其悬停状态气动性能不一定优于常规旋翼.Rozhdestensky[3]在1996年同样针对剪刀式尾桨进行了悬停试验研究,试验结果表明剪刀式尾桨的气动特性优于常规尾桨.Sullivan等[4]在2005年针对非等间距分布旋翼中的调制效应进行了试验研究,试验结果表明采用非等间距角布置的旋翼在气动性能方面与常规旋翼类似.2001年,南京航空航天大学的Xu等[5]对不同剪刀角配置下的剪刀式尾桨的诱导速度场和气动特性进行了测试,研究表明剪刀角对剪刀式尾桨性能影响很大,采用合适的剪刀角可以提高尾桨气动特性,相反也有可能降低其性能.在数值模拟方面,Brentner等[6]较早采用升力线模型对非等间距旋翼(尾桨)进行了桨叶表面载荷分析,并利用所求得的桨叶载荷计算其噪声特性,但是升力线模型不能很好地模拟桨叶之间的复杂气动干扰,因此无法精确获得桨叶表面载荷.随后,Xu等[7]采用自由尾迹方法对剪刀式尾桨的气动性能进行了分析,但是剪刀式尾桨桨叶展弦比小、三维效应大,采用自由尾迹方法在模拟流场精度方面存在一定局限性.最近,樊枫等[8]、Zhu等[9]应用先进的CFD方法对剪刀式尾桨流场开展了数值计算,得到了一些结论,但是对剪刀式尾桨复杂的涡尾迹研究较少,没有揭示涡尾迹的运动和强度演变规律.
综合目前的研究工作,以往对剪刀式尾桨的研究主要采用试验的方法,且进行数值模拟研究的方法不够精确,较少开展剪刀式尾桨干扰涡流场高精度数值模拟研究,并且无论是试验方法还是理论方法对剪刀式尾桨流场中复杂的涡干扰现象研究仍不够深入,不同研究结果甚至存在一些分歧. 鉴于此,本文基于计算流体力学方法,建立了适合于悬停状态下剪刀式尾桨流场分析的高精度数值模拟方法. 应用所建立的方法,对悬停状态下不同构型剪刀式尾桨的涡流场进行模拟研究,深入分析和揭示不同构型剪刀式尾桨上下桨叶涡尾迹运动形态、涡/涡干扰和涡/桨干扰机理,并研究了剪刀角和轴间距参数对剪刀式尾桨气动性能的影响规律,得出了一些有意义的结论.
1 数值计算方法与验证 1.1 嵌套网格方法网格生成是计算流体力学(computational fluid dynamics,CFD)方法的基础.本文首先通过求解泊松方程[10]来生成围绕翼型剖面的网格,然后桨叶段网格通过展向剖面间插值完成.考虑到C-O型网格可以更好地捕捉桨尖涡细节,本文采用绕翼型中弧线翻折策略生成桨叶的C-O型结构网格[11].剪刀式尾桨由于轴间距以及较小的剪刀角的存在,相邻桨叶网格之间可能会发生交叉重叠,对嵌套网格方法中的流场信息交换产生不利影响,为了解决这个问题,本文采用了一种类似纺锤体外形的桨叶网格方法.
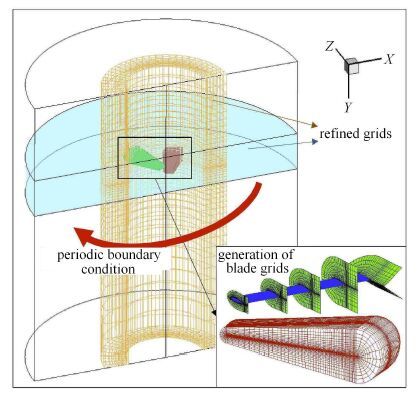
图 1给出了本文建立的嵌套网格系统示意图.四片桨叶的剪刀式尾桨在构型上仍然是中心对称的,可假定其悬停流场是准定常,采用旋转坐标系下的流场控制方程来求解. 但在引入周期性边界条件[12]时,需要通过两片相邻桨叶的模拟来代替四片桨叶,为此本文背景网格采用了半圆柱形结构网格.相比于一般计算采用的长方体背景网格和四个桨叶网格,本文的方法可以显著地提高流场计算效率.同时,采用"透视图"挖洞方法[13-14]来解决背景网格和桨叶网格之间的嵌套关系,并结合Inverse Map方法[15]和伪贡献单元搜寻法(PSSDE)[16]对背景网格洞边界单元的贡献单元进行快速搜寻.为了更好地捕捉桨尖涡细节特征,对半圆柱形背景网格进行了局部网格加密.
|
图 1 嵌套网格系统示意图 Fig. 1 Schematic of embedded grid system |
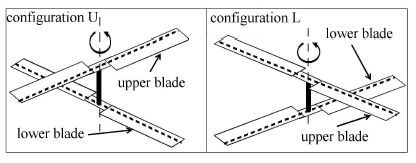
剪刀式尾桨由共轴、同向旋转的上、下两副旋翼桨叶构成,并且存在一定的轴间距.剪刀式尾桨分为两种构型,即"L构型"和"U构型". 其中,"L构型"定义为旋转在前(前行)的桨叶低于旋转在后(后行)的桨叶,"U构型"定义为旋转在前的桨叶高于旋转在后的桨叶.图 2中通过网格系统的俯视图和侧视图表明了"剪刀角"和"轴间距"的含义,其中,剪刀角始终定义为小于90°.图 3为两种构型剪刀式尾桨的示意图.

|
图 2 "剪刀角"和"轴间距"含义示意图 Fig. 2 Schematic of definition of "scissors angle" and "vertical space" |
|
图 3 U构型和L构型剪刀式尾桨示意图 Fig. 3 Schematic of scissors tail rotors with configuration U and configuration L |
悬停状态计算时,在随叶坐标系上建立以绝对物理量为参数的守恒的积分形式的雷诺平均Navier-Stoke (RANS)方程[17],方程如下
| ${\partial \over {\partial t}}\mathop{\int\!\!\!\int\!\!\!\int}\limits_{\kern-5.5pt V} W dV + \int\!\!\!\int\limits_S {({F_{\rm{c}}} - {F_{\rm{v}}})} \cdot ndS = \mathop{\int\!\!\!\int\!\!\!\int}\limits_{\kern-5.5pt V} Q dV$ | (1) |
其中,向量W 为守恒变量、 Q为由旋转带来的源项、 F c和 Fv分别为无黏通量和黏性通量, n为单元表面法矢量,S为控制体表面积,V为控制体体积.
采用Baldwin-Lomax湍流模型[18]计算黏性系数,桨叶表面采用无滑移条件.
为了提高流场求解的效率,本文的时间推进方法采用隐式LU-SGS格式[19].首先对控制方程中的时间导数进行离散后得
| $\eqalign{ & V \cdot {{{W^{m + 1}} - {W^m}} \over {\Delta t}} + \mathop \int\!\!\!\int \limits_{\partial V} (F_n^{{\rm{c}},m + 1} - F_n^{c,m})dS - \cr & \mathop \int\!\!\!\int \limits_{\partial V} (F_n^{{\rm{v}},m + 1} - F_n^{{\rm{v}},m})dS - V \cdot ({Q^{m + 1}} - {Q^m}) = Re{s^m} \cr} $ | (2) |
式中,m为推进层数, Res为残值.然后可对上式采用LU-SGS格式进行求解.
空间离散采用有限体积法,对于交界面上的对流通量,采用Roe格式[20-21]计算无黏通量.
| $\eqalign{ & {({F_{\rm{c}}})_{i + 1/2}} = {1 \over 2}[{F_{\rm{c}}}({W_{\rm{R}}}) + {F_{\rm{c}}}({W_{\rm{L}}}) - \cr & {\left| {{A_{{\rm{Roe}}}}} \right|_{i + 1/2}}({W_{\rm{R}}} - {W_{\rm{L}}})] \cr} $ | (3) |
式中, A Roe表示Roe平均雅克比矩阵,此矩阵同时考虑近似Riemann问题的波的大小及传播方向;W L和 W R分别表示交界面左右两边的守恒变量,下标i + 1 / 2表示单元交界面.
网格面上的流动变量采用三阶单调迎风MUSCL格式[22]差值获得,与二阶中心差分格式相比,可有效地减少由于截断误差和人工黏性导致的桨叶尾迹数值耗散,其格式如下
| ${\matrix{ {{W_{\rm{R}}} = {W_{i + 1}} - {1 \over 4}[(1 + \xi ){\Delta ^ - } + (1 - \xi ){\Delta ^ + }]{W_{i + 1}}} \hfill \cr {{W_{\rm{L}}} = {W_i} + {1 \over 4}[(1 + \xi ){\Delta ^ + } + (1 - \xi ){\Delta ^ - }]{W_i}} \hfill \cr } }$ | (4) |
式中,Δ - 和Δ+ 分别为后差算子和前差算子,参数ξ取为ξ = 1/3.为避免Roe格式中可能产生的非物理解,引入Harten熵修正[23].
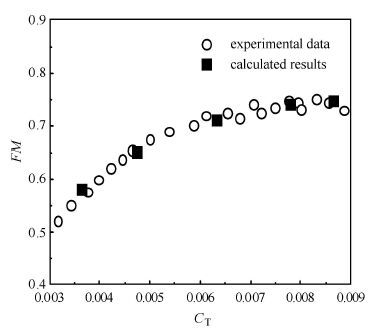
1.3 方法验证本文选用与剪刀式尾桨一样拥有4片桨叶的Helishape 7A旋翼[24]作为验证算例.只需要在CFD程序中将剪刀角设置为90°,轴间距设置为0,仍然采用剪刀式尾桨半圆柱形背景网格,采用周期性对称边界条件,实际计算两片桨叶,这样就可以来验证本文建立的CFD方法.本文计算采用的桨叶网格大小为247 × 40 × 76,背景网格大小为181 × 221 × 143.Helishape 7A旋翼直径为4.2 m,弦长0.14 m,计算状态为桨尖马赫数0.662、总距角7.5°.图 4展现了本文方法计算的Helishape 7A旋翼气动性能的计算值与试验值的对比. 悬停效率$FM$定义如下
| $FM = {{{C_{\rm{T}}} \cdot \sqrt {{C_{\rm{T}}}/2} } \over {{C_{\rm{Q}}}}}$ | (5) |
|
图 4 7A旋翼气动性能的计算值与试验值对比 Fig. 4 Comparisons of aerodynamic characteristics of Helishape 7A rotor between numerical results and experimental data |
其中,CT表示拉力系数、CQ表示扭矩系数.从图 4可以看出,本文建立的旋翼流场CFD方法可以准确地预测旋翼的气动性能.
图 5所示为"Caradonna-Tung"(C-T)旋翼悬停试验所测量的桨尖涡涡核位置[25]与计算值的对比.计算状态为转速1 250 r/min、总距角8°,图中φ表示涡龄角,r表示径向位置,y表示轴向位置,R表示桨叶半径.为了研究网格疏密对涡捕捉精度的影响,此算例给出了两组疏密不同的背景网格的结果对比.桨叶网格大小均为247 × 40 × 76,较密的背景网格大小为181 × 221 × 143,较疏的背景网格大小为121 × 131× 71. 可以看出,采用密网格更能准确地捕捉涡尾迹[26].但是采用疏网格和密网格计算的涡尾迹空间位置的差别尚在可接受范围之内,且二者涡的演变趋势较为一致.

|
图 5 C-T模型旋翼桨尖涡涡核位置的计算值与试验值对比 Fig. 5 Comparisons of the calculated position of blade-tip vortex core of C-T model rotor between numerical results and experimental data |
本文采用文献[2]中的剪刀式尾桨桨叶为算例模型.该剪刀式尾桨模型有4片相同桨叶,剖面翼型为NACA0012,半径1.35 m,弦长0.22 m,无负扭转,桨叶平面形状为矩形.本文计算采用的桨叶网格大小为247 × 40 × 76,背景网格大小为181 × 221 × 143.首先对本文计算的剪刀式尾桨进行命名,例如"L-45-0.1"代表剪刀角为45°、轴间距为0.1R的L构型剪刀式尾桨.本文计算的L构型和U构型剪刀式尾桨的剪刀角分别为30°,45°,60°,75°和90°,以及轴间距分别为0.1 R和0.15 R 计算状态:桨尖马赫数为0.65、总距角为12°的悬停状态.
图 6(a)、图 6(b)、图 6(c)和图 7(a)、图 7(b)、图 7(c)分别给出了L-45-0.1,L-75-0.1,L-45-0.15以及U-45-0.1,U-75-0.1,U-45-0.15等6种构型的剪刀式尾桨的涡量等值面图,涡量大小为0.5,可以看到本文的流场模拟方法可以准确地捕捉涡流场细节.观察图 6(a)和图 6(b)典型的L构型尾桨可知,L构型的下桨叶会受到前面上桨叶拖出的桨尖涡和下洗流的影响,实际迎角减小,会导致拉力的损失[27],桨尖涡甚至直接撞击到下桨叶,如图中圆圈所示.由于剪刀角小于90°,L构型的上桨叶距离前面下桨叶的桨尖涡比常规尾桨的近,但是轴间距的存在使得上桨叶受前行下桨叶的下洗流影响小. 随着剪刀角的增大,上桨 叶逐渐远离下桨叶的桨尖涡和下洗流的影响,而下桨叶受到上桨叶逸出桨尖涡的干扰会逐渐增强.比较图 6(a)与图 6(c)可知,轴间距的增大使得L构型下桨叶受上桨叶桨尖涡的干扰增强,而上桨叶则远离前行下桨叶的干扰.

|
图 6 L构型尾桨涡量等值面图 Fig. 6 Iso-surfaces of vorticity magnitude for scissors tail rotors with configuration L |

|
图 7 U构型尾桨涡量等值面图 Fig. 7 Iso-surfaces of vorticity magnitude for scissors tail rotors with configuration U |
观察图 7(a)和图 7(b)中U构型尾桨可知,U构型的下桨叶受到了来自上桨叶的严重的气动干扰,如图中圆圈所示.由于轴间距和剪刀角的存在,U构型的下桨叶处于前行上桨叶的下洗流之中,而U构型的上桨叶却远离下桨叶的干扰.随着剪刀角的增大,下桨叶所受气动干扰逐渐减小.比较图 7(a)与图 7(c)可知,即使轴间距增大,下桨叶依然受到强烈的下洗流影响.
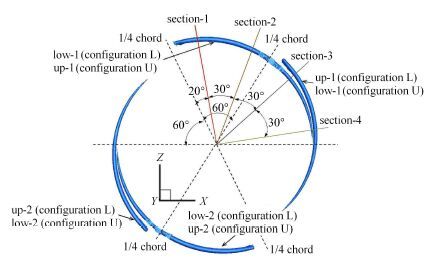
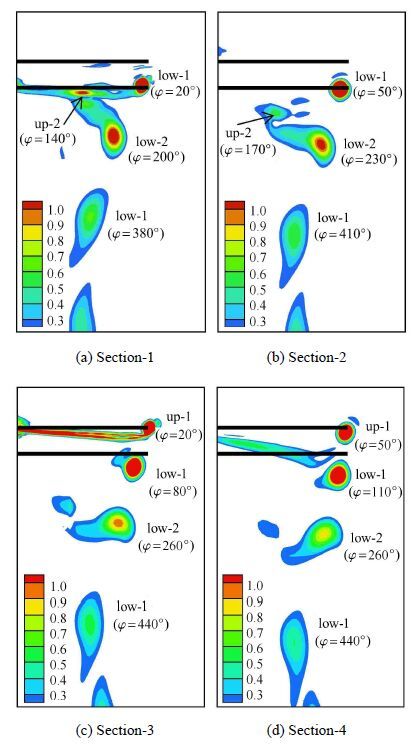
为了更加直观地观察不同桨叶桨尖涡的运动轨迹以及相互干扰的细节特征,本文选取了流场中4个典型周向位置的截面来反映桨尖涡的形态.图 8给出了各个尾迹截面以及桨尖涡命名示意图(对应于两种构型尾桨上下桨叶桨尖涡分别为up-1,up-2,low-1和low-2),相邻截面之间方位角均相差30°.以L-60-0.1和U-60-0.1两种典型的剪刀式尾桨为例,图 9和图 11分别给出了不同尾迹截面的涡量云图. 涡龄角等于0°的位置定义为桨叶1/4弦线处.图 10和图 12则分别给出了一个旋转周期内两个典型剪刀式尾桨上下桨叶的桨尖涡强度和涡核位置随涡龄角的变化,横坐标为前行桨叶的涡龄角.
|
图 8 尾迹截面示意图 Fig. 8 Schematic of sections for wake trajectory |
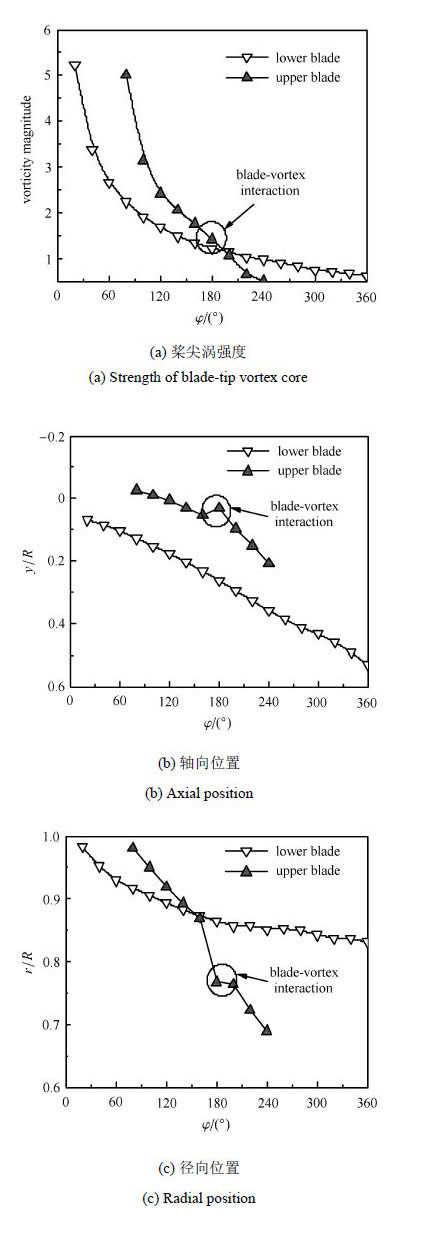
从图 9和图 10可以看出,L构型上桨叶拖出的桨尖涡up-2对下桨叶造成干扰,桨尖涡up-2结构也受到破坏,桨尖涡破碎影响到了下桨叶的下洗流.从图 10可以看出,随着涡龄角的增大,上桨叶桨尖涡up-2与下桨叶干扰之后强度减弱,逐渐消失,径向位置和轴向位置发生改变,并且持续影响到了桨尖涡low-2的运动形态和强度.观察图 9(c)与图 9(d)中与桨尖涡连成一体的是物面的附面层结构[28-29],随着桨尖涡up-1涡龄角的增大,附面层尾迹受到下洗速度的影响向下发展,并且其向下发展的速度大于桨尖涡.在图 9(d)中,桨尖涡up-1的附面层尾迹受桨尖涡low-1旋转速度的影响,尾迹形状向漩涡方向弯曲.
|
图 9 L构型剪刀式尾桨的涡量云图 Fig. 9 Vorticity magnitude contours of scissors tail rotor with configuration L |
|
图 10 L构型剪刀式尾桨桨尖涡涡核强度和位置 Fig. 10 Positions and strength of blade-tip vortex core for scissors vskip -1mm tail rotor with configuration L |
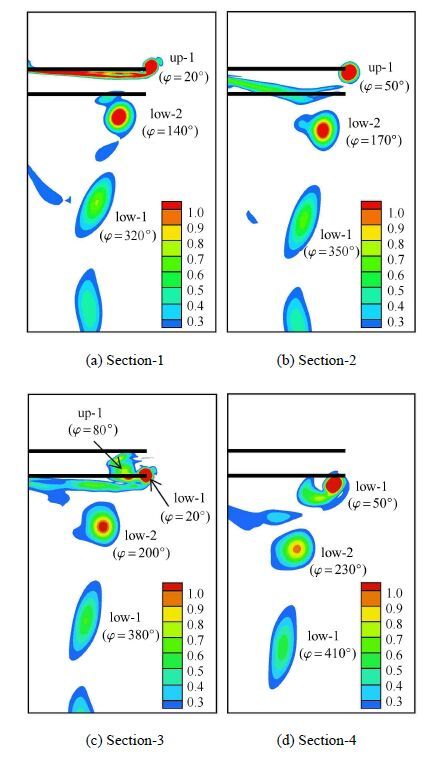
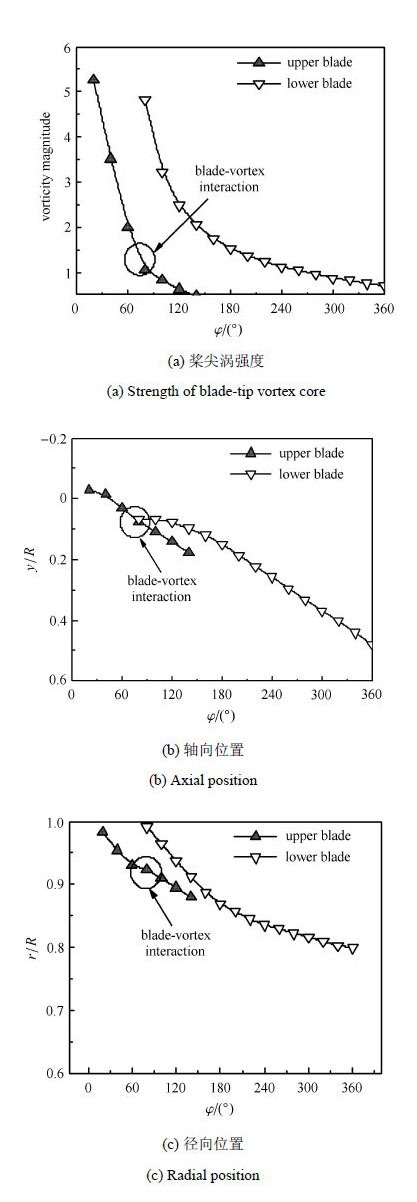
从图 11(a)和图 11(b)可以看出,上桨叶的附面层尾迹随着涡龄角的增大而向下发展,之后对下桨叶造成干扰.从图 11(c)、图 11(d)和图 12可知,上桨叶的桨尖涡up-1和下桨叶发生了碰撞,导致桨尖涡破碎,运动形态和涡核位置发生改变[30].尤其是桨尖涡up-1和下桨叶干扰之后强度迅速减弱,并且逐渐和下桨叶拖出的桨尖涡low-1融合,产生了复杂的涡-涡干扰[31].上桨叶的桨尖涡up-1和下桨叶干扰之后又对下桨叶的附面层尾迹的运动形态产生影响,使其迅速消亡.
|
图 11 U构型剪刀式尾桨的涡量云图 Fig. 11 Vorticity magnitude contours of scissors tail rotor with configuration U |
|
图 12 U 构型剪刀式尾桨桨尖涡涡核强度和位置 Fig. 12 Position and strength of blade-tip vortex core for scissors tail rotor with configuration U |
综合比较L构型与U构型剪刀式尾桨的涡流场特征可知,上桨叶的桨尖涡和下洗流均会对下桨叶产生干扰,而且干扰发生之后上桨叶桨尖涡自身也会发生畸变,期间存在这复杂的桨-涡干扰和涡-涡干扰现象.不同的是,L构型的桨尖涡从产生到与下桨叶发生干扰时的涡龄角比U构型的大,相应的桨尖涡强度也弱,所以U构型的下桨叶承受了更加强烈的气动干扰.另一方面,U构型的上桨叶离下桨叶的桨尖涡距离比L构型的远,因此U构型上桨叶所受桨尖涡干扰比L构型的小.上述剪刀式尾桨流场中存在的复杂的桨-涡干扰和涡-涡干扰现象将会对剪刀式尾桨的气动性能产生重要影响.
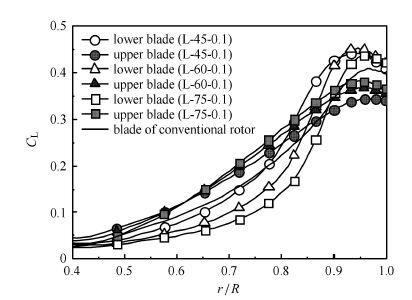
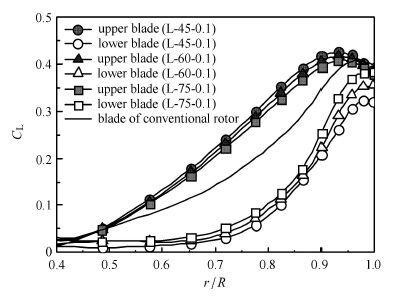
3 气动特性分析对于尾桨来说,悬停状态的轴向拉力可以提供反扭矩以及航向操纵的功能,因此本文的气动特性分析主要侧重于剪刀式尾桨的拉力计算.图 13和图 14为轴间距为0.1R时L构型和U构型桨叶展向拉力系数曲线,图中黑色的直线为相同桨叶参数和工作状态的常规尾桨的展向拉力系数.其中C L表示展向拉力系数. 从图 13和图 14中可以看出,随着剪刀角的增大,L构型的上桨叶拉力和U构型的下桨叶拉力也随之增大,而L构型的下桨叶拉力和U构型的上桨叶拉力随之减小.从图 13中可以看出,对于L构型来说,下桨叶在桨叶尖部的拉力比上桨叶大,也比常规尾桨桨叶大,而上桨叶在桨叶中段的拉力比下桨叶和常规尾桨桨叶的拉力大.从图 14中可以看出,对于U构型来说,上桨叶的拉力明显大于下桨叶和常规尾桨桨叶的拉力.U构型下桨叶中段受上桨叶下洗流干扰严重,导致桨叶中段拉力损失较大.
|
图 13 L构型桨叶展向拉力系数 Fig. 13 Spanwise distribution of lift coefficient for scissors tail rotor with configuration L |
|
图 14 U构型桨叶展向拉力系数 Fig. 14 Spanwise distribution of lift coefficient for scissors tail rotor with configuration U |
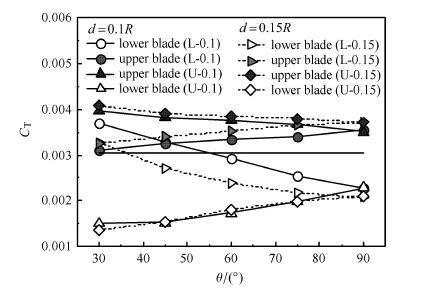
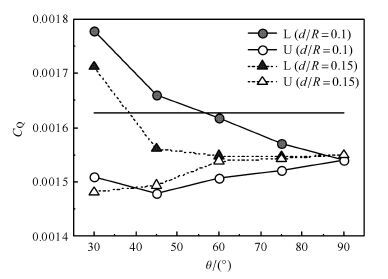
图 15和图 16为轴间距分别为0.1R和0.15R时,L构型和U构型剪刀式尾桨单片桨叶拉力系数和总拉力系数随剪刀角的变化曲线. 其中θ表示剪刀角、d表示轴间距. 图 17和图 18所示为扭矩和悬停效率的计算结果.
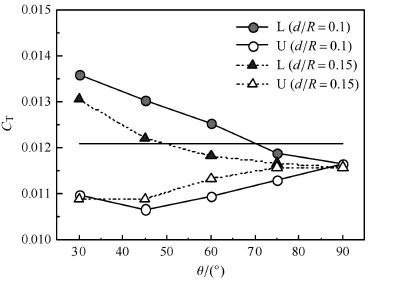
从图 15可以看出,对于L构型来说,下桨叶拉力随剪刀角增大而减小,甚至剪刀角较小时下桨叶拉力大于上桨叶和常规尾桨桨叶的拉力.这是因为剪刀角越小,前行上桨叶拖出的桨尖涡和下桨叶干扰时的涡龄角越大,强度越弱,下桨叶所受干扰也越小.随着剪刀角增大,L构型上桨叶远离前行下桨叶的桨尖涡,所以上桨叶拉力也随之增大,并且一直大于常规尾桨桨叶拉力.当轴间距从0.1R增加到0.15R时,L构型下桨叶拉力减小,而上桨叶拉力增大.从前文可知,这是因为轴间距的增大使得在本文的工作状态下桨尖涡对下桨叶的干扰加大,而上桨叶却远离下桨叶的影响.从图 16可以看出,随着剪刀角的增大,L构型总拉力随之减小;随着轴间距的增大,L构型总拉力也随之减小.
|
图 15 不同轴间距时单片桨叶拉力系数随剪刀角的变化 Fig. 15 Thrust coefficient of scissors rotor blade varies with scissors angle for different vertical space |
|
图 16 不同轴间距时总拉力系数随剪刀角的变化 Fig. 16 Total thrust coefficient of scissors rotor varies with scissors angle for different vertical space |
对于U构型来说,受相邻上桨叶下洗流和桨尖涡的影响,下桨叶遭受了强烈的气动干扰,拉力始终低于上桨叶和常规尾桨桨叶,而上桨叶所受其他桨叶影响小,拉力反而大于L构型桨叶和常规构型桨叶的拉力.随着剪刀角的增大,下桨叶所受上桨叶影响减小,因此拉力增大.从图 16中的总拉力变化曲线可知,总体而言,U构型总拉力随剪刀角增大而增大,随轴间距增大而增大.比较相同剪刀角和轴间距的U构型和L构型总拉力,在本文的计算状态下,L构型拉力总是大于U构型的拉力.
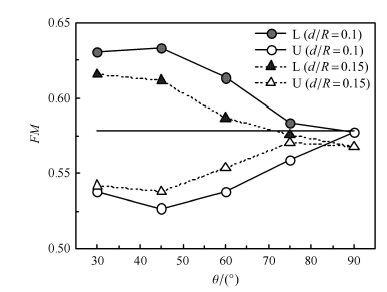
从图 17中可以看出,扭矩的变化趋势基本与拉力的变化趋势相同.从图 18可以看出,L构型的悬停效率普遍高于U构型,且存在一个最优剪刀角和轴间距的配置使得悬停效率最大.通过选取构型参数配置可以使剪刀式尾桨拉力增大,但是同时也不可避免地增加了扭矩. 因此,可以通过优化设计方法来合理选择剪刀式尾桨的外形参数.
|
图 17 不同轴间距时扭矩系数随剪刀角的变化 Fig. 17 Torque coefficient of scissors rotor varies with scissors angle for different vertical space |
|
图 18 不同轴间距时悬停效率随剪刀角的变化 Fig. 18 Figure of merit of scissors rotor varies with scissors angle for different vertical space |
兼顾计算精度和效率,建立了悬停状态下剪刀式尾桨流场计算的高精度数值模拟方法,着重分析了剪刀式尾桨涡干扰流场特征,以及构型参数对剪刀式尾桨的气动性能的影响规律. 在本文的计算状态下,结果表明:
(1) 剪刀式尾桨中存在着严重的桨-涡干扰现象.上桨叶的桨尖涡甚至会直接与下桨叶发生碰撞,一方面导致下桨叶拉力损失,另一方面碰撞后的桨尖涡会破碎、涡核运动轨迹发生改变、强度减弱. 而上桨叶的下洗流则会使得下桨叶的实际迎角减小,同样导致下桨叶拉力减小.其中,U构型下桨叶所受的干扰比L构型下桨叶所受干扰要强烈;
(2) 剪刀式尾桨中存在着复杂的涡-涡干扰现象.一方面上桨叶的桨尖涡和下桨叶干扰之后导致自身强度和轨迹发生突变,随后会与下桨叶的桨尖涡相互干扰、融合,并且对下桨叶桨尖涡强度和轨迹也造成影响;另一方面,上桨叶桨尖涡和下桨叶桨尖涡在运动过程由于距离较近,相互之间也会发生一定程度的干扰,甚至互相吸收融合;
(3) 剪刀角和轴间距对剪刀式尾桨的气动力有重要影响.总体来说,相同剪刀角和相同轴间距配置时,L构型剪刀式尾桨的拉力和悬停效率均大于U构型剪刀式尾桨.L构型剪刀式尾桨的气动力随着剪刀角的增大而增大,随着轴间距的增大而减小;U构型剪刀式尾桨的气动力随着剪刀角的增大而减小,随着轴间距的增大而增大.
| [1] |
Amer KB, Prouty RW. Technology advances in the AH-64 advanced attack helicopter[J].
Vertica,1984, 8 (2) : 133-164.
( 0) 0)
|
| [2] |
Sonneborn WGO, Drees JM. The scissors rotor[J].
Journal of the American Helicopter Society,1975, 20 (3) : 18-27.
DOI: 10.4050/JAHS.20.18. ( 0) 0)
|
| [3] |
Rozhdestensky MG. Scissors rotor concept: new results obtained[J].
American Helicopter Society 52nd Annual Forum,Washington, DC,1996 : 1231-1241.
( 0) 0)
|
| [4] |
Sullivan BM, Edwards BD, Brentner KS, et al. A subjective test of modulated blade spacing for helicopter main rotors[J].
Journal of the American Helicopter Society,2005, 50 (1) : 26-32.
DOI: 10.4050/1.3092840. ( 0) 0)
|
| [5] |
Xu GH, Wang SC, Zhao JG. Experimental and analytical investigation on aerodynamic characteristics of helicopter scissors tail rotor[J].
Chinese Journal of Aeronautics,2001, 14 (4) : 193-199.
( 0) 0)
|
| [6] |
Brentner KS, Edwards BD, Riley R. Predicted noise for a main rotor with modulated blade spacing[J].
Journal of the American Helicopter Society,2005, 50 (1) : 18-25.
DOI: 10.4050/1.3092839. ( 0) 0)
|
| [7] |
Xu GH, Zhao QJ, Peng YH. Study on the induced velocity and noise characteristics of a scissors rotor[J].
Journal of Aircraft,2007, 44 (3) : 806-811.
DOI: 10.2514/1.24460. ( 0) 0)
|
| [8] |
樊枫, 史勇杰, 徐国华. 剪刀式尾桨悬停状态气动力及噪声特性计算研究[J].
航空学报,2013, 34 (9) : 2100-2109.
( Fan Feng, Shi Yongjie, Xu Guohua. Computational research on aerodynamic and aeroacoustic characteristics of scissors tail-rotor in hover[J].
Acta Aeronautica Astronautica Sinica,2013, 34 (9) : 2100-2109.
(in Chinese) ) ( 0) 0)
|
| [9] |
Zhu Z, Zhao QJ. Numerical analyses for aerodynamic and noise characteristics of helicopter scissors tail rotor. American Helicopter Society 70th Annual Forum, Montreal, 2014: 1186-1198
( 0) 0)
|
| [10] |
Thomas PD, Middlecoff JF. Direct control of the grid point distribution in meshes generated by elliptic equations[J].
AIAA Journal,1980, 18 (6) : 652-656.
DOI: 10.2514/3.50801. ( 0) 0)
|
| [11] |
Potsdam MA, Strawn RC. CFD simulations of tiltrotor configurations in hover[J].
Journal of the American Helicopter Society,2005, 50 (1) : 82-94.
DOI: 10.4050/1.3092845. ( 0) 0)
|
| [12] |
Song WP, Han ZH, Qiao ZD. Prediction of hovering rotor noise based on Reynolds-averaged Navier-Stokes simulation[J].
Journal of Aircraft,2007, 44 (4) : 1391-1394.
DOI: 10.2514/1.28310. ( 0) 0)
|
| [13] |
Zhao QJ, Xu GH, Zhao JG. New hybrid method for predicting the flowfields of helicopter rotors[J].
Journal of Aircraft,2006, 43 (2) : 372-380.
DOI: 10.2514/1.14863. ( 0) 0)
|
| [14] |
Wang B, Zhao QJ, Xu GH, et al. Numerical analysis on noise of rotor with unconventional blade-tips based on CFD/Kirchhoff method[J].
Chinese Journal of Aeronautics,2013, 26 (3) : 572-582.
DOI: 10.1016/j.cja.2013.04.045. ( 0) 0)
|
| [15] |
Meakin RL. A new method for establishing intergrid communication among systems of overset grids. AIAA Paper 91-1586, 1991
( 0) 0)
|
| [16] |
Zhao QJ, Xu GH, Zhao JG. Numerical simulations of the unsteady flowfield of helicopter rotors on moving embedded grids[J].
Aerospace Science and Technology,2005, 9 (2) : 117-124.
DOI: 10.1016/j.ast.2004.10.004. ( 0) 0)
|
| [17] |
Zhao QJ, Xu GH. A study on aerodynamic and acoustic characteristics of advanced tip-shape rotors[J].
Journal of American Helicopter Society,2007, 52 (3) : 201-213.
DOI: 10.4050/JAHS.52.201. ( 0) 0)
|
| [18] |
Lomax H, Baldwin BS. Thin layer approximation and algebraic model for separated turbulent flows. AIAA Paper 78-257, 1978
( 0) 0)
|
| [19] |
Luo H, Baum JD, Löhner R. A fast, matrix-free implicit method for compressible flows on unstructured grids[J].
Journal of Computational Physics,1998, 146 (2) : 664-690.
DOI: 10.1006/jcph.1998.6076. ( 0) 0)
|
| [20] |
Roe PL. Approximate Riemann solvers, parameter vectors and difference schemes[J].
Journal of Computational Physics,1981, 43 (2) : 357-372.
DOI: 10.1016/0021-9991(81)90128-5. ( 0) 0)
|
| [21] |
刘强, 刘周, 白鹏, 等. 低雷诺数翼型蒙皮主动振动气动特性及流场结构数值研究[J].
力学学报,2015, 48 (2) : 269-277.
( Liu Qiang, Liu Zhou, Bai Peng, et al. Numerical study about aerodynamic characteristics and flow field structures for a skin of airfoil with active oscillation at low reynolds number[J].
Chinese Journal of Theoretical and Applied Mechanics,2015, 48 (2) : 269-277.
(in Chinese) ) ( 0) 0)
|
| [22] |
Van Leer B. Towards the ultimate conservative difference scheme. V. A second-order sequel to Godunov’s method[J].
Journal of Computational Physics,1979, 32 (1) : 101-136.
DOI: 10.1016/0021-9991(79)90145-1. ( 0) 0)
|
| [23] |
Harten A, Hyman JM. Self adjusting grid methods for onedimensional hyperbolic conservation laws[J].
Journal of Computational Physics,1983, 50 (2) : 235-269.
DOI: 10.1016/0021-9991(83)90066-9. ( 0) 0)
|
| [24] |
Pomin H, Wagner S. Navier-Stokes analysis of helicopter rotor aerodynamics in hover and forward flight[J].
Journal of Aircraft,2002, 39 (5) : 813-821.
DOI: 10.2514/2.3001. ( 0) 0)
|
| [25] |
Caradonna FX, Tung C. Experimental and analytical studies of a model helicopter rotor in hover[J].
Vertica,1981, 5 (2) : 149-161.
( 0) 0)
|
| [26] |
张涵信, 呙超, 宗文刚. 网格与高精度差分计算问题[J].
力学学报,1999, 31 (4) : 398-405.
( Zhang Hanxin, Guo Chao, Zong Wengang. Problems about grid and high order schemes[J].
Acta Mechanica Sinica,1999, 31 (4) : 398-405.
(in Chinese) ) ( 0) 0)
|
| [27] |
Yu YH. Rotor blade-vortex interaction noise[J].
Progress in Aerospace Sciences,2000, 36 (2) : 97-115.
DOI: 10.1016/S0376-0421(99)00012-3. ( 0) 0)
|
| [28] |
Lakshminarayan VK, Baeder JD. High-resolution computational investigation of trimmed coaxial rotor aerodynamics in hover[J].
Journal of the American Helicopter Society,2009, 54 (4) : 42008.
DOI: 10.4050/JAHS.54.042008. ( 0) 0)
|
| [29] |
Lakshminarayan VK, Baeder JD. Computational investigation of micro-scale coaxial rotor aerodynamics in hover[J].
Journal of Aircraft,2010, 47 (3) : 940-955.
DOI: 10.2514/1.46530. ( 0) 0)
|
| [30] |
Tauszig L, Gandhi F. Influence of blade-to-blade dissimilarity on alleviation of helicopter blade-vortex interactions[J].
Mathematical and Computer Modelling,2001, 33 (10) : 1139-1154.
( 0) 0)
|
| [31] |
朱正, 招启军, 李鹏. 悬停状态共轴刚性双旋翼非定常流动干扰机理[J].
航空学报,2016, 37 (2) : 568-578.
( Zhu Zheng, Zhao Qijun, Li Peng. Investigations on unsteady flow interaction mechanism of coaxial rigid rotors in hover[J].
Acta Aeronautica et Astronautica Sinica,2016, 37 (2) : 568-578.
(in Chinese) ) ( 0) 0)
|
 2016, Vol. 48
2016, Vol. 48
