高升阻比是高超声速飞行器气动性能研究的主要追求指标. 然而,在高速飞行条件下,由于激波阻力和摩擦阻力急剧增加,飞行器的气动性能急剧下降,形成所谓的"升阻比屏障"[1],给飞行器气动性能提升带来极大挑战. 就已有文献看,现有高升阻比构型主要包括翼身组合体[2-4]、翼身融合体[5-6]和乘波体[7]等几种方案. 翼身组合体主要由机体和机翼两部分构成,其中机翼充当主要升力部件,机体为飞行器提供足够的容积. 翼身融合体的主要特点为机体和机翼融合,二者没有明显界限,飞行器上表面适当隆起满足容积需求. 下表面为升力面,通过合理设计飞行攻角提供所需升力. 乘波体是一种较为特殊的升力体构型,在设计条件下,其前缘激波附着于乘波体边缘,激波后的高压区被完全包裹于飞行器下表面,因而可获得相对较高的升阻比.
气动外形优化设计是提升高超声速飞行器升阻比的重要手段,也是目前的研究热点之一. 其中,飞行器前缘线形状直接决定其有效升力面积,对升阻特性影响十分明显,同时与容积和机体结构等方面的耦合程度相对较弱,因此一般是气动外形优化中的首选部位. 文献[8]对一种翼身组合型的弧形翼导弹的翼前缘线进行优化,使升阻比提升约9.22%. 文献[9]基于一种采用翼身融合体设计的吸气式高超声速飞机概念构型,同样选取前缘线作为设计变量开展气动优化,其升阻比亦获得约10%的提升.
前缘线优化设计对于乘波体而言同样至关重要. 乘波体的设计原则是对给定流场进行部分切割,依据这一思想,当源流场给定后,前缘线的形状直接决定乘波体的气动性能.正因如此,乘波体前缘线优化设计一直是是国内外研究的热点领域[10-18].其中最具代表的是Bowcutt等[19]和Corda等[20]分别基于圆锥基准流场和幂次曲线轴对称体基准流场所生成的乘波体,采用参考温度法计算摩擦阻力,以非线性单纯形法为优化方法选择前缘线形状,获得了一系列黏性优化乘波体,并突破了"升阻比屏障".上述结果表明,对于前述各类飞行器构型,前缘线优化设计均是提升其升阻比的有效手段.
高超声速飞行条件下强激波的存在使升阻比和容积间的矛盾关系愈发突出,缓解这一矛盾的一般方法是采用多目标优化设计[21-23].这种做法本质上是一种折中手段,即在升阻比和容积之间选择牺牲较小的一项来换取另一项的较大提升,进而改善其综合性能.例如,文献[21]以升阻比和容积两项指标的加权乘积为目标进行优化,尽管其容积获得了一定程度的提升,但数值计算和实验结果表明,在马赫数3.5条件下其最大升阻比仅为2.62,较一般乘波体而言大幅下降.
高压捕获翼(high pressure capturing wing,HCW)构型[24-25]主要针对升阻比与容积间的矛盾而提出.该构型的主要思想为在大容积条件下,在机体背风面增加了与来流方向平行的曲面翼,通过捕获翼位置的合理设定[26],可充分利用机体上壁面对来流压缩所产生的高压区产生升力,同时,由于翼面厚度较小,所产生的附加阻力也较小,因此飞行器的升阻比也可获得大幅提高.在概念研究基础上,文献[26]基于二维流场数值分析和多维空间曲面拟合理论提出了一种捕获翼位置设计的有效方法.已有研究中,捕获翼外形设计均基于二维分析,其前缘线俯视形状为直线.如前所述,飞行器主升力面的前缘线形状对其气动性能影响十分明显.因此,发展适合于高压捕获翼的前缘型线参数化设计方法,开展优化设计进而评估翼前缘线形状对其气动性能的影响程度是研究中必须考虑的问题.
本文主要针对这一问题,采用幂次函数和余弦函数组合形式对翼前缘型线进行了参数化设计,并基于均匀实验设计和计算流体力学分析对多项式/径向基函数两种代理模型的拟合精度进行了比较,之后选用拟合精度更好的径向基函数代理模型,以升阻比最大化为目标采用遗传算法进行了优化设计,最后在最优点附近开展了单参数灵敏度分析.
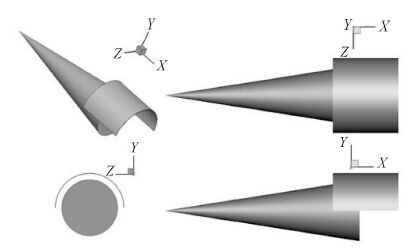
1 基准构型简介及性能评估 1.1 基准构型简介为突出重点并缩减计算量,基准构型采用圆锥机体与高压捕获翼组合的概念构型,其三维效果图和三视图如图 1所示.机体半锥角为9°,长度为1 m.捕获翼位置采用文献[26]中的方法基于二维流场分析给定,依据前缘点落在锥体激波面,同时反射激波刚好掠过机体尾缘端最高点的原则,前缘点位于X=0.862 5 m处.捕获翼基准外形为半圆柱壳体,其前缘线俯视投影为直线,尾缘端选取至X=1.2 m处,捕获翼厚度为2 mm,前缘采取圆弧钝化.
|
图 1 基准构型三维效果图和三视图 Fig. 1 Three dimensional and three-view of the baseline configuration |
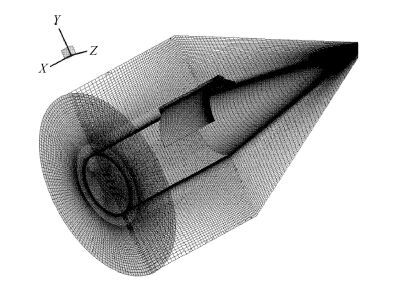
基准构型气动性能评估采用计算流体力学模拟.计算网格采用结构网格,近壁面网格进行加密,捕获翼与机体采用网格嵌套技术,总网格单元个数为340万,物面网格及对称面网格如图 2所示.数值分析采用总变差减小格式,时间推进选用隐式格式,湍流模型为k-ε模型.本文选择的网格及计算参数与文献[26]中相同,由于文献中已对数值结果的可靠性进行了验证和分析,此处不再赘述.
|
图 2 基准构型计算网格示意图 Fig. 2 Illustration of computational grid |
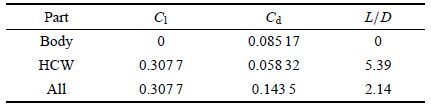
给定计算条件如下:来流马赫数7,远场静温为240 K,来流静压400 Pa,飞行攻角为0°. 升阻力系数计算时以锥体流向投影面积为参考面积,阻力计算不含底阻. 计算结果如表 1所示. 其中"Body"代表机体部分,"HCW"代表捕获翼部分,"All"代表上述两部分之和,即总升阻力参数. 从结果可见,由于机体为轴对称锥体,故其自身升阻比为0,在添加捕获翼后,升阻比获得明显提升,整体升阻比为2.14,其中捕获翼为构型升力的唯一来源,但结果同时也表明,捕获翼对于总阻力的贡献也十分明显,相对比例达40.6%.
| 表 1 基准构型各部件升阻力系数及升阻比 Table 1 Aerodynamic coefficients of the baseline configuration |
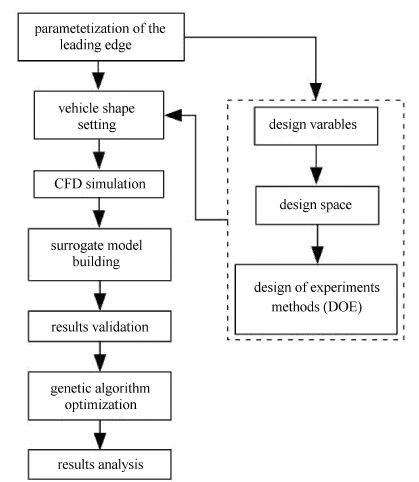
优化设计流程如图 3所示,简要解释如下:以基准构型为出发点,首先对捕获翼前缘线形状进行参数化描述,确定设计变量个数及含义;然后根据实际情况给定各参数的设计空间,选择均匀实验设计表生成设计变量集,并获得一系列典型的飞行器样本构型;之后利用数值模拟对前述样本集中的飞行器外形分别进行计算分析,获得其气动性能参数;继而根据上述数据构建不同的代理模型,通过对比选择精度较高的模型,并采用遗传算法以升阻比最大化为目标进行优化;最后通过优化外形与基准外形的比较,以及最优值的单参数灵敏度分析,总结分析捕获翼前缘线形状对飞行器气动性能的影响.
|
图 3 优化设计流程图 Fig. 3 Flowchart of the optimization |
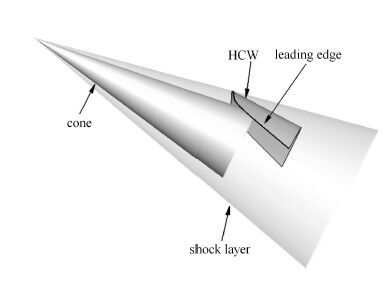
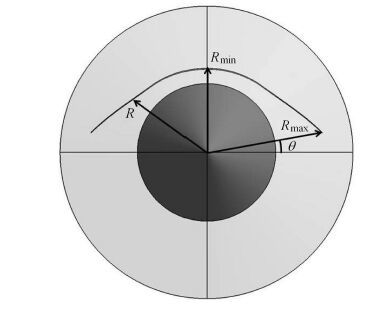
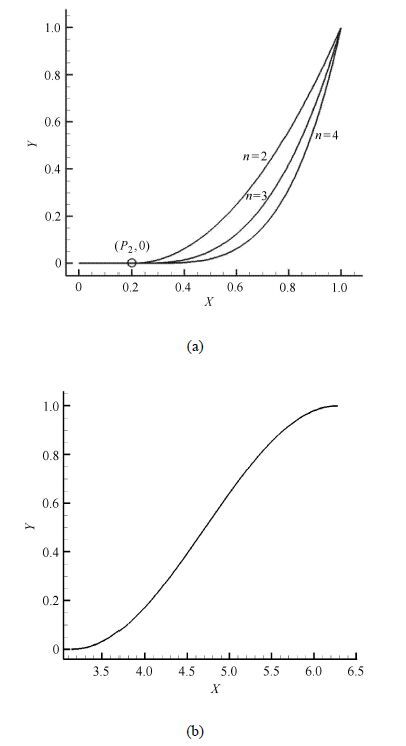
根据捕获翼的设计原理,为充分捕捉来流压缩产生的高压,捕获翼前缘线应落在机体产生的激波面上.当机体为锥体时,激波面可由Taylor-Maccoll方程求出,激波面上的前缘线给定后,沿来流方向拉伸所得到的柱面即为捕获翼外形.基于这样的思路,当捕获翼长度确定后,捕获翼外形主要由其沿流向的投影形状确定,如图 4所示.从流向正视图(图 5)看,在极坐标系统下,控制参数为对应于激波面上的半径R和两侧的截取角度 θ,具体表达式如式(1),其中Rmin为对称面上所对应的半径,即对应于基准外形的半径,Rmax为两侧端点对应的半径.为保证捕获翼前缘线为后掠形式,半径R由Rmin逐渐增加过渡到Rmax.其中过渡曲线选择幂次曲线和余弦曲线组合的形式,如式(2)和式(3)所示,对应的函数曲线如图 6所示.其中n为幂次,P1为幂次曲线所占比重,P2为幂次曲线起始点位置.
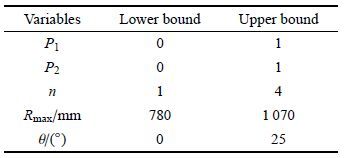
经上述参数化设计后,在保证捕获翼长度与基准构型一致时,捕获翼前缘线共采用5个设计变量描述,即两侧端点的最大半径Rmax,控制幂次函数和余弦函数的比例参数P1,幂次函数的参数P2和n,以及控制两侧截取角度的参数θ. 表 2给定了各设计参数的上下界范围,即设计空间. 其中P1和P2均为无量纲归一化参数,其取值范围为[0,1],n取为[1,4],Rmax的上边界由捕获翼尾部对应的激波位置决定,为1 070 mm,当Rmax取值与Rmin相等时,即对应于基准外形.参数 θ 主要决定捕获翼的升力面积,此处最大值取值为25°.
|
图 4 锥体组合捕获翼构型设计图示 Fig. 4 Illustration of the design of cone combination with HCW |
|
图 5 前缘线控制参数 Fig. 5 Control parameters of the leading edge along the flow direction |
|
图 6 幂次(a)和余弦(b)控制函数曲线 Fig. 6 Curves of the power (a) and cosine (b) control function |
| $$\eqalign{ & R\left( {{P_1},{P_2},n} \right) = \cr & {R_{\min }} + ({R_{\max }} - {R_{\min }})\left[ {{P_1}{f_1}({P_{2,}}n) + (1 - {P_1}){f_2}} \right] \cr} $$ | (1) |
| $${f_1}({P_{2,}}n) = \left\{ {\matrix{ {0,t \in [0,{P_2}]} \cr {{{\left( {{{t - {P_2}} \over {1 - {P_2}}}} \right)}^n},t \in ({P_2},1)} \cr } } \right.$$ | (2) |
| $${f_2} = {{\cos \alpha + 1} \over 2},\alpha \in \left[ {\pi ,2\pi } \right]$$ | (3) |
| 表 2 设计变量取值范围 Table 2 Boundary values of the design space |
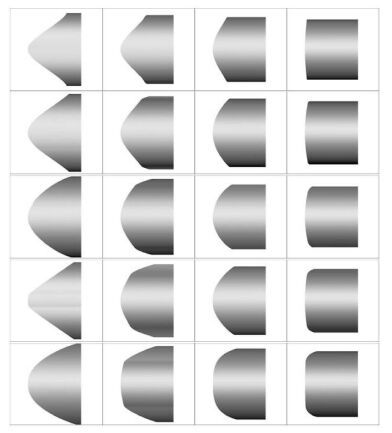
为覆盖整个设计空间,构造合适的代理模型,本文采用实际中广泛使用的均匀实验设计方法[27] 生成训练样本集.该方法基于数论理论在整个设计空间内构造合理的均匀设计表并获得样本集,被广泛应用于代理模型的构建.本文结合采用好格子点法和方幂好格子点法,根据表 2给出的设计空间,生成了水平值为20的实验设计表,图 7给出了所有20个样本的捕获翼俯视外形,从图中可以看出,参数化方法可以灵活调整捕获翼的前缘线设计形状,实验设计方法生成了外形差异明显的样本集.
|
图 7 构型样本集 Fig. 7 Sample set of configurations |
根据上述生成的捕获翼外形,结合基准外形的锥体生成整机构型,采用计算流体力学模拟对其气动性能进行评估.网格尺度、飞行条件及计算格式等均与基准构型保持一致.气动力系数计算时不考虑机体底阻,参考面积采用锥体流向的投影面积.计算得出各样本点构型对应的气动参数响应值,从而获得代理模型构建的样本集.
2.3 代理模型构建采用代理模型方法,可以有效的减少分析次数以提高整个优化设计效率. 这类方法基于有限个样本数据(即样本集)建立设计变量与目标函数间的近似响应关系,并以近似响应关系替代学科分析模块完成优化设计. 目前最常用的代理模型主要有多项式代理模型、径向基函数代理模型、Kriging模型和人工神经元网络模型等. 本文选择了最为常用的两种代理模型,即多项式和径向基函数两种模型,并对其拟合精度进行了比较. 两种模型构造时,均以前述5个设计变量(经归一化)为输入量,模型输出量为构型的升阻比.
多项式代理模型采用多项式对样本进行回归拟合,获得设计目标与设计变量之间的近似解析关系. 该方法在处理线性或弱非线性问题时,一般可以得到满意的结果,由于该方法易于实现,在飞行器优化设计中得到广泛应用[28-29]. 本文选用无交叉项的多项式模型,其表达式如式(4)所示.
| $$y\left( x \right) = {a_0} + \sum\limits_{i = 1}^n {{a_i}} {x_i} + \sum\limits_{\matrix{ {i = 1} \cr {j = 1} \cr } }^n {{a_{ij}}} {x_i}{x_j}$$ | (4) |
采用上述均匀实验设计得到的20组训练样本点及对应的目标函数值,构造多项式代理模型,相应的待定参数采用最小二乘法. 为保证检验结果的覆盖性和正交性,测试样本集采用7水平的均匀实验设计表生成. 结果表明,生成的多项式代理模型训练精度和测试精度均在5%左右,即使将测试样本集加入训练样本集中重新构建代理模型,仍无法提高其训练精度.
径向基函数代理模型以径向函数为基函数,通过线性叠加的方式获得,是一种灵活性较好,计算量相对较小且效率较高的代理模型,具有较强的非线性拟合能力,在飞行器优化设计中亦有广泛的应用[30-31].本文选用Guass径向基函数代理模型,其表达式如式(5)和式(6)所示.
| $$y(x) = \sum\limits_{i = 1}^P {{w_i}} \cdot \varphi \left( {\left\| {x - {x_i}} \right\|} \right)$$ | (5) |
| $$\varphi (\left\| {x - {x_i}} \right\|) = \varphi (r) = \exp ( - {{{r^2}} \over {2{\delta ^2}}})$$ | (6) |
模型训练仍基于上述20组样本,模型中心点个数选为17,基函数扩展常数为2.0. 同样以上述7水平的测试样本集对代理模型进行测试. 结果表明训练精度可以达到1%以内,测试样本有3组数据在1%以内,其余4组数据最大误差达到4%. 为进一步提高模型的精度,将测试精度差的4组数据加入到训练样本集中重新构建,得到的训练精度和测试精度均在2%以内,图 8给出了多项式代理模型与径向基函数代理模型训练精度和测试精度与样本的关系,可以看出,径向基函数模型的训练精度明显优于多项式代理模型,因此选用该代理模型对捕获翼前缘线形状进行优化和分析.

|
图 8 多项式(POL)和径向基函数(RBF)代理模型精度对比 Fig. 8 Precision comparison between the polynomial model (POL) and the RBF model (RBF) |
优化目标为构型升阻比最大化,具体使用时采用升阻比负值最小化表达优化目标. 优化算法采用实际中广泛使用的遗传算法,该方法基于自然选择和基因遗传学原理而提出,特别适用于处理传统搜索方法难以解决的复杂和非线性问题. 本文实际应用中种群规模为31,采用双矢量编码,每一代保留精英数目2个,遗传过程中采用高斯变异函数且交叉概率为0.8,变异概率为0.2.
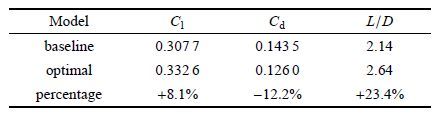
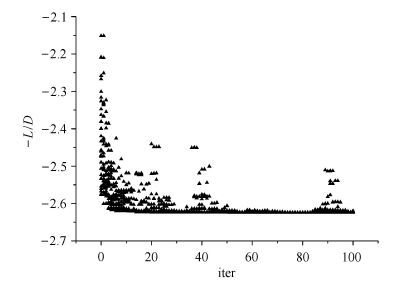
3 优化结果与分析优化目标(升阻比负值)的收敛历史曲线如图 9所示,可以看出,经40次迭代后目标函数基本收敛,至迭代100次后已完全收敛,且升阻比获得明显提升. 所得最优升阻比为2.62.为进一步检验,将最优外形采用计算流体力学分析获得其气动参数,计算结果如表 3所示.从表中数据可以看出,首先,计算流体力学计算所得升阻比为2.64,与代理模型输出结果的相对误差仅为0.8%,这表明代理模型具有很好的拟合精度.其次,经优化后,构型的升力系数增加8.1%,阻力系数减小12.2%,综合导致优化构型的升阻比增加23.4%,即优化设计同时起到了增升和减阻的作用,且使升阻比大幅增加.
|
图 9 目标函数收敛曲线 Fig. 9 The convergence history of the objective function |
| 表 3 优化外形和基准外形气动参数对比 Table 3 Comparison of the aerodynamic parameters between the optimal and the baseline configurations |
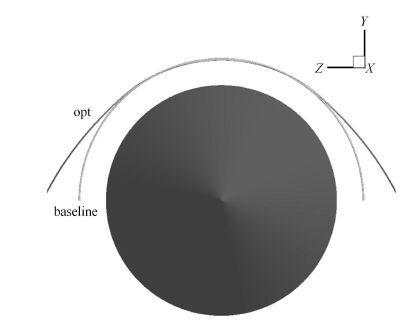
最优构型的5个设计变量数值及其与基准外形的对比如表 4所示.优化构型与基准构型的轴向比较如图 10所示,其垂向外形比较及表面压力云图比较如图 11所示,优化外形对称面的压力分布云图如图 12所示.从表 4可以看出,经优化后,5个设计变量的数值均有明显改变,因此导致优化外形与基准构型的差别较大.
从图 11和图 12可以看出,捕获翼头部由于钝化作用的影响产生弓形激波,压力急剧增加,之后经膨胀作用压力逐渐减小. 但捕获翼处于锥形流场激波内部,经激波作用的不均匀气流对捕获翼再次产生压缩,而靠近锥体的压力较大,故激波强度逐渐增强,导致捕获翼下表面压力逐渐增加,再次形成较大的高压区,之后经尾部的膨胀作用逐渐减小,故形成了图 11中所示的压力分布.此外,从图 11中还可看出,基准构型的高压区分布更为集中,而优化构型由于在两侧对应于激波面的半径逐渐增加,形成后掠翼型,且两侧区域更加平缓,导致明显的三维流动,使两侧压力值减小.但从整体来看,优化构型的升力面积有明显增加,相对于基准构型增加了约11%,因此升力明显增加.捕获翼为平行于来流方向的平面,故阻力主要来源于有厚度的前缘区域,从图 11可以发现,由于优化构型前缘线在两侧存在明显后掠现象,其前缘的压缩作用明显减弱,故阻力减小.
| 表 4 基准外形与优化外形的设计参数比较 Table 4 Comparison of the design parameters between the baseline and the optimal configurations |
|
图 10 优化外形和基准外形比较(轴向) Fig. 10 Shape comparison between the optimal and the baseline configurations (in axial direction) |
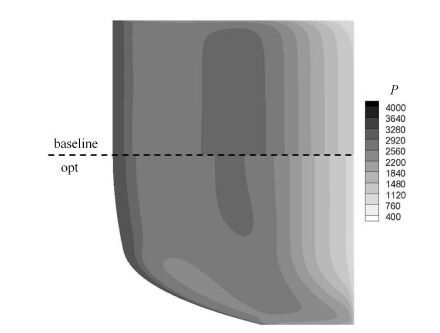
|
图 11 优化外形与基准外形下表面压力云图对比 Fig. 11 Pressure contours comparison between the optimal and the baseline configurations (on the lower surface) |
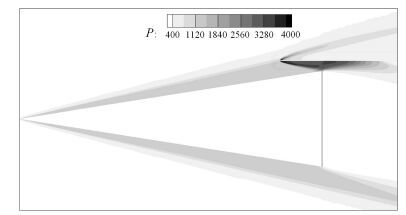
|
图 12 优化外形对称面压力分布云图 Fig. 12 The pressure contours in the symmetry plane of the optimal configuration |
为进一步分析最优值附近的参数灵敏度,以最优值为基准开展单参数轮转分析,获得了升阻比对应于每个设计参数的变化曲线,如图 13所示. 为便于比较,将每个设计变量依据取值范围进行归一化处理. 从图中可见,升阻比均在最优设计点处存在拐点,这表明优化设计是成功的. 同时随各参数在最优值附近变化时,升阻比变化均比较平缓,且幅度较小,这表明升阻比在最优值点附近对参数的变化不敏感,外形参数的小幅变化并不会导致升阻比的明显下降,即捕获翼构型的鲁棒性较好,这对于实际设计非常有利.
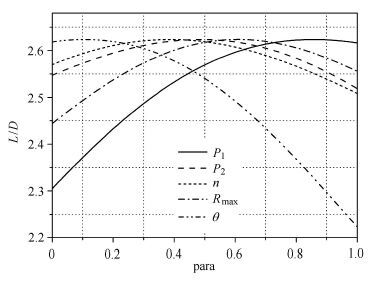
|
图 13 升阻比与设计参数的变化曲线 Fig. 13 Curves of the $L/D$ versus each design parameter |
从图 13中还可以看出,升阻比与各设计参数均呈非线性关系,其中 θ 控制展向角度(余角即为展向角度),对升阻比的影响最大,当 θ 增加时,捕获翼的升力面积减小,导致升力减小,而且 θ 越小,其两侧部分升力面的面积分量越小,故升阻比与 θ 值基本呈抛物线趋势. P1控制幂次曲线所占比例,决定着前缘线的过渡趋势,与升阻比基本呈现正比关系,从图 11的优化外形可以看出,当该参数取值较大时,对称面附近压力较大的区域前缘线半径过渡平缓,可以保证较大的升力面积,两侧以幂次曲线急剧增加,保持较强的后掠特性,使阻力大幅减小. 其他3个参数,即幂次曲线起始点参数P2、幂次n和最大激波面半径Rmax对升阻比均呈非线性关系且对升阻比影响相对较弱.
4 结论本文基于一种锥体组合捕获翼的高压捕获翼气动概念构型,以捕获翼前缘线三维形状经参数化后作为设计变量,结合使用实验设计方法、计算流体力学和代理模型构建等主要手段,在比较了多项式和径向基函数两种代理模型基础上,采用遗传算法以升阻比最大化为目标做了优化设计和结果分析,并且基于最优值结果开展了相应的单参数灵敏度分析.
计算结果表明,通过优化设计,构型的升力增加了约8.1%,阻力减小了约12.2%,升阻比提高了约23.4%. 从优化外形与基准外形的比较可以看出,当参数选择合理时,捕获翼对称面附近前缘线过渡平缓,两侧采用大后掠形状,不仅可以有效提高升力,同时具有较好的减阻效果,使升阻比获得大幅提高. 此外,从最优值的单参数灵敏度分析可以发现,升阻比与各参数均呈非线性关系,且展向角度对升阻比影响最大,其次为幂次曲线的比例参数,其他3个参数对升阻比的影响相对较弱.
本文工作仅针对固定圆锥机体及飞行条件下的捕获翼外形优化分析,尚未考虑不同组合机体及飞行条件的影响.在下一步的工作中,可考虑引入更多的设计参数进行更加细致的优化.但从结果来看,优化设计可以较大幅度的提高捕获翼构型的升阻比,证实了该构型优化的有效性和必要性,同时,为捕获翼的设计和下一步的构型选择提供了一定的参考.
| [1] |
Kuchemann D.
The Aerodynamic Design of Aircraft[M]. Oxford: Pergamon Press, 1978 .
( 0) 0)
|
| [2] |
叶友达. 近空间高速飞行器气动特性研究与构型设计优化[J].
力学进展,2009, 39 (6) : 683-694.
( Ye Youda. Study on aerodynamic characteristic and design of optimization for high speed near space vehicles[J].
Advances in Mechanics,2009, 39 (6) : 683-694.
(in Chinese) ) ( 0) 0)
|
| [3] |
Sullivan RB, Winters B. X-34 program overview. AIAA Paper 1998-3516, 1998
( 0) 0)
|
| [4] |
Jazra T, Preller D, Smart MK. Design of an airbreathing second stage for a rocket-scramjet-rocket launch vehicle[J].
Journal of Spacecraft and Rockets,2013, 50 (2) : 411-422.
DOI: 10.2514/1.A32381. ( 0) 0)
|
| [5] |
Walker S, Sherk J, Shell D, et al. The DARPA/AF Falcon Program: The Hypersonic Technology Vehicle #2 (HTV-2) flight demonstration phase. AIAA Paper 2008-2539, 2008
( 0) 0)
|
| [6] |
Walker S, Tang M, Mamplata C. TBCC propulsion for a mach 6 hypersonic airplane. AIAA Paper 2009-7238, 2009
( 0) 0)
|
| [7] |
Nonweiler TRF. Delta wings of shapes amenable to exact shockwave theory[J].
Journal of the Royal Aeronautical Society,1963, 67 : 39-40.
DOI: 10.1017/S0368393100090027. ( 0) 0)
|
| [8] |
崔凯, 杨国伟. 基于CFD 分析的弧形翼导弹气动外形优化[J].
中国科学:物理学力学天文学,2009, 39 (6) : 865-873.
( Cui Kai, Yang Guowei. Shape optimization for hypersonic arc-wing missiles based on CFD[J].
Sci Sin-Phys Mech Astron,2009, 39 (6) : 865-873.
(in Chinese) ) ( 0) 0)
|
| [9] |
胡守超, 崔凯, 李广利, 等. 基于DOE 方法的高超声速飞机前缘型线优化分析[J].
力学学报,2015, 48 (2) : 290-299.
( Hu Shouchao, Cui Kai, Li Guangli, et al. Optimization and analysis of the leading edge shape for hypersonic airplanes based on DOE methods[J].
Chinese Jounal of Theoretical and Applied Mechanics,2015, 48 (2) : 290-299.
(in Chinese) ) ( 0) 0)
|
| [10] |
Mangin B, Benay R, Chanetz B, et al. Optimization of viscous waveriders derived from axisymmetric power-law blunt body flows[J].
Journal of Spacecraft and Rockets,2006, 43 (5) : 990-998.
DOI: 10.2514/1.20079. ( 0) 0)
|
| [11] |
Lobbia M, Suzuki K. Multidisciplinary design optimization of hypersonic transport configurations using waveriders. AIAA Paper 2014-2359, 2014
( 0) 0)
|
| [12] |
Graves R. Continuum-limit design and optimization of an osculating-cones waverider at Mach 20. AIAA Paper 2013-1096, 2013
( 0) 0)
|
| [13] |
Lobbia M. Optimization of waverider-derived crew reentry vehicles using a rapid aerodynamics analysis approach. AIAA Paper 2015-0757, 2015
( 0) 0)
|
| [14] |
Knittel J, Lewis M. Multidisciplinary optimization of starbody waverider shapes for lifting aerocapture with orbital plane change. AIAA-2012-5809, 2012
( 0) 0)
|
| [15] |
张锋涛, 崔凯, 杨国伟, 等. 基于神经网络技术的乘波体优化设计[J].
力学学报,2009, 41 (3) : 418-424.
( Zhang Fengtao, Cui Kai, Yang Guowei, et al. Optimization design of waverider based on the artificial neural networks[J].
Chinese Jounal of Theoretical and Applied Mechanics,2009, 41 (3) : 418-424.
(in Chinese) ) ( 0) 0)
|
| [16] |
Cui K, YangGW. The effect of conical flowfields on the performance of waveriders at Mach 6[J].
Chinese Science Bulletin,2007, 52 (1) : 51-64.
( 0) 0)
|
| [17] |
朱旭程, 侯志强, 李日华. 基于样条曲线的乘波体外形优化方法[J].
空气动力学学报,2007, 25 (3) : 396-399.
( Zhu Xucheng, Hou Zhiqiang, Li Rihua. Spline-based waverider configuration optimization method[J].
Acta Aerodynamica Sinica,2007, 25 (3) : 396-399.
(in Chinese) ) ( 0) 0)
|
| [18] |
刘济民, 侯志强, 宋贵宝, 等. 高超声速巡航导弹乘波体构型优化设计与性能分析[J].
空气动力学学报,2011, 29 (1) : 118-123.
( Liu Jimin, Hou Zhiqiang, Song Guibao, et al. Optimization design and aerodynamic characteristic analysis of waverider based hypersonic cruise missile configuration[J].
Acta Aerodynamica Sinica,2011, 29 (1) : 118-123.
(in Chinese) ) ( 0) 0)
|
| [19] |
Bowcutt KG, Anderson JD, Capriotti D. Viscous optimized hypersonic waveriders. AIAA Paper 1987-0272, 1987
( 0) 0)
|
| [20] |
Corda S, Anderson JD. Viscous optimized hypersonic waveriders designed from axisymmertirc flow fields. AIAA-88-0396, 1988
( 0) 0)
|
| [21] |
Lobbia M, Suzuki K. Experimental investigation of a Mach 3.5 waverider designed using computational fluid dynamics[J].
AIAA Journal,2014, 53 (6) : 1590-1601.
( 0) 0)
|
| [22] |
高太元, 崔凯, 胡守超, 等. 高超声速飞行器上壁面多目标优化及性能分析[J].
力学学报,2013, 45 (2) : 193-201.
( Gao Taiyuan, Cui Kai, Hu Shouchao, et al. Multi-objective optimization and aerodynamic performance analysis of the upper surface for hypersonic vehicles[J].
Chinese Journal of Theoretical and Applied Mechanics,2013, 45 (2) : 193-201.
(in Chinese) ) ( 0) 0)
|
| [23] |
崔凯, 胡守超, 李广利等. 尖/钝化前缘乘波体压缩面优化分析. CSTAM 2012-B03-0305
( Cui Kai, Hu Shouchao, Li Guangli, et al. Optimization and analysis of waverider compression surface with sharp or blunted leading edges. CSTAM 2012-B03-0305 (in Chinese)
) ( 0) 0)
|
| [24] |
崔凯, 李广利, 胡守超, 等. 高速飞行器高压捕获翼气动布局概念研究[J].
中国科学: 物理学力学天文学,2013, 43 (5) : 652-661.
DOI: 10.1360/132013-60. ( Cui Kai, Li Guangli, Hu Shouchao, et al. Conceptual studies of the high pressure zone capture wing configuration for high speed air vehicles[J].
Sci Sin-Phys Mech Astron,2013, 43 (5) : 652-661.
(in Chinese) DOI: 10.1360/132013-60. ) ( 0) 0)
|
| [25] |
Cui K, Li GL, Xiao Y. Aerodynamic performance study of high pressure capturing wing configuration. AIAA Paper 2015-3388, 2015
( 0) 0)
|
| [26] |
李广利, 崔凯, 肖尧, 等. 高压捕获翼位置设计方法研究[J].
力学学报,2016, 48 (3) : 576-584.
( Li Guangli, Cui Kai, Xiao Yao, et al. The design method research for the position of high pressure capturing wing[J].
Chinese Journal of Theoretical and Applied Mechanics,2016, 48 (3) : 576-584.
(in Chinese) ) ( 0) 0)
|
| [27] |
方开泰, 刘民千, 周永道.
试验设计与建模[M]. 北京: 高等教育出版社, 2011 .
( Fang Kaitai, Liu Minqian, Zhou Yongdao.
Design and Modeling of Experiments[M]. Beijing: Higher Education Press, 2011 .
(in Chinese) ) ( 0) 0)
|
| [28] |
Yang G, Chen D, Cui K. Response surface technique for static aeroelastic optimization on a high-aspect-ratio wing[J].
Journal of Aircraft,2009, 46 (4) : 1444-1450.
DOI: 10.2514/1.42370. ( 0) 0)
|
| [29] |
张来平, 马戎, 常兴华, 等. 虚拟飞行中气动、运动和控制耦合的数值模拟技术[J].
力学进展,2014, 44 : 201410.
( 0) 0)
|
| [30] |
邓磊, 乔志德, 杨旭东, 等. 基于响应面法的低速翼型气动优化设计[J].
空气动力学学报,2010, 28 (4) : 430-435.
( Deng Lei, Qiao Zhide, Yang Xudong, et al. Aerodynamic optimization design of low-speed airfoil based on response surface methodology[J].
Acta Aerodynamica Sinica,2010, 28 (4) : 430-435.
(in Chinese) ) ( 0) 0)
|
| [31] |
熊伟, 张艳玲, 洪蓓, 等. 基于RBF 神经网络的轴对称飞行器弹道设计研究[J].
导弹与航天运载技术,2014 (4) : 9-13.
( 0) 0)
|
 2016, Vol. 48
2016, Vol. 48