流动聚焦(flowfocusing)是一种毛细流动现象,在这种结构的芯片中,连续相流体从离散相两侧的通道中流出,对离散相产生夹流"聚焦"的效果,形成稳定的微滴[1-3].与传统制备方法相比,流动聚焦技术稳定、易操作、适用范围广泛、没有苛刻的环境条件,可以一步到位制备出分布均匀、形态相同的微液滴、微气泡、微颗粒和微胶囊等微粒子[4-8].近年来,学者们基于流动聚焦技术展开了一系列相关研究[9-19],结果表明该技术可以利用互不相溶的液相在微型装置中连续、可控地生产具有高度单分散尺寸的单乳液滴和多重乳液液滴,并且可以对乳液液滴的结构(如乳液内部包含液滴的组分、数目、尺寸、比例以及外部液层的组分、厚度等)进行精确调控,在制备微颗粒功能材料方面展现出了其他技术无法比拟的优越性.
Martín-Banderas等[20-21]利用微流控技术制备荧光粒子时,通过改变荧光素的成分、类型和大小得到了不同粒径、大小均匀的球形微粒以满足不同需求.Holgado等[22]比较了流动聚焦与传统溶剂蒸发方法在合成麻醉剂微颗粒方面的应用,发现流动聚焦制备的微粒有更窄的粒径分布,更高的药物装载量和更慢的药物失效速率.Gañán-Calvo等[23]通过流动聚焦技术成功用一定配比的水、甘油、表面活性剂制备出直径在50∼80 μm之间的稳定均匀气泡. Karnik等[24]利用水动力流动聚焦(hydrodynamic flowfocusing)合成了粒径分布在10∼50 nm范围的共聚物纳米粒子------聚乳酸-co-乙醇酸-b-聚乙二醇(PLGA-b-PEG),并成功将其应用于药物包裹及控释. Zhang等[25]利用类似的流动聚焦结构,合成出直径在100∼200 nm范围的固态脂质纳米粒子(solid lipid nanoparticles,SLNs).
尽管基于流动聚焦技术制备微粒子较传统制备方法而言存在显著优势,但目前大部分学者更多关注于对微粒子合成方法及手段的研究,而对如何进一步优化通道结构、提高合成微液滴/气泡等的均一度和可靠性的研究还相对较少.但是流动聚焦合成微液滴的粒径和效率往往又与其通道结构和尺寸密切相关,有鉴于此,本文将研究通道深度、缩颈段长度、两相夹角等几何构型因素对流动聚焦生成微液滴直径及其生成周期各阶段的影响.尽管在工程实际中通过改变通道结构和尺寸来调节液滴大小及其生产效率并不经济,但能为进一步优化流道设计,提高合成微粒子的均一度和稳定性,以及后续研发和产品转化提供指导.
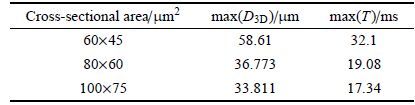
1 1 几何模型图 1为假定两相夹角 θ =90°的情形下,流动聚焦型微通道的三维几何结构及尺寸示意图, 微通道的水平段与垂直段横截面皆为矩形.为保证两相流在微通道内充分发展,参考文献[26-27]的相关结论,设定分散相和连续相入口段通道长度为5Wc (Wc为连续相入口段宽度),出口段主通道长度为16Wc.
|
图 1 流动聚焦型微通道三维几何结构及尺寸示意图(假定两相夹角 θ = 90°) Fig. 1 Scheme of three-dimensional geometry and size of flow focusing micro-channel (assuming in the case of θ = 90°) |
Tan等[28]发现在聚焦出口处设置开放式结构能够使喷嘴处的压力快速得到释放,让连续相产生的剪切力在一定程度上得到增强,从而更有利其对于分散相的挤压和断裂,使整个通道内部的压力状况更稳定,生成的液滴更为均一.另外,基于本课题组前期关于出口扩角改变对微液滴生成质量影响的模拟结果发现出口扩角取为135°时,液滴的稳定性和均一度均较好,所以设置几何模型的出口扩角为135°. 本文以硅油为连续相(ρ°=935 kg⋅m^{-3},µ°=10 mPa⋅s),去离子水为分散相(ρ w=998.2 kg⋅m-3,µ w=1.005 mPa⋅s),两相界面张力σ =15.21 mN/m.分散相速度范围为0.001∼0.015 m/s,连续相速度范围为0.01∼0.025 m/s.
2 数值分析方法及可行性验证考虑到二维模型中界面曲率和界面张力只存在于平面,无法真实反映实际情况下液滴的生成机理[14],因此本文采用计算流体力学软件Fluent对流动聚焦型微通道中液滴的生成过程进行三维数值模拟.在微尺度条件下,液液两相流速较低,因此可将液液两相均视作不可压缩黏性流.计算模型选用VOF标准模型,其中连续方程和动量方程为
| ${{\partial \rho } \over {\partial t}} + \nabla \cdot \left( {\rho v} \right) = 0$ | (1) |
| ${{\partial \rho v} \over {\partial t}} + \nabla \left( {\rho vv} \right) = - \nabla p + \nabla \left[ {\mu \left( {\nabla v + \nabla {v^\tau }} \right) + \rho g + F} \right]$ | (2) |
式中,ρ 为流体密度,v为流体速度矢量,t为时间,µ 为动力学黏度,∇p为单位体积流体所受压强梯度,∇ ⋅ [µ +( {∇ v + ∇ vτ)为单位体积流体受的黏性力,ρg为单位体积流体受与质量有关的力,F为与表面张力相关的动量源项,只存在于包含界面的控制单元内.
两相界面运动的捕捉可通过计算一个网格单元中连续相和分散相体积分数φ c和φd的分布来表征,其中 φ c=1且φd=0 代表连续相,φd=1且φ c=0代表分散相. 故一个计算单元中两相交界面依赖于 φ c和φ d在0∼1间的取值大小.两相混合单元中,式(1)和式(2)有关两相混合密度和黏度的计算可由式(3)和式(4)得到
| $\rho = {\varphi _d}{\rho _d} + \left( {1 + {\varphi _d}} \right){\rho _c}$ | (3) |
| $\mu = {\varphi _d}{\rho _d} + \left( {1 - {\varphi _d}} \right){\mu _c}$ | (4) |
另外,体积分数 φ d可以通过求解体积分数的连续方程得到
| ${{\partial {\varphi _{\rm{d}}}} \over {\partial t}} + v\nabla {\varphi _{\rm{d}}} = 0$ | (5) |
设置边界条件为壁面无滑移,微通道内部液体为不可压缩定常流动,采用速度入口和压力出口.参考文献[29-32]关于两相流动数值模拟的相关结论,引入接触角模型来表征壁面润湿性的影响.为使分散相不浸润通道壁并保证液滴顺利生成,模型在固壁面上使用预先定义的非润湿壁面边界条件,接触角设为140°,以符合实际实验中PDMS基微通道壁面的疏水特性.
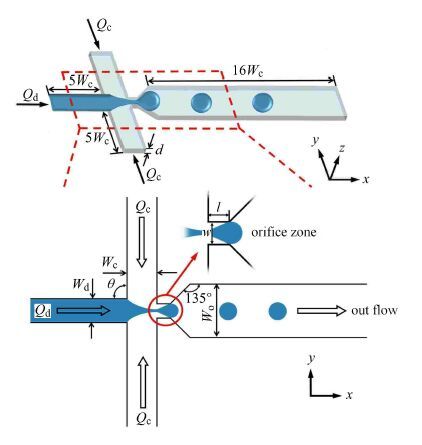
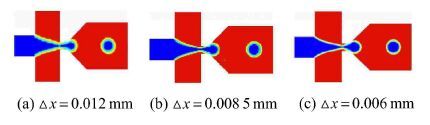
由于计算结果(特别是界面形状和界面曲率)的准确性直接取决于网格大小,为寻找最适网格尺寸,取 w=l= 80 μm,d =60 μm,θ =90°情形下的三维几何模型,采用六面体结构化网格 (网格划分如图 2),分别设置了3种网格尺寸(Δ x=0.012 mm,Δ x=0.008 5 mm,Δ x=0.006 mm)进行网格独立性验证. 图 3为不同网格下算得的液滴脱离瞬间的两相云图,发现微液滴的形成和运输的过程差异不大.故在后续研究中控制最小网格单元尺寸Δ x=0.008 5 mm, 既保证了计算结果的准确性,又显著降低了网格量,提升了计算效率.

|
图 2 数值分析过程的三维网格划分情况 Fig. 2 Three-dimensional grid division of simulation analysis |
|
图 3 数值分析过程的网格独立性验证(Δ x表示最小网格单元尺寸,两相流速比Vwater/Voil=1:3,V water=0.005 m/s Fig. 3 The independence test of simulation on grids (Δ x represents the smallest grid size, discrete/continuous phase flow rateratio vskip -1mm Vwater/Voil=1:3,V water=0.005 m/s |
Wu等[33]用硅油和去离子水为流质,研究了聚焦处的液丝尺寸(thread sizes)随流量比q (q=Qoil/Qwater) 的变化关系,并用高速相机拍摄了典型流量比下液滴的破裂过程.为了对数值分析的可行性和准确性进行验证,本文选取相同的通道结构,利用Fluent软件模拟不同流量比下液滴的破裂过程(图 4).

|
图 4 液滴破裂过程的数值模拟与试验结果[33]对比 Fig. 4 Comparison of numerical and experimental droplets[33] rupture process under different flow |
对比可知,数值模拟得到的液滴破裂过程与文献[33]的实验结果吻合较好,证明使用此数值模拟方法对流动聚焦型微通道内的两相流动形态进行表征是准确且可行的.
3 3 结果分析及讨论
为确保数值模拟结果的可信度,选取缩颈段宽度分别为w=60 μ m,w=80 μ m和w=100 μm三组独立的结构进行数值模拟,考虑通道深度d、缩颈段长度l、连续相与离散相夹角θ的变化对流动聚焦生成微液滴的影响.在进行试验数据处理时,首先在微通道中心对称平面(即z=d/2的中截面)的两相云图中,选取5∼6个大小均一的连续液滴,然后利用图像分析软件ImageJ分别测定各个液滴的外径Di(第i个液滴的测量直径,i=1, 2,3,…),最后取其平均值定义为液滴外径的测量值
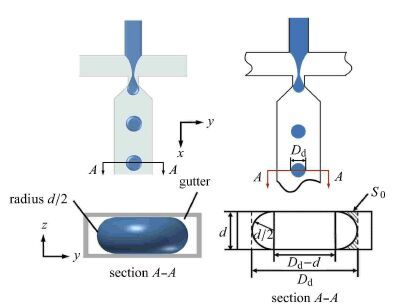
当液滴直径小于通道深度时,液滴不受外力作用,为了保持能量最低状态,液滴通常成球型.液滴直径大于通道深度时,液滴受到微通道上下壁面的挤压力作用,成圆盘型(图 5),且在液滴与壁面之间会形成一层较薄的液膜(液膜厚度远小于通道深度d,故在盘型液滴的体积求解中可近似认为液滴的界面与壁面相接触).由于球型液滴与盘型液滴不具有可比性,因此本文利用等体积原理,将盘型液滴转化为与之等价的球形液滴,并定义一个新变量------等价直径D3D,作为后续液滴大小的评价指标. 对于球型液滴而言,D 3D=Dd;对于盘型液滴,先利用式(6)和式(7)[26-27]计算盘型液滴的近似体积Vd
|
图 5 三维盘型液滴及其对应二维结构在x-y截面和y-z截面分布情况的示意图 Fig. 5 Schematic view of a 3D dish droplet and its 2D shape of droplet at x-yand y-z cross-section structure distribution |
| ${V_{\rm{d}}} = \pi D_{\rm{d}}^2d/4 - {S_0}\pi {D_{\rm{d}}}$ | (6) |
| ${S_0} = {d^2}(1/2 - \pi /8)$ | (7) |
再利用式(8)
| ${D_{{\rm{3D}}}} = {(6{V_{\rm{d}}}/\pi )^{1/3}}$ | (8) |
求得盘型液滴的等价直径D 3D. 式中Dd为液滴外径测量值(μm),d为通道深度(μm),S0为阴影部分面积.
随着液液两相工质物性、流动参数以及微流控装置几何结构和尺寸的变化,流动聚焦型微通道中液液两相流型主要表现为挤压式(squeezing)、滴流式(dripping)、射流式(jetting)以及各种不生成微液滴的类环状流(如节状形变流、管状流和滑移流)[32]. 只有挤压式、滴流式和单分散射流式能够产生具有较高均一度和单分散度的微液滴[34],而在合成液滴大小和稳定性方面以滴流式最优(合成的微液滴不但尺寸较小、粒径分布范围较宽且该流型占据整个流型图的绝大部分,易于实现).因此,经过大量调试后本文固定离散相流速Vwater=0.005 m/s,两相流速比Vwater/Voil=1:3,保证液滴生成过程为滴流式以获得大小均一、空间分布均匀的连续液滴串.在滴流式里分散相流体形成一个液滴后可能会发生周期性回缩现象,也有可能不回缩,而是在孔口上游形成一个稳定的锥形,这与两相流体的相对压力密切相关[34],而本文中液滴的形成过程主要表现为回缩式滴流.在回缩式滴流中根据液滴在生成过程中的不同状态,可分为4个阶段:迟滞阶段、填充阶段、缩颈阶段和脱离阶段,如图 6所示.其中:

|
图 6 流动聚焦型微通道中液滴生成过程的数值模拟(两相流速比V water/Voil=1:3, Vwater=0.005 m/s Fig. 6 Horizontal cross-section view of simulation results on the detailed droplet breakup process in flow-focusing micro-channel \(Discrete phase and continuous phase flow rate ratio V water/Voil=1:3, Vwater=0.005 m/s |
(1) 迟滞阶段:上一液滴脱离后的一瞬间,分散相界面出现回缩现象(图 6(b));
(2) 填充阶段:分散相界面逐渐运动填充主通道的过程(图 6(c));
(3) 颈缩阶段:连续相持续挤压离散相的同时由于毛细力造成液滴发生颈缩(图 6(d));
(4) 脱离阶段:颈缩结束后液滴脱离,开始进入下一液滴的迟滞阶段(图 6(e)).
为确保计算结果的准确性,在形成大小均一的连续液滴后,将某液滴脱离瞬间定义为计时起点t0 =0. 从t0开始到下一微液滴脱离瞬间定义为一个完整的液滴生成周期T.在该生成周期中,从t0到各阶段(迟滞、填充、缩颈、脱离阶段)结束时刻所对应的时间t,分别称为各阶段结束所耗时间t迟, t填, t缩和t脱. 在之前的研究中,学者们[35-38]仅就液滴生成周期这一单一变量进行分析,却很少关注于液滴生成过程中各阶段所发生的变化.而事实上这些变化是导致液滴直径及生成周期变化的主要因素,同时各阶段的耗时长短又侧面反映了在液滴生成过程中连续相黏滞力、挤压力与离散相冲力和界面张力的大小及其动态平衡关系.故本论文将研究焦点定于各自变量对液滴直径及生成周期各阶段的影响上.通过数据曲线拟合发现,填充、缩颈和脱离阶段结束所耗时间随微通道几何构型的变化遵循类似规律(t填, t缩和t脱随各自变量变化的规律基本相同). 因此,为了简化分析; 本文仅拟合了迟滞时刻t迟和脱离时刻t脱随各自变量变化的曲线来表征聚焦处几何参数对液滴生成周期各阶段的影响规律.
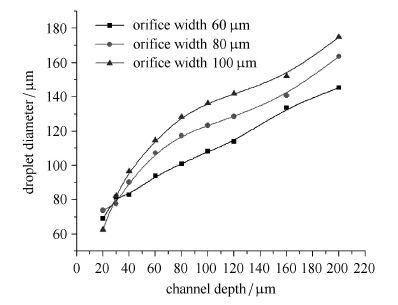
3.1 通道深度对流动聚焦生成微液滴的影响固定w=l,θ=90º,图 7和图 8分别为不同缩颈段宽度下,液滴直径D3D和生成周期中t迟和t脱随通道深度d变化的关系曲线.
液滴直径D3D及其生成周期中t迟 和 t脱受缩颈段宽度w和通道深度d的共同影响. 由图 7可知,当缩颈段宽度一定时,D3D随d的增加近似呈线性增大;另外,当通道深度一定时(在d ≥30 µm的情形下),随着缩颈段宽度的增加,两相流体交汇处的压力减小,导致颈缩半径增加,液滴尺寸增大.由图 8(a)可知,缩颈段宽度一定时,t迟随着通道深度d的增加呈指数曲线趋势递减,侧面反映出随着d的增加连续相黏滞力、挤压力的递增幅度大于离散相冲力和界面张力的递增幅度.由图 8(b)可知,当30 µm < d ≤ 80 µm时,t脱随d的增加而增大,但w=60 µm的曲线变化特征不很明显,这可能是由于缩颈段宽度降至一定程度时,Rayleigh毛细不稳定性显著增强,扰动增加,导致液滴离散相流柱提前断裂,形成单分散液滴. 当d > 80 μm时,t脱随d的增加先小幅递减后逐渐趋于稳定,此时通道深度不再是影响微液滴生成周期长短的关键因素.
|
图 7 微液滴直径D3D随通道深度d的变化规律 Fig. 7 Curves of droplet diameter versus channel depth |

|
图 8 微液滴生成周期T随通道深度d的变化规律 Fig. 8 Curves of droplet cycle versus channel depth |
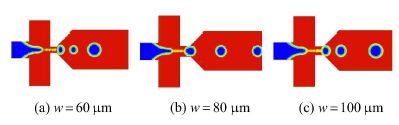
图 9为d=20µm时,不同缩颈段宽度下液滴脱离瞬间的两相云图. 结合图 8(b)和图 9可知,当0 < d ≤30µ m时,t脱随d的减小骤然陡升. 这是由于通道深度降至一定程度时,毛细作用显著增强, 液滴生成过程的不稳定性增加,出现若干碎裂小液滴聚合为稳定大液滴的情形,导致t脱呈骤升趋势.
|
图 9 d =20µm时不同缩颈段宽度下液滴脱离时刻两相云图 Fig. 9 Droplet breaking up under different orifice width at channel depth d =20µm |
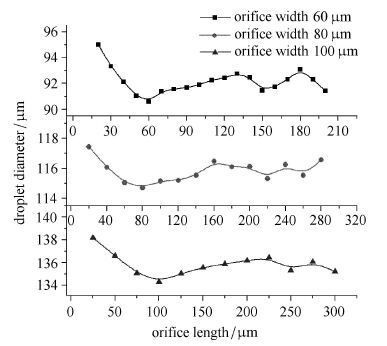
在分析通道深度d对流动聚焦生成微液滴影响的基础上,根据单变量原则,固定d=0.75 w,研究缩颈段长度l对液滴直径D3D和生成周期各阶段的影响规律(图 10和图 11).计算表明,缩颈段长度l对液滴直径D3D和生成周期各阶段的影响远小于通道深度d和缩颈段宽度w对其影响,且其变化幅度
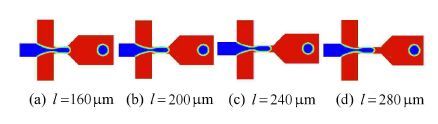
定义长宽比γ =l/w,由图 10和图 11可知,当0 < γ ≤ 1时,D3D随l的增加而显著减小.液滴生成过程中t迟随l的增加而增大,而t脱随着l的增加呈指数曲线趋势递减,这与毛细现象未充分发展时,管长增加Rayleigh毛细不稳定性增强是相吻合的;当1 < γ ≤2时,D3D随着l的增加而略微增大.t迟随l的增加呈先减小后增大的变化趋势,而t脱基本保持恒定,不再随l而变化;当γ> 2时,随着l的增加,D3D和t迟均维持在一个平均值中间呈"小幅波动"趋势变化,其中D3D的最大波幅约为1 μm,t迟的最大波幅约为0.125 ms.此时,缩颈段长度不再是影响微液滴直径和生成周期各阶段的主要因素.由不同缩颈段长度下液滴脱离瞬间的两相云图(图 12)可知,在其他条件固定时,离散相流柱在两相作用力下达到动态平衡时,断裂液柱的体积是接近恒定的.
|
图 10 微液滴直径D3D随缩颈段长度l的变化规律 Fig. 10 Curves of droplet diameter versus orifice length |

|
图 11 微液滴生成周期随缩颈段长度l的变化规律 Fig. 11 Curves of droplet cycle versus orifice length |
|
图 12 不同缩颈段长度下微液滴脱离瞬间的两相云图(w=80 μm,d =0.75 w,θ =90°时对应的物理模型) Fig. 12 Droplet breaking up under different orifice length (physical model when w=80 μm,d =0.75 w,θ =90°) |
由此看出,相对于缩颈段宽度w和通道深度h对液滴直径D3D及其生成周期各阶段的影响而言,缩颈段长度l的影响较小. 因此,若采用改变缩颈段长度的方法来调节液滴大小及其生成频率是非常不经济的,但可以为流道设计带来参考价值.
3.3 两相夹角对流动聚焦生成微液滴的影响为简化研究对象,在保证微液滴生成质量的前提下,固定l=w, d=0.75 w,进一步研究连续相与离散相夹角 θ变化对D3D,t迟和t脱的影响规律.
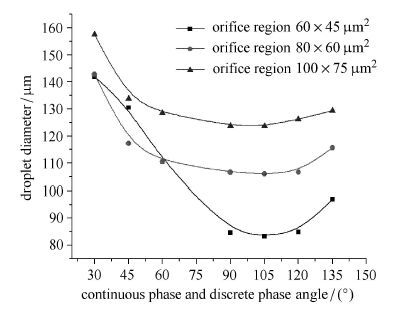
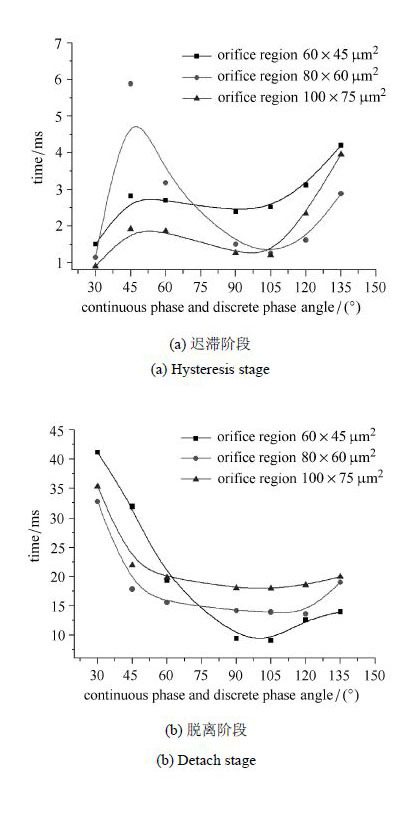
图 13和图 14 (b)分别为液滴直径D3D和脱离时刻t脱随两相夹角 θ变化的关系曲线.由图 13和图 14 (b)可知:当 θ 满足30° ≤ θ ≤ 105° 时,定义平均变化率为δ,经式(9)计算得 θ 每变化15°所对应的D3D和t脱的平均递减率δ分别为6.76∼11.72 μm/(°)和3.47∼6.42 ms/(°). 当> θ满足105° < \theta ≤ 135°时,D3D和t脱随 θ的增加呈小幅递增,其增幅分别为该区域平均值的4.5%∼15.4%和10.8%∼41.4%.
| $\delta = 15 \cdot \Delta y/\Delta x$ | (9) |
|
图 13 微液滴直径随两相夹角θ的变化规律 Fig. 13 Curves of droplet diameter versus angle between continuous and discrete phase |
|
图 14 微液滴生成周期随两相夹角θ 的变化规律 Fig. 14 Curves of droplet cycle versus angle between continuous and discrete phase |
式中Δx表示图 13和图 14(b)中横坐标的改变量,Δy为对应于Δx的纵坐标的改变量.
图 14(a) 为迟滞时间t迟随两相夹角 θ 变化的关系曲线. 由图 14(a)可知:当30° <θ ≤ 45>°时,t迟随 θ 的增加而增大;当45° < θ≤ 105°时,t迟随 θ 的增加而减小;当$105° < θ ≤ 135°时,t迟随 θ 的增加又呈现递增趋势.在整个过程中,t迟随 θ 变化的最大偏差在2∼3 ms之间.
表 1为不同缩颈段截面积下,液滴直径D3D和生成周期T随 θ 变化的最大偏差值. 由表 1可知,当两相夹角 θ 在30°∼135° 范围内变化时,缩颈段尺寸愈小,曲线的变化趋势越陡(即随 θ 改变,液滴直径D3D和生成周期T的差别愈大).
| 表 1 D3D和T随 θ 变化的最大偏差值 Table 1 The deviation maximum ofD3D and T versus θ |
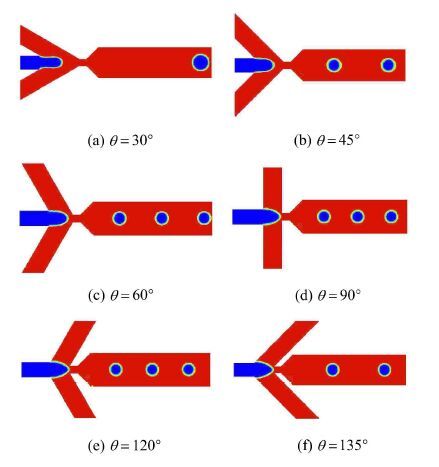
图 15为 w =80 μm时,不同两相夹角 θ 下,液滴形成过程的两相云图.分析可知,合成微液滴的大小取决于离散相流柱的延伸长度和形状. 在两相夹角θ∈ [30°,90°时,随着 θ 的递增,连续相对离散相流柱的挤压力不断加大(θ =90° 时达到最大值),致使流柱很快发生颈缩,并在Rayleigh毛细不稳定作用下发生断裂形成液滴. 随着 θ 的增加,水相流柱的伸展长度不断缩短,流柱头部由"塞段状"逐渐变为"子弹状",其内包含的液相体积也不断减小,生成微液滴直径变小,t脱变短. 当θ∈ (90°,135°] 时,连续相流速在水平方向的分量与离散相流速相反,阻碍了离散相水柱的伸展,且 θ 越大,连续相流速在水平方向的分量越大,对离散相流柱的阻碍作用越强,流柱克服连续相的黏滞阻力和挤压力的时间越长,生成的液滴直径越大,t脱越长.
|
图 15 不同两相夹角 θ 下液滴形成过程的两相云图(w=l =80 μm ,d =0.75 w,θ =90°时对应的物理模型) Fig. 15 Droplet breaking up under different angle between two-phase(w=l =80 μm ,d =0.75 w,θ =90°) |
(1) 在流动聚焦型微通道中,液滴直径D3D随通道深度d的增加近似呈线性增大. 当通道深度小于30 μm时, 液滴的生成周期T在毛细力的强烈作用下呈骤升趋势,当 d∈ (30,80] μm时,液滴生成周期T随d的增加而增大, 此后将逐渐趋于恒定. 此外,缩颈段宽度增加,液滴直径也会显著增大,这些变化规律均为设计最优通道结构以合成规定大小的微液滴提供了重要参考.
(2) 缩颈段长度l对液滴生成过程的影响不大,在整个过程中由缩颈段长度改变造成的影响仅为其平均值的3%∼5%左右. 故通过改变缩颈段长度来调节微液滴尺寸及其合成效率的作用并不理想,但能为流道设计提供参考价值.
(3) 流动聚焦法合成微液滴的过程受两相夹角θ的影响较大. 保持液滴生成方式为回缩式滴流,当θ∈[30°, 135°]时,液滴直径D3D及其生成周期T随两相夹角 θ的增加呈先大幅递减后逐渐增加的变化趋势,且当θ =90°时液滴尺寸及其生成频率均达到最优.
| [1] |
Hao G, Duits MHG, Frieder M. Droplets formation and merging in two-phase flow microfluidics[J].
International Journal of Molecular Sciences,2011, 12 (4) : 2572-2597.
( 0) 0)
|
| [2] |
司廷, 尹协振. 流动聚焦研究进展及其应用[J].
科学通报,2011, 56 (8) : 537-546.
DOI: 10.1360/972010-1639. ( Si Ting, Yin Xiezhen. Progress and application of flow focusing[J].
Chinese Science Bulletin,2011, 56 (8) : 537-546.
(in Chinese) DOI: 10.1360/972010-1639. ) ( 0) 0)
|
| [3] |
Barrero A, Loscertales IG. Micro-and nanoparticles via capillary flows[J].
Annual Review of Fluid Mechanics,2006, 39 (1) : 89-106.
( 0) 0)
|
| [4] |
GaÑ AM. Generation of steady liquid microthreads and micronsized monodisperse sprays in gas streams[J].
Physical Review Letters,1998, 80 (2) : 285-288.
DOI: 10.1103/PhysRevLett.80.285. ( 0) 0)
|
| [5] |
Gañán AM. A novel pneumatic technique to generate steady capillary microjets[J].
Journal of Aerosol Science,1999, 30 (1) : 117-125.
DOI: 10.1016/S0021-8502(98)00029-9. ( 0) 0)
|
| [6] |
Gañán-Calvo M, Gordillo JM. Perfectly monodisperse microbubbling by capillary flow focusing[J].
Physical Review Letters,2001, 87 (27 Pt 1) : 455-475.
( 0) 0)
|
| [7] |
李战华, 吴健康, 胡国庆, 等.
微流控芯片中的流体流动[M]. 北京: 科学出版社, 2012 .
( Li Zhanhua, Wu Jiankang, Hu Guoqing, et al.
Fluid Flow in Microfluidic Chips[M]. Beijing: Science Press, 2012 .
(in Chinese) ) ( 0) 0)
|
| [8] |
陈晓东, 胡国庆. 微流控器件中的多相流动[J].
力学进展,2015, 45 : 201503.
( Chen Xiaodong, Hu Guoqing. Multiphase flow in microfluidic devices[J].
Advances in Mechanics,2015, 45 : 201503.
(in Chinese) ) ( 0) 0)
|
| [9] |
Yow HN. Formation of liquid core-polymer shell microcapsules[J].
Soft Matter,2006, 2 (2) : 940-949.
( 0) 0)
|
| [10] |
Esserkahn AP, Odom SA, Sottos NR, et al. Triggered release from polymer capsules[J].
Macromolecules,2011, 44 (14) : 5539-5553.
DOI: 10.1021/ma201014n. ( 0) 0)
|
| [11] |
Nakashima T, Shimizu M, Kukizaki M. Particle control of emulsion by membrane emulsification and its applications[J].
Advance Drug Delivery Review,2000, 45 (1) : 47-56.
DOI: 10.1016/S0169-409X(00)00099-5. ( 0) 0)
|
| [12] |
Atencia J, Beebe DJ. Controlled microfluidic interfaces[J].
Nature,2005, 437 (7059) : 648-655.
DOI: 10.1038/nature04163. ( 0) 0)
|
| [13] |
Joanicot M, Ajdari A. Droplet control for microfluidics[J].
Science,2005, 309 (5736) : 887-888.
DOI: 10.1126/science.1112615. ( 0) 0)
|
| [14] |
Sahoo HR, Kralj JG, Jensen KF. Multistep continuous-flow microchemical synthesis involving multiple reactions and separations[J].
Angewandte Chemie International Edition,2007, 46 : 5704-5708.
DOI: 10.1002/(ISSN)1521-3773. ( 0) 0)
|
| [15] |
Seemann R, Brinkmann M, Pfohl T, et al. Droplet based microfluidics[J].
Reports on Progress in Physics,2012, 75 (1) : 016601-016601.
DOI: 10.1088/0034-4885/75/1/016601. ( 0) 0)
|
| [16] |
Teh SY, Lin R, Hung LH, et al. Droplet microfluidics[J].
Lab on A Chip,2008, 8 (2) : 198-220.
DOI: 10.1039/b715524g. ( 0) 0)
|
| [17] |
Belder D. Microfluidics with droplets[J].
Angewandte Chemie International Edition,2005, 44 (23) : 3521-3522.
DOI: 10.1002/(ISSN)1521-3773. ( 0) 0)
|
| [18] |
Chu L, Utada A, Shah R, et al. Controllable monodisperse multiple emulsions[J].
Angewandte Chemie,2007, 119 : 9128-9132.
DOI: 10.1002/(ISSN)1521-3757. ( 0) 0)
|
| [19] |
林炳承, 秦建华. 微流控芯片分析化学实验室[J].
高等学校化学学报,2009, 30 (3) : 433-445.
( Lin Bingcheng, Qin Jianhua. Microfluidic analytical chemistry laboratory[J].
Chemical Journal of Chinese Universities,2009, 30 (3) : 433-445.
(in Chinese) ) ( 0) 0)
|
| [20] |
Martín-Banderas L, Flores-Mosquera M, Riesco-Chueca P, et al. Flow focusing: A versatile technology to produce size-controlled and specific-morphology microparticles[J].
Small,2005, 1 (7) : 688-692.
DOI: 10.1002/(ISSN)1613-6829. ( 0) 0)
|
| [21] |
Martín-Banderas L, Rodríguez-Gil A, Cebolla Á, et al. Towards high-throughput production of uniformly encoded microparticles[J].
Advance Materials,2006, 18 (5) : 559-564.
DOI: 10.1002/(ISSN)1521-4095. ( 0) 0)
|
| [22] |
Holgado MA, Arias JL, Cózar MJ, et al. Synthesis of lidocaineloaded PLGA microparticales by flow focusing: effects on drug loading and release properties[J].
International Journal of Pharmaceutics,2008, 358 (1-2) : 27-35.
DOI: 10.1016/j.ijpharm.2008.02.012. ( 0) 0)
|
| [23] |
Gañán-Calvo AM, Martín-Banderas L, González-Prieto R, et al. Straightforward production of encoded microbeads by flow focusing: Potential applications for biomolecule detection[J].
International Journal of Pharmaceutics,2006, 324 (1) : 19-26.
DOI: 10.1016/j.ijpharm.2006.05.032. ( 0) 0)
|
| [24] |
Karnik R, Gu F, Basto P, et al. Microfluidic platform for controlled synthesis of polymeric nanoparticles[J].
Nano Letters,2008, 8 .
( 0) 0)
|
| [25] |
Zhang S, Yun J, Shen S, et al. Formation of solid lipid nanoparticles in a microchannel system with a cross-shaped junction[J].
Chemical Engineering Science,2008, 63 (23) : 5600-5605.
DOI: 10.1016/j.ces.2008.08.005. ( 0) 0)
|
| [26] |
刘赵淼, 刘丽昆, 申峰. Y 型微通道中两相界面特性变化分析[J].
机械工程学报,2014, 50 (8) : 189-196.
DOI: 10.3901/JME.2014.08.189. ( Liu Zhaomiao, Liu Likun, Shen Feng. Numerical analysis on two-phase flow characteristics at convection microfluidic Y-junctions[J].
Journal of Mechanical Engineering,2014, 50 (8) : 189-196.
(in Chinese) DOI: 10.3901/JME.2014.08.189. ) ( 0) 0)
|
| [27] |
刘赵淼, 刘丽昆, 申峰. Y 型微通道两相流内部流动特性[J].
力学学报,2014, 46 (2) : 209-216.
( Liu Zhaomiao, Liu Likun, Shen Feng. Two-phase flow characteristics in Y-junction microchannel[J].
Chinese Journal of Theoretical and Applied Mechanics,2014, 46 (2) : 209-216.
(in Chinese) ) ( 0) 0)
|
| [28] |
Tan YC, Cristini V, Lee AP. Monodispersed microfluidic droplet generation by shear focusing microfluidic device[J].
Sensors & Actuator B Chemical,2006, 114 (1) : 350-356.
( 0) 0)
|
| [29] |
刘赵淼, 刘佳, 申峰. 不同重力下90° 弯管内气液两相流流型及流动特性研究[J].
力学学报,2015, 47 (2) : 223-230.
( Liu Zhaomiao, Liu Jia, Shen Feng. Simulation on flow patterns and characteristics of two-phase gas-liquid flow in a 90° bend under different gravity[J].
Chinese Journal of Theoretical and Applied Mechanics,2015, 47 (2) : 223-230.
(in Chinese) ) ( 0) 0)
|
| [30] |
Fu T, Wu Y, Ma Y, et al. Droplet formation and breakup dynamics in microfluidic flow-focusing devices: From dripping to jetting[J].
Chemical Engineering Science,2012, 84 (52) : 207-217.
( 0) 0)
|
| [31] |
董立春, 吴纪周, 任桂香, 等. T 型微流控通道中微液滴形成机制的CFD 模拟[J].
重庆大学学报,2011, 34 (1) : 134-139.
( Dong Lichun, Wu Jizhou, Ren Guixiang, et al. CFD simulation of droplet formulation in a microfluidic T-junction[J].
Journal of Chongqing University,2011, 34 (1) : 134-139.
(in Chinese) ) ( 0) 0)
|
| [32] |
王维萌, 马一萍, 陈斌. 十字交叉微通道内液滴生成过程的数值模拟[J].
化工学报,2015 (5) : 1633-1641.
( Wang Weimeng, Ma Yipping, Chen Bin. Numerical simulation of droplet generation in crossing micro-channel[J].
CIESC Journal,2015 (5) : 1633-1641.
(in Chinese) ) ( 0) 0)
|
| [33] |
Wu P, Luo ZF, Liu ZF, et al. Drag-induced breakup mechanism for droplet generation in dripping within flow focusing microfluidics[J].
Chinese Journal of Chemical Engineering,2014, 23 (1) : 7-14.
( 0) 0)
|
| [34] |
吴平. 液滴微流控的实验应用和理论研究. [博士论文]. 安徽: 中国科学技术大学,2014
( Wu Ping. Experiments and theories of droplet-based microfluidics. [PhD Thesis]. Anhui: University of Science and Technology of China, 2014 (in Chinese)
) ( 0) 0)
|
| [35] |
De Menech M, Garstecki P, Jousse F, et al. Transition from squeezing to dripping in a microfluidic T-shaped junction[J].
Journal of Fluid Mechanics,2008, 595 (3) : 141-161.
( 0) 0)
|
| [36] |
Glawdel T, Elbuken C, Ren CL. Droplet formation in microfluidic T-junction generators operating in the transitional regime[J].
Physical Review E Statistical Nonlinear & Soft Matter Physics,2012, 85 (1-2) : 377-402.
( 0) 0)
|
| [37] |
Glawdel T, Elbuken C, Ren CL. Droplet Formation in microfluidic T-junction generators operating in the transitional regime[J].
Modeling. Physical Review E,20112, 85 : 016323.
( 0) 0)
|
| [38] |
Chen X, Glawdel T, Cui N, et al. Model of droplet generation in flow focusing generators operating in the squeezing regime[J].
Microfluidics & Nanofluidics,2014, 18 (5-6) : 1341-1353.
( 0) 0)
|
 2016, Vol. 48
2016, Vol. 48