随着柴油机喷油压力的不断提高,喷油过程中的超空化现象已变得日益突出.超空化射流时,空化气泡会随燃油液体一起从喷孔喷出. 许多研究表明[1-6],超空化射流部分分裂液滴内存在的空化气泡的生长及溃灭会对射流分裂液滴的二次分裂及雾化产生重要影响.
气泡生长及溃灭研究一直以来就是气泡动力学的一个重要研究方向.Rayleigh[7]首次提出了描述无限液体域内气泡生长及溃灭的运动方程;Plesset等[8-9]通过考虑液体黏性及表面张力作用,完善了Rayleigh的气泡运动方程;Robinson和Judd[10]对无限液体域内单个气泡的生长过程进行了数值模拟研究;张凌新[11-12]对无限液体域内单个气泡的生长及溃灭过程进行了解析和数值模拟分析.
目前,针对单液滴内空化气泡生长及溃灭的研究还较少.由于受到实验技术水平的限制,对单液滴内空化气泡生长及溃灭的实验研究还很难进行;目前,对单液滴内空化气泡生长及溃灭研究采用的方法大都是解析方法[13-14].而在解析研究方法中,由于采用了过多的假设或简化处理(如假设空泡半径以指数形式变化,将研究对象简化为无黏不可压缩流体等),因此无法对空泡生长及溃灭过程的更多细节问题(如空泡生长的控制机理、空泡溃灭的相变过程等)进行研究.
鉴于目前实验研究条件和实验手段的限制及解析方法的不足,本文将基于VOF方法对柴油射流分裂液滴内空化气泡的生长及溃灭过程进行数值模拟研究,探讨液滴内空泡生长的控制机理,分析液滴内气泡溃灭过程及其特征参数的变化规律.
1 VOF方法及计算模型 1.1 VOF方法气液两相流动研究中的关键问题是确定相界面位置和各相分布.VOF方法是一种求解气液两相流动和自由表面流动的数值计算方法,由美国Los Alamos科学实验室开发.
VOF方法通过引入流体体积组分 α 函数及其控制方程来表示混合流体的物性参数并跟踪自由面的位置.VOF方法通过控制单元及与之相连控制单元的 α函数值,并依据某一种界面捕捉方法对相界面形状及尺寸进行确定. α 函数定义为
| $\alpha (x,t) = \left\{ {\matrix{ {1,} \hfill & {{\rm{liquidarea}}} \hfill & {} \hfill & {} \hfill \cr 0 \hfill & {lt;\alpha } \hfill & {lt;1,} \hfill & {{\rm{gas - liquidarea}}} \hfill \cr {0,} \hfill & {{\rm{gasarea}}} \hfill & {} \hfill & {} \hfill \cr } } \right.$ | (1) |
在使用VOF方法进行数值模拟时,需要给出物性方程;物性方程就是不同体积组分时流体物性的表达式. 对于两相流体,物性方程可以表示为
| $\rho = \alpha _1 \rho _1 + \alpha _2 \rho _2 $ | (2) |
| $\mu = \alpha _1 \mu _1 + \alpha _2 \mu _2 $ | (3) |
| $\alpha _1 + \alpha _2 = 1 $ | (4) |
式中,ρ和μ分别为混合流体的密度和黏性系数; α 为体积组分;下标1和2分别代表第一相和第二相.
在采用VOF方法时,需要解决气液相界面的捕捉问题和相界面随时间的推进问题.相界面捕捉方法主要有分段常数界面构造方法 (PCIC) 和分段线性界面构造方法(PLIC);本文将使用精度较高的PLIC方法中的Yongs相界面捕捉方法对气液相界面进行捕捉.相界面的时间推进方法主要有算子分裂算法和算子不分裂算法;本文将采用精度较高的算子不分裂算法进行相界面的时间推进.
1.2 控制方程假设研究对象由黏性不可压缩液滴、黏性不可压缩空气以及黏性可压缩空化气泡组成;气液两相温度相同;气液相界面处无相变发生,不存在传质、传热过程;忽略流体重力影响;则流体运动满足如下控制方程[12, 15]
| ${{{\rm{D}}{\rho _i}} \over {{\rm{D}}t}} + {\rho _i}\nabla \cdot {V_i} = 0$ | (5) |
| ${\rho _i}{{{\rm{D}}{V_i}} \over {{\rm{D}}t}} = - \nabla {p_i} + {\mu _i}{\nabla ^2}{V_i} + {1 \over 3}{\mu _i}\nabla \left( {\nabla \cdot {V_i}} \right) + \sigma kn$ | (6) |
| ${{\partial {\alpha _i}} \over {\partial t}} + \left( {{V_i} \cdot \nabla } \right){\alpha _i} = 0$ | (7) |
| $\dfrac{\partial p_3 }{\partial \rho _3 } = c $ | (8) |
式中,V为速度;p为压强; σ 为表面张力系数;
在控制方程式(6)中,等号右边最后一项考虑了液滴内外表面受到的表面张力的作用;采用连续表面张力模型(CSF模型[16])对作用在气液两相界面的力进行计算.
本文采用基于有限容积法的开源CFD软件工具包OpenFOAM[17]对控制方程进行数值求解.控制方程的时间项采用二阶精度的 Crank Nicholson格式离散;控制方程的梯度项(如 ∇ p项)采用二阶精度的Gausslinear格式离散;由于液体体积分数在相界面两侧存在阶跃,为了避免发散,体积分数输运控制方程式(7)中的对流项采用二阶精度的Gaussvan Leer差分格式离散;控制方程中其余的对流项均采用二阶精度的Gaussupwind差分格式离散;动量守恒方程式(6)中的Laplacian项采用二阶精度的Gauss linear corrected格式离散.
本文采用适合非定常流动计算的压力隐式分裂算法(PISO算法)进行计算.
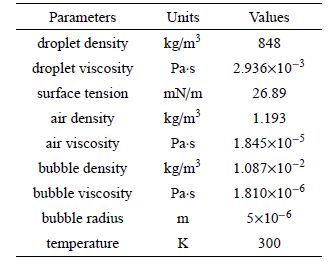
1.3 参数选取本文以柴油液滴作为研究对象. 在进行液滴内空化气泡生长过程研究时,采用的相关参数如表 1所示[18-24].
| 表 1 计算时采用的相关参数 Table 1 Parameters used in the calculation |
由于本文研究的问题属于轴对称问题,且分析的参数主要是空泡半径的变化,因此本文将研究对象简化为二维平面问题[25-29].在进行液滴内空泡生长及溃灭过程数值模拟时,将液滴周围空气、液滴及其内部气泡均纳入到计算域中.参考文献[12],将计算域取为0.2 mm × 0.2 mm正方形,气泡初始半径为5 μm.
初始计算域设置为:计算域中心至半径5 μm区域为气泡;半径5 μm至半径10 μ m区域为柴油液滴;液滴外边界至计算域边界区域为空气;如图 1linebreak 所示.
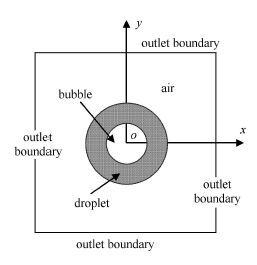
|
图 1 计算域示意图 Fig. 1 Schematic of computational domain |
出口边界设定为零压力梯度. 结合Fath等[30]的实验结果,确定数值计算的初始条件,如表 2所示.将液滴内部及周围空气初始压力设定为1×105 Pa,在进行液滴内空泡生长过程模拟时,将气泡初始压力设定为9×105 Pa;在进行液滴内气泡溃灭过程模拟时,将气泡初始压力设定为1×103 Pa.
| 表 2 初始条件设置 Table 2 The set-up of initial conditions |
在进行数值计算之前,还需要对时间步长进行设置. 本文将时间步长设置为自动调节时间步长,时间步长的初始值设置为2×10-8 s.
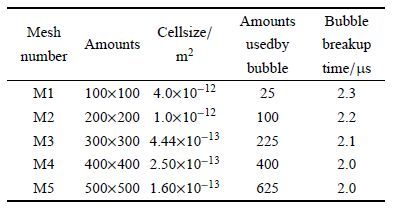
1.5 网格独立性分析及模型验证本文采用结构化网格;利用Gambit软件对计算域进行网格划分. 为了验证网格独立性,本文设置了5种不同的计算网格,并对不同网格的计算结果进行了对比;网格划分及结果对比如表 3所示.
| 表 3 不同网格的结果对比 Table 3 Comparison of different meshes |
从表 3中可以看到,随着网格数的增加,网格单元尺寸减小,气泡占据的网格数增多,各相及相界面的划分将会越精确. 从气泡破碎时刻来看,当网格数加密至编号M4时,气泡破碎时刻的计算结果基本不再变化;为此,选用编号为M4的网格作为最终计算网格,其网格数为400×400,网格单元尺寸为2.50×10- 13 m2.
为了对上述数值方法进行验证,对单个空泡在无限液体域中的溃灭过程进行了数值模拟.模拟计算时,采用文献[12]中的算例参数.将无限液体域中的模拟结果与文献[7]中的单气泡Rayleigh溃灭解析解及文献[12]中的数值模拟结果进行对比,如图 2所示;图中,气泡体积及溃灭时间分别用初始气泡体积和Rayleigh溃灭时间[12]无量纲化.
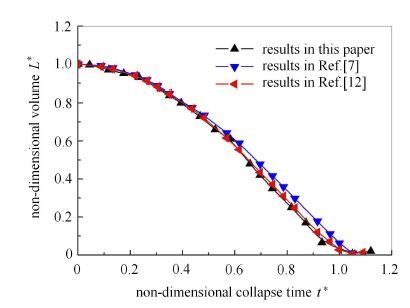
|
图 2 无限液体域中气泡溃灭与文献 [7, 12]数据比较 Fig. 2 Comparison of the simulation results of bubble collapse with the data in Refs.[7, 12] |
从图 2可以看到,无限液体域中空化气泡溃灭的模拟结果与文献[12]给出的模拟结果非常吻合.由于单气泡Rayleigh溃灭解析解中忽略了气泡周围液体黏性力和表面张力的影响,因此数值模拟结果与解析解之间存在一定偏差.
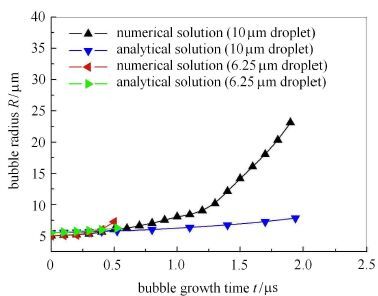
图 3给出的是单液滴内空泡生长过程的数值模拟结果与文献[14]的解析结果的比较. 文献[14]给出的单液滴内空泡生长解析解是通过线性稳定性理论得到的,其假设空化气泡与液滴交界面处的扰动具有球对称性,且扰动振幅以指数形式增长.
从图 3可以看到,对于较小的液滴来说,空泡生长的数值模拟结果与解析解比较一致. 液滴较大时,空泡生长初期的数值模拟结果与解析解比较一致;一定时间后,两种方法得到的空泡半径则存在着较大的偏差,数值模拟结果明显大于解析解,但两种方法得到的空泡破碎时间基本一致. 解析解对初始扰动及扰动振幅的假设是造成空泡生长数值模拟结果与解析结果间偏差的主要原因.
|
图 3 空泡生长数值模拟结果与解析解[14]的比较 Fig. 3 Comparison of numerical simulation results of bubble growth with theoretical results[14] |
液滴内空化气泡的生长是导致液滴破碎的关键因素之一. 单液滴内空化气泡生长过程的数值模拟结果可以更好地揭示空泡生长的变化历程.
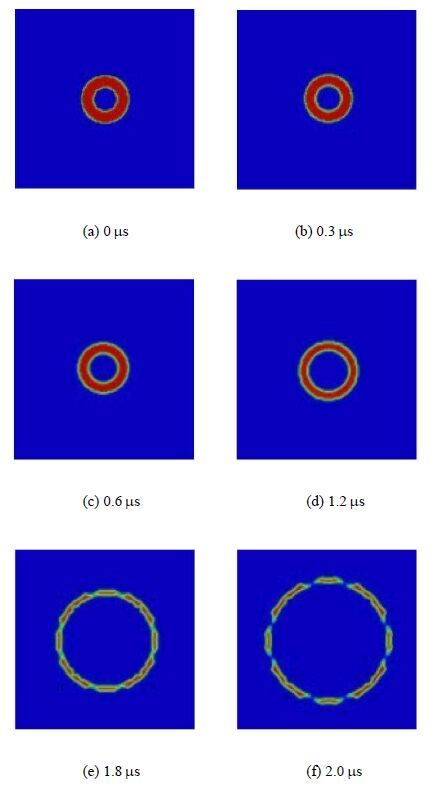
2.1 液滴内空泡生长过程为了直观的反映单液滴内空化气泡的生长过程,图 4给出了在空化气泡生长过程中不同时间时空泡及其周围液滴的相分布.
从图 4可以看到,在本文给出的计算参数下,液滴内的空化气泡在前0.3 μs内空泡半径的变化较小,在0.3 μs ∼ 1.2 μs间空泡半径的增加逐渐明显,在1.2 μs后空泡半径的增加更加显著;2.0 μs左右时空泡发生破碎.
|
图 4 不同时间时的相分布 Fig. 4 Phase distribution at different times |
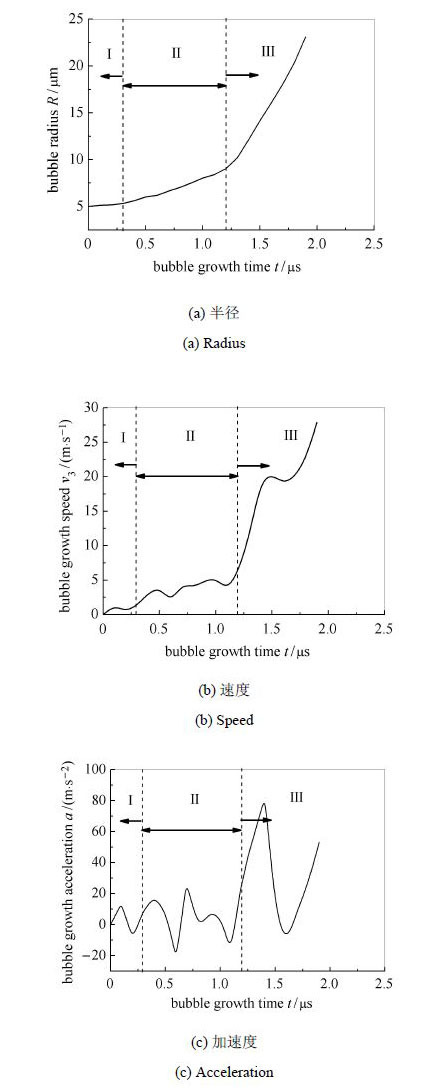
图 5给出的是在空化气泡生长过程中,单液滴内空泡半径、空泡生长速度及加速度随时间的变化.
|
图 5 液滴内空泡生长过程 Fig. 5 Growth process of cavitation bubble within the droplet |
根据图 5(a)给出的单液滴内空泡半径随时间的变化历程,可以将空泡半径随时间的变化划分为缓、中、急3个不同生长阶段.
从图 5(b)可以看到,在第I生长阶段,空泡生长速度较低,在2 m/s以内;在第Ⅱ生长阶段,空泡生长速度有所提高,处于3 ∼ 6 m/s之间;在第Ⅲ生长阶段,空泡生长速度迅速提高至20 m/s左右,维持一段时间后,生长速度再次提高直至空泡破碎.
空泡生长的加速度变化同样反映出了空泡生长缓、中、急3个不同生长阶段的特征. 从图 5(c)可以看到,在第I生长阶段,空泡生长加速度在15 m/s2以内;在第Ⅱ长阶段,空泡生长加速度有所提高,最高加速度在30 m/s2左右;在第Ⅲ生长阶段,空泡生长加速度最大可以达到80 m/s2左右.
因此,可将单液滴内空化气泡的生长划分为缓(I)、中(Ⅱ)、急(Ⅲ) 3个阶段. 在空化气泡生长的3个不同阶段中,必有其不同的生长控制机理.
2.2 液滴内空泡生长控制机理利用单液滴内空泡生长过程的数值模拟结果,结合Rayleigh-Plesset方程,对单液滴内空化气泡3个生长阶段的控制机理进行讨论与分析.
Rayleigh-Plesset方程可以表示为[9]
| ${p_3} - {p_\infty } = {{2\sigma } \over R} + {\rho _1}R{{{d^2}R} \over {d{t^2}}} + {3 \over 2}{\rho _1}{\left( {{{dR} \over {dt}}} \right)^2} + {{4{\mu _1}} \over R}{{dR} \over {dt}}$ | (9) |
式中,p3为空泡内的压力,p∞为环境压力,σ为表面张力系数,σ1为液体密度,μ1为液体黏度,R为空泡半径.
式(9)右边第1项体现的是表面张力对空泡生长的作用,第2项和第3项体现的是惯性力对空泡生长的作用,第4项体现的是黏性力对空泡生长的作用. 式(9)说明,决定空化气泡生长的空泡内外的压差主要受到3种力的作用:表面张力、惯性力及黏性力;正是这3种力的作用影响了单液滴内空化气泡的生长过程.
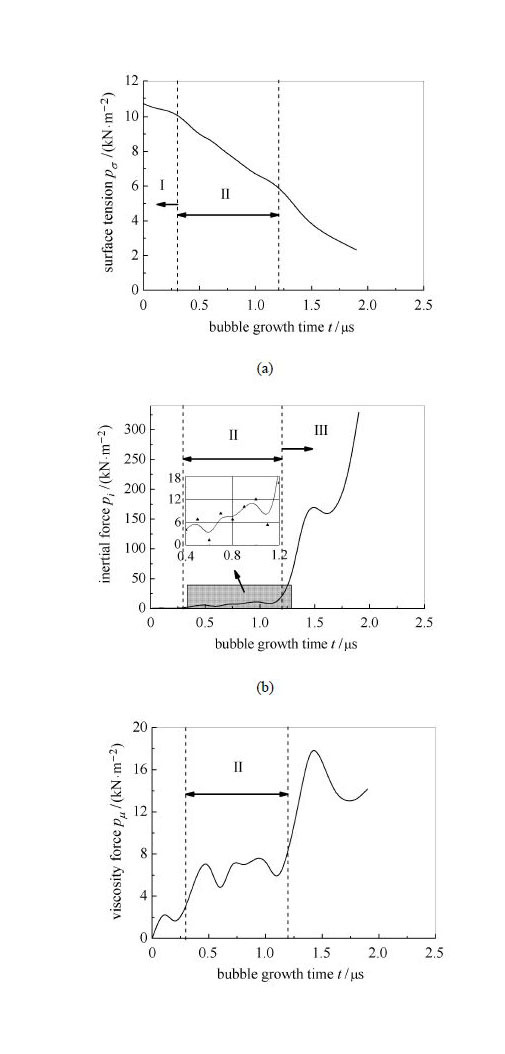
图 6给出的是在单液滴内空化气泡生长过程中,空泡所受的表面张力、惯性力以及黏性力随时间的变化关系.
|
图 6 空泡受力随时间的变化 Fig. 6 Forces acting on cavitation bubble versus time |
需要注意的是,在进行图 6中的空泡受力计算时,为了便于对比力的大小从而确定空泡生长的控制机理,均采用了空泡受力的绝对值来计算.从图 6中可以看到,在空泡生长的第I阶段,作用在气液界面上的表面张力基本在10 kN/m2以上,且以较小幅度下降;作用在气液界面上的惯性力近似为0,黏性力在3 kN/m2以下.因此,空泡生长的第I阶段主要受表面张力的控制作用,空泡的生长速率主要取决于表面张力的减小速率;惯性力对空泡生长的促进作用以及黏性力对空泡生长的抑制作用基本可以忽略.
在空泡生长第Ⅱ阶段,作用在气液界面上的表面张力逐渐从10 kN/m2左右下降至6 kN/m2左右;作用在气液界面上的惯性力在1 ∼ 16 kN/m2之间波动;作用在气液界面上的黏性力在3 ∼ 8 kN/m2之间变化. 因此,空泡生长的第Ⅱ阶段受到表面张力、惯性力及黏性力三者的综合控制作用,空泡的生长速率是促进空泡生长的惯性力和抑制空泡生长的表面张力及黏性力三者相互竞争、共同作用的结果.
在空泡生长的第Ⅲ阶段,作用在气液界面上的表面张力减小到6 kN/m2以下,黏性力不超过19 kN/m2,而惯性力则高居56 ∼ 330 kN/m2之间. 因此,空泡生长的第Ⅲ阶段主要受惯性力的控制作用,空泡的生长速率由于惯性力的迅速增加而急剧增大;而抑制空泡生长的表面张力及黏性力的作用则基本可以忽略.
3 3 空泡溃灭过程及其特征参数的变化超空化射流时,除了分裂液滴内一部分空化气泡会因泡内压力大于环境压力而迅速生长并破碎外,另一部分空化气泡则有可能因泡内压力小于环境压力而发生溃灭. 空化气泡的溃灭同样会对射流的雾化产生重要影响.
3.1 液滴内空泡溃灭过程为了直观地反映单液滴内空泡的溃灭过程,图 7给出了空泡溃灭过程中不同时刻空泡及其周围液滴的相分布.
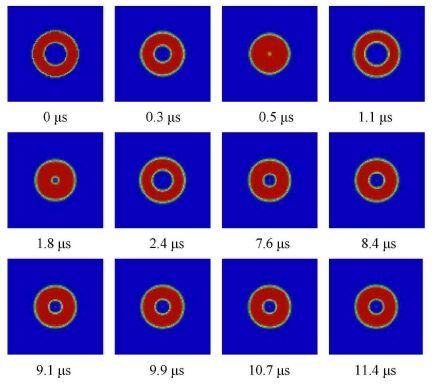
|
图 7 液滴内空泡的溃灭过程 Fig. 7 Collapse process of bubble within a droplet |
从图 7中可以看到,在给定的计算参数下,在0 μs ∼ 0.5 μs期间,液滴内的空泡半径迅速减小(0.5 μs时半径达到最小),同时空泡周围液滴的半径亦迅速减小;在0.5 μs ∼1.1 μs期间,液滴内空泡开始反弹,直至1.1 μs时半径达到最大,此时空泡半径与初始时刻空泡半径近似相等;从1.1 μs到2.4 μs,液滴内空泡半径再次经历了先减小(1.8 μs时半径达到最小)后增大(2.4 μs时半径达到最大)的过程,但1.8 μs时的空泡半径略大于0.5 μs时的空泡半径,2.4 μs时的空泡半径略小于0 μs及1.1 μs时的空泡;从2.4 μs到11.4 μs,液滴内的空泡半径不断重复先减小后增大的过程,且在此过程中,每次空泡半径达到最小值所用时间与空泡半径达到最大值所用时间基本一致;11.4 μs后,空泡半径基本不再变化,液滴内的空泡达到"稳定"状态.
计算结果表明,液滴内空泡的溃灭过程由多个溃灭阶段和反弹阶段所构成. 如果将空泡体积由最大值溃灭到最小值(溃灭阶段)再反弹到最大值(反弹阶段)的时间称为一个溃灭周期,则液滴内空泡溃灭的过程由多个溃灭周期所组成.
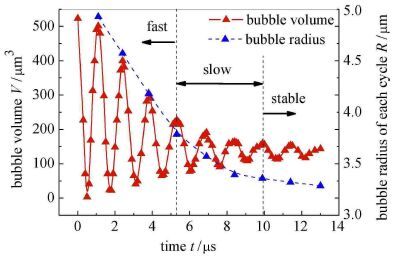
图 8给出的是在与图 7相同的计算条件下,液滴内空泡体积及每个溃灭周期结束时空泡半径随时间的变化历程.
|
图 8 空泡体积及每个溃灭周期结束时空泡半径随时间变化 Fig. 8 Variation of bubble volume and radius with time |
从图 8中可以看到,在空泡溃灭过程中,空泡体积随时间呈近似周期性变化,空泡体积的幅值随时间不断减小;在溃灭过程后期,空泡体积的变化逐渐趋于稳定. 液滴内的空泡溃灭过程类似于有阻尼弹簧振子的振动过程. 在空泡溃灭过程中,随着时间的增加,空泡体积最大值逐渐减小,空泡体积最小值逐渐增大,空泡反弹时体积最大值的减小程度远大于空泡溃灭时体积最小值的增大程度.
从图 8中可以发现,通过每个溃灭周期结束时空泡半径随时间的变化历程,可以将空泡的溃灭过程分为3个阶段,即快速溃灭期、缓慢溃灭期以及稳定期. 在快速溃灭期中,每个溃灭周期结束时的空泡半径与上一个溃灭周期相比显著下降,空泡体积随时间的变化亦非常剧烈,空泡体积反弹到最大值时与上一个溃灭周期相比明显减小. 在缓慢溃灭期中,每个溃灭周期结束时的空泡半径与上一个溃灭周期相比变化则相对平缓;空泡体积的变化小于快速溃灭期,但仍比较明显,空泡体积反弹到最大值时与上一个溃灭周期相比减小的程度明显减缓. 在稳定期中,每个溃灭周期结束时空泡半径的变化明显减小;尽管此时空泡体积随时间仍有一定变化,但变化已非常平缓,且空泡体积反弹到最大值时与上一个溃灭周期相比变化已经很小.
3.2 空泡溃灭过程特征参数的变化规律在液滴内空泡的溃灭过程中,特征参数的变化是空泡溃灭特性的直接反映. 为了研究方便,下面首先对空泡溃灭过程的特征参数进行定义. 图 9给出的是空泡溃灭过程中特征参数定义的示意图.
从图 9中可以看到,在液滴内空泡溃灭过程中,空泡体积随时间的变化存在着许多波谷和波峰;将波谷处的空泡体积称为空泡溃灭体积,波谷处的空泡压力称为空泡溃灭压力;将波峰处的空泡体积称为空泡反弹体积,波峰处的空泡压力称为空泡反弹压力.
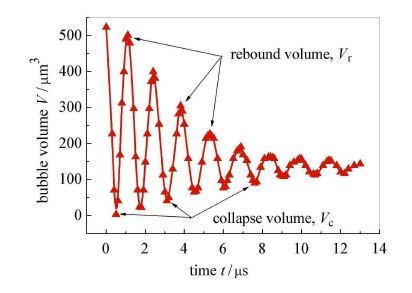
|
图 9 空泡溃灭过程特征参数定义示意图 Fig. 9 Schematic of characteristic parameters in bubble collapse |
空泡溃灭体积和空泡反弹体积的变化均可反映空泡溃灭过程的剧烈程度. 图 10和图 11分别给出的是在液滴内空泡溃灭过程中,空泡溃灭体积和空泡反弹体积随时间的变化.
从图 10和图 11中可以看到,空泡溃灭体积和空泡反弹体积随时间的变化亦反映出比较明显的空泡溃灭过程的3个阶段,即快速溃灭期、缓慢溃灭期和稳定期.在快速溃灭期,空泡溃灭体积和空泡反弹体积随时间的变化非常剧烈,空泡溃灭体积增大19.1倍,空泡反弹体积减小54.7%.在缓慢溃灭期,空泡溃灭体积和空泡反弹体积随时间的变化明显变缓,空泡溃灭体积增大0.6倍,空泡反弹体积减小30.3%,
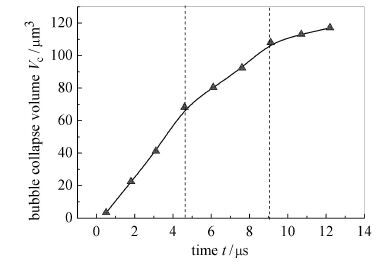
|
图 10 空泡溃灭体积随时间的变化 Fig. 10 Bubble collapse volume versus time |

|
图 11 空泡反弹体积随时间的变化 Fig. 11 Bubble rebound volume versus time |
空泡溃灭过程的剧烈程度明显降低.在稳定期,空泡溃灭体积和空泡反弹体积随时间的变化已经很小,空泡溃灭体积仅增大0.1倍,空泡反弹体积仅减小9.3%,空泡溃灭体积和反弹体积趋于稳定.
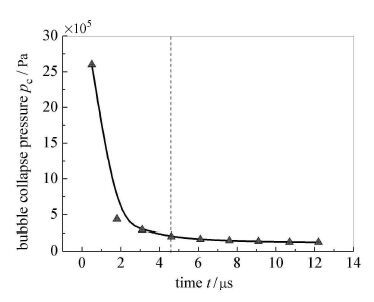
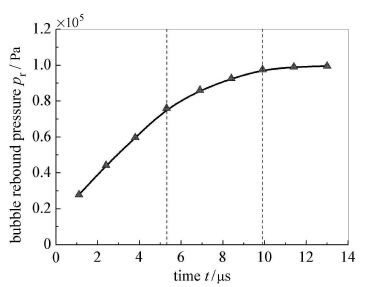
空泡溃灭体积和反弹体积随时间的变化,其根本原因在于空泡溃灭过程中空泡内压力的变化.图 12和图 13分别给出的是在液滴内空泡溃灭过程中,空泡溃灭压力和空泡反弹压力随时间的变化.
|
图 12 空泡溃灭压力随时间的变化 Fig. 12 Bubble collapse pressure versus time |
|
图 13 空泡反弹压力随时间的变化 Fig. 13 Bubble rebound pressure versus time |
空泡溃灭压力随时间的增加而降低.从图 12中可以发现,在空泡溃灭的初期,空泡溃灭压力的变化非常剧烈;随后,虽然空泡溃灭压力随时间仍呈下降趋势,但下降幅度已非常有限.对比图 12和图 10可以看到,尽管溃灭初期空泡溃灭压力的变化非常剧烈,但空泡溃灭体积的变化则要相对平缓得多.
空泡反弹压力随时间的变化与空泡反弹体积随时间的变化基本相对应.对比图 13和图 11可以看到,在溃灭初期,空泡反弹压力的变化相对较大,空泡反弹体积的变化也相对比较明显;随后,随着空泡反弹压力变化的逐渐减小,空泡反弹体积的变化也开始变缓.
4 结论(1) 基于VOF方法建立了描述单液滴内空化气泡生长及溃灭的计算模型. 验证结果表明,所建模型的数值模拟结果正确合理.
(2) 单液滴内空化气泡的生长过程可以按照控制机理划分为表面张力控制阶段、综合竞争阶段和惯性力控制阶段等三个不同阶段. 在第I生长阶段,空泡的生长主要受表面张力的控制作用,惯性力对空泡生长的促进作用及黏性力对空泡生长的抑制作用可以忽略;在第Ⅱ生长阶段,空泡的生长受表面张力、惯性力及黏性力三者的综合作用,空泡的生长速率是促进空泡生长的惯性力和抑制空泡生长的表面张力及黏性力相互竞争、共同作用的结果;在第Ⅲ生长阶段,空泡的生长主要受惯性力的控制作用,抑制空泡生长的表面张力及黏性力的作用基本可以忽略.
(3) 单液滴内空化气泡的溃灭过程由多个溃灭阶段和反弹阶段构成,类似于有阻尼弹簧振子的振动过程. 根据每个溃灭周期结束时空泡半径随时间的变化历程,可以将空泡的溃灭分为快速溃灭期、缓慢溃灭期以及稳定期. 溃灭初期空泡溃灭压力的变化非常剧烈,但空泡溃灭体积的变化则要相对平缓得多;空泡反弹压力随时间的变化与空泡反弹体积随时间的变化基本对应.
| [1] |
Safari SD. Effects of cavitation on high-pressure atomization. [PhD Thesis]. Irvine: University of California at Irvine, 2009
( 0) 0)
|
| [2] |
Sou A, Tomiyama A, Hosokawa S, et al. Cavitation in a twodimensional nozzle and liquid jet atomization[J].
JSME International Journal,2006, 49 (4) : 1253-1259.
DOI: 10.1299/jsmeb.49.1253. ( 0) 0)
|
| [3] |
Sou A, Hosokawa S, Tomiyama A. Effects of cavitation in a nozzle on liquid jet atomization[J].
International Journal of Heat and Mass Transfer,2007, 50 (17-18) : 3575-3582.
DOI: 10.1016/j.ijheatmasstransfer.2006.12.033. ( 0) 0)
|
| [4] |
Payri R, Salvador FJ, Gimeno J, et al. Study of cavitation phenomena based on a technique for visualizing bubbles in a liquid pressurized chamber[J].
International Journal of Heat and Fluid Flow,2009, 30 : 768-777.
DOI: 10.1016/j.ijheatfluidflow.2009.03.011. ( 0) 0)
|
| [5] |
Desantes JM, Payri R, Salvador FJ, et al. Influence of cavitation phenomenon on primary break-up and spray behavior at stationary conditions[J].
Fuel,2010, 89 : 3033-3041.
DOI: 10.1016/j.fuel.2010.06.004. ( 0) 0)
|
| [6] |
Suh HK, Lee CS. Effect of cavitation in nozzle orifice on the diesel fuel atomization characteristics[J].
International Journal of Heat and Fluid Flow,2008, 29 : 1001-1009.
DOI: 10.1016/j.ijheatfluidflow.2008.03.014. ( 0) 0)
|
| [7] |
Rayleigh L. On the pressure developed in a liquid during the collapse of a spherical cavity[J].
Philosophical Magazine,1917, 34 : 94-98.
DOI: 10.1080/14786440808635681. ( 0) 0)
|
| [8] |
Plesset MS, Calif P. The dynamics of cavitation bubbles[J].
ASME Journal of Applied Mechanics,1949, 16 : 228-231.
( 0) 0)
|
| [9] |
Plesset MS, Prosperetti A. Bubble dynamics and cavitation[J].
Annual Review of Fluid Mechanics,1977, 9 : 145-185.
DOI: 10.1146/annurev.fl.09.010177.001045. ( 0) 0)
|
| [10] |
Robinson AJ, Judd RL. The dynamics of spherical bubble growth[J].
International Journal of Heat and Mass Transfer,2004, 47 : 5101-5113.
DOI: 10.1016/j.ijheatmasstransfer.2004.05.023. ( 0) 0)
|
| [11] |
张凌新, 尹琴, 邵雪明. 水中气泡溃灭的理论与数值研究[J].
水动力学研究与进展,2012, 27 (1) : 68-73.
( Zhang Lingxin, Yin Qin, Shao Xueming. Theoretical and numerical studies on the bubble collapse in water[J].
Chinese Journal of Hydrodynamics,2012, 27 (1) : 68-73.
(in Chinese) ) ( 0) 0)
|
| [12] |
张凌新, 闻仲卿, 邵雪明. 多泡相互作用对气泡溃灭的影响[J].
力学学报,2013, 45 (6) : 861-867.
( Zhang Lingxin, Wen Zhongqing, Shao Xueming. Investigation of bubble-bubble interaction effect during the collapse of multi-bubble system[J].
Chinese Journal of Theoretical and Applied Mechanics,2013, 45 (6) : 861-867.
(in Chinese) ) ( 0) 0)
|
| [13] |
Zeng Y. Modeling of multicomponent fuel vaporization in internal combustion engines. [PhD Thesis]. Illinois: University of Illinois at Urbana-Champaign, 2000
https://www.ideals.illinois.edu/handle/2142/84012 ( 0) 0)
|
| [14] |
Lü Ming, Ning Zhi, Yan Kai, et al. The breakup of cavitation bubbles within the diesel droplet[J].
Chinese Journal of Mechanical Engineering,2014, 27 (1) : 198-204.
DOI: 10.3901/CJME.2014.01.198. ( 0) 0)
|
| [15] |
刘红, 解茂昭, 刘宏升, 等. 单液滴在多孔介质内碰壁过程的数值模拟[J].
燃烧科学与技术,2011, 17 (4) : 287-294.
( Liu Hong, Xie Maozhao, Liu Hongsheng, et al. Modeling of single droplet impingement onto cell wall inside porous medium[J].
Journal of Combustion Science and Technology,2011, 17 (4) : 287-294.
(in Chinese) ) ( 0) 0)
|
| [16] |
Brackbill JU, Kothe DB, Zemach C. A continuum method for modeling surface tension[J].
Journal of Computational Physics,1992, 100 : 335-354.
DOI: 10.1016/0021-9991(92)90240-Y. ( 0) 0)
|
| [17] |
OpenFOAM website. http://www.openfoam.org.
( 0) 0)
|
| [18] |
Mulemane A, Subramaniyam S, Lu PH, et al. Comparing cavitation in diesel injectors based on different modeling approaches. SAE Paper, 2004-01-0027, 2004
http://papers.sae.org/2004-01-0027/ ( 0) 0)
|
| [19] |
Jia M, Hou D, Li J, et al. A micro-variable circular orifice fuel injector for HCCI-conventional engine combustion– Part I numerical simulation of cavitation. SAE Paper, 2007-01-0249, 2007
http://papers.sae.org/2007-01-0249/ ( 0) 0)
|
| [20] |
Wang X, Su WH. A numerical study of cavitating flows in highpressure diesel injection nozzle holes using a two-fluid model[J].
Chinese Science Bulletin,2009, 54 (10) : 1655-1662.
( 0) 0)
|
| [21] |
Lalanne B, Tanguy S, Risso F. Effect of rising motion on the damped shape oscillations of drops and bubbles[J].
Physics of Fluids,2013, 25 (11) : 112107-1-112107-22.
DOI: 10.1063/1.4829366. ( 0) 0)
|
| [22] |
吕明, 宁智, 阎凯, 等. 同轴旋转可压缩流动中液体射流稳定性[J].
力学学报,2013, 45 (3) : 323-330.
( Lü Ming, Ning Zhi, Yan Kai, et al. Study on the stability of liquid jet in coaxial swirling compressible flow under supercavitation[J].
Chinese Journal of Theoretical and Applied Mechanics,2013, 45 (3) : 323-330.
(in Chinese) ) ( 0) 0)
|
| [23] |
Wang Q, Siegel M, Booty M R. Numerical simulation of drop and bubble dynamics with soluble surfactant[J].
Physics of Fluids,2014, 26 (5) : 052102-1-052102-27.
DOI: 10.1063/1.4872174. ( 0) 0)
|
| [24] |
Pelletier E, Béguin C, Étienne S. Experiments of air bubbles impacting a rigid wall in tap water[J].
Physics of Fluids,2015, 27 (12) : 123302-1-123302-16.
DOI: 10.1063/1.4936877. ( 0) 0)
|
| [25] |
Premlata AR, Tripathi MK, Sahu KC. Dynamics of rising bubble inside a viscosity-stratified medium[J].
Physics of Fluids,2015, 27 (7) : 072105-1-072105-15.
DOI: 10.1063/1.4927521. ( 0) 0)
|
| [26] |
宋云超, 宁智, 孙春华, 等. 液滴撞击湿润壁面的运动形态及飞溅运动机制[J].
力学学报,2013, 45 (6) : 833-842.
( Song Yunchao, Ning Zhi, Sun Chunhua, et al. Movement and splashing of a droplet impacting on a wet wall[J].
Chinese Journal of Theoretical and Applied Mechanics,2013, 45 (6) : 833-842.
(in Chinese) ) ( 0) 0)
|
| [27] |
孙鹏楠, 李云波, 明付仁. 自由上浮气泡运动特性的光滑粒子流体动力学模拟[J].
物理学报,2015, 64 (17) : 174701-1-174701-15.
( Sun Pengnan, Li Yunbo, Ming Furen. Numerical simulation on the motion characteristics of freely rising bubbles using smoothed particle hydrodynamics method[J].
Acta Physica Sinica,2015, 64 (17) : 174701-1-174701-15.
(in Chinese) ) ( 0) 0)
|
| [28] |
李隆键, 张磊, 朱文冰, 等. 基于VOSET 方法模拟并排气泡的上升过程[J].
计算物理,2015, 32 (5) : 545-552.
( Li Longjian, Zhang Lei, Zhu Wenbing, et al. Simulation of a pair of bubbles rising side by side using VOSET method[J].
Chinese Journal of Computational Physics,2015, 32 (5) : 545-552.
(in Chinese) ) ( 0) 0)
|
| [29] |
戴剑锋, 樊学萍, 蒙波, 等. 单液滴撞击倾斜液膜飞溅过程的耦合 Level Set-VOF 模拟[J].
物理学报,2015, 64 (9) : 094704-1-094704-6.
( Dai Jianfeng, Pan Xueping, Meng Bo, et al. A coupled level-set and volume-of-fluid simulation for splashing of single droplet impact on an inclined liquid film[J].
Acta Physica Sinica,2015, 64 (9) : 094704-1-094704-6.
(in Chinese) ) ( 0) 0)
|
| [30] |
Fath A, Fettes C, Leipertz A. Investigation of the diesel spray breakup close to the nozzle at different injection conditions.//Proceedings of the International Symposium on Diagnostics and Modeling of Combustion in Internal Combustion Engines, COMODIA, 1998: 429-434
( 0) 0)
|
 2016, Vol. 48
2016, Vol. 48