0 引言
随着航天器、机器人、现代兵器系统朝着复杂化、大型化、轻质化、高速化发展,部件的柔性效应越来越明显,传统的多刚体系统模型已无法正确描述该类系统的动力学性态.在此背景下各国学者针对多体系统的柔性效应展开研究,中心刚体-柔性梁系统大范围转动[1-11]、平动[12-13]、考虑附加质量[14]、考虑阻尼效应[15],中心刚体-变截面梁系统[16],柔性矩形薄板[17-18],柔性杆柔性铰全柔机器人[19-25]等动力学问题被广泛研究,并取得了相应的研究成果.然而上述柔性多体系统动力学研究中柔性体变形场离散方法主要采用的是假设模态法(assumed mode method,AMM)[2-5, 12-13, 15-16, 21-25]和有限元法(finite element method,FEM)[7-9, 11, 14].假设模态法源于结构动力学中梁的固有振型,其突出优点在于能通过较少模态来获得较好的逼近结果,计算效率较高.但当柔性体为非规则形状时,求解柔性体的振动振型本身就是难题,且假设模态法源于小变形假设,其在大变形问题中的适用性有待商榷. 有限元法是一种通用性很强的变形体离散法,但其前处理繁琐,需要花费大量时间划分网格、不易构造出高阶连续的形函数,通常只是位移连续而非应力应变连续.且系统的广义坐标为有限元节点坐标,由此得到的动力学方程广义坐标数目巨大,对于处理诸如由多个柔性杆件连接而成的空间柔性机器人的动力学实时计算时显得效率较低.因此,高效精确的变形场离散方法研究已经成为复杂柔性多体系统,尤其是柔性机器人动力学快速实时计算方面急需解决的难点问题.
文献[26-27]理论推导了Bezier插值方法(Bezier interpolation method,BIM)、B样条插值方法(B-spline interpolationmethod,BSIM)与绝对节点坐标方法下有限元法的关系,从而实现计算机辅助设计(computer aided design,CAD)中的几何造型与计算机辅助分析(computer aided analysis,CAA)中变形场描述的统一.文献[28-29]进一步研究了Bezier插值、B样条插值等计算几何方法和绝对节点坐标有限元法之间的转化,并给出仿真实例,研究表明将CAD中几何造型法和CAA中变形场描述相统一既能达到CAD和CAA之间的同几何分析,又可以提高CAA分析精度和效率.随后文献[30-32]将Bezier插值方法和B样条插值方法运用到柔性体变形场的描述中,并对旋转柔性悬臂梁和旋转柔性锥形梁的动力学问题进行研究.文献[33-34]将光滑节点插值法和径向基点插值法应用于柔性梁的变形场离散,并对大范围旋转柔性梁动力学问题进行研究,从而丰富了柔性梁变形场描述理论.
然而,上述诸如Bezier插值方法、B样条插值方法等计算几何法以及光滑节点插值法和径向基点插值法等无网格法,只是针对单个柔性梁做大范围运动的动力学问题的适用性进行了初步探索,尚未见其在复杂柔性机器人这类由多个柔性体构成的多体系统中的应用.本文将Bezier插值方法、B样条插值方法作为变形体新的离散方法,研究其在柔性机器人动力学中的建模方法和动力学分析中的性能,并与目前运用广泛的假设模态法和有限元法构造统一格式,方便柔性机器人动力学方程的推导及动力学仿真软件的编制.在本文提出的动力学模型中,构成机器人系统的柔性杆考虑其横向弯曲变形、纵向拉伸变形和扭转变形,同时计及横向弯曲变形引起的纵向缩短量,即非线性耦合项.对于连接机器人各杆件的关节铰,考虑其柔性效应以及质量效应,从而形成了柔性杆柔性铰空间构型和柔性杆三维空间变形的全柔复杂机器人动力学模型. 为了提高计算效率,论文采用了递推策略进行动力学建模.论文采用C++语言编制了基于假设模态法、有限元法、Bezier插值方法和B样条插值方法4种离散方法的空间多杆柔性机器人动力学仿真软件.论文给出了3个不同物理模型的柔性机器人动力学的仿真算例,以此来研究本文采用的4种变形场离散方法在柔性机器人变形场离散中的可行性和优缺点,并展示了所研制软件在处理复杂柔性机器人动力学方面的性能.
1 多杆柔性杆柔性铰机器人动力学方程
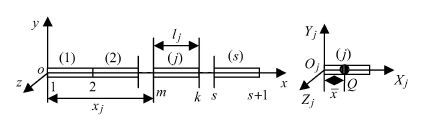
图 1所示为n个柔性杆件通过n个柔性铰连接而成的空间多杆链式柔性机器人.
运用4×4齐次变换矩阵和D-H坐标系法描述系统的运动和变形[22-24].其中柔性杆变形充分考虑了轴向拉伸变形、横向弯曲变形以及绕杆中心线的扭转变形,并计入柔性杆横向弯曲变形引起的纵向缩短,而与杆件连接的柔性关节简化成线性扭转弹簧,并考虑铰的质量效应. 通过Lagrange方程可得系统动力学方程为[25]
式中,J为系统的广义质量阵,R为系统的广义力阵,z为广义坐标列阵.
2 变形场的描述
与多刚体系统不同,柔性多体系统动力学模型是由非线性、时变和强耦合的偏微分方程描述,一般不易得到方程精确的解析解.因此,需采用离散方法对柔性体变形场进行描述,将偏微分方程转化为常微分方程处理,即把无限自由度的连续系统离散为有限自由度的系统,由此求解原系统的近似解.柔性杆的变形场描述主要是对柔性杆上任意点变形前后产生的变形位移进行分离变量处理,则第$i$根柔性杆上任意点的变形位移可表示为[25]
|
$\left. \matrix{
u_x^i = u_{x1}^i + u_{x2}^i = \sum\limits_{j = 1}^{{N_i}} {{\delta _{ij}}} {x_{ij}}\left( x \right) - {1 \over 2}\sum\limits_{k = 1}^{{N_i}} {\sum\limits_{l = 1}^{{N_i}} {{\delta _{ik}}{\delta _{il}}} } {H_{kl}}\left( x \right) \hfill \cr
u_y^i = \sum\limits_{j = 1}^{{N_i}} {{\delta _{ij}}} {y_{ij}}\left( x \right) \hfill \cr
u_z^i = \sum\limits_{j = 1}^{{N_i}} {{\delta _{ij}}} {z_{ij}}\left( x \right) \hfill \cr} \right\}$
|
(2) |
其中,$u_{x1}^i = \sum\limits_{j = 1}^{{N_i}} {{\delta _{ij}}} {x_{ij}}\left( x \right)$为杆轴向(s方向上)伸长量,uyi和uzi表示杆在y和z方向上的横向弯曲变形,$u_{x2}^i = -
\dfrac{1}{2}\sum_{k = 1}^{N_i } {\sum_{l = 1}^{N_i } {\delta _{ik} \delta _{il} } } H_{kl} \left( x
\right)$为杆横向弯曲变形引起的纵向缩短量,即非线性耦合项,其中Hkl (x)是采用非线性应变场所产生的耦合项
|
${{H}_{kl}}\left( x \right)=\int_{0}^{x}{\left( \frac{\partial {{y}_{ik}}\left( \xi \right)}{\partial \xi }\cdot \frac{\partial {{y}_{il}}\left( \xi \right)}{\partial \xi }+\frac{\partial {{z}_{ik}}\left( \xi \right)}{\partial \xi }\cdot \frac{\partial {{z}_{il}}\left( \xi \right)}{\partial \xi } \right)}d\xi $
|
(3) |
采用上述变形描述而建立的机器人动力学模型将是一次刚柔耦合层次的动力学模型[22-23, 25],能处理高速,并且柔性部件处于较大变形的柔性机器人动力学问题.
2.1 假设模态法
通过假设模态函数将第i根柔性杆上任意点的轴向s方向变形ux1i
、横向y方向变形uyi以及横向z方向变形uzi表示为
|
$\left. \begin{align}
& u_{x1}^{i}(x,t)={{x}_{i}}(x){{\delta }_{i}}{{(t)}^{\text{T}}} \\
& u_{y}^{i}(x,t)={{y}_{i}}(x){{\delta }_{i}}{{(t)}^{\text{T}}} \\
& u_{z}^{i}(x,t)={{z}_{i}}(x){{\delta }_{i}}{{(t)}^{\text{T}}} \\
\end{align} \right\}$
|
(4) |
其中,${ x}_i (x) \in R^{1\times N_i }$,${ y}_i (x) \in R^{1\times N_i }$和${ z}_i
(x) \in R^{1\times N_i
}$分别为杆的轴向振动、横向y方向和横向z方向振动的模态函数行向量,$\delta
_i (t) \in R^{1\times N_i }$是轴向、横向y方向和z方向的模态坐标. 分别为
|
$\left. \matrix{
{x_i}(x) = [{x_{ij}}] = [\phi _{i1}^{(1)}(x),\phi _{i2}^{(1)}(x), \cdots , \hfill \cr
\phi _{i{N_{ix}}}^{(1)}(x),0, \cdots ,0,0, \cdots ,0] \hfill \cr
{y_i}(x) = [{y_{ij}}] = [0, \cdots ,0,\phi _{i1}^{(2)}(x),\phi _{i2}^{(2)}(x), \cdots , \hfill \cr
\phi _{i{N_{iy}}}^{(2)}(x),0 \cdots ,0] \hfill \cr
{z_i}(x) = [{z_{ij}}] = [0, \cdots ,0,0 \cdots ,0,\phi _{i1}^{(2)}(x),\phi _{i2}^{(2)}(x), \cdots , \hfill \cr
\phi _{i{N_{iz}}}^{(2)}(x)]{\delta _i}(t) = [{\delta _{i1}}(t),{\delta _{i2}}(t), \cdots ,{\delta _{i{N_i}}}(t)] \hfill \cr} \right\}$
|
(5) |
若φi(1) (x) 和φi(2) (x)采用固定边界悬臂杆的模态函数,其元素分别为
|
$\left. \matrix{
\phi _{ij}^{(1)}(x) = \sin {{(2j - 1)\pi } \over {2{L_i}}}x,j = 1,2, \cdots ,{N_{ix}} \hfill \cr
\phi _{ij}^{(2)}(x) = \cos {\beta _j}x - \cosh {\beta _j}x + {\gamma _i}(\sin {\beta _j}x - \hfill \cr
\sinh {\beta _j}x),\quad j = 1,2, \cdots ,{N_{iy}}{\rm{or}}{N_{iz}} \hfill \cr} \right\}$
|
(6) |
其中
|
${\matrix{
{{\beta _1}{L_i} = 1.875} \hfill \cr
{{\beta _2}{L_i} = 4.694} \hfill \cr
{{\beta _j}{L_i} = (j - 0.5)\pi ,j{\rm{ }} \ge 3} \hfill \cr
} }$
|
(7) |
|
${{\gamma }_{j}}=-\frac{\cos {{\beta }_{j}}{{L}_{i}}+\cosh {{\beta }_{j}}{{L}_{i}}}{\sin {{\beta }_{j}}{{L}_{i}}+\sinh {{\beta }_{j}}{{L}_{i}}}$
|
(8) |
式中,Li为第i根杆的长度. 横向弯曲变形引起的纵向缩短量,即非线性耦合项为
|
$
u_{x2}^i = - \dfrac{1}{2}\sum_{k = 1}^{N_i } \sum_{l = 1}^{N_i } \delta _{ik} \delta _{il} H_{kl}
$
|
(9) |
其中
|
${{H}_{kl}}(x)=\int_{0}^{x}{\left( \frac{\partial {{y}_{ik}}}{\partial \xi }\cdot \frac{\partial {{y}_{il}}}{\partial \xi }+\frac{\partial {{z}_{ik}}}{\partial \xi }\cdot \frac{\partial {{z}_{il}}}{\partial \xi } \right)}\text{ }d\xi $
|
(10) |
将式(4)、式(9)和式(10)代入式(2)能得到假设模态法描述的第i根柔性杆上任意点的变形位移.
2.2 有限元法
有限元法离散:将杆分成s个单元,通过单元形函数将单元j(j = 1,2,…,s)内任意点Q的x,y,z方向变形ux1 ,uy ,uz 表示为单元节点变形的线性插值
|
$
u_{x1} = { N}_{j,1} (\bar {x}){ P}_j ,u_y = { N}_{j,2} (\bar {x}){ P}_j ,\
u_z ={ N}_{j,3} (\bar {x}){ P}_j $
|
(11) |
其中,x为Q关于单元坐标系$O_j - X_j Y_j Z_j $的纵坐标.设单元j的长度$l_j $,$\hat {x} = \bar {x} / l_j $,则形函数阵为
|
$\left. \begin{align}
& {{N}_{j,1}}(\bar{x})=\left[ \begin{matrix}
{{N}_{11}} & 0 & 0 & 0 & 0 & {{N}_{12}} & 0 & 0 & 0 & 0 \\
\end{matrix} \right] \\
& {{N}_{j,2}}(\bar{x})=\left[ \begin{matrix}
0 & {{N}_{12}} & {{N}_{13}} & 0 & 0 & 0 & {{N}_{22}} & {{N}_{32}} & 0 & 0 \\
\end{matrix} \right] \\
& {{N}_{j,3}}(\bar{x})=\left[ \begin{matrix}
0 & 0 & 0 & {{N}_{21}} & {{N}_{31}} & 0 & 0 & 0 & {{N}_{22}} & {{N}_{32}} \\
\end{matrix} \right] \\
\end{align} \right\}$
|
(12) |
其中
|
$\left. \matrix{
{N_{11}} = 1 - \hat x,{N_{12}} = \hat x \hfill \cr
{N_{21}} = 1 - 3{{\hat x}^2} + 2{{\hat x}^3},{N_{31}} = {l_j}(\hat x - 2{{\hat x}^2} + {{\hat x}^3}) \hfill \cr
{N_{22}} = 3{{\hat x}^2} - 2{{\hat x}^3},{N_{32}} = {l_j}( - {{\hat x}^2} + {{\hat x}^3}) \hfill \cr} \right\}$
|
(13) |
柔性杆的有限元离散模型见图 2.
单元节点的变形位移列阵为
|
$\left. \matrix{
{P_j} = {[P_{j,m}^{\rm{T}}P_{j,k}^{\rm{T}}]^{\rm{T}}} \hfill \cr
{P_{j,q}} = {[{w_{1q}}{w_{2q}}{\theta _{2q}}{w_{3q}}{\theta _{3q}}]^{\rm{T}}},q = m,k \hfill \cr} \right\}$
|
(14) |
其中w1m,w2m,w3m和w1k,w2k,w3k分别表示节点m和k的轴向以及横向变形位移,而$\theta
_{2m} $,$\theta _{2k} $,$\theta _{3m} $和$\theta _{3k} $为
|
$\left. \matrix{
{\theta _{2m}} = {{\partial {w_2}} \over {\partial \bar x}}(0),{\theta _{2k}} = {{\partial {w_2}} \over {\partial \bar x}}({l_j}) \hfill \cr
{\theta _{3m}} = {{\partial {w_3}} \over {\partial \bar x}}(0),{\theta _{3k}} = {{\partial {w_3}} \over {\partial \bar x}}({l_j}) \hfill \cr} \right\}$
|
(15) |
设Bj为由单位编号决定的定位矩阵, P为总体变形位移列阵,则有
|
$
{ P}_j = { B}_j { P} $
|
(16) |
其中
|
$\eqalign{
& P = [{w_{11}}{w_{21}}{\theta _{21}}{w_{31}}{\theta _{31}} \cdots \cr
& {w_{1s + 1}}{w_{2s + 1}}{\theta _{2s + 1}}{w_{3s + 1}}{\theta _{3s + 1}}{]^T} \cr
& \matrix{
{{\rm{No}}.} & 1 & 2 & \cdots & m & \cdots & k & \cdots & {s + 1} \cr
} \cr
& {B_j} = \left[ {\matrix{
0 & 0 & \cdots & {{I_{5 \times 5}}} & \cdots & 0 & \cdots & 0 \cr
0 & 0 & \cdots & 0 & \cdots & {{I_{5 \times 5}}} & \cdots & 0 \cr
} } \right] \cr} $
|
(17) |
根据杆的边界条件,P可表示为
其中,p为独立总体变形位移矩阵,R为转化矩阵.对于一端固支悬臂杆,杆悬臂端节点轴向变形和横向弯曲变形及转角均为零($w_{11} = 0,w_{21} = 0,\theta _{21} = 0,
w_{31} = 0,\theta _{31} = 0$),R和p分别为
|
$\left. \matrix{
R = {\left[ {\matrix{
{{{\bf{0}}_{5 \times 5s}}} \hfill \cr
{{I_{5s \times 5s}}} \hfill \cr
} } \right]_{5(s + 1) \times 5s}} \hfill \cr
p = {[{w_{12}}{w_{22}}{\theta _{22}}{w_{32}}{\theta _{32}} \cdots {w_{1s + 1}}{w_{2s + 1}}{\theta _{2s + 1}}{w_{3s + 1}}{\theta _{3s + 1}}]^{\rm{T}}} \hfill \cr} \right\}$
|
(19) |
于是
|
${u_{x1}} = {S_1}p,{u_y} = {S_2}p,{u_z} = {S_3}p$
|
(20) |
其中
|
${S_1} = {N_{j,1}}{B_j}R,{S_2} = {N_{j,2}}{B_j}R,{S_3} = {N_{j,3}}{B_j}R$
|
(21) |
令
|
$\left. \matrix{
{\delta _i}(t) = [{\delta _{i1}}{\delta _{i2}} \cdots {\delta _{i{N_i}}}] = {p_i} = [w_{12}^iw_{22}^i\theta _{22}^iw_{32}^i \hfill \cr
\theta _{32}^i \cdots w_{1s + 1}^iw_{2s + 1}^i\theta _{2s + 1}^iw_{3s + 1}^i\theta _{3s + 1}^i] \hfill \cr
{x_i}(x) = [{x_{ij}}] = {S_1} \hfill \cr
{y_i}(x) = [{y_{ij}}] = {S_2} \hfill \cr
{z_i}(x) = [{z_{ij}}] = {S_3} \hfill \cr} \right\}$
|
(22) |
i代表系统中的第i根杆,Ni 为有限元法对第i杆离散的广义坐标数,其为第i杆离散单元数的5倍.非线性耦合项为
|
$u_{x2}^i = - {1 \over 2}\sum\limits_{k = 1}^{{N_i}} {\sum\limits_{l = 1}^{{N_i}} {{\delta _{ik}}} } {\delta _{il}}\left[ {{H_{kl}}(x - \sum\limits_{r = 1}^{j - 1} {{l_r}} ) + \sum\limits_{m = 1}^{j - 1} {{H_{kl}}} ({l_m})} \right]$
|
(23) |
其中
|
${H_{kl}}(\eta ) = \int_0^\eta {\left( {{{\partial {y_{ik}}} \over {\partial \xi }} \cdot {{\partial {y_{il}}} \over {\partial \xi }} + {{\partial {z_{ik}}} \over {\partial \xi }} \cdot {{\partial {z_{il}}} \over {\partial \xi }}} \right)} d\xi $
|
(24) |
将式(22) ∼式(24)代入式(2)能得到有限元法描述的第i根柔性杆上任意点的变形位移.
2.3 Bezier插值方法
Bezier插值离散方法通过特征控制多边形顶点的变形与伯恩斯坦基函数的线性组合来描述柔性梁变形场[31-32]. 本文选取5次Bezier插值,则令第i根杆的广义坐标和广义形函数为
|
$\left. {\matrix{
\matrix{
{\delta _i}(t) = [{\delta _{ij}}] = [V_1^iV_2^iV_3^iV_4^iV_5^iV_6^iV_7^i \hfill \cr
V_8^iV_9^iV_{10}^iV_{11}^iV_{12}^i] \hfill \cr} \hfill \cr
\matrix{
{x_i}(x) = [{x_{ij}}] = [{J_{5,2}}({x \over {{L_i}}}){J_{5,3}}({x \over {{L_i}}}){J_{5,4}}({x \over {{L_i}}}){J_{5,5}}({x \over {{L_i}}}) \hfill \cr
00000000] \hfill \cr
{y_i}(x) = [{x_{ij}}] = [0000{J_{5,2}}({x \over {{L_i}}}){J_{5,3}}({x \over {{L_i}}}) \hfill \cr
{J_{5,4}}({x \over {{L_i}}}){J_{5,5}}({x \over {{L_i}}})0000] \hfill \cr} \hfill \cr
\matrix{
{z_i}(x) = [{x_{ij}}] = [00000000 \hfill \cr
{J_{5,2}}({x \over {{L_i}}}){J_{5,3}}({x \over {{L_i}}}){J_{5,4}}({x \over {{L_i}}}){J_{5,5}}({x \over {{L_i}}})] \hfill \cr} \hfill \cr
} } \right\}$
|
(25) |
其中Li为第i根杆的总长度,广义坐标量Ni为12,Vi是特征多边形顶点的变形,${J_{5,2}}({x \over {{L_i}}})$等是伯恩斯坦基函数,具体表达形式见文献 [31-32].横向弯曲变形引起的纵向缩短量,即非线性耦合项为
|
$u_{x2}^i = - {1 \over 2}\sum\limits_{k = 1}^{12} {\sum\limits_{l = 1}^{12} {{\delta _{ik}}} } {\delta _{il}}{H_{kl}}$
|
(26) |
其中Hkl为
|
${H_{kl}}(x) = \int_0^x {\left( {{{\partial {y_{ik}}} \over {\partial \xi }} \cdot {{\partial {y_{il}}} \over {\partial \xi }} + {{\partial {z_{ik}}} \over {\partial \xi }} \cdot {{\partial {z_{il}}} \over {\partial \xi }}} \right)} d\xi $
|
(27) |
将式(25) ∼式(27)代入式(2)能得到Bezier插值方法描述的第i根柔性杆上任意点的变形位移.
2.4 B样条插值方法
B样条插值方法是现代函数逼近中一个十分活跃的分支,是计算方法的重要基础,应用很广泛,可以利用它创造出结构分析的新方法. 在杆轴上沿s方向作一个样条分划,即
|
$\left. \matrix{
0 = {x_0} < {x_1} < {x_2} < \cdots < {x_m} < l \hfill \cr
{x_i} = {x_0} + ih,h = {x_{i + 1}} - {x_i} = l/m \hfill \cr} \right\}$
|
(28) |
将杆轴向区间 [0,l]划分为m等份,取杆轴向和横向变形位移函数为
|
$\left. {\matrix{
{{u_x} = \phi {a_x}} \hfill \cr
{{u_y} = \phi {a_y}} \hfill \cr
{{u_z} = \phi {a_z}} \hfill \cr
} } \right\}$
|
(29) |
其中
|
$\left. \matrix{
{a_x} = {[{w_{0x}}{{w'}_{0x}}{a_{1x}} \cdots {a_{m - 1x}}{w_{mx}}{{w'}_{mx}}]^{\rm{T}}} \hfill \cr
{a_y} = {[{w_{0y}}{{w'}_{0y}}{a_{1y}} \cdots {a_{m - 1y}}{w_{my}}{{w'}_{my}}]^{\rm{T}}} \hfill \cr
{a_z} = {[{w_{0z}}{{w'}_{0z}}{a_{1z}} \cdots {a_{m - 1z}}{w_{mz}}{{w'}_{mz}}]^{\rm{T}}} \hfill \cr
\phi = [{\phi _{ - 1}}{\phi _0}{\phi _1} \cdots {\phi _{m - 1}}{\phi _m}{\phi _{m + 1}}] \hfill \cr} \right\}$
|
(30) |
其中$w_{0x} ,w_{0y} ,w_{0z} ,w'_{0x} ,w'_{0y},
w'_{0z} $分别为杆左端(x = 0)处的轴向变形和横向变形及转角,$w_{nx},w_{ny},w_{nz},w'_{nx},w'_{ny},w'_{nz} $分别为杆右端(x = l)处的轴向变形和横向变形及转角,而${{a}_{1x}},\cdots ,{{a}_{m-1x}},{{a}_{1y}},\cdots ,{{a}_{m-1y}},{{a}_{1z}},\cdots ,{{a}_{m-1z}}$为特征多边形顶点的变形时间变量. 采用混合参数法,利用3次B样条函数φ 3 (η)构造基函数Φi (x)[30].
本文中柔性杆是以悬臂方式连接,即边界条件为杆左端纵向变形、横向弯曲变形及转角为零.则令
|
$\left. \matrix{
{\delta _i}(t) = [{\delta _{ij}}] = \hfill \cr
[a_{1x}^i \cdots a_{m - 1x}^iw_{mx}^iw_{mx}^{'i}a_{1y}^i \cdots a_{m - 1y}^iw_{my}^iw_{my}^{'i}a_{1z}^i \hfill \cr
\cdots a_{m - 1z}^iw_{mz}^iw_{mz}^{'i}] \hfill \cr
{x_i}(x) = [{x_{ij}}] = \hfill \cr
[{\phi _1}\;{\phi _2}\;\; \cdots \;\;{\phi _{m + 1}}\;0\;\;0\;\; \cdots \;\;0\;\;0\;\;0\;\; \cdots \;\;0] \hfill \cr
{y_i}(x) = [{y_{ij}}] = \hfill \cr
[0\;\;0\;\; \cdots 0\;\;{\phi _1}\;\;{\phi _2}\;\; \cdots \;\;{\phi _{m + 1}}\;\;0\;\;0\;\; \cdots \;\;0] \hfill \cr
{z_i}(x) = [{z_{ij}}] = \hfill \cr
[0\;\;0\;\; \cdots 0\;\;0\;\;0\;\; \cdots \;\;0\;\;{\phi _1}\;\;{\phi _2}\;\; \cdots \;\;{\phi _{m + 1}}] \hfill \cr} \right\}$
|
(31) |
其中m为第i根杆的段数,广义坐标量Ni为3m + 3.则第i根柔性杆上任意点的变形位移可表示为
|
$\left. {\matrix{
{u_x^i = u_{x1}^i + u_{x2}^i = \sum\limits_{j = 1}^{{N_i}} {{\delta _{ij}}} {x_{ij}}\left( x \right) - } \hfill \cr
{{1 \over 2}\sum\limits_{k = 1}^{{N_i}} {\sum\limits_{l = 1}^{{N_i}} {{\delta _{ik}}{\delta _{il}}} } {H_{kl}}\left( x \right)} \hfill \cr
{u_y^i = \sum\limits_{j = 1}^{{N_i}} {{\delta _{ij}}} {y_{ij}}\left( x \right)} \hfill \cr
{u_z^i = \sum\limits_{j = 1}^{{N_i}} {{\delta _{ij}}} {z_{ij}}\left( x \right)} \hfill \cr
} } \right\}$
|
(32) |
其中ux2i 为横向弯曲变形引起的纵向缩短量,即非线性耦合项. Hkl(x)为
|
${H_{kl}}(x) = \int_0^x {\left( {{{\partial {y_{ik}}} \over {\partial \xi }} \cdot {{\partial {y_{il}}} \over {\partial \xi }} + {{\partial {z_{ik}}} \over {\partial \xi }} \cdot {{\partial {z_{il}}} \over {\partial \xi }}} \right)} d\xi $
|
(33) |
3 动力学仿真
3.1 4种变形场离散方法适用性比较
论文基于柔性机器人动力学方程(1)和上述4种变形场离散法,采用C++计算机编程语言研制了多杆柔性杆柔性铰机器人动力学仿真软件,仿真软件采用阿当姆斯预报校正法求解常微分方程.为验证4种变形场离散方法在柔性机器人变形场离散中的适用性及其性能,首先以单杆柔性机械臂绕基座做大范围旋转运动为例进行研究,忽略重力的作用.柔性杆的参数与文献[2, 30-31]中的参数相同:长度L = 8 m,横截面积S0 =7.296 8× 10-5 m2,截面惯性矩I0 = 8.218 9× 10-9 m4,体积密度ρ = 2.766 7× 103 kg/m3,弹性模量E =6.895 2× 1010 N/m2. 假定该柔性机械臂由静止开始作大范围旋转运动,大范围运动角速度规律取为
|
$\dot \theta = \left\{ {\matrix{
{{{{\Omega _0}} \over T}t - {{{\Omega _0}} \over {2\pi }}\sin ({{2\pi } \over T}t),} & {0 \le t \le T} \cr
{{\Omega _0},} & {t > T} \cr
} } \right.$
|
(34) |
其中,T = 15 s,系统在T = 15 s时角速度达到Ω0 ,仿真中Ω0分别取 4 rad/s和
10 rad/s.
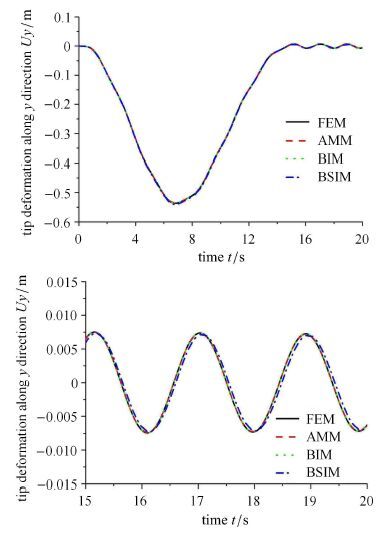
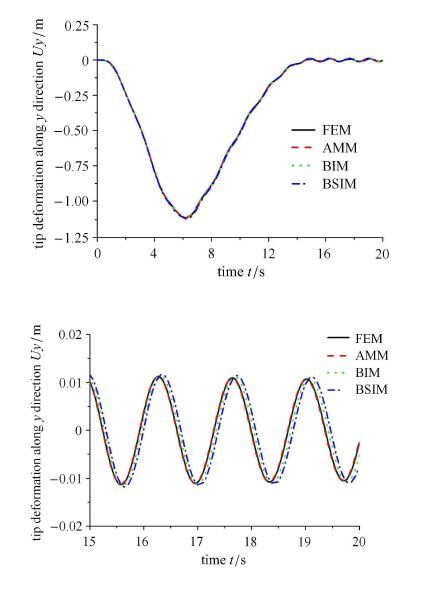
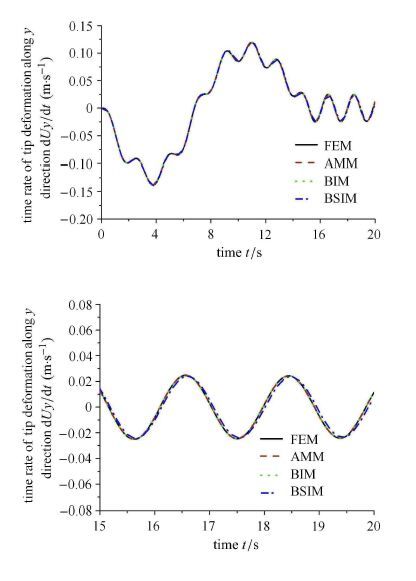
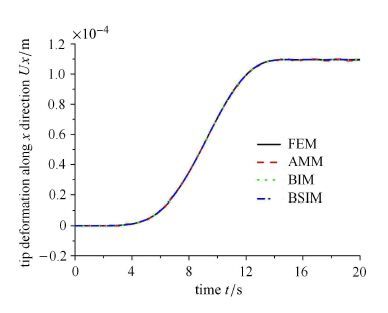
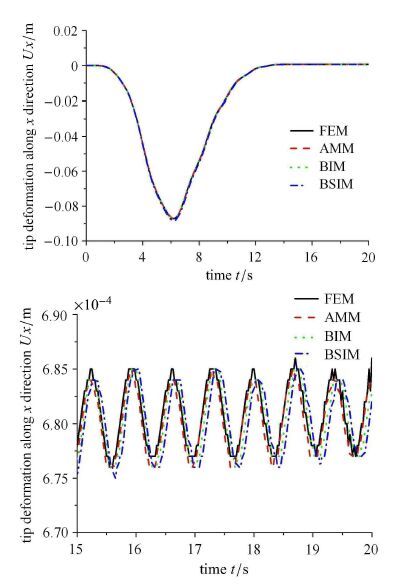
图 3和图 4分别表示Ω0 = 4 rad/s 和Ω0= 10 rad/s时柔性杆末端横向弯曲变形,从局部放大图可知,有限元法、Bezier插值方法、B样条插值方法与假设模态法大范围运动恒定时的响应振幅以及频率基本一致,且与文献[2, 30-31]中的仿真结果相同.图 5和图 6分别表示柔性杆末端的横向变形速度,如图可知4种离散方法的仿真结果基本一致.图 7表示柔性杆末端纵向变形位移,该纵向变形位移中没有计入横向弯曲变形引起的纵向缩短量.图 8表示柔性杆末端纵向变形位移,该纵向变形位移中考虑了横向弯曲变形引起的纵向缩短.比较图 7和图 8的数值量级,可以发现纵向变形位移中轴向变形相对于横向弯曲变形引起的纵向缩短是微小的,而横向弯曲变形引起的纵向缩短则不可忽略.
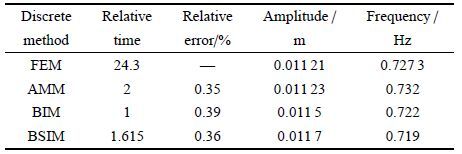
表 1和表 2分别给出了Ω0 = 4 rad/s和Ω0 =10 rad/s时4种离散方法的计算效率、误差以及大范围运动恒定时的响应频率、振幅,表 3表示在不同大范围运动角速度时假设模态法、Bezier插值方法和B样条插值方法的仿真结果与有限元结果之间的误差.该算例中,有限元法把杆分成5个单元;假设模态法则取悬臂梁自由振动的前4阶固有振型;Bezier插值方法取5次伯恩斯坦基函数;B样条插值方法选取3次B样条函数构成的混合参数法.如表 1和表 2所示,4种离散方法在大范围运动恒定下的响应频率以及振幅基本一致.计算效率方面,有限元法的计算效率最低,Bezier插值方法的最高,B样条插值方法的其次.如表 3所示,在大范围运动角速度Ω0变大时,假设模态法的计算误差变化趋势相对Bezier插值方法和B样条插值方法的要大. 因此随着角速度Ω0的增大,若要保证假设模态法的计算精度,有必要增加模态阶数. 然而,增加模态阶数则又会降低计算效率.另外,研究发现,当柔性杆处于较大变形时,假设模态法的精度大大降低,以致引起数值发散[31].
表 1(Table 1)

表 1 >4种离散方法的计算时间、误差和大范围运动恒定时响应频率、振幅(Ω0 rad/s)
Table 1 The relative time,the relative error,the amplitude and the frequency of these four discrete methods (Ω0 = 4 rad/s)
|
表 1 >4种离散方法的计算时间、误差和大范围运动恒定时响应频率、振幅(Ω0 rad/s)
Table 1 The relative time,the relative error,the amplitude and the frequency of these four discrete methods (Ω0 = 4 rad/s)
|
表 2(Table 2)

表 2 4种离散方法的计算时间、误差和大范围运动恒定时响应频率、振幅(Ω0 =10 rad/s)
Table 2 The relative time,the relative error,the amplitude and the frequency of these four discrete methods (Ω0 = 10 rad/s)
|
表 2 4种离散方法的计算时间、误差和大范围运动恒定时响应频率、振幅(Ω0 =10 rad/s)
Table 2 The relative time,the relative error,the amplitude and the frequency of these four discrete methods (Ω0 = 10 rad/s)
|
表 3(Table 3)

表 3 不同大范围运动角速度时计算误差变化趋势
Table 3 The trend of calculation error with different angular velocity
|
表 3 不同大范围运动角速度时计算误差变化趋势
Table 3 The trend of calculation error with different angular velocity
|
3.2 双杆柔性机械臂自由落体动力学仿真
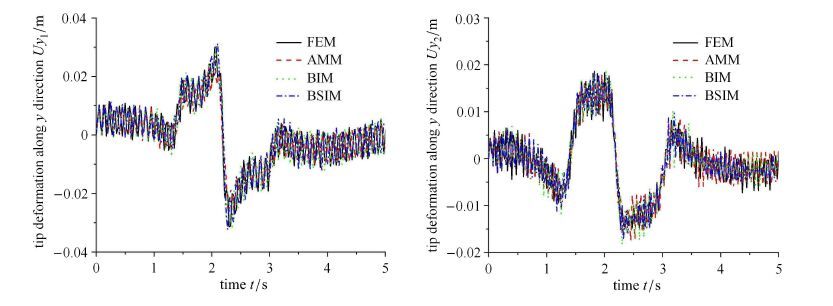
图 9所示为双杆柔性机械臂动力学模型,已知柔性机械臂在重力作用下做自由落体运动,杆的参数取为:杆长L1= L2= 7.11 m,杆的质量L1=L2 = 314.88 kg,抗拉压刚度为E1A1=E2A2 = 2.84×107 N,抗弯刚度E1I1=E2I2 = 3.8× 106 N⋅m2.
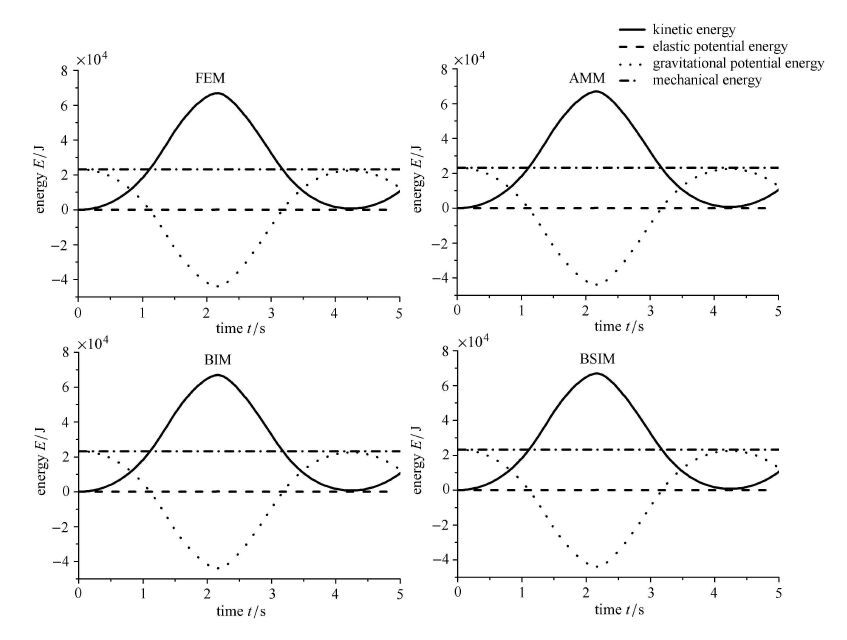
图 10分别表示第1根以及第2根柔性杆横向弯曲变形,4种离散方法的计算结果基本一致.图 11表示系统的能量,从4张小图也能看到4种离散方法的能量变化是一致的,主要是重力势能与动能的转换,弹性势能相对较小;且从图中可知机械能守恒,符合保守系统机械能始终守恒定律,这也说明了本文软件的正确性.
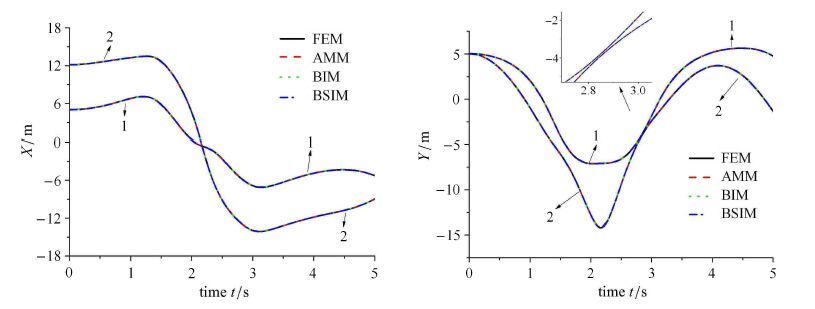
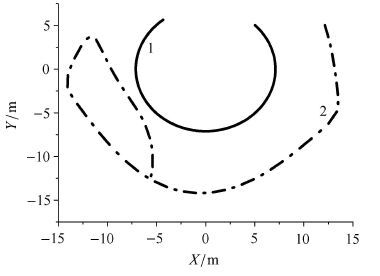
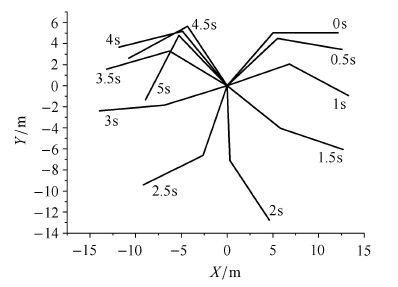
图 12表示杆1和杆2末端水平、竖直方向位移.图 13表示双杆柔性机械臂末端点轨迹,从图 13可知,杆1运动轨迹近似圆弧,而杆2的运动轨迹则无明显规律.图 14给出了系统在不同时刻的整体位形. 在4种离散方法的精度和效率的比较中得出了与算例1同样的结论.
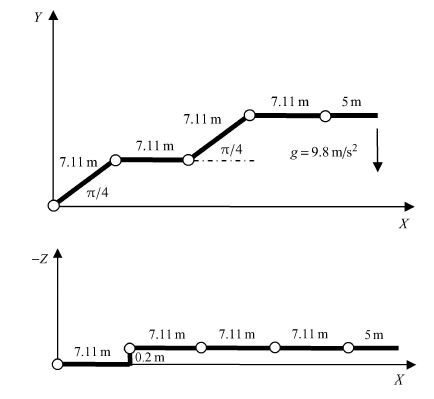
3.3 空间五根柔性杆机械臂自由落体动力学仿真
为了展示本文算法和软件对复杂系统的适应性,考虑图 15所示空间五根柔性杆机械臂物理模型,已知系统在重力的作用下做自由落体运动. 杆1与杆2之间存在0.2 m的偏置距离.本仿真算例考虑柔性杆轴向拉伸变形、y和z方向两维横向弯曲变形,以及杆的扭转变形,并计入柔性杆横向弯曲变形引起的纵向缩短.
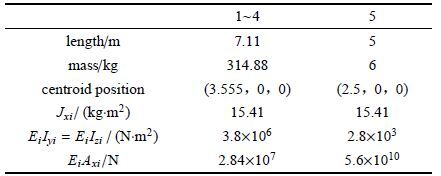
杆的参数选取参考Canadarm2[25]机械臂的参数,如表 4所示.本仿真算例选取计算效率和计算精度相对较高的Bezier插值离散法对柔性杆变形场进行描述.
表 4(Table 4)

表 4 柔性杆物理模型参数
Table 4 The physical model parameters of flexible links
|
表 4 柔性杆物理模型参数
Table 4 The physical model parameters of flexible links
|
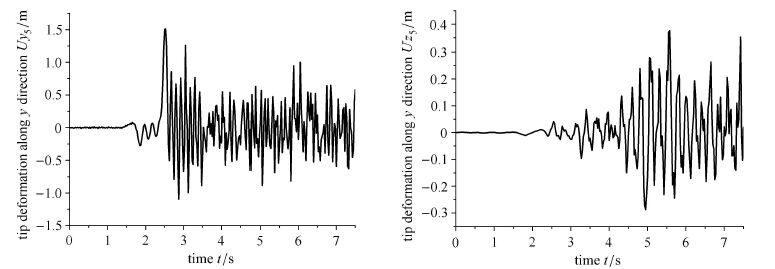
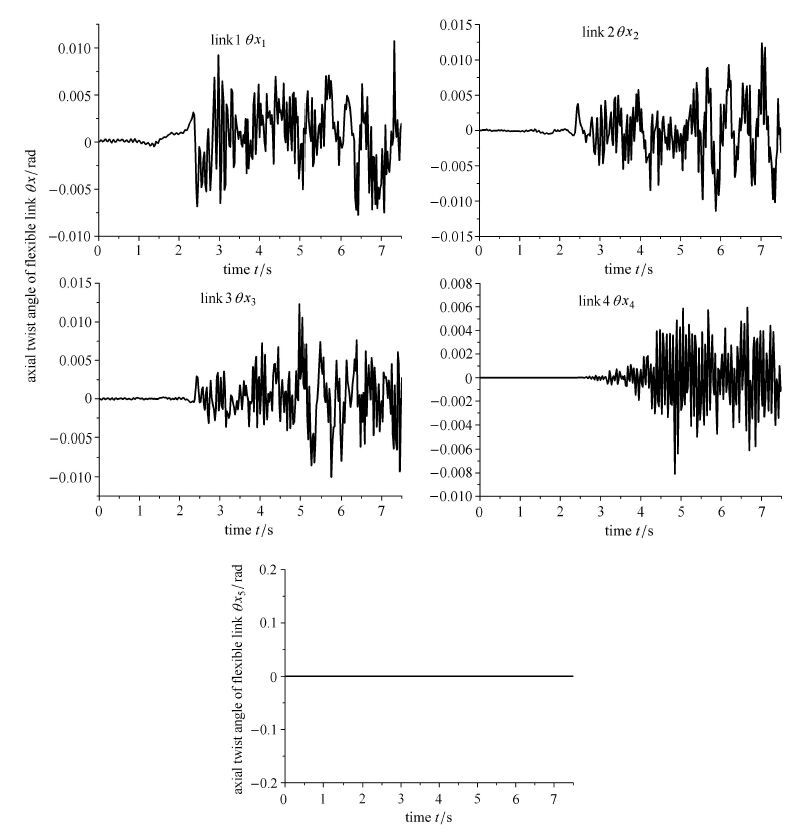
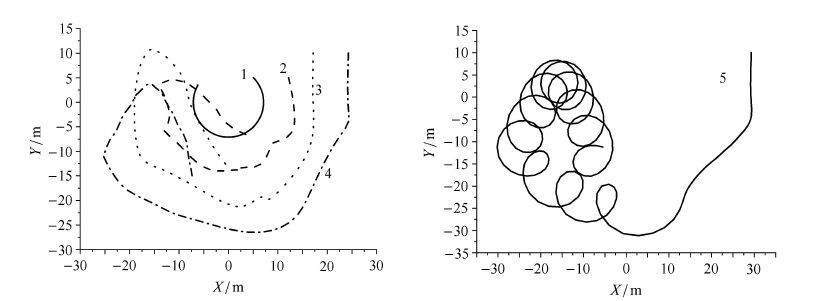
图 16表示模型第5根柔性杆y方向和z方向的横向弯曲变形,其柔性效应明显,y方向横向弯曲变形已经达到杆长的30%,属较大变形范围. 图 17表示柔性杆末端扭转角.由图 17所知,杆1、杆2、杆3和杆4末端产生了扭转变形,而杆5末端没有产生扭转变形.系统运动不是平面运动而是空间运动,柔性杆产生了三维空间变形. 图 18表示系统柔性杆末端点$XY$平面轨迹图,从图中能明显地看出杆5是做旋转运动.图 19表示系统中第五根柔性杆整体横向弯曲变形图. 图 20表示系统在不同时刻的整体空间位形.图 21表示系统的能量变化,如图可知机械能守恒,同时系统的动能、弹性势能、重力势能相互转化.
4 4 结论
本文将Bezier 插值方法和B样条插值方法作为变形体新的离散方法,
研究其在柔性机器人动力学中的建模方法和动力学分析中的性能,并同运用广泛的假设模态法和有限元法构造统一格式,方便了柔性机器人动力学方程的推导及动力学仿真软件的编制.通过仿真算例可知:在处理柔性机器人小变形动力学问题时,4种方法均能很好地描述变形场;而处理较大变形动力学问题时,假设模态法离散的仿真结果误差比较大;从计算效率考虑,有限元法最低,Bezier插值方法最佳,B样条插值方法其次,从计算精度考虑,Bezier插值方法最高,B样条插值方法其次.算例也表明,本文采用的动力学建模理论和变形场离散方法,以及在此基础上研制而成的动力学仿真软件能够处理复杂柔性机器人的动力学仿真问题.
参考文献
| [1] |
Kane TR, Ryan RR, Banerjee AK. Dynamics of a cantilever beam attached to a moving base[J].
Journal of Guidance, Control and Dynamics,1987, 10 (2) : 139-150.
DOI: 10.2514/3.20195. ( 0) 0)
|
| [2] |
蔡国平, 洪嘉振. 旋转运动柔性梁的假设模态方法研究[J].
力学学报,2005, 37 (1) : 48-56.
( Cai Guoping, Hong Jiazhen. Assumed mode method of a rotating flexible beam[J].
Chinese Journal of Theoretical and Applied Mechanics,2005, 37 (1) : 48-56.
(in Chinese) ) ( 0) 0)
|
| [3] |
方建士, 章定国. 旋转悬臂梁的刚柔耦合动力学建模与频率分析[J].
计算力学学报,2012, 29 (3) : 333-339.
( Fang Jianshi, Zhang Dingguo. Rigid-flexible coupling dynamic modeling and frequency analysis of a rotating cantilever beam[J].
Chinese Journal of Computational Mechanics,2012, 29 (3) : 333-339.
(in Chinese) ) ( 0) 0)
|
| [4] |
Liu JY, Hong JZ. Geometric stiffening effect on rigid-flexible coupling dynamics of an elastic beam[J].
Journal of Sound and Vibration,2004, 278 : 1147-1162.
DOI: 10.1016/j.jsv.2003.10.014. ( 0) 0)
|
| [5] |
陈思佳, 章定国, 洪嘉振. 大变形旋转柔性梁的一种高次刚柔耦合动力学模型[J].
力学学报,2013, 45 (2) : 251-256.
( Chen Sijia, Zhang Dingguo, Hong Jiazhen. A high-order rigid-flexible coupling model of a rotating flexible beam under large deformation[J].
Chinese Journal of Theoretical and Applied Mechanics,2013, 45 (2) : 251-256.
(in Chinese) ) ( 0) 0)
|
| [6] |
章定国, 余纪邦. 作大范围运动的柔性梁的动力学分析[J].
振动工程学报,2006, 19 (4) : 475-479.
( Zhang Dingguo, Yu Jibang. Dynamical analysis of a flexible cantilever beam with large overall motions[J].
Journal of Vibration Engineering,2006, 19 (4) : 475-479.
(in Chinese) ) ( 0) 0)
|
| [7] |
刘锦阳, 李彬, 洪嘉振. 作大范围空间运动柔性梁的刚-柔耦合动力学[J].
力学学报,2006, 38 (2) : 276-282.
( Liu Jinyang, Li Bin, Hong Jiazhen. Rigid-flexible coupling dynamics of a flexible beam with three-dimensional large overall motion[J].
Chinese Journal of Theoretical and Applied Mechanics,2006, 38 (2) : 276-282.
(in Chinese) ) ( 0) 0)
|
| [8] |
董兴建, 孟光, 蔡国平, 等. 旋转柔性梁的动力学建模及分析[J].
振动工程学报,2006, 19 (4) : 488-493.
( Dong Xingjian, Meng Guang, Cai Guoping, et al. Dynamic modelling and analysis of a rotating flexible beam[J].
Journal of Vibration Engineering,2006, 19 (4) : 488-493.
(in Chinese) ) ( 0) 0)
|
| [9] |
蔡国平, 洪嘉振. 中心刚体-柔性悬臂梁系统的动力特性研究[J].
航空学报,2004, 25 (3) : 248-253.
( Cai Guoping, Hong Jiazhen. Dynamic analysis of a flexible hub-beam system[J].
Acta Aeronautica et Astronautica Sinica,2004, 25 (3) : 248-253.
(in Chinese) ) ( 0) 0)
|
| [10] |
邓峰岩, 和兴锁, 李亮, 等. 耦合变形对大范围运动柔性梁动力学建模的影响[J].
计算力学学报,2006, 23 (5) : 599-606.
( Deng Fengyan, He Xingsuo, Li Liang, et al. Dynamics modeling of the elastic beam undergoing large overall motion considering coupling effect in deformation[J].
Chinese Journal of Computational Mechanics,2006, 23 (5) : 599-606.
(in Chinese) ) ( 0) 0)
|
| [11] |
和兴锁, 邓峰岩, 王睿. 具有大范围运动和非线性变形的空间柔性梁的精确动力学建模[J].
物理学报,2010, 59 (3) : 1428-1436.
( He Xingsuo, Deng Fengyan, Wang Rui. Exact dynamic modeling of a spatial flexible beam with large overall motion and nonlinear deformation[J].
Acta Physica Sinica,2010, 59 (3) : 1428-1436.
(in Chinese) ) ( 0) 0)
|
| [12] |
Liu JY, Hong JZ. Dynamics of three-dimensional beams undergoing large overall motion[J].
European Journal of Mechanics,2004, 23 : 1051-1068.
DOI: 10.1016/j.euromechsol.2004.08.003. ( 0) 0)
|
| [13] |
吴胜宝, 章定国. 大范围运动刚体-柔性梁刚柔耦合动力学分析[J].
振动工程学报,2011, 24 (1) : 1-7.
( Wu Shengbao, Zhang Dingguo. Rigid-flexible coupling dynamic analysis of hub-flexible beam with large overall motion[J].
Journal of Vibration Engineering,2011, 24 (1) : 1-7.
(in Chinese) ) ( 0) 0)
|
| [14] |
蔡国平, 洪嘉振. 考虑附加质量的中心刚体-柔性悬臂梁系统的动力特性研究[J].
机械工程学报,2005, 41 (2) : 33-40.
DOI: 10.3901/JME.2005.02.033. ( Cai Guoping, Hong Jiazhen. Dynamics study of hub-beam system with tip mass[J].
Journal of Mechanical Engineering,2005, 41 (2) : 33-40.
(in Chinese) DOI: 10.3901/JME.2005.02.033. ) ( 0) 0)
|
| [15] |
Cai GP, Lim CW. Dynamics studies of a flexible hub–beam system with significant damping effect[J].
Journal of Sound and Vibration,2008, 318 : 1-17.
DOI: 10.1016/j.jsv.2008.06.009. ( 0) 0)
|
| [16] |
陈思佳, 章定国. 中心刚体-变截面梁系统的动力学特性研究[J].
力学学报,2011, 43 (4) : 790-794.
( Chen Sijia, Zhang Dingguo. Dynamics of hub-variable section beam systems[J].
Chinese Journal of Theoretical and Applied Mechanics,2011, 43 (4) : 790-794.
(in Chinese) ) ( 0) 0)
|
| [17] |
Liu JY, Ma YZ, Hong JZ. Geometric nonlinear formulation for a rectangular plate with large deformation[J].
Journal of Shanghai Jiaotong University (Science),2007, 12 (6) : 831-837.
( 0) 0)
|
| [18] |
Li L, Zhang DG. Free vibration analysis of rotating functionally graded rectangular plates[J].
Composite Structures,2016, 136 : 493-504.
DOI: 10.1016/j.compstruct.2015.10.013. ( 0) 0)
|
| [19] |
Mehrdad F, Stanislaw A, Lukasiewicz. Dynamic modeling of spatial manipulators with flexible links and joints[J].
Computers and Structures,2000 (75) : 419-437.
( 0) 0)
|
| [20] |
Na KS, Kim JH. Deployment of a multi-link flexible structure[J].
Journal of Sound and Vibration,2006, 294 : 298-313.
DOI: 10.1016/j.jsv.2005.11.018. ( 0) 0)
|
| [21] |
Liu JY, Hong JZ. Geometric stiffening of flexible link system with large overall motion[J].
Computers and Structures,2003, 81 : 2829-2841.
DOI: 10.1016/j.compstruc.2003.07.001. ( 0) 0)
|
| [22] |
Chen SJ, Zhang DG, Liu J. Dynamic analysis of multi-link spatial flexible manipulator arms with dynamic stiffening effects[J].
Theoretical and Applied Mechanics Letters,2012, 2 (6) : 063003.
DOI: 10.1063/2.1206303. ( 0) 0)
|
| [23] |
Qian ZJ, Zhang DG, Liu J. Recursive formulation for dynamic modeling and simulation of multilink spatial flexible robotic manipulators[J].
Advances in Mechanical Engineering,2013, 5 : 216014.
( 0) 0)
|
| [24] |
Zhang DG. Recursive Lagrangian dynamic modeling and simulation of multi-link spatial flexible manipulator arms[J].
Applied Mathematics and Mechanics,2009, 30 : 1283-1294.
DOI: 10.1007/s10483-009-1008-2. ( 0) 0)
|
| [25] |
刘俊. 柔性杆柔性铰机器人刚柔耦合动力学. [硕士论文]. 南京: 南京理工大学,2006
( Liu Jun. Dynamic analysis for rigid-flexible coupling flexible robots. [Master Thesis]. Nanjjing: Nanjing University of Science and Technology, 2006 (in Chinese)
) ( 0) 0)
|
| [26] |
Sanborn GG, Shabana AA. On the integration of computer aided design and analysis using the finite element absolute nodal coordinate formulation[J].
Multibody Syst Dyn,2009, 22 (2) : 181-197.
DOI: 10.1007/s11044-009-9157-3. ( 0) 0)
|
| [27] |
Sanborn GG, Shabana AA. A rational finite element method based on the absolute nodal coordinate formulation[J].
Nonlinear Dyn,2009, 58 (3) : 565-572.
DOI: 10.1007/s11071-009-9501-4. ( 0) 0)
|
| [28] |
Lan P, Shabana AA. Rational finite elements and flexible body dynamics[J].
Journal of Vibration and Acoustics,2010, 132 (4) : 041007-1.
DOI: 10.1115/1.4000970. ( 0) 0)
|
| [29] |
Lan P, Shabana AA. Integration of B-spline geometry and ANCF finite element analysis[J].
Nolinear Dyn,2010, 61 (1-2) : 193-206.
DOI: 10.1007/s11071-009-9641-6. ( 0) 0)
|
| [30] |
范纪华, 章定国. 旋转悬臂梁动力学的B 样条插值方法[J].
机械工程学报,2012, 48 (23) : 59-64.
DOI: 10.3901/JME.2012.23.059. ( Fan Jihua, Zhang Dingguo. Bspline interpolation method for the dynamics of rotating cantilever beam[J].
Journal of Mechanical Engineering,2012, 48 (23) : 59-64.
(in Chinese) DOI: 10.3901/JME.2012.23.059. ) ( 0) 0)
|
| [31] |
范纪华, 章定国. 旋转柔性悬臂梁动力学的Bezier 插值离散方法研究[J].
物理学报,2014, 63 (15) : 154501.
( Fan Jihua, Zhang Dingguo. Bezier interpolation method for the dynamics of rotating flexible cantilever beam[J].
Acta Physica Sinica,2014, 63 (15) : 154501.
(in Chinese) ) ( 0) 0)
|
| [32] |
范纪华, 章定国, 洪嘉振. 基于Bezier 插值方法的作大范围旋转运动锥形悬臂梁动力学研究[J].
动力学与控制学报,2012, 10 (4) : 347-354.
( Fan Jihua, Zhang Dingguo, Hong Jiazhen. Dynamic analysis of a rotating tapered cantilever beam based on Bezier curve interpolation[J].
Journal of dynamics and control,2012, 10 (4) : 347-354.
(in Chinese) ) ( 0) 0)
|
| [33] |
杜超凡, 章定国, 洪嘉振. 径向基点插值法在旋转柔性梁动力学中的应用[J].
力学学报,2015, 47 (2) : 279-288.
( Du Chaofan, Zhang Dingguo, Hong Jiazhen. A meshfree method based on radial point interpolation method for the dynamic analysis of rotating flexible beams[J].
Chinese Journal of Theoretical and Applied Mechanics,2015, 47 (2) : 279-288.
(in Chinese) ) ( 0) 0)
|
| [34] |
杜超凡, 章定国. 光滑节点插值法:计算固有频率下界值的新方法[J].
力学学报,2015, 47 (5) : 839-847.
( Du Chaofan, Zhang Dingguo. Node-based smoothed point interpolation method: a new method for computing lower bound of natural frequency[J].
Chinese Journal of Theoretical and Applied Mechanics,2015, 47 (5) : 839-847.
(in Chinese) ) ( 0) 0)
|
DYNAMIC MODELING AND SIMULATION OF FLEXIBLE ROBOTS BASED ON DIFFERENT DISCRETIZATION METHODS
Fan Jihua1,3,
Zhang Dingguo2

1. School of Mechatronics-Engineering and Automotive, Jiangsu University of Science and Technology, Zhangjiagang 215600, Jiangsu, China
;
2. School of Sciences, Nanjing University of Science and Technology, Nanjing 210094, China
;
3. Suzhou Institute of Technology, Jiangsu University of Science and Technology, Zhangjiagang 215600, Jiangsu, China
Abstract:
Dynamic modeling and simulation of flexible robots based on different discretization methods are investigated in this paper. Firstly, the physical model of flexible robots consisting of n links and n revolute joints is established. Secondly, the assumed mode method, finite element method, Bezier interpolation method and B-spline interpolation method are used to describe the deformation of the flexible link. Then, kinematics of both rotary-joint motion and link deformation is described by 4×4 homogenous transformation matrices, and the Lagrangian equations are used to derive the governing equations of motion of the system. The longitudinal deformation and the transverse deformation of the flexible link are considered, and the coupling term of the deformation which is caused by the transverse deformation is included in the total longitudinal deformation. Then, a software package for the dynamic simulation of the flexible robots based on the different discretization methods is developed, after that, the dynamic analysis for flexible robots are studied by three examples. The simulation results show that the computational efficiency of finite element method is the lowest, and the Bezier interpolation method and B-spline interpolation method are better than the assumed mode method in dealing with the large deformation dynamic problem. As new discretization methods, Bezier interpolation method and B-spline interpolation method can be used to describe the deformation of the flexible link, and they can be extended to the dynamic modeling for spatial flexible robots.
Key words: assumed mode method finite element method Bezier interpolation method B-spline interpolation method flexible robots






 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 2016, Vol. 48
2016, Vol. 48