太空自然环境恶劣,宇航员出舱活动会面临很多危险,而空间机器人的应用可以减少宇航员出舱次数,或者辅助其完成复杂的任务. 太空在轨服务空间机器人的工作任务包括:空间站部件的组装,轨道废弃卫星的移除,为卫星加注控制液等[1-2]. 由于在太空的失重环境下,机器人系统运动过程中各个机械臂与漂浮的载体基座间存在动力学耦合作用,因此空间机器人系统的控制难度明显高于地面机器人系统. 特别是空间机器人系统存在不确定参数[3-4]时会影响系统的控制精度,而空间站的组装和卫星的燃料加注都需要较高的控制精度. 随着航天技术的发展,空间机器人在太空中应用不断增加,虽然相关的理论研究越来越多[5-8],但是空间机器人系统研究成果的数量远不及地面机器人系统. 需要注意的是目前的研究成果对双臂空间机器人系统的关注少于单臂空间机器人系统[9-12],双臂空间机器人系统与单臂空间机器人系统相比,具有更大的负载能力及更好的运动稳定性,是未来空间机器人发展的重要方向. 由于双臂空间机器人与人类的双臂相似,更有利于搬运物体并保证控制精度,其双边抓取操作明显较单边抓取操作的成功率更高,所以美国的"FREND"[13]及"Phoenix"[14]计划,德国"DEOS"[15]项目与欧洲的"SMART-OLEV"[16]系统后期多采用双臂捕获技术. 遥控机械臂系统上的双臂专用机器手SPDM[17]已在空间站上投入使用,这是双臂空间机器人已经开始应用于太空中的标志. 因此,对于双臂空间机器人系统的理论研究,是非常有必要的. 另外,由于实验室模拟太空失重状态非常困难,地面实验所需的费用昂贵,计算机仿真实验不失为一种有效的方案,并被国际上大多数航天机构所采用[18-19].
双臂空间机器人系统为了实现上述在轨服务目标,会与被捕获卫星发生碰撞,并最终形成闭链系统[20].然而这样的闭链混合体系统是不稳定的,需要进行镇定运动控制,否则大角度的翻转会导致空间仪器设备的损坏.同时,双臂空间机器人完成捕获操作前后存在开闭环变拓扑及动量、动量矩的转换;形成的混合体系统中存在闭环结构及控制器冗余的情况,需要解决左右机械臂镇定运动的协调控制问题,导致其控制系统设计难于开环系统.Rathee等[21]基于光滑的多项式函数,对漂浮基双臂空间机器人提出了点到点路径规划方案. 梁捷等[22- 23]针对开链双臂空间机器人系统,提出了惯性空间的轨迹跟踪控制方案.然而这些研究未考虑空间机器人系统与目标接触碰撞的过程.Takahashi等[24]研究了双臂机器人与自由漂浮目标碰撞后的影响.Shah等[25]研究了双臂空间机器人捕获卫星操作对载体姿态干扰最小的最优运动规划.郭闻昊等[26]利用冲量-动量方程及粒子群算法,找出了双臂空间机器人抓捕前较理想的碰撞构型,使碰撞后系统角动量尽量小.Jia 等[27]对闭链双臂空间机器人提出了自适应控制方案.但是上述研究主要涉及空间机器人系统轨迹规划及运动学控制,未考虑捕获过程动力学演化分析及其后镇定运动控制问题.
基于上述讨论,本文根据拉格朗日方程及牛顿-欧拉法,分别建立了双臂空间机械臂及被捕获目标的动力学方程.根据力的传递规律及几何运动关系,进行冲击动力学建模,多角度分析了系统受到冲击后的影响.利用闭链系统的闭环约束关系,获得了系统的闭链混合体系统动力学方程. 以上冲击效应分析有助于获得合理的捕获策略.鉴于空间机器人控制设计的高可靠性要求,空间技术一般尝试将地面成熟控制方案应用于空间机器人系统.文中基于获得的闭链混合体系统动力学方程,提出了镇定运动模糊H∞控制方案.利用模糊逻辑系统逼近动力学方程未知非线性部分,消除系统参数不确定的影响. 引入H∞控制,保证了系统误差跟踪精度. 所提控制方案最终能够有效完成镇定运动控制.最后,通过数值仿真模拟了碰撞冲击效应,并验证了所提控制方案的有效性.
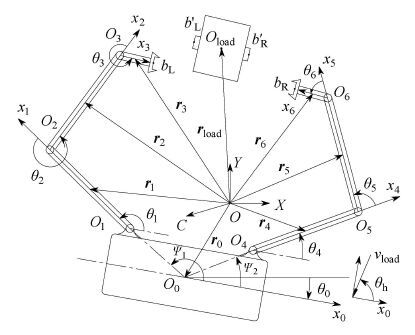
1 空间机器人捕获自旋目标卫星操作过程动力学演化分析考虑作平面运动的双臂空间机器人系统及目标系统如图 1所示.
|
图 1 双臂空间机器人系统及目标系统 Fig.1 Dual-arm space robot system and target system |
任意取一点O为原点,建立平动的惯性坐标系XOY. 建立双臂空间机器人各分体的主轴连体坐标系
将被捕获卫星系统视作刚体目标,目标质心的位置坐标及姿态角列向量为
| ${{M}_{\text{load}}}{{\ddot{q}}_{\text{load}}}=J_{\text{load}}^{\text{T}}{F}'$ | (1) |
式中,
定义
设双臂空间机器人各部分为均质刚体,其中
| $\left. \begin{align} & {{r}_{0}}=\left( {{x}_{0}}{{y}_{0}} \right) \\ & {{r}_{1}}={{r}_{0}}+{{d}_{0}}{{e}_{\text{L}}}+{{d}_{1}}{{e}_{1}} \\ & {{r}_{2}}={{r}_{0}}+{{d}_{0}}{{e}_{\text{L}}}+{{l}_{1}}{{e}_{1}}+{{d}_{2}}{{e}_{2}} \\ & {{r}_{3}}={{r}_{0}}+{{d}_{0}}{{e}_{\text{L}}}+{{l}_{1}}{{e}_{1}}+{{l}_{2}}{{e}_{2}}+{{d}_{3}}{{e}_{3}} \\ & {{r}_{4}}={{r}_{0}}+{{d}_{0}}{{e}_{\text{R}}}+{{d}_{4}}{{e}_{4}} \\ & {{r}_{5}}={{r}_{0}}+{{d}_{0}}{{e}_{\text{R}}}+{{l}_{4}}{{e}_{4}}+{{d}_{5}}{{e}_{5}} \\ & {{r}_{6}}={{r}_{0}}+{{d}_{0}}{{e}_{\text{R}}}+{{l}_{4}}{{e}_{4}}+{{l}_{5}}{{e}_{5}}+{{d}_{6}}{{e}_{6}} \\ \end{align} \right\}$ | (2) |
其中,$\theta _0 $为基座姿态角,x0和y0为基座质心位置坐标. 对式(2)求导可得
| $\left. \begin{array}{*{35}{l}} {{{\dot{r}}}_{0}}=\left( {{{\dot{x}}}_{0}}{{{\dot{y}}}_{0}} \right) \\ {{{\dot{r}}}_{1}}={{{\dot{r}}}_{0}}+{{d}_{0}}{{{\dot{e}}}_{\text{L}}}+{{d}_{1}}{{{\dot{e}}}_{1}} \\ {{{\dot{r}}}_{2}}={{{\dot{r}}}_{0}}+{{d}_{0}}{{{\dot{e}}}_{\text{L}}}+{{l}_{1}}{{{\dot{e}}}_{1}}+{{d}_{2}}{{{\dot{e}}}_{2}} \\ {{{\dot{r}}}_{3}}={{{\dot{r}}}_{0}}+{{d}_{0}}{{{\dot{e}}}_{\text{L}}}+{{l}_{1}}{{{\dot{e}}}_{1}}+{{l}_{2}}{{{\dot{e}}}_{2}}+{{d}_{3}}{{{\dot{e}}}_{3}} \\ {{{\dot{r}}}_{4}}={{{\dot{r}}}_{0}}+{{d}_{0}}{{{\dot{e}}}_{\text{R}}}+{{d}_{4}}{{{\dot{e}}}_{4}} \\ {{{\dot{r}}}_{5}}={{{\dot{r}}}_{0}}+{{d}_{0}}{{{\dot{e}}}_{\text{R}}}+{{l}_{4}}{{{\dot{e}}}_{4}}+{{d}_{5}}{{{\dot{e}}}_{5}} \\ {{{\dot{r}}}_{6}}={{{\dot{r}}}_{0}}+{{d}_{0}}{{{\dot{e}}}_{\text{R}}}+{{l}_{4}}{{{\dot{e}}}_{4}}+{{l}_{5}}{{{\dot{e}}}_{5}}+{{d}_{6}}{{{\dot{e}}}_{6}} \\ \end{array} \right\}$ | (3) |
结合式(3)可以获得双臂空间机器人系统的动能为
| $\left. \begin{align} & {{T}_{\text{r}}}=\sum\limits_{\text{0}}^{6}{{{T}_{i}}} \\ & {{T}_{i}}=\frac{1}{2}{{m}_{i}}\dot{r}_{i}^{2}+\frac{1}{2}{{I}_{i}}\omega _{i}^{2},\quad i=0,1,\cdots 6 \\ \end{align} \right\}$ | (4) |
式中,
忽略轨道动力学因素,结合拉格朗日第二类方程获得基座位置不受控、姿态受控的双臂空间机器人碰撞前瞬间开环系统动力学方程为
| $M(q)\ddot{q}+H(q,\dot{q})\dot{q}={{\tau }_{\text{M}}}+{{J}^{\text{T}}}F$ | (5) |
式中,
根据牛顿第三定律有
| ${F}'=-F$ | (6) |
由运动几何关系可知,两机械臂末端速度与广义坐标的关系为
| ${{s}_{\text{b}}}=J\dot{q}$ | (7) |
其中,
同理可得被捕获目标上的捕获位置
| ${{s}_{{\text{{b}'}}}}={{J}_{\text{load}}}{{\dot{q}}_{\text{load}}}$ | (8) |
其中,
空间机器人与目标之间的相互作用力,使各自的运动状态发生了改变. 目标捕获位置上的力可分解为
| ${F}'={{(J_{\text{load}}^{\text{T}})}^{+}}{{M}_{\text{load}}}{{\ddot{q}}_{\text{load}}}+{{F}_{\text{I}}}$ | (9) |
式中,
| $\begin{align} & M(q)\ddot{q}+H(q,\dot{q})\dot{q}= \\ & {{\tau }_{\text{M}}}-{{J}^{\text{T}}}{{(J_{\text{load}}^{\text{T}})}^{+}}{{M}_{\text{load}}}{{{\ddot{q}}}_{\text{load}}}-{{J}^{\text{T}}}{{F}_{\text{I}}} \\ \end{align}$ | (10) |
根据冲量定理,对上式两端积分得
| $\begin{align} & \int_{{{t}_{0}}}^{{{t}_{0}}+\Delta t}{[M(q)\ddot{q}+H(q,\dot{q})\dot{q}]}dt= \\ & \int_{{{t}_{0}}}^{{{t}_{0}}+\Delta t}{[}{{\tau }_{\text{M}}}-{{J}^{\text{T}}}{{(J_{\text{load}}^{\text{T}})}^{+}}{{M}_{\text{load}}}{{{\ddot{q}}}_{\text{load}}}-{{J}^{\text{T}}}{{F}_{\text{I}}}]dt \\ \end{align}$ | (11) |
其中,t0为碰撞前瞬间时刻. 在短暂接触时间Δt内,产生了很大的瞬间冲击力,可近似认为该时刻广义坐标无明显变化,而广义速度和广义加速度将发生突变,可以用数学形式表示为
| $\begin{align} & \Delta t=O\left( \iota \right) \\ & \ddot{q},{{{\ddot{q}}}_{\text{load}}}=O\left( \frac{\mathbf{1}}{\iota } \right) \\ & q,\dot{q},{{q}_{\text{load}}},{{{\dot{q}}}_{\text{load}}}=O\left( \mathbf{1} \right) \\ \end{align}$ |
其中,
同时,为避免关节受到过大的冲击力,二者接触时刻空间机器人各关节处于自由状态. 同时,由于
| $\begin{align} & M\left[ \dot{q}({{t}_{0}}+\Delta t)-\dot{q}({{t}_{0}}) \right]+ \\ & {{J}^{\text{T}}}\left[ {{(J_{\text{load}}^{\text{T}})}^{+}}{{M}_{\text{load}}}({{{\dot{q}}}_{\text{load}}}({{t}_{0}}+\Delta t)-{{{\dot{q}}}_{\text{load}}}({{t}_{0}}) \right]=\mathbf{0} \\ \end{align}$ | (12) |
抓取操作完成后,空间机器人与目标物锁紧固连. 设
| ${{J}_{\text{L}}}{{\dot{q}}_{\text{f}}}(t)={{J}_{\text{lL}}}{{\dot{q}}_{\text{load}}}(t)$ | (13) |
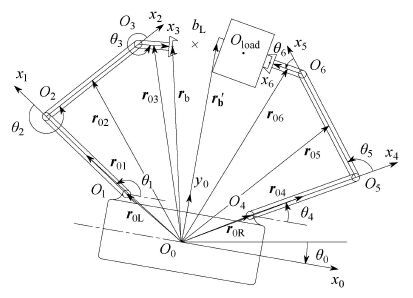
为获得闭链系统运动约束方程,首先将闭链系统在左端断开,如图 2所示,设断开的接触点
|
图 2 捕获后闭链双臂空间机器人系统 Fig.2 Dual-arm space robot with closed chain after the capture |
| $\begin{align} & {{r}_{\text{b}}}={{r}_{0\text{L}}}+{{l}_{1}}{{e}_{\text{0}1}}+{{l}_{2}}{{e}_{\text{0}2}}+{{l}_{3}}{{e}_{03}} \\ & {{r}_{{\text{{b}'}}}}={{r}_{0\text{R}}}+{{l}_{4}}{{e}_{04}}+{{l}_{5}}{{e}_{05}}+({{l}_{6}}+{{d}_{\text{L}}}+{{d}_{\text{R}}}){{e}_{06}} \\ \end{align}$ | (14) |
其中
在连体坐标系
| ${{\dot{r}}_{\text{b}}}={{\dot{r}}_{{\text{{b}'}}}}$ | (15) |
同理,被虚拟断开而形成的两个部分具有相同的角速度,可知
| ${{\dot{\theta }}_{1}}+{{\dot{\theta }}_{2}}+{{\dot{\theta }}_{3}}={{\dot{\theta }}_{4}}+{{\dot{\theta }}_{5}}+{{\dot{\theta }}_{6}}$ | (16) |
式(15)及式(16)可重写为如下形式
| ${{J}_{\text{0L}}}{{\dot{\theta }}_{\text{L}}}={{J}_{\text{0R}}}{{\dot{\theta }}_{\text{R}}}$ | (17) |
| ${{\dot{\theta }}_{1}}+{{\dot{\theta }}_{2}}+{{\dot{\theta }}_{3}}-{{\dot{\theta }}_{4}}-{{\dot{\theta }}_{5}}-{{\dot{\theta }}_{6}}=0$ | (18) |
式中,
综合式(17)及式(18) 可以得到如下关系
| ${{G}_{\text{L}}}{{\dot{\theta }}_{\text{L}}}={{G}_{\text{R}}}{{\dot{\theta }}_{\text{R}}}$ | (19) |
其中,
对式(18)积分可得
| ${{\theta }_{1}}+{{\theta }_{2}}+{{\theta }_{3}}-{{\theta }_{4}}-{{\theta }_{5}}-{{\theta }_{6}}=c$ | (20) |
此式即表征六边形内角和定理,
令
| $U=[{{I}_{6\times 6}}U_{1}^{\text{T}}]$ | (21) |
| ${{U}_{1}}=[{{O}_{3\times 3}}G_{\text{R}}^{-1}{{G}_{L}}]$ | (22) |
其中,
联合式(19)、 式(21)及式(22)可推得
| $\dot{q}={{U}^{\text{T}}}{{\dot{q}}_{\text{f}}}$ | (23) |
由式(13)可知碰撞结束后被捕获目标与闭链混合体系统广义坐标运动学关系为
| ${{\dot{q}}_{\text{load}}}({{t}_{0}}+\Delta t)=J_{\text{lL}}^{-1}{{J}_{\text{L}}}{{\dot{q}}_{\text{f}}}({{t}_{0}}+\Delta t)$ | (24) |
将式(23)和式(24)代入式(12)得
| $\begin{align} & UM{{U}^{\text{T}}}\left[ {{{\dot{q}}}_{\text{f}}}({{t}_{0}}+\Delta t)-{{{\dot{q}}}_{\text{f}}}({{t}_{0}}) \right]+ \\ & U{{J}^{\text{T}}}{{(J_{\text{load}}^{\text{T}})}^{+}}{{M}_{\text{load}}}\left[ J_{\text{lL}}^{-1}{{J}_{\text{L}}}{{{\dot{q}}}_{\text{f}}}({{t}_{0}}+\Delta t)-{{{\dot{q}}}_{\text{load}}}({{t}_{0}}) \right]=\mathbf{0} \\ \end{align}$ | (25) |
令
| $R=UM{{U}^{\text{T}}}$ | (26) |
由式(25)可解得
| $\begin{align} & {{{\dot{q}}}_{\text{f}}}({{t}_{0}}+\Delta t)= \\ & {{L}^{-1}}\left[ R{{{\dot{q}}}_{\text{f}}}({{t}_{0}})+U{{J}^{\text{T}}}{{(J_{\text{load}}^{\text{T}})}^{+}}{{M}_{\text{load}}}{{{\dot{q}}}_{\text{load}}}({{t}_{0}}) \right] \\ \end{align}$ | (27) |
其中,
上述推导过程获得了捕获操作后闭链混合体系统广义速度的计算公式.下一部分将以碰撞冲击分析为基础,对失稳的闭链混合体系统进行镇定运动控制设计.
为获得闭链混合体系统动力学方程,首先对式(13)及式(23)求导并整理得
| ${{\ddot{q}}_{\text{load}}}=J_{\text{lL}}^{-1}{{\dot{J}}_{\text{L}}}{{\dot{q}}_{\text{f}}}+J_{\text{lL}}^{-1}{{J}_{\text{L}}}{{\ddot{q}}_{\text{f}}}-J_{\text{lL}}^{-1}{{\dot{J}}_{\text{L}}}{{\dot{q}}_{\text{load}}}$ | (28) |
| $\ddot{q}={{U}^{\text{T}}}{{\ddot{q}}_{\text{f}}}+{{\dot{U}}^{\text{T}}}{{\dot{q}}_{\text{f}}}$ | (29) |
将式(13)、 (23)、 (28)和式(29)代入式(10)得
| $\bar{M}{{\ddot{q}}_{\text{f}}}+\bar{H}{{\dot{q}}_{\text{f}}}=U{{\tau }_{\text{M}}}-U{{J}^{\text{T}}}F$ | (30) |
其中
| $\begin{align} & \bar{M}=R+U{{J}^{\text{T}}}{{(J_{\text{load}}^{\text{T}})}^{+}}{{M}_{\text{load}}}J_{\text{lL}}^{-1}{{J}_{\text{L}}} \\ & \bar{H}=U(H{{U}^{\text{T}}}+M{{{\dot{U}}}^{\text{T}}})+ \\ & U{{J}^{\text{T}}}{{(J_{\text{load}}^{\text{T}})}^{+}}{{M}_{\text{load}}}J_{\text{lL}}^{-1}({{{\dot{J}}}_{\text{L}}}-{{{\dot{J}}}_{\text{lL}}}J_{\text{lL}}^{-1}{{{\dot{J}}}_{\text{L}}}) \\ \end{align}$ |
令
| $\bar{\tau }=U{{\tau }_{\text{M}}}{{\bar{F}}_{\text{I}}}=U{{J}^{\text{T}}}{{F}_{\text{I}}}$ | (31) |
将
| $\begin{align} & \bar{\tau }={{[\bar{\tau }_{\text{a}}^{\text{T}}\bar{\tau }_{\text{b}}^{\text{T}}]}^{\text{T}}}, \\ & {{{\bar{F}}}_{\text{I}}}={{[\bar{F}_{\text{1a}}^{\text{T}}\bar{F}_{\text{Ib}}^{\text{T}}]}^{\text{T}}} \\ \end{align}$ | (32) |
其中,
| ${{\bar{\tau }}_{\text{a}}}={{\tau }_{\text{N}}}={{\left[ 00{{\tau }_{\text{o}}} \right]}^{\text{T}}}$ | (33) |
| $\Omega {{\left[ \tau _{\text{L}}^{\text{T}}\tau _{\text{R}}^{\text{T}} \right]}^{\text{T}}}={{\bar{\tau }}_{\text{b}}}$ | (34) |
| ${{\bar{F}}_{\text{I}}}={{[\text{00}\bar{F}_{\text{Ib}}^{\text{T}}]}^{\text{T}}}$ | (35) |
式中,
| $\begin{align} & \left[ \begin{matrix} {{{\bar{M}}}_{11}} & {{{\bar{M}}}_{12}} \\ {{{\bar{M}}}_{21}} & {{{\bar{M}}}_{22}} \\ \end{matrix} \right]{{{\ddot{q}}}_{\text{f}}}+\left[ \begin{matrix} {{{\bar{H}}}_{11}} & {{{\bar{H}}}_{12}} \\ {{{\bar{H}}}_{21}} & {{{\bar{H}}}_{22}} \\ \end{matrix} \right]{{{\dot{q}}}_{\text{f}}}= \\ & \left[ \begin{matrix} {{\mathbf{0}}_{2\times 1}} \\ {{{\bar{\tau }}}_{\text{c}}} \\ \end{matrix} \right]-\left[ \begin{matrix} {{\mathbf{0}}_{2\times 1}} \\ {{{\bar{F}}}_{\text{Ib}}} \\ \end{matrix} \right] \\ \end{align}$ | (36) |
其中,
由于闭链混合体不受其他外力的作用,根据动力学方程的推导过程可知
| ${{\bar{M}}_{\text{c}}}{{\ddot{q}}_{\text{c}}}+{{\bar{H}}_{\text{c}}}{{\dot{q}}_{\text{c}}}={{\bar{\tau }}_{\text{c}}}-{{\bar{F}}_{\text{Ib}}}$ | (37) |
式中
| $\begin{align} & {{q}_{\text{c}}}={{[{{\theta }_{0}}\theta _{\text{L}}^{\text{T}}]}^{\text{T}}} \\ & {{{\bar{M}}}_{\text{c}}}={{{\bar{M}}}_{22}}-{{{\bar{M}}}_{21}}\bar{M}_{11}^{-1}{{{\bar{M}}}_{12}} \\ & {{{\bar{H}}}_{\text{c}}}={{{\bar{H}}}_{22}}-{{{\bar{M}}}_{21}}\bar{M}_{11}^{-1}{{{\bar{H}}}_{12}} \\ \end{align}$ |
抓取操作完成后,假设机械臂末端执行器与目标上对应的捕获点锁紧,形成整体,闭链混合体系统的内力项对系统运动无影响,则动力学方程(28)可改写为
| ${{\bar{M}}_{\text{c}}}{{\ddot{q}}_{\text{c}}}+{{\bar{H}}_{\text{c}}}{{\dot{q}}_{\text{c}}}={{\bar{\tau }}_{\text{c}}}$ | (38) |
上式即为捕获操作结束后的系统完全驱动形式的动力学方程.式(38)可通过将对称的内力项
空间机器人的系统动力学模型是难以精确获得的,存在一定程度的参数摄动,惯量矩阵可表示为
| $\begin{align} & {{{\bar{M}}}_{\text{c}}}={{{\hat{\bar{M}}}}_{\text{c}}}+\Delta {{{\bar{M}}}_{\text{c}}} \\ & {{{\bar{H}}}_{\text{c}}}={{{\hat{\bar{H}}}}_{\text{c}}}+\Delta {{{\bar{H}}}_{\text{c}}} \\ \end{align}$ |
其中,
| ${{\hat{\bar{M}}}_{\text{c}}}{{\ddot{q}}_{\text{c}}}+{{\hat{\bar{H}}}_{\text{c}}}{{\dot{q}}_{\text{c}}}={{\bar{\tau }}_{\text{c}}}+\xi $ | (39) |
式中,
采用单点模糊化、乘积推理和中心平均加权去模糊化构成的模糊系统输出为[29-30]
| $f(y)={{W}^{\text{T}}}\zeta (y)$ | (40) |
式中,W是权值矩阵,
| ${{\zeta }_{k}}({{y}_{1}},{{y}_{2}},\cdots ,{{y}_{n}})=\frac{\prod\limits_{j=1}^{n}{{{\mu }_{F_{j}^{k}}}}({{y}_{j}})}{\sum\limits_{k=1}^{n}{[}\prod\limits_{j=1}^{n}{{{\mu }_{iF_{j}^{k}}}}]({{y}_{j}})]}$ |
隶属度函数选取高斯基函数
| ${{\mu }_{F_{j}^{k}}}={{\exp }^{-[({{y}_{j}}-a_{jk}^{2})/b_{jk}^{2}]}}$ |
定理(万能逼近定理)[31]:设g(y)是定义在致密集
| $\underset{x\in U}{\mathop{\text{sup}}}\,|f(y)-g(y)|<\varepsilon $ | (41) |
为便于分析,引入状态变量
| $\dot{x}=Ax+BG(X,{{\bar{\tau }}_{\text{c}}})$ | (42) |
式中,
| $\begin{align} & A=\text{diag}({{A}_{1}}{{A}_{2}}{{A}_{3}}{{A}_{4}}),{{A}_{j}}=\left[ \begin{matrix} 0 & 1 \\ 0 & 0 \\ \end{matrix} \right] \\ & B=\text{diag}({{B}_{1}}{{B}_{2}}{{B}_{3}}{{B}_{4}}),{{B}_{j}}=\left[ \begin{matrix} 0 \\ 1 \\ \end{matrix} \right], \\ & j=1,2,3,4 \\ & G=\text{diag}({{G}_{1}}{{G}_{2}}{{G}_{3}}{{G}_{4}}) \\ & G=-[{{{\hat{\bar{M}}}}^{-1}}(\hat{\bar{H}}{{{\dot{q}}}_{\text{c}}}-\xi -{{{\bar{\tau }}}_{c}})] \\ \end{align}$ |
假设系统状态完全可测,根据模糊逻辑系统设计一个自适应模糊控制器,使得整个闭环系统趋于稳定,系统(42)可表示为
| $\dot{x}=Ax+B[\Delta G(x,{{\bar{\tau }}_{\text{c}}})+{{\hat{\bar{\tau }}}_{c}}]$ | (43) |
其中
| $\begin{align} & \Delta G(x,{{{\bar{\tau }}}_{\text{c}}})=-({{{\hat{\bar{\tau }}}}_{\text{c}}}-G) \\ & {{{\bar{\tau }}}_{\text{c}}}={{{\hat{h}}}^{-1}}(x,{{{\hat{\bar{\tau }}}}_{\text{c}}}) \\ & \hat{h}(x,t)=-[{{{\hat{\bar{M}}}}^{-1}}(\hat{\bar{H}}{{{\dot{q}}}_{\text{c}}}-\xi )]+{{{\hat{\bar{M}}}}^{-1}}{{{\bar{\tau }}}_{\text{c}}} \\ \end{align}$ |
且
设
| ${{e}_{\text{c}}}={{q}_{\text{c}}}-{{q}_{\text{cd}}}$ | (44) |
其中
设计控制器如下
| ${{\hat{\bar{\tau }}}_{\text{c}j}}={{\tau }_{\text{d}j}}+{{\tau }_{\text{f}j}}+{{\tau }_{\text{h}j}}$ | (45) |
| ${{\tau }_{\text{d}j}}={{\ddot{q}}_{\text{d}j}}+{{K}_{j}}{{\Xi }_{j}}$ | (46) |
| ${{\tau }_{\text{f}j}}(x|{{w}_{j}})=w_{j}^{\text{T}}{{\zeta }_{j}}(x)$ | (47) |
其中,
| ${{P}_{j}}{{A}_{\text{k}j}}+A_{\text{k}j}^{\text{T}}{{P}_{j}}-(\frac{2}{\lambda }-\frac{1}{{{\rho }^{2}}}){{P}_{j}}{{B}_{j}}B_{j}^{\text{T}}{{P}_{j}}=-{{Q}_{j}}$ | (49) |
其中,
定义模糊系统权值向量逼近误差为
| ${{\tilde{w}}_{j}}=w_{j}^{*}-{{w}_{j}}$ | (50) |
据自适应模糊的万能逼近特性,存在
| $w_{j}^{*}=\underset{{{w}_{j}}\in {{R}^{n}}}{\mathop{\text{argmin}}}\,[\underset{x\in {{R}^{n}}}{\mathop{\text{sup}}}\,|w_{j}^{\text{T}}{{\zeta }_{j}}(x)-\tau _{\text{f}j}^{*}|]$ |
选取权值向量的自适应律为
| ${{\dot{w}}_{j}}=-{{\eta }_{j}}\Xi _{j}^{\text{T}}{{P}_{j}}{{B}_{j}}{{\zeta }_{j}}(x)$ | (51) |
将控制律式(45)代入到式(43)中得到误差方程为
| ${{\overset{.}{\mathop{\text{ }\Xi }}\,}_{j}}={{A}_{\text{k}j}}\text{ }{{\Xi }_{j}}+{{B}_{j}}{{\tau }_{\text{h}j}}+{{B}_{j}}\tilde{w}_{j}^{\text{T}}{{\zeta }_{j}}+{{B}_{j}}{{\omega }_{j}}$ | (52) |
系统控制器采用输入方案(45),选取自适应律式(51),对于给定的抑制水平ρ > 0,且满足
| $\begin{align} & \int_{\text{0}}^{T}{{{\Xi }^{\text{T}}}}Q\Xi dt\le {{\Xi }^{\text{T}}}(0)P\Xi (0)+\frac{1}{\eta }{{{\tilde{W}}}^{\text{T}}}(0)\tilde{W}(0)+ \\ & {{\rho }^{2}}\int_{0}^{T}{{{\omega }^{\text{T}}}}\omega dt \\ \end{align}$ | (53) |
其中,
证明:选取李雅普诺夫函数为
| $V={{V}_{1}}+{{V}_{2}}+{{V}_{3}}+{{V}_{4}}$ | (54) |
| ${{V}_{j}}=\frac{1}{2}\Xi _{j}^{\text{T}}P\text{ }{{\Xi }_{j}}+\frac{1}{2{{\eta }_{j}}}\tilde{w}_{j}^{\text{T}}{{\tilde{w}}_{j}}(j=1,2,3,4)$ | (55) |
上式对时间微分
| $\begin{align} & {{{\dot{V}}}_{j}}=\frac{1}{2}\Xi _{j}^{\text{T}}{{P}_{j}}{{\Xi }_{j}}+\frac{1}{2}\Xi _{j}^{\text{T}}{{P}_{j}}{{\Xi }_{j}}+\frac{1}{{{\eta }_{j}}}\tilde{w}_{j}^{\text{T}}{{{\dot{\tilde{w}}}}_{j}}= \\ & \frac{1}{2}(\Xi _{j}^{\text{T}}A_{\text{k}j}^{\text{T}}{{P}_{j}}{{\Xi }_{j}}+{{\tau }_{hi}}B_{j}^{\text{T}}{{P}_{j}}{{\Xi }_{j}}+\tilde{w}_{j}^{\text{T}}{{\zeta }_{j}}B_{j}^{\text{T}}{{P}_{j}}{{\Xi }_{j}}+ \\ & {{\omega }_{j}}B_{j}^{\text{T}}{{P}_{j}}{{\Xi }_{j}}+\Xi _{j}^{\text{T}}{{P}_{j}}{{A}_{\text{k}j}}{{\Xi }_{j}}+\Xi _{j}^{\text{T}}{{P}_{j}}{{B}_{j}}{{\tau }_{hi}}+ \\ & \Xi _{j}^{\text{T}}{{P}_{j}}{{B}_{j}}\tilde{w}_{j}^{\text{T}}{{\zeta }_{j}}+{{\omega }_{j}}\Xi _{j}^{\text{T}}{{P}_{j}}{{B}_{j}})+\frac{1}{{{\eta }_{j}}}\tilde{w}_{j}^{\text{T}}{{{\dot{\tilde{w}}}}_{j}}= \\ & \frac{1}{2}\Xi _{j}^{\text{T}}(A_{\text{k}j}^{\text{T}}P+{{P}_{j}}A_{\text{k}j}^{\text{T}}-\frac{2}{\lambda }{{P}_{j}}{{B}_{j}}B_{j}^{\text{T}}{{P}_{j}}){{\Xi }_{j}}+ \\ & \frac{1}{2}{{\omega }_{j}}(\Xi _{j}^{\text{T}}{{P}_{j}}{{B}_{j}}+B_{j}^{\text{T}}{{P}_{j}}{{\Xi }_{j}})+ \\ & \tilde{w}_{j}^{\text{T}}(\Xi _{j}^{\text{T}}{{P}_{j}}{{B}_{j}}{{\zeta }_{j}}+\frac{1}{{{\eta }_{j}}}{{{\dot{\tilde{w}}}}_{j}}) \\ \end{align}$ | (56) |
考虑
| $\begin{align} & {{{\dot{V}}}_{j}}=-\frac{1}{2}{{(\frac{1}{\rho }B_{j}^{\text{T}}{{P}_{j}}{{\Xi }_{j}}-\rho {{\omega }_{j}})}^{2}} \\ & -\frac{1}{2}\Xi _{j}^{\text{T}}{{Q}_{j}}{{\Xi }_{j}}+\frac{1}{2}{{\rho }^{2}}\omega _{j}^{2}\le \\ & -\frac{1}{2}\Xi _{j}^{\text{T}}{{Q}_{j}}{{\Xi }_{j}}+\frac{1}{2}{{\rho }^{2}}\omega _{j}^{2} \\ \end{align}$ | (57) |
对式(57)两边求积分得
| ${{V}_{j}}(T)-{{V}_{j}}(0)\le \int_{0}^{T}{(}-\frac{1}{2}\Xi _{j}^{\text{T}}{{Q}_{j}}{{\Xi }_{j}}+\frac{1}{2}{{\rho }^{2}}\omega _{j}^{2})dt$ | (58) |
设
| $\begin{align} & \int_{\text{0}}^{T}{{{\Xi }^{\text{T}}}}Q\Xi dt\le {{\Xi }^{\text{T}}}(0)P\Xi (0)+ \\ & \frac{1}{\eta }{{{\tilde{W}}}^{\text{T}}}(0)\tilde{W}(0)+{{\rho }^{2}}\int_{0}^{T}{{{\omega }^{\text{T}}}}\omega dt \\ \end{align}$ |
即系统跟踪误差满足
由于
| $\left[ \begin{matrix} {{\tau }_{\text{L}}} \\ {{\tau }_{\text{R}}} \\ \end{matrix} \right]=E{{\Omega }^{\text{T}}}{{\left( \Omega E{{\Omega }^{\text{T}}} \right)}^{-1}}{{\bar{\tau }}_{\text{b}}}$ | (59) |
其中,
以做平面运动的双臂空间机器人系统捕获目标过程为例.
双臂空间机器人系统惯性参数选取为:
设双臂空间机器人捕获时初始构型为
| $q={{[0.3\text{m}0.3\text{m}{{0}^{{}^\circ }}{{120}^{{}^\circ }}-{{60}^{{}^\circ }}-{{60}^{{}^\circ }}{{60}^{{}^\circ }}{{60}^{{}^\circ }}{{60}^{{}^\circ }}]}^{\text{T}}}$ |
被捕获目标初始速度值为
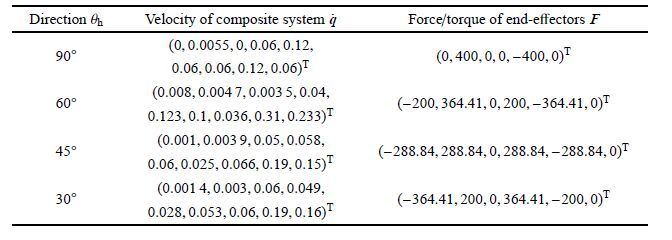
| 表 1 不同角度冲击效应比较(目标无角速度) Table 1 Impact effect of different angle (target without angular velocity) |
| 表 2 不同角度冲击效应比较(目标有角速度) Table 2 Impact effect of different angle(target with angular velocity) |
从表 1及表 2作用力对比中可以看出,
在太空条件下,更需要控制负载姿态(如释放卫星)及载体姿态(如通信需求),负载姿态可通过如下公式获得
| ${{q}_{\text{load}}}={{\theta }_{\text{0}}}+{{\theta }_{\text{1}}}+{{\theta }_{\text{2}}}+{{\theta }_{\text{3}}}$ |
已知左臂各关节角度
仍选取上述初始捕获构型及捕获目标初始速度值,
控制器相关参数选取为:
仿真时设碰撞后瞬时时刻为初始时间,控制要求为:在2 s的反应时间后启动控制器,将系统恢复至初始状态并稳定,镇定运动过程仿真时间取18 s.
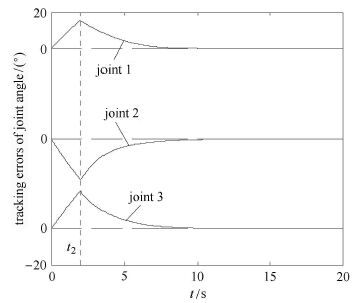
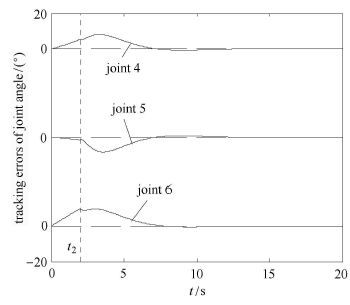
图 3 $\sim$图 5为镇定运动过程,其中负载姿态角跟踪误差指其偏离初始位置的偏离量.图 3为载体、载荷误差收敛情况,两根零线之间所代表的角度差值为20°.图 4及图 5为左右机械臂关节角误差收敛情况,两根零线之间所代表的角度差值为50°.仿真结果表明,双臂空间机器人系统受到冲击后,载体、臂杆产生了一定幅度的晃动.设碰撞冲击2 s后的瞬时时刻为t2,结合上述推导过程及数值仿真分析,可获得在t2时刻混合体系统的载体姿态及关节角形成新的姿态构型为
| $\begin{align} & {{q}_{\theta }}=[{{\theta }_{0}}\theta _{\text{L}}^{\text{T}}\theta _{\text{R}}^{\text{T}}]=[{{2.7}^{{}^\circ }}{{135.5}^{{}^\circ }}-{{82.5}^{{}^\circ }}-{{39.3}^{{}^\circ }} \\ & {{65.3}^{{}^\circ }}{{58.7}^{{}^\circ }}{{69.9}^{{}^\circ }}] \\ \end{align}$ |

|
图 3 控制开启后载体及负载姿态角跟踪误差 Fig.3 Attitude angle tracking errors of base and load with control |
|
图 4 控制开启后左臂关节角跟踪误差 Fig.4 Joint angle tracking errors of left arm with control |
|
图 5 控制开启后右臂关节角跟踪误差 Fig.5 Joint angle tracking errors of right arm with control |
t2时刻系统的载体姿态及关节角瞬时角速度为
| $\begin{align} & {{{\dot{q}}}_{\theta }}=[0.0220 0.1267-0.1700 0.1658 \\ & 0.0568-0.0185 0.0841]\text{rad/s} \\ \end{align}$ |
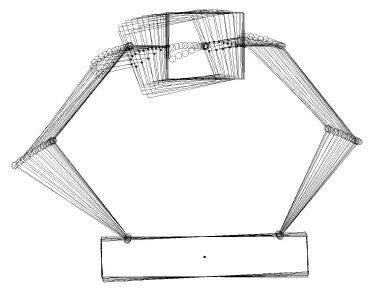
对于不稳定的混合体系统,若不及时采用有效的镇定运动控制方案,基座将产生更大角度的无规律翻滚,而空间设备一般携带有接收器、摄像机等精密设备以及液体燃料仓,不稳定的翻滚状态有可能对设备产生破坏,甚至导致空间任务的失败.开启控制器后,载体、载荷的控制误差渐进收敛于期望轨迹,完成干扰运动镇定控制(消旋运动).图 6为协调镇定运动过程的闭链双臂空间机器人载体姿态、关节角运动过程动态模拟图.
|
图 6 控制开启后载体、臂杆姿态运动过程动态模拟图 Fig.6 Motion of base attitude and joint angles with control |
本文在多刚体动力学理论的基础上,结合动量守恒定律,对空间机器人双臂抓取目标卫星的过程进行了碰撞过程动力学演化分析,利用闭链系统几何及运动学约束关系推导了捕获操作结束后混合体系统的动力学方程,对失去稳定性的闭链混合体系统提出了镇定控制方案.并可得到如下结论:
(1) 双臂空间机器人姿态与目标冲击方向的相对角度较大时,会产生较大的垂直于杆件的力.目标卫星具有角速度的情况下,会导致左右臂杆末端执行器受到不同大小的反作用力.
(2) 双臂空间机器人姿态与目标冲击方向的相对角度越小,载体受冲击后的干扰运动越明显.可根据实际情况,适当选取双臂空间机器人与自旋卫星冲击方向的相对角度,将冲击对基座的影响及冲击产生的垂直于臂杆的力调整在合理的范围.
(3) 所提控制方案具有无需获得系统的精确动力学模型,也不要求系统动力学方程为关于惯性参数的线性函数的优点.开启控制器之后,系统能够逐渐恢复至稳定状态,以准备执行下一步的太空任务.文中控制方案经适当扩充,可推广应用于三维空间运动的空间机器人系统中.
| [1] |
Abad AF, Ma O, Pham K, et al. A review of space robotics technologies for on-orbit servicing[J].
Progress in Aerospace Sciences,2014, 68 : 1-26.
DOI: 10.1016/j.paerosci.2014.03.002. ( 0) 0)
|
| [2] |
Yoshida K, Nakanishi H, Ueno N, et al. Dynamics, control and impedance matching for robotic capture of a non-cooperative satellite[J].
Advanced Robotics,2004, 2 (2) : 175-198.
( 0) 0)
|
| [3] |
Walker MW. Adaptive control of space-based robot manipulators[J].
IEEE Transactions on Robotics and Automation,1992, 7 (6) : 828-835.
( 0) 0)
|
| [4] |
谢立敏, 陈力. 漂浮基柔性空间机器人的鲁棒控制及振动抑制[J].
力学学报,2012, 44 (3) : 1057-1065.
( Xie Limin, Chen Li. Robust control and vibration suppression of free-floating flexible space robot[J].
Chinese Journal of Theoretical and Applied Mechanics,2012, 44 (3) : 1057-1065.
(in Chinese) ) ( 0) 0)
|
| [5] |
Narikiyo T, Ohmiya M. Control of a planar space robot: Theory and experiments[J].
Control Engineering,2006, 8 (14) : 875-883.
( 0) 0)
|
| [6] |
程靖, 陈力. 漂浮基空间机器人捕获卫星过程冲击动力学建模及基于非线性滤波器的镇定运动控制[J].
载人航天,2016, 22 (1) : 34-38.
( Cheng Jing, Chen Li. Impact dynamic calming control based on nonlinear filter for free-floating space robot capturing a satellite[J].
Manned Spaceflight,2016, 22 (1) : 34-38.
(in Chinese) ) ( 0) 0)
|
| [7] |
王靖森, 刘晓峰, 段柳成, 等. 考虑关节摩擦的空间机器人动力学建模与参数辨识[J].
力学季刊,2015, 36 (44) : 594-601.
( Wang Jingsen, Liu Xiaofeng, Duan Liucheng, et al. Dynamic modeling and parameter identification of a space robot considering joint friction[J].
Chinese Quarter of Mechanics,2015, 36 (44) : 594-601.
(in Chinese) ) ( 0) 0)
|
| [8] |
戈新生, 孙鹏伟. 自由漂浮空间机械臂非完整运动规划的粒子群优化算法[J].
机械工程学报,2007, 43 (4) : 34-38.
DOI: 10.3901/JME.2007.04.034. ( Ge Xinsheng, Sun Pengwei. Nonholonomic motion planning of space manipulator system using particle swarm optimization[J].
Chinese Journal of Mechanical Engineering,2007, 43 (4) : 34-38.
(in Chinese) DOI: 10.3901/JME.2007.04.034. ) ( 0) 0)
|
| [9] |
Dubanchet V, Saussie D, Alazard D, et al. Modeling and control of a space robot for active debris removal[J].
CEAS Space Journal,2015, 7 (2) : 203-218.
DOI: 10.1007/s12567-015-0082-4. ( 0) 0)
|
| [10] |
Chen J, Chen L. Decentralized adaptive neural network stabilization control and vibration suppression of flexible robot manipulator during capture a target.//The 66rd International Astronautical Congress. Jerusalem, 2015
( 0) 0)
|
| [11] |
Oki T, Nakanishi H, Youshida K. Whole-body motion control for capturing a tumbling target by a free-floating space robot.//Proceeding of the 2007 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Diego, CA: IEEE, 2007: 2256-2261
( 0) 0)
|
| [12] |
Rekleitis, G, Papadopoulos E. On orbit cooperating space robotic servicers handling a passive object[J].
IEEE Transaction on Aerospace and Electronic System,2015, 51 (2) : 803-814.
( 0) 0)
|
| [13] |
Debus TJ, Dougherty SP. Overview and performance of the frontend robotics enabling near-term demonstration (FREND) robotic arm. In: AIAA Infotech and Aerospace Conference. Seattle, Washington, USA: AIAA, 2009: 2009-1870
( 0) 0)
|
| [14] |
Barnhart D, Sullivan B, Hunter R, et al. Phoenix Program Status-2013. In: AIAA Space 2013 Conference and Exposition, San Diego, CA: AIAA, 2013: 1-17
( 0) 0)
|
| [15] |
Reintsema D, Thaeter J, Rathke A, et al. DEOS-the German robotics approach to secure and de-orbit malfunctioned satellites from low earth orbit.//The 10th International Symposium on Artificial Intelligence, Robotics and Automation in Space. Sapporo, Japan, 2010: 244-251
( 0) 0)
|
| [16] |
Kaiser C, Berg F, Delcura JM, et al. SMART-OLEV-An orbit life extension vehicle for servicing commercial spacecrafts in GEO[J].
Acta Astronautica,2008, 63 : 400-410.
DOI: 10.1016/j.actaastro.2007.12.053. ( 0) 0)
|
| [17] |
Sachdev S, Marcotte B, Gibbs G. Canada and the international space station program: overview and status.//International Astronautical Federation-55th International Astronautical Congress 2004. Paris, France: IAF, 2004: 7405-7415
( 0) 0)
|
| [18] |
Afanasiev V, Braigozin D, Kazanski I, et al. RTR-trees for robotics behavior simulation and visualization[J].
Visual Computer,2007, 23 (2) : 347-358.
( 0) 0)
|
| [19] |
Quiocho LJ, Huynh A, Edwin Z. Application of multibody dynamics to on-orbit manipulator simulations.//ASME 2005 International Design Engineering Technical Conferences. Long Beach, California: ASME. 2005: 81-87
( 0) 0)
|
| [20] |
Obermark J, Greamer G, Kelm BE, et al. SUMO/FREND: vision system for autonomous satellite grapple.//Proceeding of SPIESensor and System for Space Applications. Orlando, Florida: SPIE, 2007: 65550Y-1–65550Y-11
( 0) 0)
|
| [21] |
Rathee R, Pathak P. Dual arm free flying space robot trajectory planning using polynomial[J].
Journal of Robotics,2015 : 1-11.
( 0) 0)
|
| [22] |
梁捷, 陈力. 基于标称计算力矩控制器的双臂空间机器人惯性空间轨迹跟踪的模糊自适应补偿控制[J].
工程力学,2010, 27 (11) : 221-228.
( Liang Jie, Chen Li. Fuzzy logic adaptive compensation control for duan-arm space robot based on computed torque control to track desired trajectory in inertia space[J].
Enigieering Mechanics,2010, 27 (11) : 221-228.
(in Chinese) ) ( 0) 0)
|
| [23] |
陈志勇, 陈力. 具有外部扰动及不确定载荷参数双臂空间机器人的拟增广鲁棒与自适应混合控制[J].
工程力学,2010, 27 (12) : 27-33.
( Chen Zhiyong, Chen Li. Robusted-adaptive combined control for dual-arm space robot with external disturbances and uncertain parameters[J].
Engineering Mechanics,2010, 27 (12) : 27-33.
(in Chinese) ) ( 0) 0)
|
| [24] |
Takahashi R, Ise H, Sato D, et al. Hybrid simulation of a dual-arm space robot colliding with a floating object. In: Proceeding of the 2008 IEEE International Conference on Robotics and Automation. Pasadena: IEEE, 2008: 1202-1206
( 0) 0)
|
| [25] |
Shah SV, Sharf I, Misra AK. Reactionless path planning strategies for capture of tumbling objects in space using a dual-arm robotic system. In: AIAA Guidance, Navigation, and Control (GNC) Conference, Guidance, Navigation, and Control and Co-located Conferences, Boston, MA: AIAA, 2013-4521
( 0) 0)
|
| [26] |
郭闻昊, 王天舒. 空间机器人抓捕目标星碰撞前构型优化[J].
宇航学报,2015, 36 (4) : 390-396.
( Guo Wenhao, Wang Tianshu. Pre-impact configuration optimization for a space robot capturing target satellite[J].
Journal of Astronautics,2015, 36 (4) : 390-396.
(in Chinese) ) ( 0) 0)
|
| [27] |
Jia YH, Hu Q, Xu SJ. Dynamics and adaptive control of a dual-arm space robot with closed-loop constraints and uncertain inertial parameters[J].
Acta Mechanica Sinica,2014, 30 (1) : 112-124.
DOI: 10.1007/s10409-014-0005-1. ( 0) 0)
|
| [28] |
Moosavian SF, Papadoupoulos E. On the control of space free-flyer using multiple impedance control. In: Proceeding of the 1997 IEEE International Conference on Robotics and Automation. Albuquerque, New Mexico: IEEE, 1997: 853-858
( 0) 0)
|
| [29] |
Passino KM.
Fuzzy Control[M]. New York: Addison Wesley Longman Press, 1998 .
( 0) 0)
|
| [30] |
Kovacic Z, Bojdan S.
Fuzzy Controller Design Theory and Application[M]. Florida: CRC Press, 2005 .
( 0) 0)
|
| [31] |
Wang LX. Stable adaptive fuzzy control of nonlinear systems[J].
IEEE Transaction on Fuzzy Systems,1993, 1 (2) : 146-155.
DOI: 10.1109/91.227383. ( 0) 0)
|
| [32] |
Rubaai A. Direct adaptive fuzzy control design achieving H1 tracking for high performance servo drives[J].
IEEE Transaction on Energy Conversion,1999, 14 (4) : 1199-1208.
DOI: 10.1109/60.815047. ( 0) 0)
|
 2016, Vol. 48
2016, Vol. 48