引言
水下滑翔机作为一种用于海洋探测的水下自主航行观测平台,最早由HenryStommel于1989年提出[1],因其能够实现大范围海域长时间的探测,而在世界海洋调查领域被广泛使用.目前国际上比较典型的水下滑翔机主要有3种,分别是由Webb实验室Webb等研制的Slocum滑翔机[2]、由Washington大学Eriksen等研制的Seaglider滑翔机[3]以及由Scripps海洋研究所Sherman等研制的Spray滑翔机[4].
传统水下滑翔机通过改变自身净浮力,并依靠固定于机身的机翼产生水平方向的分力,实现锯齿形的下潜和上浮运动.它具有功耗低、航程长、工作时间长、隐蔽性高等优点.但由于自身结构限制,传统水下滑翔机又具有速度慢、机动性差、运动形式单一等缺点,不能实现特殊场合的调查任务或者海洋探测.而混合驱动水下滑翔机(hybrid-driven underwater gliders,HUG)通过改变自身净浮力或开启螺旋桨来实现混合驱动,不仅具备了传统水下滑翔机的优点,而且具有良好的自主性和机动性能. 其能够实现3种不同模式的运动,即滑翔模式运动、AUV模式运动和混合驱动模式运动.
目前,国外的混合驱动水下滑翔机主要有韦伯研究公司研制的SlocumAUV[5],北约水下研究中心研制的Folaga-Ⅲ[6]和ACSA Underwater GPS 研制的SeaExplore[7].在国内天津大学于2007年成功研制了第一台混合驱动水下滑翔机,随后于2014年研制出"海燕"混合驱动水下滑翔机,并完成了一系列海试实验,具体如图 1所示.
水下机器人动力学模型参数辨识是水下机器人运动状态控制、路径跟踪、状态监测、故障诊断及容错系统开发的基础,是水下机器人研究的核心内容之一[8].为了对混合驱动水下滑翔机不同运动模式进行准确控制以及精确导航,使其在不同海况下顺利地完成各种复杂任务,获得准确混合驱动水下滑翔机的动力学模型(包括水动力数学模型)以及水动力参数是关键问题.
针对水下潜器的水动力数学模型,国内外学者做了大量细致的工作,如根据翼型理论和势流理论计算并通过实验验证的水下潜器的水动力数学模型[9],依据线性理论表示的鱼雷水动力数学模型[10],以及依据泰勒级数展开公式所表示的非线性鱼雷水动力数学模型和潜艇水动力数学模型[10-11].
对于不同类型的水下机器人,在不可预知的海洋环境中,其水动力参数是不确定的.而水动力参数详细描述了在水下环境中作用在机器人上的水动力和水动力矩,其准确与否直接关系到水下滑翔机的运动结果[9].因此,在混合驱动水下滑翔机动力学模型(包括水动力学模型)已知的基础上,如何获得准确的水动力参数成为本文主要研究的内容.
总的来说,获得水动力参数的方法主要包括:解析法[12-13]、试验法[14]、计算流体力学(computationalfluid dynamics,CFD)方法[15-18]、 半经验法[19]和参数辨识方法[20]. 其中,解析法依据strip理论获得水动力参数,对于细长体外形和航行参数小范围变化的运动过程,该方法得到的水动力参数是可以接受的;而对于其他外形如比目鱼形状,航行参数大范围变化的运动过程,其获得的水动力参数则与试验结果存在较大差距.试验方法主要包括风洞试验、水池试验和拖拽试验等,但其成本高并耗时长.CFD方法具有成本低,时间周期短,能够计算各种复杂外形不同航行参数(如大攻角)条件下的航行器水动力参数等特点.但CFD方法结果需要得到风洞试验、水池试验或实际物理流场的验证.这是由于CFD方法的计算结果往往取决于对复杂流场仿真前置处理时的边界条件、物理参数等的定义是否符合实际,以及计算方法与后置处理是否准确. 半经验法是通过试验得出的相关准则来估计一般形状物体的水动力参数,由于该方法需要将科学理论、经验、专家判断以及试验相结合,针对某些特殊外形模型参数估计,其估计结果是不理想的.参数辨识是系统辨识的一部分,具体是指在模型辨识完成的基础上,根据试验数据,利用参数辨识方法对模型中的未知参数进行估计.该方法多应用于飞行器的气动参数辨识中[21- 25].常用的参数辨识方法是极大似然法,因其具有完备的理论体系,以及良好的有效性、渐近一致性、渐近正态性等性质,在飞行器等系统的参数辨识中,应用十分广泛[26].在水下潜器的动力学建模以及水动力参数的获取方面,系统辨识也有部分应用.如,傅慧萍[27]应用系统辨识技术对潜射导弹运载器的水下弹道动力学系统进行了建模;刘建成等[28]利用基于极大似然准则的系统辨识技术实现了对水下机器人的水平面动力学建模.马岭等[29]基于最小二乘准则,以收缩映射遗传算法为辨识算法,对载人潜水器水动力参数进行辨识,获得了水平面动力学模型.朱大奇等[8]利用量子粒子群算法对水下机器人参数进行了辨识.另外,澳大利亚海上平台部门的Jones等[9],详细地阐述了水动力学模型的构建和参数计算方法,提高了水下潜器动力学模型的精度.美国弗吉尼亚理工学院暨州立大学Geisbert[19]利用计算流体力学方法对两种不同形状水下滑翔机的水动力参数进行计算.美国普林斯顿大学Graver等[20]利用模型参数辨识来匹配滑翔试验数据,从而得到相关水动力参数.美国佐治亚技术研究所Wang等[30]利用理论计算方法、计算流体力学方法仿真以及场地试验,获得了EcoMapper的全部水动力参数.
上述涉及的方法,一方面需要获得水下潜器诸如速度、纵倾角以及攻角等航行参数,以及测量或者计算得到的水动力(矩),从而进一步求解水动力参数(这就需要传感器设备对相关物理量如航行参数、力、力矩等进行测量);另一方面计算结果需与实验结果进行验证,方可得到相对可靠的水动力参数.目前针对混合驱动水下滑翔机的水动力参数辨识,少有文献涉及.而且滑翔机自身搭载的传感设备有限,如测量滑翔速度、攻角物理量的传感器目前无法集成,因此这些参数无法直接得到.为了克服滑翔机搭载传感器有限的困难,以及充分利用现场试验数据,本文提出一种在有限航行参数条件下,基于大数据统计分析的计算流体力学和参数辨识相结合来获取混合驱动水下滑翔机的水动力参数的方法.具体过程为:首先,根据"海燕"水下滑翔机的实际运动,建立其动力学模型,并推导出稳态数据和所求水动力参数之间的关系.接着,采用CFD方法得到其航行升力系数.在此基础上,采用大数据统计分析方法从大量滑翔实验数据中获取所需稳态数据,仅利用单一航行参数纵倾角即可辨识出其滑翔运动模式下的水动力参数.最后,根据其混合驱动实验数据辨识出与螺旋桨相关的水动力参数,从而得到所需全部水动力参数.根据得到的纵平面水动力参数,对其运动进行仿真并与实验结果对比分析,验证了该方法的准确性.
1 动力学建模
1.1 "海燕"水下滑翔机结构
"海燕"混合驱动水下滑翔机主要由滑翔机壳体、固定质量(包括配重块、机翼及附件等)、螺旋桨推进单元、浮力驱动单元、俯仰调节单元和滚转调节单元组成. 在建模时,可将上述单元抽象成一系列质点,滑翔机整体可看作由这些质点组成的系统,具体滑翔机质量分布如图 2所示.
图中,壳体的质量为$m_{\rm h} $,配重块的质量为$m_{\rm w} $,这两部分质量的位置是固定不变的.滑翔机通过安装在其头部的浮力驱动单元改变自身体积从而实现净浮力的变化.在这里可以将浮力驱动单元抽象成可变质量为$m_{\rm b} $的质量块,但其位置固定.俯仰调节单元可以看作是沿滑翔机主轴线方向移动的质量块$\bar{m}$,其通过自身移动产生俯仰力矩来实现滑翔机俯仰姿态的调节.滚转调节单元可以看作是绕主轴线转动的偏心质量块,其通过自身转动产生对滑翔机主轴的滚转力矩来调节滑翔机的滚转姿态.在实际设计中,"海燕"水下滑翔机的俯仰调节单元与滚转调节单元是同一质量块为$\bar {m}$.螺旋桨推进单元安装在滑翔机尾部,滑翔机通过螺旋桨转动产生推力实现推进运动.
1.2 纵平面动力学模型
水下滑翔机的运动形式主要是在纵平面的"之"字形运动,因此,在参数辨识前首先需要建立其在纵平面内的动力学模型.
(1) 坐标系的建立
为描述水下滑翔机的动力学模型,首先需要定义惯性坐标系和体坐标系. 惯性坐标系(o-xyz)选取水平面上任意一点为原点,ox轴方向沿着滑翔机主航向方向,oz轴竖直向下,oy轴方向满足右手定则. 体坐标系($o_{1}$-$e_{1}e_{2}e_{3}$)的原点位于滑翔机的浮心CB处,$o_{1}e_{1}$轴沿着滑翔机主体轴线指向头部,$o_{1}e_{3}$垂直于$o_{1}e_{1}$轴并指向滑翔机的下方,$o_{1}e_{2}$方向满足右手定则,具体坐标系的定义如图 3所示.
(2)水动力模型
水下滑翔机在水下运动时,会受到水动力的作用,而水动力的大小直接决定着滑翔机的运动结果. 水下滑翔机在纵平面运动时,所受到的水动力主要有升力L,阻力D和纵倾力矩M,文献[31]研究表明,升力和纵倾力矩与攻角之间为近似线性关系、阻力与攻角之间为近似二次函数关系,并可表示如下[31]
|
$D=\frac{1}{2}\rho {{C}_{D}}(\alpha )A{{V}^{2}}\approx ({{K}_{{{D}_{0}}}}+{{K}_{D}}{{\alpha }^{2}})(v_{1}^{2}+v_{3}^{2})$
|
(1) |
|
$L=\frac{1}{2}\rho {{C}_{L}}(\alpha )A{{V}^{2}}\approx ({{K}_{{{L}_{0}}}}+{{K}_{L}}\alpha )(v_{1}^{2}+v_{3}^{2})$
|
(2) |
|
${{M}_{DL}}=\frac{1}{2}\rho {{C}_{M}}(\alpha )A{{V}^{2}}\approx ({{K}_{{{M}_{0}}}}+{{K}_{M}}\alpha )(v_{1}^{2}+v_{3}^{2})$
|
(3) |
式中,ρ是海水的密度,A是滑翔机的横截面积,V是滑翔机的合速度,v1和v3是合速度水平和竖直分量,α是攻角,$C_D (\alpha )$,$C_L(\alpha )$,$C_M (\alpha )$是需要辨识的水动力参数,在三者已知的基础上,即可进一步求得水动力参数$K_{D_0 } $,KD ,$K_{L_0 } $,KL ,$K_{M_0 } $和KM.
(3)螺旋桨推力模型
螺旋桨的推力可以用下式表示[32]
|
$T={{K}_{T}}\rho d_{\text{p}}^{4}{{n}^{2}}$
|
(4) |
式中,KT 是需要辨识的螺旋桨推力系数,$d_{\rm p} $是螺旋桨的直径,n是螺旋桨的转速.
(4)水下滑翔机动力学模型
根据水下滑翔机的受力分析,具体如图 3所示,采用拉格朗日方法建立混合驱动水下滑翔机在纵平面内的动力学方程,如下所示[31]
|
$\dot{x}={{v}_{1}}\cos \theta +{{v}_{3}}\sin \theta $
|
(5) |
|
$\dot{z}=-{{v}_{1}}\sin \theta +{{v}_{3}}\cos \theta $
|
(6) |
|
$\dot{\theta }={{\Omega }_{2}}$
|
(7) |
|
$\begin{align}
& {{{\dot{\Omega }}}_{2}}=\frac{1}{{{J}_{2}}}[({{m}_{3}}-{{m}_{1}}){{v}_{1}}{{v}_{3}}-({{r}_{\text{P1}}}{{P}_{\text{P1}}}+{{r}_{\text{P3}}}{{P}_{\text{P3}}}){{\Omega }_{2}}- \\
& \bar{m}\text{g}({{r}_{\text{P1}}}\cos \theta +{{r}_{\text{P3}}}\sin \theta )+{{M}_{DL}}-{{r}_{\text{P3}}}{{u}_{1}}+{{r}_{\text{P1}}}{{u}_{3}}] \\
\end{align}$
|
(8) |
|
$\begin{align}
& {{{\dot{v}}}_{1}}=\frac{1}{{{m}_{1}}}(-{{m}_{3}}{{v}_{3}}{{\Omega }_{2}}-{{P}_{P3}}{{\Omega }_{2}}-{{m}_{0}}\text{g}\sin \theta + \\
& L\sin \alpha -D\cos \alpha -{{u}_{1}}+T) \\
\end{align}$
|
(9) |
|
$\begin{align}
& {{{\dot{v}}}_{3}}=\frac{1}{{{m}_{3}}}({{m}_{1}}{{v}_{1}}{{\Omega }_{2}}+{{P}_{P1}}{{\Omega }_{2}}+{{m}_{0}}\text{g}\cos \theta - \\
& L\cos \alpha -D\sin \alpha -{{u}_{3}}) \\
\end{align}$
|
(10) |
|
${{\dot{r}}_{P1}}=\frac{1}{{\bar{m}}}{{P}_{\text{P1}}}-{{v}_{1}}-{{r}_{\text{P3}}}{{\Omega }_{2}}$
|
(11) |
|
${{\dot{r}}_{P3}}=\frac{1}{{\bar{m}}}{{P}_{\text{P3}}}-{{v}_{3}}-{{r}_{\text{P1}}}{{\Omega }_{2}}$
|
(12) |
|
${{\dot{P}}_{\text{P1}}}={{u}_{1}}$
|
(13) |
|
${{\dot{P}}_{\text{P3}}}={{u}_{3}}$
|
(14) |
|
${{\dot{m}}_{\text{b}}}={{u}_{4}}$
|
(15) |
|
$T={{K}_{T}}\rho d_{\text{p}}^{4}{{n}^{2}}$
|
(16) |
2 水动力参数辨识
为了利用实验数据对水动力参数进行辨识,需要得到水下滑翔机在稳态运动时的平衡方程.根据实际稳态运动情况,将式(8)至式(15)等号左半部分设为零,即可得到水下滑翔机的稳态平衡方程,具体如下
|
$\dot{x}={{v}_{1}}\cos \theta +{{v}_{3}}\sin \theta $
|
(17) |
|
$\dot{z}=-{{v}_{1}}\sin \theta +{{v}_{3}}\cos \theta $
|
(18) |
|
$\begin{align}
& 0=({{m}_{f3}}-{{m}_{f1}}){{v}_{\text{1eq}}}{{v}_{\text{3eq}}}- \\
& \bar{m}g({{r}_{\text{P1eq}}}\cos {{\theta }_{\text{eq}}}+{{r}_{\text{P3eq}}}\sin {{\theta }_{\text{eq}}})- \\
& {{m}_{{{b}_{eq}}}}g({{r}_{\text{B1}}}\cos {{\theta }_{\text{eq}}}+{{r}_{\text{B3}}}\sin {{\theta }_{\text{eq}}})- \\
& {{m}_{w}}g({{r}_{\text{W1}}}\cos {{\theta }_{\text{eq}}}+{{r}_{\text{W3}}}\sin {{\theta }_{\text{eq}}})+{{M}_{DL}} \\
\end{align}$
|
(19) |
|
$0={{L}_{\text{eq}}}\sin {{\alpha }_{\text{eq}}}-{{D}_{\text{eq}}}\cos {{\alpha }_{\text{eq}}}-{{m}_{{{0}_{\text{eq}}}}}g\sin {{\theta }_{\text{eq}}}+{{T}_{\text{eq}}}$
|
(20) |
|
$0={{L}_{\text{eq}}}\cos {{\alpha }_{\text{eq}}}+{{D}_{\text{eq}}}\sin {{\alpha }_{\text{eq}}}-{{m}_{{{0}_{\text{eq}}}}}g\cos {{\theta }_{\text{eq}}}$
|
(21) |
由图 3可以得到滑翔角与纵倾角的关系为
|
$\xi =\theta -\alpha $
|
(22) |
水下滑翔机稳态运动时,升力和阻力之间的关系满足下式
|
${{\xi }_{\text{eq}}}=-{{\tan }^{-1}}(\frac{{{D}_{\text{eq}}}}{{{L}_{\text{eq}}}})$
|
(23) |
水下滑翔机速度之间的关系如下所示
|
$V=\sqrt{v_{1}^{2}+v_{3}^{2}}$
|
(24) |
水下滑翔机下潜深度与速度之间的关系如下所示
|
$\dot{z}=-V\sin \xi =-V\sin (\theta -\alpha )$
|
(25) |
|
$V=\left| \frac{{\dot{z}}}{\sin (\theta -\alpha )} \right|$
|
(26) |
为了得到水下滑翔机的水动力参数和螺旋桨的推力系数,将辨识分为两个过程来进行. 首先,通过滑翔模式下的运动参数得到升力、阻力和纵倾力矩参数. 然后在这3组水动力参数已知的基础上,利用螺旋桨推进模式下的滑翔运动参数辨识出螺旋桨的推力系数.
将式(26)和水动力式(1)到式(3)代入式(20)和式(21)中,可以得到如下方程
|
$\begin{align}
& \frac{1}{2}\rho {{C}_{L}}({{\alpha }_{\text{eq}}})A{{\left( \frac{{{{\dot{z}}}_{\text{eq}}}}{\sin ({{\theta }_{\text{eq}}}-{{\alpha }_{\text{eq}}})} \right)}^{2}}\sin {{\alpha }_{\text{eq}}}- \\
& \frac{1}{2}\rho {{C}_{D}}({{\alpha }_{\text{eq}}})A{{\left( \frac{{{{\dot{z}}}_{\text{eq}}}}{\sin ({{\theta }_{\text{eq}}}-{{\alpha }_{\text{eq}}})} \right)}^{2}}\cos {{\alpha }_{\text{eq}}}- \\
& {{m}_{{{0}_{\text{eq}}}}}g\sin {{\theta }_{\text{eq}}}+{{T}_{\text{eq}}}=0 \\
\end{align}$
|
(27) |
|
$\begin{align}
& \frac{1}{2}\rho {{C}_{L}}({{\alpha }_{\text{eq}}})A{{\left( \frac{{{{\dot{z}}}_{\text{eq}}}}{\sin ({{\theta }_{\text{eq}}}-{{\alpha }_{\text{eq}}})} \right)}^{2}}\cos {{\alpha }_{\text{eq}}}+ \\
& \frac{1}{2}\rho {{C}_{D}}({{\alpha }_{\text{eq}}})A{{\left( \frac{{{{\dot{z}}}_{\text{eq}}}}{\sin ({{\theta }_{\text{eq}}}-{{\alpha }_{\text{eq}}})} \right)}^{2}}\sin {{\alpha }_{\text{eq}}}- \\
& {{m}_{{{0}_{\text{eq}}}}}g\cos {{\theta }_{\text{eq}}}=0 \\
\end{align}$
|
(28) |
2.1 升力系数
为了辨识出水下滑翔机的水动力参数,只有式(27)和式(28)是不能求解的,因为方程未知量(攻角、升力系数、阻力系数和螺旋桨推力系数)的个数大于方程组的个数.而水动力参数辨识的关键是得到攻角的数值,由于实际水下滑翔机没有集成可测量攻角的传感器,需采用其他方法求得.而且在进行水下滑翔机初始方案设计阶段,CFD方法能够为设计者提供极大的方便.所以,本文先通过CFD方法辨识出一个水动力参数,比如升力系数.在此基础上,方程未知量还包括:攻角、阻力系数和螺旋桨推力系数,如果进一步假定螺旋桨不工作,即水下滑翔机作纯滑翔运动,那么由于此时未知量(攻角、阻力系数)的个数等于方程组个数,接着利用测量得到的水下滑翔机的单一航行参数纵倾角θ、竖直下降/上升速度(可以通过搭载于滑翔机本体上的温盐深传感器间接测量得到),即可求得攻角数值大小,从而顺利实现后续水动力参数的辨识.当通过水下滑翔机纯滑翔运动的实验数据辨识出阻力系数以后,再进一步利用螺旋桨开启工作时的混合推进实验数据,即可辨识出螺旋桨推力系数.
对于水下滑翔机升力系数的辨识,具体CFD计算方案如表 1所示.
表 1(Table 1)

表 1 CFD计算方案
Table 1 Calculation schemes of CFD
|
表 1 CFD计算方案
Table 1 Calculation schemes of CFD
|
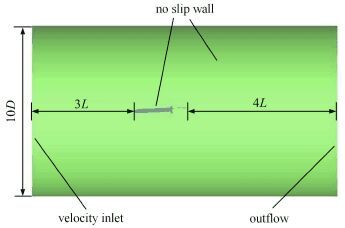
在CFD计算过程中,将计算域设为圆柱形,其直径为水下滑翔机主体最大直径的10倍,前侧面距水下滑翔机头部3倍主体长度,后侧面距水下滑翔机尾部4倍主体长度,具体如图 4所示.采用八叉树的方法对计算域进行非结构网格划分,最终的网格划分结果如图 5所示.
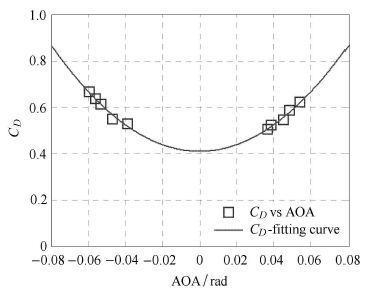
最后采用Standard $k$-$\omega$湍流计算模型对水动力进行求解计算,计算结果如图 6所示,其中AOA (angle
of attack)表示攻角.
根据图 6的计算结果,采用最小二乘法拟合即可得到升力系数与攻角的函数关系
|
${{C}_{L}}(\alpha )=17.9691\alpha -0.0088$
|
(29) |
根据CFD计算求得的升力系数,将式(29)代入到式(27)和式(28)中,并消去阻力系数可以得到
|
$\begin{align}
& 0={{L}_{\text{eq}}}\sin {{\alpha }_{\text{eq}}}-{{m}_{{{0}_{\text{eq}}}}}g\sin {{\theta }_{\text{eq}}}- \\
& \frac{{{L}_{\text{eq}}}\cos {{\alpha }_{\text{eq}}}-{{m}_{{{0}_{\text{eq}}}}}g\cos {{\theta }_{\text{eq}}}}{\sin {{\alpha }_{\text{eq}}}}\cos {{\alpha }_{\text{eq}}}+{{T}_{\text{eq}}} \\
\end{align}$
|
(30) |
|
${{L}_{\text{eq}}}=\frac{1}{2}\rho {{C}_{L}}({{\alpha }_{\text{eq}}})A{{\left( \frac{{{{\dot{z}}}_{\text{eq}}}}{\sin ({{\theta }_{\text{eq}}}-{{\alpha }_{\text{eq}}})} \right)}^{2}}$
|
(31) |
在水下滑翔机稳态纵倾角和稳态竖直下降/上升速度已知的前提下,将式(31)以及$T_{\rm eq}=0$代入方程(30)中,即可求得水下滑翔机稳态运动时的攻角数值大小.
2.2 阻力系数
在求解攻角过程中,需要已知水下滑翔机的稳态纵倾角和稳态竖直下降/上升速度. 水下滑翔机的纵倾角可以通过集成在滑翔机本体上的电子罗盘传感器测量得到;竖直下降/上升速度可以通过搭载于滑翔机本体上的温盐深传感器间接测量得到.因而,为了求得攻角数值,首先需要测量水下滑翔机的纵倾角度和竖直下降/上升速度数据.
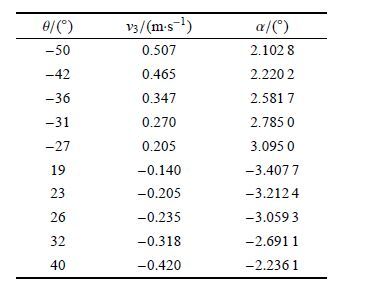
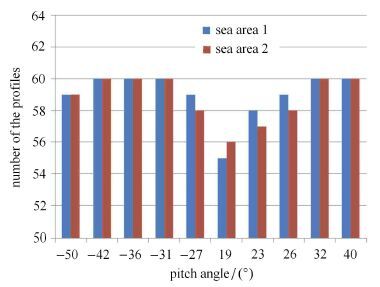
为了测量得到上述数据,以及充分测试水下滑翔机的动力学行为,项目组在南海海域进行了大规模大范围不同纵倾角条件下的海试实验,实验区域如图 7所示. 海试试验整个过程中一共进行了900多组的剖面和直航数据,对于水下潜器来说这是数据量非常大.因此,基于大量现场实验数据,避免单个剖面数据带来的偶然性误差,本文采用大数据统计分析方法获取辨识过程中用到的稳态试验数据. 即首先对海域1内进行的不同目标纵倾角的海试实验进行分层抽样,然后对海域2内进行的不同目标纵倾角的海试实验进行分层抽样,样本总数量为600个.这里需要注意的是,由于实际试验过程中会遇到强海流或者台风以及鱼群等因素的干扰,因此,在选择数据时,需要选择有效的稳态数据作为样本数据.例如,对于图 8所示的实验数据,在滑翔机下潜阶段,选取1 500 s∼4 000 s的稳态纵倾角数值$-27^\circ$作为一组有效值;在滑翔机上浮阶段,选取5 200 s∼6 800 s的稳态纵倾角数值23°作为一组有效值.
最后利用直方图法对测量得到的有效实验数据进行处理,统计结果如图 9所示.
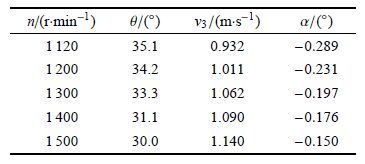
根据得到的纵倾角实验统计结果,以及相应的竖直下降/上升速度,即可求得不同纵倾角下的攻角数值,进而实现对水动力参数的辨识,具体辨识用到的实验数据如表 2所示.
表 2(Table 2)

表 2 辨识采用实验数据
Table 2 Experimental data for identification
|
表 2 辨识采用实验数据
Table 2 Experimental data for identification
|
根据表 2中实验数据以及求得的攻角数值,利用式(27)和式(29)即可计算出阻力系数的大小.
绘制不同攻角下的阻力系数大小关系,如图 10所示. 采用最小二乘法拟合,即可得到阻力系数与攻角的函数关系
|
${{C}_{D}}(\alpha )=71.7{{\alpha }^{2}}+0.4108$
|
(32) |
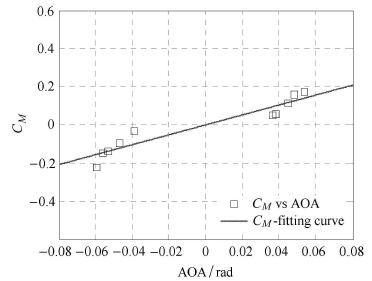
2.3 纵倾力矩系数
考虑到为了能够辨识出纵倾力矩系数,需要利用方程(19),故将惯性水动力矩和黏性水动力矩一起计入到纵倾力矩系数中,具体如下式所示
|
$\frac{1}{2}\rho {{C}_{M}}(\alpha )A{{V}^{2}}=({{m}_{\text{f3}}}-{{m}_{\text{f1}}}){{v}_{\text{1eq}}}{{v}_{\text{3eq}}}+{{M}_{D{{L}_{\text{eq}}}}}$
|
(33) |
将式(33)代入式(3),可以得到如下形式
|
$\begin{align}
& \frac{1}{2}\rho {{C}_{M}}(\alpha )A{{V}^{2}}=\bar{m}g({{r}_{\text{P1eq}}}\cos {{\theta }_{\text{eq}}}+{{r}_{\text{P3eq}}}\sin {{\theta }_{\text{eq}}})+ \\
& {{m}_{{{\text{b}}_{\text{eq}}}}}g({{r}_{\text{B1}}}\cos {{\theta }_{\text{eq}}}+{{r}_{\text{B3}}}\sin {{\theta }_{\text{eq}}})+ \\
& {{m}_{\text{w}}}g({{r}_{\text{W1}}}\cos {{\theta }_{\text{eq}}}+{{r}_{\text{W3}}}\sin {{\theta }_{\text{eq}}}) \\
\end{align}$
|
(34) |
依据表 2中的数据以及式(34),即可计算出不同攻角下的纵倾力矩大小,如图 11所示.采用最小二乘法拟合,即可得到纵倾力矩系数与攻角的函数关系
|
${{C}_{M}}(\alpha )=2.598\alpha $
|
(35) |
2.4 螺旋桨推力系数KT
为了辨识出螺旋桨推力系数,首先也要对螺旋桨推进模式下的攻角数值进行求解. 为了得到攻角数值,将上述求得的水动力系数$C_L (\alpha )$和$C_D (\alpha )$代入到式(28)中,得到
|
$\begin{align}
& \frac{1}{2}\rho (17.9691{{\alpha }_{\text{eq}}}-0.00898)A{{\left( \frac{{{{\dot{z}}}_{\text{eq}}}}{\sin ({{\theta }_{\text{eq}}}-{{\alpha }_{\text{eq}}})} \right)}^{2}}\cos {{\alpha }_{\text{eq}}}+ \\
& \frac{1}{2}\rho (71.7\alpha _{\text{eq}}^{2}+0.4108)A{{\left( \frac{{{{\dot{z}}}_{\text{eq}}}}{\sin ({{\theta }_{\text{eq}}}-{{\alpha }_{\text{eq}}})} \right)}^{2}}\sin {{\alpha }_{\text{eq}}} \\
& -{{m}_{{{0}_{\text{eq}}}}}g\cos {{\theta }_{\text{eq}}}=0 \\
\end{align}$
|
(36) |
式(36)中,只有攻角是未知量,将螺旋桨开启时的相关实验数据代入方程求解,即可得到攻角的实际值.
在攻角已知的基础上,通过对方程(27)进行变换,得到稳态运动时的螺旋桨推力与攻角的关系表达式,具体如下所示
|
$\begin{align}
& {{T}_{\text{eq}}}=-\frac{1}{2}\rho {{C}_{L}}({{\alpha }_{\text{eq}}})A{{\left( \frac{{{{\dot{z}}}_{\text{eq}}}}{\sin ({{\theta }_{\text{eq}}}-{{\alpha }_{\text{eq}}})} \right)}^{2}}\sin {{\alpha }_{\text{eq}}}+ \\
& \frac{1}{2}\rho {{C}_{D}}({{\alpha }_{\text{eq}}})A{{\left( \frac{{{{\dot{z}}}_{\text{eq}}}}{\sin ({{\theta }_{\text{eq}}}-{{\alpha }_{\text{eq}}})} \right)}^{2}}\cos {{\alpha }_{\text{eq}}} \\
& +{{m}_{0\text{eq}}}g\sin {{\theta }_{\text{eq}}} \\
\end{align}$
|
(37) |
辨识时采用的实验数据如表 3所示.
表 3(Table 3)

表 3 辨识采用实验数据
Table 3 Experimental data for identification
|
表 3 辨识采用实验数据
Table 3 Experimental data for identification
|
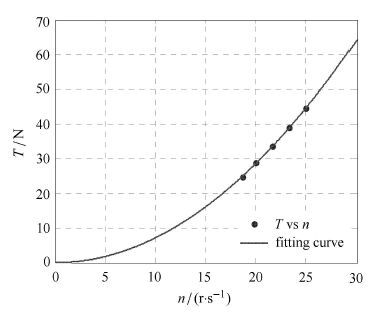
将表 3中的数据代入式(37)中,即可计算得到不同转速下的螺旋桨实际推力大小,具体如图 12所示. 根据采用最小二乘法拟合的结果,如图 12所示以及式(4)所表示的螺旋桨推力与转速的函数关系,即可得到KT 的数值为 0.033 71.与根据推力系数与进速比图谱查到的KT=0.034有差别,但差别很小,表明利用该辨识方法得出的推力系数是有效的,更能反映螺旋桨的实际工作情况.
3 实验验证
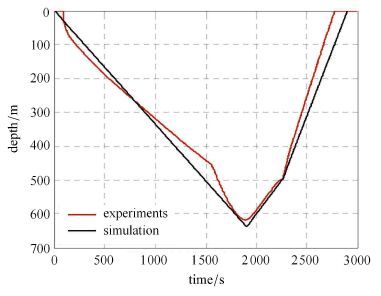
为验证所辨识的水动力参数的正确性,在相同输入条件下,采用辨识出的水动力参数对水下滑翔机动力学方程进行仿真并与实验结果进行对比,对比结果如图 13 ∼图 16所示.
其中图 13与图 14所示的剖面,水下滑翔机在下潜阶段是纯滑翔运动,在上浮阶段开启螺旋桨即混合推进运动.图 15和图 16是螺旋桨工作时的水下定深航行运动.
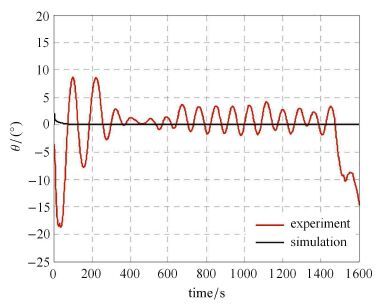
从仿真和实验结果的对比可以看出,除水下滑翔机初始回油阶段和上浮过渡排油阶段以及水面等待阶段外,水下滑翔机在纯滑翔运动时,稳态纵倾角度的仿真值(平均为-26°)与实验结果(平均为-29°)最大误差不超过3°;在混合推进运动时,稳态纵倾角度的仿真值(平均为35°)与实验结果(平均为31°)最大误差不超过4°,具体如图 14所示;水下滑翔机在定深航行时,稳态纵倾角度仿真值(平均为0°)与实验结果(在2°∼4°之间变化)最大误差不超过4°,具体如图 16所示.即纵倾角的仿真结果比较接近实验值.
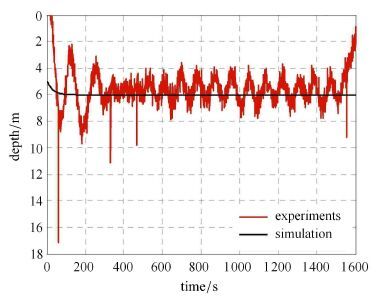
对于滑翔运动和定深运动,下潜深度的仿真值与实验结果对比如图 13和图 15所示. 其中,图 13中,纯滑翔和混合推进阶段,除回排油以及水面等待阶段外,误差都在40 m之内,出现稍大误差的原因有可能是在海试试验时遇到海洋中海流的作用,这在本文的模型中并未考虑.定深运动阶段,如图 15所示,深度的仿真值(平均为6 m)和实验值(在4 m∼8 m之间变化)的最大误差为2 m.因此,可以认为仿真值较好地预测了水下滑翔机的实际定深轨迹.
综上可知,仿真结果与实验吻合较好,验证了所辨识水动力参数的正确性和有效性.
4 结论
由于混合驱动水下滑翔机所搭载的传感器有限,测量滑翔机本体速度和攻角的传感器是未安装的,而为了尽可能准确地得到混合驱动水下滑翔机的水动力参数,本文提出一种在有限航行参数条件下,基于大数据统计分析的计算流体力学和参数辨识相结合来获取水动力参数的方法.根据水下滑翔机方案设计阶段的CFD仿真以及对纯滑翔模式下的大量实验数据的统计分析,辨识出了水下滑翔机的升力系数、阻力系数和纵倾力矩系数.在此基础上,根据螺旋桨混合驱动模式下的实验数据辨识出了水下滑翔机的螺旋桨推力系数.
为验证该方法的正确性和有效性,根据辨识出的水动力参数对水下滑翔机动力学模型进行了仿真. 仿真结果与海试实验结果对比,验证了所提出方法的正确性和辨识结果的准确性. 该方法对混合驱动水下滑翔机的运动仿真和设计具有较好的指导作用.
参考文献
| [1] |
Stommel H. The Slocum mission[J].
Oceanography,1989, 2 (1) : 22-25.
DOI: 10.5670/oceanog. ( 0) 0)
|
| [2] |
Webb DC, Simonetti PJ, Jones CP. SLOCUM, an underwater glider propelled by environmental energy[J].
IEEE Journal of Oceanic Engineering,2001, 26 (4) : 447-452.
DOI: 10.1109/48.972077. ( 0) 0)
|
| [3] |
Eriksen CC, Osse TJ, Light RD, et al. Seaglider: A long range autonomous underwater vehicle for oceanographic research[J].
IEEE Journal of Oceanic Engineering,2001, 26 : 424-436.
DOI: 10.1109/48.972073. ( 0) 0)
|
| [4] |
Sherman J, Davis RE, Owens WB, et al. The autonomous underwater glider ‘Spray'[J].
IEEE Journal of Oceanic Engineering,2001, 26 : 437-446.
DOI: 10.1109/48.972076. ( 0) 0)
|
| [5] |
Blidberg DR. The development of autonomous underwater vehicles (AUV). In: IEEE International Conference on Robotics and Automation, Seoul, May, 2001, 1-12
( 0) 0)
|
| [6] |
Alvarez A, Caffaz A, Caiti A, et al. Folaga: A low-cost autonomous underwater vehicle combining glider and AUV capabilities[J].
Ocean Engineering,2009, 36 (1) : 24-38.
DOI: 10.1016/j.oceaneng.2008.08.014. ( 0) 0)
|
| [7] |
La Spezia. Inovative glider technology. Technical Report, ACSA Underwater GPS, 2008
( 0) 0)
|
| [8] |
朱大奇, 袁义丽, 邓志刚. 水下机器人参数辨识的量子粒子群算法[J].
控制工程,2015, 22 (3) : 531-537.
( 0) 0)
|
| [9] |
Jones DA, Clarke DB, Brayshaw IB, et al. The calculation of hydrodynamic coefficients for underwater vehicles. Victoria: DSTO Platforms Sciences Laboratory, 2002
( 0) 0)
|
| [10] |
李天森.
鱼雷操纵性[M]. 北京: 国防工业出版社, 1999 .
( Li Tiansen.
Torpedo Maneuverability[M]. Beijing: National Defence Industry Press, 1999 .
(in Chinese) ) ( 0) 0)
|
| [11] |
施生达.
潜艇操纵性[M]. 北京: 国防工业出版社, 1995 .
( Shi Shengda.
Submarine Maneuverability[M]. Beijing: National Defence Industry Press, 1995 .
(in Chinese) ) ( 0) 0)
|
| [12] |
Etkin B.
Dynamics of Flight[M]. New York: Wiley, 1959 .
( 0) 0)
|
| [13] |
McCormick BW.
Aerodynamics Aeronautics and Flight Mechanics[M]. New York: Wiley, 1979 .
( 0) 0)
|
| [14] |
Grauer JA, Hubbard Jr JE. Flight Dynamics and System Identification for Modern Feedback Control, Avian-Inspired Robots. Philadelphia: Woodhead Publishing, 2013
( 0) 0)
|
| [15] |
王金强, 于凯, 马学文. 基于CFD 的碟形深潜器阻力性能数值计算分析[J].
中国水运,2015 (4) : 62-63.
( Wang Jinqiang, Yu Kai, Ma Xuewen. Dish submersible resistance performance numerical analysis based on CFD[J].
China Shipping (second half),2015 (4) : 62-63.
(in Chinese) ) ( 0) 0)
|
| [16] |
Kim H, Leong ZQ, Ranmuthugala SD, et al. Free running simulation of an autonomous underwater vehicle undergoing a straight line manoeuvre via computational fluid dynamics. In: Proceedings of the Pacific International Maritime Conference, Glebe Island, October, 2015. 1-14
( 0) 0)
|
| [17] |
Gungor E, Ozdemir IB. Design and analyses of a propeller for underwater vehicles using computational fluid dynamics[J].
Applied Mechanics and Materials, Trans Tech Publications,2015, 798 : 155-159.
DOI: 10.4028/www.scientific.net/AMM.798. ( 0) 0)
|
| [18] |
Barrio R, Blanco E, Fernández J, et al. The use of computational fluid dynamics to estimate fluid residence time and flow hydrodynamics in open digesters of wastewater treatment plants: a case study[J].
Desalination and Water Treatment,2015, 53 (10) : 2613-2622.
DOI: 10.1080/19443994.2013.868831. ( 0) 0)
|
| [19] |
Geisbert JS. Hydrodynamic modeling for autonomous underwater vehicles using computational and semi-empirical methods. [Master Thesis]. Blacksburg: Virginia Polytechnic Institute and State University, 2007
( 0) 0)
|
| [20] |
Graver JG, Bachmayer R, Leonard NE, et al. Underwater glider model parameter identification. In: Proceedings of the 13th International Symposium on Unmanned Untethered Submersible Technology, New Hampshire, August, 2003
( 0) 0)
|
| [21] |
张天姣, 钱炜祺, 何开锋, 等. 基于最大似然法的风洞自由飞试验气动力参数辨识技术研究[J].
实验流体力学,2015, 29 (5) : 8-14.
( Zhang Tianjiao, Qian Weiqi, He Kaifeng, et al. Research on aerodynamic parameter identification technology in wind tunnel free-flight test based on maximum likelihood estimation[J].
Journal of Experiments in Fluid Mechanics,2015, 29 (5) : 8-14.
(in Chinese) ) ( 0) 0)
|
| [22] |
周思达, 刘莉, 李昱霖, 等. 高速飞行器热结构工作时变模态参数辨识[J].
航空学报,2015, 36 (1) : 373-380.
( Zhou Sida, Liu Li, Li Yulin, et al. Operational identification of time-varying modal parameters for thermal structures of high-speed aerial vehicles[J].
Acta Aeronautica et Astronautica Sinica,2015, 36 (1) : 373-380.
(in Chinese) ) ( 0) 0)
|
| [23] |
齐万涛, 吕新波, 钱炜祺. 调整试飞阶段的某型飞机气动参数辨识实现方法[J].
科学技术与工程,2015 (16) : 222-225.
( Qi Wantao, Lü Xinbo, Qian Weiqi. Aerodynamic parameter identification of an aircraft implementation during adjustment of the flight test phase[J].
Science Technology and Engineering,2015 (16) : 222-225.
(in Chinese) ) ( 0) 0)
|
| [24] |
王俭臣, 齐晓慧. 基于气动参数辨识的飞控系统传感器故障估计[J].
兵工学报,2015, 36 (1) : 103-110.
( Wang Jianchen, Qi Xiaohui. Sensor fault estimation method for flight control systems based on aerodynamic parameter identification[J].
ActaArmamentarii,2015, 36 (1) : 103-110.
(in Chinese) ) ( 0) 0)
|
| [25] |
崔乃刚, 卢宝刚, 傅瑜, 等. 基于卡尔曼滤波的再入飞行器气动参数辨识[J].
中国惯性技术学报,2014 (6) : 755-758.
( Cui Naigang, Lu Baogang, Fu Yu, et al. Aerodynamic parameter identification of a reentry vehicle based on Kalman filter method[J].
Journal of Chinese Inertial Technology,2014 (6) : 755-758.
(in Chinese) ) ( 0) 0)
|
| [26] |
陈少敏. 飞行器气动参数辨识方法研究. [硕士论文]. 哈尔滨: 哈尔滨工业大学, 2014
( Chen Shaomin. Aerodynamic parameter identification for aircraft. [Master Thesis]. Harbin :Harbin Institute of Technology, 2014 (in Chinese)
) ( 0) 0)
|
| [27] |
傅慧萍.潜射导弹运载器弹道水动力学系统建模及其应用研究. [博士论文]. 西安:西北工业大学,2000
( Fu Huiping. Theory and application study on underwater trajectory dynamic system modeling of submarine launched missile carrier. [PhD Thesis]. Xi'an: Northwestern Polytechnical University, 2000(in Chinese)
) ( 0) 0)
|
| [28] |
刘建成, 刘学敏, 徐玉如. 极大似然法在水下机器人系统辨识中的应用[J].
哈尔滨工程大学学报,2001, 22 (5) : 1-4.
( Liu Jianchen, Liu Xuemin, Xu Yuru. Maximum likelihood method application of underwater vehicle system identification[J].
Journal of Harbin Engineering University,2001, 22 (5) : 1-4.
(in Chinese) ) ( 0) 0)
|
| [29] |
马岭, 崔维成. 载人潜水器水平面动力学模型系统辨识[J].
中国造船,2006, 47 (2) : 76-81.
( Ma Ling, Cui Weicheng. Manned submersible horizontal dynamics model system identification[J].
Shipbuilding of China,2006, 47 (2) : 76-81.
(in Chinese) ) ( 0) 0)
|
| [30] |
Wang CF, Zhang FM, Schaefer D. Dynamic modeling of an autonomous underwater vehicle[J].
Journal of Marine Science and Technology,2015, 20 (2) : 199-212.
DOI: 10.1007/s00773-014-0259-0. ( 0) 0)
|
| [31] |
Leonard NE, Graver JG. Model-based feedback control of autonomous underwater gliders[J].
Oceanic Engineering,2001, 26 (4) : 633-645.
DOI: 10.1109/48.972106. ( 0) 0)
|
| [32] |
王同苏. 深海无人潜器高效推进器的设计研究. [硕士论文]. 哈尔滨:哈尔滨工程大学,2012
( Wang Tongsu. Research of effi-cient thruster of deep sea unmanned submersible. [Master Thesis]. Harbin: Harbin Engineering University, 2012 (in Chinese)
) ( 0) 0)
|
HYDRODYNAMIC PARAMETER IDENTIFICATION OF HYBRID-DRIVEN UNDERWATER GLIDER
Niu Wendong,
Wang Yanhui,
Yang Yanpeng,
Zhu Yaqiang,
Wang Shuxin

Tianjin University, Tianjin 300354, China
Abstract:
Compared with traditional autonomous underwater gliders (AUGs), hybrid-driven underwater gliders (HUGs) can achieve different motion modes by buoyancy driven system and propeller driven system, which are characterized by low power consumption, long endurance and high manoeuvrability, thus being widely used in various oceanographic monitoring missions. An accurate dynamics model with a series of exact enough hydrodynamic parameters is the basis of control system as well as navigation. The main issue of this paper is how to get the accurate hydrodynamic parameters based on the known dynamic model of HUG. In this paper, an HUG named as Petrel which is developed by Tianjin University is selected as the research object. A new method based on large data statistical analysis which combines computational fluid dynamics (CFD) and parameter identification is proposed for hydrodynamic parameter identification. Firstly, dynamic model of Petrel with hydrodynamic model is established. Secondly, lift coefficient is solved by CFD method. Then, other hydrodynamic parameters in the buoyancy driven gliding mode are calculated by large data statistical analysis using a large amount of experimental data. Finally a set of hydrodynamic parameters including the propeller thrust coefficient is obtained. The simulation results show a good agreement with the experimental results, thus verifying validity and availability of this method. And this work paves the way for further design.
Key words: hybrid-driven underwater gliders CFD parameter identification motion simulation sea trial








 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 2016, Vol. 48
2016, Vol. 48