在过去的二十年中,并联机器人因其更高的运动速度、加速度、刚度,逐渐成为了一个研究热点,并被广泛用于机床[1-3]、微动机构[4-5]、射电望远镜[6]、医疗机器人[7-9]、工业输送[10-12]等领域.目前对于并联机器人运动学的研究已经成熟[13-15],但动力学特性研究,特别是实验研究相对较少,原因是并联机器人机械结构复杂,包含较多被动铰链,也因此引入了较多时变、非线性环节,很难在理论上建立高精度的动力学模型.虽然目前已有部分学者针对铰链间隙、刚度、阻尼等非线性环节对动力学特性的影响开展研究[16-18],但这些研究几乎只进行理论仿真,其结果在很大程度上受到相关数值算法精度的影响,并且在实际的实验过程中很难直接测量相关变量以验证理论的正确性. 因此通过实验结合理论的方式研究并联机器人的主要动力学特性成为亟待解决的问题.
惯量是表征机器人动力学特性的最重要参数,在很大程度上影响并联机器人的动态特性.在已知的研究中,Shao等[19]对并联机器人关节空间惯量匹配问题进行了研究,并以Stewart平台为例研究并联机器人各驱动轴电机惯量与负载惯量的配比问题.Liu等[20]对并联机器人惯量矩阵进行奇异值分解,以最大奇异值作为并联机器人的惯量指标,并研究解耦空间的动态性能.Yang等[21]基于惯量解耦分析,针对一种六自由度并联机器人设计了解耦控制器.这些研究充分说明了惯量特性是并联机器人研究过程中的重要问题.何景峰等[22]最先针对一种液压驱动的Stewart平台提出了一种有效的耦合特性分析方法,将耦合惯量与自身负载惯量进行比较,但没有直接评价耦合惯量以及进一步给出惯量耦合特性在并联机器人整个工作空间中的变化规律,同时也缺乏相应的时域验证实验.随着对并联机器人运动速度、加速度越来越高的要求,并联机器人因其多支链耦合结构特点而产生的惯量耦合[23]特性将越发突出,在高速、高加速度的运动过程中,并联机器人各驱动轴因耦合惯量而产生的耦合干扰力矩,在动态过程中将导致控制超调、振动等现象,严重影响机器人的动态性能,因此需要针对并联机器人惯量耦合特性开展进一步研究.
本文以3-PRS并联机器人为研究对象,开展并联机器人惯量耦合特性研究. 首先基于虚功原理推导动力学方程与惯量矩阵,为评价惯量耦合特性,从伺服控制观点出发,提出惯量耦合指标,在此基础上分析了3-PRS并联机器人的惯量耦合指标在工作空间内的分布规律. 最后在一台典型3-PRS并联机器人样机上进行实验验证. 该研究为后续根据惯量耦合特性进行机构参数优化,设计补偿控制器及进行伺服参数匹配提供了理论基础.
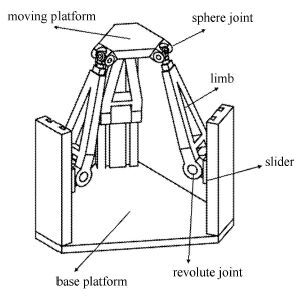
1 运动学建模 1.1 位置分析图 1所示为典型3-PRS并联机器人,3-PRS并联机器人由完全相同的三条支链连接动、静平台,每条支链包括一个移动副、一个转动副与一个球副,每一个驱动轴的滑块由伺服电机通过滚珠丝杠驱动,终端动平台可实现两转动自由度和一个移动自由度的运动[24-25].
|
图 1 典型3-PRS并联机器人 Fig.1 A typical 3-PRS parallel robot |
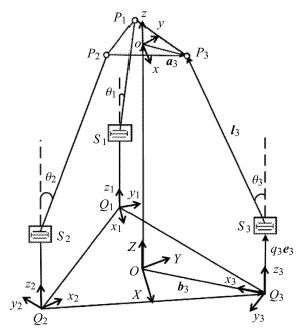
3-PRS机器人运动学模型如图 2所示,在静平台Q1 Q2 Q3中心O处建立固定坐标系O-XYZ,这里Q1 Q2 Q3是正三角形;同时在动平台P1 P2P3中心o处建立动坐标系o-xyz,这里P1 P2 P3也为正三角形. 为不失一般性,令OX轴沿向量 Q1O 方向,ox轴沿向量 P1 o 方向;在静平台Q1 Q2 Q3的端点处建立关节坐标系Qi - xi yi zi ,Qi xi 轴沿向量 QiO 方向. 根据图 2可写出3-PRS机器人第i (i=1,2,3)个矢量环方程
| $t+{{T}^{o}}{{a}_{i}}={{b}_{i}}+{{q}_{i}}{{e}_{3}}+{{l}_{i}}$ | (1) |
|
图 2 3-PRS并联机器人结构简图 Fig.2 Schematic diagram of the 3-PRS parallel robot |
式中
| $\begin{align} & T=R\left( x,\alpha \right)R\left( y,\beta \right)R\left( z,\gamma \right)= \\ & \left[ \begin{matrix} \cos \beta \cos \gamma & -\cos \beta \sin \gamma & \sin \beta \\ \sin \alpha \sin \beta \cos \gamma +\cos \alpha \sin \gamma & -\sin \alpha \sin \beta \sin \gamma +\cos \alpha \cos \gamma & -\sin \alpha \cos \beta \\ -\cos \alpha \sin \beta \cos \gamma +\sin \alpha \sin \gamma & \cos \alpha \sin \beta \sin \gamma +\sin \alpha \cos \gamma & \cos \alpha \cos \beta \\ \end{matrix} \right] \\ \end{align}$ | (2) |
由于3-PRS三个转动副的布置特点,动平台无法沿转动副轴向运动,因此可以得到约束方程如下
| $u_{i}^{\text{T}}{{l}_{i}}=u_{i}^{\text{T}}\left( t+{{a}_{i}} \right)=0$ | (3) |
式中,ui为转动副轴向单位向量,ai= To ai,联立式(1)和式(3)可解得3-PRS并联机器人伴生运动[26]
| $\left. \begin{array}{*{35}{l}} x=\frac{r}{2}\left[ \cos \gamma \left( \cos \alpha -\cos \beta \right)-\sin \alpha \sin \beta \sin \gamma \right] \\ y=r\left( \sin \alpha \sin \beta \cos \gamma +\cos \alpha \sin \gamma \right) \\ \gamma =a\tan \left( \frac{-\sin \alpha \sin \beta }{\cos \alpha +\cos \beta } \right) \\ \end{array} \right\}$ | (4) |
式中,R与r分别为向量 Qi O 与Pi o的模,将伴生运动的解代入矢量环方程(1)即可得到滑块位移
| ${{q}_{i}}=z+{{a}_{iz}}-{{b}_{iz}}-\sqrt{{{l}^{2}}-{{\left( x+{{a}_{ix}}-{{b}_{ix}} \right)}^{2}}-{{\left( y+{{a}_{iy}}-{{b}_{iy}} \right)}^{2}}}$ | (5) |
式中,
对矢量环方程(1)进行求导,通过向量运算可得
| ${{\dot{q}}_{i}}=\left[ \begin{matrix} \frac{l_{1}^{\text{T}}}{l_{1}^{\text{T}}{{e}_{3}}} & \frac{{{\left( {{a}_{1}}\times {{l}_{1}} \right)}^{\text{T}}}}{l_{1}^{\text{T}}{{e}_{3}}} \\ \frac{l_{2}^{\text{T}}}{l_{2}^{\text{T}}{{e}_{3}}} & \frac{{{\left( {{a}_{2}}\times {{l}_{2}} \right)}^{\text{T}}}}{l_{2}^{\text{T}}{{e}_{3}}} \\ \frac{l_{3}^{\text{T}}}{l_{3}^{\text{T}}{{e}_{3}}} & \frac{{{\left( {{a}_{3}}\times {{l}_{3}} \right)}^{\text{T}}}}{l_{3}^{\text{T}}{{e}_{3}}} \\ \end{matrix} \right]\left[ \begin{matrix} v \\ \omega \\ \end{matrix} \right]={{J}_{a}}\dot{X}$ | (6) |
式中,Ja为驱动雅可比矩阵,
利用约束方程可得
| $\mathbf{0}=\left[ \begin{matrix} u_{1}^{\text{T}} & {{\left( {{a}_{1}}\times {{u}_{1}} \right)}^{\text{T}}} \\ u_{2}^{\text{T}} & {{\left( {{a}_{2}}\times {{u}_{2}} \right)}^{\text{T}}} \\ u_{3}^{\text{T}} & {{\left( {{a}_{3}}\times {{u}_{3}} \right)}^{\text{T}}} \\ \end{matrix} \right]\left[ \begin{matrix} v \\ \omega \\ \end{matrix} \right]={{J}_{c}}\left[ \begin{matrix} v \\ \omega \\ \end{matrix} \right]$ | (7) |
式中,Jc为约束雅可比矩阵,联立式(6)与式(7)可得
| $\left[ \begin{matrix} {\dot{q}} \\ \mathbf{0} \\ \end{matrix} \right]=\left[ \begin{matrix} {{J}_{a}} \\ {{J}_{c}} \\ \end{matrix} \right]\dot{X}=J\dot{X}$ | (8) |
式中,J为广义雅可比矩阵[27],且有
| $G\left[ \begin{matrix} {\dot{q}} \\ \mathbf{0} \\ \end{matrix} \right]=\dot{X}$ | (9) |
式中,
对于支链速度求解,由质心矢量环方程可得
| $\left[ \begin{matrix} {{v}_{i}} \\ {{\omega }_{i}} \\ \end{matrix} \right]=\left[ \begin{matrix} {{J}_{iv}} \\ {{J}_{i\omega }} \\ \end{matrix} \right]\left[ \begin{matrix} v \\ \omega \\ \end{matrix} \right]={{J}_{iv\omega }}\dot{X}$ | (10) |
式中,
| ${{J}_{i\omega }}=\frac{1}{{{l}^{2}}}\left[ \left( \left[ {{l}_{i}}\times \right]-\left[ {{l}_{i}}\times \right]\left[ {{a}_{i}}\times \right] \right)-\left( {{l}_{i}}\times {{e}_{3}} \right){{J}_{ai}} \right]$ | (11) |
| ${{J}_{iv}}=\left( E-\left[ {{a}_{i}}\times \right] \right)+\frac{1}{2}\left[ {{l}_{i}}\times \right]{{J}_{i\omega }}$ | (12) |
对矢量环方程(1)二次求导可得滑块加速度
| ${{\ddot{q}}_{i}}={{J}_{ai}}\ddot{X}+\frac{-{{\omega }^{2}}l_{i}^{\text{T}}{{a}_{i}}+\omega _{i}^{2}{{l}^{2}}}{l_{i}^{\text{T}}{{e}_{3}}}$ | (13) |
式中,
| ${{\dot{\omega }}_{i}}={{J}_{i\omega }}\ddot{X}+\frac{{{l}_{i}}\times \left[ \omega \times \left( \omega \times {{a}_{i}} \right) \right]}{{{l}^{2}}}$ | (14) |
| ${{\dot{v}}_{i}}={{J}_{iv}}\ddot{X}+\omega \times \left( \omega \times {{a}_{i}} \right)-\frac{1}{2}{{\omega }_{i}}\times \left( {{\omega }_{i}}\times {{l}_{i}} \right)$ | (15) |
式中,
在不考虑摩擦力的情况下,动平台受力可表示为
| ${{Q}_{\text{P}}}=\left[ \begin{matrix} {{f}_{\text{p}}} \\ {{n}_{\text{p}}} \\ \end{matrix} \right]=\left[ \begin{matrix} {{f}_{\text{e}}}+{{m}_{\text{p}}}g-{{m}_{\text{p}}}\dot{v} \\ {{n}_{\text{e}}}-{{I}_{\text{p}}}\dot{\omega }-\omega \times \left( {{I}_{\text{p}}}\omega \right) \\ \end{matrix} \right]$ | (16) |
式中,
| ${{I}_{\text{p}}}=T{{I}_{\text{p}o}}{{T}^{\text{T}}}$ | (17) |
这里
在不考虑摩擦力情况下,第i个支链受力可表示为
| ${{Q}_{i}}=\left[ \begin{matrix} {{f}_{i}} \\ {{n}_{i}} \\ \end{matrix} \right]=\left[ \begin{matrix} {{m}_{i}}g-m{{{\dot{v}}}_{i}} \\ -{{I}_{i}}{{{\dot{\omega }}}_{i}} \\ \end{matrix} \right]$ | (18) |
式中,mi为支链质量,Ii为支链相对坐标系O-XYZ的惯量矩阵.
滑块受力为
| ${{Q}_{\text{s}i}}=\left[ \begin{matrix} {{m}_{\text{s}i}}g-{{m}_{\text{s}i}}{{{\ddot{q}}}_{i}}{{e}_{3}} \\ Z \\ \end{matrix} \right]$ | (19) |
式中,
最后对电机驱动轴进行受力分析可得
| ${{Q}_{\text{m}i}}=\left[ \begin{matrix} Z \\ \left( {{\tau }_{i}}-{{J}_{\text{m}}}{{{\ddot{\theta }}}_{i}} \right){{e}_{3}} \\ \end{matrix} \right]$ | (20) |
式中
| ${{\theta }_{i}}=\frac{2\pi }{{{P}_{\text{h}}}}{{q}_{i}}$ | (21) |
式中
由虚功原理可得
| $\begin{align} & {{\left[ \begin{matrix} \delta v \\ \delta \omega \\ \end{matrix} \right]}^{\text{T}}}{{Q}_{\text{p}}}+\sum\limits_{i=1}^{3}{{{\left[ \begin{matrix} \delta {{v}_{i}} \\ \delta {{\omega }_{i}} \\ \end{matrix} \right]}^{\text{T}}}}{{Q}_{i}}+ \\ & \sum\limits_{i=1}^{3}{\delta }{{q}_{i}}e_{3}^{\text{T}}\left( {{m}_{\text{s}i}}g-{{m}_{\text{s}i}}{{{\ddot{q}}}_{i}}{{e}_{3}} \right)+ \\ & \sum\limits_{i=1}^{3}{\delta }{{\theta }_{i}}e_{3}^{\text{T}}\left( {{\tau }_{i}}-{{J}_{\text{m}}}\ddot{\theta } \right){{e}_{3}}=0 \\ \end{align}$ | (22) |
整理后可得驱动力表达式
| $\begin{align} & \tau =\frac{{{P}_{\text{h}}}}{2\pi }[{{\left( \frac{2\pi }{{{P}_{\text{h}}}} \right)}^{2}}{{J}_{\text{m}}}{{{\ddot{q}}}_{i}}+{{M}_{\text{s}}}\left( {{{\ddot{q}}}_{i}}-g \right)- \\ & G_{\text{a}}^{\text{T}}{{Q}_{\text{p}}}-\sum\limits_{i=1}^{3}{G_{\text{a}}^{\text{T}}}J_{iv\omega }^{\text{T}}{{Q}_{i}}] \\ \end{align}$ | (23) |
式中
由并联机器人速度映射关系可得
| $\left. \begin{array}{*{35}{l}} \ddot{X}={{G}_{\text{a}}}\left( \ddot{q}-{{{\dot{J}}}_{\text{a}}}\dot{X} \right) \\ \left[ \begin{matrix} {{{\dot{v}}}_{i}} \\ {{{\dot{\omega }}}_{i}} \\ \end{matrix} \right]={{J}_{iv\omega }}{{G}_{\text{a}}}\ddot{q}+\left( {{{\dot{J}}}_{iv\omega }}-{{J}_{iv\omega }}{{G}_{\text{a}}}{{{\dot{J}}}_{\text{a}}} \right)\dot{X} \\ \end{array} \right\}$ | (24) |
将以上映射关系代入驱动力表达式(23)可得3-PRS并联机器人惯量矩阵为
| $\begin{align} & {{M}_{\text{I}}}=\frac{{{P}_{\text{h}}}}{2\pi }[{{\left( \frac{2\pi }{{{P}_{\text{h}}}} \right)}^{2}}{{J}_{\text{m}}}+{{M}_{\text{s}}}+G_{\text{a}}^{\text{T}}{{M}_{\text{p}}}{{G}_{\text{a}}}+ \\ & \sum\limits_{i=1}^{3}{G_{\text{a}}^{\text{T}}}J_{iv\omega }^{\text{T}}{{M}_{i}}{{J}_{iv\omega }}{{G}_{\text{a}}}] \\ \end{align}$ | (25) |
式中,
| ${{M}_{\text{I}}}=\left[ \begin{matrix} {{J}_{11}} & {{J}_{12}} & {{J}_{13}} \\ {{J}_{21}} & {{J}_{22}} & {{J}_{23}} \\ {{J}_{31}} & {{J}_{32}} & {{J}_{33}} \\ \end{matrix} \right]$ | (26) |
式中,
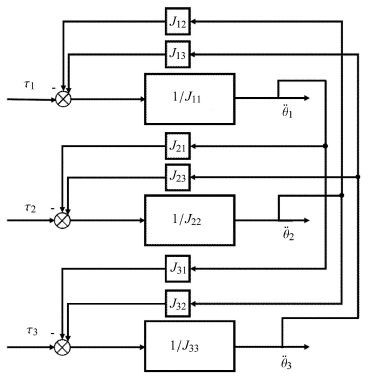
目前驱动关节空间控制仍为并联机器人最主要的控制方法[28-30],以3-PRS并联机器人为例,主要考虑惯量影响,图 3所示为其关节空间控制简图.
|
图 3 3-PRS并联机器人关节空间控制简图 Fig.3 Control structure of the 3-PRS parallel robot in joint space |
3-PRS并联机器人有三条控制回路,
基于以上分析,为直接评价并联机器人惯量耦合特性,对惯量矩阵每一行除对角元外的其他元素进行绝对值求和可得
| $\left. \begin{align} & IC{{I}_{1}}=\left| {{J}_{12}} \right|+\left| {{J}_{13}} \right| \\ & IC{{I}_{2}}=\left| {{J}_{21}} \right|+\left| {{J}_{23}} \right| \\ & IC{{I}_{3}}=\left| {{J}_{31}} \right|+\left| {{J}_{32}} \right| \\ \end{align} \right\}$ | (27) |
式中
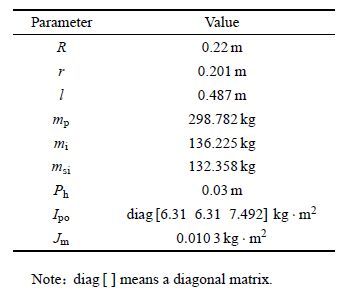
| 表 1 3-PRS并联机器人几何及惯量参数 Table 1 Geometrical and inertia parameters of the 3-PRS parallel robot |
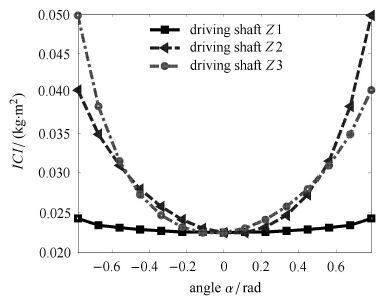
3-PRS并联机器人终端摆角α与β运动范围设定为
|
图 4 3-PRS并联机器人惯量耦合指标沿α方向分布 Fig.4 The distribution of the ICI along the α direction |
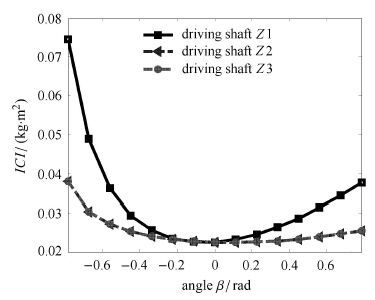
惯量耦合指标沿β方向分布如图 5所示,此时α = 0,Z = 1.2 m. 从图中可以看到,当3-PRS并联机器人进行β方向摆动时,驱动轴Z1的惯量耦合指标大于驱动轴Z2与驱动轴Z3的惯量耦合指标,驱动轴Z2与驱动轴Z3的惯量耦合指标相同. 与图 4情况相同,各驱动轴的惯量耦合指标随β的绝对值增大而增大.
|
图 5 3-PRS并联机器人惯量耦合指标沿β方向分布 Fig.5 The distribution of the ICI along the β direction |
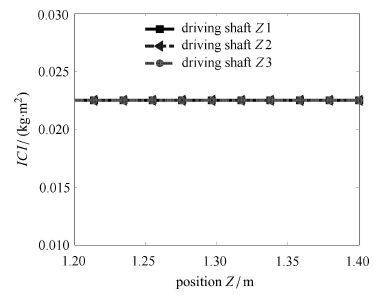
惯量耦合指标沿Z方向分布如图 6所示,此时α = β = 0. 从图中可以看到,3-PRS并联机器人各驱动轴惯量耦合指标沿Z方向没有变化,Z方向位移并不会对指标产生影响. 因此对于3-PRS并联机器人,惯量耦合指标主要取决于终端动平台的摆角大小.
|
图 6 3-PRS并联机器人惯量耦合指标沿Z方向分布 Fig.6 The distribution of the ICI along the Z direction |
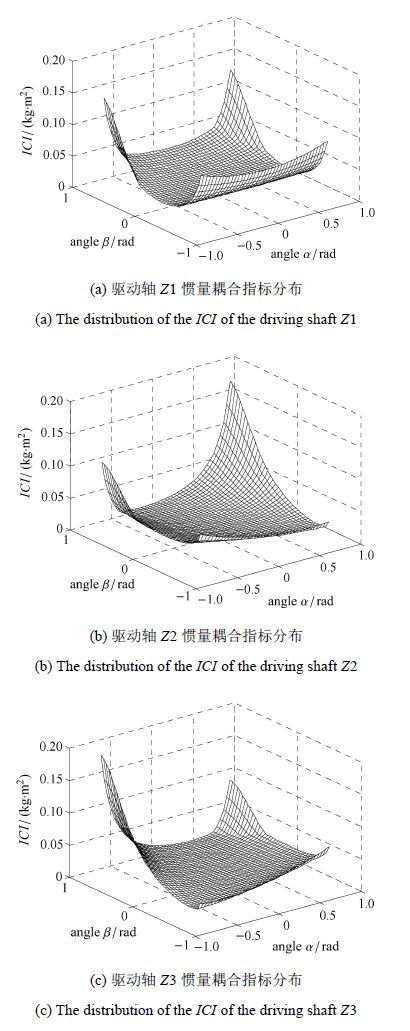
为进一步分析惯量耦合指标在整个工作空间内的分布情况,同时考虑摆角α和β的影响,得到如图 7所示各驱动轴惯量耦合指标在整个工作空间内的分布结果,这里工作空间范围为:
|
图 7 3-PRS并联机器人各驱动轴惯量耦合指标分布 Fig.7 The distribution of the ICI of the 3-PRS parallel manipulator |
为探求耦合惯量在实际并联机器人运动过程中对动态特性的影响,验证所提出惯量耦合指标的有效性,在一台3-PRS并联机器人样机上进行实验验证. 实验样机的几何及惯量参数与表 1相对应.
如图 3所示,当运动条件一定时,耦合惯量变化会导致各驱动轴所受干扰力矩变化从而影响各驱动轴负载. 在实际运动过程中,并联机器人各驱动轴电机的驱动电流能够表征驱动轴的负载,因此可以通过测量不同位姿下各驱动轴电流来反映各驱动轴负载情况从而达到对比耦合惯量的目的. 为验证耦合惯量对驱动轴动态特性的影响,首先在
| $\left. \begin{array}{*{35}{l}} v=50\text{mm/s} \\ {{a}_{\max }}=1\text{m/}{{\text{s}}^{2}} \\ \end{array} \right\}$ | (28) |
图 8所示为实验1中Z3轴的电流情况,电流的幅值大小代表了运动过程中Z3轴的负载情况,电流绝对值越大可以认为此时驱动轴承受的负载越大.

|
图 8 α=0° β=0°时实验1中Z3轴驱动电流 Fig.8 The current of Z3 in experiment 1 when α=0° β=0° |
之后进行实验2:在相同的运动条件下,令Z3轴与Z2轴进行与前述相同的往复运动,在这个过程中Z1轴不运动,保持静止,同样可以得到这个过程中Z3轴的电机驱动电流

|
图 9 α=0° β=0°时实验2中Z3轴驱动电流 Fig.9 The current of Z3 in experiment 2 when α=0° β=0° |
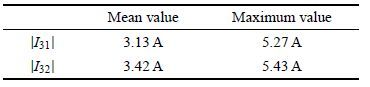
实验1与实验2的区别在于驱动轴Z1的运动状态,同时因为运动行程较短,终端动平台的姿态变化量可基本忽略.因此通过对比两次实验中驱动轴Z3的驱动电流情况,就能够反映因驱动轴Z1的运动状态改变对Z3轴负载的影响,这种影响正是由Z3轴与Z1轴间的耦合惯量造成的,负载的变化将最终影响驱动轴的动态性能.为更好地对比两次实验结果,计算两次实验过程中电流的平均值与最大值,以这两项指标对负载情况进行评价,这里需要指出,因为电流正负只代表电流方向,因此对电流取绝对值后进行运算.
| 表 2 α=0° β=0°时电流数值 Table 2 Numerical value of current when α=0° β=0° |
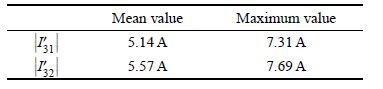
为探寻不同位姿下并联机器人耦合惯量的变化情况,改变并联机器人终端位姿至α= 20° ,β = 0°,在同样的条件下重复之前的实验1与实验2,可以得到Z3轴电流
| 表 3 α= 0° ,β = 0°时电流数值 Table 3 Numerical value of current when α= 0° ,β = 0° |
同时需要指出的是,在实验中所使用的伺服参数均是保守参数,当驱动轴负载变大时,若使用较大的伺服参数可能在换向过程中引起振动等不稳定现象.
5 结论本文针对3-PRS并联机器人惯量耦合特性开展研究,得到如下结论:
(1) 基于惯量矩阵直接对耦合惯量开展研究,提出各驱动轴惯量耦合指标,该指标的大小表征各驱动轴在当前位姿下的耦合惯量的大小,并给出该指标在机器人工作空间内的分布规律. 结果表明各驱动轴惯量耦合程度主要受并联机器人终端动平台摆角影响,随摆角绝对值变大而变大.
(2) 利用驱动电流表征驱动轴负载情况,在一台3-PRS并联机器人样机上进行实验. 在一组保守的控制参数下通过实验验证了耦合惯量在运动过程中会对驱动轴负载造成影响,最终将影响动态性能,同时随着摆角增大,耦合惯量增大,负载波动变大,实验结果与理论分析一致.
(3) 经过实验验证,本文所提出的惯量耦合指标能够很好地表征并联机器人惯量耦合特性,后续可用于工作空间优化及控制参数整定,以提高并联机器人在运动过程中的动态性能.
| [1] |
1Wu J, WangJS, WangLP, et al. Dynamics and control of a planar 3-DOF parallel manipulator with actuation redundancy[J].
Mechanism and Machine Theory,2009, 44 (4) : 835-849.
( 0) 0)
|
| [2] |
Gao Z, Zhang D. Performance analysis, mapping, and multiobjective optimization of a hybrid robotic machine tool[J].
IEEE Transactions on Industrial Electronics,2015, 62 (1) : 423-433.
DOI: 10.1109/TIE.2014.2327008. ( 0) 0)
|
| [3] |
Wu J, Chen XM, Li TM, et al. Optimal design of a 2-DOF parallel manipulator with actuation redundancy considering kinematics and natural frequency[J].
Robotics and Computer-Integrated Manufacturing,2013, 29 (1) : 80-85.
DOI: 10.1016/j.rcim.2012.07.005. ( 0) 0)
|
| [4] |
Xu QS. Design and development of a compact flexure-based XY precision positioning system with centimeter range[J].
IEEE Transactions on Industrial Electronics,2014, 61 (2) : 893-903.
DOI: 10.1109/TIE.2013.2257139. ( 0) 0)
|
| [5] |
Ramadan AA, Takubo T, Mae Y, et al. Developmental process of a chopstick-like hybrid-structure two-fingered micromanipulator hand for 3-D manipulation of microscopic objects[J].
IEEE Transactions on Industrial Electronics,2009, 56 (4) : 1121-1135.
DOI: 10.1109/TIE.2008.2008753. ( 0) 0)
|
| [6] |
Yao R, Tang XQ, Wang JS, et al. Dimensional optimization design of the four-cable-driven parallel manipulator in FAST[J].
IEEE/ASME Transactions on Mechatronics,2010, 15 (6) : 932-941.
( 0) 0)
|
| [7] |
Li YM, Xu QS. Design and development of a medical parallel robot for cardiopulmonary resuscitation[J].
IEEE/ASME Transactions on Mechatronics,2007, 12 (3) : 265-273.
DOI: 10.1109/TMECH.2007.897257. ( 0) 0)
|
| [8] |
Xu WL, Pap JS, Bronlund J. Design of a biologically inspired parallel robot for foods chewing[J].
IEEE Transactions on Industrial Electronics,2008, 55 (2) : 832-841.
DOI: 10.1109/TIE.2007.909067. ( 0) 0)
|
| [9] |
Xu WL, Torrance DJ, Chen BQ, et al. Kinematics and experiments of a life-sized masticatory robot for characterizing food texture[J].
IEEE Transactions on Industrial Electronics,2008, 55 (5) : 2121-2132.
DOI: 10.1109/TIE.2008.918641. ( 0) 0)
|
| [10] |
Pierrot F, Nabat V, Company O, et al. Optimal design of a 4-DOF parallel manipulator: from academia to industry[J].
IEEE Transactions on Robotics,2009, 25 (2) : 213-224.
DOI: 10.1109/TRO.2008.2011412. ( 0) 0)
|
| [11] |
Bourbonnais F, Bigras P, Bonev IA. Minimum-time trajectory planning and control of a pick-and-place five-bar parallel robot[J].
IEEE/ASME Transactions on Mechatronics,2015, 20 (2) : 740-749.
DOI: 10.1109/TMECH.2014.2318999. ( 0) 0)
|
| [12] |
Wu J, Chen XL, Wang LP, et al. Dynamic load-carrying capacity of a novel redundantly actuated parallel conveyor[J].
Nonlinear Dynamics,2014, 78 (1) : 241-250.
DOI: 10.1007/s11071-014-1436-8. ( 0) 0)
|
| [13] |
Zhang D, Gao Z. Optimal kinematic calibration of parallel manipulators with pseudoerror theory and cooperative coevolutionary network[J].
IEEE Transactions on Industrial Electronics,2012, 59 (8) : 3221-3231.
DOI: 10.1109/TIE.2011.2166229. ( 0) 0)
|
| [14] |
Xie FG, Liu XJ, Wang JS. A 3-DOF parallel manufacturing module and its kinematic optimization[J].
Robotics and Computer-Integrated Manufacturing,2012, 28 (3) : 334-343.
DOI: 10.1016/j.rcim.2011.10.003. ( 0) 0)
|
| [15] |
Liu XJ, Li J, Zhou YH. Kinematic optimal design of a 2-degree-offreedom 3-parallelogram planar parallel manipulator[J].
Mechanism and Machine Theory,2015, 87 : 1-17.
DOI: 10.1016/j.mechmachtheory.2014.12.014. ( 0) 0)
|
| [16] |
Shiau TN, Tsai YJ, Tsai MS. Nonlinear dynamic analysis of a parallel mechanism with consideration of joint effects[J].
Mechanism and Machine Theory,2008, 43 (1) : 491-505.
( 0) 0)
|
| [17] |
Liu XF, Xu YD, Yao JT, et al. Control-faced dynamics with deformation compatibility for a 5-DOF active over-constrained spatial parallel manipulator 6PUS–UPU[J].
Mechatronics,2015, 30 : 107-115.
DOI: 10.1016/j.mechatronics.2015.06.014. ( 0) 0)
|
| [18] |
Zhang J, Zhao YQ. Elastodynamic modeling and joint reaction prediction for 3-PRS PKM[J].
Journal of Central South University,, 22 (8) : 2971-2979.
DOI: 10.1007/s11771-015-2833-y. ( 0) 0)
|
| [19] |
Shao ZF, Tang XT, Chen X, et al. Research on the inertia matching of the Stewart parallel manipulator[J].
Robotics and Computer Integrated Manufacturing,2012, 28 (6) : 649-659.
DOI: 10.1016/j.rcim.2012.04.001. ( 0) 0)
|
| [20] |
Liu ZH, Tang XQ, Shao ZF, et al. Dimensional optimization of the Stewart platform based on inertia decoupling characteristic. Robotica, 2014: publish online
( 0) 0)
|
| [21] |
Yang CF, Qu Z, Han J. Decoupled-space control and experimental evaluation of spatial electrohydraulic robotic manipulators using singular value decomposition algorithms[J].
IEEE Transactions on Industrial Electronics,2014, 61 (7) : 3427-3438.
DOI: 10.1109/TIE.2013.2278958. ( 0) 0)
|
| [22] |
何景峰, 叶正茂, 姜洪洲, 等. 基于关节空间模型的并联机器人耦合性分析[J].
机械工程学报,2006, 42 (6) : 161-165.
DOI: 10.3901/JME.2006.06.161. ( He Jingfeng, Ye Zhengmao, Jiang Hongzhou, et al. Coupling analysis on joint-space model of parallel robot[J].
Chinese Journal of Mechanical Engineering,2006, 42 (6) : 161-165.
(in Chinese) DOI: 10.3901/JME.2006.06.161. ) ( 0) 0)
|
| [23] |
Yang CF, Han J. Dynamic coupling analysis of a spatial 6-DOF electro-hydraulic parallel manipulator using a modal decoupling method[J].
International Journal of Advanced Robotic Systems,2013, 10 (104) : 1-8.
( 0) 0)
|
| [24] |
Li QC, Chen Z, Chen QH, et al. Parasitic motion comparison of 3-PRS parallel mechanism with different limb arrangements[J].
Robotics and Computer-Integrated Manufacturing,2011, 27 (2) : 389-396.
DOI: 10.1016/j.rcim.2010.08.007. ( 0) 0)
|
| [25] |
Li YM, Xu QS. Kinematics and inverse dynamics analysis for a general 3-PRS spatial parallel mechanism[J].
Robotica,2005, 23 (2) : 219-229.
DOI: 10.1017/S0263574704000797. ( 0) 0)
|
| [26] |
Carretero JA, Podhorodeski RP, Nahon MA, et al. Kinematic analysis and optimization of a new three degree-of-freedom spatial parallel manipulator[J].
Journal of Mechanical Design,2000, 122 (1) : 17-24.
DOI: 10.1115/1.533542. ( 0) 0)
|
| [27] |
刘海涛. 少自由度机器人机构一体化建模理论、方法及工程应用. [博士论文]. 天津:天津大学,2010
( Liu Haitao. Unified parameter modeling of lower mobility robotic manipulators: theory, methodology and application. [PhD Thesis]. Tianjin: Tianjin University, 2010(in Chinese)
) ( 0) 0)
|
| [28] |
Wu J, Wang D, Wang LP. A control strategy of a two degrees-offreedom heavy duty parallel manipulator[J].
Journal of Dynamic Systems, Measurement and Control Transactions of the ASME,2015, 37 (6) : 061007-1.
( 0) 0)
|
| [29] |
Liu ZH, Tang XQ, Wang LP. Research on the dynamic coupling of the rigid-flexible manipulator[J].
Robotics and Computer-Integrated Manufacturing,2015, 32 : 72-82.
DOI: 10.1016/j.rcim.2014.10.001. ( 0) 0)
|
| [30] |
Dumlu A, Erenturk K. Trajectory tracking control for a 3-DOF parallel manipulator using fractional-order PIλDμ control[J].
IEEE Transactions on Industrial Electronics,2014, 61 (7) : 3417-3426.
DOI: 10.1109/TIE.2013.2278964. ( 0) 0)
|
 2016, Vol. 48
2016, Vol. 48