众所周知,蚯蚓等软体动物通过蠕动实现运动,这种运动形式看似简单,却凭借其一大优势-无足,吸引了众多学者的关注[1-6]. 受此启发,一类新型的运动模型-振动驱动系统,近年来得到了广泛的研究[7-25]. 这种运动模型继承了蚯蚓运动的优势-不需要外部驱动部件,如腿或轮子,因此易于实现结构的微型化,密封化. 可以预见,基于振动驱动这一思想的机器人能更好地适应多种环境,甚至有学者期望将其制成微型胶囊机器人进入人体肠道甚至血管中治疗疾病.
2005年,Chernousko[7]研究了两个质量块系统的直线运动,通过选择合适的物理参数并合理地控制两个质量块之间的相互作用力,实现了该系统的最快平均速度.在此基础上,其首次提出了由一个内部质量块和一个外部箱型刚体构成的振动驱动系统模型[8].在该模型中,内部质量块相对于外部箱体做周期运动,通过合理设计内部质量块的周期运动形式,外部箱体可以在内部质量块对其作用力以及支撑面对其摩擦力的共同作用下,实现周期平移运动.因而,对质量块的相对运动形式进行设计和优化以实现系统最大平均速度是该类系统研究的一个关键问题.纵观之前的研究,质量块的控制模式大致分为两类:对称控制和非对称控制.对称控制意味着内部质量块的相对运动形式具有对称性,也更容易实现,比如正弦驱动,但是往往需要环境提供能使系统发生刚体位移的异性摩擦.2012年,Fang等[9]在研究三模块振动驱动系统时使用了正弦驱动,他们发现通过优化各模块中正弦驱动的初始相位差,能够有效地提高系统的稳态平均速度.2014年,Fang等[10]研究了正弦驱动下,单模块振动驱动系统的运动,重点从滑移分岔的角度分析了系统的粘滑运动,加深了人们对该类系统粘滑运动的认识. 对称驱动的研究总的来说并不如非对称驱动的研究多.早在2005年Chernousko[7]就提出了两种非对称驱动模式-两相驱动和三相驱动,对实现振动驱动系统的运动都行之有效.2006年,Chernousko[11]研究了两相驱动模式,这种驱动模式下,内部质量块一个周期内的相对运动被分为两段,每段上的相对运动速度均为常数. 以实现系统的最大稳态平均速度为目标,对两相驱动参数进行了优化.2007年,Chernousko[12]研究了三相驱动下振动驱动系统的运动.该种情形下,内部质量块一个周期内的相对运动被分为三段,每段上的加速度大小为常数.由于库伦干摩擦的存在,以及不同时间域内,内部质量块的相对加速度不同,加上系统速度的不断变化,因而系统会发生复杂的粘滑运动.2011年,Fang等[13]运用平均法研究了三相驱动的单模块振动驱动系统在不存在粘滑效应时的速度.但是当考虑粘滑效应时,平均法不再适用,根据粘滑运动发生情况,系统运动可以被细分成8种情况.2011年,Fang等[14]在研究两模块振动驱动系统时,在两个模块中也分别施加了这种三相驱动,通过调节两组振动的相位差实现了系统的较快运动速度. 可见,三相驱动在振动驱动系统的控制中占有重要的地位.此外,2006年Li等[15]使用的四步驱动以及 2011年 Huda等[16] 使用的四相驱动也属于非对称驱动.
除了上文中内部质量块的相对运动形式以外,另外一个对振动驱动系统的运动行为起很大影响的是系统受到的外部摩擦.2007年,Chernousko[12]研究了非对称黏性摩擦下振动驱动系统的运动,这种环境模拟了系统在液体环境中的运动.研究针对振动驱动系统速度进行了控制参数优化,并加以实验验证. 2009年,Bolotnik等[17]研究了平方阻尼作用下系统的运动情况,这种运动常常在系统运动速度较快、雷诺数较大的环境下发生.研究表明,在平方阻尼作用下,即使是各向同性的阻力,系统也能实现向前运动.2011年,Fang等[13]研究了振动驱动系统在非对称库伦干摩擦下的运动情况,由于干摩擦存在,观察到了前面所述的粘滑运动.
事实上,粘滑效应至今为止仍然是振动驱动系统中的一大难题.一方面,粘滑效应使得运动情况复杂多样,难以分析,另一方面,充分利用粘滑效应也是提高系统运动性能的重要措施.粘滑运动往往都是在库伦摩擦之下发生,这一点,不仅在振动驱动系统中得到体现,而且在其他系统中也有发现并被研究[18, 26-28].库伦摩擦之所以能引起粘滑运动,是因为其不连续性.从运动状态场的角度看,这种由摩擦力引起的不连续系统,是一类典型的Filippov系统[29-30],而Filippov系统最突出的就是利用滑移和滑移分岔理论巧妙地分析系统中的不连续性对运动的影响. 2010年,Guardia等[26]通过滑移分岔理论研究了一个干摩擦下的弹簧振子,研究证实系统存在两参数滑移分岔,并得到了其中一条余维一分岔曲线的解析表达式.2007年,Kowalczyk等[27]也通过Filippov系统模型研究了干摩擦下的弹簧振子,发现了系统中的余维二分岔,并解释了可能发生的混沌现象. Filippov系统理论为研究干摩擦下的弹簧振子这类系统行为,提供了重要的分析方法[18, 26-28].受此启发,2011年,Fang等[10]也利用Filippov系统描述了非对称干摩擦下受正弦驱动的振动驱动系统,首次从滑移分岔角度阐明了粘滑效应下系统的运动情况,优化结果显示,合理优化系统驱动参数和摩擦系数,能实现系统无后退移动.
回顾振动驱动系统十年来的研究[7-25],无论是内部驱动的设计,还是外部阻力的分类,抑或是研究方法的选用,都得到了长足的发展. 值得注意的是,绝大部分研究更多地是关注了摩擦力为各向异性时的情况,而对于同性摩擦的情形讨论较少.因此,本文重点研究了各向同性干摩擦下的振动驱动系统的运动.由于摩擦的各向同性,本文中将采用三相驱动这一非对称驱动以保证系统定向移动的实现.此外,干摩擦条件下,系统的不连续性会诱发粘滑运动,这种运动的复杂性也对研究工作形成了挑战.借助分岔理论可知,本文中所考虑的振动驱动系统也是Filippov系统,因此可以从滑移分岔的角度对系统的运动进行分类.这种分类有效地揭示了各向同性干摩擦下振动驱动系统多样的运动行为,对参数的设计起到一定的指导作用.最后,我们用数值方法对理论分析得到的运动分类以及运动特性进行了验证.
1 振动驱动系统 1.1 动力学方程振动驱动系统的基本模型如图 1所示. 系统由两个部分组成,分别为质量为M的刚性箱体以及质量为m的内部质量块. 由前人的工作可知,通过m相对于M的特定振动,可以实现系统在水平直线上的定向移动,由此称其为振动驱动系统. 易知,系统有两个自由度,因而可以取两组独立的广义坐标,分别为m相对于M的位移ξ,以及M的绝对位移y,来表示系统的运动情况.

|
图 1 振动驱动系统 Fig.1 Vibration-driven system |
由牛顿第二运动定律,可得运动方程
| $(M+m)\ddot{y}=-m\ddot{\xi }-R(\dot{y})$ | (1) |
式中,
| $R(\dot{y})=\left\{ \begin{array}{*{35}{l}} f(M+m)g\text{sgn}(\dot{y}), & \dot{y}e0 \\ R(0), & \dot{y}=0 \\ \end{array} \right.$ |
式中sgn (x)表示符号函数. 式(1)两边同时除以(M+m),得到
| $\ddot{y}=-\mu \ddot{\xi }-r(\dot{y})$ | (2) |
式中
| $\mu =\frac{m}{M+m},r(\dot{y})=\left\{ \begin{array}{*{35}{l}} fg\text{sgn}(\dot{y}), & \dot{y}e0 \\ r(0), & \dot{y}=0 \\ \end{array} \right.$ |
需要注意的是,上面的R (0)表示速度为0时,系统所受的摩擦阻力. 因此,如果内部振动提供的驱动力不足以克服库伦摩擦,那么摩擦力就与该力等大反向,维持系统静止状态. 如果内部振动提供的驱动力大于最大静摩擦力,那么系统有运动的趋势,此时摩擦力的大小就是最大静摩擦力. 为了简便分析,本文中最大静摩擦力近似认为等于滑动摩擦力. 所以有
| $r(0)=\frac{R(0)}{M+m}=\left\{ \begin{array}{*{35}{l}} -\mu \ddot{\xi }, & |\mu \ddot{\xi }|\le fg \\ -fg\text{sgn}\left( {\ddot{\xi }} \right), & |\mu \ddot{\xi }|>fg \\ \end{array} \right.$ | (3) |
式(2)和式(3)是振动驱动的基本力学模型.
1.2 三相驱动假设箱体内允许质量块运动的区间长度为L,那么对于任意时刻t,有
| $0\le \xi (t)\le L$ | (4) |
并且由振动的周期性,有
| $\left. \begin{array}{*{35}{l}} \xi (0)=\xi (T)=0 \\ \dot{\xi }(0)=\dot{\xi }(T)=0 \\ \end{array} \right\}$ | (5) |
为了充分利用箱体的空间,同时又保证箱体和质量块之间不会发生碰撞,我们可以知道,存在某个时刻
| $\xi (\theta )=L,\dot{\xi }(\theta )=0$ | (6) |
在满足式(4) ∼式(6)的条件下,Chernousko[8]提出了三相驱动模式.
三相驱动模式的基本思想是将内部质量块一个周期的相对振动在时间上分为三段,三段区间的长度分别为τ1,τ2 ,τ3 . 并且,在每段时间区间内,质量块m相对于M均做匀变速直线运动,由式(5)∼式(7)易知,第一、三段中m相对运动的加速度为正常数,第二段中m相对运动的加速度为负常数.一个周期内,m相对运动的数学表达式如下
| $\ddot{\xi }(t)=\left\{ \begin{matrix} {{w}_{1}}, & t\in (0,{{\tau }_{1}}) \\ -{{w}_{2}}, & t\in ({{\tau }_{1}},{{\tau }_{1}}+{{\tau }_{2}}) \\ {{w}_{3}}, & t\in ({{\tau }_{1}}+{{\tau }_{2}},T) \\ \end{matrix} \right.$ | (7) |
其中,
| $\ddot{\xi }(t)=\left\{ \begin{align} & {{w}_{1}}-h(t-{{t}_{1}})({{w}_{2}}+{{w}_{1}})+ \\ & h(t-{{t}_{2}})({{w}_{2}}+{{w}_{3}}), t\in [0,T) \\ & \ddot{\xi }(t(\text{mod}T)), t\notin [0,T) \\ \end{align} \right.$ | (8) |
其中h(t)表示Heaviside函数,mod 表示取模运算. 这里,为了方便
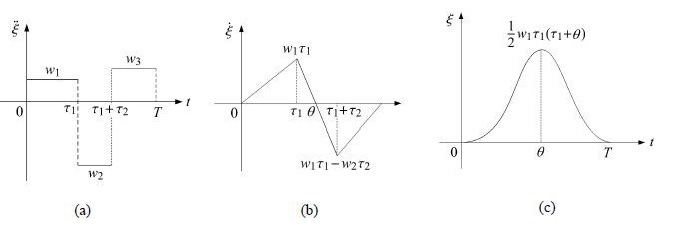
三相驱动模式下内部质量块相对运动图像如图 2所示.
|
图 2 三相控制模式下m的(a)相对加速度、(b)速度和(c)位移 Fig.2 m's (a) relative acceleration,(b) velocity and (c) displacement under three-phase control |
三相驱动中,独立的控制变量有3个,本文使用
| $\left. \begin{align} & \theta =\sqrt{\frac{2L({{w}_{1}}+{{w}_{2}})}{{{w}_{1}}{{w}_{2}}}} \\ & {{\tau }_{1}}=\sqrt{\frac{2L{{w}_{2}}}{{{w}_{1}}({{w}_{1}}+{{w}_{2}})}} \\ & {{\tau }_{2}}=\sqrt{\frac{2L}{{{w}_{2}}}}(\sqrt{\frac{{{w}_{3}}}{{{w}_{2}}+{{w}_{3}}}}+\sqrt{\frac{{{w}_{1}}}{{{w}_{1}}+{{w}_{2}}}}) \\ & {{\tau }_{3}}=\sqrt{\frac{2L{{w}_{2}}}{{{w}_{3}}({{w}_{2}}+{{w}_{3}})}} \\ \end{align} \right\}$ | (9) |
振动驱动系统的运动情况不仅取决于内部质量块的相对振动,而且与其所受的外部阻力有关. 本文中系统所受的阻力为库伦干摩擦,干摩擦的复杂性在于其不连续性,即当系统速度方向改变时,摩擦力的变化是阶跃的. 因此,就其本质而言,本文所研究的系统,也就是式(2)和式(8) 所决定的振动驱动系统,是一种右端不连续的微分方程系统. 这种不连续的复杂性体现在力学现象上,就是系统会发生粘滑运动,而这种特殊的运动模式又让传统的分析方法显得无能为力. 为了更好地从数学上描述运动方程,以及从力学角度更好地解释各种运动情形的发生,本文采用Filippov系统的相关理论分析振动驱动系统. 这样做的好处是,Filippov滑移分岔理论能有效地解释振动驱动系统中的粘滑效应. 需要注意的是,Filippov系统中所谓的滑移运动,其实就对应了振动驱动系统粘滑运动中的黏滞状态.
采用Filippov系统分析的步骤是:建立系统一阶状态微分方程;确定滑移区域;具体讨论在滑移区域的边界是否发生滑移分岔. 当然,由于本文中采用的驱动是三相驱动,本身也存在不连续现象,所以这又增加了分析的复杂性. 基于此,文中通过分类讨论,将振动驱动系统中可能发生的各种滑移分岔现象进行了详细的罗列、归纳.
具体地,我们首先将(2)式由二阶非自治系统转化为一阶自治系统,即将t作为状态变量,引入变量替换,令
| $x=\left( \begin{matrix} {{x}_{1}} \\ {{x}_{2}} \\ t \\ \end{matrix} \right)=\left( \begin{matrix} y \\ {\dot{y}} \\ t(\text{mod}T) \\ \end{matrix} \right)$ | (10) |
这里,
| $\sum{=\{x\in {{R}^{3}}|H(x)={{x}_{2}}=0\}}$ | (11) |
可以将整个状态空间分为两个部分,分别为
| $\left. \begin{align} & {{G}_{1}}=\{x\in {{R}^{3}}|H(x)>0 \\ & {{G}_{2}}=\{x\in {{R}^{3}}|H(x)<0 \\ \end{align} \right\}$ | (12) |
据此,可以将式(2)表示为
| $\dot{x}=\left\{ \begin{array}{*{35}{l}} {{F}_{1}}(x,\mu ),x\in {{G}_{1}} \\ {{F}_{2}}(x,\mu ),x\in {{G}_{2}} \\ \end{array} \right.$ | (13) |
这里,有
| ${{F}_{1}}=\left( \begin{matrix} {{x}_{2}} \\ -\mu \ddot{\xi }-fg \\ 1 \\ \end{matrix} \right),{{F}_{2}}=\left( \begin{matrix} {{x}_{2}} \\ -\mu \ddot{\xi }+fg \\ 1 \\ \end{matrix} \right)$ | (14) |
如果在G1和G2两个子空间上,向量场F1和F2都局部地指向不连续界面Σ,这就意味着系统的流形在局部受到Σ面的约束. 其数学表述为
| ${{H}_{x}}{{F}_{1}}\le 0\le {{H}_{x}}F$ | (15) |
式中,Hx=0是 x的法向量.
分界面上满足这一条件的区域称为滑移区域(sliding region),记为
根据Utkin等效控制理论,滑移区域上的运动由两个部分构成. 一个是F1和F2平均值,另一个是控制函数
| $\left. \begin{align} & {{F}_{s}}=\frac{{{F}_{1}}+{{F}_{2}}}{2}+\frac{{{F}_{2}}-{{F}_{1}}}{2}\beta (x) \\ & \beta (x)=-\frac{{{H}_{x}}{{F}_{1}}+{{H}_{x}}{{F}_{2}}}{{{H}_{x}}{{F}_{2}}-{{H}_{x}}{{F}_{1}}} \\ \end{align} \right\}$ | (16) |
将式(11)和式(14)代入式(16),有
| $\beta (x)=\frac{\mu \ddot{\xi }(t)}{fg}$ | (17) |
当
| $\hat{\Sigma }=\{x\in \Sigma -1\le \beta (x)\le 1\}$ | (18) |
它的边界又可以表示为
| $\partial {{\hat{\Sigma }}^{\pm }}=\{x\in \Sigma |\beta (x)=\pm 1\}$ | (19) |
从式(7)、式(17)和式(18) 可以看出,自变量
|
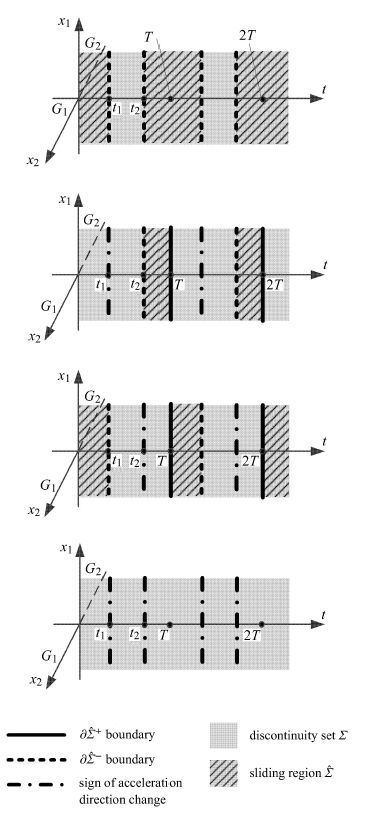
图 3 下的滑移区域示意图 Fig.3 Sliding regions for systems under four situations |
| 表 1 粘滑运动的4种情形 Table 1 Four situations for stick-slip motions |
此时,由表 1中的第一行数据,等价地得到μw1 ≤ fg,μw2 > fg,μw3 ≤ fg.由式(17)和式(18)判定,可知不连续界面在(t2 ,T + t1 )的时间区域内为滑移区域,此时滑移区域示意图如图 3(a). 结合稳态运动的周期性观察可知,系统有两个可能存在滑移分岔的位置
| $x_{1}^{*}=(x_{1}^{*},0,{{t}_{1}}),\quad x_{2}^{*}=(x_{1}^{*},0,{{t}_{2}})$ |
由于有刚体位移,可知,x1的取值为任意值,这里都用
| $\begin{array}{*{35}{l}} \underset{t\to t_{1}^{-},x\to x_{1}^{*}}{\mathop{\lim }}\,{{H}_{x}}{{F}_{s}}(x)=0 \\ \underset{t\to t_{1}^{+},x\to x_{1}^{*}}{\mathop{\lim }}\,{{H}_{x}}{{F}_{1}}(x)=\mu {{w}_{2}}-fg>0 \\ \end{array}$ |
所以可以补充定义
| $\left. \begin{align} & H(x_{i}^{*})=0,{{H}_{x}}(x_{i}^{*})\ne \mathbf{1},i=1,2 \\ & {{H}_{x}}{{F}_{1}}(x_{1}^{*})=0,{{H}_{x}}{{F}_{1}}(x_{2}^{*})=0 \\ \end{align} \right\}$ | (20) |
对于非退化条件,借助式(8),得到如下表达
| $\left. \begin{align} & {{({{H}_{x}}{{F}_{1}})}_{x}}{{F}_{1}}(x_{1}^{*})=\mu ({{w}_{1}}+{{w}_{2}})\delta (0)\to +\infty >0 \\ & {{({{H}_{x}}{{F}_{1}})}_{x}}{{F}_{1}}(x_{2}^{*})=-\mu ({{w}_{2}}+{{w}_{3}})\delta (0)\to -\infty <0 \\ \end{align} \right\}$ | (21) |
注意到
分析该运动过程,首先假设x2 (0) = 0. 考虑到(0,t1 )上,分界面为滑移区域,初始状态x2 (0)落在滑移区域上,因此系统发生滑移运动,即保持黏滞的状态到t1,因而有x2 (t1 ) = 0. (t1 ,t2)上,系统加速度为正常数
注意x2 (t1 )=0,x2 (t2 ) >0,也就是可能发生滑移分岔位置的速度符号确定,因而两点处均不会发生分岔. 此时,系统的运动状态示意图对应于图 5(a).
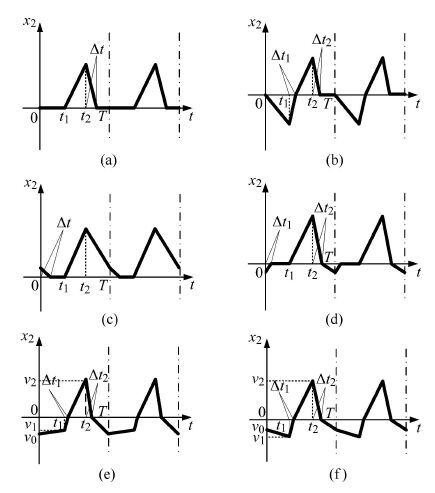
|
图 5 系统的6种运动形态 Fig.5 Six motion types for vibration-driven system |
此时,
注意到x2 (t2 ) > 0,x2 (T) = 0,也就是分岔位置处速度的符号确定,因而两点处均不会发生分岔. 系统的运动状态唯一,如图 5(b).
2.3 情形3
此时,μw1 ≤ fg,μw2 > fg,μw3 > fg,滑移区域示意图如图 3(c)所示,有两个可能的滑移分岔位置:
| ${{P}_{1}}=(\mu {{w}_{2}}-fg){{\tau }_{2}}-(\mu {{w}_{3}}+fg){{\tau }_{3}}$ | (22) |
虽然这里的表达式与情形1中x2 (T)的表达式一样,但是需要注意的是,由于wi (i =1,2,3)的取值范围与情形一中不同,故而得不到P1 <0的结论,因而这里P1的符号是不定的.根据分岔点的非退化条件,可知P1 = 0意味着系统在
| $\begin{align} & {{P}_{2}}=({{\tau }_{3}}-\frac{\mu {{w}_{2}}-fg}{\mu {{w}_{3}}+fg}{{\tau }_{2}})(-\mu {{w}_{3}}+fg)+ \\ & (-\mu {{w}_{1}}+fg){{\tau }_{1}} \\ \end{align}$ | (23) |
根据非退化条件并结合运动,可知P2=0意味着系统在 x1*处发生crossing-sliding分岔,而且由稳态运动的周期性,可知假设x2 (t1 ) =0正确,因此分析符合实际.
综上所述,P1=0表示系统在x2*处发生switching-sliding分岔,分岔示意图如图 4(a),其中轨迹B对应P1 = 0,C对应P1 <0,A对应P1 > 0. 当P1 <0时,P2 = 0表示系统在x1*处发生crossing-sliding分岔,分岔示意图如图 4(b),其中轨迹B对应P2 = 0,C对应P2 > 0,A对应P2 <0.
因此,在这种情形(情形3)下,系统的运动状态有3种:① P1 > 0,运动形态如图 5(c);② P1 <0,P2 >0,运动形态如图 5(d);③ P1 <0,P2 <0,运动形态如图 5(e).
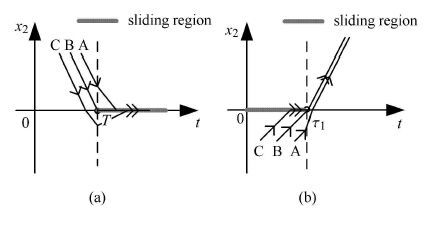
|
图 4 系统的两种分岔示意图 Fig.4 Two kinds of bifurcations for system |
此时,μ w1 > fg,μ w2 > fg,μ w3 > fg,易知,系统不存在滑移区域,如图 3(d)所示.这种情形中,系统将不会发生黏滞. 因此,系统运动的拓扑结构唯一,且相对简单,系统做无黏滞的周期振动,运动示意图见图 5(f).
3 分岔第2节中通过对系统运动分情形进行分析,观察到系统运动出现了滑移分岔现象,也得到了6种形式的粘滑运动.但是需要注意的是,这并不意味着这6种运动形式定性上各不相同.本节将先从滑移分岔的观点分析上述各运动属于何种滑移运动类型.然后再具体分析各种不同运动发生的条件,探究随着参数变化它们之间如何通过滑移分岔实现相互切换.
3.1 归纳Filippov滑移分岔理论指出,右端不连续系统在不连续界面上可能会发生4种滑移分岔(crossing-sliding,grazing-sliding,switching-sliding,adding-sliding)[29],这4种分岔的名称也可以被借用来命名滑移运动的类型.利用图 3(a),可以看到在图 5(a)中,系统从G1 空间进入滑移区域之后,并不进入G2空间,而是保持滑移运动直到再次进入G1空间.可以简单地理解成系统的运动状态轨迹擦过滑移区域,因而这种滑移运动称为grazing-sliding.同样可以看到,图 5(c)中的滑移运动也可以看成是一种grazing-sliding.这两种运动形态可以被归纳为同一种滑移运动类型.
观察图 5(b),并结合图 3(b)可知,系统由G1空间进入滑移区域后保持滑移运动至
观察图 5(d),并结合图 3(d)可知,系统由G1空间直接进入G2空间,然后又回到滑移区域. 由G2空间进入滑移区域后,系统滑移运动至
图 5(e)和图 5(f)属于同一类运动,且都不发生滑移运动.
综上,系统存在4种定性不同的运动类型,其中3种运动中存在黏滞,1种无黏滞发生.
3.2 分岔图
为了更清晰地描述滑移分岔发生的条件,判断系统滑移运动的类型,引入符号
| ${{\tilde{\tau }}_{i}}=\sqrt{\frac{fg}{2\mu L}}{{\tau }_{i}},i=1,2,3$ | (24) |
代入式(9),经计算,可知
| $\left. \begin{array}{*{35}{l}} {{{\tilde{\tau }}}_{1}}=\sqrt{\frac{{{u}_{2}}}{{{u}_{1}}({{u}_{1}}+{{u}_{2}})}} \\ {{{\tilde{\tau }}}_{2}}=\sqrt{\frac{1}{{{u}_{2}}}}(\sqrt{\frac{{{u}_{3}}}{{{u}_{2}}+{{u}_{3}}}}+\sqrt{\frac{{{u}_{1}}}{{{u}_{1}}+{{u}_{2}}}}) \\ {{{\tilde{\tau }}}_{3}}=\sqrt{\frac{{{u}_{2}}}{{{u}_{3}}({{u}_{2}}+{{u}_{3}})}} \\ \end{array} \right\}$ | (25) |
根据式(22) $\sim$式(25),可知
| $\left. \begin{align} & {{P}_{1}}=\sqrt{2\mu Lfg}[({{u}_{2}}-1){{{\tilde{\tau }}}_{2}}-({{u}_{3}}+1){{{\tilde{\tau }}}_{3}}] \\ & {{P}_{2}}=\sqrt{2\mu Lfg}[({{{\tilde{\tau }}}_{3}}-\frac{{{u}_{2}}-1}{{{u}_{3}}+1}{{{\tilde{\tau }}}_{2}})(-{{u}_{3}}+1)+ \\ & (-{{u}_{1}}+1){{{\tilde{\tau }}}_{1}}] \\ \end{align} \right\}$ | (26) |
记
| $\left. \begin{array}{*{35}{l}} {{{\tilde{P}}}_{1}}=({{u}_{2}}-1){{{\tilde{\tau }}}_{2}}-({{u}_{3}}+1){{{\tilde{\tau }}}_{3}} \\ {{{\tilde{P}}}_{2}}=({{{\tilde{\tau }}}_{3}}-\frac{{{u}_{2}}-1}{{{u}_{3}}+1}{{{\tilde{\tau }}}_{2}})(-{{u}_{3}}+1)+(-{{u}_{1}}+1){{{\tilde{\tau }}}_{1}} \\ \end{array} \right\}$ | (27) |
由第二节的分析,不难发现,如果知道一个系统ui (i = 1,2,3)的取值,以及P1和P2的正负号情况,那么系统的运动状态可以确定. 从式(26)和式(27)可以看出,P1和P2的正负号情况分别与
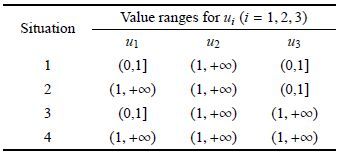
由3.1的分析可知,grading-sliding运动类型的发生有两种可能:一种u1 ≤1,u2 > 1,u3 ≤ 1,运动状态如图 5(a)所示,另一种
根据表 2,可以绘制出当u2给定后,振动驱动系统在u1-u3参数平面的分岔图. 如图 6所示,本文分别选取了两种具有代表性的情况,图 6 (a) u2=3,图 6 (b) u2=5. 图中,点划线表示
| 表 2 4种粘滑运动的发生条件 Table 2 Corresponding conditions for four types of \stick-slip motions |
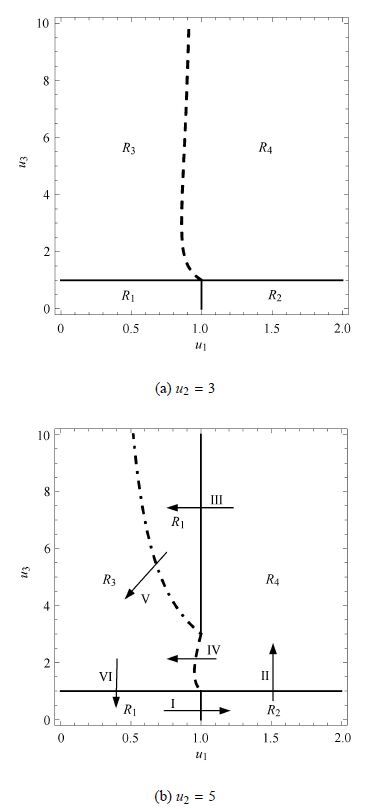
|
图 6 振动驱动系统在u1-u3平面的分岔图 Fig.6 Bifurcation diagrams in u1-u3 plane for vibration-driven system |
当u2较大时,运动分类情况较为典型也较为丰富. 以图 5(b)为例,从左下角的R1出发逆时针绕一圈,研究各分岔线或分界线对运动行为的影响. 从R1出发,当u1的值增加时,系统跨过u1=1分界线进入R2 (箭头I),运动类型由grazing-sliding (图 5(a))变成crossing-sliding (图 5(b)). 这是因为随着u1增加,系统在第一段时间上的黏滞区域逐步地变为非黏滞区域,无法再保证系统不发生后退运动. 从R2出发,当u3的值增加时,系统跨过u3 = 1分界线进入R4 (箭头Ⅱ),运动类型由crossing-sliding(图 5(b))变成无黏滞运动(图 5(f)). 这是因为,随着u3的增加,仅存的黏滞区域也逐步变成非黏滞区域,因而系统将不再黏滞. 注意到
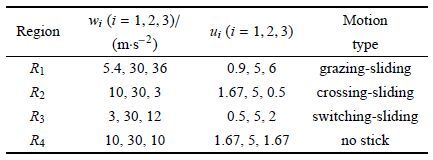
由第3节可知,决定系统分岔特性的变量是驱动参数ui (i = 1,2,3),为了验证分岔结果是否正确,以及运动特性是否与理论分析一致,有必要对其进行数值计算的验证.本节中物理参数固定,唯一改变的是驱动参数. 这里选定L =1 m,μ = 0.333 3,g =10 m/s2,f=0.2,通过改变控制驱动参数wi (i = 1,2,3),可以得到所有类型的运动特性图形. 本节中取u2 =5,这样系统的粘滑运动类型可以由图 6(b)直观地看出. 图 7通过数值计算,得到了系统在不同区域的速度时间图.通过比较表 3和图 7,发现理论分析出的运动类型和数值计算的运动形态吻合. 通过对比图 5和图 7,发现运动形态的理论分析和数值计算结果吻合. 由此,验证了本文中理论分析的正确性.
| 表 3 数值计算四组驱动参数 Table 3 Four groups of driving parameters for numerical calculations |
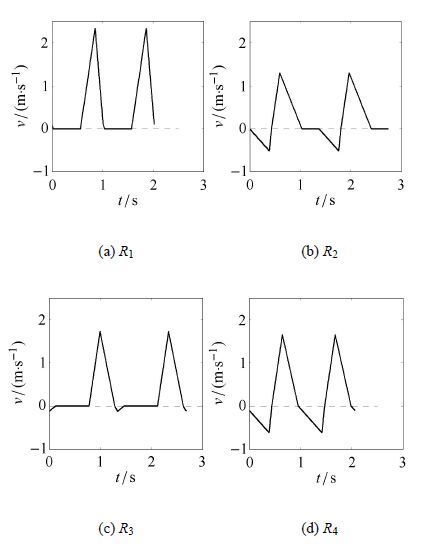
|
图 7 数值方法得到的系统在不同区域的速度时程图 Fig.7 Velocities derived from numerical method versus time for systems in different regions |
本文研究了受三相驱动的振动驱动系统在水平面上的直线运动. 不同于以往的研究,本文重点关注了系统在各向同性干摩擦下的运动. 这种环境与物理实际比较吻合,研究工作具有潜在的实用价值.
含库伦干摩擦的振动驱动系统是一种Filippov系统,因而本文采用滑移分岔的理论分析了其粘滑运动. 在只考虑系统向前运动的情况下,可以将运动分成4种基本情形. 对4种情形分类讨论,并加以归纳,最终得到4种不同的粘滑运动. 借助理论分析得到的分岔条件,我们给出了在驱动参数wi(i = 1,2,3)变化时,系统运动的分岔图. 通过数值模拟,运动分类以及各种运动形态的正确性都得到了验证.
通过本文的滑移分岔分析,可以看到,三相振动驱动系统在各向同性干摩擦环境下具有丰富的动力学行为,值得进一步的实验验证和探究. 此外,从结构上改善和提升振动驱动系统,使其更好地适应各向同性干摩擦环境,也是未来值得思考的问题.
| [1] |
Fang HB, Wang CH, Li SY, et al. A comprehensive study on the locomotion characteristics of a metameric earthworm-like robot[J].
Multibody System Dynamics,2015, 35 (2) : 153-177.
DOI: 10.1007/s11044-014-9428-5. ( 0) 0)
|
| [2] |
Kano T, Kobayashi R, Ishiguro A, et al. Decentralized control scheme for adaptive earthworm locomotion using continuummodel-based analysis[J].
Advanced Robotics,2014, 28 (3) : 197-202.
DOI: 10.1080/01691864.2013.861770. ( 0) 0)
|
| [3] |
Glozman D, Hassidov N, Senesh M, et al. A self-propelled inflatable earthworm-like endoscope actuated by single supply line[J].
IEEE Transactions on Biomedical Engineering,2010, 57 (6) : 1264-1272.
DOI: 10.1109/TBME.2010.2040617. ( 0) 0)
|
| [4] |
Marvi H, Bridges J, Hu DL. Snakes mimic earthworms: propulsion using rectilinear travelling waves[J].
Journal of the Royal Society Interface,2013, 10 (84) : 20130188.
DOI: 10.1098/rsif.2013.0188. ( 0) 0)
|
| [5] |
Wang KD, Yan GZ, Ma GY, et al. An earthworm-like robotic endoscope system for human intestine: design, analysis, and experiment[J].
Annals of Biomedical Engineering,2009, 37 (1) : 210-221.
DOI: 10.1007/s10439-008-9597-6. ( 0) 0)
|
| [6] |
Wang KD, Yan GZ. An earthworm-like microrobot for colonoscopy[J].
Biomedical Instrument and Technology,2006, 40 (6) : 471-478.
DOI: 10.2345/i0899-8205-40-6-471.1. ( 0) 0)
|
| [7] |
Chernousko FL. The optimum rectilinear motion of a two-mass system[J].
Journal of Applied Mathematics and Mechanics,2002, 66 (1) : 1-7.
DOI: 10.1016/S0021-8928(02)00002-3. ( 0) 0)
|
| [8] |
Chernousko FL. Analysis and optimization of the motion of a body controlled by means of a movable internal mass[J].
Journal of Applied Mathematics and Mechanics,2006, 70 (6) : 819-842.
DOI: 10.1016/j.jappmathmech.2007.01.003. ( 0) 0)
|
| [9] |
Fang HB, Xu J. Dynamics of a three-module vibration-driven system with non-symmetric Coulomb's dry friction[J].
Multibody System Dynamics,2012, 27 (4) : 455-485.
DOI: 10.1007/s11044-012-9304-0. ( 0) 0)
|
| [10] |
Fang HB, Xu J. Stiffck-slip effect in a vibration-driven system with dry friction: sliding bifurcations and optimization[J].
Journal of Applied Mechanics,2014, 81 (5) : 051001.
( 0) 0)
|
| [11] |
Chernousko FL. On the optimal motion of a body with an internal mass in a resistive medium[J].
Journal of Vibration and Control,2008, 14 (1-2) : 197-208.
DOI: 10.1177/1077546307079398. ( 0) 0)
|
| [12] |
Chernousko FL. Dynamics of a body controlled by internal motions. IUTAM Symposium on Dynamics and Control of Nonlinear Systems with Uncertainty, Springer Netherlands, 2007
( 0) 0)
|
| [13] |
Fang HB, Xu J. Dynamics of a mobile system with an internal acceleration-controlled mass in a resistive medium[J].
Journal of Sound and Vibration,2011, 330 (16) : 4002-4018.
DOI: 10.1016/j.jsv.2011.03.010. ( 0) 0)
|
| [14] |
Fang HB, Xu J. Controlled motion of a two-module vibration-driven system induced by internal acceleration-controlled masses[J].
Archive of Applied Mechanics,2012, 82 (4) : 461-477.
DOI: 10.1007/s00419-011-0567-3. ( 0) 0)
|
| [15] |
Li HY, Furuta K, Chernousko FL. Motion generation of the capsubot using internal force and static friction. 45th IEEE Conference on Decision and Control, IEEE, 2006
( 0) 0)
|
| [16] |
Huda MN, Yu HN, Wane SO. Self-contained capsubot propulsion mechanism[J].
International Journal of Automation and Computing,2011, 8 (3) : 348-356.
DOI: 10.1007/s11633-011-0591-3. ( 0) 0)
|
| [17] |
Bolotnik NN, Chernousko FL, Figurina TY. Control of Vibration-Driven Systems Moving in Resistive Media. Motion and Vibration Control, Springer Netherlands, 2009: 31-40
( 0) 0)
|
| [18] |
Galvanetto U. Some discontinuous bifurcations in a two-block stick–slip system[J].
Journal of Sound and Vibration,2001, 248 (4) : 653-669.
DOI: 10.1006/jsvi.2001.3809. ( 0) 0)
|
| [19] |
Chernousko FL. Optimal periodic motions of two-mass systems in resistive media[J].
IFAC Proceedings Volumes on Periodic Control Systems,2007, 40 (14) : 13-19.
DOI: 10.3182/20070829-3-RU-4912.00003. ( 0) 0)
|
| [20] |
Fang HB, Xu J. Dynamic analysis and optimization of a three-phase control mode of a mobile system with an internal mass[J].
Journal of Vibration and Control,2011, 17 (1) : 19-26.
DOI: 10.1177/1077546309345631. ( 0) 0)
|
| [21] |
Bolotnik NN, Figurina TY. Optimal control of the rectilinear motion of a rigid body on a rough plane by means of the motion of two internal masses[J].
Journal of Applied Mathematics and Mechanics,2008, 72 (2) : 126-135.
DOI: 10.1016/j.jappmathmech.2008.04.013. ( 0) 0)
|
| [22] |
Li HY, Furuta K, Chernousko FL. A pendulum-driven cart via internal force and static friction. In: Proceedings of 2005 International Conference on Physics and Control. IEEE, 2005
( 0) 0)
|
| [23] |
Liu Y, Wiercigroch M, Pavlovskaia E, et al. Modelling of a vibroimpact capsule system[J].
International Journal of Mechanical Sciences,2013, 66 : 2-11.
DOI: 10.1016/j.ijmecsci.2012.09.012. ( 0) 0)
|
| [24] |
Liu Y, Pavlovskaia E, Hendry D, et al. Vibro-impact responses of capsule system with various friction models[J].
International Journal of Mechanical Sciences,2013, 72 : 39-54.
DOI: 10.1016/j.ijmecsci.2013.03.009. ( 0) 0)
|
| [25] |
Liu Y, Pavlovskaia E, Wiercigroch M, et al. Forward and backward motion control of a vibro-impact capsule system[J].
International Journal of Non-Linear Mechanics,2015, 70 : 30-46.
DOI: 10.1016/j.ijnonlinmec.2014.10.009. ( 0) 0)
|
| [26] |
Guardia M, Hogan SJ, Seara TM. An analytical approach to codimension-2 sliding bifurcations in the dry-friction oscillator[J].
SIAM Journal on Applied Dynamical Systems,2010, 9 (3) : 769-798.
DOI: 10.1137/090766826. ( 0) 0)
|
| [27] |
Kowalczyk P, Piiroinen PT. Two-parameter sliding bifurcations of periodic solutions in a dry-friction oscillator[J].
Physica D: Nonlinear Phenomena,2008, 237 (8) : 1053-1073.
DOI: 10.1016/j.physd.2007.12.007. ( 0) 0)
|
| [28] |
Bernardo MD, Kowalczyk P, Nordmark A. Sliding bifurcations: a novel mechanism for the sudden onset of chaos in dry friction oscillators[J].
International Journal of Bifurcation and Chaos,2003, 13 (10) : 2935-2948.
DOI: 10.1142/S021812740300834X. ( 0) 0)
|
| [29] |
Bernardo MD, Budd CJ, Champneys AR, et al.
Piecewise-smooth Dynamical Systems: Theory and Applications[M]. Springer Science & Business Media, 2008 .
( 0) 0)
|
| [30] |
Filippov AF, Arscott FM.
Differential Equations with Discontinuous Righthand Sides[M]. Springer Science & Business Media, 1988 .
( 0) 0)
|
 2016, Vol. 48
2016, Vol. 48