自然界中的水合物地层特别是海域水合物地层通常处于欠固结状态且存在一定的坡度. 水合物开采钻井引起的钻具摩擦生热和钻井液盐分变化等因素均会引起水合物的分解，削弱水合物地层强度，对井壁稳定性十分不利^[1]；开采过程中的水合物分解会引起地层强度大幅度降低，可能导致地层变形、滑动、生产平台下陷倒塌等工程地质灾害，对水合物开采安全性构成严重威胁^[2]. 对含水合物沉积物的工程力学特性进行深入研究并建立相关理论模型是水合物开采安全性评价的前提条件^[3].

目前，国内外已报道的含水合物沉积物力学性质研究主要集中在三轴剪切试验方面. 温特斯等^[4]针对加拿大马更些冻土区的含水合物沉积物试样和室内合成的含水合物渥太华砂样品进行了三轴剪切试验，重点分析了水合物含量和沉积物性质等因素对样品强度的影响；兵藤等^[5]对人工制备的含水合物砂样品进行了三轴剪切实验，探讨了温度、有效围压和初始孔隙比等因素对样品力学性质的影响；松井等^[6]对取自日本南海海槽的含水合物沉积物试样和室内重塑含水合物砂样品进行了三轴剪切试验，指出样品强度和割线模量均随水合物含量的增加而变大，而泊松比变化不大；兵藤等^[7]对室内合成的含水合物砂样品进行了三轴剪切试验，探讨了加热分解与降压分解过程中样品力学性质的变化规律；国内学者也开展了系列含水合物沉积物的三轴剪切试验，进一步研究了水合物类型^[8]、水合物饱和度^[9,10]、温度^[11]和有效围压^[12]等因素对力学性质的影响关系. 然而，现有的三轴剪切试验通常根据分解产气量^[4,8,10]、孔隙水含量^[7,9]和气体压力降低幅值^[10]等参数反演计算获得样品中水合物的含量，往往存在一定误差且很难对水合物饱和度进行实时准确控制；虽然直接挤压纯水合物与砂粒制样法^[5,11,12]可以准确控制水合物饱和度，但是由该方法制备的样品与自然界的样品存在较大的差别. 时域反射(time domain reflectometry)技术测量水合物饱和度具有结果可靠和实时原位探测等优点^[13,14]，能够较好地解决上述不足.

随着低温高压三轴剪切试验技术的不断发展，国内外学者对含水合物沉积物力学性质的认识逐渐深入^[15,16]，针对含水合物沉积物本构关系模型的研究也相继展开.苏丹等^[17]基于剑桥模型提出了一个考虑水合物饱和度影响的含水合物沉积物本构关系模型，能够模拟其骨架结构破坏及软化现象，但是该模型的参数较多，且其预测的应力-应变曲线仅仅在变化趋势上与试验结果相同.宮崎等^[18]基于邓肯-张模型提出了一个考虑水合物含量和有效围压共同影响的含水合物沉积物本构关系模型，其预测的应力-应变曲线与试验结果符合良好.基于摩尔-库伦破坏准则和广义虎克定律，平克特等^[19]将含水合物沉积物视为沉积物骨架和水合物的组合体而提出一个考虑水合物饱和度和有效围压共同影响的本构关系模型，其预测的应力-应变曲线与试验结果符合良好，最后指出丰浦(Toyoura)砂和另外两种硅砂的模型参数取值基本相同，有利于该本构关系模型的推广应用. 吴二林等^[20,21]基于复合材料的混合律理论和常规土体的统计损伤理论提出一个考虑水合物饱和度和有效围压共同影响的含水合物沉积物本构关系模型，证明了混合律理论和统计损伤理论在描述含水合物沉积物力学性质方面的可行性与合理性，但是该模型采用的沃伊特模型在实际情况中往往不能精确描述复合材料的等效割线模量^[22]，并且其采用的德鲁克-普拉格(Drucker-Prager)破坏准则较为保守，使其岩土微元强度确定的合理性受到限制^[23].

本文将采用饱和样品利用气体扩散法制备含水合物沉积物，通过时域反射技术实时监测并控制水合物含量，利用三轴剪切试验获得系列应力-应变曲线；基于改进的等效割线模量混合律模型与损伤统计理论，结合摩尔-库破坏准则，提出较为合理的含水合物沉积物本构关系模型，为水合物开采安全性评价提供本构模型依据.

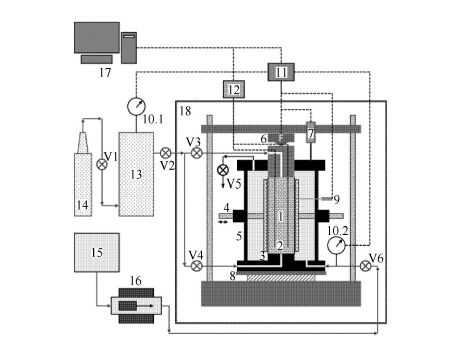
以南京宁曦土壤仪器有限公司生产的TSZ-2型三轴剪切仪为基础，增加温度控制、流体供给和时域反射测量等模块，经系统改造后形成一套具备水合物含量实时测量能力的含水合物沉积物力学性质测试装置(图1).为了尽可能降低时域反射探针对含水合物沉积物力学性质的影响，该装置采用柔性纯铜丝替代常规刚性探针.主要技术参数：含水合物沉积物样品直径为39.1 mm，高为120 mm；通过压力室内蒸馏水传递加载围压，其上限为10 MPa； 轴向荷载施加上限为30 kN；温度控制范围-10℃~30℃；压力室内布置精度为$\pm 0.1$℃的T型热电偶温度探头以测量土样温度变化，测量范围-10℃ $\sim$ 100℃；压力传感器由上海天沐公司生产，测量范围0$\sim $10 MPa，精度为$\pm $0.1%FS；柔性纯铜丝探针长度为11 cm，直径为0.2 mm；用于时域反射波形采集的时域反射仪(型号：TDR100)由美国坎贝尔科技(Campbell Scientific)公司生产.

图1(Fig.1)

图1 含水合物沉积物力学性质测试实验装置结构示意图 Fig.1 Sketch of the triaxial shear test apparatus for mechanical properties of HBS

图中,1为含水合物沉积物，2为时域反射探针，3为橡胶筒，4为不锈钢半开模，5为压力室，6为压力传感器，7为位移传感器，8为可移动底座，9为温度探头，10.1和10.2为压力表，11为数据采集模块，12为时域反射仪，13为气室，14为甲烷气瓶，15为水箱，16为围压泵，17为工控机，18为恒温空气浴，V1,V2,V3,V4,V5和V6为阀门.

本文试验所用材料主要包括：取自青岛海滩的天然海砂筛分制成的粒径为0.18 mm$\sim $0.25 mm的细砂，主要成分为石英，样品干密度为1.53 g/cm$^{3}$，孔隙度为38%，砂颗粒的相对密度为2.47； 纯度为99.9%的甲烷气体，由青岛瑞丰气体有限公司生产；自行配置的十二烷基硫酸钠水溶液，质量浓度为0.03%，用于促进甲烷水合物的快速合成^[24].

时域反射技术最初用于电缆探伤，后来被赖特等^[25]推广应用于含水合物沉积物的含水量测量，通过含水量变化确定水合物饱和度. 饱和状态的含水合物沉积物中水合物饱和度$S_{\rm h} $可按下式计算

试验的具体步骤如下：(1)焊接两根时域反射探针；(2)安装橡胶筒，拧紧不锈钢半开模，翻转压力室后将海砂分5次装填入橡胶筒内，同时将十二烷基硫酸钠水溶液分5次加入海砂直到饱和，该过程中不断震动以增加海砂的密实性；(3)安装压力室底座，连接管路；(4)施加1.0 MPa围压后加入甲烷气体冲洗管路，排除杂异气体；(5)逐级施加围压并注入甲烷气体，始终保持孔隙压力至少小于围压0.5 MPa，常温放置12 h以促进甲烷气体溶解于孔隙水； (6)启动恒温空气浴降温以合成水合物，目标温度设定为1.0$℃；(7)待孔隙压力变化不大时水合物合成结束，拧开不锈钢半开模，调整有效围压至设定值，以0.8 mm/min的剪切速率进行排水三轴剪切试验，同时记录应力、应变和孔隙压力数据.

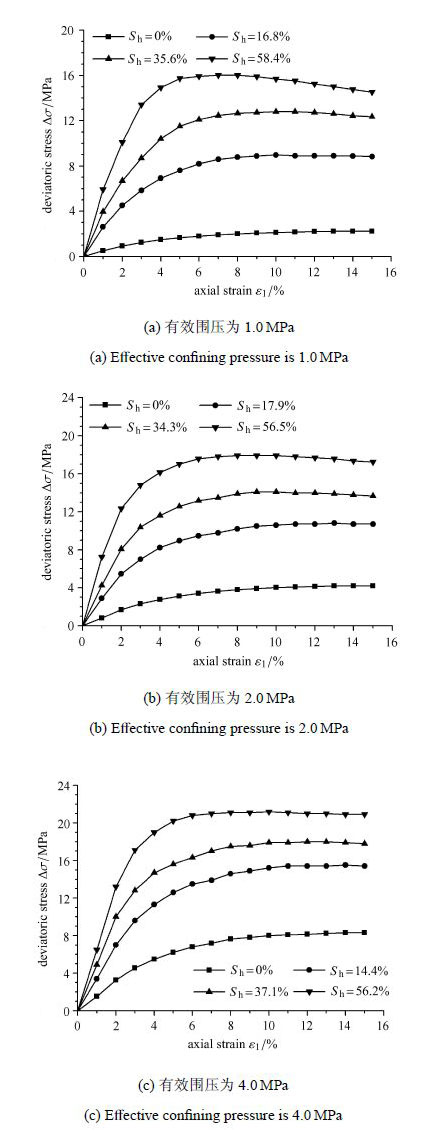
不同有效围压下含水合物沉积物应力-应变关系曲线如图2所示. 可以看出: 水合物饱和度较低时，应力-应变曲线没有明显的峰值点；随着水合物饱和度的增加，应力-应变曲线逐渐具有明显的峰值点；有效围压越小，水合物含量较高的沉积物的应力-应变曲线峰值点越明显.水合物在沉积物中含量较高时，将与土颗粒骨架一起作为持力体存在^[27]，三轴剪切过程中，除了发生土颗粒旋转滑移，水合物还会发生损伤和破碎，而水合物与冰一样脆性较强，导致应力-应变曲线出现应变软化现象.水合物饱和度越高，这种应变软化现象越明显.有效围压较低时，土颗粒以及水合物颗粒之间的结合由于限制减小而更容易发生损伤与破坏，应变软化现象更容易出现.因此，含水合物沉积物在三轴剪切试验过程中是否出现应变软化现象由水合物饱和度和有效围压共同决定.

图2(Fig.2)

图2 不同有效围压下含水合物沉积物应力--应变关系曲线 Fig.2 Stress-strain curves of hydrate-bearing sands with different effective confining pressures

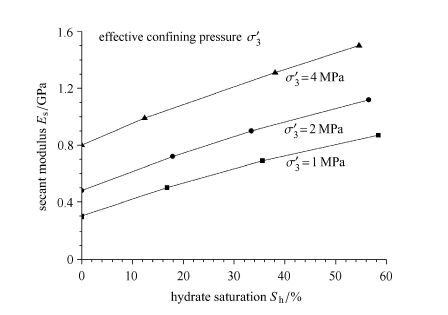
割线模量反应了含水合物沉积物的平均刚度特性.不同有效围压下含水合物沉积物的割线模量随水合物饱和度变化曲线如图3所示.图中的割线模量定义为1%应变对应的割线模量.可以看出，相同有效围压下含水合物沉积物的割线模量随着水合物饱和度的增加而增大.水合物随其含量的增加以胶结的形式逐渐填充于土颗粒之间的孔隙，土颗粒之间的胶结作用逐步加强，含水合物沉积物的整体刚度有所增加，表现为割线模量有所增大. 相同水合物饱和度下含水合物沉积物的割线模量随着有效围压的增大而单调增加.有效围压既能够起到约束含水合物沉积物的作用，割线模量随围压增加而增加；有效围压增大将会引起土颗粒之间形成的胶结遭到破坏，导致含水合物沉积物的整体刚度降低，割线模量随围压增加而有所降低.割线模量随着有效围压的增大而单调增加说明了有效围压的约束作用在试验过程中始终处于主导地位.

图3(Fig.3)

图3 不同有效围压下含水合物沉积物割线模量随水合物饱和度变化曲线 Fig.3 Relationships between secant modulus and hydrate saturation of hydrate-bearing sands with different effective confining pressures

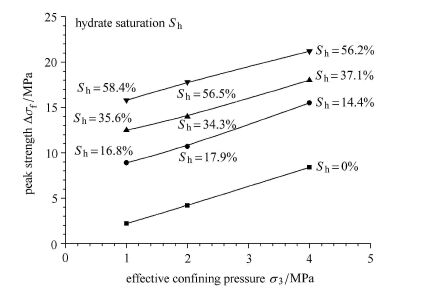
不同水合物饱和度下含水合物沉积物峰值强度(对于应力-应变曲线无明显峰值的情况，以15%应变对应的应力值作为强度值)与有效围压关系如图4所示.可以看出，相同有效围压下含水合物沉积物峰值强度随水合物饱和度的增加而变大；相同水合物饱和度下含水合物沉积物峰值强度随有效围压的变大而增加.

图4(Fig.4)

图4 不同水合物饱和度下含水合物沉积物破坏强度与有效围压关系 Fig.4 Relationships between strength and effective confining pressure

不同水合物饱和度下含水合物沉积物的强度指标(黏聚力$c$和内摩擦角$ffarphi $)如图5所示.可以看出，内摩擦角$ffarphi $相差并不明显，即水合物饱和度对含水合物沉积物的内摩擦角$ffarphi $影响不大，而含水合物沉积物的黏聚力$c$随着水合物饱和度的增加而明显变大.因此，水合物对含水合物沉积物强度的贡献主要体现在增加砂颗粒间的胶结能力，进而引起黏聚力$c$的明显增加，而对内摩擦角$ffarphi $的影响较小. 相关研究^[28]表明，在渥太华砂样中采用气体扩散法制备含水合物沉积物，其内摩擦角$ffarphi $在水合物饱和度小于60%时基本保持在32$^{\circ}$上下不变，而在水合物饱和度大于60%时有所降低；黏聚力$c$随着水合物饱和度的增加而明显增大. 松井等^[29]、宮崎等^[30]和刘芳等^[31]均发现了类似的实验现象.本文中水合物饱和度始终小于60%，内摩擦角$ffarphi $ 随着水合物饱和度的增加基本保持在32$^{\circ}$上下不变，而黏聚力$c$随着水合物饱和度的增加而明显增大，说明了试验结果的可靠性.

图5(Fig.5)

图5 不同水合物饱和度下含水合物沉积物强度指标 Fig.5 Strength parameters of hydrate-bearing sands with different hydrate saturations

含水合物沉积物是一种多相介质，弹性常数由所有组成相的性质决定.在本节将借鉴复合材料的相关理论，建立等效弹性模量和泊松比与各组分参数之间的关系.分析中将做如下假设：含水合物沉积物为一种复合材料，由沉积物骨架(海砂)、水合物和孔隙水组成；饱和海砂沉积物(海砂颗粒和孔隙水)为复合材料的基相并为均匀连续体；水合物为复合材料的夹杂相并与基相之间完全黏结；基相、夹杂相以及复合材料总体均为各向同性材料.

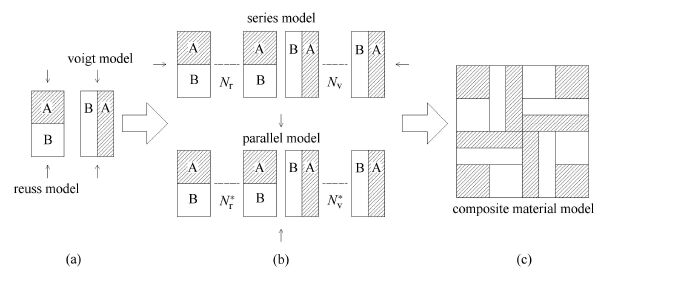
由于独立使用罗伊斯模型或者沃伊特模型预测复合材料等效弹性模量存在较大误差^[22]；两者算术平均模型^[32]的物理意义不明确，无法反应复合材料的微观情况.本文首先将罗伊斯模型和沃伊特模型组成各向异性的串并联单元，然后再将两个串联单元和两个并联单元组成各向同性的复合材料模型.

假设含水合物沉积物的结构可以用图6所示的复合材料模型表述,A表示复合材料基相(海砂颗粒和孔隙水),B表示复合材料夹杂相(水合物).这个模型的特点是各向同性的复合材料模型由2个串联单元和2个并联单元组成，而每个串联单元或并联单元均由若干个罗伊斯应力串联模型和若干个沃伊特应变并联模型组成^[33]，其中，罗伊斯应力串联模型的等效弹性模量$E_{\rm r}$可由下式确定

图6(Fig.6)

图6 含水合物沉积物复合材料模型示意图 Fig.6 Diagram of the composite-material model for hydrate-bearing sands

式中，$n_{\rm A} $和$n_{\rm B} $分别表示基相和夹杂相的体积分数，取值分别为$1 - \phi S_{\rm h} $和$\phi S_{\rm h} $；$E_{\rm A} $表示基相的弹性模量，根据饱和水纯砂样品的应力-应变曲线确定，$E_{\rm B} $表示夹杂相的弹性模量，取值为纯水合物的弹性模量. 沃伊特应变并联模型的等效弹性模量$E_{\rm v} $可由下式确定

类似地，各向同性含水合物沉积物符合材料的泊松比$\nu $可由相同方法估算，即

假设含水合物沉积物的三轴应力-应变关系服从广义虎克定律，即有

假设含水合物沉积物在三轴剪切过程中的损伤是一个连续过程，各微元强度在概率统计上服从威布尔(Weibull)分布规律^[37]，损伤变量$D$可由下式确定

摩尔-库伦准则是基于大量试验数据而建立的，能够较准确的反应岩土材料的承载力. 基于摩尔-库伦准则，含水合物沉积物微元强度威布尔分布的分布变量$F$具有如下形式^[23]

当轴向应变$ffarepsilon _1 $等于峰值应变$ffarepsilon _{\rm f} $时，轴向偏应力$\Delta \sigma $等于峰值应力$\Delta \sigma _{\rm f} $，并且$\Delta \sigma $对$ffarepsilon _1 $的一阶导数为0，即

用上述建立的本构关系预测不同有效围压条件下三轴剪切试验的应力-应变曲线的参数如表1所示.其中，基相的体积分数$n_{\rm A} $和夹杂相的体积分数$n_B $的取值分别为$1 - \phi S_{\rm h} $和$\phi S_{\rm h }$，孔隙率$\phi $的取值为0.38；基相的弹性模量$E_{\rm A} $的取值为水合物含量为零时沉积物的割线模量；沃伊特应变并联模型对应的力链比例$f_{\rm v} $根据割线模量试验数据拟合获得，如图7所示；威布尔分布参数$m$和$F_0 $分别由式(23)和式(24)计算获得.根据已经报道的试验数据，纯水合物的弹性模量为9.0 GPa^[39]，取其为夹杂相的弹性模量$E_{\rm B} $；水合物含量为零时沉积物和纯水合物的泊松比取值分别为0.2和0.219^[21].

图7(Fig.7)

图7 不同有效围压下含水合物沉积物割线模量试验结果与混合律模型预测曲线的对比 Fig.7 Comparison of experimental results and predicting curves by the mixed model of secant modulus of hydrate-bearing sands with different effective confining pressures

表1(Table 1)

表1 本构关系预测不同有效围压条件下应力--应变曲线 所用参数Table 1 Parameters for prediction of experimental stress-strain curves by constitutive model under different effective confining pressure $\sigma $3/MPa S h=% nA nB EA/GPa fv m F0/MPa 1 0 1 0 0.3 0.51 0.360 0.09 16.8 0.936 0.064 0.513 6.60 35.6 0.865 0.135 0.582 11.55 58.4 0.778 0.222 0.686 17.12 2 0 1 0 0.48 0.43 0.440 1.65 17.9 0.932 0.068 0.518 8.42 34.3 0.870 0.130 0.568 12.88 56.5 0.785 0.215 0.632 18.61 4 0 1 0 0.8 0.24 0.478 3.80 14.4 0.945 0.055 0.553 12.01 37.1 0.859 0.141 0.540 14.25 56.2 0.786 0.214 0.586 19.05

表1 本构关系预测不同有效围压条件下应力--应变曲线 所用参数 Table 1 Parameters for prediction of experimental stress-strain curves by constitutive model under different effective confining pressure

在不同有效围压下，含水合物沉积物割线模量的模型预测值与试验数据的对比情况如图7所示，含水合物沉积物应力-应变曲线的模型预测值与试验数据的对比情况如图8所示. 从图7可以看出，含水合物沉积物割线模量的试验数据全部分布于模型预测的等效弹性模量上限值与下限值之间，并且该模型能够较好地预测不同有效围压下含水合物沉积物割线模量随水合物饱和度而变化的过程.从图8可以看出，含水合物沉积物应力-应变曲线的模型预测结果与试验数据在水合物饱和度较低时符合良好，而在水合物饱和度较高时存在一定差别，但是仍然能够较好地反映含水合物沉积物应力-应变发展过程，即剪切初期为弹性变形，随后为硬化屈服，达到峰值应变之后发生不同程度软化.综上所述，本文模型能够反应含水合物沉积物中水合物与沉积物骨架解胶结以及固体水合物颗粒破损等损伤效应，较好地预测了含水合物沉积物割线模量和应力-应变曲线的变化情况，特别适用于描述含水合物沉积物的应变软化行为，具有良好的适用性.

图8(Fig.8)

图8 不同有效围压下含水合物沉积物应力--应变试验数据与 本构关系模型预测结果的对比 Fig.8 Comparison of experimental and theoretical stress-strain curves of hydrate-bearing sands with different effective confining pressures

本文开展了含水合物沉积物样品制备与排水三轴剪切试验，实时测量了水合物饱和度；提出了一个等效弹性模量细观力学混合律模型，改进了含水合物沉积物的损伤统计本构关系模型. 主要结论如下：

(1)随着水合物饱和度的增加和有效围压的降低，应力-应变曲线由应变硬化型逐渐变为应变软化型，割线模量和峰值强度均随着水合物饱和度和有效围压的增加而变大，水合物含量对粘聚力的影响明显，而对内摩擦角的影响较小；

(2)提出的细观力学混合律模型能够较好地预测不同有效围压下等效弹性模量随水合物饱和度的变化规律，一定程度上反应了含水合物沉积物的细观结构；

(3)基于细观力学混合律和损伤统计理论改进的本构关系模型能够反映水合物饱和度增加引起的应变软化现象，具有良好的适用性.

Liu Lele, Zhang Xuhui, Liu Changling, Ye Yuguang