引言
结构动力失稳是造成工程结构系统失效的主要原因之一。多数作用在结构上的动力载荷(如地震动、强风以及巨浪)则表现出明显的随机性。因此,结构随机动力稳定性分析是进行复杂工程结构分析、设计的关键问题之一。
关于结构稳定性的研究,经历了一个观念逐步演进的过程。在经典时期(欧拉时期,1774年)[1, 2],结构稳定性是指先于强度失效的可能性。在达到临界载荷时,结构会在微小扰动下偏离初始平衡位置,导致结构失稳(失去关于平衡位置的稳定性)。对经典稳定问题的研究导致能量准则:当体系处于稳定平衡状态时,其总势能为最小值[3]。在本质上,这一准则属于静力学判据。仅从系统"处于平衡位置是否稳定"这一观念出发讨论动力稳定性问题,会忽略动力系统的运动学属性,因此,静力学判据不适用于动力系统。1892年,俄国学者李雅普诺夫从动力系统在状态空间中的轨迹是否对初始扰动(初始条件)敏感的角度定义动力稳定性[4, 5]:若初始条件的微小变化只引起系统响应的微小变化,则称该结构是稳定的。李雅普诺夫动力稳定性扩展了经典稳定性的观念、也使稳定性问题的提法有了关键性的概念变化:从本质上的系统平衡方程解的多值性、转化为系统平衡方程解对于初始条件的敏感性。因此,李雅普诺夫动力稳定性与静力稳定性虽有共性的一面:系统失稳与否,但其间的差别则更值得关注:经典稳定性概念关注于寻找系统平衡状态;而李雅普诺夫动力稳定性则关注于系统对于初始条件的敏感性。事实上,经典稳定性研究、李雅普诺夫意义上的稳定性研究,最终都归结为对结构自身特性的研究,无论是静力问题的能量判据,还是动力问题稳定性判别的李雅普诺夫函数,经典稳定性研究多关注于平衡微分方程的定性性质,并利用这种定性性质考察系统的稳定性。显然,这种思想在本质上属于封闭系统的思想,它们忽略了系统动力过程中外部作用的变化及由之导致的系统能量消长,我们认为:这极可能是经典研究难以应用于复杂工程系统的根源。
在另一方面,随机动力稳定性研究则基本限制在李雅普诺夫意义上的动力稳定定性方法。大量的研究工作集中于获得微分方程解保持矩稳定性[6]及样本稳定性的稳定边界[7]。在这些工作中,仅可以定性地导出动力系统保持样本稳定性的充分条件[8, 9, 10, 11]、依概率1动力稳定与否的稳定边界[12]。 但是,对于如何定量地分析结构的动力失稳概率,迄今为止的研究却都无能为力。 究其原因:在于李雅普诺夫意义上的经典动力稳定性及其分析方法(如样本稳定性[13, 14]与矩稳定性[15, 16]分析)本质上属于定性分析而不是定量的物理分析。
有鉴于此,本文试图在概率密度演化理论基础之上,发展结构随机动力稳定性的定量分析方法。
1 经典随机动力稳定性回顾
在发展结构随机动力稳定性定量分析方法之前,不妨首先回顾一下经典随机动力稳定性的定义。 不失一般性,考虑一般的随机动力系统
|
$\dot X = {\bf{f}}(X,\theta ,t){\rm{ }}$
|
(1) |
式中,${ X}(t)$为 $2n$维状态向量; $\theta $为该随机动力系统中所有随机变量组成的随机向量; ${\bf f}(\cdot)$为$2n$ 维向量算子。
在经典随机动力稳定性定义中,要求初始条件不含随机性,即初始条件依概率1的为 ${ X}(0)={ X}_0$。一般地,取 ${ X}_0={\bf 0}$,并且要求 $(X,\theta ,t) = {\bf{0}}$,
这就将问题转化为0解的稳定性。
以 $\| { X}(t)\|$表示 ${ X}(t)$的某种范数,随机动力稳定性可以有如下几种不同的定义[17, 18, 19, 20]。
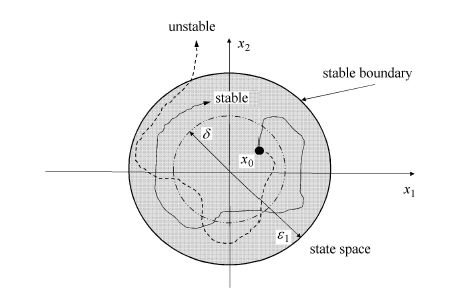
(1) 依概率为1的稳定性(almost-sure stability):给定任意 ${\varepsilon _1},{\varepsilon _2} > 0$,存在平凡解且$\delta ({\varepsilon _1},{\varepsilon _2},{t_0}) > 0$,使得
|
${\rm{Pr}}(\bigcup\limits_{{X_0} \le \delta } \{ \mathop {{\rm{sup}}}\limits_{t \ge {t_0}} X(t) \ge {\rm{ }}{\varepsilon _1}\} ) \le {\varepsilon _2}{\rm{ }}$
|
(2) |
成立,该平凡解在李雅普诺夫意义上依概率为1 稳定或几乎必然稳定。 这里Pr表示概率。
式(2)的物理意义在于:在整个时间区段$[t_0,\infty)$,保证其最大值超越边界${\varepsilon _1}$的样本个数占所有样本个数的比例(频率)不超过${\varepsilon _2}$。事实上,这里要求${\varepsilon _2} \to 0$。 因此,依概率为1的稳定性又称为样本稳定性[20]。
(2) 依概率为1的渐进稳定性(almost-sure asymptotic stability):假定每一个$\varepsilon > 0$,存在平凡解且$\delta '(\varepsilon ,t)$,使得
|
$\mathop {{\text{lim}}}\limits_{{t_1} \to \infty } {\text{Pr}}(\mathop {{\text{sup}}}\limits_{t{t_1}} X(t)\varepsilon ) = 0,\left\| {{X_0}} \right\|{\text{ < }}\delta '$
|
(3) |
成立,称平凡解在李雅普诺夫意义上依概率为1渐进稳定或几乎必然渐进稳定性。
式(3)较式(2)降低了要求,即仅要求随机过程的最终状态始终在稳定边界内,而对其中间过程并不关心。
事实上,式(2)与(3)与随机过程$\| { X} (t) \|$在整个时间区段$[t_0,\infty)$
内的收敛性有关。 然而,在实际动力系统中这两个式子常常难以得到满足[21]。 因此,需要定义其他的随机动力稳定性的概念。
(3) 依概率的稳定性(stability in probability): 给定${\varepsilon _1},{\varepsilon _2} > 0$,存在平凡解且
|
${\text{Pr}}(X(t){\varepsilon _1}){\varepsilon _2}$
|
(4) |
$\delta ({\varepsilon _1},{\varepsilon _2},{t_0}) > 0$,使得
成立,则称该平凡解是概率稳定的。
式(4)表示在任意时刻$t$超过稳定边界$\varepsilon_1$的样本个数占总样本个数的比例(频率)不超过$\varepsilon_2$,如图1所示。事实上,$\varepsilon_2$即为系统失稳概率。
(4) 矩稳定性(stability in $n$th statistical moment): 给定$\varepsilon>0$,存在平凡解且 $\delta(\varepsilon,t_0)>0$,使得
|
${\text{E}}[{\left\| {X(t)} \right\|^n}]\varepsilon ,n > 0,t{t_0}$
|
(5) |
成立,则称该平凡解的$n$阶矩是稳定的。 ${\rm E} [\cdot]$表示集合平均。
可以注意到:不等式(4)与式(5)仅仅与任意$t$时刻的$ \| { X} (t) \|$值有关。
令人遗憾的是,在既有随机动力稳定性研究中,很少直接运用上述随机动力稳定性的基本定义。 原因主要在于:(1) 稳定边界值$\varepsilon_1$在李雅普诺夫意义的稳定概念中没有统一地确定方法;(2) 经典随机动力稳定性分析理论是定性分析理论,它只研究系统是否出现动力失稳,而并不关心有多大的概率出现失稳(也从来没有研究者能够计算这一概率)。 因此,失稳概率$\varepsilon_2$从未被用来衡量随机动力系统保持动力稳定性或失去动力稳定性的可能性程度。
针对上述局限性,本文致力于发展结构随机动力稳定性能评价的定量方法------结构动力稳定性概率的精细分析方法。 通过建立这一方法,实现在定量概率意义上评价结构动力稳定性。 为此,首先要研究结构动力稳定性判别准则。
2 结构动力稳定性判别准则
前已述及:经典静力稳定性与李雅普诺夫动力稳定性研究认为:仅结构自身的性质会影响结构的动力稳定性态。 这种思想在本质上忽略了结构动力系统中的外部作用。因此,采用经典动力稳定性准则判定复杂结构在动力作用下(如地震动,强风等)的稳定性时常常会导致误判。 在本文作者的研究中,发展了一类新的结构动力稳定性判别准则[22, 23],简介如下。
在随机激励作用下,多自由度随机非线性系统的运动方程可表示为
|
$M(\theta )\ddot Z + C(\theta )\dot Z + G(\theta ,Z) = F(\theta ,t)$
|
(6) |
式中,${ Z}$为系统状态量,${ M}$和${ C}$分别为$n\times n$质量矩阵与阻尼矩阵;${ G}$为$n\times1$线性/非线性恢复力向量; ${ F}$为$n\times 1$外激励向量;$\theta = ({\theta _1},{\theta _2},\cdots ,{\theta _s})$为由结构与载荷中$s$个独立随机变量所组成的随机向量,其概率密度函数可表示为${p_\theta }(\theta ) = \mathop \prod \limits_{j = 1}^s {p_{{\theta _j}}}({\theta _j})$。
式(6)的初始条件为
|
$Z({t_0}) = {Z_0},\dot Z({t_0}) = {\dot Z_0}$
|
(7) |
在动力系统中,结构动力稳定性不仅仅只与结构自身的性质有关,同时也与外部作用过程有密切联系。 因此,可定义如下的动力稳定性函数
|
$S(t) = {E_{{\rm{input}}}}(t) - {E_{{\rm{intr}}}}(t){\rm{ }}{\rm{}}$
|
(8) |
其中
|
$E_{\rm input}(t)=\int^t_0{ F}^{\rm T}(t) \dot{ Z}(t) d t +E_0 $
|
(9) |
$E_{\rm intr}(t)=| W_{\rm ext}(t)-W_{\rm int}(t) | =$
|
$|{[F(t) - (M\ddot Z(t) + C\dot Z(t))]^{\text{T}}}Z(t) - \int_0^Z G (Z,t)dZ|$
|
(10) |
式(9)中,$E_{\rm input}(t)$表示输入到系统中的总能量,$E_0$为初始条件所贡献的输入能量;式(10)中,$E_{\rm intr}(t)$表示系统的特征能量,其中,$W_{\rm ext}(t)$为"即时外力功",$W_{\rm int}(t)$为"累积内力功"。
结构发生动力失稳的本质在于[22, 23]:在振动过程中,除去结构动能、阻尼耗能吸收一部分能量之外,结构非线性恢复力将耗散或吸收大量能量,如果输入到结构中的总能量与上述耗能总量相平衡,则结构是动力稳定的;反之,如果输入的能量小于上述总耗能,则必然在结构内部存在其他的吸收能量的过程,这一吸收能量的过程即为系统从原运动状态进入新的运动状态---失稳的过程。 结构在系统吸收能量总量大于结构总输入能量的时刻发生突变,即发生动力失稳。 换句话说,动力失稳的本质在于能量平衡的失稳:结构振动过程中所消耗的能量大于输入系统的能量。
据此,可定义如下动力稳定准则
|
$\left. \matrix{
S(t) > 0 \hfill \cr
S(t) = 0 \hfill \cr
S(t) < 0 \hfill \cr} \right\}$
|
(11) |
显然,上述准则同时反映了结构自身性质与外部作用对结构动力稳定性能的综合影响。
通过引入动力稳定函数,系统稳定概率可用时间$[0,T]$
范围内系统动力稳定性函数大于0的概率度量
|
$R = {\rm{Pr}}(\bigcap\limits_{t \in [0,T]} S (t) \ge 0){\rm{ }}12$
|
(12) |
于是,参照经典随机动力稳定性的定义,结构随机动力稳定性可有如下定义:
(1) 依概率为1的结构随机动力稳定性:给定结构参数及外部载荷,使得
恒成立,则称该系统依概率为1稳定。
(2) 依概率的结构随机动力稳定性:给定结构参数及外部载荷并规定结构允许发生动力失稳的概率为$p_{\rm f}$,使得
|
$1 - R \le {p_{\rm{f}}}{\rm{ }}$
|
(14) |
成立,则称该系统是依概率$R$稳定的。
3 结构随机动力稳定性分析的概率密度演化
经典随机动力稳定性分析的目的在于获得依概率为1或依概率稳定的稳定边界。 如本文第一部分所述,这些定性分析无法给出定量的结构稳定概率。 因此,有必要在上述动力稳定性准则基础上发展定量计算结构稳定或不稳定概率的新方法。 由本文第一作者及其合作者发展的概率密度演化理论可用于实现这一目标[24, 25, 26]。 事实上,通过引入结构动力失稳的物理机制,这一理论可进一步推广至概率耗散系统。
对于概率保守系统而言,与方程(6)相应的广义概率密度演化方程可表示为[25]
|
${{\partial {p_{Z\theta }}(z,\theta ,t)} \over {\partial t}} + \sum\limits_{j = 1}^n {{{\dot Z}_j}} (\theta ,t){{\partial {p_{Z\theta }}(z,\theta ,t)} \over {\partial {z_j}}} = 0{\rm{ }}$
|
(15) |
式中,${p_{Z\theta }}(z,\theta ,t)$ 为$(Z(t),\theta )$的联合概率密度函数。
对于概率耗散系统,一旦发生动力失稳$(S(t)<0)$,结构响应所携带的概率将发生耗散。 耗散概率$\delta P$可表示为
|
$\delta P = - H(S(t)) \cdot {\rm{Pr}}[(Z(t),\theta )]{\rm{ }}$
|
(16) |
式中,${\cal H}$称为概率耗散因子,可定义为
|
$H(S(t)) = \left\{ \matrix{
0,S(t) \ge 0 \hfill \cr
1,S(t) < 0 \hfill \cr} \right.$
|
(17) |
注意到
|
${\text{Pr}}[Z(t),\theta ] = [\int_{\Omega \times \Omega \theta } {{p_{Z\theta }}} (z,\theta ,t)dzd\theta ]$
|
(18) |
结合上式,假定概率耗散发生在$[t,t+\Delta t]$时刻范围内,式(16)可改写为
|
$\delta P = - H(S(t)) \cdot [\int_{\Omega \times {\Omega _\theta }} {{{\tilde p}_{Z\theta }}} (z,\theta ,t)dzd\theta ]$
|
(19) |
式中,${\tilde p_{Z{\rm{ }}\theta }}(z,\theta ,t)$ 称为时间间隔$[t,t+\Delta
t]$内的平均耗散概率密度
|
${\tilde p_{Z{\rm{ }}\theta }}(z,\theta ,t) = {{{p_{Z{\rm{ }}\vartheta }}(z,\theta ,t)} \over {\Delta t}} $
|
(20) |
显然,当$\Delta t \to 0$,下式成立
|
${\tilde p_{Z\varpi }}(z,\theta ,t) = {p_{Z\theta }}(z,\theta ,t)$
|
(21) |
对于式(6)所示的动力系统,考虑动力失稳的可能性,在任意时间区间$[t,t+\Delta t]$
内,依据概率守恒原理[26] 可知有
|
${\rm{Pr}}\{ (Z(t + \Delta t),)\theta \} - {\rm{Pr}}\{ (Z(t),\theta )\} = \delta P$
|
(22) |
以式(16)和式(18)代入上式有
|
$\eqalign{
& \int_{{\Omega _{t + \Delta t}} \times \Omega \theta } {{p_{Z\theta }}} (z,\theta ,t + \Delta t)d\tilde zd\theta - \cr
& \int_{{\Omega _t} \times {\Omega _Q}} {{p_{Z\theta }}} (z,\theta ,t)dzd\theta = \cr
& - H(S(t)) \cdot \int_{{\Omega _t} \times \Omega \theta } {{{\tilde p}_{Z\theta }}} (z,\theta ,t)\Delta tdzd\theta \cr} $
|
(23) |
|
$d\tilde z = |J|dz{\rm{ }}$
|
(24) |
其中,$\tilde{ z}={ z}(t+\Delta t)$,且有
这里,$| { J} |$表示雅克比量
|
$|J| = [1 + \sum\limits_{l = 1}^m {\frac{{\partial {{\dot Z}_l}(\theta ,t)\Delta t}}{{\partial {z_l}}}} ]$
|
(25) |
可以证明$|{ J}|=1$,因此
|
$\eqalign{
& \int_{{\Omega _{t + \Delta t}} \times \Omega \theta } {{p_{Z\theta }}} (z,\theta ,t + \Delta t)d\tilde zd\theta - \cr
& \int_{{\Omega _t} \times {\Omega _\theta }} {{p_{Z\theta }}} (z,\theta ,t)dzd\theta = \cr
& - H(S(t)) \cdot \int_{{\Omega _t} \times \Omega \theta } {{{\tilde p}_{Z\theta }}} (z,\theta ,t)\Delta tdzd\theta \cr} $
|
(26) |
将上式两端同除以$\Delta t$,并令$\Delta t \to 0$,则有
|
$\eqalign{
& {{\rm{D}} \over {{\rm{D}}t}}\int_{{\Omega _t} \times \Omega \theta } {{p_{Z\theta }}} (z,\theta ,t)dzd\theta = \cr
& - H(S(t)) \cdot \int_{{\Omega _t} \times \Omega \theta } {{p_{Z\theta }}} (z,\theta ,t)dzd\theta \cr} $
|
(27) |
由此,可导出概率耗散系统的广义概率密度演化方程
|
$\eqalign{
& {{\partial {p_{Z\theta }}(z,\theta ,t)} \over {\partial t}} + \sum\limits_{j = 1}^n {{{\dot Z}_j}} (\theta ,t){{\partial {p_{Z\theta }}(z,\theta ,t)} \over {\partial {z_j}}} = \cr
& - H(S(t)) \cdot {p_{Z\theta }}(z,\theta ,t) \cr} $
|
(28) |
注意到:当系统始终保持动力稳定时(${\cal H}(S(t))=0$),式(28)将转化为概率保守系统概率密度演化方程(式(15))。
式(28)的一维形式为
|
$\eqalign{
& {{\partial {p_{{Z_l}\theta }}({z_l},\theta ,t)} \over {\partial t}} + {{\dot Z}_l}(\theta ,t){{\partial {p_{{Z_l}\theta }}({z_l},\theta ,t)} \over {\partial {z_l}}} = \cr
& H(S(t)){p_{Z\theta }}({Z_l},\theta ,t) \cr} $
|
(29) |
初始条件为
|
${p_{{Z_l}\theta }}({z_l},\theta ,t){|_{t = {t_0}}} = \delta (z - {z_{l,0}}){p_\theta }(\theta )$
|
(30) |
系统发生概率耗散后的剩余概率密度函数为
|
${p_{{z_l}}}({z_l},t) = \int_{\Omega \theta } {{p_{{Z_l}\theta }}} ({z_l},\theta ,t)d\theta {\rm{ (}}$
|
(31) |
显然,系统稳定概率为
|
$R = R(T) = \int_{ - \infty }^{ + \infty } {{p_{{Z_l}}}} ({z_l},T)d{z_l}{\rm{ (}})$
|
(32) |
失稳概率为
|
${p_{\text{f}}} = 1 - R$
|
(33) |
据此,可以定量分析结构随机动力稳定性。 具体数值解法如下:
(1) 在概率空间$\Omega \theta $选取代表点集${\theta}_q$
并确立相应的赋得概率${P_q}(q = 1,2,\cdots ,{n_{{\rm{pt}}}})$,$n_{\rm pt}$
为代表点集中的点数;
(2) 对于给定的$\theta = {\theta _q}$求解结构动力方程,获得
$\dot Z_l({ \theta}_q,t)$及动力稳定函数$S(t)$;
(3) 通过有限差分方法求解耗散系统密度演化方程(29)以获得${p_{{Z_l}\theta }}({z_l},{\theta _q},t)$,若$S(t)<0$,则 ${p_{{Z_l}\theta }}({z_l},{\theta _q},t) = 0$;
(4) 将上述${p_{{Z_l}\theta }}({z_l},{\theta _q},t) = 0(\$ q = 1,2,\cdots ,{n_{{\rm{pt}}}}$累计求和,可获得系统发生概率耗散后的剩余概率密度函数
$p_{Z_l}(z_l,t)$,对该概率密度函数进行积分(式(32)),即可获得系统稳定概率。
4 数值算例
本节选用两个经典的用于结构动力稳定分析的基准模型,验证上述理论的正确性与有效性.
4.1 参数激励系统
单自由度参数激励系统方程可表示为
|
$m\ddot x + c\dot x + k(1 + lv(t)x = 0$
|
(34) |
式中,$m,c$和$k$分别为无量纲正态分布随机变量,均值: $m_0=1$,$c_0=0.63$,$k_0=39.48$,变异系数:
$\delta_m=\delta_c=\delta_k=0.2$;初始条件为: $x_0=0.0$,$\dot x_0=0.1$. $v(t)$
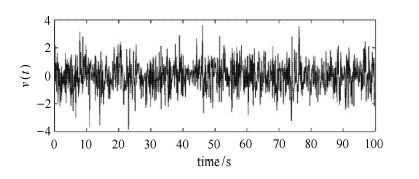
为宽带白噪声(均值为0,标准差为1),其典型样本过程如图2所示; $l=0.7$为加载系数。
实质上,式(34)可以描述诸如压杆失稳、梁弯扭失稳等诸多动力失稳现象,因此,具有一定的普遍性。
令${ Z}(t)=[x(t)]$,采用数论选点法[27, 28]在三维正态分布空间选取290个离散代表点进行随机动力分析。
首先,设置概率耗散的边界为$S(t)=\infty$ (即概率保守系统),利用广义概率密度演化方程可计算给出无概率耗散时的
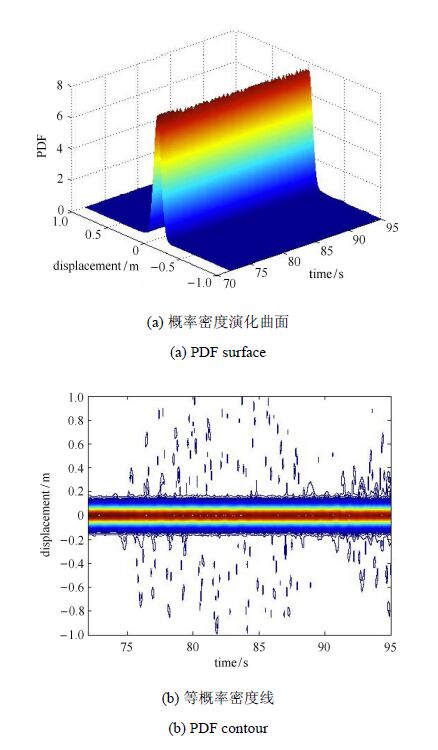
$x(t)$概率密度演化过程,如图3所示;然后,将概率耗散的边界设为$S(t)=0$,即结构 动力失稳将触发概率耗散,可利用上节建议方法得到考虑概率耗散的$x(t)$ 概率密度演化过程(图4)。对比图3与图4可见:概率耗散对结构位移响应概率密度的演化过程有显著的影响。
表1给出了针对不同控制参数$l$该系统的稳定概率。 同时,采用蒙特卡洛模拟(简记为MCS)来验证本文建议方法的正确性。在模拟中,系统动力稳定概率可由下式计算
|
${R_{\rm{S}}} = 1 - {{n(min(S(t)) < 0} \over N}$
|
(35) |
式中,$N$为总的蒙特卡洛模拟次数(本文取10万次),$n$ 为发生动力失稳样本的个数。可见本文建议算法结果与蒙特卡洛模拟的计算结果十分接近,由此验证了基于耗散系统广义概率密度演化方程计算结构动力稳定概率的正确性与有效性。 显然,本文建议方法的计算效率远优于蒙特卡洛模拟方法。
表1(Table 1)

表1 稳定概率的对比Table 1 Comparison of stable probabilities
| Loading factor l | Stable probability (proposed method) | Stable probability (MCS) |
| 0.50 | 0.999 97 | 0.999 93 |
| 0.53 | 0.998 96 | 0.998 84 |
| 0.56 | 0.998 64 | 0.998 52 |
| 0.59 | 0.997 65 | 0.997 81 |
| 0.62 | 0.994 56 | 0.994 47 |
| 0.65 | 0.984 02 | 0.984 29 |
| 0.66 | 0.982 27 | 0.982 31 |
| 0.67 | 0.978 03 | 0.977 96 |
| 0.68 | 0.977 53 | 0.977 54 |
| 0.69 | 0.951 16 | 0.951 28 |
| 0.70 | 0.940 67 | 0.940 91 |
|
表1 稳定概率的对比
Table 1 Comparison of stable probabilities |
4.2 非弹性两杆桁架
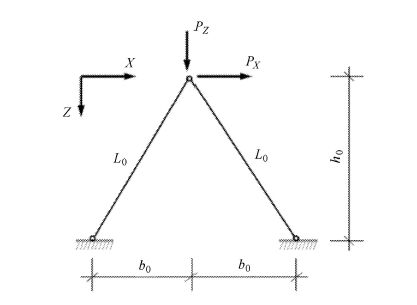
考虑一两杆桁架结构动力稳定问题。 桁架结构模型如图5所示。这一模型代表一类在稳定性分析中的典型结构系统(如框架结构,壳结构)的失稳特征以及与分叉失稳有关的物理现象,因而被广泛应用。
模型中的结构参数取值如下[29]: 弹性模量$E= 200$ kPa; 屈服应力$\sigma_{\rm y}=4.239\times 10^4$ Pa;
截面积$A= 0.1$ m$^{2}$; 半跨长$b_{0} = 5$ m; 高度$h_{0} =15$ m;阻尼比$\xi=0.03$;
质量密度$\rho=300$ kg/m$^3$。
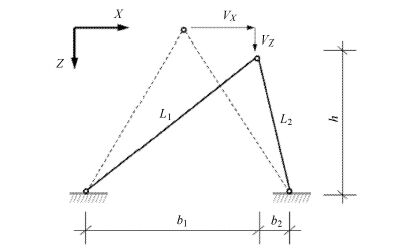
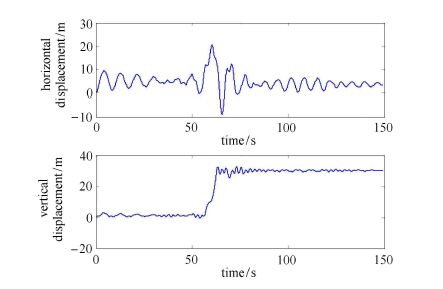
结构变形后的形态如图6所示,其中$V_x$
为水平位移,$V_Z$为竖向位移。 结构的运动方程可写为
|
$M\ddot V(t) + C\dot V(t) + G(V(t)) = P(t)$
|
(36) |
|
${K_e} = \frac{{EA}}{{{L_0}}}\left| \begin{gathered}
2{\left( {\frac{{{b_0}}}{{{L_0}}}} \right)^2}0 \hfill \\
0{\left( {\frac{{{h_0}}}{{{L_0}}}} \right)^2} \hfill \\
\end{gathered} \right|$
|
(37) |
式中,${ V}=[V_X,V_Z]^{\rm T}$表示位移向量,质量矩阵${ M}$
与初始刚度矩阵${ K}_{\rm e}$为动力分析中采用瑞利阻尼
|
$C = aM + b{K_{\text{e}}}$
|
(38) |
其中,$a=0.043 2$,$b=0.007 5$。
结构非线性内力可表示为[29]
|
$G(V) = \left[\matrix{
{G_X}({V_X},{V_Z}) \hfill \cr
{G_Z}({V_X},{V_Z}) \hfill \cr} \right] = EA\left[\matrix{
{{{b_1}} \over {{L_0}}} - {{{b_1}} \over {{L_1}}} - {{{b_2}} \over {{L_0}}} + {{{b_2}} \over {{L_2}}} \hfill \cr
{h \over {{L_1}}} + {h \over {{L_2}}} - {{2h} \over {{L_0}}} \hfill \cr} \right]$
|
(39) |
每根杆件的非弹性应力可表示为
|
${\sigma _i} = \left\{ \begin{gathered}
E \cdot ({l_i}/{L_0} - 1),{l_i}/{L_0} < {\varepsilon _{\text{y}}} \hfill \\
{\sigma _{\text{y}}},{l_i}/{L_0}{\varepsilon _{\text{y}}}i \hfill \\
\end{gathered} \right. = 1,2$
|
(40) |
式中,${\varepsilon _{\text{y}}} = {\sigma _{\text{y}}}/E$表示屈服应变。
结构外部激励为
|
$P(t) = \left| \matrix{
{P_X} \hfill \cr
{P_Z} \hfill \cr} \right| - M\left| \matrix{
{A_1}{{\ddot x}_g}(t) \hfill \cr
{A_2}{{\ddot x}_g}(t) \hfill \cr} \right|$
|
(41) |
式中,$P_X=1 000$ N和$P_Z=800 $N
为施加在结构上的静力载荷;$A_1$为水平地震动加速度峰值,取为正态分布随机变量(均值为3,变异系数为0.2),$A_2=\eta A_1$为竖向地震动加速度峰值,其中$\eta$ 为另一个正态分布随机变量(均值为0.35,变异系数为0.2);$\ddot
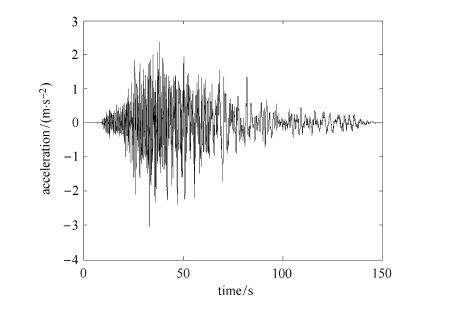
x_g(t)$ 取1999年集集(Chi-Chi) CHY017台站记录的地震动加速度过程,如图7所示。
在本例中,由于仅有两个随机变量,采用张量积方法[30]在二维正态分布空间中选取121个离散代表点。
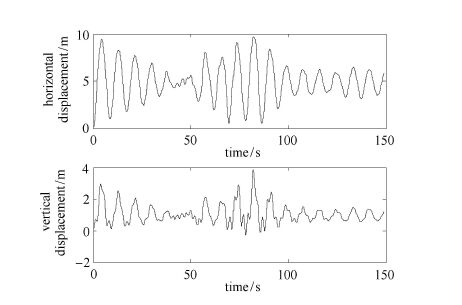
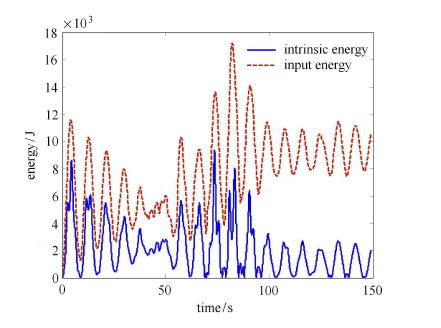
利用动力时程积分方法计算结构动力响应,典型样本过程如图8所示($A_1=-0.928 9$,$\eta=0$)。可以看到:此时结构位移响应并未发生很大的变化。若从经典静力稳定性或李雅普诺夫动力稳定性出发判定该结构动力稳定性,则一旦结构切线刚度的特征值出现负值,结构发生动力失稳。以每个时刻结构切线刚度特征值最小值作为特征过程,结果如图9所示。可见:切线刚度特征过程在零线附近不断地来回跳跃。若仅从结构自身特性(切线刚度)来判断,此时结构已经发生动力失稳,很显然,该判断是不正确的,因为结构事实上仍保持动力稳定状态。 而按照本文式(11)准则判断,结构系统特征能量与输入到该系统中总能量的关系将如图10所示。由图可见:此时结构的特征能量很小、在整个过程中均未超过输入到系统中的总能量,结构处于动力稳定状态。 该结论与结构的位移响应信息(图8)是一致的。
若进一步考察动力失稳典型样本响应($A_1=3.936 2$,$\eta=-5.188 0$),如图11所示。 动力稳定函数中能量响应见图12。可见:按照本文中的动力稳定判别准则,能够准确地判别结构何时进入动力失稳状态,且这种判断为图11所验证。
进一步采用本文建议方法分析该系统动力稳定概率。 首先不考虑概率耗散,采用式(15)分析结构顶点竖向位移$V_Z(t)$的概率密度演化过程;其次,考察因动力失稳引发的概率耗散,由式(29)分析$V_Z(t)$概率密度演化过程。
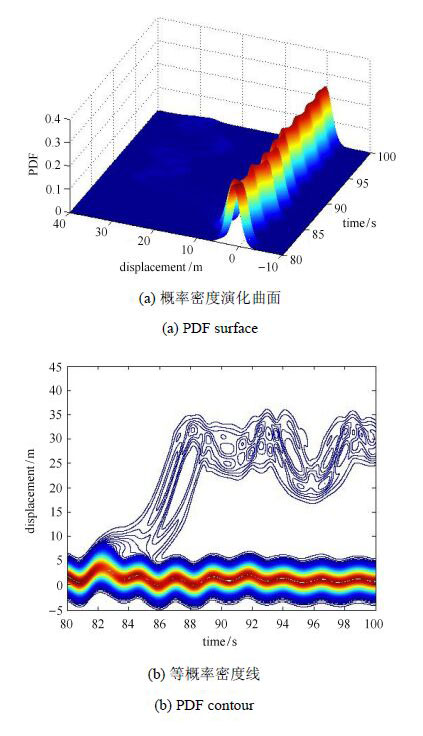
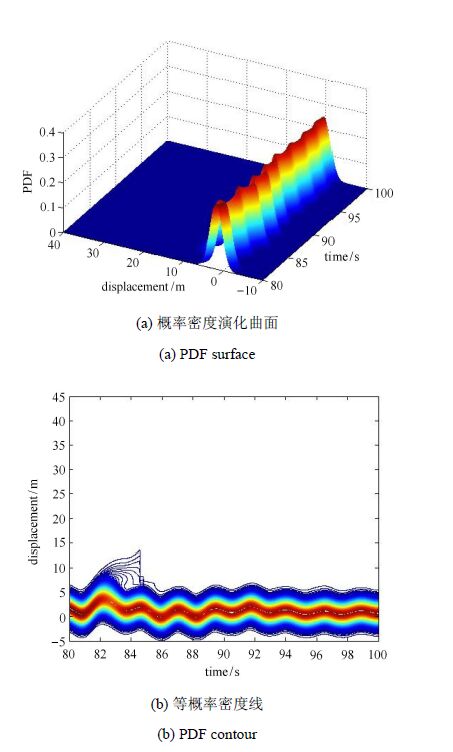
图13所示为不考虑概率耗散时结构竖向位移$V_Z(t)$在[80, 100]s内概率密度演化过程,可以清楚地看到结构响应概率密度演化过程出现了随机分叉现象,即$V_Z(t)$
的概率密度演化过程中分为两个分支:稳定响应与跳跃失稳响应。
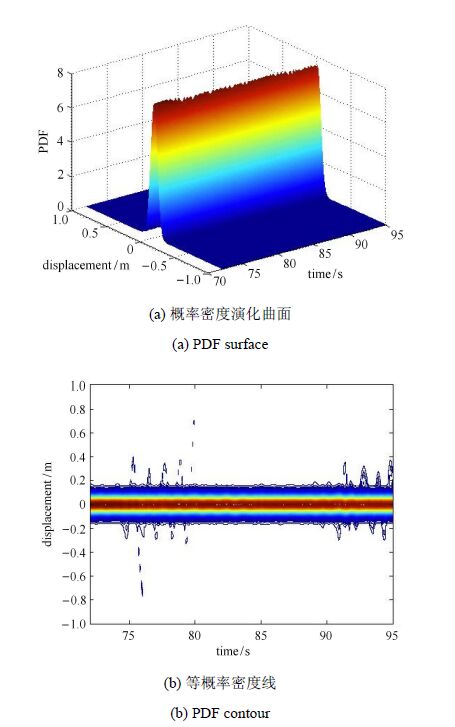
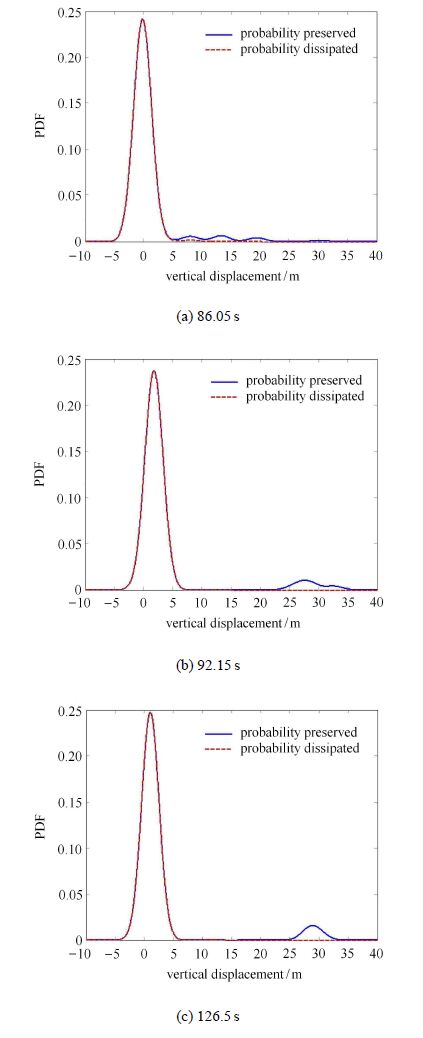
考虑结构动力失稳引起的概率耗散,结构系统响应$V_Z(t)$ 的概率密度演化过程将如图14所示。显然,由于流向跳跃失稳位置的概率信息(不稳定随机动力响应)被耗散,剩余的概率信息仅为稳定随机动力响应。 图15所示为有、无概率耗散时$V_Z(t)$在典型时刻的概率密度函数对比。由此可见:概率耗散过程对概率密度演化过程会产生明显的影响。
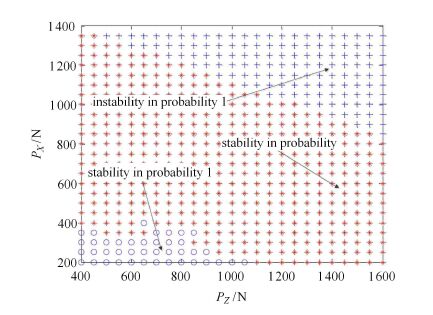
将$P_Z$-$P_X$在参数空间[400,1 600]N×[200,1 400]N 划分为25×25 网格点。在每个网格点上,可利用本文建议方法计算给出该网格点所代表的静力载荷作用下的结构动力稳定概率。若考虑依概率为1的结构随机动力稳定性,可将稳定概率为1的点标记为"o"。据此,可获得在依概率为1的结构随机动力稳定性意义上的稳定边界,如图16所示。这意味着:若$P_Z$与$P_X$在此区域内取值,结构可以始终"百分之百"地保持动力稳定性。 在图16中将失稳概率为1的点标记为"+",则给出稳定边界与失稳边界,而界于稳定边界与失稳边界之间的部分代表着结构在概率意义上保持动力稳定,图中以"*"所标示,在这一区间,结构具体的失稳概率可由本文建议方法逐步求出。
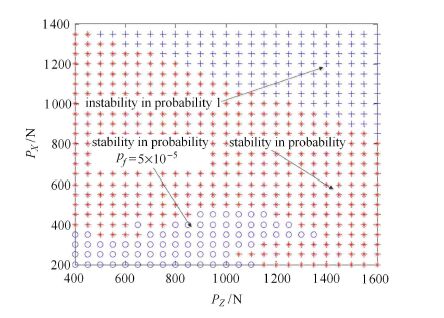
不难推断,当在定量概率意义上评价结构的动力失稳概率时,结构失稳边界将发生变化,图17与图
18给出了两个典型结果,其中图13对应的失稳界限概率$p_{\rm f}$ 为十万分之五,而图14则为万分之一。可以清晰地看到:失稳边界随着不同水平下的失稳概率而发生变化。 这是非常有趣而富有现实工程价值的。
在表2和表3中,分别给出了按本文建议方法计算的若干工况的结构稳定概率和按蒙特卡洛模拟(3万次)的计算结果。 可见:
在不同静力载荷作用下,本文建议方法均具有很好的精度。 事实上,稳定概率的计算精度也进一步验证了图11 $\sim $图13所示的概率意义上稳定边界的正确性。 而在经典研究中,获得这样的结果几乎是不可能的。
表2(Table 2)

表2 稳定概率(本文建议方法)Table 2 Probability of stability by the proposed approach
| PX | PZ |
| 800N | 900N | 1 000N | 1 100N | 1 200N |
| 600N | 0.999 8 | 0.993 1 | 0.993 1 | 0.993 1 | 0.993 0 |
| 650N | 0.999 8 | 0.998 8 | 0.996 0 | 0.993 1 | 0.992 6 |
| 700N | 0.999 8 | 0.994 8 | 0.993 1 | 0.992 6 | 0.967 4 |
| 750N | 0.998 8 | 0.994 7 | 0.992 6 | 0.967 4 | 0.925 2 |
| 800N | 0.993 5 | 0.992 6 | 0.942 9 | 0.944 0 | 0.848 9 |
|
表2 稳定概率(本文建议方法)
Table 2 Probability of stability by the proposed approach |
表3(Table 3)

表3 稳定概率(蒙特卡洛模拟)Table 3 Probability of stability by MCS
| PX | PZ | |
| 800N | 900N | 1 000N | 1 100N | 1 200N | |
| 600N | 0.999 8 | 0.993 3 | 0.993 2 | 0.993 1 | 0.993 0 |
| 650N | 0.999 8 | 0.998 5 | 0.996 0 | 0.993 3 | 0.992 8 |
| 700N | 0.999 8 | 0.994 9 | 0.992 9 | 0.992 8 | 0.967 4 |
| 750N | 0.998 6 | 0.994 7 | 0.992 7 | 0.967 1 | 0.925 5 |
| 800N | 0.993 7 | 0.992 3 | 0.943 0 | 0.944 1 | 0.848 9 |
|
表3 稳定概率(蒙特卡洛模拟)
Table 3 Probability of stability by MCS |
5 结语
本文提出了结构随机动力稳定性的定量分析方法. 研究表明:
(1) 结构的动力稳定性能不仅与结构自身性质有关,而且与结构的外部作用密切相关。 据此,引入了一类新的结构动力稳定性判别准则;
(2) 结构动力稳定概率可以利用概率密度演化理论加以分析。 在本文中,依据概率守恒原理推导了概率耗散系统的广义概率密度演化方程,给出了数值求解途径,据此,可以定量地计算结构的动力稳定概率。
(3) 对典型动力稳定系统的分析表明:本文方法可以定量地给出实际工程系统发生动力失稳的概率、动力稳定边界与依给定概率意义上的动力失稳边界。
参考文献
| [1] |
Bažant ZP, Cedolin L. Stability of Structures: Elastic, Inelastic, Fracture and Damage Theories. Singapore: World Scientific Publishing Company Incorporated, 2010 |
| [2] |
周绪红. 结构稳定理论. 北京:高等教育出版社, 2010 (Zhou Xuhong. Theory of Structural Stability. Beijing: Higher Education Press, 2010 (in Chinese)) |
| [3] |
Simitses GJ, Hutchinson J. An introduction to the elastic stability of Structures. Journal of Applied Mechanics, 1976, 43(2): 383 |
| [4] |
Lasallae J, Lefschetz S. Stability by Lyapunov's Direct Method with Applications. New York: Academic Press, 1960 |
| [5] |
秦元勋, 王慕秋, 王联. 运动稳定性理论与应用. 北京:科学出版社, 1981 (Qin Yuanxun, Wang Muqiu, Wang Lian. Motion Stability Theory and Application. Beijing: Science Press, 1981 (in Chinese)) |
| [6] |
Ariaratnam S, Tam D. Moment stability of coupled linear systems under combined harmonic and stochastic excitation. In: Proc. of Stochastic Problems in Dynamics, Pitman, London, 1977 |
| [7] |
Potapov V, Marasanov A. The investigation of the stability of elastic and viscoelastic rods under a stochastic excitation. International Journal of Solids and Structures, 1997, 34(11): 1367-1377 |
| [8] |
Ariaratnam S, Ly B. Almost-sure stability of some linear stochastic Systems. Journal of Applied Mechanics, 1989, 56(1): 175-178 |
| [9] |
Lin Y, Ariaratnam S. Stability of bridge motion in turbulent winds. Journal of Structural Mechanics, 1980, 8(1): 1-15 |
| [10] |
Bucher CG, Lin YK. Stochastic stability of bridges considering coupled Modes. Journal of Engineering Mechanics, 1988, 114(12):2055-2071 |
| [11] |
Xie WC. Dynamic stability of structures. New York: Cambridge University Press, 2006 |
| [12] |
Williamson EB, Rungamornrat J. Numerical analysis of dynamic stability under random excitation. Engineering Structures, 2002,24(4): 479-490 |
| [13] |
Arnold L. A formula connecting sample and moment stability of linear stochastic systems. SIAM Journal on Applied Mathematics,1984, 44(4): 793-802 |
| [14] |
Kozin F. On almost sure stability of linear systems with random coe fficients. Journal of Mathematics and Physics, 1963, 42: 59-67 |
| [15] |
Ariaratnam S, Tam D. Moment stability of coupled linear systems under combined harmonic and stochastic excitation. In: Proc. of Stochastic Problems in Dynamics, Pitman, London, 1977: 90-103 |
| [16] |
Ma F, Caughey T. Moment stability of linear stochastic difference Systems. Mechanics Research Communications, 1981, 8(3): 143-151 |
| [17] |
Kozin F. A survey of stability of stochastic systems. Automatica,1969, 5(1): 95-112 |
| [18] |
Kushner HJ. Stochastic Stability. Germany: Springer, 1972 |
| [19] |
朱位秋. 随机振动. 北京: 科学出版社, 1992 (ZhuWeiqiu. Random Vibration. Beijing: Science Press, 1992 (in Chinese)) |
| [20] |
Lin YK, Li QC. Stochastic stability of wind excited structures. Journal of Wind Engineering and Industrial Aerodynamics, 1995, 54:75-82 |
| [21] |
Lin YK. Stochastic stability of wind-excited long-span bridges. Probabilistic Engineering Mechanics, 1996, 11(4): 257-261 |
| [22] |
Xu J, Li J. An energetic criterion for dynamic instability of structures under arbitrary excitations. International Journal of Structural Stability and Dynamics, 2015. 15(2): 1-32 |
| [23] |
李杰, 徐军. 结构动力稳定性判定新准则. 同济大学学报:自然科学版, 2015, 43(7): 965-971 (Li Jie, Xu Jun. Novel criterion for identification of dynamic stability of structures. Journal of Tongji University (Natural Science Edition), 2015, 43 (7): 965-971 (in Chinese)) |
| [24] |
Li J, Chen JB. The probability density evolution method for dynamic response analysis of nonlinear stochastic structures. International Journal for Numerical Methods in Engineering, 2006, 65(6): 882-903 |
| [25] |
Li J, Chen JB. Stochastic Dynamics of Structures. Singapore: John Wiley & Sons, 2009 |
| [26] |
Li J, Chen JB. The principle of preservation of probability and the generalized density evolution equation. Structural Safety, 2008,30(1): 65-77 |
| [27] |
Li J, Chen JB. The number theoretical method in response analysis of nonlinear stochastic structures. Computational Mechanics, 2006,39(6): 693-708 |
| [28] |
Hua LK, Wang Y. Applications of Number Theory to Numerical Analysis. Germany: Springer Science & Business Media, 2012 |
| [29] |
Nawrotzki P, Eller C. Numerical stability analysis in structural dynamics. Computer Methods in Applied Mechanics and Engineering,2000, 189(3): 915-929 |
| [30] |
Xu J, Chen JB, Li J. Probability density evolution analysis of engineering structures via cubature points. Computational Mechanics,2012, 50(1): 135-156 |
A QUANTITATIVE APPROACH TO STOCHASTIC DYNAMIC STABILITY OF STRUCTURES
Li Jie, Xu Jun
1. School of Civil Engineering, Tongji University, Shanghai 200092, China;
2. State Key Laboratory of Disaster Reduction in Civil Engineering, Shanghai 200092, China
Abstract: A quantitative approach is proposed for stochastic dynamic stability analysis of structures. The classical concept of stochastic dynamic stability is firstly revisited. It is pointed that the dynamic stability of structures not only depends on structural parameters, but also relates to the applied external excitations. A new criterion for identifying dynamic stability of structures is introduced and the definition of stochastic dynamic stability of structures is therefore formulated based on the criterion. According to the principle of preservation of probability, the generalized density evolution equation for probability-preserved system is introduced firstly and then the equation for probability-dissipated system is derived. On the basis, the probability of stability/instability can be obtained via solving the equation for probability-dissipated system by introducing the physical mechanism of dynamic instability of structures as the triggering force of probability dissipation. Numerical algorithms for solving the generalized density evolution equation for probability-dissipated system are provided. According to the obtained probability, it is readily applicable to quantitatively evaluate stochastic dynamic stability of structures in the sense of stability in probability 1 or a given probability. Stochastic dynamic stability analyses of typical structural dynamic systems are carried out by the proposed approach, where the results by Monte Carlo simulations are employed for comparisons. The numerical results verify the e ectiveness of the proposed approach.
Key words:
stochastic dynamic stability quantitative approach probability-dissipated system probability density evolution equation

 2016, Vol. 48
2016, Vol. 48