引言
黏弹性材料作为一种耗能减振材料受到广大学者的关注,采用黏弹性材料制作而成的黏弹性阻尼器已广泛应用于航空航天、机械工程、土木工程等领域的振动控制[1, 2, 3, 4, 5].近年来,对黏弹性材料的研究主要集中在高性能黏弹性材料研制、力学模型研究、减震应用等[6, 7, 8, 9].目前绝大多数关于黏弹性材料的研究和应用是针对地震、风振等毫米级以上的普通振动控制.然而关于黏弹性材料和阻尼器用于微振动(微米级振动)控制研究较少.微振动是一类主要由环境变化、机械运转等所产生的微幅机械振动,对精密设备工作精度、精密制造加工精度等有较大影响[10, 11, 12, 13],因此采用黏弹性减振技术对微振动进行抑制是一个非常有意义的课题.
黏弹性材料力学模型是黏弹性材料应用的理论基础.对于黏弹性材料在普通振动幅值下的力学模型,主要包括Maxwell模型、Kelvin模型以及线性固体模型等,上述模型只能描述黏弹性材料的力学性能与频率的关系,有较大局限性.徐赵东等[14, 15]提出了一种可以考虑温度影响的等效标准固体力学模型和分数等效Kelvin模型.Lewandowski等[16]提出了分数Kelvin模型和分数Maxwell模型.周云等[17]采用五单元模型描述黏弹性阻尼器的力学性能.郭亚娟等[18]研究了黏弹性材料的ADF模型,提出一种新的参数识别方法.张针粒等[19]提出了黏弹性阻尼材料温度谱模型来描述温度对黏弹性阻尼材料的影响.高庆等[20]基于ZN17黏弹性材料的蠕变试验,提出一种新的蠕变型本构方程描述黏弹性材料的非线性蠕变特性.康永刚等[21]基于可变粘性元件构造出非定常黏弹性本构模型.石银明等[22]提出黏弹性材料的微振子模型及参数确定方法.上述所提到的多种力学模型都是唯象模型,即是基于黏弹性材料宏观试验现象提出的力学模型,该类模型不能反映黏弹性材料的微观结构与其力学性能的关系和微观结构对黏弹性材料力学性能的影响.
黏弹性材料是一类高分子基复合材料,材料的微观结构较复杂且对材料宏观力学性能有较大影响[23, 24]. 近些年来,一些学者利用多尺度研究方法,研究了材料微观结构同宏观性能的联系[25, 26],提出了一些相应的链网络模型,这类模型从微观分子链层面解释了橡胶类材料的超弹性[27].然而针对此类材料的耗能和黏弹性性能,从材料微观结构方面研究取得成果较少.
本文分析了微观分子链结构对黏弹性材料在微振动条件下动态力学性能的影响.结合温频等效原理,提出一种微振激励下黏弹性阻尼器微观链结构力学模型.该模型能够反映黏弹性材料微观结构中两种主要分子链结构对黏弹性阻尼器在微振激励下动态力学性能的影响,同时该模型宏观上反映了温度和频率对黏弹性阻尼器在微振激励下的力学性能影响.模型参数物理意义明确,可以为黏弹性材料的研制和分析提供理论依据.对黏弹性阻尼器在不同温度、频率和幅值下进行动态力学性能试验,分析黏弹性阻尼器的耗能能力和动态力学性能,并利用试验结果对该模型的有效性进行了验证分析.
1 黏弹性材料的微观链结构
由于交联作用,在黏弹性减振材料中主要是硫化作用,基体高聚物的分子链之间发生复杂的变化,一部分通过交联作用形成相应的交联网络,另一部分以自由链形式存在.这两种形式的分子链,力学性能有较大不同,分别在不同方面影响着黏弹性材料的宏观力学性能.本文将从黏弹性材料两种微观链结构出发,研究黏弹性材料的耗能和动态力学性能.
黏弹性材料的微观结构可以抽象为图1所示的链结构,其主要是网络链和自由链两类分子链结构,将材料中未参与交联作用的分子链以及主链支链等都假定为自由链. 这两类分子链的性能决定着黏弹性材料的宏观力学性能,分别对其弹性和黏性起着不同作用[25].目前,从微观分子链结构研究高分子材料的超弹性有着较多研究,并且提出了多种描述材料超弹性的力学模型.其中主要是依据分子链的统计特性而提出的高斯链网络模型和非高斯链网络模型[27].类比于橡胶材料超弹性模型研究方法,分别研究两类分子链结构的力学性能.
1.1 黏弹性材料网络链结构
如上所述,黏弹性材料的微观分子链结构中,一部分的分子链由交联或是缠结作用,相互一起形成网状结构[28].在黏弹性材料发生变形过程中,此部分的分子链拉伸并起到传递应力作用,在外界作用撤消后,由于分子热运动作用,此部分的分子链恢复原状,表现出相应的弹性特性;同时在变形过程中,分子链不可避免的受到相邻分子链及分子链段间的作用,即分子链在变形恢复过程中受到阻力作用,分子链运动表现出滞后特性.因此,黏弹性材料对应的分子链在变形过程中表现出相应的弹性能,并且能够耗散一部分运动能量.
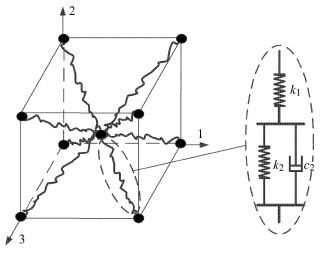
在超弹性研究中,八链模型能够较好地描述黏弹性材料在几种变形模式下的超弹性性能.如图2所示,八链网络模型的8条分子链一端在立方体中心交联,另一端位于立方体的8个顶点,该结构具有较强对称性.因此,在变形过程中交联点始终处于中心位置,并且各条分子链具有相同的伸长比.
网络链中单个高分子链在宏观上表现为黏弹性特性.目前,描述黏弹性性能的力学模型主要有Maxwell模型、Kelvin模型、标准线性固体模型等.为了表示网络链中单条分子链的黏弹性,采用标准线性固体模型表示单个链的黏弹性,如图2所示.该模型能够描述材料的瞬态弹性响应和渐近弹性性质,同所研究的分子链表现的特性一致.
由图2所示的标准线性固体模型,可以直接写
|
\[{{F}_{\text{s1}}}=\frac{{{k}_{1}}\left( {{k}_{2}}+\text{j}\omega {{c}_{2}} \right)}{\left( {{k}_{1}}+{{k}_{2}} \right)+\text{j}\omega {{c}_{2}}}\Delta x={{E}_{\text{s1}}}\Delta x\]
|
(1) |
式中,$k_1 $,$k_2 $,$c_2 $均为模型参数,表示分子链的弹性和黏性;$\Delta x$为分子链两端变形,$F_{\rm s1}$为相应变形下分子链端作用力,$\omega $为作用在分子链端交变应变或应力的圆频率.
高分子热力学理论可知,由于分子链发生热运动,高分子链的长度及末端距在空间上随机分布.因此,需要对分子链的统计特性进行研究.在橡胶材料超弹性研究中,分别采用高斯函数和非高斯函数来描述分子链的统计特性.为了方便应用,此处分子链末端距作为一个待拟合的参数出现.
引入分子链末端距概念,单个分子链在变形过程中的作用力由式(1)可改写为下式
|
\[{{F}_{\text{s1}}}=\frac{{{k}_{1}}\left( {{k}_{2}}+\text{j}\omega {{c}_{2}} \right)}{\left( {{k}_{1}}+{{k}_{2}} \right)+\text{j}\omega {{c}_{2}}}(r-{{r}_{\text{0s}}})={{E}_{\text{s1}}}\left( r-{{r}_{\text{0s}}} \right)\]
|
(2) |
式中,$r$,$r_{\rm 0s} $分别为变形后和变形前分子链末端距. 同理,单个分子链在变形后的应变能可以定义为
|
\[{{\varphi }_{\text{s1}}}={{F}_{\text{s1}}}\left( r-{{r}_{\text{0s}}} \right)\]
|
(3) |
对此模型来说,可以得到单位体积中单个分子链的总能量,即
|
\[{{\phi }_{\text{s1}}}=\frac{3\sqrt{3}}{2r_{\text{0s}}^{3}}\cdot \frac{1}{8}{{E}_{\text{s1}}}\cdot {{\left( r-{{r}_{\text{0s}}} \right)}^{2}}\]
|
(4) |
1.2 黏弹性材料自由链结构
黏弹性材料微观分子链结构中,一部分并没有参与构成网络结构的自由链,由叠加自由链和相应分子链的侧链等组成.该部分分子链在运动过程中主要受到周围其他分子链的阻碍,在宏观上主要表现为材料的黏性性能;由于自由分子链相对于形成网络链的分子链,柔性较大,弹性效应较弱.
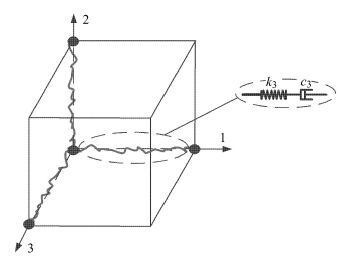
为了描述该部分分子链的力学性能,本文以三链网络模型为基础,其3条链分布在立方体相互正交的3条边上,在变形过程中,3条链发生仿射形变. 此处采用三链网络模型同样是为了便于同上面八链网络模型结合,最终提出本文的力学模型.
对模型中的每个分子链采用Maxwell模型来描述其在变形过程中的力学性能.Maxwell模型能够较好地反应材料的流变性质,与所研究的自由分子链性能相符合,如图3.由图3所示Maxwell模型可以直接得到单个分子链的力和位移关系,即
|
\[{{F}_{\text{c1}}}=\frac{{{k}_{3}}\cdot \text{j}\omega {{c}_{3}}}{{{k}_{3}}+\text{j}\omega {{c}_{3}}}\left( r-{{r}_{\text{0c}}} \right)={{E}_{\text{c1}}}\left( r-{{r}_{\text{0c}}} \right)\]
|
(5) |
式中,$k_3 $和 $c_3 $均为模型参数,同分子链的弹性和黏性相关;$\omega $为相应交变应变或应力的圆频率,$r$和$r_{\rm 0c} $ 分别为变形后和变形前分子链末端距. 同理,单个分子链在变形后的应变能可以定义为
|
\[{{\varphi }_{\text{c1}}}={{F}_{\text{c1}}}\left( r-{{r}_{\text{0c}}} \right)\]
|
(6) |
故可得到单位体积中单个分子链的总能量
|
\[{{\phi }_{\text{c1}}}=\frac{1}{2r_{\text{0c}}^{3}}\cdot \frac{1}{3}\sum\limits_{i=1}^{3}{{{E}_{\text{c1}}}}\cdot {{({{r}_{i}}-{{r}_{\text{0c}}})}^{2}}\]
|
(7) |
2 微振激励下黏弹性阻尼器力学模型
2.1 微观链结构模型
以上述分析为基础,综合考虑两种微观链结构对黏弹性材料力学性能的影响,提出微观链结构模型. 变形过程中黏弹性材料单位体积所具有的总能量为两类分子链能量之和
|
\[\phi ={{n}_{\text{s1}}}{{\phi }_{\text{s1}}}+{{n}_{\text{c1}}}{{\phi }_{\text{c1}}}\]
|
(8) |
式中$n_{\rm s1} $和$n_{\rm c1} $分别为单位体积中网络链和自由链的分子链个数. 材料的应力和应变关系可以表示为
|
\[{{\sigma }_{i}}={{\lambda }_{i}}\frac{\partial \varphi }{\partial {{\lambda }_{i}}}\left( i=1,2,3 \right)\]
|
(9) |
式中$\lambda _i $为$i$方向的伸长率.
黏弹性阻尼器在工作过程中,黏弹性材料一般处于是剪切变形状态,因此本文只研究剪切模式这一种情况. 此时,材料的剪切应力应变关系也可以写为如下形式
|
\[{{\sigma }_{i}}=G{{\varepsilon }_{i}}\left( i=1,2,3 \right)\]
|
(10) |
式中$\varepsilon _i = \lambda _i-1$为$i$方向的剪切主应变;$G$为相应的复模量,实部为黏弹性材料的储能模量,虚部为黏弹性材料的损耗模量,虚部同实部的比值为损耗因子
|
\[\eta =\frac{\text{Im}(G)}{\text{Re}(G)}\]
|
(11) |
材料的分子链变形假定符合仿射变形,因此分子链的构象变形与材料的宏观变形关系为
|
\[r=F\cdot {{r}_{0}}\]
|
(12) |
式中$F$为材料相应变形模式下的形变梯度. 对于剪切模式(假定轴1-2平面内),$\lambda_1 = \lambda $,$\lambda _2 = \lambda ^{-1}$,$\lambda _3 =1$,即形变梯度为
|
\[{{F}_{\text{sh}}}={{\lambda }_{1}}{{\mathbf{e}}_{1}}\otimes {{\mathbf{e}}_{1}}+\lambda _{1}^{-1}{{\mathbf{e}}_{2}}\otimes {{\mathbf{e}}_{2}}+{{\mathbf{e}}_{3}}\otimes {{\mathbf{e}}_{3}}\]
|
(13) |
其中,$\det F_{\rm sh} = \lambda _1 \lambda _2 \lambda _3 = 1$,满足不可压缩条件.
由此,可由式(9)得到应力和应变表达式为
|
\[{{\sigma }_{i}}={{\lambda }_{i}}\frac{{{n}_{\text{s1}}}3\sqrt{3}}{8{{r}_{\text{0s}}}}{{E}_{\text{s1}}}\left( {{\lambda }_{i}}-1 \right)+{{\lambda }_{i}}\frac{{{n}_{\text{c1}}}}{3{{r}_{\text{0c}}}}{{E}_{\text{c1}}}\left( {{\lambda }_{i}}-1 \right)\]
|
(14) |
假定在1轴上施加相应的循环应变荷载$\varepsilon _1 = \varepsilon _0 \sin\left( {\omega t} \right)$,式(14)可以写为
|
\[\begin{align}
& {{\sigma }_{1}}={{\lambda }_{1}}\frac{{{n}_{\text{s1}}}3\sqrt{3}}{8{{r}_{\text{0s}}}}{{E}_{s1}}\left( {{\lambda }_{1}}-1 \right)+{{\lambda }_{1}}\frac{{{n}_{\text{c1}}}}{3{{r}_{\text{0c}}}}{{E}_{c1}}\left( {{\lambda }_{1}}-1 \right)= \\
& \varepsilon _{1}^{2}\left( \frac{{{n}_{\text{s1}}}3\sqrt{3}}{8{{r}_{\text{0s}}}}{{E}_{\text{s1}}}+\frac{{{n}_{\text{c1}}}}{3{{r}_{\text{0c}}}}{{E}_{\text{c1}}} \right)+ \\
& {{\varepsilon }_{1}}\left( \frac{{{n}_{\text{s1}}}3\sqrt{3}}{8{{r}_{\text{0s}}}}{{E}_{\text{s1}}}+\frac{{{n}_{c1}}}{3{{r}_{\text{0c}}}}{{E}_{\text{c1}}} \right) \\
\end{align}\]
|
(15) |
由于本文考虑的是微振动条件,振动过程中的应变幅值较小,因此应变项的二次方项$\varepsilon _1^2 $可以忽略.
上式可以简化为
|
\[{{\sigma }_{1}}={{\varepsilon }_{1}}\left( \frac{{{n}_{\text{s1}}}3\sqrt{3}}{8{{r}_{\text{0s}}}}{{E}_{\text{s1}}}+\frac{{{n}_{\text{c1}}}}{3{{r}_{\text{0c}}}}{{E}_{\text{c1}}} \right)\]
|
(16) |
因此,由式(10)和式(16)得到材料的复模量如下
|
\[\begin{align}
& G=\frac{{{n}_{\text{s1}}}3\sqrt{3}}{8{{r}_{\text{0s}}}}{{E}_{\text{s1}}}+\frac{{{n}_{\text{c1}}}}{3{{r}_{\text{0c}}}}{{E}_{\text{c1}}}= \\
& \frac{{{n}_{\text{s1}}}3\sqrt{3}}{8{{r}_{\text{0s}}}}\left( \frac{k_{1}^{2}{{k}_{2}}+{{k}_{1}}k_{2}^{2}+{{k}_{1}}{{\omega }^{2}}c_{2}^{2}}{{{\left( {{k}_{1}}+{{k}_{2}} \right)}^{2}}+{{\omega }^{2}}c_{2}^{2}}+ \right. \\
& \left. \text{j}\frac{k_{1}^{2}\omega {{c}_{2}}}{{{\left( {{k}_{1}}+{{k}_{2}} \right)}^{2}}+{{\omega }^{2}}c_{2}^{2}} \right)+ \\
& \frac{{{n}_{\text{c1}}}}{3{{r}_{\text{0c}}}}\left( \frac{{{k}_{3}}{{\omega }^{2}}c_{3}^{2}}{k_{3}^{2}+\omega _{3}^{2}c_{3}^{2}}+\text{j}\frac{k_{3}^{2}\omega {{c}_{3}}}{k_{3}^{2}+{{\omega }^{2}}c_{3}^{2}} \right) \\
\end{align}\]
|
(17) |
由上述分析可得到,黏弹性材料的储能模量、损耗模量和损耗因子分别为
|
\[\begin{align}
& {{G}_{1}}=\text{Re}\left( G \right)=\frac{{{n}_{\text{s1}}}3\sqrt{3}}{8{{r}_{\text{0s}}}}\frac{k_{1}^{2}{{k}_{2}}+{{k}_{1}}k_{2}^{2}+{{k}_{1}}{{\omega }^{2}}c_{2}^{2}}{{{\left( {{k}_{1}}+{{k}_{2}} \right)}^{2}}+{{\omega }^{2}}c_{2}^{2}}+ \\
& \frac{{{n}_{\text{c1}}}}{3{{r}_{\text{0c}}}}\frac{{{k}_{3}}{{\omega }^{2}}c_{3}^{2}}{k_{3}^{2}+{{\omega }^{2}}c_{3}^{2}}(18\text{a}) \\
\end{align}\]
|
(18a) |
|
\[\begin{align}
& {{G}_{2}}=\text{Im}\left( G \right)=\frac{{{n}_{\text{s1}}}3\sqrt{3}}{8{{r}_{\text{0s}}}}\frac{k_{1}^{2}\omega {{c}_{2}}}{{{\left( {{k}_{1}}+{{k}_{2}} \right)}^{2}}+{{\omega }^{2}}c_{2}^{2}}+ \\
& \frac{{{n}_{c1}}}{3{{r}_{\text{0c}}}}\frac{k_{3}^{2}\omega {{c}_{3}}}{k_{3}^{2}+{{\omega }^{2}}c_{3}^{2}} \\
\end{align}\]
|
(18b) |
|
\[\eta =\frac{{{G}_{2}}}{{{G}_{1}}}\]
|
(18c) |
上述模型(18)从微观链结构给出了黏弹性阻尼器在微振动环境下的动态力学性能指标,式中各参数均有明确物理意义,可以从微观层面解释黏弹性材料的耗能规律.
2.2 黏弹性阻尼器力学模型
模型(18)只能考虑频率对黏弹性材料力学性能的影响. 试验和研究结果表明[29, 30],温度对黏弹性材料的力学性能有较大影响. 下文将结合模型(18),引入温频等效原理,提出微振激励下黏弹性阻尼器力学模型.
黏弹性材料的储能剪切模量和损耗因子随温度和频率的变化关系是不完全相同的,当温度处在玻璃态转变温度$T_{\rm g}$至$T_{\rm g} + 100^ \circ$C范围内时,多数黏弹性材料的温度和频率之间存在等效关系,即温频等效原理[31]. 如果将温度和频率对黏弹性材料性能的影响进行综合考虑,那么将有
|
\[\left. \begin{matrix}
{{G}_{1}}(\omega ,T)={{G}_{1}}({{\alpha }_{T}}\omega ,{{T}_{0}}) \\
\eta (\omega ,T)=\eta ({{\alpha }_{T}}\omega ,{{T}_{0}}) \\
\end{matrix} \right\}\]
|
(19) |
式中,$T_0 $为参考温度,$\alpha _T $为温度的函数
|
\[{{\alpha }_{T}}={{10}^{-12(T-{{T}_{0}})/[525+(T-{{T}_{0}})]}}\]
|
(20) |
将式(19)和式(20)代入式(18)得到下式
|
\[\begin{align}
& {{G}_{1}}\left( \omega ,T \right)=\frac{{{n}_{\text{s1}}}3\sqrt{3}}{8{{r}_{\text{0s}}}}\frac{k_{1}^{2}{{k}_{2}}+{{k}_{1}}k_{2}^{2}+{{k}_{1}}\alpha _{T}^{2}{{\omega }^{2}}c_{2}^{2}}{{{\left( {{k}_{1}}+{{k}_{2}} \right)}^{2}}+\alpha _{T}^{2}{{\omega }^{2}}c_{2}^{2}}+ \\
& \frac{{{n}_{\text{c1}}}}{3{{r}_{\text{0c}}}}\frac{{{k}_{3}}\alpha _{T}^{2}{{\omega }^{2}}c_{3}^{2}}{k_{3}^{2}+\alpha _{T}^{2}{{\omega }^{2}}c_{3}^{2}} \\
\end{align}\]
|
(21a) |
|
\[\begin{align}
& {{G}_{2}}\left( \omega ,T \right)=\frac{{{n}_{\text{s1}}}3\sqrt{3}}{8{{r}_{\text{0s}}}}\frac{k_{1}^{2}\alpha _{T}^{\omega }{{c}_{2}}}{{{\left( {{k}_{1}}+{{k}_{2}} \right)}^{2}}+\alpha _{T}^{2}{{\omega }^{2}}c_{2}^{2}}+ \\
& \frac{{{n}_{\text{c1}}}}{3{{r}_{\text{0c}}}}\frac{k_{3}^{2}\alpha _{T}^{\omega }{{c}_{3}}}{k_{3}^{2}+\alpha _{T}^{2}{{\omega }^{2}}c_{3}^{2}} \\
\end{align}\]
|
(21b) |
|
\[\eta \left( \omega ,T \right)=\frac{{{G}_{2}}\left( \omega ,T \right)}{{{G}_{1}}\left( \omega ,T \right)}\]
|
(21c) |
所得式(21)即为微振激励下黏弹性阻尼器力学模型,该模型能够同时反映温度和频率对黏弹性微振阻尼器的力学性能的影响.
3 模型试验验证
3.1 试验概况
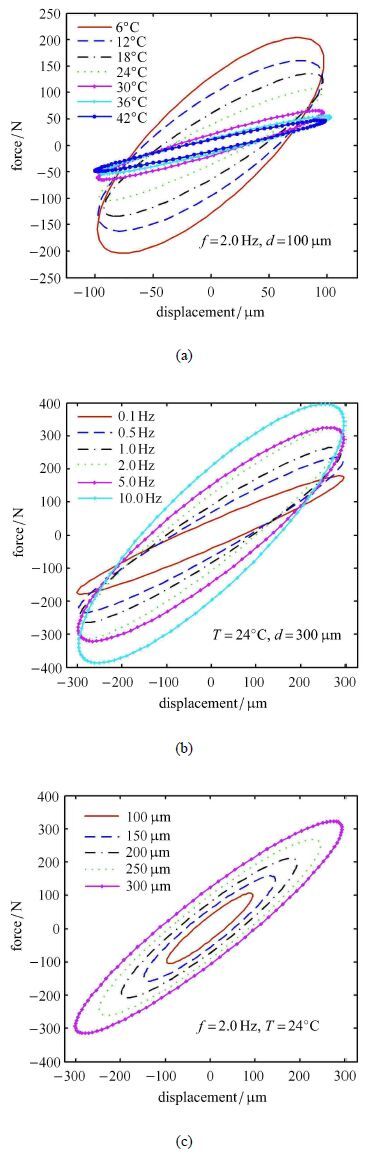
本次试验所采用的阻尼器为三块钢板间夹两层黏弹性层制作而成,其构造及尺寸如图4所示.动态力学性能试验在南京理工大学力学实验室进行,试验采用正弦位移加载控制,记录试验过程中阻尼器力位移曲线.本次试验主要测试黏弹性阻尼器在不同工作条件下的力学性能,即考察不同温度、频率和幅值对黏弹性阻尼器的力学性能的影响.
试验过程中采用的温度范围为黏弹性阻尼器的工作温度范围(6$℃$~$42$℃),温度的控制采用自主设计的小型温控箱,如图4所示. 具体试验工况见表1 所示.
表1(Table 1)

表1 试验工况Table 1 Loading condition of property tests
| Temperature ℃ | Frequency Hz | Displacement/$\mu $m | Cycle number |
| 6,12,18,24, 30,36,42 | 0.1,0.5,1.0,2.0,5.0,10.0 | 100,150,200,250,300 | 20 |
|
表1 试验工况
Table 1 Loading condition of property tests |
3.2 试验结果分析
试验滞回曲线如图5所示.从图中可以看出,在不同工况条件下,黏弹性阻尼器的滞回曲线为饱满的椭圆,表明黏弹性阻尼器具有较好的耗能能力.试验温度和加载频率对黏弹性阻尼器的滞回曲线的饱满程度和长轴斜率影响较明显,加载幅值的影响较小,即温度和频率对黏弹性阻尼器的刚度和耗能能力有较大影响.随着温度的增加,椭圆饱满程度和斜率均在下降,表明阻尼器的耗能能力和刚度随温度上升而下降.随着频率增加,椭圆饱满程度和斜率均在增加.在试验幅值范围内,椭圆饱满程度和斜率随幅值变化较小,即幅值对黏弹性阻尼器的影响较小,在后面的分析中将忽略幅值的影响.
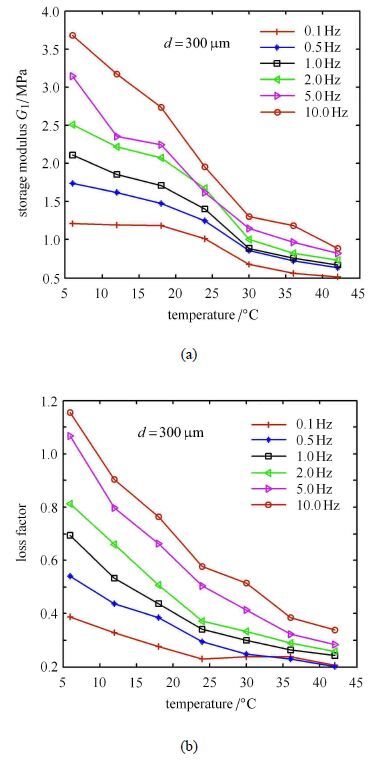
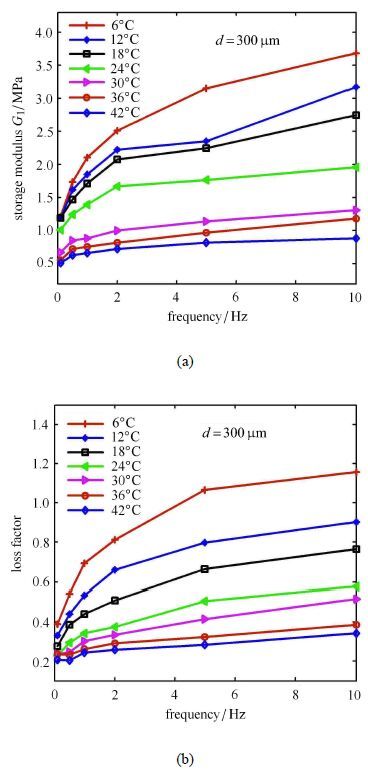
由滞回曲线可以看出温度和频率对微振激励下黏弹性阻尼器力学性能影响明显.下文分别就温度和频率对黏弹性阻尼器的动态力学性能指标的影响进行分析.图6为黏弹性阻尼器储能模量和损耗因子随环境温度的变化曲线. 由图6可以看出,在同样的频率和幅值条件下,储能模量和损耗因子随着温度的增加显著减少.在频率较高时,储能模量和损耗因子随温度增加减小比起在较低频率条件下的要更为明显.例如,在10 Hz时当温度从6$℃增加到42$℃时,黏弹性阻尼器的储能模量从3.68 MPa 随着频率的增加而增加,在温度较低时增加的更为减少到0.88 MPa,损耗因子从1.15减少到0.34.图7为黏弹性阻尼器储能模量和损耗因子随加载频率的变化曲线.可以明显看出,储能模量和损耗因子随着温度的增加而增加,在温度较低时增加得更为明显.例如在6$℃时,当频率由0.1 Hz增加到10 Hz 时,黏弹性阻尼器的储能模量从1.16 MPa增加到3.68 MPa,损耗因子从0.39增加到1.36.
3.3 模型验证
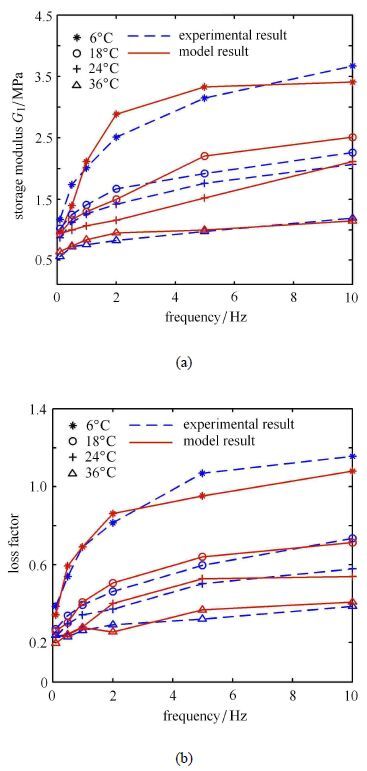
基于微振激励下黏弹性阻尼器的试验数据,为所提出的微振激励下黏弹性阻尼器微观链结构力学模型编制了MATLAB程序,采用非线性最小二乘法对模型的未知参数进行识别,识别得到各参数值为:$k_1 = 2.93\times 10^{-7}$,$k_2 = 6.09\times 10^{-3}$,$c_2 = 6.25\times 10^{-
7}$,$k_3 = 9.88\times 10^{-6}$,$c_3 = 4.47\times 10^{-6}$,$n_{\rm s1} = 2.54\times 10^{15}$,$n_{\rm c1} = 1.48\times 10^9$,$r_{\rm 0s} = r_{\rm 0c} = 1.94\times 10^{-4}$,$T_0 = 195^ \circ$C.利用该模型对黏弹性阻尼器力学性能参数进行计算,并与试验值进行比较,进而考察该模型的有效性. 由模型计算得到不同温度和不同频率的储能模量. 和损耗因子同试验所测得的储能模量和损耗因子比较见图8.为便于分析,图8中只给出了几种温度条件下的计算值和试验值的对比.从图8可以看出,所提出的模型能够精确的反映微振激励下黏弹性阻尼器储能模量和损耗因子随温度和频率的变化趋势.黏弹性阻尼器力学模型计算得到的储能模量和损耗因子在不同温度和频率条件下都与试验值较为接近.在一些点处出现误差,但误差是在可接受的范围内,其产生的主要原因可能是在建立本模型的过程中只考虑了两种微观分子链的影响,黏弹性材料的结构十分复杂,除了这两种分子链的影响,其他次要因素也会影响到其力学性能,最终导致模型数值产生误差.结果表明,所提出的模型能够较好描述微振激励下黏弹性阻尼器的力学性能.分析也发现,该模型对储能模量的描述精度高于对损耗因子的描述.例如在6℃时,储能模量和损耗因子的最大误差分别为15%和22%.此现象可以从模型的推导计算过程解释,在推导过程中,由式(18)直接获得储能模量和损耗模量,储能模量是直接获得的,误差较小,而损耗因子是由储能模量和损耗模量比值得到的,由于在计算储能模量和损耗模量的过程中都会产生误差,因此计算损耗因子会导致累计误差产生,计算所得损耗因子误差较大.
4 结论
本文分析了黏弹性材料所包含的两种微观分子链结构,并基于微观分子链结构和温频等效原理提出了一种微振激励下黏弹性阻尼器微观链结构力学模型;对黏弹性阻尼器微振激励下进行动态力学性能试验;对模型计算值与试验值进行对比验证,得出如下结论:
(1) 黏弹性材料的动态力学性能与材料的微观结构密切相关,材料的微观结构决定了黏弹性材料的力学性能.所提模型参数同黏弹性材料微观结构相关,具有明确物理意义.
(2)黏弹性阻尼器试验结果表明,温度和频率对其力学性能影响较大,黏弹性阻尼器储能模量和损耗因子在试验温度和频率范围内随温度升高而降低,随频率增加而增加.
(3)模型计算结果与试验值对比可知,所提出的微振激励下黏弹性阻尼器微观链结构力学模型能够准确地描述黏弹性阻尼器在不同频率和温度下动态力学性能,可以利用该模型预测黏弹性阻尼器的动态力学性能.
参考文献
| [1] |
赵云峰. 高性能黏弹性阻尼材料及其应用. 宇航材料工艺, 2009,(5): 1-6 (Zhao Yunfeng. Properties and application of advancedviscoelastic damping materials. Aerospace Material & Technology,2009, (5): 1-6 (in Chinese)) |
| [2] |
张少辉, 柴洪友, 马海全等. 黏弹阻尼技术在航天器上的应用与展望. 航天器工程, 2011, 20(1): 120-128 (Zhang Shaohui, ChaiHongyou, Ma Haiquan, et al. Progress and perspect on viscoelasticdamping technology for spacecraft application. Spacecraft Engineering,2011, 20(1): 120-128 (in Chinese)) |
| [3] |
Mazza F, Vulcano A. Control of the earthquake and wind dynamic response of steel-framed buildings by using additional braces and/or viscoelastic dampers. Earthquake Engineering & Structural Dynamics,2011, 40(2): 155-174 |
| [4] |
Rashid A, Nicolescu CM. Design and implementation of tuned viscoelastic dampers for vibration control in milling. International Journal of Machine Tools and Manufacture, 2008, 48(9): 1036-1053 |
| [5] |
Moliner E, Museros P, Martínez-Rodrigo MD. Retrofit of existing railway bridges of short to medium spans for high-speed traffic using viscoelastic dampers. Engineering Structures, 2012, 40: 519-528 |
| [6] |
Rao MD. Recent applications of viscoelastic damping for noise control in automobiles and commercial airplanes. Journal of Sound and Vibration, 2003, 262(3): 457-474 |
| [7] |
黄微波, 刘超, 黄舰. 高分子阻尼材料研究进展及发展趋势. 材料导报, 2012, 26(11): 89-91,100 (Huang Weibo, Liu Chao, Huang Jian. Progress and trends in polymer damping materials. Materials Review, 2012, 26(11): 89-91,100 (in Chinese)) |
| [8] |
路纯红, 白鸿柏. 黏弹性材料本构模型的研究. 高分子材料科学与工程, 2007, 23(6): 28-31,35 (Lu Chunhong, Bai Hongbai. Study on constitutive model of viscoelastic material. Polymer Materials Science & Engineering, 2007, 23(6): 28-31,35 (in Chinese)) |
| [9] |
Saidi I, Gad EF, Wilson JL, et al. Development of passive viscoelastic damper to attenuate excessive floor vibrations. Engineering Structures, 2011, 33(12): 3317-3328 |
| [10] |
张振华, 杨雷, 庞世伟. 高精度航天器微振动力学环境分析. 航天器环境工程, 2009, 26(6): 528-534 (Zhang Zhenhua, Yang Lei, Pang Shiwei. Jitter environment analysis for micro-precision spacecraft. Spacecraft Environment Engineering, 2009, 26(6): 528-534 (in Chinese)) |
| [11] |
Zhang Z, Aglietti GS, Zhou WY. Microvibrations induced by a cantilevered wheel assembly with a soft-suspension system. AIAA Journal,2011, 49(5): 1067-1079 |
| [12] |
Zhou WY, Aglietti GS, Zhang Z. Modelling and testing of a soft suspension design for a reaction/momentum wheel assembly. Journal of Sound and Vibration, 2011, 330(18): 4596-4610 |
| [13] |
Liu CC, Jing XJ, Daley S, et al. Recent advances in micro-vibration isolation. Mechanical Systems and Signal Processing, 2015, 56: 55-80 |
| [14] |
Xu ZD, Wang DX, Shi CF. Model, tests and application design for viscoelastic dampers. Journal of Vibration and Control, 2011, 17(9):1359-1370 |
| [15] |
Xu ZD, Xu C, Hu J. Equivalent fractional Kelvin model and experimental study on viscoelastic damper. Journal of Vibration and Control, 2015, 21(13): 2536-2552 |
| [16] |
Lewandowski R, Pawlak Z. Dynamic analysis of frames with viscoelastic dampers modelled by rheological models with fractional derivatives. Journal of Sound and Vibration, 2011, 330(5): 923-936 |
| [17] |
周云, 松本達治, 田中和宏等. 高阻尼黏弹性阻尼器性能与力学模型研究. 振动与冲击, 2015, 34(7): 1-7 (Zhou Yun, Matsumoto Tatsuji, Tanaka Kazuhiro, et al. Performance and mechanical model of high damping viscoelastic dampers. Journal of Vibration and Shock,2015, 34(7): 1-7 (in Chinese)) |
| [18] |
郭亚娟, 李鸿光, 孟光. 黏弹性材料的ADF 模型研究. 振动与冲击, 2007, 26(10): 145-147, 168 (Guo Yajuan, Li Hongguang, Meng Guang. Study on ADF model of viscoelastic material. Journal of Vibration and Shock , 2007, 26(10): 145-147, 168 (in Chinese)) |
| [19] |
张针粒, 李世其, 朱文革. 黏弹性阻尼材料动态力学性能温度谱模型. 机械工程学报, 2011, 47(20): 135-140 (Zhang Zhenli, Li Shiqi, Zhu Wenge. Temperature spectrum model of dynamic mechanical properties for viscoelastic damping materials. Journal of Mechanical Engineering, 2011, 47(20): 135-140 (in Chinese)) |
| [20] |
高庆, 林松, 杨显杰. 丁基橡胶黏弹性材料的非线性蠕变本构描述. 应用力学学报, 2007, 24(3): 386-390, 503 (Gao Qing, Lin Song, Yang Xianjie. Constitutive description for nonlinear creep behavior of viscoelastic material buty1. Chinese Journal of Applied Mechanics,2007, 24(3): 386-390, 503 (in Chinese)) |
| [21] |
康永刚, 张秀娥. 非定常微分型黏弹性本构模型. 力学学报, 2012,44(2): 456-459 (Kang Yonggang, Zhang Xiu'e. The non-stationary differential constitutive models of viscoelasticity. Chinese Journal of Theoretical and Applied Mechanics, 2012, 44(2): 456-459 (in Chinese)) |
| [22] |
石银明, 华宏星, 傅志方. 黏弹性材料的微振子模型研究. 振动工程学报, 2001, 14(1): 100-104 (Shi Yinming, Hua Hongxing, Fu Zhifang. The mini-oscillator model research for viscoelastic material. Journal of Vibration Engineering, 2001, 14(1): 100-104 (in Chinese)) |
| [23] |
Fröhlich J, NiedermeierW, Luginsland HD. The effect of filler-filler and filler-elastomer interaction on rubber reinforcement. Composites Part A: Applied Science and Manufacturing, 2005, 36(4): 449-460 |
| [24] |
Prabhu R, Klitkou R, Medvedev GA, et al. A critical analysis of the effect of crosslinking on the linear viscoelastic behavior of styrene- butadiene rubber and other elastomers. Journal of Polymer Science Part B: Polymer Physics, 2013, 51(2): 687-697 |
| [25] |
Tang S, Greene MS, Liu WK. Two-scale mechanism-based theory of nonlinear viscoelasticity. Journal of the Mechanics and Physics of Solids, 2012, 60(2): 199-226 |
| [26] |
Miehe C, Göktepe S. A micro-macro approach to rubber-like materials. Part II: the micro-sphere model of finite rubber viscoelasticity. Journal of the Mechanics and Physics of Solids, 2005, 53(10): 2231-2258 |
| [27] |
谭江华, 罗文波. 橡胶材料分子链网络本构模型的研究进展. 材料导报, 2008, 22(7): 31-34 (Tan Jianghua, Luo Wenbo. Advances in studies on molecular chain-network based constitutive models of rubber materials. Materials Review, 2008, 22(7): 31-34 (in Chinese)) |
| [28] |
Svaneborg C, Grest GS, Everaers R. Strain-dependent localization, microscopic deformations, and macroscopic normal tensions in model polymer networks. Physical Review Letters, 2004, 93(25):257801 |
| [29] |
Min KW, Kim J, Lee SH. Vibration tests of 5-storey steel frame with viscoelastic dampers. Engineering Structures, 2004, 26(6): 831-839 |
| [30] |
Bhatti AQ. Performance of viscoelastic dampers (VED) under various temperatures and application of magnetorheological dampers (MRD) for seismic control of structures. Mechanics of Time- Dependent Materials, 2013, 17(3): 275-284 |
| [31] |
Richard MC. Theory of Viscoelasticity, 2nd edn. New York: Dover Publications, 2003 |
MICROSCOPIC MOLECULAR CHAIN STRUCTURE MODEL OF VISCOELASTIC DAMPER UNDER MICRO-VIBRATION EXCITATIONS
Xu Zhaodong , Xu Chao, Xu Yeshou
, Xu Chao, Xu Yeshou
Key Laboratory of Concrete and Prestressed Concrete Structures of Ministry of Education, Southeast University, Nanjing 210096, China
Abstract: It is of great importance to reduce micro-vibration e ect on precision instrument, and employing viscoelastic damper to reduce micro-vibration is an innovative and challenging issue. In this paper, the molecular chain network model is employed to analyze the viscoelastic material microstructures, and the e ect of the network chains and free chains on the viscoelastic properties of viscoelastic material is comprehensively considered, and then a mechanical model of VE damper under micro-vibration is proposed based on molecular chain structures. The standard linear solid model and Maxwell model are adopted to describe the mechanical behaviors of the single network chain and single free chain, respectively. Moreover, eight-chain network model and three-chain network model are then employed. Additionally, temperature-frequency equivalent theory is adopted to reflect the temperature e ect. The proposed model is able to describe the mechanical properties of viscoelastic damper at di erent frequencies and temperatures, and this model can reflect the material microstructure e ect on its viscoelastic properties. To verify the proposed model and reveal the mechanical behavior of viscoelastic damper under micro-vibration excitations, tests on viscoelastic damper are carried out. The results show that viscoelastic damper has good energy dissipation capacity; the dynamic properties are significantly influenced by frequency and temperature, and the proposed model can accurately describe the dynamic properties of viscoelastic damper at di erent temperatures and frequencies under micro-vibration excitations.
Key words:
microscopic chain structure mechanical model viscoelastic damper micro-vibration property test temperature-frequency equivalent theory


 2016, Vol. 48
2016, Vol. 48