0 引言
唯象学本构理论是目前应用最广泛的材料本构理论之一,根据其弹性本构方程的形式可分为次弹性-塑性本构理论和超弹性-塑性本构理论两类.超弹性-有限塑性本构模型引入了 Hemholz
自由能,在推导本构方程时利用了热力学第二定律,因而克服了次弹性模型的主要缺点------本构表达式不可积.因此,以超弹性理论为基础的有限弹塑性本构模型在过去的20年里得到了广泛的接受与应用,至今也被看作是现象学本构理论发展的最高水平而被拓展到不同的力学领域,如土体塑性[1, 2]、损伤力学[2, 3, 4]以及晶体塑性[5]等.
材料在低应变率下的塑性行为可近似看作是率无关的,其塑性流动的描述需要引入屈服面方程,而通过屈服面的膨胀、收缩以及平移、扭转来分别描述材料的各向同性硬化和各向异性硬化[6, 7, 8, 9].目前,最简单也是最常用的描述屈服面各向同性硬化的方法是引入一个标量内变量$k$,利用$k$的演化过程来反映屈服面大小的变化;而屈服面的各向异性硬化则只考虑其平移------即随动硬化部分,其在不同的本构理论中有不同的描述方式.对于次弹性本构理论,由于其本构方程在形式上与小变形理论基本一致,故小变形理论中的经典随动硬化法则,如
Armstrong-Frederick (A-F)随动硬化法则[10],Chaboche 随动硬化法则[11, 12],Ohno-Wang (O-W)随动硬化法则[13]以及 Karim-Ohno
(K-O)随动硬化法则[14]等,只需根据普拉格(Prager)一致性准则[15]将硬化模型中背应力的物质导数替换为其相应的客观应力率即可[16].而超弹性本构理论由于包含了不同的构型,故背应力的引入需要依托于中间构型的概念[17, 18, 19, 20, 21]. Lion
[17]基于变形梯度的乘法分解定理[22],并结合直观的非线性流变学模型,将总体变形梯度${
F}$的塑性分解部分${ F}^{\rm p}$再次以乘法形式分解为两部分:能量部分${ F}^{\rm pe}$和耗散部分${
F}^{\rm pd}$,即${ F}^{\rm p} = { F}^{\rm pe} { F}^{\rm
pd}$,并将相应的中间构型称之为随动硬化中间构型,在此基础上假定由力学机制所引起的亥姆霍兹自由能${\psi
}$可表示为两部分之和:弹性变形部分所储存的自由能${\psi }^{\rm e}$和随动硬化部分所储存的自由能 ${\psi
}^{\rm pe}$,利用热力学第二定律,随动硬化背应力可表示为自由能 ${\psi }^{\rm
pe}$相对于随动硬化变形的偏导数,即变形梯度 ${ F}^{\rm pe}$的张量函数,再通过引入 ${ F}^{\rm
pe}$的演化方程来反映背应力的演化过程,从而确定随动硬化法则的形式. 显然,多种构型的引入以及热动力学法则的限制使得超弹性理论中的随动硬化法则相对复杂.目前,多数文献将A-F随动硬化法则应用到超弹性-塑性本构理论中,而将Chaboche模型、O-W模型以及K-O模型中背应力的加法分解性质及其演化的临界面阶跃特性引入超弹性理论则存在一定的复杂性. Zhu
等[23]首次利用K-O随动硬化法则构建了超弹性-塑性本构模型,但并未对其背后的构型分解理论做相应的物理阐释.
本文基于 Lion [17]变形分解理论以及Yilin Zhu
等[23]的超弹性-塑性本构理论,引入了多机制过程并明确提出了多重中间构型的概念,在此基础上对经典理论中客观性的定义进行了概念上的推广,同时发展了一类新的超弹性-有限塑性本构模型.这类本构模型通过适当地选择Hemholz自由能分量${{\psi }^{\text{pe}}}$的形式,在满足热动力学法则的基础上,可融合多种小变形循环塑性理论中经典的随动硬化法则(如Chaboche
模型,O-W模型以及K-O模型等),且随动硬化法则中背应力的加法分解性质及其演化的临界面阶跃特性在该本构理论中均有所体现.
1 变形运动学
1.1 基本理论
考虑一个各向同性的变形体,在某一时间间隔内经历一个连续光滑的有限变形过程,变形体的初始状态记为固定的参考构型$C_{0}$,变形结束后的状态记为当前构型$C$,变形体的某一物质点在初始构型$C_{0}$中的空间位置向量记为${
X}$,在当前构型$C$中的空间位置向量记为${ x}$,在时间间隔$l$内经历的变形过程可以用一个映射$\chi
$来表示,定义为 ${ x} =\chi ({ X},t)$,$t$代表时间,而变形梯度的表达式为
|
$F=\frac{\partial x}{\partial X}F=\text{det}F>0$
|
(1) |
根据极分解定理,变形梯度可以唯一地分解为伸长张量与正交张量的乘积
式中,${ V}$和${ U}$为正定对称二阶张量,分别称为左伸长张量和右伸长张量,${ R}$是一个正交张量.
速度矢量和速度梯度张量如下
|
$\begin{align}
& \text{L= D + W (4a)} \\
& D=\frac{L+{{L}^{\text{T}}}}{2},W=\frac{L-{{L}^{\text{T}}}}{2}(4b) \\
\end{align}$
|
(3) |
式中,字母的上标"$\dot{ }$"表示对相应的量求物质导数. 速度梯度张量可以唯一地分解为对称部分和反对称部分
式中,${ D}$ 称为变形率张量,${ W}$称为涡旋张量,有些文献中也将${
W}$称为物质旋率张量. 下面通过变形梯度的极分解定理定义两个对称正定二阶张量
|
${{U}^{2}}={{F}^{\text{T}}}F=C$
|
(5) |
|
${{V}^{2}}=F{{F}^{\text{T}}}=B$
|
(6) |
式中,${ C}$和${ B}$分别称为右 Cauchy-Green
(C-G)张量和左C-G张量,分别与${ U}$和${ V}$拥有相同的特征子空间.
1.2 变形梯度乘法分解定理
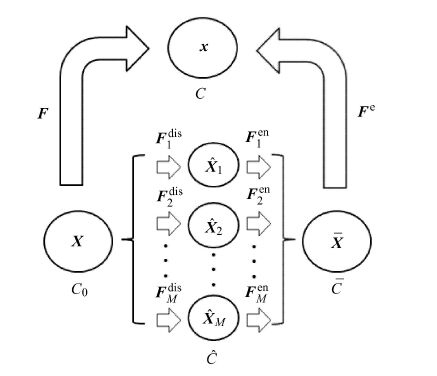
在有限变形理论中,变形梯度${ F}$的乘法分解[24]是其常用的理论基础,中心思想是局部卸载构型的引入:假定材料的每一个物质点在变形过程中的任意时刻都可以通过一个假想的局部卸载过程得到相应的无应力卸载构型,其示意图如图1.
变形梯度的乘法分解假定从参考构型$C_{0}$到即时构型$C$的变形分为两步. 第一步,由参考构型$C_{0}$通过变形梯度${ F}^{\rm p}$先变到一中间构型$\bar C$,物质点的空间位置向量由${ X}$变为$\bar {
X}$,其周围微小邻域内的物质线元由$\text{dX}$
变为$
\text{d}\bar{X}$
,仿照式(1),变形梯度${ F}^{\rm p}$
可表示为
|
${{F}^{\text{p}}}=\frac{\partial \bar{X}}{\partial X},{{J}^{\text{p}}}=\det {{F}^{\text{p}}}=1$
|
(7) |
|
$d\bar{X}={{F}^{\text{p}}}\text{d}X$
|
(8) |
物质线元$d{ X}$与$d\bar { X}$之间的关系为
然后进行第二步,由中间构型$\bar C$到即时构型$C$,物质点的空间位置向量由 $\bar{ X}$变为${
x}$,物质线元由$d \bar{ X}$ 变为$d{ x}$,变形梯度与线元变换公式各为
|
${{F}^{\text{e}}}=\frac{\partial x}{\partial \bar{X}},{{J}^{\text{e}}}=\det {{F}^{\text{e}}}>0$
|
(9) |
|
$\text{d}x={{F}^{\text{e}}}d\bar{X}$
|
(10) |
根据总的变形过程,线元变换公式为
|
$\text{d}x=F\text{ d}X$
|
(11) |
将式(8)代入式(10),得
|
$\text{d}x={{F}^{\text{e}}}{{F}^{\text{p}}}\text{ }\backslash \text{ d}X$
|
(12) |
比较式(11)与式(12),并注意线元$
\text{dX}$
的任意性,可得
|
$F={{F}^{\text{e}}}{{F}^{\text{p}}}\text{ }$
|
(13) |
上式为变形梯度的乘法分解定理,这个定理假定中间构型$\bar C$
是由即时构型$C$卸载而得,也称为卸载构型. 如果每点附近的小邻域都完全卸载,那么由于出现不可逆的塑性变形,卸载后的各个微元之间变形可能不协调,卸载构型不可能是一个连续体. 因此乘法分解定理只局限于物质点${ X}$的一个小邻域,想象把它从物体的其余部分分割开,而中间构型$\bar C$
专指此一个小邻域的卸载构型. 因此${ F}^{\rm e}$和${ F}^{\rm p}$都只是局部的量,不能对它们进行空间的微分运算,而只能对时间$t$进行微分运算(即求物质导数).${ F}^{\rm e}$和${ F}^{\rm p}$各称为弹性变形梯度与塑性变形梯度. 分解式(13)最早是由文献[22]提出的,可称为变形梯度${ F}$的弹塑性分解式.
实际上,将物体所受的外荷载卸去以后,物体内部将出现残余应力,不可能做到使体内所有的微元都完全卸载. 如果所有的微元都完全卸载,这些微元就好像一组积木块,不可能拼成一个连续无缝的整体. 因此,如果要保持为一连续整体,每个微元只能卸载到残余应力的状态,再经过各自的旋转,合成一个连续体.
另外,如图2所示,从即时构型$C$完全卸载到中间构型$\bar C$
的过程中不产生新的反向塑性变形,即卸载过程是完全的弹性卸载过程,期间不再发生任何的非弹性变形. 以图2所示的出现随动硬化的单向拉伸过程(包辛格效应)为例,$O$点相当于参考构型$C_{0}$,$B$点相当于即时构型$C$,而卸载构型相当于$A$点. 尽管实际上从$B$点卸载还未到达$A$点之前由于随动硬化已经开始产生新的反向塑性变形,但是仍然假定有一个状态即$A$,为卸载状态.
将分解式(13)代入速度梯度计算式(3),经过代数处理,可得速度梯度分解式
|
$L={{L}^{\text{e}}}+{{F}^{\text{e}}}{{L}^{p}}{{({{F}^{\text{e}}})}^{-1}}$
|
(14) |
对变形梯度${ F}^{\rm e}$和${ F}^{\rm p}$
应用极分解定理,以构造更多的几何变形张量
|
${{F}^{\text{e}}}={{R}^{\text{e}}}{{U}^{\text{e}}}={{V}^{\text{e}}}{{R}^{\text{e}}}$
|
(15) |
|
${{F}^{\text{p}}}={{R}^{\text{p}}}{{U}^{\text{p}}}={{V}^{\text{p}}}{{R}^{\text{p}}}$
|
(16) |
仿照变形运动学基本理论中构造C-G变形张量的方式(式(5)与(6))构造弹塑性C-G变形张量
|
${{({{U}^{\text{e}}})}^{2}}={{({{F}^{\text{e}}})}^{\text{T}}}{{F}^{\text{e}}}={{C}^{\text{e}}}$
|
(17) |
|
${{({{V}^{\text{e}}})}^{2}}={{F}^{\text{e}}}{{({{F}^{\text{e}}})}^{\text{T}}}={{B}^{\text{e}}}$
|
(18) |
|
${{({{U}^{\text{p}}})}^{2}}={{({{F}^{\text{p}}})}^{\text{T}}}{{F}^{\text{p}}}={{C}^{\text{p}}}$
|
(19) |
|
${{({{V}^{\text{p}}})}^{2}}={{F}^{\text{p}}}{{({{F}^{\text{p}}})}^{\text{T}}}={{B}^{\text{p}}}$
|
(20) |
式中,${ C}^{\rm e}$,${ B}^{\rm e}$,${ C}^{\rm p}$和${ B}^{\rm
p}$分别称为弹性右C-G变形张量、弹性左C-G变形张量、塑性右C-G变形张量和塑性左C-G变形张量.
2 变形梯度分解理论的拓展
为了考虑塑性流动的能量存储机制,Lion引进了塑性变形梯度${ F}^{\rm p}$的乘法分解定理[17]
|
${{F}^{\text{p}}}={{F}^{\text{en}}}{{F}^{\text{dis}}},\text{ }\det {{F}^{\text{en}}}=\det {{F}^{\text{dis}}}=1\text{ }$
|
(21) |
莱昂将变形梯度${ F}^{\rm dis}$所确定的中间构型称为"随动硬化中间构型",其分解理论的直观示意图与流变学模型分别见图3与图4.
为了将小变形理论中常用的背应力分解假定拓展应用到大变形领域,现假定Lion塑性变形梯度分解过程(即式(21))是一个多重机制过程,即
|
$\begin{align}
& {{F}^{\text{p}}}=F_{1}^{\text{en}}F_{1}^{\text{dis}}=F_{2}^{\text{en}}F_{2}^{\text{dis}}=\cdots =F_{M}^{\text{en}}F_{M}^{\text{dis}} \\
& \det F_{i}^{\text{en}}=\det F_{i}^{\text{dis}}=1,i=1,2,\cdots ,M \\
\end{align}$
|
(22) |
类似于式(14),可知
|
${{L}^{\text{p}}}=L_{i}^{\text{en}}+F_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{\text{en}}L_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{\text{dis}}{{(F_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{\text{en}})}^{-1}}\text{ }$
|
(23) |
式中,$\underline{i}$表示不对指标$i$求和,下文亦是如此. 上述分解理论的直观示意图与流变学模型见图5与图6.
由图6的流变学模型可以看出,这个多机制过程反映了背应力产生机制的多样性与复杂性,在晶体塑性领域,可将背应力产生的微观机制分为三类:不同晶粒间的相互作用力,晶粒交界面处堆叠位错线间的相互作用力,以及晶粒内部位错线间的相互作用力[24],这些作用力的宏观表现即可解释为本文引入的多机制过程.
利用极分解定理,可得
|
$F_{i}^{\text{en}}=R_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{\text{en}}U_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{\text{en}}=V_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{\text{en}}R_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{\text{en}}\text{ }$
|
(24) |
相应的左、右C-G张量为
|
$B_{i}^{\text{en}}=F_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{\text{en}}{{(F_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{\text{en}})}^{\text{T}}}={{(V_{i}^{\text{en}})}^{2}}\text{ }$
|
(25) |
|
$C_{i}^{\text{en}}={{(F_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{\text{en}})}^{\text{T}}}F_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{\text{en}}={{(U_{i}^{\text{en}})}^{2}}\text{ }$
|
(26) |
假定单位参考构型体积的Hemholz自由能$\psi $具有如下的弹塑性分解形式
|
$\psi =\text{ }{{\psi }^{\text{e}}}({{B}^{\text{e}}})+\text{ }\psi _{1}^{\text{en}}(B_{1}^{\text{en}})+\psi _{2}^{\text{en}}(B_{2}^{\text{en}})+\cdots +\text{ }\psi _{M}^{\text{en}}(B_{M}^{\text{en}})\text{ }$
|
(27) |
$\psi $
本文只考虑各向同性材料,因此,式(26)中$\psi^{\rm e}({ C}^{\rm e})$及$\psi _i^{\rm en}({
B}_i^{\rm en})$分别为其自变量${ C}^{\rm e}$和 ${ B}_i^{\rm
en}$的各向同性标量函数,仿照Lion[17]以及文献[21]的定义,将第$i$个背应力分量${ S}_i^{\rm en}$定义为
|
$S_{i}^{\text{en}}=\text{sy}{{\text{m}}_{0}}(2\frac{\partial \psi _{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{\text{en}}(B_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{\text{en}})}{\partial B_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{\text{en}}}B_{i}^{\text{en}})$
|
(28) |
式中,运算符
${\rm sym}_0( )$表示对圆括号中的二阶张量取对称偏量. 总的背应力
${ S}^{\rm en}$可表示为
|
${{S}^{\text{en}}}=\sum\limits_{i=1}^{M}{S_{i}^{\text{en}}}\text{ }$
|
(29) |
基于以上理论,现对应力功率${ \tau }:{ L}$进行分解,由式(14)可知
$\tau :L=\tau :{{L}^{\text{e}}}+[{{({{F}^{\text{e}}})}^{\text{T}}}\tau {{({{F}^{\text{e}}})}^{\text{-T}}}]:{{L}^{\text{p}}}$
上式也可写为
|
$\tau :L\tau :L=\tau :{{L}^{\text{e}}}+[{{({{F}^{\text{e}}})}^{\text{T}}}\tau {{({{F}^{\text{e}}})}^{\text{-T}}}-{{S}^{\text{en}}}]:{{L}^{p}}+{{S}^{\text{en}}}:{{L}^{\text{p}}}$
|
(30) |
将式(23)与式(29)代入式(30)左端第3项,经过简单的代数运算,可得
|
$\begin{align}
& \tau :L=\tau :{{L}^{e}}+[{{({{F}^{e}})}^{T}}\tau {{({{F}^{e}})}^{-T}}-{{S}^{en}}]:{{L}^{p}}+ \\
& \sum\limits_{i=1}^{M}{S_{i}^{en}}:L_{i}^{en}+\sum\limits_{i=1}^{M}{[{{(F_{i}^{en})}^{T}}S_{i}^{en}{{(F_{i}^{en})}^{-T}}]}:L_{i}^{dis} \\
\end{align}$
|
(31) |
考虑到${ \tau }$与 ${ S}_i ^{\rm en}$的对称性,式(31)又可记为
$$
|
$\begin{align}
& \tau :D=\tau :{{D}^{\text{e}}}+[{{({{F}^{\text{e}}})}^{\text{T}}}\tau {{({{F}^{\text{e}}})}^{\text{-T}}}-{{S}^{\text{en}}}]:{{L}^{\text{p}}}+ \\
& \sum\limits_{i=1}^{M}{S_{i}^{en}:D_{i}^{en}+}\sum\limits_{i=1}^{M}{[{{(F_{i}^{\text{en}})}^{\text{T}}}S_{i}^{en}{{(F_{i}^{\text{en}})}^{\text{-T}}}]:L_{i}^{\text{dis}}} \\
\end{align}$
|
(32) |
式中,$({ F}^{\rm e})^{\rm T}{ \tau}{ F}^{\rm e})^{\rm - T}$与 ${ S}_i^{\rm en}({
F}_i^{\rm en})^{\rm -T}$ 分别称为弹性 Mandel 应力与塑性 Mandel应力,即
|
${{M}^{e}}={{({{F}^{\text{e}}})}^{\text{T}}}\tau {{({{F}^{\text{e}}})}^{\text{-T}}}$
|
(33) |
|
$M_{i}^{\text{en}}={{(F_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{\text{en}})}^{\text{T}}}S_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{\text{en}}{{(F_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{\text{en}})}^{\text{-T}}}$
|
(34) |
与 Kirchhoff 应力 ${ \tau}$和背应力${ S}^{\rm en}_i$不同,上述两类
Mandel应力通常不具备对称性.
3 客观性
客观性又称为标架不变性,是连续固体介质力学中的一个重要概念,它强调了本构关系与刚体转动无关,也即材料的本构关系不因观察者不同而发生形式上的变化,这就要求在构建材料本构关系时所采用的变量必须具备客观性.经典理论中客观性的定义仅局限于初始构型和当前构型,众所周知,经典理论中的 Truesdell 客观张量只包含定义在当前构型中的张量,Hill 客观张量是定义在当前构型中的客观张量,而两点客观张量也仅仅涉及初始和当前构型,这对于次弹性-塑性本构理论已经足够(次弹性-塑性理论只涉及初始和当前构型两个构型),而现如今,超弹性理论已经发展的很完善,多种构型分解理论业已提出,因此本节利用中间构型的概念,将现有客观性的定义进行适当的推广,得到适用于超弹性本构理论的转换关系,并对各种转换关系进行了分类,进一步加深了对客观性定义的理解.
由第2节的论述可知,若采用拓展的Lion塑性梯度分解理论,则材料点在某个变形状态下的卸载构型仅由梯度张量${ F}^{\rm p}$所确定,而随动硬化中间构型则可由多个梯度张量${ F}_i^{\rm dis}$ ($i =1,2,\cdots,n)$所确定,为了论述上的方便,现仅考虑其中某一个随动硬化构型,且略去下角标$i$,即假定其由梯度张量${ F}^{\rm dis}$所确定.
客观性的定义依托于材料点的等价运动,即材料点在变形过程中若不加以限制,可对当前构型和中间构型进行任意的平移与刚性转动而不改变材料的本构特性. 通常意义下,这种叠加的刚性转动和平移运动可表示为时间$t$的函数,且不同的构型可叠加不同的转动与平移. 由于构型的平移运动对材料点的运动学变量无影响,故只需考虑每个构型的刚性转动,现将当前构型、卸载构型和随动硬化中间构型的刚性转动张量分别记为${ Q}_{1}(t)$,${ Q}_{2}(t)$和${ Q}_{3}(t)$,下文将讨论这些转动张量对各运动学变量的影响.
3.1 转换关系
记二阶张量${ A}$在刚性转动后变为
$\tilde { A}$,略去简单的代数推导过程,将一些显而易见的结果列出如下
|
$\tilde{F}={{Q}_{1}}F=({{Q}_{1}}\mathbf{1})_{*}^{*}F$
|
(35) |
|
${{\tilde{F}}^{\text{p}}}={{Q}_{2}}{{F}^{\text{p}}}=({{Q}_{2}}\mathbf{1})_{*}^{*}{{F}^{\text{p}}}$
|
(36) |
|
${{\tilde{F}}^{\text{dis}}}={{Q}_{3}}{{F}^{\text{dis}}}=({{Q}_{3}}\mathbf{1})_{*}^{*}{{F}^{\text{dis}}}$
|
(37) |
|
${{\tilde{F}}^{\text{e}}}={{Q}_{1}}{{F}^{\text{e}}}Q_{2}^{\text{T}}=({{Q}_{1}}{{Q}_{2}})_{*}^{*}{{F}^{\text{e}}}$
|
(38) |
|
${{\tilde{F}}^{\text{en}}}={{Q}_{2}}{{F}^{\text{en}}}Q_{3}^{\text{T}}=({{Q}_{2}}{{Q}_{3}})_{*}^{*}{{F}^{\text{en}}}$
|
(39) |
式中,${\bf 1}$代表三维空间中的二阶单位张量,运算符$( )_\ast ^\ast $
表示圆括号中的两个二阶张量分别左乘运算符右端二阶张量并矢式中的两个向量. 由以上各式,可得左右C-G张量的转换关系
|
$\tilde{B}=({{Q}_{1}}{{Q}_{1}})_{*}^{*}B$
|
(40a) |
|
${{\tilde{B}}^{\text{p}}}=({{Q}_{2}}{{Q}_{2}})_{*}^{*}{{B}^{\text{p}}}$
|
(41a) |
|
${{\tilde{C}}^{\text{p}}}={{C}^{\text{p}}}$
|
(41b) |
|
${{\tilde{B}}^{\text{dis}}}=({{Q}_{3}}{{Q}_{3}})_{*}^{*}{{B}^{\text{dis}}}$
|
(42a) |
|
${{\tilde{C}}^{\text{dis}}}={{C}^{\text{dis}}}$
|
(42b) |
|
${{\tilde{B}}^{\text{e}}}=({{Q}_{1}}{{Q}_{1}})_{*}^{*}{{B}^{\text{e}}}$
|
(43a) |
|
${{\tilde{C}}^{\text{e}}}=({{Q}_{2}}{{Q}_{2}})_{*}^{*}{{C}^{\text{e}}}$
|
(43b) |
|
${{\tilde{B}}^{\text{en}}}=({{Q}_{2}}{{Q}_{2}})_{*}^{*}{{B}^{\text{en}}}$
|
(44a) |
|
${{\tilde{C}}^{\text{en}}}=({{Q}_{3}}{{Q}_{3}})_{*}^{*}{{C}^{\text{en}}}$
|
(44b) |
以上各式中,类似于变形梯度${ F}^{\rm en}$的左、右C-G张量分别为 ${ B}^{\rm en}$,
${ C}^{\rm en}$ (式 (25)和式(26)),记 ${ B}^{\rm dis}$,${ C}^{\rm dis}$分别为变形梯度 ${
F}^{\rm dis}$的左、右C-G张量,其表达式与式(25)、式(26)类似,即
$\begin{align}
& {{B}^{\text{dis}}}={{F}^{\text{dis}}}{{({{F}^{\text{dis}}})}^{\text{T}}}={{({{V}^{\text{dis}}})}^{\text{2}}} \\
& {{C}^{\text{dis}}}={{({{F}^{\text{dis}}})}^{\text{T}}}{{F}^{\text{dis}}}={{({{U}^{\text{dis}}})}^{\text{2}}} \\
\end{align}$
由于变形率张量${ D}$和涡旋张量${ W}$涉及到了变形梯度的物质导数,其转换关系并不像式(35)$\sim$式(44)那样简洁,记正交张量${ Q}_{1}$,${ Q}_{2}$和${ Q}_{3}$的旋率张量分别为${
\Omega}_{1}$,${ \Omega }_{2}$和${ \Omega }_{3}$,即
|
${{\dot{Q}}_{1}}={{\Omega }_{1}}{{Q}_{1}}$
|
(45) |
|
${{\dot{Q}}_{2}}={{\Omega }_{2}}{{Q}_{2}}$
|
(46) |
|
${{\dot{Q}}_{3}}={{\Omega }_{3}}{{Q}_{3}}$
|
(47) |
由速度梯度张量${ L}$的表达式(3)以及转换关系式(35),可得
|
$\tilde{L}=({{Q}_{1}}{{Q}_{1}})_{*}^{*}L+{{\Omega }_{1}}$
|
(48) |
由上式可得${ D}$与${ W}$的转换关系式
|
$\tilde{D}=({{Q}_{1}}{{Q}_{1}})_{*}^{*}D$
|
(49) |
|
$\tilde{W}=({{Q}_{1}}{{Q}_{1}})_{*}^{*}W+{{\Omega }_{1}}$
|
(50) |
将以上过程应用于式(36)$\sim$式(39)中的各变形梯度,便可得到相应的变形率张量与涡旋张量的转换关系,现略去代数推演过程,直接将结果列出如下
|
${{\tilde{D}}^{\text{p}}}=({{Q}_{2}}{{Q}_{2}})_{*}^{*}{{D}^{\text{p}}}$
|
(51) |
|
${{\tilde{W}}^{\text{p}}}=({{Q}_{2}}{{Q}_{2}})_{*}^{*}{{W}^{\text{p}}}+{{\Omega }_{2}}$
|
(52) |
|
${{\tilde{D}}^{\text{dis}}}=({{Q}_{3}}{{Q}_{3}})_{*}^{*}{{D}^{\text{dis}}}$
|
(53) |
|
${{\tilde{W}}^{\text{dis}}}=({{Q}_{3}}{{Q}_{3}})_{*}^{*}{{W}^{\text{dis}}}+{{\Omega }_{3}}$
|
(54) |
|
${{\tilde{D}}^{\text{e}}}=({{Q}_{1}}{{Q}_{1}})_{*}^{*}{{D}^{\text{e}}}-\text{sym}({{\tilde{F}}^{\text{e}}}{{\Omega }_{2}}{{({{\tilde{F}}^{\text{e}}})}^{-1}})$
|
(55) |
|
${{\tilde{W}}^{\text{e}}}=({{Q}_{1}}{{Q}_{1}})_{*}^{*}{{W}^{\text{e}}}+{{\Omega }_{1}}\text{ }\!\!\ddot{\ }\!\!\text{ }C\text{skw}({{\tilde{F}}^{\text{e}}}{{\Omega }_{2}}{{({{\tilde{F}}^{\text{e}}})}^{-1}})$
|
(56) |
|
${{\tilde{D}}^{\text{en}}}=({{Q}_{2}}{{Q}_{2}})_{*}^{*}{{D}^{\text{en}}}-\text{sym}({{\tilde{F}}^{\text{en}}}{{\Omega }_{3}}{{({{\tilde{F}}^{\text{e}}})}^{-1}})$
|
(57) |
|
${{\tilde{W}}^{\text{en}}}=({{Q}_{2}}{{Q}_{2}})_{*}^{*}{{W}^{\text{en}}}+{{\Omega }_{2}}\text{ }\!\!\ddot{\ }\!\!\text{ }C\text{skw}({{\tilde{F}}^{\text{en}}}{{\Omega }_{3}}{{({{\tilde{F}}^{\text{en}}})}^{-1}})$
|
(58) |
以上各式中,类比于式(3)和式(4)对总体变形率张量${ D}$和涡旋张量${
W}$的定义,以上各张量定义如下
$\eqalign{
& {D^{\text{p}}} = {\text{sym}}({{\dot F}^{\text{p}}}{({F^{\text{p}}})^{ - 1}}),{W^{\text{p}}} = {\text{skw}}({{\dot F}^{\text{p}}}{({F^{\text{p}}})^{ - 1}}) \cr
& {D^{{\text{dis}}}} = {\text{sym}}({{\dot F}^{{\text{dis}}}}{({F^{{\text{dis}}}})^{ - 1}}),X{W^{{\text{dis}}}} = {\text{skw}}({{\dot F}^{{\text{dis}}}}{({F^{{\text{dis}}}})^{ - 1}}) \cr
& {D^{\text{e}}} = {\text{sym}}({{\dot F}^{\text{e}}}{({F^{\text{e}}})^{ - 1}}),{W^{\text{e}}} = {\text{skw}}({{\dot F}^{\text{e}}}{({F^{\text{e}}})^{ - 1}}) \cr
& {D^{{\text{en}}}} = {\text{sym}}({{\dot F}^{{\text{en}}}}{({F^{{\text{en}}}})^{ - 1}}),{W^{{\text{en}}}} = {\text{skw}}({{\dot F}^{{\text{en}}}}{({F^{{\text{en}}}})^{ - 1}}) \cr} $
以上各式中,运算符"sym( )"和"skw( )"分别表示对括号中的二阶张量去对称运算和反对称运算.
3.2 两点客观性、Truesdell客观性与Hill客观性
观察以上转换关系式(35) $\sim$式(44),式(49) $\sim$式(58),根据其转换特征可将其分为5类:
(1) 转换关系 $\mathop { A}\limits^{\sim} = ({ Q}_i { Q}_j )_\ast ^\ast { A}$,其中$i$,$j
=0$,1,2,3,且
$i \ne j,{Q_0} = {\bf{1}}$
满足上述转换关系的二阶张量具有两点客观性,易知这类张量是定义在两个不同构型中. 式(35)$\sim$式(39)中的各梯度张量均为两点客观张量,且定义在不同的构型中,如变形梯度张量${
F}$是定义在初始构型和当前构型中的两点客观张量(见式(35)),而其弹性分量${ F}^{\rm
e}$则是定义在当前构型和卸载构型中的两点客观张量(见式(38)).
(2) 转换关系$\mathop A\limits^{\sim }= ({ Q}_i { Q}_i )_\ast ^\ast { A}$,其中$i =1,2,3$
满足上述转换关系的二阶张量具有Truesdell客观性. 式(40a) $\sim$式(42a),式(43) $\sim$式(44)以及式(49),式(51)和式(53)中的二阶张量均为Truesdell客观张量.易知,Truesdell客观张量是定义在单一构型中的客观张量,如二阶张量${ B}$,${ B}^{\rm e}$和${
D}$是定义在当前构型中的客观张量(见式(40a),式(43a)和式(49)),${ C}^{\rm e}$,${ B}^{\rm p}$,${
B}^{\rm en}$和${ D}^{\rm p}$是定义在卸载构型中的客观张量(见式(43b),式(41a),式(44a)和式(51)),而${
C}^{\rm en}$,${ B}^{\rm dis}$和${ D}^{\rm dis}$
则是定义在随动硬化中间构型中的客观张量(见式(44b),式(42a)和式(53)).
(3) 转换关系$ \tilde{ A} = { A}$
称满足上述转换关系的二阶张量具有Hill客观性. 式(40b) $\sim$式(42b)中的二阶张量(${ C}$,${ C}^{\rm
p}$和${ C}^{\rm dis}$)均为Hill客观张量,易知,Hill客观张量是定义在初始构型中的客观张量.
(4) 转换关系$\mathop A\limits^{\sim }=( { Q}_i { Q}_i)_\ast ^\ast { A} + { \Omega }_i $,其中$i =1,2,3$
满足这类转换关系的二阶张量通常情况下均为速度梯度张量或涡旋张量,它们定义在单一构型中却不具备任何客观性,如${
L}$,${ L}^{\rm p}$和${ L}^{\rm dis}$以及${ W}$(式(50)),${ W}^{\rm p}$(式(52))和${
W}^{\rm dis}$ (式(54)).然而这类涡旋张量与Truesdell客观张量的物质导数进行适当的代数运算能构建出满足Truesdell客观性的二阶张量(如次弹性本构关系中常用的客观共旋率张量),即若${
X}$满足转换关系(2),${ Y}$和${ Z}$满足转换关系(4),它们是定义在同一构型中的二阶张量,而张量${
H}$与张量 ${ X}$,${ Y}$,${ Z}$满足如下关系
|
$H=\dot{X}-(Y\mathbf{1})_{*}^{*}X-(\mathbf{1}Z)_{*}^{*}X$
|
(59) |
则张量${ H}$满足转换关系(2).
上述定理的证明很简单,根据式(59)可知
|
$\tilde{H}=\dot{\tilde{X}}-(\tilde{Y}\mathbf{1})_{*}^{*}\tilde{X}-(\mathbf{1}\tilde{Z})_{*}^{*}\tilde{X}\text{ }$
|
(60) |
将张量${ X}$的转换关系$\tilde{ X}= ({ Q}_{\underline i } { Q}_{\underline i } )_\ast ^\ast
{ X}$ 以及${ Y}$ 和${ Z}$的转换关系$\tilde{ A} ({ Q}_{\underline i } { Q}_{\underline
i } )_\ast ^\ast A + {\Omega }_i $ (${ A}$取${ Y}$或${ Z}$)代入式(60),并利用关系式$\dot{ Q}_i ={ \Omega }_i { Q}_i $,很容易得出
|
$\tilde{H}=({{Q}_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}}{{Q}_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}})_{*}^{*}H$
|
(61) |
故二阶张量${ H}$为Truesdell客观张量. 当${ Y}$与${ Z}$取相同的涡旋张量时(${
W}$或其他旋率张量,如 ${ W}^{\rm R} = \dot { R} { R}^{\rm T}$或著名的对数旋率张量 ${
W}^{\log }$等),称张量${ H}$为张量 ${ X}$的客观共旋率.
(5) 其他转换关系
由式(55) $\sim$式(58)可知,其中的张量${ D}^{\rm e}$,${ W}^{\rm e}$,${ D}^{\rm en}$和${
W}^{\rm
en}$均是定义在两个构型中的两点张量,不具备任何客观性,但是若限定叠加在某些构型上的刚性转动形式,如对于二阶张量${
D}^{\rm en}$ 和${ W}^{\rm en}$,限定叠加在随动硬化构型上的刚性转动${ Q}_{3}(t)$为常量,即${
Q}_{3}(t) = { Q}_{0}$,${ \Omega }_{3}={\bf 0}$,则式(57)退化为转换关系(2),${ D}^{\rm
en}$退化为Truesdell客观张量,而式(58)则退化为转换关系(4),${ W}^{\rm en}$则满足通常的涡旋张量转换关系式.类似的情况同样适用于二阶张量 ${ D}^{\rm e}$和${ W}^{\rm e}$.
4 本构理论
适用于大变形领域的材料本构模型的发展必须以热动力学理论为基础,并结合适当的变形运动学假定. 变形梯度的乘法分解定理以及Lion的塑性变形分解理论由于其直观的现象学定义以及合理的材料微观解释而被广泛接受. 但由于变形梯度乘法分解理论的复杂性以及热动力学方面的限制,将一些适用于小变形情况下的变形假定或本构关系推广到大变形领域时,会面临许多理论上的困难. 下文将在大变形理论框架下发展一类严格满足热力学理论的本构模型,其考虑了材料的随动硬化和各项同性硬化,尤其是可以融合多种适用于小变形理论中的经典的随动硬化法则.
4.1 热力学第二定律
热力学第二定律又称为熵增定律或 Clausius-Duhem
(C-D)不等式,其反映了材料体在变形过程中宏观物理现象的不可逆性.若假定材料体的变形过程是一个等温绝热过程,则热力学第二定律可简单的表示为
|
$\tau :D-\dot{\psi }\text{ }\ge 0$
|
(62) |
上式中个符号意义同前. 若单位参考构型体积的Hemholz自由能 $\psi $具有式(27)的形式,则
|
$\dot{\psi }=\frac{\partial {{\psi }^{\text{e}}}}{\partial {{B}^{\text{e}}}}:{{\dot{B}}^{\text{e}}}+\sum\limits_{i=1}^{M}{\frac{\partial \psi _{i}^{\text{en}}}{\partial B_{i}^{\text{en}}}}:\dot{B}_{i}^{\text{en}}\text{ }$
|
(63) |
由式(18)易知
|
${{\dot{B}}^{\text{e}}}={{L}^{\text{e}}}{{B}^{\text{e}}}+{{({{B}^{\text{e}}}{{L}^{\text{e}}})}^{\text{T}}}\text{ }$
|
(64) |
由此可知
|
$\frac{\partial {{\psi }^{\text{e}}}}{\partial {{B}^{\text{e}}}}:{{\dot{B}}^{\text{e}}}=({{B}^{\text{e}}}\frac{\partial {{\psi }^{\text{e}}}}{\partial {{B}^{\text{e}}}}+\frac{\partial {{\psi }^{\text{e}}}}{\partial {{B}^{\text{e}}}}{{B}^{\text{e}}}):{{L}^{\text{e}}}$
|
(65) |
本文只考虑各向同性材料,故上式可写为
|
$\frac{\partial {{\psi }^{\text{e}}}}{\partial {{B}^{\text{e}}}}:{{\dot{B}}^{\text{e}}}=(2\frac{\partial {{\psi }^{\text{e}}}}{\partial {{B}^{\text{e}}}}{{B}^{\text{e}}}):{{D}^{\text{e}}}$
|
(66) |
同理可得
|
$\frac{\partial \psi _{i}^{\text{en}}}{\partial B_{i}^{\text{en}}}:\dot{B}_{i}^{\text{en}}=(2\frac{\partial \psi _{i}^{\text{en}}}{\partial B_{i}^{\text{en}}}B_{i}^{\text{en}}):D_{i}^{\text{en}}$
|
(67) |
考虑到塑性变形无体积变化($\det { F}_i^{\rm en} = \det { F}_i^{\rm dis} =
1$,$i = 1,2,\cdots,M$),可得
|
$\text{tr}{{D}^{\text{p}}}=\text{tr}D_{i}^{\text{en}}=\text{tr}D_{i}^{\text{dis}}=0\text{ }$
|
(68) |
故变形率张量${ D}^{\rm p}$,
${ D}_i^{\rm en}$ 及
${ D}_i^{\rm dis} $均为偏量,结合
${ D}_i^{\rm en} $的偏量性质及背应力
${ S}_i^{\rm en}$的定义式(28),式(67)可重新写为
|
$\begin{align}
& \frac{\partial \psi _{i}^{\text{en}}}{\partial B_{i}^{\text{en}}}:\dot{B}_{i}^{\text{en}}=\text{sy}{{\text{m}}_{0}}(2\frac{\partial \psi _{i}^{\text{en}}}{\partial B_{i}^{\text{en}}}B_{i}^{\text{en}}):D_{i}^{\text{en}}= \\
& S_{i}^{\text{en}}:D_{i}^{\text{en}} \\
\end{align}$
|
(69) |
将式(66)和式(69)代入式(63),可得
|
$\dot{\psi }=(2\frac{\partial {{\psi }^{\text{e}}}}{\partial {{B}^{\text{e}}}}{{B}^{\text{e}}}):{{D}^{\text{e}}}+\sum\limits_{i=1}^{M}{S_{i}^{\text{en}}}:D_{i}^{\text{en}}$
|
(70) |
将式(32)和式(70)代入式(62),则热力学第二定律的表达式变为
$$
|
$\begin{align}
& (\tau -2\frac{\partial {{\psi }^{\text{e}}}}{\partial {{B}^{\text{e}}}}{{B}^{\text{e}}}):{{D}^{\text{e}}}+({{M}^{\text{e}}}-{{S}^{\text{en}}}):{{L}^{\text{p}}}+ \\
& \sum\limits_{i=1}^{M}{M_{i}^{\text{en}}}:L_{i}^{\text{dis}}\ge 0 \\
\end{align}$
|
(71) |
上式对于任意加卸载过程均成立,若假定材料点经历弹性卸载过程:
$({ D} ={ D}^{\rm e})$,则上式退化为
|
$(\tau -2\frac{\partial {{\psi }^{\text{e}}}}{\partial {{B}^{\text{e}}}}{{B}^{\text{e}}}):D\text{ }\ge 0$
|
(72) |
式(72)对任意的弹性卸载变形率张量${ D}$均成立,而上式左端括号内的二阶张量为状态量,故可得材料的超弹性本构关系
|
$\tau =2\frac{\partial {{\psi }^{\text{e}}}}{\partial {{B}^{\text{e}}}}{{B}^{\text{e}}}$
|
(73) |
由上式以及式(28)可知,Kirchhoff应力张量${ \tau }$以及背应力偏量${ S}_i^{\rm en} $分别为变形张量${ B}^{\rm e}$和${ B}_i^{\rm
en}$的各向同性张量函数,故结合Mandel应力的表达式(33)和式(34)易知,${ M}^{\rm e}$与 ${ M}_i ^{\rm
en}$均为对称张量,而由${ S}_i^{\rm en}$ 的偏量性质进一步可推得塑性Mandel应力${ M}_i ^{\rm
en}$也为偏量.
将式(73)代入式(71),并结合Mandel应力的对称性以及 ${ D}^{\rm p}$和${ D}_i^{\rm dis} $的偏量性,式
(71)可重新写为
|
$(M_{0}^{\text{e}}-{{S}^{\text{en}}}):{{D}^{\text{p}}}+\sum\limits_{i=1}^{M}{M_{i}^{\text{en}}}:D_{i}^{\text{dis}}\text{ }\ge 0$
|
(74) |
上式又称为内耗不等式,${ M}_0 ^{\rm e}$表示为Mandel应力
${ M}^{\rm e}$的偏量部分. 材料的流动法则及随动硬化法则均根据内耗不等式 (74)进行构建.
4.2 流动法则与随动硬化法则
为了满足内耗不等式(74),通常情况下需要做出更强的假定,即
|
$(M_{0}^{\text{e}}-{{S}^{\text{en}}}):{{D}^{\text{p}}}\ge 0$
|
(75) |
|
$M_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{\text{en}}:D_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{\text{dis}}\ge 0,i=1,2,\cdots ,M$
|
(76) |
现引入文献[25]关于耗散共轭对、演化项和驱动力的概念. 观察两个耗散项(75)和(76),二者在形式上均为状态张量与变形率张量的内积,以塑性耗散部分$ ({ M}_0^{\rm e}
- { S}^{\rm en}):{ D}^{\rm p}$为例,现形象地将状态张量
$({ M}_0^{\rm e} - { S}^{\rm
en}$)称为驱动力,意为其为引起耗散的"不平衡力",而产生的塑性变形率${ D}^{\rm
p}$称为演化项,意为驱动力驱使其朝某个方向演化,二者共同构成一对耗散共轭对,相同地概念同样应用于式(76).为了满足其内积非负,最自然、简单的做法便是假定演化项是沿着驱动力方向演化的,因此流动法则为
|
${{D}^{\text{p}}}=\sqrt{\frac{3}{2}}{{\dot{\kappa }}^{\text{p}}}\frac{M_{0}^{\text{e}}-{{S}^{\text{en}}}}{\left\| M_{0}^{\text{e}}-{{S}^{\text{en}}} \right\|}$
|
(77a) |
|
$\left\| M_{0}^{\text{e}}-{{S}^{\text{en}}} \right\|=\sqrt{(M_{0}^{\text{e}}-{{S}^{\text{en}}}):(M_{0}^{\text{e}}-{{S}^{\text{en}}})}$
|
(77b) |
式中,$\dot {\kappa }^{\rm p} ≥ 0$,称其为塑性乘子,其确定需要用到一致性条件(又称为
Kuhn-Tucker条件).式(76)对应的便是随动硬化法则,为了将小变形情况下的经典随动硬化法则推广到大变形情况,需要对叠加在随动硬化中间构型上的刚性转动张量${
Q}_{3}(t)$(见前文第3节)作适当的限制,现以小变形理论中常用的K-$\!$O随动硬化法则为例进行说明
$$
|
$\begin{align}
& \alpha =\sum\limits_{i=1}^{M}{{{\alpha }_{i}}} \\
& {{{\dot{\alpha }}}_{i}}=\frac{2}{3}{{r}_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}}{{\gamma }_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}}{{D}^{\text{p}}}-\left[{{\mu }_{i}}{{{\dot{\kappa }}}^{\text{p}}}+\left\langle {{{\dot{\lambda }}}_{i}} \right\rangle \cdot H\left( \frac{3}{2}{{\alpha }_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}}:{{\alpha }_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}}-r_{i}^{2} \right) \right]{{\gamma }_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}}{{\alpha }_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}} \\
\end{align}$
|
(78) |
式中,$\mu_i,\gamma_i$和$r_i$
均为材料常数,${ \alpha }$为总的背应力偏量,其可以表示为多个背应力分量
${\alpha }_i $之和,$\dot {\lambda }_i = \left( {\dfrac{{ D}^{\rm p}}{\left\| {{ D}^{\rm p}}
\right\|}:\dfrac{ {\alpha }_i }{\left\| { {\alpha }_i } \right\|} - \mu _i } \right)\dot {\kappa
}^{\rm p}$,MacCauley 运算符: $\left\langle y \right\rangle = \dfrac{\left| y \right| + y}{2}$,
Heaviside 阶跃函数$H(x)$定义如下
|
$H(x)=\left\{ \begin{align}
& 1,x\ge 0 \\
& 0,x<0 \\
\end{align} \right.$
|
(79) |
在小变形理论中,由于忽略了不同构型之间的异同,可直接引入背应力的概念以描述材料的随动硬化,然而,在大变形理论中,特别是引入了Lion塑性变形分解理论中随动硬化中间构型的概念,背应力则必须与相应的塑性变形联系起来(如式(28)),而背应力的率则应替换为相应的塑性变形率张量${ D}_{i}^{\rm en}
$,因此,K-O随动硬化法则在大变形理论中的示意形式应为
|
${{k}_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}}D_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{\text{en}}={{C}_{i}}{{D}^{\text{p}}}-{{\dot{\kappa }}^{\text{p}}}{{S}_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}}\left( {{D}^{\text{p}}},B_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{\text{en}} \right)\text{ }$
|
(80) |
式中,$k_{i }$ 与$C_i $可看作材料常数,${ S}_{i } \left( {{ D}^{\rm p},{ B}_{i}^{\rm en} }
\right)$为${ D}^{\rm p}$和${ B}_{i}^{\rm en}$ 的各向同性张量函数. 式
(80)仅为K-O随动硬化法则在大变形问题中的示意形式,其具体的解析表达式后文会给出.由前文3.2节的分析可知,二阶张量 ${ D}^{\rm p}$,${ S}_{i} \left( {{ D}^{\rm p},{ B}_{i}^{\rm
en} } \right)$均为定义在卸载构型中的Truesdell客观张量,满足转换关系 (2);而二阶张量 ${ D}_{i}^{\rm en}$
则为定义在随动硬化构型和卸载构型中的两点张量,其满足转换关系 (5)且不具备任何客观性,故在不对随动硬化中间构型加以限制的情况下,式(80)由于不满足标架不变性(或客观性)而不可能成立. 因此,为了使小变形随动硬化理论顺利推广应用到大变形领域,现规定所有随动硬化中间构型的涡旋张量均为${\bf 0}$,即
|
$W_{i}^{\text{dis}}=\mathbf{0},i=1,2,\cdots ,M$
|
(81) |
由转换关系式(54)可知,欲使式(81)对所有的等价运动过程均成立,叠加在随动硬化构型上的转动张量 ${
Q}_{3}(t)$旋率必须为 {\bf 0},即${ \Omega }_{3}= {\bf 0}$,因此 ${ Q}_{3}(t)$应为常张量,即${
Q}_{3}(t)= { Q}_{0}$;由3.2节的分析可知,变形率张量${ D}_{i}^{\rm en}
$满足转换关系(2),退化为定义在卸载构型中的Truesdell客观张量,此时,式(80)满足标架不变性,其可作为大变形理论中的本构方程以描述材料的随动硬化特征. 在后文的分析中,均假定式(81)成立,将其代入到式(23)中可得
|
${{L}^{\text{p}}}=L_{i}^{\text{en}}+F_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{\text{en}}D_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{\text{dis}}{{(F_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{\text{en}})}^{-1}}$
|
(82) |
现讨论式(80)的具体解析表达式,为了满足耗散不等式(76),现假定变形率张量 ${ D}_i^{\rm dis} $的演化方程为
|
$D_{i}^{\text{dis}}=\frac{3}{2}\left[{{\mu }_{i}}{{{\dot{\kappa }}}^{\text{p}}}+\left\langle {{{\dot{\lambda }}}_{i}} \right\rangle \cdot H\left( \frac{3}{2}M_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{\text{en}}:{{(M_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{\text{en}})}^{\text{T}}}-r_{i}^{2} \right) \right]\frac{M_{i}^{\text{en}}}{{{r}_{i}}}$
|
(83) |
式中,$ \dot {\lambda }_i = \left( {\dfrac{{ D}^{\rm p}}{\left\| {{ D}^{\rm p}}
\right\|}:\dfrac{{ S}_i^{\rm en} }{\left\| {{ S}_i^{\rm en} } \right\|} - \mu_i } \right) \dot
{\kappa }^{\rm p}$,其余符号意义同前. 由式(83)可推得二阶张量 ${ F}_{\underline i}^{\rm en} {
D}_{\underline i}^{\rm dis} ({ F}_{\underline i}^{\rm en})^{ - 1}$ 的表达式如下
|
$\begin{align}
& F_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{\text{en}}D_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{\text{dis}}{{(F_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{\text{en}})}^{-1}}=\frac{3}{2}[{{\mu }_{i}}{{{\dot{\kappa }}}^{\text{p}}}+\left\langle {{{\dot{\lambda }}}_{i}} \right\rangle \cdot \\
& H\left( \frac{3}{2}S_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{\text{en}}:S_{\text{i}}^{\text{en}}-r_{i}^{2} \right)]\frac{B_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{\text{en}}S_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{\text{en}}{{(B_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{\text{en}})}^{-1}}}{{{r}_{i}}} \\
\end{align}$
|
(84) |
由于背应力分量${ S}_i^{\rm en} $是
${ B}_i^{\rm en}$ 的各向同性张量函数,故上式又可进一步写为
|
$\begin{align}
& F_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{\text{en}}D_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{\text{dis}}{{(F_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{\text{en}})}^{-1}}=\frac{3}{2}[{{\mu }_{i}}{{{\dot{\kappa }}}^{\text{p}}}+\left\langle {{{\dot{\lambda }}}_{i}} \right\rangle \cdot \\
& H\left( \frac{3}{2}S_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{\text{en}}:S_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{\text{en}}-r_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{2} \right)]\frac{S_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{\text{en}}}{{{r}_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}}} \\
\end{align}$
|
(85) |
由此可知,二阶张量
${ F}_{\underline i}^{\rm en} { D}_{\underline i}^{\rm dis} ({ F}_{\underline i}^{\rm en})^{ - 1}$
为对称张量,将上式代入式 (82),并经过简单的代数整理可得
|
$\begin{align}
& \frac{2}{3}{{r}_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}}{{\gamma }_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}}D_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{\text{en}}=\frac{2}{3}{{r}_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}}{{\gamma }_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}}{{D}^{\text{p}}}-[{{\mu }_{i}}{{{\dot{\kappa }}}^{\text{p}}}+\left\langle {{{\dot{\lambda }}}_{i}} \right\rangle \cdot \\
& H\left( \frac{3}{2}S_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{\text{en}}:S_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{\text{en}}-r_{i}^{2} \right)]{{\gamma }_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}}S_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{\text{en}}85 \\
\end{align}$
|
(85) |
上式便为K-O随动硬化法则在大变形问题中的表达式. 应注意,上式的得出需要利用式(82),而式(82)是假定随动硬化中间构型涡旋张量为 {\bf 0}(式(81))的直接结果.
将式(85)与小变形理论中的表达式(78)进行对比,式(85)等号左端的 $\dfrac{2}{3}r_{\underline i} \gamma
_{\underline i} { D}_{\underline i}^{\rm en} $是否可以写成背应力偏量
${ S}_i^{\rm en}$ 的某种客观导数?为了论述这一问题,现引入 Hencky 对数应变
|
$h_{i}^{\text{en}}=\frac{1}{2}\ln B_{i}^{\text{en}}\text{ }$
|
(86) |
考虑到塑性变形无体积变化($
\det { F}_i^{\rm en} = \det { F}_i^{\rm dis} = 1$,$i =1,2,\cdots ,M $),
对数应变${ h}_i^{\rm en}$ 应为偏量,即
|
$\text{tr}h_{i}^{\text{en}}=0\text{ }$
|
(87) |
现将经典的小变形各向同性情况下经典的Hemholz自由能 $\psi _i^{\rm en}$的表达形式推广应用到本文模型,即假定 $
\psi _i^{\rm en}$ 具有如下形式
$$
\psi _i^{\rm en} ({ B}_{ i}^{\rm en} ) = \dfrac{1}{3}r_{ \underline i} \gamma _{\underline i} \left\|
{({ h}_i^{\rm en} )_0 } \right\|^2 + \dfrac{1}{2}K \cdot ( {\rm tr}{ h}_i^{\rm en} )^2
$$
式中,$\dfrac{1}{3}r_{\underline i} \gamma _{\underline i}$为剪切模量,而$K$为体积模量,$({ h}_i^{\rm en} )_0 $表示为
${ h}^{\rm en} $的偏量,将式 (87)代入上式,得到
$\psi _i^{\rm en} $的最终表达式
|
$\psi _{i}^{\text{en}}(B_{i}^{\text{en}})=\frac{1}{3}{{r}_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}}{{\gamma }_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}}{{\left\| h_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{\text{en}} \right\|}^{2}}$
|
(88) |
将其代入${ S}_i^{\rm en} $的表达式 (28)可得
|
$S_{i}^{\text{en}}=\frac{2}{3}{{r}_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}}{{\gamma }_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}}h_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{\text{en}}\text{ }$
|
(89) |
而Hencky对数应变的对数共旋率等于变形率张量,即
|
${{(\overset{.}{\mathop{\overline{h_{i}^{\text{en}}}}}\,)}^{\log }}=D_{i}^{\text{en}}\text{ }$
|
(90) |
式中,$( \dot{\overline{ { h}_i^{\rm en}}} )^{\log }$代表Hencky对数应变的对数共旋率,其表达式为
|
${{(\overset{.}{\mathop{\overline{h_{i}^{\text{en}}}}}\,)}^{\log }}=\overset{.}{\mathop{\overline{h_{i}^{\text{en}}}}}\,-\Omega _{i}^{\log }h_{i}^{\text{en}}+h_{i}^{\text{en}}\Omega _{i}^{\log }$
|
(91) |
对数旋率${\Omega }_i^{\log } $的表达式为
|
$\Omega _{i}^{\log }=W_{i}^{\text{en}}+N_{i}^{\log }$
|
(92) |
式中,涡旋张量${ W}_i^{\rm en}$ 其实与塑性旋率${ W}^{\rm p}$相等,这一结论可由式 (82)得出. 对式(82)两端取反对称运算,结合二阶张量$ { F}_{\underline i}^{\rm en} { D}_{\underline i}^{\rm dis}
({ F}_{\underline i}^{\rm en})^{-1}$的对称性,便可得出
|
${{W}^{p}}=W_{i}^{\text{en}},i=1,2,\cdots ,M\text{ }$
|
(93) |
于是式(92)便可重新写为
|
$\Omega _{i}^{\log }={{W}^{\text{p}}}+N_{i}^{\log }$
|
(94) |
${ N}_i^{\log } $的表达式如下
|
$N_{i}^{\log }=\left\{ \begin{align}
& \mathbf{0},{{b}_{1}}={{b}_{2}}={{b}_{3}} \\
& \nu \left[B_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{\text{en}}D_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{\text{en}} \right],{{b}_{1}}e{{b}_{2}}={{b}_{3}} \\
& {{\nu }_{1}}\left[B_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{\text{en}}D_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{\text{en}} \right]+{{\nu }_{2}}\left[{{(B_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{\text{en}})}^{2}}D_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{\text{en}} \right]+ \\
& {{\nu }_{3}}\left[{{(B_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{\text{en}})}^{2}}D_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{\text{en}}B_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{\text{en}} \right],{{b}_{1}}\ne {{b}_{2}}\ne {{b}_{3}}\ne {{b}_{1}} \\
\end{align} \right.$
|
(95) |
式中,$b_1$,$b_2$ 和$b_3 $为变形张量$ { B}_{\underline i }^{\rm en} $的3个非零特征值,且
$\begin{align}
& \left[A \right]=2skw(A) \\
& \nu =\frac{1}{{{b}_{1}}-{{b}_{2}}}\left[\frac{1+{{b}_{1}}/{{b}_{2}}}{1-{{b}_{1}}/{{b}_{2}}}+\frac{2}{\ln ({{b}_{1}}/{{b}_{2}})} \right] \\
& {{\nu }_{k}}=\frac{1}{\Delta }\sum\limits_{i=1}^{3}{{{(-{{b}_{i}})}^{3-k}}}\left( \frac{1+{{\varepsilon }_{i}}}{1-{{\varepsilon }_{i}}}+\frac{2}{\ln {{\varepsilon }_{i}}} \right),k=1,2,3 \\
& {{\varepsilon }_{1}}={{b}_{2}}/{{b}_{3}},{{\varepsilon }_{2}}={{b}_{3}}/{{b}_{1}},{{\varepsilon }_{3}}={{b}_{1}}/{{b}_{2}} \\
& \Delta =({{b}_{1}}-{{b}_{2}})({{b}_{2}}-{{b}_{3}})({{b}_{3}}-{{b}_{1}}) \\
\end{align}$
由式(89)和式(90),可知
|
${{(\overset{.}{\mathop{\overline{S_{i}^{\text{en}}}}}\,)}^{\log }}=\frac{2}{3}{{r}_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}}{{\gamma }_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}}{{(\dot{h}_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{\text{en}})}^{\log }}=\frac{2}{3}{{r}_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}}{{\gamma }_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}}D_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{\text{en}}$
|
(96) |
将上式代入式(85),便可得到大变形理论中的K-O随动硬化法则
|
$\begin{align}
& {{(\overset{.}{\mathop{\overline{S_{i}^{\text{en}}}}}\,)}^{\log }}=\frac{2}{3}{{r}_{\underset{-}{\mathop{i}}\,}}{{\gamma }_{\underset{-}{\mathop{i}}\,}}{{D}^{\text{p}}}-\left[{{\mu }_{i}}{{{\dot{\kappa }}}^{\text{p}}}+\left\langle {{{\dot{\lambda }}}_{i}} \right\rangle \cdot \right. \\
& \left. H\left( \frac{3}{2}S_{\underset{-}{\mathop{i}}\,}^{\text{en}}:S_{\underset{-}{\mathop{i}}\,}^{\text{en}}-r_{i}^{2} \right) \right]{{\gamma }_{\underset{-}{\mathop{i}}\,}}S_{\underset{-}{\mathop{i}}\,}^{\text{en}} \\
\end{align}$
|
(97) |
由此可知,合理地选择Hemholz自由能塑性分量部分 $\psi _i^{\rm en} $ 的表达形式(式
(88)),可以使大变形和小变形问题中的K-O随动硬化法则在形式上完全对等(对比式(97)和式(78)).
同理,若假定变形率张量 ${ D}_i^{\rm dis} $
的演化方程为其它形式,则经过相同的推演过程,便可得到其它随动硬化法则在大变形问题中的表达形式,下文将分别简述四类经典随动硬化模型的结果.
(1) A-F随动硬化法则
若假定背应力分支总数$M
=1$,则拓展的Lion塑性变形分解定理退化为原有的Lion变形梯度分解定理,此时假定变形率张量${ D}^{\rm
dis}$的演化方程为
|
${{D}^{\text{dis}}}=\frac{3}{2}{{\dot{\kappa }}^{\text{p}}}\frac{{{M}^{\text{en}}}}{r}$
|
(98) |
最终的随动硬化法则为
|
${{(\overset{.}{\mathop{\overline{{{S}^{\text{en}}}}}}\,)}^{\log }}=\frac{2}{3}r\gamma {{D}^{\text{p}}}-{{\dot{\kappa }}^{\text{p}}}\gamma {{S}^{\text{en}}}$
|
(99) |
在一维应力加载情况下,A-F随动硬化法则预测的每一次正反向循环加载的应力应变非闭合环的形状完全相同,意味着轴向平均塑性应变随着循环次数的增加以恒定的率增长,也就是说采用阿姆斯特朗-弗雷德里克模型模拟材料的单轴棘轮效应时,棘轮应变会以恒定的棘轮率增长,从而过度预测了材料的轴向应变响应[18].为了改善模拟结果,很多模型都是在A-F模型的基础上做适当改进而得到的.
(2) Chaboche随动硬化法则
若单纯从形式上讲,Chaboche随动硬化法则与A-F随动硬化法则并无本质上的区别,只是Chaboche模型中背应力分支总数取为$M =3$. 即
|
$D_{i}^{\text{dis}}=\frac{3}{2}{{\dot{\kappa }}^{\text{p}}}\frac{M_{i}^{\text{en}}}{{{r}_{i}}},i=1,2,3$
|
(100) |
最终的随动硬化法则为
|
${{(\overset{.}{\mathop{\overline{S_{i}^{\text{en}}}}}\,)}^{\log }}=\frac{2}{3}{{r}_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}}{{\gamma }_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}}{{D}^{\text{p}}}-{{\dot{\kappa }}^{\text{p}}}{{\gamma }_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}}S_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{\text{en}},i=1,2,3$
|
(101) |
实际上,在小变形理论中,Chaboche模型的三组材料参数$r_{i}$与$\gamma _{ i }$
是根据材料的单轴拉压滞回曲线决定的,背应力的每一个分支负责模拟滞回曲线的不同区间[26].
(3) O-W随动硬化法则-初始模型
若假定变形率张量${ D}_i^{\rm dis} $的演化方程为
|
$\begin{align}
& D_{i}^{\text{dis}}=\frac{3}{2}{{{\dot{\kappa }}}^{\text{p}}}\cdot \left\langle \frac{{{D}^{\text{p}}}}{\left\| {{D}^{\text{p}}} \right\|}:\frac{S_{i}^{\text{en}}}{\left\| S_{i}^{\text{en}} \right\|} \right\rangle \cdot \\
& H\left( \frac{3}{2}M_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{\text{en}}:{{(M_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{\text{en}})}^{\text{T}}}-r_{i}^{2} \right)\frac{M_{i}^{\text{en}}}{{{r}_{i}}} \\
\end{align}$
|
(102) |
则最终的随动硬化法则为
|
$\begin{align}
& {{(\overset{.}{\mathop{\overline{S_{i}^{\text{en}}}}}\,)}^{\log }}=\frac{2}{3}{{r}_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}}{{\gamma }_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}}{{D}^{\text{p}}}-{{{\dot{\kappa }}}^{\text{p}}}\cdot \left\langle \frac{{{D}^{\text{p}}}}{\left\| {{D}^{\text{p}}} \right\|}:\frac{S_{i}^{\text{en}}}{\left\| S_{i}^{\text{en}} \right\|} \right\rangle \cdot \\
& H\left( \frac{3}{2}S_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{\text{en}}:S_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{\text{en}}-r_{i}^{2} \right){{\gamma }_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}}S_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{\text{en}} \\
\end{align}$
|
(103) |
可以证明,O-W随动硬化模型的构造方式使得背应力分量 ${ S}_i^{\rm en}$ 在临界面: $f\left( {{
S}_i^{\rm en} } \right) = \dfrac{3}{2}{ S}_{\underline i }^{\rm en} :{ S}_{\underline i }^{\rm en} -
r_i^2 ≤ 0$内部演化,其演化方向与塑性应变率之间的夹角保持为锐角,即:
$( \dot {\overline{{ S}_i^{\rm en}}} )^{\log }:{ D}^p ≥ 0$
(A-F模型也满足此条件).在一维应力加载条件下,若忽略材料的各向同性硬化,O-W随动硬化模型退化为多线性模型,导致其预测的单轴应力滞回环闭合,因此,材料不会产生任何单轴棘轮效应[26]。
(4) O-W随动硬化法则-修正模型
为了更好地模拟材料的循环塑性,文献[13] 对模型做了修正,引入了非线性项,而反映到大变形理论中,即将式(102)修改为
|
$\begin{align}
& D_{i}^{\text{dis}}=\frac{3}{2}{{{\dot{\kappa }}}^{\text{p}}}\cdot \left\langle \frac{{{D}^{\text{p}}}}{\left\| {{D}^{\text{p}}} \right\|}:\frac{S_{i}^{\text{en}}}{\left\| S_{i}^{\text{en}} \right\|} \right\rangle \cdot \\
& {{(\frac{\sqrt{\frac{3}{2}M_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{\text{en}}:{{(M_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{\text{en}})}^{\text{T}}}}}{{{r}_{i}}})}^{{{m}_{i}}}}\frac{M_{i}^{\text{en}}}{{{r}_{i}}} \\
\end{align}$
|
(104) |
式中,$m_i > 0$,为材料常数,最终的随动硬化法则为
|
$\begin{align}
& {{(\overset{.}{\mathop{\overline{S_{i}^{\text{en}}}}}\,)}^{\log }}=\frac{2}{3}{{r}_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}}{{\gamma }_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}}{{D}^{\text{p}}}- \\
& {{{\dot{\kappa }}}^{\text{p}}}\cdot \left\langle \frac{{{D}^{\text{p}}}}{\left\| {{D}^{\text{p}}} \right\|}:\frac{S_{i}^{\text{en}}}{\left\| S_{i}^{\text{en}} \right\|} \right\rangle {{(\frac{\sqrt{\frac{3}{2}S_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{\text{en}}:S_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{\text{en}}}}{{{r}_{i}}})}^{{{m}_{i}}}}{{\gamma }_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}}S_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{\text{en}} \\
\end{align}$
|
(105) |
对比式(103)与(105),通过将Heaviside阶跃函数替换为一个$m_i $
次的乘子,使方程由多线性变为非线性,阻止了一维加载情况下应力控制滞回环的闭合,从而产生轴向棘轮应变,故材料系数
$m_i $
在一定程度上反映了应力控制滞回环的钢化程度,其值越小,滞回环越
"柔",棘轮现象相对明显;反之,滞回环越"刚",棘轮现象相对弱化,因此,通过适当选取材料参数
$m_i$,可使单轴棘轮模拟结果尽可能地逼近实验结果[13, 25].
4.3 屈服面方程
屈服面方程可用标量函数$f$表示,是材料在变形过程中的弹性边界,屈服面的演化可以看作是材料微观结构发生变化的宏观表现,其演化过程的描述是一个非常复杂的问题------既包含材料的各向同性硬化(屈服面的膨胀或收缩),又伴随着非各向同性硬化(屈服面的平移、扭转). 目前,最简单也是最常用的描述屈服面各向同性硬化的方法是引入标量内变量$\sigma
_{\rm y} $,利用$\sigma _{\rm y} $
的演化过程来反映屈服面大小的变化;而屈服面的非各向同性硬化则只考虑其平移------即随动硬化部分,其描述只需通过前文背应力张量
${ S}^{\rm en}$(式 (29))的变化来反映屈服面中心位置的变化. 这种通过各向同性硬化和随动硬化来描述屈服面演化过程的方法,由于其在数学处理方面的简洁而被广泛地接受与运用,但是这种相对简单的描述方法无法反映实验中观察到的扭转硬化效应、交叉效应等. 因此,许多学者又引进了额外的非各向同性硬化参数试图描述屈服面的空间扭转硬化[6 -9],本文只阐述考虑各向同性硬化和随动硬化的屈服面演化方程,即
|
$f\left( {{M}^{\text{e}}},{{S}^{\text{en}}},{{\sigma }_{\text{y}}} \right)=0$
|
(106) |
实验表明,除了初始各向异性材料(如轧制钢板,单晶体和地质材料等),材料的初始屈服面接近于von Mises屈服面,即屈服面方程取如下形式
|
$\begin{align}
& f\left( {{M}^{\text{e}}},{{S}^{\text{en}}},{{\sigma }_{\text{y}}} \right)=\quad \\
& \sqrt{\frac{3}{2}\left( \text{sy}{{\text{m}}_{0}}\left( {{M}^{\text{e}}} \right)-{{S}^{\text{en}}} \right):\left( \text{sy}{{\text{m}}_{0}}\left( {{M}^{\text{e}}} \right)-{{S}^{\text{en}}} \right)}-{{\sigma }_{\text{y}}}=0 \\
\end{align}$
|
(107) |
式中,${\rm sym}_0\left( { { M}^{\rm e}}
\right)$是弹性Mandel应力的对称偏量部分,以描述材料静水压力无关于塑性变形的特性,标量$\sigma _{\rm y}
$代表当前屈服面的尺寸用以描述材料的各向同性硬化,而背应力偏量${ S}^{\rm
en}$代表当前屈服面在应力空间中的中心位置,用以描述其随动硬化.
对于实际材料,硬化不会无限期地进行下去,而是随着塑性应变的增长而逐渐趋近于一个饱和值. 现假定$\sigma _{\rm y}$
按 "指数衰减记忆率"函数[27, 28]变化
|
${{\sigma }_{\text{y}}}\left( {{\kappa }^{\text{p}}} \right)={{\sigma }_{{{\text{y}}_{0}}}}+\left( {{\sigma }_{{{\text{y}}_{\text{s}}}}}-{{\sigma }_{{{\text{y}}_{0}}}} \right)\left( 1-{{\text{e}}^{-{{C}_{\text{iso}}}{{\kappa }^{\text{p}}}}} \right)$
|
(108) |
式中,$\sigma _{{\rm y}_0 }$,$\sigma _{{\rm y}_{\rm s} }$和$C_{\rm iso} $
是非负材料常数,分别代表屈服面的初始尺寸,饱和尺寸和各向同性硬化率;
$\kappa ^{\rm p}$是非负单增参数,在应变硬化情况下,其为累积等效塑性应变
|
${{\dot{\kappa }}^{\text{p}}}={{\left[\frac{2}{3}{{D}^{\text{p}}}:{{D}^{\text{p}}} \right]}^{1/2}}$
|
(109a) |
|
${{\kappa }^{\text{p}}}=\int{{{\left[\frac{2}{3}{{D}^{\text{p}}}:{{D}^{\text{p}}} \right]}^{1/2}}dt}$
|
(109b) |
式中,塑性乘子
|
$\begin{align}
& {{{\dot{\kappa }}}^{\text{p}}}\ge 0f\left( {{M}^{\text{e}}},{{S}^{\text{en}}},{{\sigma }_{\text{y}}} \right)\le 0,\\
& {{{\dot{\kappa }}}^{\text{p}}}f\left( {{M}^{\text{e}}},{{S}^{\text{en}}},{{\sigma }_{\text{y}}} \right)=0 \\
\end{align}$
|
(110) |
4.4 塑性旋率
由前文叙述可知,两类塑性变形梯度$F^{\rm p}$和$F_i^{\rm dis} $
分别确定了卸载构型和随动硬化构型,而为了将小变形理论中的随动硬化率在形式上推广到大变形理论中,本文假定随动硬化构型旋率为0,即$W_i^{\rm dis} = 0$(式(81),而
$D_i^{\rm dis} $则由本文的随动硬化法则(式 (83),式(98),式(100),式(102),式(104))确定,故变形梯度
$F_i^{\rm dis}$ 的演化过程由此确定为
|
$\dot{F}_{i}^{\text{dis}}=D_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{\text{dis}}F_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{\text{dis}},i=1,2,\cdots ,M$
|
(111) |
同理,卸载构型塑性变形梯度
${ F}^{\rm p}$的演化由塑性变形率
${ D}^{\rm p}$和塑性旋率
${ W}^{\rm p}$决定,${ D}^{\rm p}$的演化取决于式 (77)的流动法则,而塑性旋率
${ W}^{\rm p}$的演化则是一个相对复杂的问题. 很多学者对塑性旋率在变形梯度乘法分解理论的地位与作用进行了详细探讨[29]. Green$^{
[30]以及Casey等[31]引进了卸载构型的标架不变性原则,并将其视为与当前构型标架不变性具有同等地位的一般性原则,这种观点虽然被许多学者所驳斥[32],但对于无织构的多晶材料,其仍然适用.基于这一观点并结合 Kroner 变形分解理论,文献[33] 阐述了在各向同性塑性理论框架下,可以不失一般性地假定塑性旋率为 {\bf 0},即${ W}^{\rm p}={\bf 0}$.
根据上述讨论,同时考虑到对于各向同性材料的有限变形理论,忽略塑性旋率将使理论得到很大简化,本文假定
|
${{W}^{\text{p}}}=\mathbf{0}$
|
(112) |
故塑性变形梯度
${ F}^{\rm p}$的演化过程可完全由塑性变形率决定,即
|
${{F}^{\text{p}}}={{D}^{\text{p}}}{{F}^{\text{p}}}\text{ }$
|
(113) |
4.5 本构理论总结
本文本构理论的最大新颖之处便是将经典的背应力加法分解法则引入到超弹性本构理论中,并使其拥有直观的物理意义------即背应力产生机制的多重性,这一机制抽象出来的变形运动学便是塑性变形梯度的多重分解定理,在这一变形分解假定下,几类经常应用于小变形理论和次弹性理论中的随动硬化法则,便可在拥有合理物理解释的基础上推广应用于超弹性本构理论,而材料进入有限变形阶段后,基于变形梯度乘法分解的超弹性本构理论比基于变形率加法分解的次弹性本构理论更加合理,因此这也说明了本节本构关系在理论上的优越性.
本节本构理论总结如表1所示,其与经典次弹性-塑性本构模型的对比如表2所示.两类本构理论本质上的不同点在于其基于不同的变形运动学基础:
表1(Table 1)
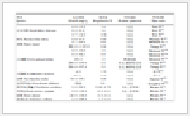
表1 本构理论总结Table 1 Summary of the constitutive model
| Multiplicative decomposition of
deformation gradient | F = FeFp |
| generalized Lion deformation
decomposition theory | $\eqalign{
& {F^p} = F_1^{en}F_1^{dis} = F_2^{en}F_2^{dis} = \cdot \cdot \cdot F_M^{en}F_M^{dis} \cr
& \det F_i^{en} = \det F_i^{dis} = 1,i = \left\{ {1,2,,M} \right\} \cr} $ |
| hyperelastic constitutive equation | $\begin{align}
& \tau =2\frac{\partial {{\psi }^{e}}}{\partial {{B}^{e}}}{{B}^{e}} \\
& S_{i}^{en}=sy{{m}_{0}}(2\frac{\partial \psi _{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{en}(B_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{en})}{\partial B_{i}^{en}}B_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{en})=\frac{2}{3}{{r}_{_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}}}{{\gamma }_{_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}}}h_{_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}}^{en} \\
& {{S}^{en}}=\sum\limits_{i=1}^{M}{S_{i}^{en}} \\
\end{align}$ |
| Mandel stress | ${{M}^{e}}={{({{F}^{e}})}^{T}}\tau {{({{F}^{e}})}^{-T}},M_{i}^{en}={{(F_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{en})}^{T}}S_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{en}{{(F_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i}}}^{en})}^{-T}}$ |
| flow rule | ${{D}^{p}}=\sqrt{\frac{3}{2}}{{\dot{k}}^{p}}\frac{M_{o}^{e}-{{S}^{en}}}{\left\| M_{o}^{e}-{{S}^{en}} \right\|},{{F}^{p}}={{D}^{p}}{{F}^{p}}$ |
| kinematic hardening rule | $\begin{align}
& D_{i}^{dis}=\frac{3}{2}\left[ {{\mu }_{i}}{{{\dot{k}}}^{p}}+\left\langle {{{\dot{\lambda }}}_{i}} \right\rangle \cdot H\left( \frac{3}{2}M_{i}^{en}:{{(M_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\dot{i}}}}^{en})}^{T}}-r_{i}^{2} \right) \right]\frac{M_{i}^{en}}{{{r}_{i}}} \\
& {{{\dot{\lambda }}}_{i}}=\left( \frac{{{D}^{p}}}{\left\| {{D}^{p}} \right\|}:\frac{S_{i}^{en}}{\left\| S_{i}^{en} \right\|}-{{\mu }_{i}} \right){{{\dot{k}}}^{p}},F_{i}^{dis}=D_{i}^{dis}F_{i}^{dis} \\
\end{align}$ |
| isotropic hardening rule | >$\begin{align}
> & f\left( {{M}^{e}},{{S}^{en}},{{\sigma }_{y}} \right)=\sqrt{\frac{3}{2}(sy{{m}_{0}}({{M}^{e}})-{{S}^{en}}):(sy{{m}_{0}}({{M}^{e}})-{{S}^{en}})}-\sigma y=0 \\
> & {{\sigma }_{y}}({{k}^{p}})={{\sigma }_{y}}_{0}+\left( {{\sigma }_{y}}_{s}-{{\sigma }_{y}}_{0} \right)\left( 1-{{e}^{-{{C}_{is{{o}^{{{K}^{P}}}}}}}} \right),{{k}^{p}}=\int{{{\left[ \frac{2}{3}{{D}^{p}}:{{D}^{p}} \right]}^{1/2}}dt} \\
>\end{align}$ |
| Kuhn--Tucker condition | ${{k}^{p}}\ge 0b\left( {{M}^{e}},{{S}^{en}},{{\sigma }_{y}} \right)\le 0,{{k}^{p}}f\left( {{M}^{e}},{{S}^{en}},{{\sigma }_{y}} \right)=0$ |
|
表1 本构理论总结
Table 1 Summary of the constitutive model |
超弹性-塑性本构理论基于变形梯度的乘法分解定理,而次弹性-塑性本构理论则基于变形率的加法分解定理,而前者的复杂程度远甚于后者.多个中间构型的引入将产生定义在不同构型上的演化方程,例如,在
表2次弹性-塑性本构模型栏中的所有方程均是定义在当前构型中的;而超弹性栏中的方程则不是如此,如流动法则是定义在载构型中的,而随动硬化法则定义在相应的随动硬化中间构型中,尽管它们与次弹性理论在形式上相似.这也使得超弹性本构理论比次弹性理论在数值计算上要复杂的多.
表2(Table 2)

表2 与次弹性--塑性本构模型的对比Table 2 The comparison with hypoelastic-plasticity constitutive model
| Hyperelastic-plasticity constitutive model | Hypoelastic-plasticity constitutive model |
| decomposition | $F={{F}^{e}}{{F}^{p}}$ | $D={{D}^{p}}+{{D}^{e}}$ |
| theory of | ${F^p} = F_1^{en}F_1^{dis} = F_2^{en}F_2^{dis} = = F_M^{en}F_M^{dis}$ |
| deformation | $\det F_i^{en} = \det F_1^{dis} = 1,i = \left\{ {1,2,M} \right\}$ |
| elastic constitutive equation | $\tau =2\frac{\partial {{\psi }^{e}}}{\partial {{B}^{e}}}{{B}^{e}}$ | ${{\tau }^{*}}={{H}^{e}}:{{D}^{e}}$ |
| kinematic hardening rule | $\mathop {\overline {(S_i^{en})} }\limits^ {\mkern 1mu} \log = \frac{2}{3}{r_{\mathop i\limits_ - }}{\gamma _{\mathop i\limits_ - }}{D^p} - \left[ {{\mu _i}{{\dot k}^p} + \left\langle {{{\dot \lambda }_i}} \right\rangle H\left( {\frac{3}{2}S_{\mathop i\limits_ - }^{en}:S_i^{en} - r_i^2} \right)} \right]$ | $\alpha _i^* = \frac{2}{3}{r_{\mathop i\limits_ - }}{\gamma _{\mathop i\limits_ - }}{D^p} - \left[ {{\mu _i}{{\dot k}^p} + \left\langle {{{\dot \lambda }_i}} \right\rangle H\left( {\frac{3}{2}{\alpha _{\mathop i\limits_ - }}:{\alpha _{\mathop i\limits_ - }} - r_i^2} \right)} \right]{\gamma _{\mathop i\limits_ - }}{\alpha _{\mathop i\limits_ - }}$ |
| ${{S}^{en}}=\sum\limits_{i=1}^{M}{S_{i}^{en}}$ | $\alpha =\sum\limits_{i=1}^{M}{{{\alpha }_{i}}}$ |
| flow rule | ${{D}^{p}}=\sqrt{\frac{3}{2}}{{{\dot{k}}}^{p}}\frac{M_{0}^{e}-{{S}^{en}}}{\left\| M_{0}^{e}-{{S}^{en}} \right\|}$ | ${{D}^{p}}=\sqrt{\frac{3}{2}}{{{\dot{k}}}^{p}}\frac{\tau '-\alpha }{\left\| \tau '-\alpha \right\|}$ |
|
表2 与次弹性--塑性本构模型的对比
Table 2 The comparison with hypoelastic-plasticity constitutive model |
5 结论
本文在Lion塑性变形分解理论的基础上,引入了多机制过程,对其进行了理论上的拓展.基于拓展的Lion塑性变形分解理论,结合变形梯度乘法分解定理,本文对经典理论中客观性的定义进行了概念上的推广,提出了一类新的超弹性-有限塑性本构模型,这类本构模型满足热动力学法则,并且可以融合多种小变形循环塑性理论中经典的随动硬化模型. 本文以K-O模型、A-F模型、Chaboche模型和
O-W模型为例进行了讨论,并着重论述了K-O模型.
K-O随动硬化模型与O-W随动硬化模型的共性在于Heaviside阶跃函数的引入,这种阶跃性质使得背应力分量始终在相应的临界面内演化,故在数值积分过程中背应力的积分需要利用径向返回映射法,同时考虑到对数共旋率以及多种构型的引入,本文本构理论的数值化过程会相对复杂一些.
参考文献
| [1] |
Coombs WM, Crouch RS, Augarde CE. A unique critical state two-surface hyperplasticity model for fine-grained particulate media. Journal of the Mechanics and Physics of Solids, 2013, 61(1):175-189 |
| [2] |
刘时鹏, 施建勇, 雷国辉等. K0 固结饱和土柱孔扩张问题弹塑性分析. 岩土力学, 2013, 34(2): 389-394+403 (Liu Shipeng, Shi Jianyong, Lei Guohui, et al. Elastoplastic analysis of cylindrical cavity expansion in K0 consolidated saturated soils. Rock and Soil Mechanics, 2013, 34(2): 389-394+403 (in Chinese)) |
| [3] |
王小莉. 橡胶隔振器多轴疲劳寿命预测方法研究. [博士论文]. 广州:华南理工大学, 2014 (Wang Xiaoli. Studies on life prediction of multiaxial fatigue for rubber isolators. [PhD Thesis]. Guangzhou: South China University of Technology, 2014 (in Chinese)) |
| [4] |
盖芳芳, 才源, 郝俊才等. 超高速撞击压力容器后壁损伤实验及建模研究. 振动与冲击, 2015, 34(13): 12-17 (Gai Fangfang, Cai Yuan, Hao Juncai, et al. Tests and modeling for damage of pressure vessels' rear wall caused by hypervelocity impact. Journal of Vibration and Shock, 2015, 34(13): 12-17 (in Chinese)) |
| [5] |
Bargmann S, Svendsen B, Ekh M. An extended crystal plasticity model for latent hardening in polycrystals. Computational Mechanics,2011, 48(6): 631-645 |
| [6] |
Ishikawa H. Subsequent yield surface probed from its current center. International Journal of Plasticity, 1997, 13(6-7): 533-549 |
| [7] |
Barlat F, Aretz H, Yoon JW, et al. Linear transformation-based anisotropic yield functions. International Journal of Plasticity,2005, 21(5): 1009-1039 |
| [8] |
Suprun AN. A constitutive model with three plastic constants: the description of anisotropic workhardening. International Journal of Plasticity, 2006, 22(7): 1217-1233 |
| [9] |
Feigenbaum HP, Dafalias YF. Directional distortional hardening in metal plasticity within thermodynamics. International Journal of Solids and Structures, 2007, 44(22-23): 7526-7542 |
| [10] |
Armstrong PJ, Frederick CO. A mathematical representation of the multiaxial bauscinger effect. CEGB Report No. RD/B/N 731, Berkeley Nuclear Laboratories, Berkeley, CA, 1966 |
| [11] |
Chaboche JL, Dang-Van K, Cordier G. Modelization of the strain memory effect on the cyclic hardening of 316 stainless steel. In: Proceedings of the 5th International Conference on SMiRT, Div. L, Berlin, Germany, 1979 |
| [12] |
Chaboche JL. Time-independent constitutive theories for cyclic plasticity. International Journal of Plasticity, 1986, 2(2): 149-188 |
| [13] |
Ohno N, Wang JD. Kinematic hardening rules with critical state of dynamic recovery, part I: formulations and basic features for ratcheting behavior. International Journal of Plasticity, 1993, 9(3): 375-390 |
| [14] |
Abdel-Karim M, Ohno N. Kinematic hardening model suitable for ratcheting with steady-state. International Journal of Plasticity,2000, 16(3-4): 225-240 |
| [15] |
Xiao H, Bruhns OT, Meyers A. Elastoplasticity beyond small deformations. Acta Mechanica, 2006, 182(1-2):31-111 |
| [16] |
Zhu Y, Kang G, Kan Q, et al. Logarithmic stress rate based constitutive model for cyclic loading in finite plasticity. International Journal of Plasticity, 2014, 54(March): 34-55 |
| [17] |
Lion A. Constitutive modelling at finite thermoviscoplasticity: a physical approach based on nonlinear rheological models. International Journal of Plasticity, 2000, 16(5): 469-494 |
| [18] |
Tsakmakis C, Willuweit A. A comparative study of kinematic hardening rules at finite deformations. International Journal of Non- Linear Mechanics, 2004, 39(4): 539-554 |
| [19] |
Shutov AV, Kreißig R. Finite strain viscoplasticity with nonlinear kinematic hardening: phenomenological modeling and time integration. Computer Methods in Applied Mechanics and Engineering,2008, 197(21-24): 2015-2029 |
| [20] |
Vladimirov IN, Pietryga MP, Reese S. On the modeling of non-linear kinematic hardening at finite strains with application to springbackcomparison of time integration algorithms. International Journal for Numerical Methods in Engineering, 2008, 75(1): 1-28 |
| [21] |
Henann DL, Anand L. A large deformation theory for ratedependent elastic-plastic materials with combined isotropic and kinematic hardening. International Journal of Plasticity, 2009,25(10): 1833-1878 |
| [22] |
Lee EH. Elastic plastic deformation at finite strains. Journal of Applied Mechanics, 1969, 36(1): 1-6 |
| [23] |
Zhu YL, Kang GH, Kan QH, et al. An extended cyclic plasticity model at finite deformations describing the Bauschinger effect and ratchetting behavior. In: 13th International Conference on Fracture June 16-21, 2013, Beijing, China |
| [24] |
Zecevic M, Knezevic M. A dislocation density based elasto-plastic self-consistent model for the prediction of cyclic deformation: Application to AA6022-T4. International Journal of Plasticity, 2015,72: 200-217 |
| [25] |
Lin RC, BrocksW, Batten J. On internal dissipation inequalities and finite strain inelastic constitutive laws: Theoretical and numerical comparisons. International Journal of Plasticity, 2006, 22: 1825-1857 |
| [26] |
Bari S, Hassan T. Anatomy of coupled constitutive models for ratcheting simulation. International Journal of Plasticity, 2000, 16(3-4):381-409 |
| [27] |
Naghdabadi R, Yeganeh M, Saidi AR. Application of corotational rates of the logarithmic strain in constitutive modeling of hardening materials at finite deformations. International Journal of Plasticity,2005, 21(8): 1546-1567 |
| [28] |
Wu HC. On stress rate and plasticity constitutive equations referred to a body-fixed coordinate system. International Journal of Plasticity,2007, 23(9): 1486-1511 |
| [29] |
Dafalias Y. Plastic spin: necessity or redundancy. International Journal of Plasticity, 1998, 14(9): 909-31 |
| [30] |
Green AE, Naghdi PM. Some remarks on elastic-plastic deformation at finite strain. International Journal of Engineering Science,1971, 9(12): 1219-1229 |
| [31] |
Casey J, Naghdi PM. A remark on the use of the decomposition F = FeFp in plasticity. Journal of Applied Mechanics, 1980, 47(3):672-675 |
| [32] |
Dashner PA. Invariance considerations in large strain elastoplasticity. Journal of Applied Mechanics, 1986, 53(1): 55-60 |
| [33] |
Gurtin ME, Anand L. The decomposition F = (FFp)-F_e, material symmetry, and plastic irrotationality for solids that are isotropicviscoplastic or amorphous. International Journal of Plasticity,2005, 21(9): 1686-1719 |
A NEW FORMULATION OF CONSTITUTIVE MODEL FOR HYPERELASTIC-CYCLIC PLASTICITY
Meng Lingkai, Zhou Changdong , Guo Kunpeng, Zhang Xiaoyang
, Guo Kunpeng, Zhang Xiaoyang
School of Civil Engineering, Beijing Jiaotong University, Beijing 100044, China
Abstract: Until now, a number of classical hyperelastic-finite plasticity constitutive models have been proposed. However, most of them are based on the classical Armstrong-Frederick kinematic hardening rule in consideration of the complexity brought by the introduction of the intermediate configuration in the hyperelasticity theory. Hence, based on the existed constitutive theories, the methodology of Lion decomposition theory was extended utilizing the notion of the multi-mechanism process and clearly put forward the conception of the multi-intermediate configuration. Furthermore, the classical concept of the objectivity in the continuum mechanics for better application to the hyperelasticity theory was generalized and then a new hyperelastic-finite plastic constitutive model was proposed. The new constitutive model not only meets the thermal dynamic laws but also can incorporate several classical kinematic hardening rules which were usually adopted in cyclic plasticity of infinitesimal deformation theory (e.g. the A-F model, Chaboche model, O-W model and the K-O model, etc.). Therefore, this model corresponding to finite deformation problems contains two typical characteristics adopted by infinitesimal deformation theory: the additive decomposition property and step mutation feature of the backstress on the critical surface. Thus, the present model can be treated as parallel to the corresponding form in the small deformation case. Finally, the situation accounting for Karim-Ohno kinematic hardening rule is under specific consideration and compared with the hypoelasticity constitutive model.
Key words:
constitutive model objectivity decomposition theory of deformation gradient kinematic hardening rule cyclic plasticity structural analysis





 2016, Vol. 48
2016, Vol. 48