引言
混凝土是土木、水利工程等领域应用最广的建筑材料.据统计,混凝土的工程用量是其他建筑材料的10倍,就我国而言,混凝土用量已超过其他所有国家的总和,约占全世界的60%,每年人均用量已达5吨[1].工程结构中的混凝土材料几乎都处在复杂的三维应力状态下工作,并且经常遭受地震、爆炸、风、冲击等动态载荷作用.混凝土材料的动态力学特性是非常复杂的,包括加载速率效应和循环效应,速率效应是指加载速率对混凝土材料力学特性的影响规律,如对强度、变形及耗能能力的影响等;循坏效应是指在往复载荷作用下混凝土的力学特性,如塑性变形的累积特性、强度与刚度的损伤退化规律等.混凝土材料的力学特性是工程结构受力分析的基础,尤其是多轴应力状态下的动态强度特性[2]已成为前沿热点课题.
目前,通过不同的试验装置已经获得了大量的动态强度试验.早期主要利用落锤装置进行应变率为10$^{-6}\sim$10s$^{-1}$的动态单轴压缩试验[3, 4, 5],但是由于落锤惯性的影响,不能获得精确的动态强度[6].霍普金森压杆SHPB(split Hopkinson pressure bar)方法减小了试件惯性效应的影响,能够进行动态压缩和劈拉试验[7, 8, 9, 10, 11],加载速率可达10$^{3}$ s$^{-1}$.轻气炮冲击加载装置用来获得更高应变率的动态强度试验[12],应变率高达10$^{4}$s$^{-1}$到10$^{5}$ s$^{-1}$.上述这些试验装置主要用来进行单轴动态强度试验,很难获得双轴或真三轴动态强度试验结果.液压伺服试验机可以进行动态多轴强度试验[13, 14, 15, 16, 17],其应变率范围为10$^{-5}\sim $ 10$^{-2}$s$^{-1}$,远小于SHPB试验装置和轻气炮冲击装置.在不同的应变率范围内,混凝土材料强度提高的机制是不同的.在低应变率范围内,混凝土动态强度的提高主要受热活化机制控制,在该区域内混凝土强度随应变率的增加变化很缓慢.在中间应变率范围内,混凝土动态强度的提高主要受黏性阻尼机制控制,在该区域混凝土动态强度的变化剧烈.在高应变率范围内,混凝土动态强度的提高主要受惯性机制控制,在该区域内混凝土强度的变化又区域平缓.
混凝土材料动态强度试验为建立混凝土材料动态强度准则提供了基础.其中,混凝土材料的动态单轴强度准则多是通过给定动态强度增长因子(dynamic increase factor,DIF)与对数应变率之间的函数关系来建立的[18, 19, 20, 21, 22, 23, 24].最具代表性的成果是欧洲规范(CEB-FIP)采用的双线性动态单轴强度准则[25],该准则的表达式简单,便于应用;不足在于强度曲线存在角点,并且强度曲线是发散的,即随着应变率的提高动态强度无限增大.杜修力等[26]提出了混凝土动态单轴强度准则,即S准则,该准则合理地描述了混凝土动态单轴强度随应变率的非线性增长规律,强度曲线是收敛的,表明混凝土材料的动态强度随着应变率的提高不是无限增大的,存在一个动态极限强度,准则给出了混凝土材料单轴压缩强度和单轴拉伸强度的率效应函数.混凝土动态多轴强度准则主要有两种建立方法,一是直接通过拟合试验结果给出混凝土多轴强度与应变率的经验关系[16],该方法给出的动态多轴强度准则的适用范围有限,无法外延应用;二是在已有的静态多轴强度准则的基础上建立[27, 28],给出静态强度参数的应变率相关表达式,进而将静态强度准则发展为动态强度准则.例如,基于库普弗-格斯尔(Kupfer--Gerstle)的双轴强度准则[29],闫东明和林皋[30]以及关萍和刘鹏[15]分别发展了混凝土动态双轴强度准则;施林林等[17]将威廉-瓦恩克(William--Warnke)五参数强度准则[31]发展为混凝土动态多轴强度准则.路德春等[32, 33, 34]基于混凝土非线性统一强度准则,发展了混凝土非线性动态多轴强度准则[35],该准则适用于不同类型的混凝土材料,能够合理地描述混凝土材料的非线性动态强度随应变率的变化规律,并且能够反映混凝土材料的极限动态多轴强度.
目前,应用最多的静态多轴强度准则是摩尔-库伦(M-C)强度理论[38]和鲁克-普拉格(D-P)强度理论[39],它们的物理概念清楚,表达式简单,便于应用,并且在常规受力状态下能够合理地描述混凝土的强度规律.松岗-中井(M-N)强度理论[40]和拉德-邓肯(L-D)强度准则[41, 42, 43]也被广泛地应用在岩土材料中,可以更好地反映岩土材料的强度规律.M-N强度理论是对M-C强度理论的拓展,考虑了中主应力对材料强度的影响,提出了空间滑动面(spatially mobilized plane,SMP)的概念.L-D强度准则是基于岩土类材料的真三轴试验规律建立的,可较合理描述岩石、混凝土的真三维强度特性.胡克-布朗(H-B)强度准则[44, 45, 46]是基于多种岩石的试验规律,提出的一种经验型强度准则,该准则仍然没有考虑中主应力的影响,建立的是大主应力与小主应力间的非线性关系,这与M-C强度理论的线性关系是不同的.另外,针对混凝土材料,提出了一系列经验的强度准则,包括赖曼准则[47]、奥托森准则[48]、谢-廷-陈准则[49]、威廉-瓦恩克准则[50]、科索沃准则[51]以及过-王准则[52]等,多是D-P类型的强度准则,即表达式为剪应力与平均应力的函数关系.本文分别将M-C强度理论、D-P强度理论、M-N强度理论、L-D强度准则和H-B强度准则的材料参数转化为混凝土的基本强度指标(单轴压缩强度和单轴拉伸强度),再利用动态单轴S准则[26]建立的单轴强度指标的率相关的表达式,将5个静态多轴强度准则发展为动态多轴强度准则.分析了每个强度准则的双轴强度曲线、子午面强度曲线、偏平面强度曲线以及主应力空间强度曲面随应变率的变化规律.利用混凝土材料的动态双轴和动态真三轴强度试验结果,分析评价了各动态多轴强度准则及各准则的应变率范围的适用性.
1 经典强度准则的参数分析
1.1 M-C强度理论
M-C理论[36]是应用最为广泛的强度理论之一,被广泛用于土、岩石和混凝土等岩土类材料[53, 54].用主应力表示的M-C强度理论,其表达式为
|
\[\frac{1}{2}\left( {{\sigma }_{1}}-{{\sigma }_{3}} \right)-\frac{1}{2}\left( {{\sigma }_{1}}+{{\sigma }_{3}} \right)\sin \varphi -c\cos \varphi =0\]
|
(1) |
本文以压应力为正,将混凝土单轴压缩下的破坏应力条件($f_{rm c}$,0,0)、单轴拉伸下的破坏应力条件(0,0,$-f_{\rm t})$分别代入式(1),并联立求解得
|
\[\varphi =\arcsin \frac{{{f}_{\text{c}}}-{{f}_{\text{t}}}}{{{f}_{\text{c}}}+{{f}_{\text{t}}}}\]
|
(2) |
|
\[c=\frac{1}{2}\sqrt{{{f}_{\text{c}}}{{f}_{\text{t}}}}\]
|
(3) |
式(2)和式(3)表明,M-C强度理论的参数可以由混凝土材料的基本强度指标单轴压缩强度$f_{\rm c }$和单轴拉伸$f_{rm t}$来表示.
1.2 D-P强度理论
D-P强度理论[39]作为最简单的强度理论之一,同样被广泛的应用于岩土类材料.其表达式如下
|
\[{{\tau }_{\text{oct}}}=\alpha {{\sigma }_{\text{oct}}}+k\]
|
(4) |
式中,$\alpha $和$k$为材料参数.
将混凝土单轴压缩下的破坏应力条件($f_{rm c}$,0,0)和单轴拉伸下的破坏应力条件(0,0,$-f_{\rm t})$分别代入式(4),并联立求解得
|
\[\alpha =\frac{3\left( {{f}_{\text{c}}}-{{f}_{\text{t}}} \right)}{{{f}_{\text{c}}}+{{f}_{\text{t}}}}\]
|
(5) |
|
\[k=\frac{2{{f}_{\text{c}}}{{f}_{\text{t}}}}{{{f}_{\text{c}}}+{{f}_{\text{t}}}}\]
|
(6) |
式(5)和式(6)表明,D-P强度理论的参数可以由混凝土材料的基本强度指标单轴压缩强度$f_{\rm c }$和单轴拉伸$f_{rm t}$来表示.
1.3 M-N强度理论
M-N强度理论[40]首先基于无黏性材料,认为材料的破坏在空间滑动面(SMP)上遵循摩擦规律,建立抗剪强度与正应力的线性关系,其表达式如下
|
\[\frac{{{\tau }_{\text{SMP}}}}{{{\sigma }_{\text{SMP}}}}=C\]
|
(7) |
式中,$\tau $$_{\rm SMP}$和$\sigma $$_{rmSMP}$分别为SMP面上的剪应力和正应力,$C$为材料参数.式(7)也可以转化为应力不变量表示,即
|
\[\frac{{{I}_{1}}{{I}_{2}}}{{{I}_{3}}}={C}'\]
|
(8) |
式中,$C'$为材料参数,$I_{1}$,$I_{2}$,$I_{3}$分别为第一、第二和第三应力不变量,表达式为
|
\[\left. \begin{array}{*{35}{l}}
{{I}_{1}}={{\sigma }_{1}}+{{\sigma }_{2}}+{{\sigma }_{3}} \\
{{I}_{2}}={{\sigma }_{1}}{{\sigma }_{2}}+{{\sigma }_{2}}{{\sigma }_{3}}+{{\sigma }_{3}}{{\sigma }_{1}} \\
{{I}_{3}}={{\sigma }_{1}}{{\sigma }_{2}}{{\sigma }_{3}} \\
\end{array} \right\}\]
|
(9) |
对于有黏聚强度的混凝土材料,可通过坐标平移的方法转化.坐标平移公式为
|
\[{{\hat{\sigma }}_{i}}={{\sigma }_{i}}+{{\sigma }_{0}}\quad (i=1,2,3)\]
|
(10) |
式中,$\sigma $$_{0}$为混凝土三向拉伸强度.扩展后的M-N准则为
|
\[\frac{{{\tau }_{\text{SMP}}}}{{{\sigma }_{\text{SMP}}}}=\sqrt{\frac{{{{\hat{I}}}_{1}}{{{\hat{I}}}_{2}}-9{{{\hat{I}}}_{3}}}{9{{{\hat{I}}}_{3}}}}=C\]
|
(11) |
将单轴压缩下的破坏应力条件($f_{rm c}$,0,0)代入式(10),得
|
\[\frac{\sqrt{2}}{3}\sqrt{\frac{f_{\text{c}}^{2}{{\sigma }_{0}}}{\sigma _{0}^{3}+{{f}_{\text{c}}}\sigma _{0}^{2}}}=C\]
|
(12) |
将单轴拉伸下的破坏应力条件(0,0,$-f_{\rm t})$代入式(10),得
|
\[\frac{\sqrt{2}}{3}\sqrt{\frac{f_{\text{t}}^{2}{{\sigma }_{0}}}{\sigma _{0}^{3}-{{f}_{\text{t}}}\sigma _{0}^{2}}}=C\]
|
(13) |
联立求解式(11)和式(12),得
|
\[{{\sigma }_{0}}=\frac{{{f}_{\text{c}}}{{f}_{\text{t}}}}{{{f}_{\text{c}}}-{{f}_{\text{t}}}}\]
|
(14) |
|
\[C=\frac{{{f}_{\text{c}}}-{{f}_{\text{t}}}}{3}\sqrt{\frac{2}{{{f}_{\text{c}}}{{f}_{\text{t}}}}}\]
|
(15) |
式(14)和式(15)表明,扩展的M-N强度理论的材料参数可由混凝土的基本强度指标单轴压缩强度$f_{\rm c }$和单轴拉伸$f_{rm t}$来表示.
1.4 L-D强度准则
拉德和邓肯根据砂土的真三轴试验成果提出无黏聚强度材料的强度准则[41]
|
\[\frac{I_{1}^{3}}{{{I}_{3}}}={{k}_{1}}\]
|
(16) |
式中,$k_{1}$是材料参数.为描述岩土类材料强度在子午面上的非线性特性,拉德将式(15)发展为
|
\[\left( \frac{I_{1}^{3}}{{{I}_{3}}}-27 \right){{\left( \frac{{{I}_{1}}}{{{p}_{\text{a}}}} \right)}^{m}}={{\eta }_{1}}\]
|
(17) |
式中,$m$和$\eta$$_{1}$为材料参数,$m$取值不同反映了子午面上强度曲线的非线性行为,当$m$=0时,退化为式(15)的强度准则.
对于混凝土等黏聚材料,通过平移主应力空间中的强度面来考虑黏聚力(三向拉伸强度)[40, 41],联立式(10)得有黏聚强度材料的强度准则为
|
\[\left( \frac{\hat{I}_{1}^{3}}{{{{\hat{I}}}_{3}}}-27 \right){{\left( \frac{{{{\hat{I}}}_{1}}}{{{p}_{\text{a}}}} \right)}^{m}}={{\eta }_{1}}\]
|
(18) |
当$m$=0,将单轴压缩下的破坏应力条件($f_{rm c}$,0,0)代入式(17),得
|
\[\frac{{{\left( 3{{\sigma }_{0}}+{{f}_{\text{c}}} \right)}^{3}}}{\sigma _{0}^{3}+{{f}_{\text{c}}}\sigma _{0}^{2}}-27={{\eta }_{1}}\]
|
(19) |
当$m=0$,将单轴拉伸下的破坏应力条件(0,0,$-f_{\rm t})$代入式(17),得
|
\[\frac{{{\left( 3{{\sigma }_{0}}-{{f}_{\text{t}}} \right)}^{3}}}{\sigma _{0}^{3}-{{f}_{\text{t}}}\sigma _{0}^{2}}-27={{\eta }_{1}}\]
|
(20) |
联立求解式(18)和式(19),得
|
\[{{\sigma }_{0}}=\frac{\sqrt{f_{\text{c}}^{2}+14{{f}_{\text{c}}}{{f}_{\text{t}}}+f_{\text{t}}^{2}}\left( {{f}_{\text{c}}}+{{f}_{\text{t}}} \right)+10{{f}_{\text{c}}}{{f}_{\text{t}}}-f_{\text{c}}^{2}-f_{\text{t}}^{2}}{18\left( {{f}_{\text{c}}}-{{f}_{\text{t}}} \right)}\]
|
(21) |
|
\[{{\eta }_{1}}=\frac{{{\left( 3{{\sigma }_{0}}+{{f}_{\text{c}}} \right)}^{3}}}{\sigma _{0}^{3}+{{f}_{\text{c}}}\sigma _{0}^{2}}-27\]
|
(22) |
式(20)和式(21)表明,有黏聚强度材料的L-D强度准则的材料参数可由混凝土的基本强度指标单轴压缩强度$f_{\rm c }$和单轴拉伸$f_{rm t}$来表示.
1.5 H-B强度准则
H-B强度准则[44, 45, 46]是根据岩石材料的三轴试验结果提出的经验型强度准则,被广泛地用于岩石工程.它是通过改进M-C强度理论,考虑了与围压相关的岩石强度. 其表达式为
|
\[{{\sigma }_{1}}={{\sigma }_{3}}+{{f}_{\text{c}}}\sqrt{m\frac{{{\sigma }_{3}}}{{{f}_{\text{c}}}}+1}\]
|
(23) |
式中,$m$是材料参数.
将单轴拉伸下的破坏应力条件(0,0,$-f_{\rm t})$代入式(22),求得
|
\[m=\frac{f_{\text{c}}^{2}-f_{\text{t}}^{2}}{{{f}_{\text{c}}}{{f}_{\text{t}}}}\]
|
(24) |
式(23)表明,H-B强度准则的材料参数可由混凝土的基本强度指标单轴压缩强度$f_{rm
c}$和单轴拉伸$f_{rm t}$来表示.
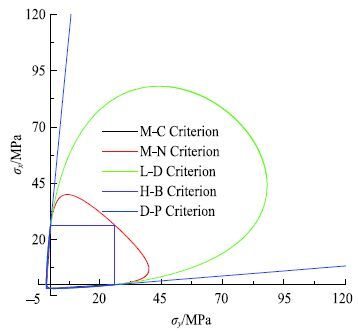
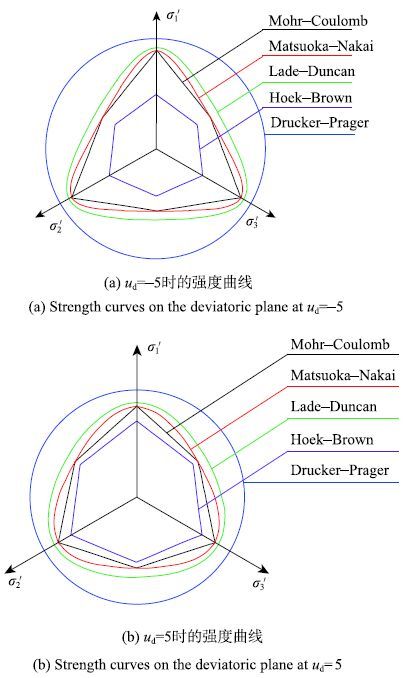
由上述分析可知,不同强度准则的强度参数与混凝土基本强度指标之间的关系是不同的.将M-C强度理论、M-N强度理论、D-P强度理论、L-D强度准则以及H-B强度准则绘制在主应力空间的偏平面上,并考虑三轴压缩条件($\sigma_{1}>\sigma _{2}=\sigma_{3}$)下各种破坏线重合,在偏平面上表示的各种强度准则如图1所示.从图中可以发现,M-C强度理论是所有强度准则的下限,并且M-N强度曲线外接于M-C强度线的6个角点,是非线性强度准则的下限;D-P强度理论是所有非线性强度准则的上限,L-D强度准则和H-B强度准则介于M-N强度理论(M-C强度理论)和D-P强度理论之间.D-P、M-N和L-D准则的强度曲线式连续光滑的,H-B准则与M-C准则类似,在三轴拉伸和三轴压缩处存在角点,在该点处强度曲线的外法线方向不唯一.
2 强度准则的率效应参数
在混凝土材料单轴动态强度试验研究成果的基础上,作者通过混凝土材料强度增长幅值的动力增长因数与对数应变速率之间关系的微分方程,建立了混凝土材料的非线性单轴动态强度准则,即J准则[26].在J准则的基础上,通过引入强度增长幅值的最大动力增长因数,将J准则改进为能描述混凝土材料动态极限强度特性的S准则[26].在多轴应力条件下,应变率通过广义剪应变率$\dot {\varepsilon }_{\rm d } $描述,非线性动态S准则的表达式[37]为
|
\[DIF=1+F\left( {{u}_{\text{d}}} \right)=1+\frac{{{F}_{\max }}}{1+\left( \frac{{{F}_{\max }}}{{{F}_{0}}}-1 \right)\exp \left[ -\xi \left( {{u}_{\text{d}}}-{{u}_{\text{d}0}} \right) \right]}\]
|
(25) |
式中,$u_{\rm d} = {\rm lg} \dot {\varepsilon }_{\rm d } $为对数广义剪应变率,$\dot {\varepsilon }_{\rm d} = {\sqrt{2\left( {\left( {\dot {\varepsilon }_{1}-\dot {\varepsilon}_{2} } \right)^2 + \left( {\dot {\varepsilon }_{2}-\dot{\varepsilon }_{3} } \right)^2 + \left( {\dot {\varepsilon }_{3}-\dot {\varepsilon }_{1} } \right)^2} \right)} }\Big/3$为广义剪应变率,$F_{\max}$为最大强度增长幅值的动力增长因数,$\xi$为反映动力增长因子随应变率增加速度的材料参数.
将式(24)代入${DIF} = {f_i^{\rm d} } / {f_i^{\rm s} }$,得
|
\[f_{i}^{\text{d}}=\left[ 1+\frac{{{F}_{i\max }}}{1+\left( \frac{{{F}_{i\max }}}{{{F}_{0}}}-1 \right)\exp \left[ -\xi \left( {{u}_{\text{d}}}-{{u}_{\text{d}0}} \right) \right]} \right]f_{i}^{\text{s}}\]
|
(26) |
式中,d代表动态,s代表静态,当$i$=c时表示单轴压缩强度,$i$=t时表示单轴拉伸强度.
将式(25)分别代入式(2)和式(3)、式(5)和式(6)、式(13)和式(14)、式(20)和式(21)以及式(23)即可得到M-C强度理论、D-P强度理论、M-N强度理论、L-D强度准则和H-B强度准则的率效应参数.将这些应变率相关的强度参数分别代入相应的静态多轴强度准则,即发展成了动态多轴强度准则.发展的动态多轴强度准则均包含6个材料参数,即$\xi $$_{\rm c }$,$F_{\rm c\max}$,$\xi $$_{\rm t}$,$F_{\rm t\max}$,$f_{ \rm c}$和$f_{rm t}$.对于不同的混凝土材料,可通过动态单轴试验确定参数$\xi$$_{\rm c}$,$F_{\rm c\max}$;$\xi $$_{\rm t}$,$F_{\rm tmax}$的取值,通过静态单轴试验确定$f_{ \rm c}$和$f_{\rm t}$的取值.
对于缺乏动态单轴试验结果的情况,作者等已根据多种混凝土材料的动态单轴抗压强度与抗拉强度试验结果,统计分析了动态强度参数[26],建议取值为$\xi$$_{\rm c}$=0.94,$F_{\rm cmax}$=2.12;$\xi $$_{\rm t}$=1.09,$F_{\rm tmax}$=6.36. 当初始状态取为$\dot {\varepsilon}_{{\rm d}0} = 1\times 10^{-4}$,$F_{0}$=0.1,则$u_{\rm d 0}$=$-$4.26,将其代入式(25)得
|
\[f_{\text{c}}^{\text{d}}=\left[ 1+\frac{2.12}{1+20.2\exp \left[ -0.94\left( {{u}_{d}}+4.26 \right) \right]} \right]{{f}_{\text{c}}}\]
|
(27) |
|
\[f_{\text{t}}^{\text{d}}=\left[ 1+\frac{6.36}{1+62.6\exp \left[ -1.09\left( {{u}_{\text{d}}}+4.26 \right) \right]} \right]{{f}_{\text{t}}}\]
|
(28) |
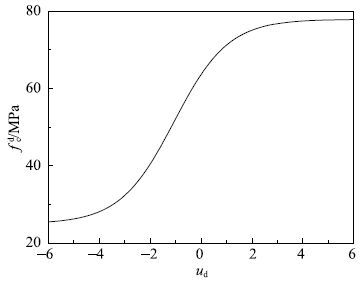
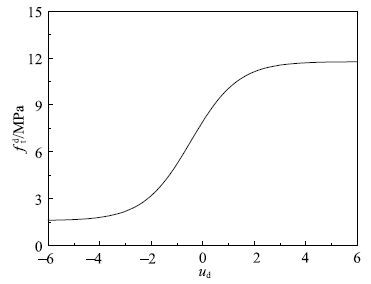
如图2和图3分别为式(26)和式(27)表示的动态单轴压缩强度与动态单轴拉伸强度随应变率的变化规律,从图中可以发现动态单轴压缩强度与动态单轴拉伸强度均随着应变率的增加而增加,动强度曲线连续光滑,并且存在极限强度.
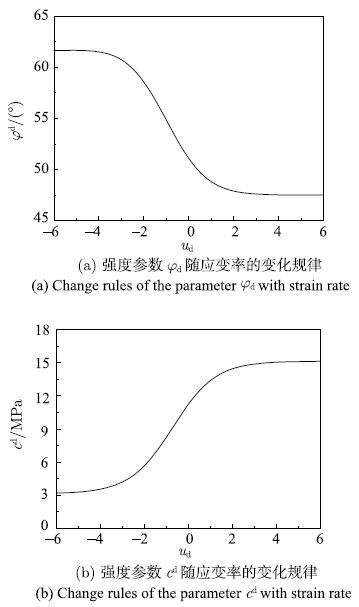
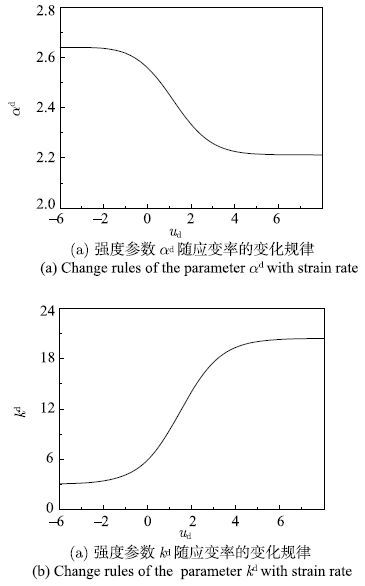
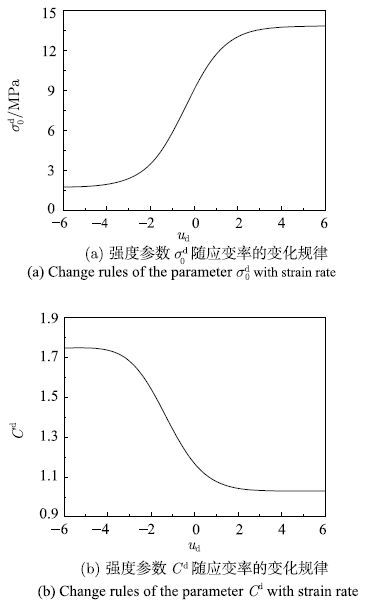
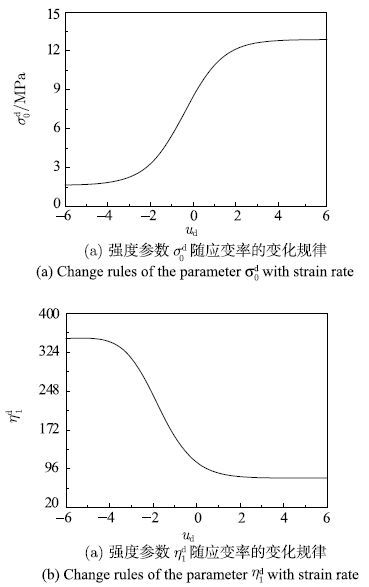
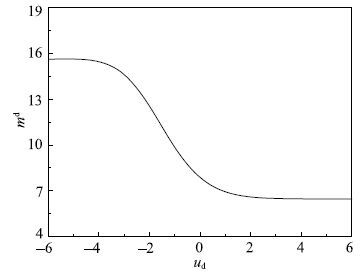
下面以作者进行的M20砂浆试验为例,来分析各动态多轴强度准则率相关参数随应变率的变化规律.砂浆的强度为$f_{rm c}=24.98~{\rm MPa}$,$f_{rm t}=1.6~{rmMPa}$. 首先将$f_{rm c}=24.98~{\rm MPa}$和$f_{rm t}=1.6~{rmMPa}$代入式(26)和式(27),然后将得到的方程分别代入各动态强度准则的应变率相关参数中,即可得到各强度参数与应变率的关系式.图4$\sim$图8分别为动态M-C准则、D-P准则、M-N准则、L-D准则和H-B准则的率相关参数与应变率的关系曲线,对应的动态强度参数变化的幅值如表1所示.从图中可以发现,控制摩擦强度的率相关参数随应变率的增加是降低的,但降低的幅度不大,例如M-C的参数$\varphi $$^{\rm d}$,D-P的参数$\alpha $$^{\rm d}$,M-N的参数$C^{\rm d}$,L-D的参数$\eta _1^{\rm d} $和H-B的参数$m^{\rm d}$;控制黏聚强度的率相关参数随应变率的增加而增大,增大的幅度相对较大,例如M-C的参数$c^{\rm d}$,D-P的参数$k^{\rm d}$,M-N的参数$\sigma _{0}^{\rm d} $,L-D的参数$\sigma _{0}^{\rm d} $和H-B的参数$f_{rm c}^{\rm d} $.本文的分析是在$\xi $$_{\rm c}=0.94$,$F_{\rm c max}=2.12$;$\xi _{\rm t}=1.09,F_{\rm tmax}=6.36$条件下得到的,对于某一具体的混凝土材料,因上述参数的不同,率相关强度参数随应变率的变化规律也会有所差别.上述规律性认识与赵坚[28]通过统计混凝土材料动态强度试验结果获得的规律一致,应变率对摩擦强度的影响较小,对黏聚强度的影响较大.
表1(Table 1)

表1 各动态多轴强度准则的应变率相关参数Table 1 Strain rate dependent parameters of each dynamic multiaxial strength criterion
| Strength criteria | Strain rate dependent equations of the strength parameters | Change rules of the parameters |
| maximum | minimum | variation |
| M-C strength criterion | $\varphi^{\rm d} = \arcsin \dfrac{f_{\rm c}^{\rm d}-f_{\rm t}^{\rm d}}{f_{\rm c}^{\rm d} + f_{\rm t}^{\rm d}}$ | 61.7 | 47.51 | $-$23% |
| $c^{\rm d} = \dfrac{1}{2}\sqrt {f_{\rm c }^{\rm d} f_{\rm t}^{\rm d} } $ | 15.1 | 3.2 | 372% |
| D-P strength criterion | $\alpha ^{\rm d} = \dfrac{3\left({f_{\rm c}^{\rm d}-f_{\rm t}^{\rm d} } \right)}{f_{\rm c}^{\rm d} + f_{\rm t}^{\rm d} }$ | 2.6 | 2.2 | $-$15% |
| $k^{\rm d} = \dfrac{2f_{\rm c}^{\rm d} f_{\rm t}^{\rm d} }{f_{\rm c}^{\rm d} + f_{\rm t}^{\rm d} }$ | 20.4 | 3.1 | 558% |
| M-N strength criterion | $C^{\rm d} = \dfrac{f_{\rm c }^{\rm d}-f_{\rm t}^{\rm d} }{3}\sqrt {\dfrac{2}{f_{\rm c}^{\rm d} f_{\rm t}^{\rm d} }} $ | 1.7 | 1.0 | $-$41% |
| $\sigma _0^{\rm d} = \dfrac{f_{\rm c}^{\rm d} f_{\rm t}^{\rm d} }{f_{\rm c}^{\rm d}-f_{\rm t}^{\rm d} }$ | 13.9 | 1.7 | 718% |
| L-D strength criterion | $\eta _1^{\rm d} = \dfrac{\left({3\sigma _0^{\rm d} + f_{\rm c}^{\rm d} } \right)^3}{\sigma_0^{{\rm d3}} + f_{\rm c}^{\rm d} \sigma _0^{{\rm d2}} }-27$ | 350.8 | 78.0 | $-$78% |
| $\sigma _0^{\rm d} = \dfrac{\sqrt {f_{\rm c}^{{\rm d2}} + 14f_{\rm c }^{\rm d} f_{\rm t}^{\rm d} + f_{\rm t}^{{\rm d2}} } \left({f_{\rm c}^{\rm d} + f_{\rm t}^{\rm d} } \right) + 10f_{\rm c }^{\rm d} f_{\rm t}^{\rm d}-f_{\rm c}^{{\rm d2}}-f_{\rm t}^{{\rm d2}} }{18\left( {f_{\rm c}^{\rm d}-f_{\rm t}^{\rm d} }\right)}$ | 12.9 | 1.7 | 659% | | H-B strength criterion | $m^{\rm d} =\dfrac{f_{\rm c}^{{\rm d2}}-f_{\rm t}^{{\rm d2}} }{f_{\rm c}^{\rm d} f_{\rm t}^{\rm d} }$ | 15.6 | 6.5 | $-$58% |
|
表1 各动态多轴强度准则的应变率相关参数
Table 1 Strain rate dependent parameters of each dynamic multiaxial strength criterion |
3 主应力空间中的动态多轴强度准则
通过强度参数随应变率的提高而变化的规律,分析混凝土材料的动态多轴强度规律.各强度准则在单轴拉伸强度和单轴压缩强度都分别相等的条件下,分别给出平面应力条件、子午面和偏平面上的动强度曲线,以及主应力空间上的动强度曲面.
根据多种混凝土材料的动态单轴压缩强度与动态单轴拉伸强度试验结果,统计分析给出的4个动态强度参数的建议值分别为[26]:$\xi
_{\rm c}=0.94$,$F_{\rm cmax}=2.12$;$\xi _{\rm t}=1.09$,$F_{\rm tmax}=6.36$. 参考强度状态取为$u_{\rm d }=-4$,$F_{0}=0.1$,则$u_{\rm d0}=-4.26$. 取单轴压缩强度为$f_{rm
c}=24.98~{\rm MPa}$,单轴拉伸强度$f_{rm t}=5~{\rm MPa}$.
3.1 平面应力条件下的动强度曲线
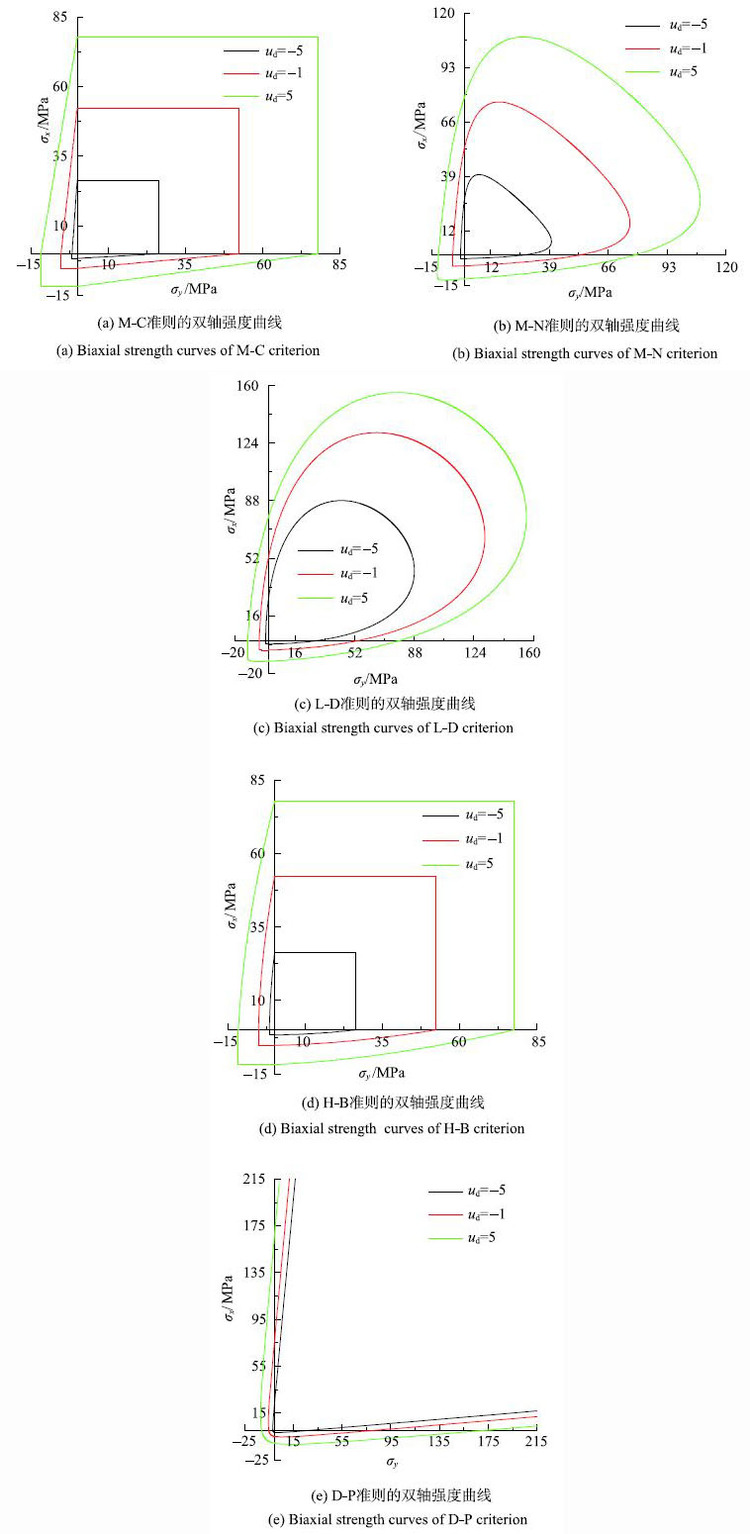
平面应力条件,三个主应力中有一个保持为零,即$\sigma _{z }= 0$.在二维主应力$\sigma _{x }-\sigma _{y}$平面内,第一象限时,$\sigma_{z}$为小主应力;在第二、第四象限时,$\sigma_{z}$为中主应力;在第三象限时,$\sigma _{z}$为大主应力.各强度准则在应变率$u_{\rm d}=-5$,$u_{\rm d}=-1$和$u_{\rm d }=5$下的双轴强度曲线如图9所示.对于同一个强度准则,随着应变率的增加,其强度曲线向外扩展,表明动态双轴强度随着应变率的提高而增大.对于动态M-C强度准则,其压压区、拉压区和拉拉区的强度线都是直线;对于M-N强度理论、L-D强度准则和D-P强度理论,其压压区、拉压区和拉拉区的强度线都是曲线;对于H-B强度准则,其压压区和拉拉区的强度线是直线,而拉压区的强度线是曲线.应变率为$u_{\rm d }=-5$时,将各动态强度准则的强度曲线绘于同一图中,如图10所示,各强度准则在拉压区和拉拉区的强度线相差不大.在压压区差别很大,M-C准则与H-B准则均没有考虑中主应力的影响,动强度曲线重合,M-N外接于M-C和H-B,L-D准则和D-P准则的强度线显著地大于M-C,M-N和H-B准则的强度线.M-C准则和H-B准则的动态双轴压缩强度与动态单轴压缩强度相等,即$f_{{rmbc}}^{\rm d} = f_{rm c}^{\rm d}$;动态双轴拉伸强度与动态单轴拉伸强度相等,即$f_{{\rm bt}}^{\rm d}= f_{rm t}^{\rm d} $.
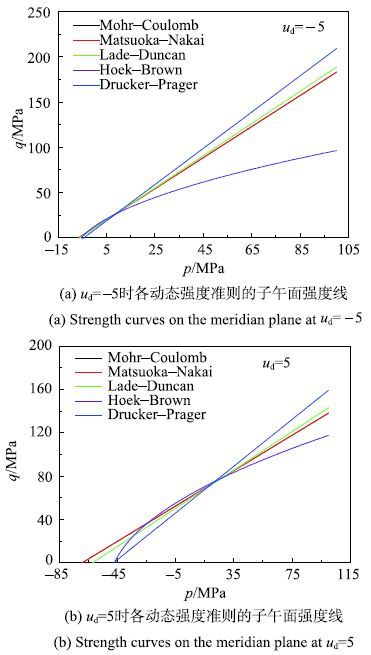
3.2 子午面上的动强度曲线
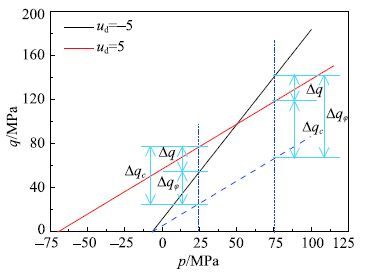
图11(a)和11(b)分别为应变率为$u_{\rm d}$=$-5$和$u_{\rm d}$=5下,动态M-C准则、M-N准则、D-P准则、L-D准则和H-B准则在三轴压缩子午面上的强度曲线.从图中可以发现,动态M-C准则和动态M-N准则的三轴压缩子午面强度曲线相同,除动态H-B准则的强度线为非线性曲线外,其他动态强度准则的强度线都是直线.当应变率为$u_{\rm d}=-5$时,各动态强度准则的三向拉伸强度基本相等,即与$p$轴的交点基本相同;而当应变率为$u_{\rm d }= 5$时,三向拉伸强度主要集中在两个区域,即动态M-C,M-N和L-D集中在一起,它们的三向拉伸强度相差不大,动态D-P和H-B集中在一起,但这两个区域的三向拉伸强度相差较大.由于动态M-C,M-N,D-P和L-D准则的子午面强度线都是直线,它们随应变率的变化规律类似,因此这里只分析动态M-C强度准则的子午面强度线随应变率的变化规律.如图12为不同应变率下动态M-C强度准则在三轴压缩子午面的强度线.在图12中,随着应变率的增加强度参数$\varphi $减小,而参数$c$(或$\sigma_{0})$增加. 分别取$p=25 ~{\rm MPa}$和$p=75~ {rmMPa}$来分析子午面上各个强度准则的强度规律. 在$p = 25~ {rmMPa}$处,黏聚强度$c$增加所贡献的抗剪强度变化值为$\Delta q_{\rm c }$,其值为正;内摩擦角$\varphi$减小所导致抗剪强度的变化值为$\Delta q_{\varphi}$,其值为负;$\Delta q_{\rm c}$的绝对值大于$\Delta q_{\varphi}$的绝对值,总体表现为抗剪强度增加,增加的值为$\Delta q=\Delta q_{\rm c}-\Delta q_{\varphi }$. 当$p=75~{\rm MPa}$时,$\Delta q_{\rm c}$的绝对值小于$\Delta q_{\varphi}$的绝对值,总体表现为抗剪强度降低,降低的值为$\Delta q=\Delta {{q}_{\varphi }}-\Delta {{q}_{\text{c}}}$.上面的分析表明,随着应变率的增大,混凝土材料的剪切破坏机制由最大应力比破坏向最大剪应力破坏转化.
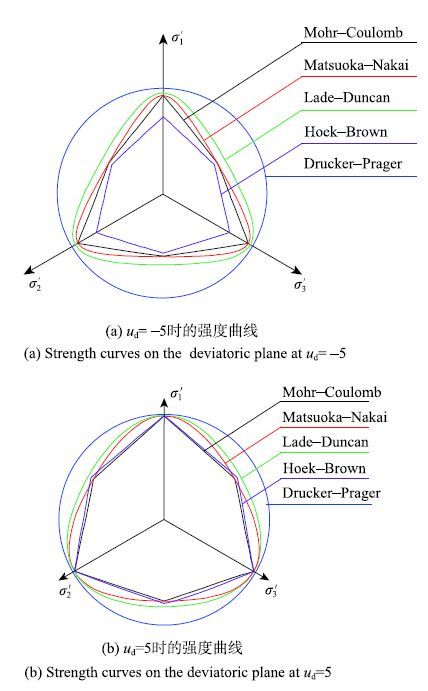
3.3 偏平面上的动强度曲线
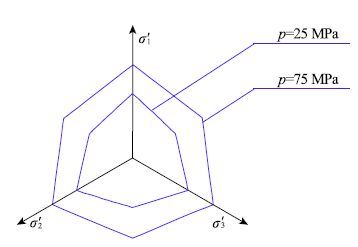
与子午面的分析相对应,在静水压力$p = 25~{\rm MPa}$和$p=75~ {rmMPa}$处给出各动态强度准则偏平面上的强度曲线,如图13和14所示.在$p=25~ {\rm MPa}$处,当$u_{\rm d }=-5$时,动强度曲线如图13(a)所示,各动态强度准则在三轴压缩处不再相交,D-P曲线最大,H-B曲线最小,M-C和M-N曲线相切,L-D曲线介于D-P和M-N曲线之间;当$u_{\rm d }=5$时(图13(b)),各动态强度准则的强度曲线在三轴压缩处基本重合.比较图13(a)和13(b)发现,在相同静水压力处,各动态强度准则偏平面曲线随着应变率的增加向外扩张,并且动态M-C,M-N,L-D和H-B强度曲线的形状都发生了变化,表现为向D-P圆过渡,其原因是随着应变率的增加,各动态强度准则的内摩擦角减小所致.如图14所示,当$p = 75~{rmMPa}$,随着应变率的增加表现出与图13相似的规律.对于动态H-B强度准则,由于子午面上的非线性特性,在相同应变率下,随着静水压力的增大,其偏平面上的强度曲线也向D-P圆过渡,如图15所示.
3.4 主应力空间中的动强度面
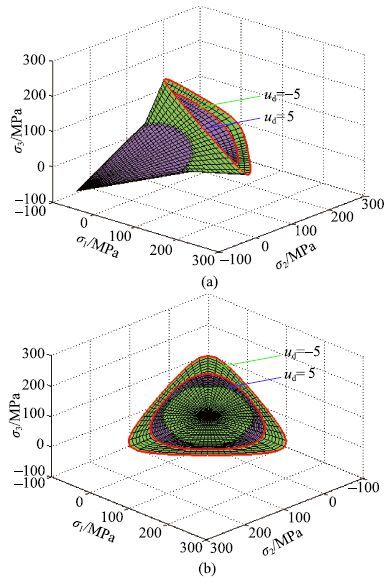
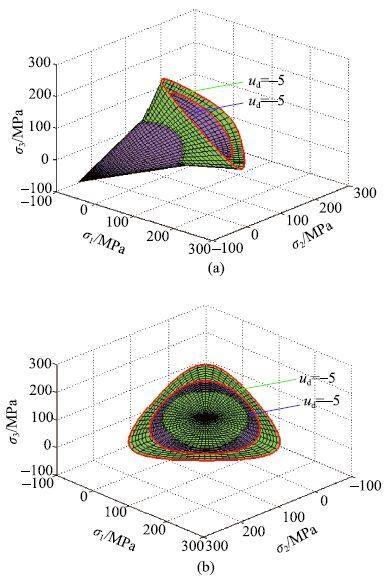
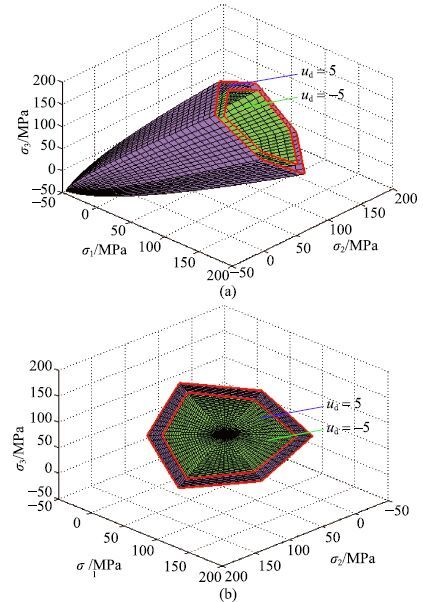
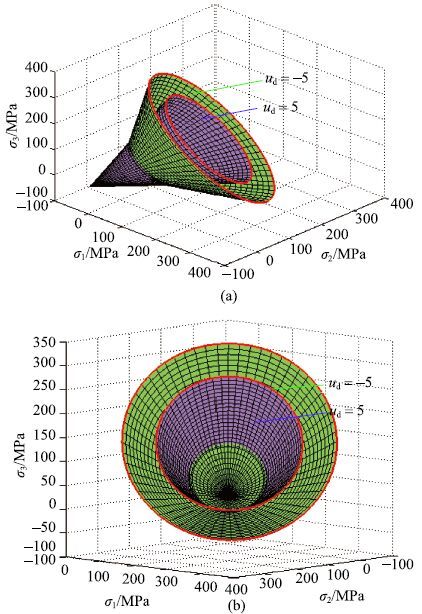
当应变率$u_{\rm d}$=$-5$和$u_{\rm d }$=5时,分别给出主应力空间中动态M-C强度准则、M-N强度准则、L-D强度准则、H-B强度准则和D-P强度准则的动强度曲面如图16至图20所示.从图中可以发现,各强度准则在主应力空间的静水压力轴上一端汇聚于一点,另一端是开口的. 对于动态M-C和H-B强度准则,主应力空间的强度面上存在6条奇异线,使得强度面不光滑.而其他准则的强度面除了在$p$轴上的奇异点外,处处都是连续光滑的.此外,H-B准则的强度面随着应变率的增加,表现出与其他准则不一样的变化规律,即不同应变率的强度面没有相交.
本文发展的各动态多轴强度准则的参数都是单轴压缩强度和单轴拉伸强度的函数,在单轴压缩和单轴拉伸条件下各动态强度准则是相同的.各动态多轴强度准则的参数都是基于单轴压缩和单轴拉伸条件确定的,因此,在单轴压缩和单轴拉伸条件下各动态强度准则是相同的.动态单轴压缩强度和拉伸强度由非线性动态单轴S准则给出,适用的应变率范围取决于单轴动态S准则,各动态多轴强度准则在单轴压缩和单轴拉伸条件下同样适用于所有的应变率范围.另外,不同的应力状态也显著地影响混凝土材料的强度特性,并与应变率具有耦合影响.由上面平面应力条件、偏平面、子午面以及主应力空间的强度规律分析可知,发展的动态D-P强度准则除确定参数的应力状态外,不适用于描述其他应力状态下混凝土材料的多轴强度随应变率的变化规律.动态M-C强度准则和H-B强度准则存在同样的问题,但较D-P准则更符合混凝土材料的强度规律;M-N强度准则和L-D强度准则能够较好地描述混凝土材料动态多轴强度特性,并且可以适用于所有的应变率范围.
4 动态强度准则与试验结果的对比分析
利用混凝土材料的三组动态双轴强度试验结果和两组动态三轴试验结果,分析评价动态多轴强度准则的适用性.因D-P准则在压压区与试验结果相差甚远,不适用于描述混凝土材料的多轴静动态强度规律,只分析了M-C,M-N,L-D和H-B准则.
4.1 动态双轴试验
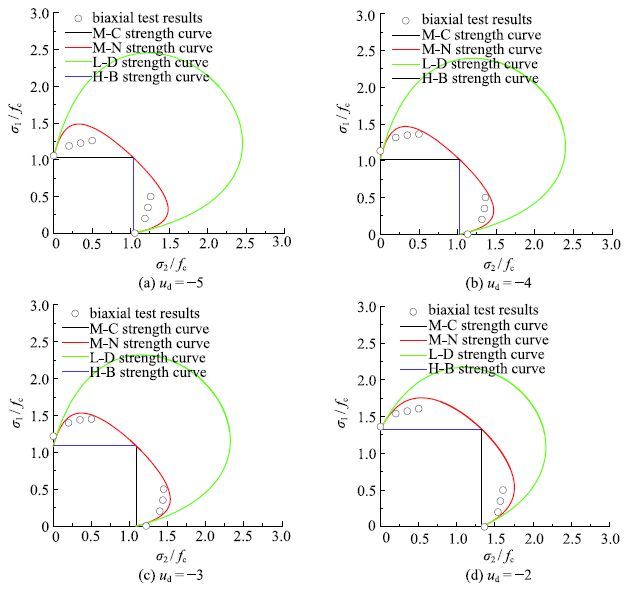
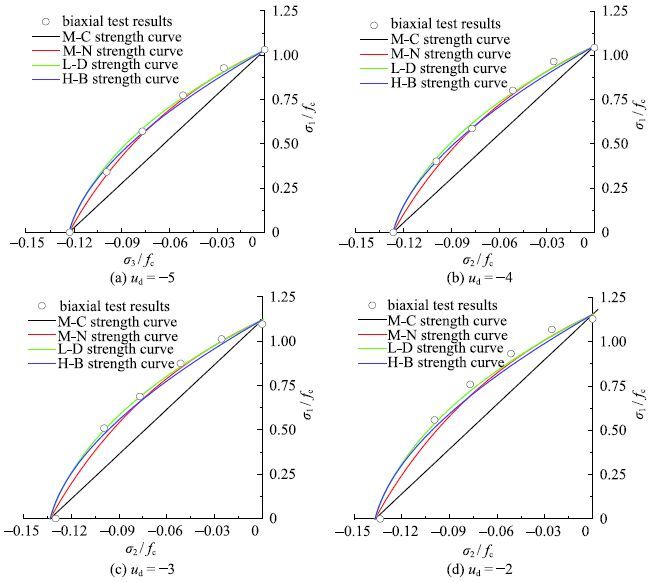
闫东明和林皋[30]开展了C10混凝土材料的双轴压-压动态加载试验,所用混凝土材料的单轴抗压强度$f_{\rm c }=9.84~ {\rm MPa}$. 试验时,控制小主应力$\sigma _{3}=0$;大主应力$\sigma_{ 1}$与中主应力$\sigma _{2}$以不同比例进行动态加载,直到试样破坏. $\sigma _{1}$与$\sigma _{2}$的比值分别为1:0, 1:0.25,1:0.5,1:0.75和1:1,加载时的应变率$u_{\rm d }$分别为$-5$,$-4$,$-3$和$-2$.试验结果[30]如图21中的点所示,各动态强度准则的计算结果如图21中的曲线所示.从图中可以发现,各动态强度准则的预测曲线相差较大,试验结果与动态M-N准则更接近,介于动态M-N和L-D准则之间.随着应变率的增加,试验结果和各动态强度准则预测曲线均向外扩张. 对于动态M-C,M-N和H-B准则,其双轴压缩强度$f _{rmbc}$是相同的,等于动态单轴强度$f _{\rm c }$,并且M-C准则与H-B准则强度曲线重合,而动态L-D准则的双轴压缩强度是大于其他动态准则的.
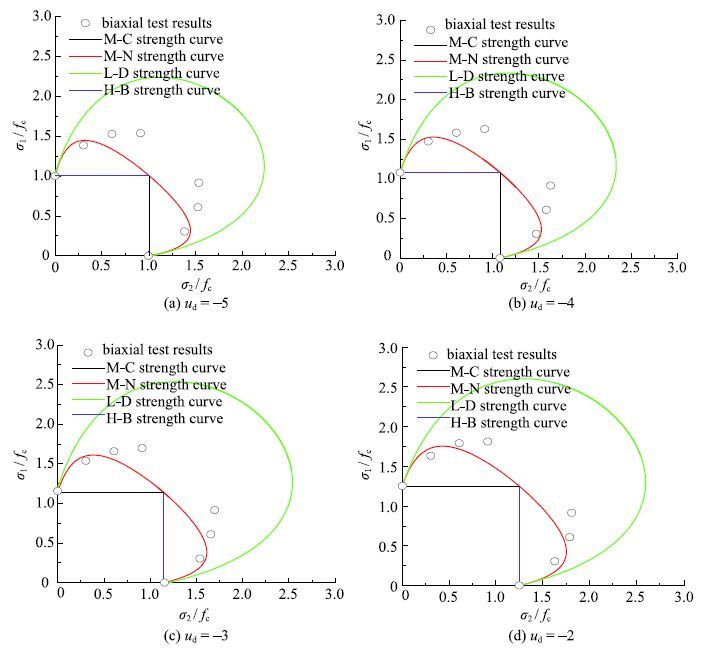
关萍[55]开展了C20混凝土材料的双轴压-压动态加载试验,所用混凝土材料的单轴抗压强度$f_{\rm c }=20.0 ~{\rm MPa}$. 试验过程中,保持小主应力$\sigma _{3}=0$; 水平向中主应力$ \sigma _{2} $首先加载至预设的侧压力值,并保持恒定,预设值分别为0,0.25$f _{\rm c}$,0.35$f$ $_{\rm c}$和0.5$f_{rm c}$;大主应力$\sigma _{1}$为动态载荷,加载时的应变率$u_{\rm d}$分别为$-5,-4,-3$和$-2$,试验结果[53]如图22中的点所示,各动态强度准则的计算结果如图22中的曲线所示.从图中可以发现,各动态强度准则的预测曲线相差较大,试验结果与动态M-N准则更接近,介于动态M-N和L-D准则之间.规律与图21类似.
尚世明等[16]开展了C30混凝土材料双轴拉压动态加载试验和单轴动态拉伸试验,所用混凝土材料的单轴抗压强度$f_{\rm c }=31.2 ~{\rm MPa}$. 双轴试验时,保持中主应力$\sigma _{2}=0$;小主应力$\sigma _{3}$为拉伸状态,首先施加拉应力分别到0~MPa,0.7 MPa,1.4 MPa,2.1Mpa和2.8 MPa,并保持不变,然后施加动态压缩载荷到试样破坏.大主应力$\sigma _{1}$动态载荷,加载时的应变率$u_{\rm d }$分别为$-5,-4$,$-3$和$-$2,试验结果[16]如图23中的点所示,各动态强度准则的计算结果如图23中的曲线所示.从图中可以发现,各动态强度准则在拉压区的预测曲线相差不大,除M-C准则外其他动态强度准则的预测曲线均与试验结果吻合较好,且随着应变率的增加,混凝土的双轴拉压强度也是增加的.
4.2 三轴试验验证
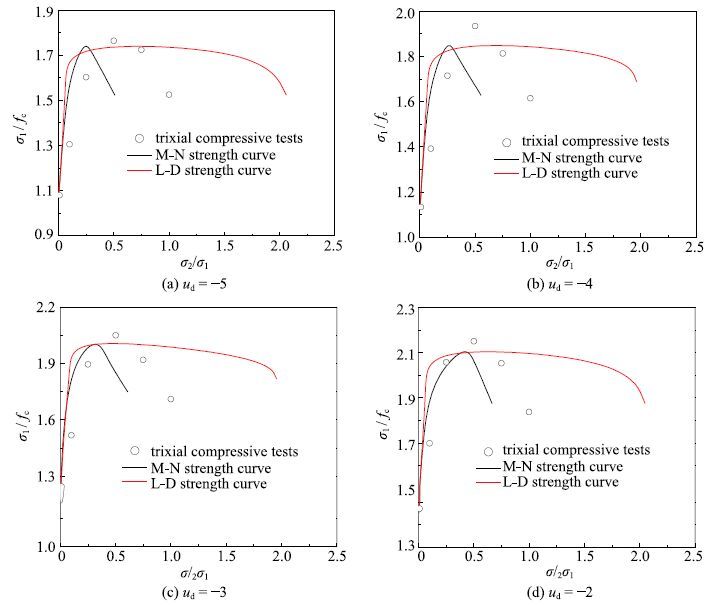
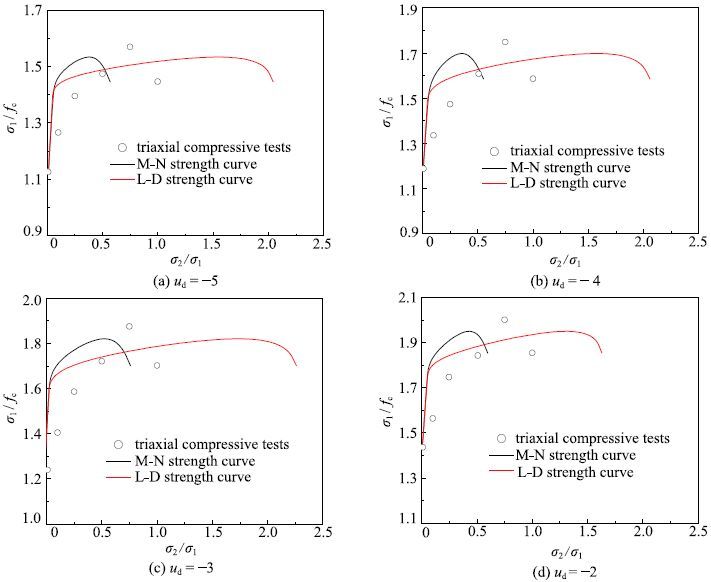
施林林等[17]开展了C20大坝混凝土和湿法过筛混凝土动态真三轴加载试验,所用混凝土材料的单轴抗压强度分别为$f_{\rm c }=19.29~{\rm MPa}$和 $f_{rm c}=24.51~{\rm MPa}$.本文采用压应力为正,在三轴压缩加载时,保持3个主应力的比值$\sigma_{ 1}$:$\sigma _{ 2}$:$\sigma _{ 3}$分别为1:0.01:0.01,1:0.1:0.01,1:0.25:0.01,1:0.5:0.01,1:0.75:0.01和1:1:0.01加载至破坏,加载时的应变率$u_{\rm d}$分别为$-$5,$-4$,$-3$和$-$2.试验结果[17]如图24(大坝混凝土)和图25(湿法过筛混凝土)中的点所示,各动态强度准则的计算结果如图24和图25中的曲线所示.由于M-C准则和H-B准则不能考虑中主应力对强度的贡献,因此,这里只进行了M-N准则和L-D准则与真三轴动态强度试验的对比分析.从图中可以发现,混凝土图的动态三轴强度试验结果介于动态M-N和L-D准则预测曲线之间.随着应变率的增加,试验结果和各动态强度准则预测曲线均向外扩张.M-N和L-D准则均较好地描述了混凝土材料的动态真三轴试验结果.
通过与3组动态双轴强度试验结果与2组动态真三轴强度试验结果的比较表明,发展的5个动态多轴强度准则除D-P准则外,均能够反映混凝土材料的动态多轴强度规律.对于双轴压压强度试验,试验结果与动态M-N准则的预测曲线更接近,介于动态M-N和L-D准则之间,这两个准则都能用于描述其他应变率范围内混凝土材料的双轴压缩强度规律. 在双轴拉压区,各准则的区别较小,除M-C强度理论外,都与试验结果吻合较好,并且能够适用于所有的应变率范围.对于真三轴强度试验,M-N准则和L-D准则均能够反映混凝土动态三轴强度规律.试验结果总体表明,在M-N准则和L-D准则之间应该存在一个强度准则,能够更好地适用于描述混凝土材料的静态和动态多轴强度特性.
5 结论
将经典的强度理论或准则,即摩尔-库伦强度理论、德鲁克-普拉格强度理论、松岗-中井强度理论、拉德-邓肯强度准则和胡克-布朗强度准则的强度参数用混凝土的基本强度指标$f_{rm c}$和$f_{\rm t}$来表示,利用混凝土材料动态单轴S准则推导了各强度准则强度参数的应变率相关表达式,进而将各静态强度准则发展为动态多轴强度准则.利用混凝土动态单轴压缩和动态单轴拉伸试验结果统计分析给出的S准则率效应参数,分析了5种强度准则中强度参数随应变率的变化规律以及取值范围.基于混凝土单轴压缩和单轴拉伸强度,分别给出了5种强度准则在子午面、偏平面和平面应力条件下的强度曲线与主应力空间中的强度曲面,对比分析了5种强度准则间的异同,以及每种强度准则随应变率的变化规律.通过分析发现,混凝土材料的抗剪强度由黏聚强度和摩擦强度两部分组成,随着应变率的增加,与静水压力无关的黏聚强度是提高的,而受静水压力影响的摩擦强度是减小的;在较低静水压力时,混凝土的抗剪强度主要受黏聚强度控制,当静水压力较高是,摩擦强度成为主要控制因素,表现为动态抗剪强度随应变率的增加而减小.
利用混凝土材料的动态双轴和动态真三轴强度试验结果,分析评价了5种动态多轴强度准则,德鲁克-普拉格强度理论在压压区与试验结果相差甚远,不适于描述混凝土材料的强度规律.动态双轴加载时,在拉压区和拉拉区各强度准则差别不大,都可较好地描述试验规律;在压压区各强度准则差别较大,松岗-中井强度理论与试验结果吻合最好,可用于描述整个应变率范围内混凝土材料的多轴动态强度特性.在动态真三轴比例加载时,摩尔-库伦强度理论和胡克-布朗强度准则无法考虑中主应力的影响;松岗-中井强度理论和拉德-邓肯强度准则都可较好地描述试验规律. 本文建立的动态多轴强度准则为率相关特性的研究提供了一系列准则.当混凝土处于双轴拉拉或拉压受力状态时,各动态强度准则都可作为强度条件,实现到有限元软件中进行混凝土结构的动力分析.当混凝土处于双轴压-压受力状态时,动态松岗-中井准则与试验结果吻合最好,也可作为强度条件实现到有限元软件中分析混凝土结构的动力响应.此外,本文提出的建立混凝土动态多轴强度准则的方法可作为一种通用的方法来建立混凝土的动态强度准则.
参考文献
| [1] |
李杰, 吴建营, 陈建兵. 混凝土随机损伤力学. 北京: 科学出版社,2014 (Li Jie, Wu Jianying, Chen Jianbing. Stochastic Damage Mechanics of Concrete Structures. Beijing: Science Press, 2014 (in Chinese)) |
| [2] |
Zhang QB, Zhao J. A review of dynamic experimental techniques and mechanical behaviour of rock materials. Rock Mechanics and Rock Engineering, 2014, 47: 1411-1478 |
| [3] |
Jones PG, Richart FE. The effect of testing speed on strength and elastic properties of concrete//Proceedings of the American Society for Testing Materials, 1936, 36: 380-392 |
| [4] |
Watstein D. Effect of straining rate on the compressive strength and elastic properties of concrete. ACI Materials Journal, 1953 49: 729-744 |
| [5] |
Hughes BP, Gregory R. Concrete subjected to high rates of loading in compression. Magazine of Concrete Research, 1972, 24: 25-36 |
| [6] |
Bischoff PH, Perry SH. Compressive behaviour of concrete at high strain rates. Materials and Structures, 1991, 24: 425-450 |
| [7] |
Ross CA, Tedesco JW, Kuennen ST. Effects of strain rate on concrete strength. ACI Materials Journal, 1995, 92-M5: 37-47. |
| [8] |
Klepaczko JR, Brara A. An experimental method for dynamic tensile testing of concrete by spalling. International Journal of Impact Engineering, 2001, 25: 387-409 |
| [9] |
Li QM, Meng H. About the dynamic strength enhancement of concrete-like materials in a split Hopkinson pressure bar test. International Journal of Solids and Structures, 2003, 40: 343-360 |
| [10] |
Lu YB, Li QM. About the dynamic uniaxial tensile strength of concrete-like materials. International Journal of Impact Engineering,2011, 38: 171-180 |
| [11] |
Al-Salloum Y, Almusallam T, Ibrahim SM, et al. Rate dependent behavior and modeling of concrete based on SHPB experiments. Cement and Concrete Composites, 2015, 55: 34-44 |
| [12] |
Liu HF, Ning JG. Mechanical behavior of reinforced concrete subjected to impact loading. Mechanics of Materials, 2009, 41: 1298-1308 |
| [13] |
Gary G, Bailly P. Behaviour of quasi-brittle material at high strain rate experiment and modelling. European Journal of Mechanics - A/Solids, 1998, 17: 403-420 |
| [14] |
Yan DM, Lin G. Dynamic behavior of concrete in biaxial compression. Magazine of Concrete Research, 2007, 59: 45-52 |
| [15] |
Guan P, Liu P. Study of strength criterion for dynamic biaxial compressive properties of concrete under constant confining pressure. Electric Technology and Civil Engineering, International Conference on IEEE. 2011, 753-755 |
| [16] |
Shang SM, Song YP. Dynamic biaxial tensile-compressive strength and failure criterion of plain concrete. Construction and Building Materials, 2013, 40: 322-329 |
| [17] |
Shi LL, Wang LC, Song YP, et al. Dynamic multiaxial strength and failure criterion of dam concrete. Construction and Building Materials,2014, 66: 181-191 |
| [18] |
Malvar LJ, Crawford JE, Wesevich JW, et al. A plasticity concrete material model for DYNA3D. International Journal of Impact Engineering,1997, 19: 847-873 |
| [19] |
Hao YF, Hao H, Jiang GP, et al. Experimental confirmation of some factors influencing dynamic concrete compressive strengths in highspeed impact tests. Cement and Concrete Research, 2013, 52: 63-70 |
| [20] |
Xu H, Wen HM. Semi-empirical equations for the dynamic strength enhancement of concrete-like materials. International Journal of Impact Engineering, 2013, 60: 76-81 |
| [21] |
Tedesco JW, Ross CA. Strain-rate-dependent constitutive equations for concrete. Journal of Pressure Vessel Technology, ASME, 1998,120: 398-405 |
| [22] |
Grote DL, Park SW, Zhou M. Dynamic behavior of concrete at high strain rates and pressures: Ⅰ. experimental characterization. International Journal of Impact Engineering, 2001, 25(9): 869-886 |
| [23] |
Li QM, Meng H. About the dynamic strength enhancement of concrete-like materials in a split Hopkinson pressure bar test. International Journal of Solids and Structures, 2003, 40: 343-360 |
| [24] |
Hao YF, Hao H. Dynamic compressive behaviour of spiral steel fibre reinforced concrete in split Hopkinson pressure bar tests. Construction and Building Materials, 2013, 48: 521-532. |
| [25] |
CEB FIP model code 1990, Comite Euro-International Du Beton[S]. |
| [26] |
杜修力, 王阳, 路德春. 混凝土材料的非线性单轴动态强度准则. 水利学报, 2010, 41(03): 300-309 (Du Xiuli, Wang Yang, Lu Dechun. Non-linear uniaxial dynamic strength criterion for concrete. Journal of Hydraulic Engineering, 2010, 41(03): 300-309 (in Chinese)) |
| [27] |
Fujikake K, Mori K, Uebayashi K, et al. Dynamic properties of concrete materials with high rates of tri-axial compressive loads//Sixth International Corference on Structures under Shock and Impact.2000, 511-522 |
| [28] |
Zhao J. Applicability of Mohr-Coulomb and Hoek-Brown strength criteria to the dynamic strength of brittle rock. International Journal of Rock Mechanics & Mining Sciences, 2000, 37: 1115-1121. |
| [29] |
Kupfer HB, Gerstle KH. Behavior of concrete under biaxial stresses. Journal of Engineering Mechanics, ASCE. 1973, 99(4): 853-866 |
| [30] |
闫东明, 林皋. 双向应力状态下混凝土的动态压缩试验研究. 工程力学, 2006, 23(9): 104-108 (Yan Dongming, Lin Gao. Effect of strain rate on the biaxial compressive behavior of concrete. Engineering Mechanics, 2008, 23(4): 385-393 (in Chinese)) |
| [31] |
Willam KL, Warnke E. Constitutive model for triaxial behavior of concrete//Proceedings of the International Assoc. for Bridge and Structural Engineering. 1975, 19: 1-30 |
| [32] |
Du XL, Lu DC, Gong QM, et al. Nonlinear unified strength criterion for concrete under three dimensional stress states. Journal of Engineering Mechanics, ASCE, 2010, 136: 51-59 |
| [33] |
路德春, 杜修力, 龚秋明等. 混凝土材料的广义非线性强度理论. 水利学报, 2009, 40(5): 542-549 (Lu Dechun, Du Xiuli, Gong Qiuming, et al. Generalized nonlinear strength theory for concrete. Journal of Hydraulic Engineering, 2009, 40(5): 542-549 (in Chinese)) |
| [34] |
路德春. 基于广义非线性强度理论的土的应力路径本构模型. [博士论文]. 北京: 北京航空航天大学, 2006 (Lu Dechun A constitutive model for soils considering wmplex stress paths based on generalized nonlinear strength theory. [PhD Thesis]. Beijing: Beihang Univesity, 2006 (in Chinese)) |
| [35] |
姚仰平, 路德春, 周安楠, 等. 广义非线性强度理论及其变换应力空间. 中国科学: 技术科学. 2004, 34(11): 1283-1299 (Yao YangPing, Lu DeChun, Zhou AnNan, et al. Generalized non-linear strength theory and transformed stress space. Science in China(Ser E), 2004, 47(6): 691-709 (in English)) |
| [36] |
Lu DC, Du XL, Wang GS, et al. A three-dimensinal elatoplastic constitutive model for concrete. Computers and Structures, 2016,163: 41-55 |
| [37] |
杜修力, 王国盛, 路德春. 混凝土材料非线性多轴动态强度准则. 中国科学: 技术科学, 2014, 44(12): 1319-1332 (Du Xiuli, Wang Gaosheng, Lu Dechun. Nonlinear multiaxial dynamic strength criterion for concrete material. Scientia Sinica Technologica, 2014,44(12): 1319-1332 (in Chinese)) |
| [38] |
Coulomb CA. Essai sur une Application des Regles de Maximis et Minimis a Quelques Problèmes de Statique, Relatifs a l'Architecture. Memoires de Mathematique et de Physique, Présentés, à l'Academie Royale des Sciences, 1776, 7: 343-382 |
| [39] |
Drucker DC, Prager W, Greenberg HJ. Extended limit design theorems for continuous media. Quarterly Applied Mathematics, 1952,9(4): 381-389 |
| [40] |
Matsuoka H, Nakai T. Stress-deformation and strength characteristics of soil under three different principal stresses// Proceedings of JSCE. 1974, 232: 59-70 |
| [41] |
Lade PV, Duncan JM. Elasto-plastic stress-strain theory for cohesionless soils. Journal of the Geotechnical Engineering Division, ASCE, 1975, 101(10): 1037-1053 |
| [42] |
Lade PV. Modelling the strengths of engineering materials in three dimensions. Mechanics of Cohesive-frictional Materials, 1997;2(4): 339-356 |
| [43] |
Lade PV. Three-parameter failure criterion for concrete. Journal of the Engineering Mechanics Division, ASCE, 1982, 108 (EM5): 850-863 |
| [44] |
Hoek E, Brown ET. Empirical strength criterion for rock masses. Journal of Geotechnical Engineering Division, ASCE. 1980, 106(9):1013-1035 |
| [45] |
Hoek E, Brown ET. The Hoek-Brown failure criterion-a 1988 update. Canadian Rock Mechanics Symposium. 1988, 31-38 |
| [46] |
Hoek E, Brown ET. Practical estimates of rock mass strength. International Journal of Rock Mechanics and Mining Sciences, 1997,34(8): 1165-1186 |
| [47] |
Podgórski J. General failure criferion for isotropic media. Journal of Engineering Mechanics ASCE, 1985, 111(2): 188-201 |
| [48] |
Ottosen NS. A failure criterion for concrete. Journal of Engineering Mechanics, ASCE, 1977, 103(4): 527-535 |
| [49] |
Hsieh SS, Ting EC, Chen WF. An elastic-fracture model for concrete// Proceeding of 3rd Engineering Mechanics Division, Special Conference ASCE, 1979, 437-440 |
| [50] |
Willam K L, Warnke E. Constitutive model for triaxial behavior of concrete//Proceedings of the International Assoc. for Bridge and Structural Engineering, 1975, 19: 1–30 |
| [51] |
Kotsovos MD. A mathematical description of the strength properties of concrete under generalized stress. Magazine of Concrete Research,1979, 31(108): 151-158 |
| [52] |
过镇海, 王传志, 张秀琴. 多轴应力下混凝土的强度和破坏准则研究. 土木工程学报, 1991, 24(3): 1-14 (Guo Zhenhai, Wang Chuanzhi, Zhang Xiuqin. Investigation of strength and failure criterion of concrete under multi-axial stresses. China Civil Engineering Journal, 1991, 24(3): 1-14 (in Chinese)) |
| [53] |
Rahman MA, Anand SC. Empirical Mohr-Coulomb failure criterion for concrete block-mortar joints. Journal of Structural Engineering,1994, 120(8): 2408-2422 |
| [54] |
Bai Y, Wierzbicki T. Application of extended Mohr–Coulomb criterion to ductile fracture. International Journal of Fracture, 2010,161(1): 1-20 |
| [55] |
关萍. 定侧压下混凝土双轴动态抗压性能的试验研究. 土木工程学报, 2009, 42(4): 33-37 (Guan Ping Experimental study on the dynamic biaxial compressive properties of concrete under constant confining pressure. China Civil Engineering Journal, 2009, 42(4):33-37 (in Chinese)) |
DYNAMIC MULTIAXIAL STRENGTH CRITERION FOR CONCRETE DEVELOPED BASED ON THE S CRITEIRON
Wang Guosheng , Lu Dechun, Du Xiuli, Li Meng
, Lu Dechun, Du Xiuli, Li Meng
Key Laboratory of Urban Security and Disaster Engineering of Ministry of Education, Beijing Univ. of Technology, Beijing 100124, China
Abstract: The classical strength criteria including Mohr-Coulomb strength theory, Drucker-Prager strength theory, Matsuoka-Nakai strength theory, Lade-Duncan strength criterion and Hoek-Brown strength criterion are developed into dynamic multiaxial strength criteria by deriving the strain-rate-dependent strength parameters of each static strength criterion. The strain-rate-dependent strength parameters are obtained by combing the dynamic uniaxial S criterion and the basic strength indexes of concrete material. Then the change rules and value range of strength parameters of five strength criteria are analyzed by these statistical material parameters of S criterion. On the basis of the uniaxial compressive and tensile strengths of concrete, the strength curves of each dynamic multiaxial strength criterion at plane stress condition, meridian plane, deviatoric plane and the strength surfaces in the principle stress space are given. Then the di erences of the five dynamic multiaxial strength criteria are analyzed. The five dynamic strength criteria are evaluated by the dynamic biaxial and true triaxial strength tests. The dynamic Drucker-Prager criterion shows big di erences with the dynamic test results of concrete. All of the dynamic strength criteria are able to reasonably describe the strength rules under biaxial compression-tension. It also shows big di erence among these dynamic strength criteria, while the dynamic Matsuoka-Nakai criteria describes the strength rules better than others. Under dynamic true triaxial proportional loading, Mohr-Coulomb and Hoek-Brown strength criteria cannot consider the influences of intermediate principal stress, while the Matsuoka-Nakai and Lade-Duncan strength criteria are capable of well describing the test results of concrete.
Key words:
concrete strain rate static multiaxial strength dynamic multiaxial strength strength criterion


 2016, Vol. 48
2016, Vol. 48