0 引言
接触非线性问题广泛存在于水利、机械等工程领域,如坝体的接缝、齿轮之间的相互咬合等.接触问题属于非保守系统和自由边界问题,其构成的泛函具有非线性和非光滑的特点,导致数学处理上的复杂与计算上的困难.
目前求解接触问题的数值方法主要采用有限元法[1, 2],边界元法[3, 4],等几何分析方法[5]等.有限元法是求解接触问题最常用、适应性最强的方法,但有限元法采用拉格朗日(Lagrange)插值函数拟合物体边界形状,精度较差,同时需要消耗大量时间进行前处理;边界元法仅离散问题的边界,降低了问题的维数,数据处理简单,但边界元中寻找问题的基本解较为困难,且方程的系数矩阵是非对称满阵;等几何分析方法(isogeometric analysis,IGA)是由休斯等[6]提出的新型数值方法,实现了计算机辅助设计与计算辅助工程的无缝对接,解决了传统数值方法中几何模型与求解域模型的非一致性问题,可精确描述求解域的边界,具有较高的计算精度与效率[7, 8],并且网格细分时具有保形性,因此近年来,等几何分析方法与各种接触约束条件施加方法相结合求解接触问题成为一个研究热点[9, 10, 11],但与有限元相同的是,等几何分析需要对整个求解域进行离散,而接触问题中确定接触区域和接触压力,本身就只关注问题的边界,计算结果对边界几何形状的变化非常敏感[12].
比例边界有限元(scaled boundary finite element method,
SBFEM)是由Wolf等[13, 14]提出的一种半解析数值方法.该方法与有限元相比,具有只需离散求解域的环向边界、在径向具有解析解、将问题降低一维的特点,与边界元相比,具有无需基本解,不存在奇异积分的特点[15, 16].
张勇等[17]提出了比例边界等几何分析算法,即将比例边界有限元与等几何分析耦合在一起.该方法继承了比例边界有限元与等几何分析的优点,具有高精度、节约计算工作量的特点,已被用于求解静力[18]、波导本征[19]、断裂[20]以及结构地基相互作用[21]等问题.
对于接触问题,当采用数值方法对接触体进行离散后,将平衡方程与接触条件相结合进行求解,求解方法主要有试验$\!$--$\!$误差迭代方法和数学规划方法.试验$\!$--$\!$误差迭代方法[22]一般利用经典的牛顿$\!$--$\!$拉普森迭代方法求解平衡方程,在迭代过程中需根据接触条件修正刚度阵和荷载项.由于接触系统的总泛函是非光滑的,导致当采用迭代法求解复杂接触问题时,适用于光滑函数的牛顿$\!$--$\!$拉普森迭代方法的收敛性难以得到保证.数学规划法将接触条件表示成线性互补模型[23, 24]、非线性互补模型[25, 26]、B可微方程组[27]等形式.在处理满足一定条件的非光滑最小化问题时,数学规划法的收敛性是具有理论保证的,其中B可微方程组模型可精确满足库伦摩擦定律.
由于比例边界等几何分析只需离散接触边界,能够精确描述接触边界,B可微方程组可精确满足库伦摩擦定律,其求解方法收敛性有理论保证,因此本文提出了比例边界等几何B可微方程组算法,用于求解摩擦接触问题.本文内容安排如下:首先介绍接触问题的基本方程,B样条与非均匀有理B样条(non-uniform rational B-spline ,NURBS);然后在比例边界等几何坐标系统下,对接触边界进行等几何离散,推导二维摩擦接触问题的边界控制方程,并介绍真实接触边界的识别方法;最后通过数值算例对本文算法的正确性与有效性进行验证.
1 接触问题的基本方程
弹性接触系统由接触体$\Omega ^1$和$\Omega ^2$组成.对于接触体$\Omega ^\alpha (\alpha = 1,2)$,其边界$\Gamma^\alpha $由三部分组成,${{\Gamma }^{\alpha }}=\Gamma _{\text{u}}^{\alpha }\cup \Gamma _{\text{q}}^{\alpha }\cup \Gamma _{\text{c}}^{\alpha }$,其中$\Gamma _{\rm u}^\alpha $,$\Gamma _{q}^{\alpha }$和$\Gamma _{\rm c}^\alpha$分别表示已知位移边界、已知外载荷边界和可能接触边界.
由于摩擦力是非保守力,使得摩擦接触问题的解与加载路径相关,因而采用增量形式进行求解.在小变形理论的假设下,弹性静力摩擦接触系统的增量方程可写成如下形式:
平衡方程
|
\[\mathbf{L}\text{d}{{\sigma }^{\alpha }}+\text{d}{{\bar{b}}^{\alpha }}=\mathbf{0}\]
|
(1) |
几何方程
|
\[\text{d}{{\varepsilon }^{\alpha }}=\widehat{\mathbf{L}}\text{d}{{u}^{\alpha }}\]
|
(2) |
物理方程
|
\[\text{d}{{\sigma }^{\alpha }}=D\text{d}{{\varepsilon }^{\alpha }}\]
|
(3) |
在边界处强制边界和自然边界条件为
|
\[\text{d}{{u}^{\alpha }}=\text{d}{{\bar{u}}^{\alpha }}\]
|
(4) |
|
\[{{({{n}^{\alpha }})}^{\text{T}}}\text{d}{{\sigma }^{\alpha }}=\text{d}{{\bar{q}}^{\alpha }}\]
|
(5) |
其中,${\rm d}{{ \sigma }}^\alpha,{\rm d}{{\varepsilon}}^\alpha$和${\rm d}{{ u}}^\alpha$分别表示应力增量、应变增量和位移增量;${\rm d}{{\bar {b}}}^{\alpha},{\rm d}{{\bar { u}}}^{\alpha}$和$ {\rm d}{{\bar{ q}}}^{\alpha}$分别表示已知体力增量、已知边界位移增量和已知边界面力增量;$\text{L},\widehat{\mathbf{L}}$表示微分算子;${{ D}}$表示材料的弹性矩阵.
在边界处的接触边界条件为
|
\[\left. \begin{matrix}
\text{d}u_{n}^{1}-\text{d}u_{n}^{2}+{{\delta }_{n}}\ge 0,\ \ {{p}_{n}}\le 0 \\
{{p}_{n}}\left( \text{d}u_{n}^{1}-\text{d}u_{n}^{2}+{{\delta }_{n}} \right)=0 \\
\left| {{p}_{\tau }} \right|<-\mu {{p}_{n}}\Rightarrow \left| \text{d}u_{\tau }^{1}-\text{d}u_{\tau }^{2}+{{\delta }_{\tau }} \right|=0 \\
\left| {{p}_{\tau }} \right|=-\mu {{p}_{n}}\Rightarrow \left| \text{d}u_{\tau }^{1}-\text{d}u_{\tau }^{2}+{{\delta }_{\tau }} \right|\ge 0 \\
\end{matrix} \right\}\]
|
(6) |
其中,${\rm d}u_n^\alpha $和${\rm d}u_\tau ^\alpha$分别表示接触体$\Omega ^\alpha $的法向和切向位移增量;$\delta_n$和$\delta _\tau$分别表示可能接触面之间的法向和切向初始间隙;$p{ }_n$和$p_\tau$分别表示可能接触面的法向和切向接触应力,$p_n $受压为正;$\mu$表示摩擦系数.
2 B样条与非均匀有理B样条基函数
2.1 B样条
B样条基函数通过一组节点向量进行定义
|
\[s=\left[ {{s}_{0}},{{s}_{1}},\cdots ,{{s}_{n+p}} \right]\]
|
(7) |
其中,$n$表示控制点的个数,$p$表示基函数的阶数,$[s_0 ,s_{n + p}]$表示一个单片,$[s_i ,s_{i + 1}]$表示第$i +1$个节点区间,与物理空间中的单元$V_i $相对应. 若节点向量${{s}}$两端的节点均是$p + 1$重的,则称该组节点向量为开放性节点向量.开放性节点向量在端点处满足克罗内克$\delta $(Kronecker-delta)性质,本文采用的是开放性节点向量.
一维B样条基函数考克斯$\!$--$\!$德布尔(Cox-de Boor)公式[28],递归定义如下
|
\[\left. \begin{array}{*{35}{l}}
{{N}_{i,0}}=\left\{ \begin{array}{*{35}{l}}
1, & s\in [{{s}_{i}},{{s}_{i+1}}] \\
0, & 否则 \\
\end{array} \right.\text{ } \\
{{N}_{i,p}}=\frac{s-{{s}_{i}}}{{{s}_{i+p}}-{{s}_{i}}}{{N}_{i,p-1}}(s)+ \\
~~~~~~~~~~\frac{{{s}_{i+p+1}}-s}{{{s}_{i+p+1}}-{{s}_{i+1}}}{{N}_{i+1,p-1}}(s),\ p\ge 1 \\
\end{array} \right\}\]
|
(8) |
B样条基函数的基本性质:非负性,单位分解性,高阶连续性,紧支性,线性无关性等.
2.2 非均匀有理B样条基函数
非均匀有理B样条基函数是在B样条基础上采用有理分式和引入权的方式构造的基函数,一维非均匀有理B样条基函数的表达式
|
\[R_{i}^{p}\left( s \right)=\frac{{{\omega }_{i}}{{N}_{i,p}}\left( s \right)}{\sum\limits_{j=0}^{n}{{{\omega }_{j}}{{N}_{j,p}}\left( s \right)}}\]
|
(9) |
其中,$\omega _i $为$N_{i,p} \left( s \right)$相应的权值.
非均匀有理B样条基函数具有与B样条基函数一样的性质.与B样条相比,非均匀有理B样条基函数通过改变权值可以更准确地建立二次曲线或曲面;权值相同时,非均匀有理B样条基函数将退化为B样条基函数.
非均匀有理B样条基函数的单位分解性、线性无关性、紧支性和有限元方法中的拉格朗日基函数是一致的,非均匀有理B样条基函数的高阶连续性可以保证单元间至少具有$C^1$连续,拉格朗日基函数在单元间是$C^0$连续,因此非均匀有理B样条基函数有利于构造高阶连续的未知变量场;非均匀有理B样条基函数的非负性,能够保证在求解接触问题时各点的接触力为正值,拉格朗日基函数不具有非负性,会出现负的接触力;同时非均匀有理B样条基函数具有的保型细分性,可以保证采用节点插入算法进行细分时不改变几何体的实际形状.
非均匀有理B样条曲线可由控制点及其相对应的非均匀有理B样条基函数构造,形式如下
|
\[C\left( s \right)=\sum\limits_{i=0}^{n}{R_{i}^{p}\left( s \right)}{{P}_{i}}\]
|
(10) |
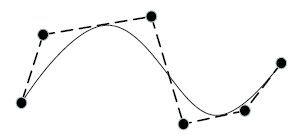
其中,$P_i $为非均匀有理B样条曲线的控制点.图1为一条典型的非均匀有理B样条曲线,其采用的基函数如图2所示.
3 弹性静力摩擦接触问题的比例边界等几何分析方程推导
3.1 比例边界坐标变换
下面所用到的变量和符号,除特殊说明外,均适用于整个接触系统,故省略上标$\alpha$.
对于弹性静力摩擦接触问题的比例边界等几何分析方程的推导,需建立笛卡尔坐标系与比例边界等几何坐标系的转换关系.对任一接触体$\Omega$,如图3所示,其相似中心为$O$,边界$\Gamma$由侧面边界$\Gamma _{\rm s} $和外边界$\Gamma _{\rm b}$组成,侧面边界$\Gamma _{\rm s} $不需要离散,外边界$\Gamma_{\rm b}$为非均匀有理B样条曲线,并用非均匀有理B样条基函数进行离散,实心圆点为控制点,虚线为控制点网格,空心点为$\Gamma_{\rm b} $边界单元节点,加粗黑线为可能接触边界$\Gamma _{\rm c}$. 环向坐标$\eta $与径向坐标$\xi$构成了比例边界等几何坐标系,环向坐标$\eta $张成外边界$\Gamma_{\rm b} $的非均匀有理B样条参数空间,径向坐标$\xi$是无量纲的比例坐标,表示外边界$\Gamma _{\rm b}$的"缩放因子".
实体空间内任意一点的笛卡尔坐标与参数空间内比例边界等几何坐标的映射关系
|
\[\left. \begin{array}{*{35}{l}}
\hat{x}=\xi (x(\eta )-{{{\hat{x}}}_{0}}))+{{{\hat{x}}}_{0}}=\xi (R(\eta )x-{{{\hat{x}}}_{0}})+{{{\hat{x}}}_{0}} \\
\hat{y}=\xi (y(\eta )-{{{\hat{y}}}_{0}}))+{{{\hat{y}}}_{0}}=\xi (R(\eta )y-{{{\hat{y}}}_{0}})+{{{\hat{y}}}_{0}} \\
\end{array} \right\}\]
|
(11) |
其中,$\xi$和$\eta $表示比例边界等几何坐标,$0 \le \xi \le1$;$(\hat {x},\hat {y})$表示计算域内点的笛卡尔坐标;$(\hat {x}_0,\hat {y}_0 )$表示相似中心笛卡尔坐标;$(x(\eta )$和$(\eta))$表示边界$\xi = 1$上非均匀有理B样条曲线节点的笛卡尔坐标;${ {x}} = \{x_1 ,x_2 ,\cdots \},{{ y}} = \{y_1 ,y_2 ,\cdots\}$表示与边界等几何单元相关联的控制点笛卡尔坐标;$R(\eta ) = [R_1(\eta ){\kern 1pt} \quad R_2 (\eta ){\kern 1pt} \quad \cdots]$表示与边界等几何单元相关联的非均匀有理B样条形函数.
边界等几何单元的雅可比矩阵可表示为
|
\[\hat{J}(\xi ,\eta )=\left[ \begin{matrix}
{{{\hat{x}}}_{,\xi }} & {{{\hat{y}}}_{,\xi }} \\
{{{\hat{x}}}_{,\eta }} & {{{\hat{y}}}_{,\eta }} \\
\end{matrix} \right]=\left[ \begin{matrix}
1 & {} \\
{} & \xi \\
\end{matrix} \right]{{J}_{\xi }}(\eta )\]
|
(12) |
其中,${{ J}}_\xi (\eta)$表示边界雅可比矩阵,其逆矩阵可写成如下形式
|
\[J_{\xi }^{-1}(\eta )=\left[ \begin{matrix}
{{j}_{11}} & {{j}_{12}} \\
{{j}_{21}} & {{j}_{22}} \\
\end{matrix} \right]\]
|
(13) |
对域内任意一个微小单元面积${\rm d}\Omega $可表示为
|
\[\text{d}\Omega =\left| {\hat{J}} \right|\text{d}\xi \text{d}\eta =\xi \left| J \right|\text{d}\xi \text{d}\eta \]
|
(14) |
引入笛卡尔坐标系下的微分算子
|
\[\mathbf{L}={{b}_{1}}\frac{\partial }{\partial \xi }+\frac{1}{\xi }{{b}_{2}}\frac{\partial }{\partial \eta }\]
|
(15) |
其中
|
\[{{b}_{1}}=\left[ \begin{matrix}
{{j}_{11}} & {} \\
{} & {{j}_{21}} \\
{{j}_{21}} & {{j}_{11}} \\
\end{matrix} \right],\quad {{b}_{2}}=\left[ \begin{matrix}
{{j}_{12}} & {} \\
{} & {{j}_{22}} \\
{{j}_{22}} & {{j}_{12}} \\
\end{matrix} \right]\]
|
(16) |
根据等参概念,位移场变量可采用与坐标相同的非均匀有理B样条形函数表示
|
\[\text{d}u(\xi ,\eta )=R\text{d}u(\xi )\]
|
(17) |
其中,$u(\xi )$表示控制点位移,是关于径向坐标的函数.
应变场为
|
\[\text{d}\varepsilon =\mathbf{L}\text{d}u(\xi )={{B}_{1}}\text{d}u{{(\xi )}_{,\xi }}+\frac{1}{\xi }{{B}_{2}}\text{d}u(\xi )\]
|
(18) |
其中
|
\[\left. \begin{array}{*{35}{l}}
{{B}_{1}}={{b}_{1}}R \\
{{B}_{2}}={{b}_{2}}{{R}_{,\eta }} \\
\end{array} \right\}\]
|
(19) |
3.2 域边界等几何离散
弹性静力摩擦接触问题的增量虚功方程为
|
\[\begin{align}
& \begin{matrix}
\int_{{{\Omega }^{1}}+{{\Omega }^{2}}}{\delta \text{d}{{\varepsilon }^{\text{T}}}\text{d}\sigma }\text{d}\Omega -\int_{{{\Omega }^{1}}+{{\Omega }^{2}}}{\delta \text{d}{{u}^{\text{T}}}\text{d}\bar{b}}\text{d}\Omega - \\
~\int_{\Gamma _{\text{bq}}^{1}+\Gamma _{\text{bq}}^{2}}{\delta \text{d}{{u}^{\text{T}}}\text{d}{{{\bar{q}}}_{\text{b}}}}\text{d}\Gamma -\int_{\Gamma _{\text{sq}}^{1}+\Gamma _{\text{sq}}^{2}}{\delta \text{d}{{{\hat{u}}}^{\text{T}}}\text{d}{{{\bar{q}}}_{\text{s}}}}\text{d}\xi - \\
\end{matrix} \\
& \int_{{{\Gamma }_{\text{c}}}}{{{(\delta \text{d}u_{\text{c}}^{1}-\delta \text{d}u_{\text{c}}^{2})}^{\text{T}}}}\text{d}{{p}_{\text{c}}}\text{d}\Gamma =0\text{ } \\
\end{align}\]
|
(20) |
|
\[\text{d}{{u}_{i}}\in {{D}_{\text{u}}}=\left\{ \text{d}{{u}_{i}}:\text{d}{{u}_{i}}=\text{d}{{{\bar{u}}}_{i}}\quad {{x}_{i}}\in {{\Gamma }_{\text{u}}} \right\}~\]
|
(21) |
其中,$d{{ u}}_{\rm c}^\alpha $表示接触体$\alpha$在公共接触边界处$\Gamma _{\rm c} $的位移增量,${\rm d}{{p}}_{\rm c} $表示接触系统在公共接触边界处$\Gamma _{\rm c}$的接触应力增量,$\Gamma _{\rm bq} ,\Gamma _{\rm sq}$分别表示存在面力增量的外边界和侧面边界,$D_{\rm u}$表示可行位移集.
将式(17),(18)代入式(20),得到
|
\[\begin{align}
& \begin{array}{*{35}{l}}
{{\left. \delta \text{d}{{u}^{\text{T}}}({{E}_{0}}\text{d}{{u}_{,\xi }}+{{({{E}_{1}})}^{\text{T}}}\text{d}u-\text{d}P-\text{d}R) \right|}_{\xi =1}}- \\
\int_{{{\xi }_{0}}}^{{{\xi }_{1}}}{\{\delta }\text{d}u{{(\xi )}^{\text{T}}}\frac{1}{\xi }[{{E}_{0}}{{\xi }^{2}}\text{d}u{{(\xi )}_{,\xi \xi }}+ \\
({{E}_{0}}+{{({{E}_{1}})}^{\text{T}}}-{{E}_{1}})\xi \text{d}u{{(\xi )}_{,\xi }}- \\
\end{array} \\
& {{E}_{2}}\text{d}u(\xi )+\text{d}F(\xi )]\}\text{d}\xi =0~~ \\
\end{align}\]
|
(22) |
其中
|
\[\left. \begin{array}{*{35}{l}}
{{E}_{0}}=\int_{{{\eta }_{i}}}^{{{\eta }_{i+1}}}{{{B}^{1}}{{(\eta )}^{\text{T}}}D{{B}^{1}}(\eta )\left| J \right|\text{d}\eta } \\
{{E}_{1}}=\int_{{{\eta }_{i}}}^{{{\eta }_{i+1}}}{{{B}^{2}}{{(\eta )}^{\text{T}}}D{{B}^{1}}(\eta )\left| J \right|\text{d}\eta } \\
{{E}_{2}}=\int_{{{\eta }_{i}}}^{{{\eta }_{i+1}}}{{{B}^{2}}{{(\eta )}^{\text{T}}}D{{B}^{2}}(\eta )\left| J \right|\text{d}\eta } \\
\text{d}P=\int_{\Gamma _{\text{bq}}^{\text{1e}}+\Gamma _{\text{bq}}^{\text{2e}}}{{{R}^{\text{T}}}\text{d}{{{\bar{q}}}_{\text{b}}}(\eta )}\text{d}\Gamma \\
\text{d}R=\int_{\Gamma _{\text{c}}^{\text{e}}}{{{R}^{\text{T}}}\text{d}{{p}_{\text{c}}}(\eta )\text{d}\Gamma } \\
\text{d}F(\xi )={{\xi }^{2}}\int_{\Gamma _{\text{b}}^{\text{e}}}{{{R}^{\text{T}}}\text{d}\bar{b}(\xi ,\eta )\left| J \right|\text{d}\eta }+\xi \text{d}{{{\bar{q}}}_{\text{s}}}(\xi ) \\
\end{array} \right\}\]
|
(23) |
式中,${{ E}}_0 ,{{ E}}_1$和${{ E}}_2$表示外边界各单元的系数矩阵,${\rm d}{{P}}$表示外边界等效控制点面力增量,${\rm d}{{R}}$表示外边界等效控制点接触力增量,${\rm d}{{F}}(\xi)$表示等效控制点体力增量.
根据$\delta {{ u}}$和$\delta {{ u}}(\xi)$的任意性,式(22)可写成如下形式
|
\[\begin{align}
& {{E}_{0}}{{\xi }^{2}}\text{d}u{{(\xi )}_{,\xi \xi }}+({{E}_{0}}+{{({{E}_{1}})}^{\text{T}}}-{{E}_{1}})\xi \text{d}u{{(\xi )}_{,\xi }}- \\
& {{E}_{2}}\text{d}u(\xi )+\text{d}F(\xi )=0 \\
\end{align}\]
|
(24) |
|
\[{{E}_{0}}\text{d}{{u}_{,\xi }}+{{({{E}_{1}})}^{\text{T}}}\text{d}u-\text{d}P-\text{d}R=0~\]
|
(25) |
式(24)为域内偏微分方程,式(25)为外边界$(\xi =1)$上的代数方程.式(24)和(25)均由一个单元$\Omega ^{rme}$导出,故边界各单元的系数矩阵、等效控制点面力、接触力和体力按照控制点自由度集成整体系数矩阵,其形式与式(24)和(25)相同.
4 弹性静力摩擦接触问题的求解
4.1 比例边界等几何分析方程的求解
域内偏微分方程(24)为二阶非齐次常微分方程,当方程中的非齐次向可以忽略时,可采用特征值[29]求解.
引入对偶变量,即等效控制点内力
|
\[\text{d}f(\xi )={{E}_{0}}\xi \text{d}{{u}_{,\xi }}+{{({{E}_{1}})}^{\text{T}}}\text{d}u\]
|
(26) |
联立式(24)和(26),得到
|
\[\xi X{{(\xi )}_{,\xi }}=-ZX(\xi )~\]
|
(27) |
|
\[Z=\left[ \begin{matrix}
{{({{E}_{0}})}^{-1}}{{({{E}_{1}})}^{\text{T}}} & -{{({{E}_{0}})}^{-1}} \\
{{E}_{1}}{{({{E}_{0}})}^{-1}}{{({{E}_{1}})}^{\text{T}}}-{{E}_{2}} & -{{E}_{1}}{{({{E}_{0}})}^{-1}} \\
\end{matrix} \right]\]
|
(28) |
|
\[X(\xi )=\left\{ \begin{matrix}
\text{d}u(\xi ) \\
\text{d}f(\xi ) \\
\end{matrix} \right\}~\]
|
(29) |
其中,${{ Z}}$为哈密顿矩阵,对其进行特征分解
|
\[Z\Phi =\Phi \text{ }\Lambda =\left[ \begin{matrix}
\text{ }{{\Phi }_{11}} & \text{ }{{\Phi }_{12}} \\
\text{ }{{\Phi }_{21}} & \text{ }{{\Phi }_{22}} \\
\end{matrix} \right]\left[ \begin{matrix}
{{\lambda }_{n}} & {} \\
{} & {{\lambda }_{p}} \\
\end{matrix} \right]\]
|
(30) |
其中,${{ \lambda }}_n $为负特征值,${{ \lambda }}_p$为正特征值,且${{ \lambda }}_n = - {{ \lambda }}_p $.
一阶微分方程(27)的通解为
|
\[X(\xi )=\left[ \begin{matrix}
\text{ }{{\Phi }_{11}} & \text{ }{{\Phi }_{12}} \\
\text{ }{{\Phi }_{21}} & \text{ }{{\Phi }_{22}} \\
\end{matrix} \right]\left[ \begin{matrix}
{{\xi }^{-{{\lambda }_{n}}}} & {} \\
{} & {{\xi }^{-{{\lambda }_{p}}}} \\
\end{matrix} \right]\left\{ \begin{matrix}
{{c}_{1}} \\
{{c}_{2}} \\
\end{matrix} \right\}\]
|
(31) |
即位移和等效控制点内力的通解为
|
\[\left. \begin{matrix}
\text{d}u(\xi )={{\Phi }_{11}}{{\xi }^{-{{\lambda }_{n}}}}{{c}_{1}}+{{\Phi }_{12}}{{\xi }^{-{{\lambda }_{p}}}}{{c}_{2}} \\
\text{d}f(\xi )={{\Phi }_{21}}{{\xi }^{-{{\lambda }_{n}}}}{{c}_{1}}+{{\Phi }_{22}}{{\xi }^{-{{\lambda }_{p}}}}{{c}_{2}} \\
\end{matrix} \right\}\]
|
(32) |
根据$\left| {{\rm d}{{ u}}(\xi = 0)} \right| < \infty
$,则系数$c_2 = 0$.
在式(26)中取$\xi = 1$,并考虑式(25)可得
|
\[\text{d}f(\xi =1)={{E}_{0}}\text{d}{{u}_{,\xi }}+{{({{E}_{1}})}^{\text{T}}}\text{d}u=\text{d}P+\text{d}R\]
|
(33) |
在式(32)中消去积分常数,并将式(33)代入可得
|
\[K\text{d}u-\text{d}P-\text{d}R=0\]
|
(34) |
|
\[K={{\Phi }_{21}}{{({{\Phi }_{11}})}^{-1}}\]
|
(35) |
式(34)为边界等几何代数方程,求解该方程获得边界位移增量$\text{d}u$,再通过式(32)获得积分常数$c_1$和域内的位移增量.
4.2 摩擦接触条件的B可微方程组
摩擦接触条件的B可微方程组表示形式如下
|
\[H_{2}^{i}=\min \left\{ r\Delta \text{d}u_{n}^{i},p_{n}^{i} \right\}=0\]
|
(36) |
|
\[H_{3}^{i}=p_{\tau }^{i}-\lambda p_{\tau }^{i}\left( r \right)=0~\]
|
(37) |
式中
|
\[\left. \begin{array}{*{35}{l}}
p_{\tau }^{i}\left( r \right)=p_{\tau }^{i}-r\Delta \text{d}u_{\tau }^{i} \\
\lambda =\min \left\{ \mu \max \left\{ p_{n}^{i},0 \right\}/\left| p_{\tau }^{i} \right|,1 \right\} \\
\end{array} \right\}\]
|
(38) |
其中,$i = 1,2,\cdots,NC$;$r$取正值,$NC$表示可能接触点对总数,$p_n^i$和$p_\tau ^i$分别表示接触点对$i$处的法向和切向接触力,$\Delta {\rm d}u_n^i$和$\Delta {\rm d}u_\tau ^i$分别表示接触点对$i$处的法向和切向相对位移增量.
将边界等几何代数方程(34)与表示接触条件的式(36)和(37)联立,得到二维弹性摩擦接触系统的边界控制方程,记为
|
\[H\left( x \right)={{\left\{ {{H}_{1}},{{H}_{2}},{{H}_{3}} \right\}}^{\text{T}}}={{\left\{ 0,0,0 \right\}}^{\text{T}}}\]
|
(39) |
式中,$H_1 =0$边界等几何代数方程,变量$x$表示节点位移和接触点对的接触力向量.式(39)可采用B可微阻尼牛顿法[30]进行求解,其收敛性具有理论保证.
4.3 真实接触区域的识别
对可能接触边界进行离散后,通过B可微阻尼牛顿法求解式(39)可获得边界单元结点的接触力.在网格较稀疏的情况下,边界单元结点难以与真实接触区域边界重合,无法获得真实的接触长度.
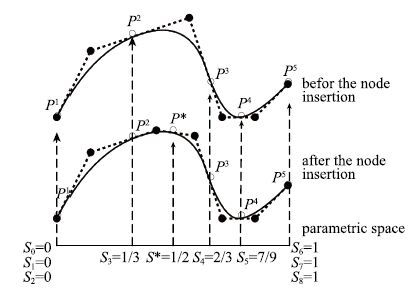
以图4为例说明如何进行真实接触区域的识别.在图4中,实线表示可能接触边界$\Gamma _{\rm c}
$,虚线表示控制点网格,实心圆表示控制点,空心圆表示单元结点,在节点矢量端点处控制点与单元结点重合.
首先根据式(39)得到边界结点$P^{i}$处的接触力$F^{i}$,若$F^{2}$不为零,$F^{3}$为零,则表示真实的接触区域边界位于$P^{2}$与$P^{3}$ 之间,在节点$S_{2}$与$S_{3}$之间插入新的节点$S*$,生成新结点$P*$;然后再次求得各结点处的接触力$F^{i}$,若$F*$等于零,则在$S_{2}$与$S*$之间插入新的节点$S'$,若$F*$不等于零,则在$S*$与$S_{3}$之间插入新的节点$S'$,生成新结点$P'$;重新计算各结点处的接触力$F^{i}$,根据$F'$判断插入节点的位置.依次类推,直至$P^{i}$与新生成的结点$P'$之间的距离小于容许误差,此时结点$P'$的位置就是真实接触区域的边界.值得注意的是:每次插入的新节点只在本次识别过程中存在,并不会引起额外的计算量.
5 数值算例
5.1 精确的几何描述
传统的数值方法如有限元方法、比例边界有限元等主要通过拉格朗日基函数描述域边界,而比例边界等几何分析中采用非均匀有理B样条基函数描述域边界.为了对比非均匀有理B样条基函数与拉格朗日基函数在描述域边界的精确性,选取如图5所示的圆弧分别采用比例边界等几何分析和比例边界有限元进行离散,离散时均采用二阶基函数,圆弧半径为1.由图6可见,除了在结点上拉格朗日单元仅可以近似的描述域边界几何形状,而非均匀有理B样条单元可逐点精确描述域边界的几何形状.非均匀有理B样条基函数的这一特性使比例边界等几何分析求解接触问题时,可以精确描述接触边界.
5.2 赫兹接触问题
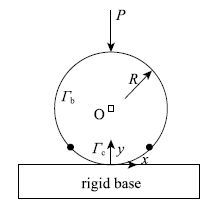
为了验证本文算法的精确性,选取具有解析解的赫兹接触问题进行对比分析.如图7所示,圆柱体与刚性基础接触,圆柱体半径$R=8$m,弹性模量$E=1~000$ Pa,泊松比$\nu =0.3$,外载荷$P=240$ N.该问题可简化为平面应变问题.
根据赫兹接触理论,圆柱体接触问题的接触区域半宽$a$和接触应力沿接触区域$a$的合力$F$可分别由式(40)和(41)求得.
|
\[a=2\sqrt{\frac{PR\left( 1-{{\nu }^{2}} \right)}{\pi LE}}\]
|
(40) |
|
\[F=\frac{P}{2}-\int_{r}^{a}{\frac{2P}{\pi {{a}^{2}}L}}\sqrt{{{a}^{2}}-{{x}^{2}}}\text{d}x,\quad r\in \left[ 0,a \right]\]
|
(41) |
由于基础为刚性,只需对圆柱体进行分析计算.圆柱体为一个封闭域,整个边界均为外边界$\Gamma _{\rm b}$,侧面边界$\Gamma _{\rm s}$不存在,将相似中心放在圆柱体中心,对外边界$\Gamma _{\rm b}$采用2阶非均匀有理B样条基函数进行描述与等几何离散后,利用节点反演算法在外边界$\Gamma_{\rm b} $上确定可能接触边界$\Gamma _{\rm c}$,并对可能接触边界$\Gamma _{\rm c}$采用$h$细分算法进行局部细分获得具有21个控制点和41个控制点的两种计算模型.
根据式(40)可求得接触区域长度$a =1.4915$,表1中列出本文算法计算出的接触区域长度,及其与赫兹解析解之间的相对误差.由表1可见,本文算法可以获得高精度的接触区域长度.
表1(Table 1)

表1 接触区域半宽Table 1 The half of contact region
| Model |
| SBIGA-model 1 | SBIGA-model 2 |
| contact region $a_0 $ | 1.499~7 | 1.484~2 |
| relative error $\dfrac{a_0 - a}{a}$ | 0.55% | 0.49% |
|
表1 接触区域半宽
Table 1 The half of contact region |
本文算法计算出的接触力合力与赫兹解析解对比如图8所示,由图8可见本文算法计算出的接触力合力与赫兹解析解相当吻合,并且随着局部加密精度进一步提高.
5.3 悬臂梁接触问题
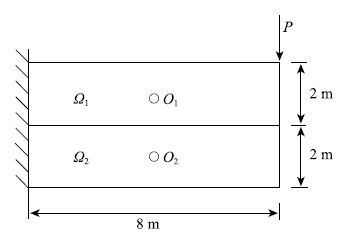
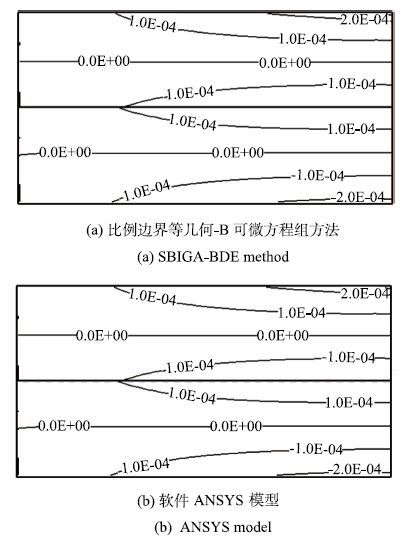
为了检验本文算法在求解带摩擦的接触问题时的正确性,考虑如图9所示的悬臂梁接触问题.图9中粗实线表示可能接触区域,$P=100$ kN.悬臂梁材料参数:弹性模量10 GPa,泊松比0.3,摩擦系数0.5.目前摩擦接触问题尚无解析解,因此本文采用软件ANSYS中的结果作为参考解.在软件ANSYS中采用较密的网格(结点数为3402),点点接触模型;本文算法模型中共216个控制点,相似中心放在$O_{1}$和$O_{2}$处.
表2中列出了本文算法与软件ANSYS点点接触模型计算出的法向和切向接触力合力,两种方法计算出的接触力合力较吻合,最大相对误差为0.127%.图10和图11分别为悬臂梁的$X$和$Y$向位移分布图,由图可见本文算法与软件ANSYS计算出的位移分布与大小基本相同.
表2(Table 2)

表2 不同接触模型接触面上总的接触力Table 2 Total contact forces for difference models
| Contact | Contact force$/$kN |
| model | normal | tangential |
| SBIGA-BDE | 53.682 | 26.841 |
| ANSYS | 53.749 | 26.875 |
| relative error $\dfrac{F_{\rm IGA - B} -F_{\rm ANSYS} }{F_{\rm {SBIGA}} }$ | 0.125% | 0.127% |
|
表2 不同接触模型接触面上总的接触力
Table 2 Total contact forces for difference models |
6 结论
在求解二维摩擦接触问题时,本文算法只需对接触边界进行离散,能够通过非均匀有理B样条精确描述接触边界,避免了几何模型与计算模型之间的误差;在对接触体离散之后,使二维问题转变为了一维问题,减少了计算量,可进行局部保形细分,并可通过节点插入算法进行真实接触区域的识别.赫兹接触算例表明,本文方法在较少控制点的情况下可获得较高精度的计算结果,计算精度随着网格加密可进一步提高;悬臂梁接触算例表明,本文方法在求解摩擦接触问题时的有效性.
参考文献
| [1] |
孙林松, 王德信, 谢能刚. 接触问题有限元分析方法综述. 水利水电科技进展, 2001, 21(3): 18-20 (Sun Linsong, Wang Dexin, Xie Nenggang. A summary of finite element analysis for contact problems. Advances in Science and Technology of Water Resources,2001, 21(3): 18-20 (in Chinese)) |
| [2] |
赵兰浩, 李同春, 牛志伟. 有初始间隙摩擦接触问题的有限元混合法. 岩土工程学报, 2006, 28(11): 2015-2018 (Zhao Lanhao, Li Tongchun, Niu Zhiwei. Mixed finite element method for contact problems with friction and initial gap. Chinese Journal of Geotechnical Engineering, 2006, 28 (11) : 2015-2018 (in Chinese)) |
| [3] |
刘永健, 姚振汉. 三维弹性体移动接触边界元法的一类新方案. 工程力学, 2005, 22(1): 6-11 (Liu Yongjian, Yao Zhenhan. A new scheme of BEM for moving contact of 3D elastic solid. Engineering Mechanics , 2005, 22 (1): 6-11 (in Chinese)) |
| [4] |
杨霞, 肖宏, 陈泽军. 基于轴承边界元法的轧机圆锥滚子轴承的载荷研究. 应用力学学报, 2014, 31(1): 137-143 (Yang Xia, Xiao Hong, Chen Zejun. Analysis of the distribution of mill conical roller bearing boundary element method, Chinese Journal of Applied Mechanism, 2014, 31 (1): 137-143 (in Chinese)) |
| [5] |
Lorenzis LD, Wriggers P, Hughes TJR. Isogeometric contact: a review. GAMM-Mitteilungen , 2014, 37 (1): 85-123 |
| [6] |
Hughes TJR, Cottrell JA, Bazilevs Y. Isogeometric analysis: CAD, finite elements, NURBS, exact geometry and mesh refinement. Computer Methods in Applied Mechanics & Engineering,2005, 194: 4135-4195 |
| [7] |
吴紫俊,黄正东,左兵权等. 等几何分析研究概述. 机械工程学报,2015, 51 (5): 114-129 (Wu Zijun, Huang Zhengdong, Zuo Bingquan,et al. Perspectives on isogeometric analysis, Journal of Mechanical Engineering, 2015, 51 (5): 114-129 (in Chinese)) |
| [8] |
Hughes TJR, Reali A, Sangalli G. Efficient quadrature for NURBSbased isogeometric analysis. Computer Methods in Applied Mechanics & Engineering, 2010, 199 (5): 301-313 |
| [9] |
Lorenzis LD, Wriggers P, Zavarise G. A mortar formulation for 3D large deformation contact using NURBS-based isogeometric analysis and the augmented Lagrangian method. Computational Mechanics,2011, 49 (1): 1-20 |
| [10] |
Dimitri R, De Lorenzis L, Scott MA, et al. Isogeometric large deformation frictionless contact using T-splines. Computer Methods in Applied Mechanics & Engineering, 2014, 269 (1): 394-414 |
| [11] |
Temizer I, Wriggers P, Hughes TJR. Three-dimensional mortarbased frictional contact treatment in isogeometric analysis with NURBS. Computer Methods in Applied Mechanics & Engineering,2012, 209 (1): 115-128 |
| [12] |
Temicer I, Wiggrs P, Hughes TJR. Three-dimensional mortar-based frictional contact treatment in isogeometric analysis with NURBS. Computer Methods in Applied Mechanics & Engineering, 2012, 209 (1):115-128 |
| [13] |
Song CM, Wolf JP. Consistent Infinitesimal finite-element cell method: three-dimensional vector wave equation. International Journal for Numerical Methods in Engineering, 1996, 39 (13):2189-2208 |
| [14] |
Deeks A J,Wolf J P. A virtual work derivation of the scaled boundary finite-element method for elastostatics. Computational Mechanics,2002, 28 (6): 489-504 |
| [15] |
Liu J Y, Lin G, Li XC, et al. Evaluation of stress intensity factors for multiple cracked circular disks under crack surface tractions with SBFEM. China Ocean Engineering, 2013, 27 (3): 417-426 |
| [16] |
Li C, Song C, Man H, et al. 2D dynamic analysis of cracks and interface cracks in piezoelectric composites using the SBFEM. International Journal of Solids & Structures, 2014, 51: 2096-2108 |
| [17] |
张勇, 林皋, 胡志强等. 基于等几何分析的比例边界有限元方法. 计算力学学报, 2012, 29 (3): 433-438 (Zhang Yong, Lin Gao, Hu Zhiqiang, et al. Scaled boundary finite element based on isogeometric analisys. Chinese Journal of Computational Mechanics, 2012,29 (3): 433-438 (in Chinese)) |
| [18] |
Lin G, Zhang Y, Hu ZQ, et al. Scaled boundary isogeometric analysis for 2D elastostatics. Science China Physics, Mechanics and Astronomy, 2014, 57 (2): 286-300 |
| [19] |
张勇, 林皋, 胡志强. 比例边界等几何分析方法I:波导本征问题. 力学学报, 2012, 44 (2): 382-392 (Zhang Yong, Lin Gao, Hu Zhiqiang. Scaled boundary isogeometric analysis and its application I: eigenvalue problem of waveguide. Chinese Journal of Theoretical and Applied Mechanics, 2012, 44 (2): 382-392 (in Chinese)) |
| [20] |
Natarajan S, Wang J, Song C, et al. Isogeometric analysis enhanced by the scaled boundary finite element method. Computer Methods in Applied Mechanics and Engineering, 2015, 283: 733-762 |
| [21] |
Lin G, Zhang Y, Wang Y, et al. Coupled isogeometric and scaled boundary isogeometric approach for earthquake response analysis of dam-reservoir-foundation system. Lisbon: 2012 |
| [22] |
Rahman MU, Rowlands RE, Cook RD, et al. An iterative procedure for finite-element stress analysis of frictional contact problems. Computers and Structures, 1984, 18 (6): 947-954 |
| [23] |
钟万勰. 弹性接触问题的参数变分原理及参数二次规划求解. 计算结构力学及其应用, 1985, 2(1): 1-9 (Zhong Wanxie. Parameter variational principle and parameter quadratic programming method for elastic contact problem. Computational Structural Mechanics and Application, 1985, 2 (1): 1-9 (in Chinese)) |
| [24] |
Klarbring A. A mathematical programming approach to threedimensional contact problems with friction. Computer Method in Applied Mechanics Engineering, 1986, 58 (2): 175-200 |
| [25] |
Leung AYT, Chen GQ, Chen WJ. Smoothing Newton method for solving two-and three-dimensional frictional contact problem. International Journal Numerical Methods in Engineering, 1998, 41 (6): 1001-1027 |
| [26] |
Li XW, Ai-Kah Soh, Chen WJ. A new nonsmooth model for three dimensional frictional contact problem. Computational Mechanics,2000, 26 (6): 528-535 |
| [27] |
Christensen P, Klarbring A, Pang JS, et al. Formulation and comparison of algorithm for frictional contact problems. International Journal Numerical Methods in Engineering, 1998, 42 (1): 145-173 |
| [28] |
Piegl L, TillerW. The NURBS Book. Berlin: Springer-Verlag, 1997 |
| [29] |
Song C, Wolf JP. Body loads in scaled boundary finite-element method. Computer Methods in Applied Mechanics & Engineering,1999, 180 (1-2): 117-135 |
| [30] |
Pang JS. Newton's method for B-differentiable equations. Mathematics of Operations Research, 1990, 15 (2): 311-341 |
ANALYSIS OF FRICTIONAL CONTACT PROBLEMS BY SBIGA-BDE METHOD
Xue Binghan , Lin Gao, Hu Zhiqiang, Pang Lin
, Lin Gao, Hu Zhiqiang, Pang Lin
Faculty of Infrastructure Engineering, Dalian University of Technology, Dalian 116024, China
Abstract: Frictional contact analysis is one of the most challenging problems in computational mechanics. The functional system of the contact problem is not only nonlinear, but also non-smooth, so in general the convergence and accuracy of contact algorithms are di cult to be guaranteed. For 2D elastic frictional contact problem, the scaled boundary isogeometric analysis combined with B di erential equation method (SBIGA-BDE method) is developed. Based on the scaled boundary isogeometric transformation, the contact equilibrium equation is derived by using virtual principle. The contact conditions are formulated as B di erential equation and satisfied rigorously. The convergence of the algorithm to solve the B di erential equation is guaranteed by the theory of mathematical programming. In the proposed method, only the outer boundary including the contact boundary need to be discretized isogeometrically, which reduces the spatial dimension by one and the boundary are represented accurately. The real contact length can be detected by the knot insertion algorithm. In addition, as the interpolatory functions used in geometry modeling and numerical analyzing are the same, the time costs in mesh generation is saved. The numerical examples, including Hertz contact problem and cantilever beams frictional contact problem, are presented and compared with analytic solution and ANSYS results. It validates the e ectiveness and accuracy of the proposed method in solving 2D elastic frictional contact problem.
Key words:
elastic frictional contact problem scaled boundary isogeometric analysis scaled boundary finite element method B dierential equation numerical modeling






 2016, Vol. 48
2016, Vol. 48