可重复使用空天飞行器起飞和再入过程中,以超声速穿过大气层,会受到剧烈的气动加热作用.飞行器表面温度可达1 100℃以上[1],需要可靠的热防护系统.传统热防护结构采用陶瓷隔热瓦和金属承载件相结合的多层结构,在陶瓷-金属界面处材料物理性能有突变,因此存在严重的热应力集中[2].1986年以来发展的功能梯度材料能有效缓解因不同材料热膨胀失配引起的热应力问题[3, 4].功能梯度材料(functionally graded materials,FGMs)是采用先进材料复合技术由2种或多种不同材料组合而成的非均质材料[5].功能梯度材料的构成要素(组份、组织、显微气孔率等)随空间位置呈梯度连续变化,因此能充分减少和克服组份材料结合部位界面性能的不匹配因素.将功能梯度壁板用于超声速飞行器,不仅能消除气动加热带来的壁板内部热应力集中,提高结构承受热载荷的能力,而且可以利用功能梯度材料的可设计特性,通过调整材料的组份,充分利用隔热和承载材料的性能,使壁板整体展现出同时兼顾热防护和承载的新的设计功能.
不同于传统均质结构,功能梯度板壳由于材料梯度分布带来结构非对称,常导致结构的中性面与几何中面不重合,使结构易发生非对称弯曲/振动、力热耦合、屈曲等问题[6, 7, 8, 9].功能梯度结构的建模理论和力-热耦合问题近年来受到广泛关注[10, 11, 12, 13, 14, 15].基尔霍夫(Kirchhoff)板理论、一阶/高阶剪切变形理论都可用于功能梯度板壳的热应力、屈曲和动力学分析[16, 17, 18, 19, 20].功能梯度壁板作为飞行器外层蒙皮结构,气动-热-结构耦合可诱发屈曲(静发散)、颤振以及二者合成的复杂力学现象[21, 22, 23, 24, 25, 26, 27].研究表明,尽管功能梯度壁板的颤振速压较高(相对于金属壁板),但壁板受热后易发生弯曲/后屈曲变形,且材料组份、温度分布、气动阻尼、边界约束等都会对壁板气动弹性变形和响应产生重要影响[28, 29].当组份材料沿板厚方向梯度分布时,由于壁板上、下表面的应力不对称,功能梯度壁板的颤振振幅也较大[30].
鉴于功能梯度壁板在高速飞行器热结构设计中良好的应用前景,以及壁板复杂的气动-热-结构耦合机制,本文拟开展超声速气流中功能梯度壁板的热气动弹性分析.考虑到当前研究多在无变形的结构初始状态下采用线性方法分析功能梯度壁板的颤振边界,本文首先分析功能梯度壁板的热过屈曲变形,然后研究后屈曲平衡态下结构的气动弹性稳定性,进而确定功能梯度壁板的非线性颤振边界.
1 力学模型 1.1 材料等效力学性能
假设功能梯度材料由陶瓷和金属复合而成,且陶瓷体积含量沿板厚方向($z$方向)的分布可表述为幂函数
\[{{V}_{\text{c}}}={{\left( \frac{z}{h}+\frac{1}{2} \right)}^{n}},-h/2\le z\le h/2\]
(1a)
\[{{V}_{\text{m}}}=1-{{V}_{\text{c}}}\]
(1b)
利用宏观力学分析的空间均质化方法,假设各组份材料承受的面内应力相同,则功能梯度壁板的宏观力学性能空间分布可由线性混合律描述
\[P(z)={{P}_{\text{c}}}{{V}_{\text{c}}}+{{P}_{\text{m}}}{{V}_{\text{m}}}\]
(2)
基于明德林(Mindlin)板理论,壁板的内部位移场可由中面位移和法线转角确定
\[\left. \begin{matrix}
u(x,y,z)={{u}_{0}}(x,y)+z{{\theta }_{y}}(x,y) \\
v(x,y,z)={{v}_{0}}(x,y)+z{{\theta }_{x}}(x,y) \\
w(x,y,z)={{w}_{0}}(x,y) \\
\end{matrix} \right\}\]
(3)

|
图1 功能梯度壁板示意图 Fig.1 Schematic of a functionally graded (FG) panel |
为考虑壁板大挠度变形的几何非线性,采用冯$ \cdot $卡门(von Karman)应变-位移关系
\[\left. \begin{array}{*{35}{l}}
{{\varepsilon }_{x}}=\frac{\partial {{u}_{0}}}{\partial x}+z\frac{\partial {{\theta }_{y}}}{\partial x}+\frac{1}{2}{{\left( \frac{\partial w}{\partial x} \right)}^{2}} \\
{{\varepsilon }_{y}}=\frac{\partial {{v}_{0}}}{\partial y}+z\frac{\partial {{\theta }_{x}}}{\partial y}+\frac{1}{2}{{\left( \frac{\partial w}{\partial y} \right)}^{2}} \\
{{\gamma }_{xy}}=\frac{\partial {{u}_{0}}}{\partial y}+\frac{\partial {{v}_{0}}}{\partial x}+z\left( \frac{\partial {{\theta }_{x}}}{\partial x}+\frac{\partial {{\theta }_{y}}}{\partial y} \right)+\frac{\partial w}{\partial x}\frac{\partial w}{\partial y} \\
\end{array} \right\}\]
(4)
并假设横向剪切应变具有一阶表达式
\[\left. \begin{array}{*{35}{l}}
{{\gamma }_{yz}}={{\theta }_{x}}+\frac{\partial w}{\partial y} \\
{{\gamma }_{zx}}={{\theta }_{y}}+\frac{\partial w}{\partial x} \\
\end{array} \right\}\]
(5)
面内应力${ \sigma } = \left[ {\sigma _x } {\sigma _y } {\tau _{xy} } \right]^{\rm T}$和面内应变${ \varepsilon } = \left[{\varepsilon _x } {\varepsilon _y } {\gamma _{xy} } \right]^{\rm T}$满足如下关系
\[\sigma =Q\left( \varepsilon -\alpha \Delta T \right)\]
(6)
\[Q=\frac{E(z)}{1-\upsilon {{\left( z \right)}^{2}}}\left[ \begin{matrix}
1 & \upsilon (z) & 0 \\
\upsilon (z) & 1 & 0 \\
0 & 0 & (1-\upsilon (z))/2 \\
\end{matrix} \right]\]
(7)
横向剪应力${ \tau } = \left[ {\tau _{yz} } {\tau _{zx} } \right]^{\rm T}$和横向剪应变${ \gamma } = \left[{\gamma _{yz} } {\gamma _{zx} } \right]^{\rm T}$关系如下
\[\tau ={{Q}_{S}}\gamma \]
(8)
\[{{Q}_{S}}=\frac{E(z)}{2\left( 1+\upsilon (z) \right)}\left[ \begin{matrix}
1 & 0 \\
0 & 1 \\
\end{matrix} \right]\]
(9)
于是,壁板中任意微元(体积 $\Omega $)的内力虚功
\[\delta W_{\text{int}}^{e}=\int_{\Omega }{\left( \delta {{\varepsilon }^{\text{T}}}\sigma +\beta \delta {{\gamma }^{\text{T}}}\tau \right)}dV\]
(10)
考虑超声速气流以速度$v$沿$x$方向流过壁板的上表面,作用于壁板表面(面积$S$)的气动压力可由一阶活塞理论的准定常公式近似描述
\[\Delta p=p-{{p}_{\infty }}=\frac{{{\rho }_{\text{a}}}{{v}^{2}}}{\sqrt{{{M}^{2}}-1}}\left( \frac{\partial w}{\partial x}+\frac{{{M}^{2}}-2}{{{M}^{2}}-1}\frac{1}{v}\frac{\partial w}{\partial t} \right)\]
(11)
由于气流参数$\rho _{\rm a} $,$v$和$M$中只有2个参数相互独立,因此可引入无量纲参数来反映气动特性
\[\lambda ={{\rho }_{\text{a}}}{{v}^{2}}{{l}^{3}}/({{D}_{\text{m}}}\sqrt{{{M}^{2}}-1})\]
(12a)
\[{{R}_{M}}={{\left( \frac{{{M}^{2}}-2}{{{M}^{2}}-1} \right)}^{2}}\frac{{{\rho }_{\text{a}}}l}{{{\rho }_{\text{m}}}h\sqrt{{{M}^{2}}-1}}\]
(12b)
式中,$D_{\rm m} = E_{\rm m} h^3 / [12(1-\upsilon _{\rm m}^2)]$为金属板弯刚度,$l$为壁板$x$方向长度.
忽略壁板的面内惯性,微元的外力虚功为
\[\delta W_{\text{ext}}^{\text{e}}=-\int_{\Omega }{\delta }w\rho \left( z \right)\ddot{w}dV-\int_{S}{\delta }w\Delta pdS\]
(13)
基于虚功原理并采用3节点三角形明德林板单元做有限元离散[17],可导出超声速气流中受热功能梯度壁板的非线性颤振运动方程
\[m\ddot{w}+{{c}_{\text{a}}}\dot{w}+\left( {{k}_{0}}+{{k}_{\text{a}}}+{{k}_{\text{G}}}-{{k}_{\text{T}}}+\frac{1}{2}{{n}_{1}}+\frac{1}{3}{{n}_{2}} \right)w={{p}_{\text{T}}}\]
(14)
运动方程(14)中忽略动态项,可写出功能梯度壁板的非线性静力平衡方程
\[\left( {{k}_{0}}+{{k}_{\text{a}}}+{{k}_{\text{G}}}-{{K}_{\text{T}}}+{{n}_{1}}/2+{{n}_{2}}/3 \right)w={{p}_{\text{T}}}\]
(15)
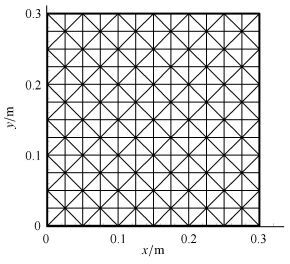
给定气流条件$\lambda $、温升条件$\Delta \text{T}$和边界约束,可采用牛顿-拉弗森(Newton-Raphson)迭代法数值求解式(15)得到功能梯度板的热屈曲变形. 以周边简支(限制$x,y,z$方向位移,但不限制转动)方形Si$_3$N$_4$/SUS304功能梯度板($l\times \text{h}=300$ mm×3 mm)为例,有限元网格划分见图2. 当$n =1$时,均匀温升下板中心无量纲变形($W = w /h$)与温升关系见图3. 陶瓷(Si$_3$N$_4$)和金属(SUS304)材料力学性能列于表1 ($\upsilon =0.3$).
|
图2 功能梯度壁板有限元模型 Fig.2 Finite element mesh of a FG panel |
|
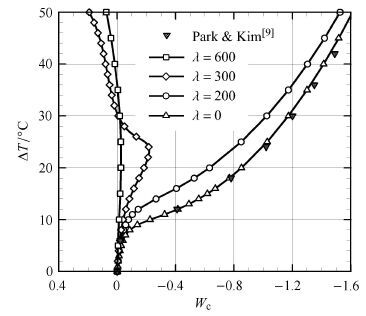
图3 功能梯度壁板的热屈曲变形 Fig.3 Thermal buckling deflection of a FG panel |
| 表1 材料力学性能参数 Table 1 Material mechanical properties |
由静力平衡方程式(15)可导出线性特征值问题求解结构的屈曲临界温度. 如不计气流影响($\lambda =0$),该简支Si$_3$N$_4 $/SUS304功能梯度板($n=1$)的屈曲临界温升为$\Delta T_{\rm cr} =11.15$℃.从图3壁板挠度方向变形曲线可见,温度稍有升高壁板就会发生弯曲变形.这是由于材料沿厚度方向梯度分布破坏了结构的对称性,导致壁板在面内热应力作用下发生指向金属较集中壁板内侧($W<0$)的热弯曲变形.当壁板温升低于屈曲临界温升($\Delta T< \Delta T_{\rm cr} $)时,壁板的弯曲变形量很小($\left| W \right| \ll 1$).如果壁板温升接近屈曲临界温升($\Delta T \to \Delta T_{\rm cr}$),壁板的弯曲变形会随着温度升高迅速增长,即壁板屈曲. 当壁板温升超过屈曲临界温升($\Delta T>\Delta T_{\rm cr}$,过屈曲),壁板弯曲变形随温度升高不断增长,很快达到板厚量级($\left| W \right| \to1$),这时几何非线性刚度${ n}_1$,${ n}_2$随弯曲变形增大迅速增长,使结构变形表现出"渐硬"特性.图3同时绘出了文献[9]基于9结点一阶剪切变形板单元的无气流影响计算结果,本文热屈曲变形曲线($\lambda=0$)与文献[9]结果符合良好.
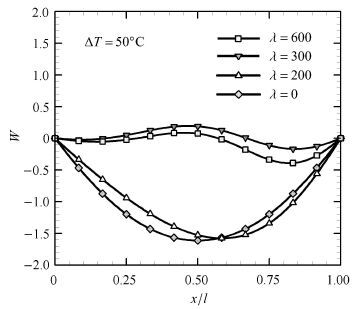
超声速气流会影响功能梯度壁板的热屈曲变形. 由图3无量纲气流速压$\lambda $为200,300,600下壁板的热屈曲变形曲线可知,随着气流速压$\lambda $增大壁板中点的弯曲变形量减小. 当气流速压足够大(如$\lambda $为300,600)时,壁板的过屈曲变形还出现了由"内凹" ($W<0$)向"外凸" ($W>0$)的转变. 温升$\Delta \text{T}$=50℃时,功能梯度壁板在不同超声速气流速压下的热过屈曲变形中线($y = l / 2$)形态见图4.
|
图4 热过屈曲变形形态 Fig.4 Thermal post-buckling deformation shape |
由活塞理论气动力式(11)可知,当壁板绕$x$轴转角为正(${\partial w} /{\partial x} > 0)$时气动力(压差)定常项为指向壁板内侧的压力,反之绕$x$轴转角为负(${\partial w} /{\partial x} <0)$时气动力的定常项为指向壁板外侧的吸力. 由于气动力定常项通过气动刚度${{k}_{a}}$影响壁板的热屈曲行为,因此壁板热过屈曲变形受到超声速气动力的影响机理如下:处于热过屈曲状态的壁板具有中心对称的后屈曲变形形态($\lambda =0$),变形最大的位置在壁板中点($x = l / 2$)处.由于壁板"内凹",在较低气流速压($\lambda =200$)下,上游半弦长范围内($x < l /2$)壁板受到指向外侧的定常气动吸力,下游半弦长范围内($x > l /2$)壁板受到指向内侧的定常气动压力,因此壁板后屈曲变形最大的位置顺气流方向($x$方向)向下游推移,这种推移同时造成气动吸力的作用面积增大,导致壁板"内凹"变形量减小. 气流速压$\lambda$越高,热屈曲变形峰值的位置推移量越大,内凹变形幅值也越小. 于是在某些较大的气流速压(如$\lambda=300$)下,壁板被吸离"内凹"状态,达到无变形初始位置($W= 0$)附近的部分"内凹"部分"外凸"的新平衡位置.如气流速压进一步增大(如$\lambda =600$),壁板热过屈曲变形幅值会受到限制,难以出现大挠度变形的情况.
3 壁板颤振
超声速气流除了改变壁板的热屈曲变形,引入的非保守力(与变形路径有关的气动力)还会影响结构的动态稳定性. 在特定壁板振动响应下,气动力持续对结构作正功,使壁板从气流中吸收能量而发生壁板颤振.经典颤振分析基于小挠度变形假设,在壁板无变形的初始位置($W =0$)对颤振方程(14)式做线性化处理,从而忽略包含弯曲变形高阶项的非线性刚度${ n}_1$和${ n}_2$.当壁板温度较高处于后屈曲状态时,结构大挠度弯曲变形很显著(图3和图4),仍基于上述线性理论忽略${n}_1$和${ n}_2$必然导致对壁板后屈曲刚度的错误估计,因此我们在热屈曲变形的基础上开展气动弹性稳定性分析.假设壁板温度变化相对于颤振响应是一个"慢"过程,可近似认为温度不随时间变化,则热过屈曲壁板的颤振稳定性可在静态变形${w}_{\rm s}$的基础上叠加动态小扰动$\delta { w}_{\rm d} $开展分析,有
\[w={{w}_{\text{s}}}+\delta {{w}_{\text{d}}}\]
(16)
\[\begin{align}
& m\delta {{{\ddot{w}}}_{\text{d}}}+{{c}_{\text{a}}}\delta {{{\dot{w}}}_{\text{d}}}+ \\
& \left( {{k}_{\text{L}}}+{{n}_{1}}\left( {{w}_{\text{s}}} \right)+{{n}_{2}}\left( {{w}_{\text{s}}} \right) \right)\delta {{w}_{\text{d}}}=0 \\
\end{align}\]
(17)
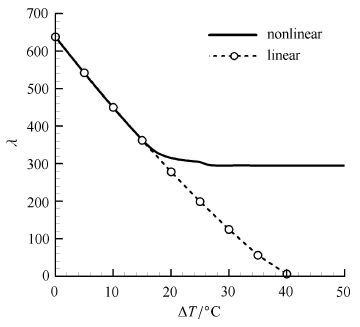
式(17)含有热过屈曲变形引入的几何非线性刚度${ n}_1$和${ n}_2$,采用$V-g$法可解得功能梯度壁板的非线性颤振边界. 图5绘制了简支Si$_3$N$_4 $/SUS304功能梯度壁板($n=1$,$R_M =0.001$)的非线性颤振边界(实线)和线性颤振边界(虚线). 可见,无量纲气流速压较高($\lambda>320$)时,两条边界曲线吻合良好. 但在无量纲气流速压较低($\lambda <320$)时,线性颤振速压远低于非线性颤振速压.由于较高无量纲气流速压下超声速气流对功能梯度壁板热过屈曲变形的影响较大(减小壁板的弯曲变形),在高无量纲气流速压下(如$\lambda=600$)壁板变形会被限制在小挠度范围内,因此热过屈曲变形的几何非线性效应对壁板颤振边界的影响在高无量纲气流速压下并不显著,却在低无量纲气流速压下表现明显.
|
图5 功能梯度壁板颤振边界 Fig.5 Flutter boundary of a FG panel |
本文首先建立了功能梯度壁板的气动弹性有限元模型,然后数值分析了功能梯度壁板的热过屈曲变形和气动弹性颤振边界,得到主要结论如下:
(1)沿板厚的材料梯度分布会破坏结构的对称性,导致陶瓷-金属功能梯度壁板在面内热应力作用下发生指向金属侧的热屈曲变形.
(2)超声速气流中壁板热屈曲变形最大的位置随气流速压增大向下游推移,并伴随有屈曲变形量的减小.无量纲气流速压足够大时,壁板热过屈曲变形的幅值会受到超声速气动力的压制,难以出现大挠度变形.
(3)热过屈曲壁板的几何非线性效应会提高壁板的颤振边界,这种影响在高温、低速压且壁板发生大挠度热屈曲变形时表现显著.较高无量纲气流速压下由于壁板的热屈曲变形被气动力限定在小挠度范围,几何非线性的影响不明显.
| [1] | Jenkins DR. Hypersonics before the shuttle: A concise history of the X-15 research airplane. Washington: NASA Publication SP-4518,2000: 11-12 |
| [2] | Cooper PA, Holloway PF. The shuttle tile story. Astronautics and Aeronautics, 1981, 19(1): 24-36 |
| [3] | Birman V, Byrd LW. Modeling and analysis of functionally graded materials and structures. Applied Mechanics Reviews, 2007, 60:195-216 |
| [4] | Reddy JN. Analysis of functionally graded plates. International Journal for Numerical Methods in Engineering, 2000, 47(1-3): 663-684 |
| [5] | 韩杰才,徐丽,王保林等. 梯度功能材料的研究进展及展望. 固体火箭技术,2004,27(3):207-215 (Han Jiecai, Xu Li,Wang Baolin, et al. Progress and prospects of functional gradient materials. Journal of Solid Rocket Technology, 2004, 27(3):207-215 (in Chinese)) |
| [6] | 仲政, 吴林志, 陈伟球. 功能梯度材料与结构的若干力学问题研究进展. 力学进展, 2010, 40(5): 528-541 (Zhong Zheng, Wu Linzhi, ChenWeiqiu. Progress in the study on mechanics problems of functionally graded materials and structures. Advances in Mechanics,2010, 40(5): 528-541 (in Chinese)) |
| [7] | Wu L. Thermal buckling of a simply supported moderately thick rectangular FGM plate. Composite Structures, 2004, 64(2): 211-218 |
| [8] | Shen HS, Wang H. Nonlinear bending and postbuckling of FGM cylindrical panels subjected to combined loadings and resting on elastic foundations in thermal environments. Composites Part BEngineering,2015, 78: 202-213 |
| [9] | Park JS, Kim JH. Thermal postbuckling and vibration analyses of functionally graded plates. Journal of Sound and Vibration, 2006,289: 77-93 |
| [10] | Jha DK, Kant T, Singh RK. A critical review of recent research on functionally graded plates. Composite Structures, 2013, 96: 833-849 |
| [11] | Thai HT, Kim SE. A review of theories for the modeling and analysis of functionally graded plates and shells. Composite Structures,2015, 128: 70-86 |
| [12] | 王铁军, 马连生, 石朝锋. 功能梯度中厚圆/环板轴对称弯曲问题的解析解. 力学学报, 2004, 36(3): 348-353 (Wang Tiejun, Ma Liansheng, Shi Zhaofeng. Analytical solutions for axisymmetric bending of functionally graded circular/annular plates. Acta Mechanica Sinica, 2004, 36(3): 348-353 (in Chinese)) |
| [13] | Shao ZS, Wang TJ, Ang KK. Transient thermomechanical stresses of functionally graded cylindrical panels. AIAA Journal, 2007,45(10): 2487-2496 |
| [14] | Zhang LW, Zhu P, Liew KM. Thermal buckling of functionally graded plates using a local Kriging meshless method. Composite Structures, 2014, 108: 472-492 |
| [15] | Liang X, Wu Z, Wang L, et al. Semianalytical three-dimensional solutions for the transient response of functionally graded material rectangular plates. Journal of Engineering Mechanics, 2015, 141(9):1-17 |
| [16] | Apuzzo A, Barretta R, Luciano R. Some analytical solutions of functionally graded Kirchhoff plates. Composites Part B-Engineering,2015, 68: 266-269 |
| [17] | Tessler A, Hughes TJR. A three-node Mindlin plate element with improved transverse shear. Computer Methods in Applied Mechanics and Engineering, 1985, 50: 71-91 |
| [18] | Huu-Tai T, Trung-Kien N, Vo TP, et al. Analysis of functionally graded sandwich plates using a new first-order shear deformation theory. European Journal of Mechanics a-Solids, 2014, 45: 211-225 |
| [19] | Satouri S, Kargarnovin MH, Allahkarami F, et al. Application of third order shear deformation theory in buckling analysis of 2Dfunctionally graded cylindrical shell reinforced by axial stiffeners. Composites Part B-Engineering, 2015, 79: 236-253 |
| [20] | Zhang JH, Li GZ, Li SR. Analysis of transient displacements for a ceramic-metal functionally graded cylindrical shell under dynamic thermal loading. Ceramics International, 2015, 41(9): 12378-12385 |
| [21] | Dowell EH. Nonlinear oscillations of a fluttering plate. AIAA Journal,1966, 4(7): 1267-1275 |
| [22] | Dixon IR, Mei C. Finite element analysis of large-amplitude panel flutter of thin laminates. AIAA Journal, 1993, 31(4): 701-707 |
| [23] | 夏巍, 杨智春. 超音速气流中受热壁板的稳定性分析. 力学学报,2007, 39(5): 602-609 (Xia Wei, Yang Zhichun. Stability analysis of heated panels in supersonic air flow. Chinese Journal of Theoretical and Applied Mechanics, 2007, 39(5): 602-609 (in Chinese)) |
| [24] | Yang C, Li G, Wan Z. Aerothermal-aeroelastic two-way coupling method for hypersonic curved panel flutter. Science China- Technological Sciences, 2012, 55(3): 831-840 |
| [25] | Yang Z, Zhou J, Gu Y. Integrated analysis on static/dynamic aeroelasticity of curved panels based on a modified local piston theory. Journal of Sound and Vibration, 2014, 333(22): 5885-5897 |
| [26] | Li P, Yang Y, Lu L. Nonlinear flutter behavior of a plate with motion constraints in subsonic flow. Meccanica, 2014, 49(12): 2797-2815 |
| [27] | Mei G, Zhang J, Xi G, et al. Analysis of supersonic and transonic panel flutter using a fluid-structure coupling algorithm. Journal of Vibration and Acoustics-Transactions of the Asme, 2014, 136(3): 1-11 |
| [28] | Sohn KJ, Kim JH. Nonlinear thermal flutter of functionally graded panels under a supersonic flow. Composite Structures, 2009, 88(3):380-387 |
| [29] | Prakash T, Singha MK, Ganapathi M. A finite element study on the large amplitude flexural vibration characteristics of FGM plates under aerodynamic load. International Journal of Non-Linear Mechanics,2012, 47(5): 439-447 |
| [30] | Haddadpour H, Navazi HM, Shadmehri F. Nonlinear oscillations of a fluttering functionally graded plate. Composite Structures, 2007,79(2): 242-250 |
 2016, Vol. 48
2016, Vol. 48