在武器弹药系统的设计、研制和工业重大爆炸灾害预防与救援的研究中,涉及了大量的爆炸与冲击问题. 爆炸与冲击问题是一个几何、材料和边界条件均为非线性的强耦合问题,涉及高速、高压、高温、相变,气体、液体和固体等多种介质间相互耦合甚至混合,材料不但会发生严重变形和破碎,还会融化甚至汽化. 由于爆炸与冲击问题的复杂性,使理论和实验研究遇到相当大的困难,而计算机数值仿真试验技术具有安全保密、设计灵活、可重复性好、环境和过程可控、效费比高等优点,是未来提高武器弹药研制和爆炸灾害预防与救援水平的有效手段. 当前,计算爆炸力学已成为由爆炸力学、材料动力学与计算数学、计算机技术交叉而产生的新的力学学科分支,该学科极大地推动了爆炸力学以及武器装备的发展[1].
爆炸与冲击问题是一个多物质在高应变率、高温及高压条件下的强非线性的瞬态动力学问题,对其进行数值模拟,不仅涉及到流体弹塑性动力学数学物理模型的建立,而且需要给出精确描述冲击波和爆轰波强间断的数值计算方法. 此外,由于工程实际问题的复杂性,需要开展三维计算分析,对求解规模提出了新的需求. 因此,针对爆炸与冲击问题的数值计算,需要开展大规模高精度分析,相关研究工作不仅具有重要的理论价值,而且具有很强的工程应用背景[2, 3].
从20世纪60年代开始,以美国三大国防实验室为代表,开始了爆炸力学数值方法的研究及仿真程序的开发工作,以美国为代表的西方发达国家先后开发了100多个与此相关的计算代码,也形成了多个著名的商业化爆炸力学数值仿真软件,包括ANSYS/LS-DYNA,AUTODYN和MSC/DYTRAN等.上述商业软件由于代码的保密性,使得我们不能加入新的算法模块,在应用上受到了很大的限制,而且计算规模受到严格的限制,难以满足工程实际的计算要求,为此,迫切需要开发出具有自主知识产权的欧拉型仿真计算软件.国内,北京应用物理与计算数学研究所[4]、北京大学[5]、清华大学[6]、总参四所[7]等单位在爆炸力学仿真软件方面取得了丰富的成果.北京理工大学宁建国领导的爆炸与冲击动力学学科组经过二十余年的积累,对爆炸力学多物质欧拉数值方法进行了深入系统的研究,开发了拥有自主知识产权的欧拉型二维及三维爆炸与冲击问题仿真软件系统[8, 9].该软件能够有效模拟炸药爆轰、爆炸冲击、侵彻等各种强冲击载荷下结构的动态响应与破坏问题,已通过国防科技成果鉴定,并在国内多家单位的武器装备研究项目及民用安全领域得到了应用,推动了我国武器装备的数字化设计与制造的发展.
本文针对爆炸与冲击问题数值模拟中的一些关键问题开展了研究,提出了适用于冲击波强间断高分辨率计算的伪弧长算法,发展了气相爆轰数值模拟中考虑刚性化学源项的附加龙格-库塔方法,给出了三维多物质流体动力学欧拉数值方法的并行化方法,解决了爆炸与冲击问题大规模、高精度计算中的一些难题,并通过聚能射流侵彻混凝土等典型工程问题验证了所研究数值方法的有效性.
1 冲击波强间断问题高分辨率数值模拟的伪弧长方法研究如何能够精确捕捉和追踪波阵面的传播过程对于研究爆炸冲击波的传播规律始终是一个非常关键而困难的课题. 为了精确捕捉波阵面,并且使得计算量保持在一定的可接受范围以内,采用自适应网格方法是一种常用的做法. 传统的自适应网格方法包括h 方法,p 方法和r 方法[10]. 其中r 方法,也叫移动网格法是一种保持总体计算过程中的网格数和原有网格连通性不变,在计算中通过重新分配网格点来达到网格自适应的方法. 汤华中和汤涛[11]提出了一种针对于一维和二维空间双曲问题的r 自适应方法,这种方法将物理方程的演化和空间网格的重构分开计算,然后通过物理量的插值重构来进行耦合. 在大量的计算实践中,已经证明这种方法对于一、二维双曲问题是有效的,但对于三维问题,则会遇到相当,这是因为没有将物理方程的演化和空间网格的变化进行有效结合. 此外,武际可等[12]通过引入弧长参数,试图求解微分方程的刚性问题.
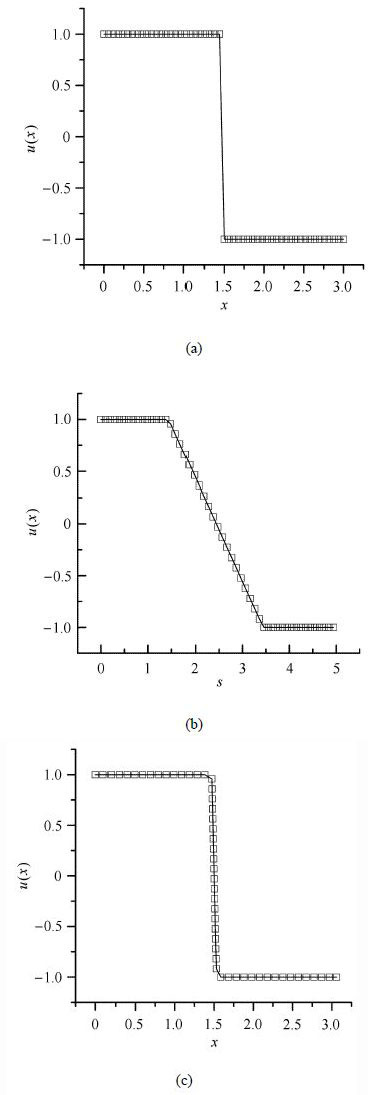
针对爆炸与冲击波的特点,本文提出了能够统一求解一维、二维和三维强冲击间断问题的伪弧长网格方法[13, 14]. 该方法通过引入弧长参数将物理空间的双曲型方程转换到基于弧长变量的控制方程,然后在弧长空间上离散求解控制方程,最后将弧长空间上的物理量值插值映射到物理空间点(图1),实现了物理方程的演化和空间网格的变化进行有效结合,使求解精度得到保证. 该方法的研究对于提高冲击波强间断处数值模拟的分辨率具有重要意义.
|
图1 应用伪弧长方法物理量空间分布变化过程 Fig.1 Physical quantities space distribution change process with pseudo arc-length method |
对于多维非定常、无黏、气体导热、无气体导热的化学反应流动问题,考虑多维空间化学反应的混合气体欧拉方程组
\[\frac{\partial }{\partial t}w+\frac{\partial }{\partial x}F\left( w \right)=s\left( w \right),t\ge 0\]
(1)
首先引入弧长参数$ {\xi } = {\xi }\left( {{ x},t} \right)$,其满足弧长表达式
\[{{\left( d\xi \right)}^{2}}={{\left( dx \right)}^{2}}+\sum\limits_{i=1}^{n}{{{\lambda }_{i}}}{{\left( d{{w}_{i}} \right)}^{2}}\]
(2)
进一步,可以定义监视函数
\[M\left( x,t \right)=\sqrt{1+\sum\limits_{i=1}^{n}{{{\lambda }_{i}}{{\left( \nabla w \right)}^{2}}}}\]
(3)
通过引入伪时间来得到多维空间中的网格移动速度的偏微分方程
\[{{x}_{t}}=\frac{1}{\tau }\frac{\partial }{\partial \xi }(M\frac{\partial x}{\partial \xi })\]
(4)
对方程(1)在每个网格单元$K$积分得到并化简得
\[\begin{align}
& |K|\frac{\partial }{\partial t}\bar{w}=-\sum\limits_{l}{h}(w_{K}^{\text{int}(l)},w_{K}^{\text{ext}(l)},n_{K}^{l})|e_{K}^{l}|- \\
& |K|s(\bar{w}) \\
\end{align}\]
(5)
进而可对系统(4)和(5)采用龙格-库塔法耦合求解. 耦合求解过程中,要保证网格物理量值插值重构的守恒性[15]
\[\sum\limits_{K}{\left| {{{\tilde{A}}}_{K}} \right|}{{\tilde{w}}_{K}}=\sum\limits_{K}{\left| {{A}_{K}} \right|}{{w}_{K}}\]
(6)
下面以一步化学反应过程为例给出计算实例
\[R\to P,\omega =-\tilde{K}\rho R\exp \left( -\tilde{T}/T \right)\]
(7)
\[E=\frac{1}{2}\rho {{u}^{2}}+\frac{p}{\gamma -1}+\rho qR\]
(8)
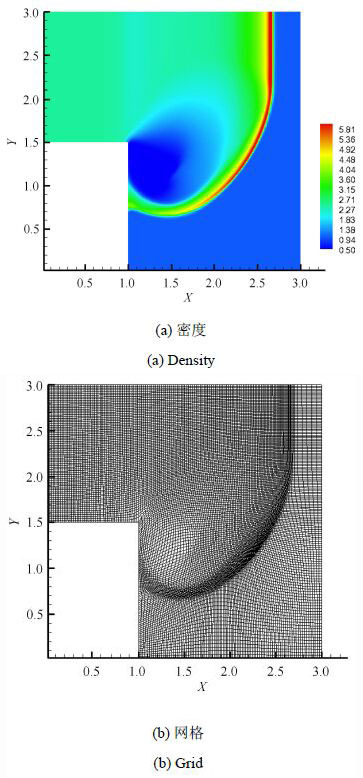
首先对二维爆轰波衍射问题进行研究. 障碍物为反射边界,其余为无限边界. 初始网格步长为$\Delta x = \Delta y = \dfrac{1}{50}$. 图2给出了当$t =0.3$时的模拟结果,结果表明网格可以随着爆轰波阵面而进行自适应变化.
|
图2 $t =0.3$时数值模拟结果 Fig.2 Numerical results at $t = 0.3$ |
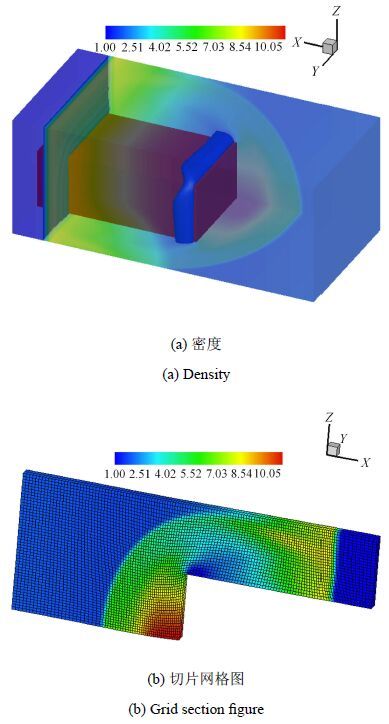
三维前台阶问题:障碍物为反射边界,计算中采用并行算法编程,使用40万网格计算结果如图3.结果表明障碍物后方存在一个低密度区,并且伪弧长移动网格法能够实现三维空间中网格的自适应变化.
|
图3 $t =0.178$时,数值模拟结果 Fig.3 Numerical results at $t = 0.178$ |
气相爆轰是流动和化学反应的强耦合过程,典型的一维爆轰波由前导激波和其后的化学反应区组成,而多维气相爆轰波波阵面则存在复杂的多波结构. 近些年,爆轰波的基本理论并没有得到太大的发展,而由于观测手段的局限对爆轰波精细结构的实验研究也存在很大困难. 而随着计算机技术的快速发展和计算能力的大幅提高,以基元反应模型为主的复杂模型成为气相爆轰数值模拟的重点,该模型求解的最大困难在于多组分反应欧拉方程的化学源项存在着很强的刚性,这种刚性主要体现在各个基元反应的时间尺度存在巨大的差异[16]. 如果使用显式格式对此类刚性方程组进行处理,格式精度所要求的时间步长将远小于由稳定性条件所决定的时间步长,这将大大增加计算时间,严重影响计算效率. 由于显式方法在处理刚性问题中存在不足,隐式方法或者半隐式方法得到了很大的应用. 考虑到多组分反应欧拉方程源项的刚性问题,采用附加龙格-库塔方法耦合方程中非刚性对流项和刚性反应源项. 根据文献[17]中的工作,附加龙格-库塔方法能够求解下述形式的常微分方程[18, 19, 20]
\[dU/dt=F(U)=\sum\limits_{\nu =1}^{N}{{{F}^{[\nu ]}}}(U)\]
(9)
\[\left. \begin{array}{*{35}{l}}
{{U}^{(i)}}={{U}^{n}}+(\Delta t)\sum\limits_{\nu =1}^{N}{\sum\limits_{j=1}^{s}{a_{ij}^{[\nu ]}}}{{F}^{[\nu ]}}({{U}^{(j)}}) \\
{{U}^{n+1}}={{U}^{n}}+(\Delta t)\sum\limits_{\nu =1}^{N}{\sum\limits_{j=1}^{s}{b_{i}^{[\nu ]}}}{{F}^{[\nu ]}}({{U}^{(j)}}) \\
\end{array} \right\}\]
(10)
应用5阶精度的加权本质无振荡格式和附加龙格-库塔方法对一维、二维气相爆轰波以及爆轰波在楔面和弯管内的传播过程进行了数值研究[19, 20]. 气相爆轰的采用基元化学反应模型(9 组分 19 反应[22]),并用70%的氩气稀释. 初始压力和温度分别为6 670 Pa和298 K.图4中给出了通过上述方法得到的二维爆轰波波阵面的精细结构,可以清楚地观察到前导激波,反应区,横波以及密度间断等结构.图5和图6分别是通过实验和数值模拟得到的胞格结构,两者都具有规则的胞格模式.

|
图4 两个不同时刻的爆轰波波阵面精细结构 (密度梯度) Fig.4 Detonation wave front fine structure at two different times (density gradient) |

|
图6 数值胞格结构 Fig.6 Numerical cell structures |
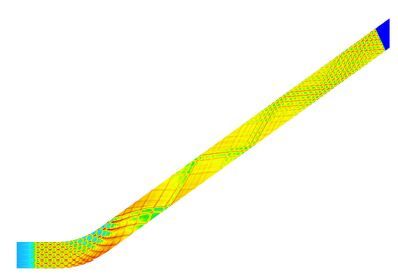
当前,对气相爆炸机理的研究是数值模拟的研究热点[24, 25]. 图7和图8分别是通过数值计算得到的爆轰波马赫反射的胞格结构和爆轰波在弯管中传播的胞格结构. 前者可以观察到爆轰波在单独压缩作用下的变化,包括三波点方向和尺寸的变化. 对后者而言,爆轰波在上壁面受到稀疏作用的影响,胞格尺寸变大,强度降低;在下壁面受到不断地压缩作用,胞格尺寸变小,强度增加. 当爆轰波通过弯管段后,经过一段距离后重新恢复到初始的状态. 通过对两者进行分析,可以研究爆轰波在反射或者衍射等作用下不同的响应机理.

|
图7 爆轰波马赫反射的胞格结构 Fig.7 The cell structure of detonation wave Mach reflection |
|
图8 爆轰波在30°弯管中传播的胞格结构 Fig.8 The cell structure of detonation wave propagation in 30° bend |
针对未来新型高效毁伤战斗部及防护结构的发展需求,仿真软件需具备从炸药爆轰、毁伤元形成直至毁伤元与目标作用全物理过程的仿真计算能力,特别是由于欧拉型软件涉及武器弹药设计和国防安全,以美国为代表的西方国家对我国是完全禁运的,必须依靠自主开发,因此开展大规模并行计算方法研究和欧拉型爆炸与冲击问题大规模仿真软件的开发是十分必要的.
针对爆炸与冲击问题的大规模计算需求,重点开展了三维多物质流体动力学欧拉数值方法特别是三维多物质界面处理算法的并行化方法研究,开发了基于消息传递接口(message passing interface,MPI)的爆炸与冲击问题并行计算程序[26].
3.1 子区域间的关联性子区域间的关联性反映了子区域与邻近子区域的重叠程度. 为了计算需要,往往要在子区域的边界增加一些网格来储存临近子区域的信息. 如图9所示,将一个二维的计算域分解成九个子区域,其中灰色网格为子区域4与周围子区域的重叠网格,称为"子区域重叠网格". 欧拉方法的子区域的关联性来源于两个方面:输运带来的关联性及数值格式带来的关联性.

|
图9 重叠子区域 Fig.9 The overlapping subdomain |
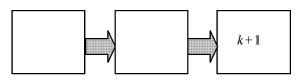
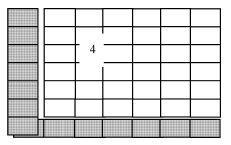
网格物理量的改变量等于该网格在3个方向流进量与流出量的差,因此在欧拉输运歩里一个网格正确的更新包含该网格与邻近网格的输运. 以单方向输运为例,如图10所示,流场速度沿着正方向,则单方向$k$网格一次正确的更新包含$k-1$和$k$网格的输运,即$k$网格物理量的改变等于$k-1$网格流进量(速度为负方向值为负)与$k$网格流出量(速度为负方向值为负)的差. 因此对于图1子区域4来说,要在其左边及下边各增加一层网格,如图11所示.
|
图10 单方向输运 Fig.10 The single direction transport |
|
图11 输运带来的关联性 Fig.11 The relevance caused by transport |
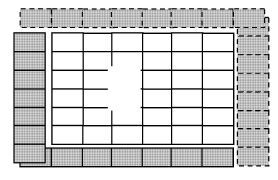
由于在实际的更新运算中,采用的数值格式往往会需要周边的网格物理量. 考虑一个简单的数值格式
\[{{u}_{k+\tfrac{1}{2}}}=\frac{1}{2}\left( {{u}_{k}}+{{u}_{k+1}} \right)\]
(11)
|
图12 输运及数值格式带来的关联性 Fig.12 The relevance caused by transport and numerical format |
由图10可知,$k-1$网格的输运会造成$k-1$和$k$网格物理量的改变,因此当$k$网格输运时,$k-1$和$k$网格物理量已经改变. 并且由于受制于CFL条件,当前网格的输运只会影响到周围26个网格,即当前网格的某种物质的输运量可写作如下函数关系式
\[\begin{align}
& \Delta {{V}_{ijk}}=f(\Delta t,\Delta x,\Delta y,\Delta z,{{V}_{ijk}},jfla{{g}_{ijk}},{{u}_{ijk}}, \\
& {{V}_{i\pm 1j\pm 1k\pm 1}},jfla{{g}_{i\pm 1j\pm 1k\pm 1}},{{u}_{i\pm 1j\pm 1k\pm 1}}) \\
\end{align}\]
(12)
| 表1 伪代码 Table 1 The pseudo code |
通过大量的爆炸与冲击问题算例,对并行程序进行了测试.考虑到基于消息传递接口并行程序的测试与调试的困难,把对并行程序的测试分为2个阶段[27]:在阶段1,不依赖于实际的物理模型,测试分区对计算结果的影响;在阶段2,设计合理的物理模型,测试计算结果是否符合物理规律.
表1中,Keb,Kee,Jeb,Jee,Ieb,Iee为计算起始位置.
图13给出了60°锥角聚能装药的考核算例,共有2 473万个网格,计算得到的射流形状及射流头部速度模拟结果与实验结果吻合较好,验证了并行程序求解工程实际问题的能力.

|
图13 聚能射流数值模拟结果(b)与实验结果(a)的对比 Fig.13 The shaped jet results of numerical simulation (b) compared with experimental results (a) |
根据上述所研究的数值方法和程序,开展了聚能装药侵彻混凝土靶的数值模拟研究. 当前,对于该类问题的研究,特别是实验工作,大多是采用小口径的药型罩[28, 29],因此无法反映混凝土的尺度效应的影响. 为此,对不同锥形药型罩成型过程进行了数值模拟研究[30],设计了一种能够侵彻厚混凝土靶板的大口径聚能装药结构. 药型罩的口径为300 mm,锥角为90°,药型罩壁厚为16 mm,装药高度为480 mm,炸药采用常用的B炸药,装药量为35.7 kg,壳体厚度为10 mm(聚能装药结构图见图14).

|
图14 聚能装药结构及尺寸 Fig.14 The structure and size of shaped charge |
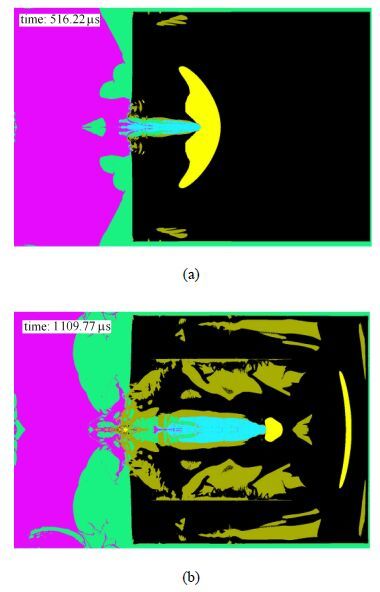
为了分析靶板的尺寸效应,采用自主开发的软件进行了4种尺寸混凝土靶侵彻效应的数值模拟研究,靶板直径分别为 2 m,3 m,4 m,5 m.从数值模拟结果可以看出,对于小于4 m直径的靶板,在射流侵彻过程中依然有可能会造成整体靶板破碎;直径4 m及以上的靶板在侵彻过程中混凝土没有出现大面积损伤,能够满足实验要求.图15为大口径聚能装药侵彻4 m直径混凝土靶板的数值模拟结果.侵彻初期,数值模拟结果表明混凝土表面的压缩破坏区面积较大,开坑孔径较大,如图15(a);随着侵彻的进行,压缩破坏区仅存在于侵彻体的头部附近,这一过程形成一个孔洞隧道区,孔洞直径基本一致,如图15(b).
|
图15 大口径聚能装药侵彻4 m直径混凝土靶的数值模拟结果 Fig.15 Numerical simulation results of heavy-caliber shaped charge penetration in 4 m diameter concrete target |
对数值分析得到的4 m混凝土靶进行实验研究.混凝土靶板的尺寸为长4 m,宽4 m,深度为2 m,混凝土整体处于地面以下,混凝土底部垫有0.5 m厚的沙石,混凝土的周边采用钢筋抱箍.爆炸之后,聚能射流将混凝土靶板穿透,留下一个直径为16 cm的孔洞,靶板表面出现了许多细小裂纹,靶板的整体保存完好,未出现整体破坏. 爆炸后的实验结果如图16(a)所示,数值模拟最终结果如图16(b)所示.数值模拟结果与实验结果较为符合,实验的混凝土表面的开坑口径也较大,后期也主要是一个孔径基本一致的隧道区.在侵彻深度方面,数值模拟未能将混凝土穿透,侵彻深度为1.74 cm,而实验将整个混凝土靶板穿透,数值模拟结果略低于实验值; 在侵彻孔径方面,数值模拟得到的侵彻孔径为上半部分为22.6 cm,下半部分为14.2 cm,而实验测得值为上半部分为16.8 cm,下半部分为14.5 cm. 在下半部分数值模拟与实验吻合较好,而在上半部分数值模拟结果略大于实验值.造成侵彻深度低于实验值以及上半部分侵彻孔径高于实验值的原因主要是数值模拟中对混凝土采用了连续介质假设,这无形中加强了混凝土的强度,导致了侵彻深度的下降.上半部分的混凝土在破坏之后还呈现连续状态,随着侵彻的进行,孔洞在逐渐增加.但总体而言,该数值模拟技术能够较好地模拟侵彻类问题,其结果与实验也较为一致.

|
图16 实验结果与数值模拟结果对比 Fig.16 Experimental results compared with numerical ones |
(1)提出了求解三维双曲守恒系统激波、接触间断等奇异性问题的伪弧长方法,数值模拟结果验证了该方法的有效性和通用性,使求解精度得到保证,该方法的提出对于提高冲击波强间断处数值模的分辨率具有重要意义;
(2)发展了一种隐-显式附加龙格-库塔算法,该算法对非刚性对流项进行显式处理,源项用半隐式格式处理,整体具有高精度和L 稳定性. 利用基元反应模型对气相爆轰问题进行了数值研究.结果表明该算法能够很好地处理源项引起的刚性问题,准确的捕捉和描述爆轰波的复杂结构和典型特征;
(3)针对爆炸与冲击问题的大规模计算需求,开展了三维多物质流体动力学欧拉数值方法特别是三维多物质界面处理算法的并行化方法研究,并对自主开发的欧拉型三维爆炸与冲击问题仿真计算程序进行了并行化设计,实现了爆炸与冲击问题的大规模并行计算;
(4)根据数值模拟得到的不同锥角的聚能装药成型规律设计了一种侵彻厚混凝土靶的聚能装药结构,并研究了靶板尺寸对聚能装药侵彻性能的影响. 对数值模拟得到的最佳混凝土靶板进行实验,实验结果表明该数值模拟技术能够有效地评估混凝土靶板的破坏情况.
| [1] | 杨桂通. 计算爆炸力学及相关进展. 科学通报, 2011, 56(31): 2544-2547 (Yang Guitong. Computational explosion mechanics and related progress. Chinese Sci Bull, 2011, 56(31): 2544-2547 (in Chinese)) |
| [2] | 宁建国, 王成, 马天宝. 爆炸与冲击动力学. 北京: 国防工业出版社, 2010 (Ning Jianguo, Wang Cheng, Ma Tianbao. Explosion and Shock Dynamics. Beijing: National Defence Industry Press, 2010 (in Chinese)) |
| [3] | 宁建国, 马天宝. 计算爆炸力学. 北京: 国防工业出版社, 2015 (Ning Jianguo, Ma Tianbao. Computational Explosion Mechanics. Beijing: National Defence Industry Press, 2003 (in Chinese)) |
| [4] | 刘军, 何长江, 梁仙红. 三维弹塑性流体力学自适应欧拉方法研究. 高压物理学报, 2008, 22(1): 72-78 (Liu Jun, He Changjiang, Liang Xianhong. An Eulerian adaptive mesh refinement method for three dimensional elastic-plastic hydrodynamic simulations. Chinese Journal of High Pressure Physics, 2008, 22(1): 72-78 (in Chinese)) |
| [5] | Wang G, Wang JT, Liu KX. New numerical algorithms in SUPER CE/SE and their applications in explosion mechanics. Science China Physics, Mechanics & Astronomy, 2010, 53(2): 237-243 |
| [6] | Ma S, Zhang X, Lian YP, et al. Simulation of high explosive explosion using adaptive material point method. CMES: Computer Modeling in Engineering & Sciences, 2009, 39(2): 101-123 |
| [7] | 杨秀敏. 爆炸冲击现象数值模拟. 合肥: 中国科学技术大学出版社, 2010 (Yang Xiumin. Numerical Simulation for Explosion and Phenomena. Hefei: Press of University of Science and Technology of China, 2010 (in Chinese)) |
| [8] | Ma TB,Wang C, Ning JG. Multi-material Eulerian formulations and hydrocode for the simulation of explosions. CMES: Computer Modeling in Engineering and Sciences, 2008, 33(2): 155-178 |
| [9] | Fei GL, Ma TB, Hao L. Large-scale high performance computation on 3D explosion and shock problems. Applied Mathematics and Mechanics, 2011, 32(3): 375-382 |
| [10] | Yang XB, Huang WZ, Qiu JX. A moving mesh WENO method for one-dimensional conservation laws. SIAM J Sci Comput, 2012,34(4): A2317-A2343 |
| [11] | Tang HZ, Tang T. Adaptive mesh methods for one- and twodimensional hyperbolic conservation laws. SIAM J Numer Anal,2003, 41(2): 487-515 |
| [12] | 武际可, 许为厚, 丁红丽. 求解微分方程初值问题的一种弧长法. 应用数学和力学, 1999, 20(8): 875-880 (Wu Jike, Xu Weihou, Yu Hongli. Arc-length method for differential equations. Applied Mathematics and Mechanics, 1999, 20(8): 875-880 (in Chinese)) |
| [13] | Wang X, Ma TB, Ning JG. A pseudo arc-length method for numerical simulation of shock waves. Chinese Physics Letters, 2014, 31:030201 |
| [14] | Wang X, Ma TB, Ren HL, et al. A local pseudo arc-length method for hyperbolic conservation laws. Acta Mechanica Sinica, 2014,30(6): 956-965 |
| [15] | Ning JG, Yuan XP, Ma TB, et al. Positivity-preserving moving mesh scheme for two-step reaction model in two dimensions. Computers and Fluids, 2015, 123: 72-86 |
| [16] | Zhong XL. Additive semi-implicit Runge-Kutta methods for computing high-speed no equilibrium reactive flows. Journal of Computational Physics, 1996, 128(1): 19-31 |
| [17] | Araújo AL, Murua A, Sanz-Serna JM. Symplectic methods based on decompositions. SIAM Journal of Numerical Analysis, 1997, 34(5):1926-1947 |
| [18] | Kennedy CA, Carpenter MH. Additive Runge-Kutta schemes for convection-diffusion-reaction equations. Applied Numerical Mathematics,2003, 44(1-2): 139-181 |
| [19] | Li J, Ren HL, Ning JG. Additive Runge-Kutta methods for H2/O2/Ar detonation with a detailed elementary chemical reaction model. Chinese Science Bulletin, 2013, 58(11): 1227 |
| [20] | Li J, Ren HL, Ning JG. Numerical application of additive Runge- Kutta methods on detonation interaction with pipe bends. International Journal of Hydrogen Energy, 2013, 38: 9016-9027 |
| [21] | Jiang GS, Shu CW. Efficient implementation of weighted ENO schemes. Journal of Computational Physics, 1996, 126(1): 202-228 |
| [22] | 胡湘渝, 张德良, 姜宗林. 气相爆轰基元反应模型数值模拟. 空气动力学学报, 2003, 21(1): 59-66 (Hu Xiangyu, Zhang Deliang, Jiang Zonglin. Numerical simulation of gaseous detonation with detailed chemical reaction model. Acta Aerodynamica Sinica, 2003,21(1): 59-66 (in Chinese)) |
| [23] | Strehlow RA. Gas phase detonations: recent developments. Combustion and Flame, 1968, 12(2): 81-101 |
| [24] | 张薇, 刘云峰, 姜宗林. 气相爆轰波胞格尺度与点火延迟时间关系研究. 力学学报, 2014, 46(6): 977-981 (ZhangWei, Liu Yunfeng, Jiang Zonglin. Study on the relationship between ignition delay time and gaseous detonation cell size. Chinese Journal of Theoretical and Applied Mechanics, 2014, 46(6): 977-981 (in Chinese)) |
| [25] | 滕宏辉, 王春, 赵伟等. 斜爆轰波面上复杂结构的数值研究. 力学学报, 2011, 43(4): 641-645 (Teng Honghui, Wang Chun, Zhao Wei, et al. Numerical research on the complicated structures on the oblique detonation wave surface. Chinese Journal of Theoretical and Applied Mechanics, 2011, 43(4): 641-645 (in Chinese)) |
| [26] | Ning JG, Ma TB, Fei GL. Multi-material Eulerian method and parallel computation for 3D explosion and impact problems. International Journal of Computational Methods, 2014, 11: 1350079 |
| [27] | 马天宝, 费广磊, 张文耀. 三维多物质弹塑性流体动力学Euler 方法的并行算法研究及程序测试. 高压物理学报, 2011, 25(6):508-513 (Ma Tianbao, Fei Guanglei, Zhang Wenyao. Study on parallel algorithm of Eulerian method for three-dimensional multimaterial plastic-elastic hydrokinetic. Chinese Journal of High Pressure Physics, 2011, 25(6): 508-513 (in Chinese)) |
| [28] | 黄风雷, 张雷雷, 段卓平. 大锥角药型罩聚能装药侵彻混凝土实验研究. 爆炸与冲击, 2008, 28(1): 17-22 (Huang Fenglei, Zhang Leilei, Duan Zhuoping. Shaped charge with large cone angle for concrete target. Explosion and Shock Waves, 2008, 28(1): 17-22 (in Chinese)) |
| [29] | 王成, 王万军, 宁建国. 聚能装药对混凝土靶板的侵彻研究. 力学学报, 2015, 47(4): 672-686 (Wang Cheng, Wang Wanjun, Ning Jianguo. Investigation on shaped charge penetration into concrete targets. Chinese Journal of Theoretical and Applied Mechanics,2015, 47(4): 672-686 (in Chinese)) |
| [30] | 许香照,马天宝,宁建国. 聚能装药侵彻混凝土数值模拟. 计算机辅助工程, 2015, 24(2): 29-35 (Xu Xiangzhao, Ma Tianbao, Ning Jianguo. Numerical simulation on concrete penetration of shaped charge. Computer Aided Engineering, 2015, 24(2): 29-35 (in Chinese) |
 2016, Vol. 48
2016, Vol. 48
