2. 上海交通大学海洋工程国家重点实验室, 上海 200240
近十年来,随着国际海洋油气开发从浅海转向深海,多立柱浮式油气生产平台(如半潜式生产平台或张力腿平台)的设计吃水不断增加,导致其在海流作用下容易产生大幅度涡激运动,这不仅会影响平台的正常生产作业,还会导致其系泊及采油立管系统产生疲劳破坏[1, 2].
单立柱深吃水(Spar)平台的涡激运动一直是海洋工程领域的重要研究课题,在其产生机理、响应特性和抑制方法等方面已有诸多研究成果[3, 4, 5, 6, 7].研究表明,当来流约化速度处于某个范围内时,漩涡脱落和平台运动固有频率保持一致,产生锁定效应.深海多立柱浮式平台一般由4个立柱组成,立柱截面形式一般以圆形、方形和倒角方形为主,并呈一定形式排列[2].当海流绕多个立柱时,立柱间的耦合干扰作用致使其绕流场结构发生复杂变化,进而导致多立柱浮式平台的涡激运动会出现诸多与单柱式平台涡激运动不同的特征[8]. 然而,目前国际上对多立柱浮式平台的涡激运动研究仍十分有限.一些研究人员[9, 10]通过循环水洞和风洞实验研究了4个固定圆柱在不同流向和组合排列下的脱涡和尾流干扰机理,分析了立柱排列和间距对各柱体升阻力系数以及涡脱频率的影响.一些研究人员[11, 12, 13, 14]通过在拖曳水池对平台模型进行拖曳实验分析了多柱式平台的横向和艏摇运动响应随约化速度的变化规律,测量了涡激运动的轨迹. 然而,以上研究鲜有涉及多立柱浮式平台涡激运动的作用机理及响应特性.此外,也有通过计算流体力学对多柱式平台涡激运动进行数值模拟,方法以雷诺平均方程(RANS)和脱体涡模拟为主[15, 16],但计算精度不甚理想.
有鉴于此,本文采用改进的延迟脱体涡方法对多立柱浮式深海平台的涡激大幅度运动进行了数值计算和分析,系统研究了流向、流速等海流环境参数对平台涡激运动响应的影响机理和规律,并分析了涡激运动中的三维流场特性.
1 数值模型 1.1 改进的延迟脱体涡方法(IDDES)
脱体涡方法的基本原理是将湍流模型的长度 $\tilde
{d}$量化为网格尺度. 早期的脱体涡方法[17]对$\tilde {d}$的定义如下
\[\tilde{d}=\min (d,{{C}_{\text{des}}}\Delta )\]
(1)
\[\tilde{d}={{\tilde{f}}_{\text{d}}}\left( 1+{{f}_{\text{e}}} \right)d+\left( 1-{{{\tilde{f}}}_{\text{d}}} \right)\psi {{C}_{\text{des}}}\text{ }{{\Delta }_{1}}\]
(2)
改进的延迟脱体涡方法通过$\tilde {f}_{\rm d} $和$f_{\rm e}$将带壁面模型的大涡模拟方法和延迟的脱体涡方法相结合[19],有效解决模型应力耗散和对数层不匹配问题,同时提高了近壁面湍流的求解质量,进而可以有效模拟大分离流动.
数值计算中,选取压力耦合方程组的半隐式(SIMPLE)算法求解压力和速度场,对流项采用混合二阶迎风格式,时间项采用二阶格式离散. 应用动网格技术,采用计算域整体运动的方法模拟流场和平台的相互作用.
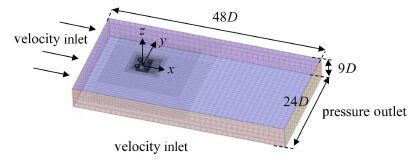
2 网格划分与边界条件研究选取四立柱张力腿(TLP)平台作为算例进行数值模拟分析,平台的主尺度(模型尺度,吃水宽度比为2.0)见文献[11].在数值算例中,由于傅氏数$F_r <0.14$,可认为自由面兴波的影响较小,计算模型仅取水面以下部分,计算域及网格划分如图1所示.为了使模型能够合理捕捉到立柱尾部的湍流特性,将入口边界条件中的湍流黏度比设置为0,初始化条件中的湍流黏度比设置为5.
|
图1 计算域及网格划分 Fig.1 Computational domain and mesh |
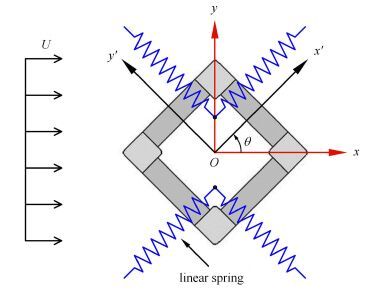
由于涡激运动主要发生在水平方向上,数值模拟仅考虑水平面上的3个自由度运动. 平台系泊系统等效为水平方向上的4根线性弹簧,如图2所示.其中,$\theta $为流向角,$Ox'y'$表示随体坐标系,$Oxy$表示为固定坐标系.定义沿$x$方向上的运动为顺流向运动,$y$方向上的运动为横向运动.
|
图2 流向角以及等效水平刚度示意图 (俯视图) Fig.2 Definition of current heading and equivalent horizontal mooring stiffness |
基于三维柱体绕流的流场特性,定义3个网格加密区(见图1),分别为:流动分离区(距尾部$0.5 D$,$D$为立柱宽度),剪切层作用区(距尾部3$D$)以及尾迹区(距尾部$10 D$).通过收敛性分析,最终选取的计算网格大小为:分离区为$0.03D$,剪切层作用区为$0.12 D$,尾流区为$0.24 D$.在近壁面使用壁面函数,$y^+$取0.3.
3 计算结果 3.1 多立柱浮式平台自由衰减数值模拟平台运动的固有周期定义为$T_n$,将数值自由衰减实验曲线经快速傅里叶变换取得的固有周期与实验值进行了比较,结果如表1所示. 从比较结果可以看出,数值衰减实验所得固有周期与实验结果较为吻合,最大误差为2.7%.分析表明,数值模型中的线性弹簧系统可以有效模拟水池实验的系泊状态.
| 表1 张力腿平台横向和艏摇运动固有周期 Table 1 Natural periods in transverse and yaw modes of a TLP platform |
平台的涡激运动幅值采用式(3)无量纲化. 其中,$\delta _1 $和$\delta _2$分别为横向和艏摇运动时间历程的方差. 约化速度由式(4)定义,$T_{n2}$和$T_{n6} $分别为平台横向和艏摇运动的固有周期,$V_{r2} $和$V_{r6}$分别定义为横向和艏摇运动约化速度
\[A/D=\sqrt{2}{{\delta }_{1}}/D,\phi =\sqrt{2}{{\delta }_{2}}\]
(3)
\[{{V}_{r2}}=U\cdot {{T}_{n2}}/D,{{V}_{r6}}=U\cdot {{T}_{n6}}/D\]
(4)
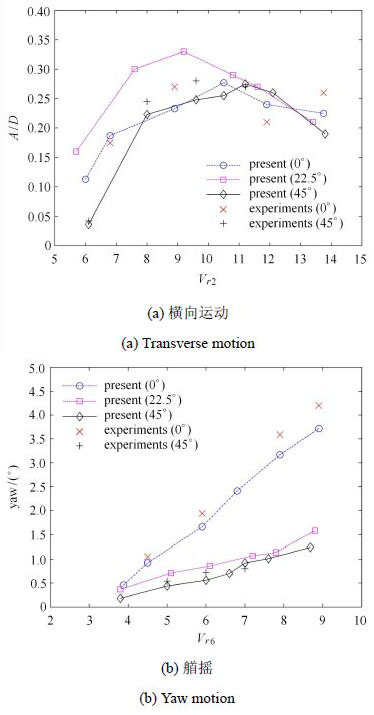
图3(a)为0°,22.5° 和45° 流向角下,计算结果和实验值的比较. 总体而言,在0°和45°流向角下,多柱式平台涡激运动响应的数值计算结果与实验值[11]基本吻合,运动幅度随约化速度的变化趋势与实验一致,从而验证了数值模型的有效性. 如图3(a)所示,当$7 <V_{r2} <14$时,横向涡激运动响应介于$0.2D \sim0.4D$之间,22.5°流向角下的横向运动响应较0°及45°流向下更大.
|
图3 涡激运动响应 Fig.3 Nominal VIM responses |
图3(b)为张力腿平台艏摇运动响应的计算结果.如图所示,艏摇响应和约化速度呈线性递增关系,表明艏摇涡激运动很可能是一种驰振. 在22.5° 和45° 流向角下,艏摇运动响应仅为0°流向角下的30%,这与0°流向角下平台所受激振力转矩较其他两个流向下较大有关.
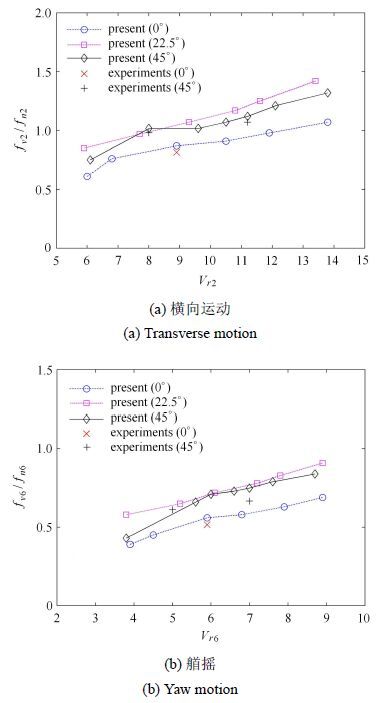
3.3 涡激运动特性分析图4比较了各流向下数值计算和模型实验的涡激运动频率比. 从图4(a)中可以看出,横向运动频率$f_{v2}$与其固有频率$f_{n2} $的比值始终保持在1.0上下,当$7 < V_{r2} <14$时,脱涡频率锁定在横向运动固有频率附近,使横向运动处于锁频状态.这表明,多立柱平台的涡激运动机理与单立柱平台相似,受脱涡激励和系泊回复力的共同作用,其运动频率长时间保持在固有频率附近,大幅度的共振运动反过来改变周围的流场,进一步加强了流固耦合效应.如图4(b)显示,多柱式平台的艏摇运动频率与固有频率的比值始终在1.0以下,但频率比随约化速度的增加逐渐接近于1.22.5°和45°流向角下,频率比随约化速度的变化曲线始终高于0°流向角下的结果.
|
图4 涡激运动频率比 Fig.4 Frequency ratio |
图5为不同流向角下平台横向运动的功率谱密度. 从图中可以看出,不同流向角下横向运动的主要能量都集中在$7 < V_{r2} <14$,而其频率均位于横向模态的固有频率附近.22.5°流向角下横向运动的能量更为集中且峰值更大,而0° 流向角下横向运动的能量谱较宽.

|
图5 横向运动的功率谱密度 Fig.5 Power spectrum density of motion in the transverse direction |
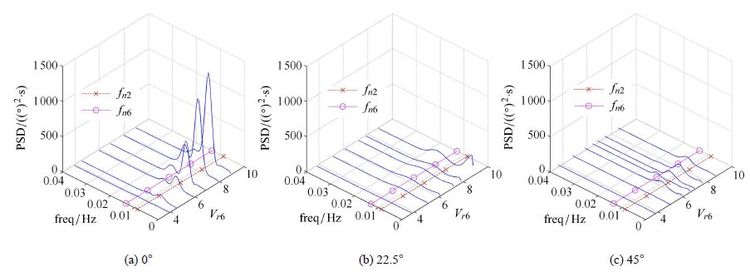
图6为平台艏摇运动的功率谱密度. 通过对比横向运动位移功率谱可见,在横向运动锁定区间内(对应的艏摇约化速度范围为$5 < V_{r6} <9$),艏摇和横向运动的频率基本一致,表明在锁频状态下,艏摇激振力矩主要受立柱上的升力控制,其激振频率与升力的作用频率相同.进一步对比可知,22.5°和45° 流向角下的艏摇能量仅为0° 流向角下的10%左右.0°流向角下的艏摇运动能量与横向运动保持在同一量级,而在22.5° 和45°流向角下,艏摇能量仅为横向运动能量的10%.
|
图6 艏摇的功率谱密度 Fig.6 Power spectrum density of yaw motion |
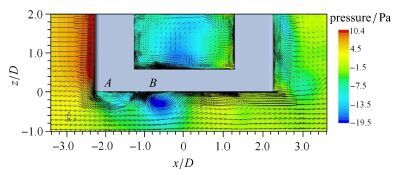
图7 为0° 流向角和约化速度$V_{r2} = 11.9$下,某时刻立柱中剖面($y = 1.8D)$上的压力云图和速度矢量分布.从图中可以看出,由于立柱的吃水宽度比较小,流体在立柱底部角区的拐点$A$处发生流动分离,剪切层的不稳定形成了明显的拱形涡结构,且流体向底面后下方扩散,这与短柱长比垂直圆柱自由边附近的流动类似[20].由于多柱式平台的浮箱底部与立柱底部平行,当流向角为0°时,浮箱的存在延长了流体在立柱底面上的作用和扩散,从而推动了底部梢涡结构(tip vortex)[21]的进一步发展,梢涡结构与拱形涡结构在底面附近的相互作用,诱导了流动分离后涡再次附着于浮箱底面$B$点.当然,平台本身的运动对其底部拐点处的流动分离也会有一定的影响.
|
图7 立柱中纵剖面上的压力分布图和速度矢量 Fig.7 Pressure contour and velocity vector in the middle section of a column of a TLP |
本文基于改进的延迟脱体涡方法实现了深海多立柱浮式平台涡激运动的三维数值模拟,计算结果与模型实验值较吻合,验证了所用数值模型的有效性. 研究发现,当$7 < V_{r2} <14$时,多柱式平台横向运动发生频率锁定,运动响应保持在较大的振幅区间,而艏摇响应随约化速度呈线性递增,和驰振有关.在锁频区间内,横向和艏摇涡激运动频率基本相同,艏摇力矩的变化主要受作用于立柱上的涡激升力控制. 22.5° 和45°流向角下的横向运动能量与0°流向角下的横向运动能量保持在同一量级上. 通过分析涡激运动时立柱底面的三维流场,发现平台浮箱底部交界处出现流动分离和涡的再次附着现象,其对平台涡激运动的影响还有待进一步研究.
| [1] | Vandiver JK, Swithenbank SB, Jaiswal V, et al. Fatigue damage from high mode number vortex-induced vibration.//Proc. of 25th International Conference on Offshore Mechanics and Arctic Engineering, Hamburg, Germany, 2006: 803-811 |
| [2] | 张新曙,尤云祥,滕明清. 深海半潜浮式平台的关键理论与技术问题. 海洋工程, 2016, 34(1): 109-115 (Zhang Xinshu, You Yunxiang, Teng Mingqing. Review of the key theories and technologies for the development of deep-sea semi-submersible floating production unit. The Ocean Engineering, 2016, 34(1): 109-115 (in Chinese)) |
| [3] | Finnigan T, Roddier D. Spar VIM model tests at supercritical Reynolds numbers.//Proc. of 26th International Conference on Off- shore Mechanics and Arctic Engineering, San Diego, USA, 2007:731-740 |
| [4] | Irani M, Perryman S, Brewer J, et al. Vortex induced motions of the horn mountain truss spar.//Proc. of 27th International Conference on Offshore Mechanics and Arctic Engineering, Estoril, Portugal,2008: 967-973 |
| [5] | Finn L, Maher J, Gupta H. The cell spar and vortex induced vibrations.// Proc. of Offshore Technology Conference, Houston, USA,2003: 1-6 |
| [6] | Halkyard J, Sirnivas S, Constantinides Y, et al. Benchmarking of truss spar vortex induced motions derived from CFD with experiments.// Proc. of 24th International Conference on Offshore Mechanics and Arctic Engineering, Halkidiki, Greece, 2005: 895-902 |
| [7] | Oakley OH, Navarro C, Constantinides Y, et al. Modeling vortex induced motions of spars in uniform and stratified flows.// Proc. of 24th International Conference on Offshore Mechanics and Arctic Engineering, Halkidiki, Greece, 2005: 885-894 |
| [8] | Waals OJ, Bultema S, Phadke AC. Flow induced motions of multi column floaters.//Proc. of 26th International Conference on Offshore Mechanics and Arctic Engineering, San Diego, USA, 2007: 669-678 |
| [9] | Lam K, Li JY, Chan KT, et al. Flow pattern and velocity field distribution of cross-flow around four cylinders in a square configuration at a low Reynolds number. Journal of Fluids & Structures, 2003,17(5): 665-679 |
| [10] | Lam K, Li JY, So RMC. Force coefficients and Strouhal numbers of four cylinders in cross flow. Journal of Fluids & Structures, 2003,18(3): 305-324 |
| [11] | Magee A, Sheikh R, Guan KYH, et al. Model tests for VIM of multicolumn floating platforms.//Proc. of 30th International Conference on Ocean, Offshore and Arctic Engineering. Rotterdam, The Netherlands,2011: 127-136 |
| [12] | 白治宁,肖龙飞,程正顺等. 深吃水半潜式平台涡激运动响应模型实验研究. 船舶力学, 2014, 18(4): 377-384 (Bai Zhining, Xiao Longfei, Cheng Zhengshun, et al. Experimental study on vortex induced motion response of a deep draft semi-submersible platform. Journal of Ship Mechanics, 2014, 18(4): 377-384 (in Chinese)) |
| [13] | 苏云龙,杨建民,吕海宁等. 新型多立柱式Spar 平台涡激运动特性研究. 海洋工程, 2015, 33(1): 14-23 (Su Yunlong, Yang Jianmin, Lv haining, et al. Study on the vortex-induced motions of a new type multi-column Spar platform. The Ocean Engineering, 2015, 33(1):14-23 (in Chinese)) |
| [14] | Gonçalves RT, Rosetti GF, Fujarra ALC, et al. Experimental study on vortex-induced motions of a semi-submersible platform with four square columns, Part I: Effects of current incidence angle and hull appendages. Ocean Engineering, 2012, 54: 150-169 |
| [15] | Tan JHC, Magee A, Kim JW, et al. CFD simulation for vortex induced motions of a multi-column floating platform.//Proc. of 32th International Conference on Ocean, Offshore and Arctic Engineering. Nantes, France, 2013 |
| [16] | 谷家扬,陶延武,杨建民等. 深水张力腿平台非线性涡激特性及水动力性能研究. 船舶力学, 2015, 19(4): 370-379 (Gu Jiayang, Tao Yanwu, Yang Jianmin, et al. Study on the nonlinear characteristics of vortex induced motion and hydrodynamic performance of deepwater TLP. Journal of Ship Mechanics, 2015, 19(4): 370-379 (in Chinese)) |
| [17] | Spalart PR, Allmaras SR. A one-equation turbulence model for aerodynamic flows. La Recherche Aérospatiale, 1992, 439(1): 5-21 |
| [18] | Shur ML, Spalart PR, Strelets MK, et al. A hybrid RANS-LES approach with delayed-DES and wall-modelled LES capabilities. International Journal of Heat and Fluid Flow, 2008, 29(6): 1638-1649 |
| [19] | Spalart PR, Deck S, Shur ML, et al. A new version of detachededdy simulation, resistant to ambiguous grid densities. Theoretical and Computational Fluid Dynamics, 2006, 20(3): 181-195 |
| [20] | Gonçalves RT, Franzini GR, Rosetti GF, et al. Flow around circular cylinders with very low aspect ratio. Journal of Fluids & Structures,2014, 54: 122-141 |
| [21] | Pattenden RJ, Turnock SR, Zhang X. Measurements of the flow over a low-aspect-ratio cylinder mounted on a ground plane. Experiments in Fluids, 2005, 39(1): 10-21 |
2. State Key Laboratory of Ocean Engineering, Shanghai Jiao Tong University, Shanghai 200240, China
 2016, Vol. 48
2016, Vol. 48