对升阻比的追求一直是高速飞行器构型设计中重点关注的问题. 在高速飞行条件下，由于激波阻力和黏性阻力急剧增加，飞行器的气动性能急剧下降，形成所谓的"升阻比屏障"^[1]，导致飞行器升阻比难以获得提高. 目前高升阻比构型主要包括翼身组合体^{[2, 3, 4]}、翼身融合体^{[5, 6]}和乘波体^[7]等几种方案. 翼身组合体主要由机体和机翼两部分构成，其中机翼一般采用大后掠三角翼/梯形翼充当主要升力部件，机体采用锥体或锥/柱组合体，为飞行器提供足够的容积. 翼身融合体以美国HTV-2为典型代表，主要特点为机体和机翼融合，二者没有明显界限，飞行器上表面适当隆起满足容积需求. 下表面为升力面，通过合理设计飞行攻角提供所需升力. 乘波体是目前公认的高升阻比构型. 在设计条件下，由于高速飞行时前缘激波附着于乘波体边缘，激波后的高压区被完全包裹于飞行器下表面，因而可获得相对较高的升阻比. 自20世纪80年代Bowcutt^[8]和Corda^[9]在考虑黏性条件下采用优化方法获得一系列黏性优化乘波体以来，该构型一直是研究热点之一，所涉及的具体问题包含构型设计^{[10, 11, 12, 13]}、分析和优化^{[14, 15, 16, 17, 18, 19]}、一体化设计^{[20, 21, 22, 23]}和热载荷分析^{[24, 25]}等诸多方面.

然而乘波体在实用化方面仍面临许多困难. 其中之一为标准乘波体上表面一般采用自由流面或弱膨胀面设计，因此厚度相对较薄，容积率偏小. 文献^{[26, 27]}提出的乘波概念飞行器为解决这一问题，将飞行器的尺寸增加至60 m左右. 但尺寸的增加不可避免地导致迎流面积和湿润面积增加，进而导致飞行器的气动阻力和重量大幅增加，给飞行器的动力系统选择及结构设计等方面带来困难.

高速飞行器最基本的功能是实现载荷的远程快速运输，除载荷需求外，燃料的装载量与航程直接呈正比，因此其重量和容积是最基本的两个追求指标. 例如，相比于吸气式飞行器，以火箭为动力的高超声速巡航飞行器是现阶段非常有竞争力的选择^[28]. 然而，火箭发动机除携带燃料外还需携带大量氧化剂，使飞行器的容积和重量均大幅增加，因而在气动设计中应提高升力以满足升重匹配，同时尽量减小阻力使其具有较优的升阻比. 文献^[29]对高超声速飞行器上壁面进行了多目标优化和性能分析，结果表明，升阻比和容积近似成线性反比关系. 文献^[30]对乘波体采用增量修正方法和微分演化方法进行了优化和分析，其结果表明升阻比不仅与容积存在矛盾，同时也同升力存在矛盾，即乘波体的高升阻比不仅建立在低阻力的基础上，同时相应升力也会减小，增加了升重匹配的难度.

针对大容积高速飞行器高升阻比的设计需求，文献^[31]基于飞行器上壁面一般为压缩面的特点，提出了一种高压捕获翼的新型气动布局概念. 与传统升力体或乘波体布局相比，该布局主要特点为在飞行器机体背风面增加了与来流方向平行的曲面翼，称之为高压捕获翼(high pressure capturing wing,HCW). 在此基础上，通过二维平面斜激波-膨胀波理论证明了捕获翼上下表面具有较大的压差，从而为飞行器提供较大的升力，此外还通过三维概念设计外形初步验证了HCW气动布局的实际效果. 结果表明，增加捕获翼后飞行器的升力大幅提升达30%以上，升阻比提升一般可达20%以上.

由于高压捕获翼构型主要利用机体上压缩面和捕获翼之间的耦合关系来改善其气动性能，因此捕获翼的位置与机体压缩激波和自身二次压缩激波直接相关，除平面二维情况外，均无法利用理论等方法直接获得. 本文主要针对这一问题，发展了一种捕获翼位置设计的有效方法. 其简要流程为：首先分析捕获翼设计位置的影响参数，在此基础上利用均匀实验设计方法在设计空间内生成一系列构型，并通过迭代使用数值模拟获得相应的捕获翼设计位置，然后构建HCW位置与设计参数之间的代理模型，获得设计参数与捕获翼位置间的直接映射关系.

图1给出了HCW的基本设计原理^[32]，为简化描述，机体上表面为尖楔形压缩，捕获翼采用无厚度的平板.高速来流经飞行器上表面压缩后，产生第一道斜激波$S_{1}$，来流经此激波压缩后，压力增加，且流动方向向上转折与机体上表面平行.之后，来流继续前进与捕获翼接触后形成第二道激波$S_{2}$，压力进一步提高.随着来流继续前进，在机体尾部产生膨胀波，经过前马赫线(FML)后压力逐渐减小，然后流向下游.根据激波和膨胀波的位置，整个流场可分为5个区域，如图1所示.区域1的压力为自由来流压力，区域2为第一压缩区，在机体压缩作用下压力增加.区域3为第二压缩区，在HCW对来流压缩的影响下，其压力进一步升高. 在第4区域，由于膨胀波的作用，压力逐渐减小.由于捕获翼平行于来流，第5区域的压力基本与自由来流压力相等.通过以上分析可知，捕获翼下表面的压力经两次压缩后将明显高于上表面压力，为飞行器提供较大的升力.当捕获翼采用薄翼设计时，其阻力增加较小，因此飞行器的升阻比也可获得大幅增加.

图1(Fig.1)

图1 HCW设计原理示意图 Fig.1 Design principle illustration of the HCW

基于上述设计原理，捕获翼的设计位置应如下选择：(1)捕获翼前缘点应落在第一道激波$S_{1}$附近(类似于乘波体的设计)，以尽可能利用机体压缩的高压区；(2)第二道压缩激波$S_{2}$应掠过机体尾部最高点后缘.若捕获翼下移使$S_{2}$与机体作用，将导致机体的阻力和负升力同时增加.而当捕获翼上移使$S_{2}$偏离机体较远时，HCW所捕获的高压区减小，使其增升效果减弱.可见，捕获翼的位置选择与前述第一道和第二道压缩激波同时相关.

若机体上表面为二维楔形体，根据斜激波-膨胀波理论可直接解析求得两道激波$S_{1}$和$S_{2}$的位置，进而确定捕获翼的设计位置.但实际中机体大多为轴对称体(如图2所示)或其他更加复杂的外形，此时将无法采用理论等方法求解两道压缩激波.即使对于简单的锥体组合HCW的构型，也只能基于无黏尖锥条件下的Taylor-Macoll(T-M)方程求得第一道压缩激波而无法求得第二道激波.若机体外形更为复杂时，第一道和第二道压缩激波的求解都将更加复杂.同时，高速飞行条件下黏性对流场的影响十分明显，边界层将直接导致激波位置的变化.此外，实际使用中出于热防护的需要，机体和捕获翼的前缘均需采取一定厚度的钝化，这进一步增加了流场的复杂性.显然，捕获翼位置的确定是该构型设计中第一个必须解决的关键问题.

图2(Fig.2)

图2 锥体(左)和任意母线旋成体(右)组合HCW示意图 Fig.2 Cone (left) and arbitrary generating line revolution (right)combination HCW

针对这一问题，本文基于代理模型发展了一种捕获翼位置设计的有效方法，其主要流程如图3所示：首先，在给定机体外形条件下，对影响HCW位置设计的参数进行分析，确定关键设计参数.其次，给定各设计参数的上下变化区间(设计空间)，并依据设计参数的个数选择合理的实验设计表，并生成一系列典型构型构成设计样本集，再次，对样本集中的每个构型通过迭代使用CFD分析获得其捕获翼的设计位置.最后，根据前述数据构建代理模型并对其进行检验，在此基础上最终获得此条件下捕获翼位置与设计参数之间的映射关系.

图3(Fig.3)

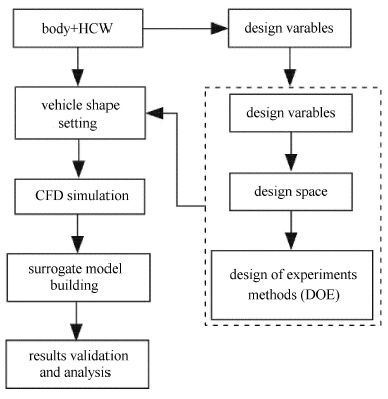
图3 捕获翼位置设计方法流程图 Fig.3 Flowchart of the design method for HCW position

由于该流程主要基于数值模拟，这里首先对CFD模块进行检验. 检验数据采用美国Langley 11英寸高超声速风洞的尖锥模型数据^[33]. 两个模型外形分别为长度127 mm、半锥角5°和长度85.471 mm、半锥角10°的锥体构型，如图4所示. 实验来流条件为马赫数9.6，飞行攻角0°.

图4(Fig.4)

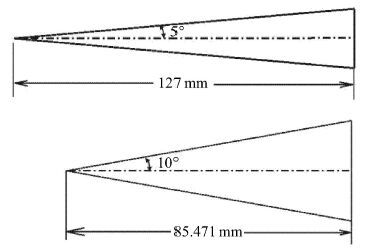
图4 模型外形示意图 Fig.4 The diagram of model configuration

数值分析采用TVD (total variation diminishing)格式，时间推进选用隐式格式，湍流模型为$k$-$\varepsilon $模型.阻力系数计算时参考面积为锥体法向投影面积.表1为半锥角5°外形在不同壁面网格尺度下对应的阻力系数$C_{d}$(不含底阻)，$\triangle n$为壁面法向第一层网格厚度，$d$为锥体的长度，可以看出，随壁面网格逐渐加密，阻力系数趋于收敛.表2选取编号4的网格尺度，分别计算了两组外形在0°攻角下的阻力系数，表中 $\alpha $ 为半锥角.结果表明CFD数值计算与实验结果拟合较好，具有较高的可信度.

表1(Table 1)

表1 网格收敛性分析结果Table 1 Results of grid convergence analysis Number $\triangle n$ $C_{d}$ 1 $d \times 10^{-2}$ 0.009 0 2 $d \times 10^{-3}$ 0.017 8 3 $d \times 10^{-4}$ 0.017 6 4 $d \times 10^{-5}$ 0.017 6 5 $d \times 10^{-6}$ 0.017 6

表1 网格收敛性分析结果 Table 1 Results of grid convergence analysis

表2(Table 2)

表2 数值结果与实验数据对比Table 2 Comparison of numerical results and experimental data $\alpha $/(°) $C_{d }$ (CFD) $C_{d}$ (experimental) 5 0.017 6 0.017 0 10 0.057 5 0.057 0

表2 数值结果与实验数据对比 Table 2 Comparison of numerical results and experimental data

为验证前述方法的有效性，这里以圆锥形机体组合捕获翼的构型为例进行计算和检验. 计算主要基于二维轴对称模型.

在无黏条件下，机体压缩激波$S_{1}$可以由锥形流T-M方程解出.但高速飞行条件下，黏性诱导的边界层效应将会影响飞行器的有效外形，从而导致外部无黏流场发生改变，可能导致激波位置发生改变.为分析黏性对机体激波的影响，这里基于数值模拟首先分析了湍流条件与无黏流场的区别，进而分析黏性对HCW设计位置的影响.

机体选用长度4 m、半锥角9°的锥体，计算来流马赫数为7. 分别采用无黏和湍流计算模型，HCW的设计位置均基于无黏流场. 图5为两种计算模型条件下的压力分布，为细致对比二者激波位置，从图中截取了$X=3$ m和$X=3.95$ m平面处压力随高度变化曲线，如图6所示. 从图中可以看出，在考虑黏性效应后，由于边界层厚度的影响，机体压缩激波和捕获翼压缩激波相对于水平面的夹角均有小幅度增加. 但从激波线在$Y$方向的偏移量可以看出，激波偏移量均在10 mm以内，对于HCW位置的设计影响相对微弱，因此，在这一构型中黏性影响可以忽略.

图5(Fig.5)

图5 湍流与无黏流场压力分布 Fig.5 Pressure contours comparison of the flow-field by the turbulent and the invisid model

图6(Fig.6)

图6 $X=3$ m和$X=3.95$ m截面处压力随$Y$值的变化曲线 Fig.6 Variations of pressure with $Y$ value at cross section $X=3$ m and $X=3.95$ m

气动加热是高速飞行器设计中必须面对的问题，这一问题在飞行器鼻锥和捕获翼前缘部分尤为严重，一般需要钝化处理以满足热防护需求. 对于锥体组合HCW飞行器构型，锥体前缘钝化和HCW前缘钝化必然导致流场发生改变. 激波形状在前缘附近由贴体直线激波变为脱体弓形激波，并且导致下游流场随之改变. 因此，锥体和捕获翼前缘钝化可能对HCW设计位置产生影响，需要对其进行分析和评估.

基于上述长度4 m,半锥角9°的锥体，对锥体前缘采取圆弧钝化的方式，钝化前缘和机体相切连接，如图7所示，图中从左到右依次为钝化半径0,10 mm,20 mm和30 mm.计算条件为：来流马赫数7，飞行攻角0°，飞行高度30 km，采用$k$-$\varepsilon $湍流模型.在不同钝化半径下，锥体产生的第一道激波位置如图8所示，其鼻锥部局部放大如图9所示.从图中可知，钝化半径为0，即尖前缘时，激波为一条直线.随着钝化半径的增加，弓形激波区域扩大，偏离尖前缘直线激波的距离增加.而在靠近机体尾部时，激波形状均基本与尖前缘直线激波一致. 这一结论与文献^[34]基本一致.为进一步说明，图10给出了$X=3$ m截面处压力随$Y$值的变化曲线，可以看出机体激波及波后压力分布基本保持不变，故机体前缘钝化的影响可以忽略.

图7(Fig.7)

图7 锥体前缘不同钝化半径模型 Fig.7 The sketch of different blunted models

图8(Fig.8)

图8 不同钝化半径对应激波位置 Fig.8 Variation of shock position with blunted radius

图9(Fig.9)

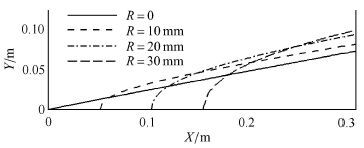
图9 不同钝化半径头部激波位置 Fig.9 Variation of shock position with blunted radius at cone front position

图10(Fig.10)

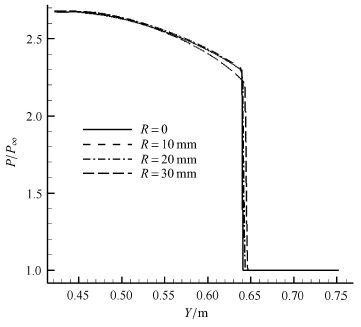
图10 $X=3$ m截面处压力随$Y$值的变化曲线 Fig.10 Variations of pressure with $Y$ value at cross section $X=3$ m

基于上述结果可知，本算例中黏性和锥体前缘钝化对机体压缩激波影响较小，由此，机体压缩激波仍可基于无黏/尖机体前缘外形，利用T-M方程求解.这里仍基于上述长度4 m、半锥角9°的锥体作为机体，在前述相同的计算条件下，分析捕获翼前缘钝化半径对其设计位置的影响.分析中，捕获翼钝化半径在0$\sim$20 mm范围内选择6个不同的值，分别为0,2.5 mm,5 mm,10 mm,15 mm和20 mm.

图11给出了前述6种外形尾部附近的流场压力云图，可以看出，通过合理调整捕获翼位置，捕获翼均可获得最优设计位置，即前缘点落于机体激波$S_{1}$上，同时捕获翼自身压缩激波掠过锥体尾部最高点后缘.而且，从结果还可以看出，随着钝化半径增加，捕获翼位置向后移动，造成这种结果的原因为：(1)为保证捕获翼整体落在锥体激波$S_{1}$后面，需使其上前缘点落在$S_{1}$上，随着钝化半径增加，驻点离$S_{1}$距离增加，为保证捕获翼自身激波不作用于机体，捕获翼必须向右移动；(2)随着钝化半径增加，前缘产生的弓形激波强度增加，为保证此激波掠过机体上，HCW位置必须向右移动.由上述分析可知，捕获翼前缘钝化半径对其设计位置的影响不能忽略.

图11(Fig.11)

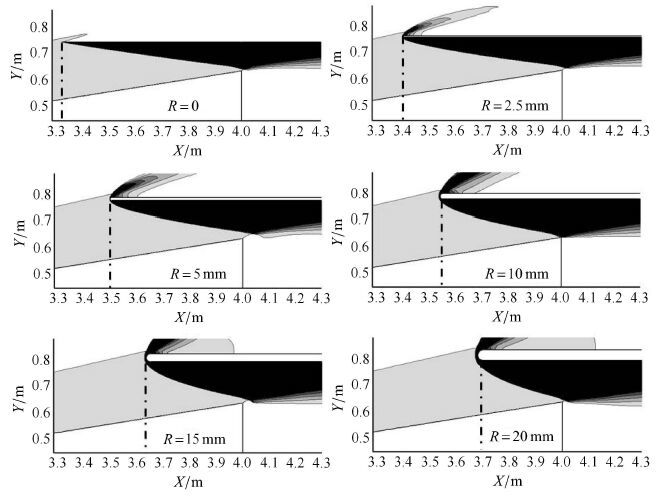
图11 不同HCW钝化半径压力分布云图 Fig.11 Pressure distribution at different blunted radius for HCW

捕获翼设计位置主要由机体压缩激波和捕获翼压缩激波确定，机体压缩角和来流马赫数是影响这两道激波位置的决定性参数，因此必须考虑.此外，通过前述分析可知，黏性效应和机体前缘钝化对两道压缩激波位置的影响可以忽略，而捕获翼前缘钝化的影响必须考虑.由此，可以得出影响HCW设计位置的3个关键参数为：机体压缩角、来流马赫数和捕获翼前缘钝化半径.为便于后续处理，将机体压缩角及捕获翼前缘钝化半径均以机体长度为参考量进行无量纲化处理.上述3个无量纲量的取值边界如表3给定.

表3(Table 3)

表3 设计参数及取值范围Table 3 Design parameters and design space Variables Lower bound Upper bound $H$ 0.105 1 0.212 6 $M$ 3 9 $R_{\rm HCW}$ 0.000 5 0.005

表3 设计参数及取值范围 Table 3 Design parameters and design space

表3中，$H$为半锥角的正切值，其有量纲上下边界分别为6°和12°，$M$为来流马赫数，$R_{rmHCW}$为无量纲化的HCW钝化半径，其有量纲上下边界分别为2 mm和20 mm.

按前述方法及流程，下一步需要在设计空间内给定样本算例进而构建代理模型. 这里样本取样方法采用实际中广泛使用的均匀实验设计方法. 该方法基于数论理论，通过在整个设计空间内构造合理的均匀设计表来获取样本集，可有效减小计算量. 这里选择变量水平值为15. 实验设计表中各样本的参数分布如表4所示.

表4(Table 4)

表4 实验设计表及对应的$X_{\rm HCW}$Table 4 Table of uniform design of experiment and corresponding values of $X_{\rm HCW}$ Number $H$ $M$ $R_{\rm HCW}$ $X_{\rm HCW}$ 1 0.108 6 4.4 0.004 25 0.812 5 2 0.115 7 6 0.003 65 0.862 5 3 0.122 8 7.6 0.003 05 0.9 4 0.129 9 3.2 0.002 45 0.737 5 5 0.137 0 4.8 0.001 85 0.825 6 0.144 1 6.4 0.001 25 0.85 7 0.151 2 8 0.000 65 0.862 5 8 0.158 4 3.6 0.004 55 0.8 9 0.165 5 5.2 0.003 95 0.862 5 10 0.172 7 6.8 0.003 35 0.9 11 0.179 9 8.4 0.002 75 0.925 12 0.187 1 4 0.002 15 0.8 13 0.194 4 5.6 0.001 55 0.85 14 0.201 6 7.2 0.000 95 0.875 15 0.208 9 8.8 0.004 85 0.95

表4 实验设计表及对应的$X_{\rm HCW}$ Table 4 Table of uniform design of experiment and corresponding values of $X_{\rm HCW}$

根据实验设计表生成的设计参数，对每个算例迭代使用CFD分析计算得出对应的捕获翼设计位置. 由于捕获翼上前缘点落在机体激波$S_{1}$上，因此仅需给定其前缘点的横向位置$X_{\rm HCW}$即可，其纵向位置可由$S_{1}$的斜率直接计算获得. 经上述计算，可获得每个样本的$X_{\rm HCW}$数值，如表4最后一列所示. 这里$X_{\rm HCW}$的数值仍以机体长度为参考量进行无量纲化表达.

利用上述均匀实验设计生成的训练样本集，构建出不带交叉项的多项式代理模型，其解析表达式如式(3)所示.

图12给出了前述15个训练样本的训练误差，图中横坐标为样本点编号，纵坐标为代理模型输出值和实际值的相对误差.可以看出，对所有样本训练精度均控制在2%以内，具有较高的精度.

图12(Fig.12)

图12 多项式代理模型训练拟合精度 Fig.12 The training fitting precision for polynomial model

为进一步验证代理模型的准确性，在设计空间内选用7水平的均匀实验设计重新生成7个训练样本，利用代理模型计算得到每个测试样本点对应的$X_{\rm HCW}$，再通过CFD计算验证捕获翼设计位置是否遵循设计准则.表5为测试样本点及利用代理模型得出的$X_{\rm HCW}$，图13给出了上述7个测试样本的计算压力分布云图.从图13可以看出，捕获翼位置均按照设计位置摆放，符合HCW的基本准则.

表5(Table 5)

表5 测试样本点及代理模型得出的$X_{\rm HCW}$Table 5 The $X_{\rm HCW}$ value computed by agent model corresponding to the test points Number $H$ $M$ $R_{\rm HCW}$ $X_{\rm HCW}$ 1 0.112 7 6 0.003 4 0.862 5 2 0.127 9 3.429 0.002 1 0.75 3 0.143 1 6.857 0.000 8 0.85 4 0.158 4 4.286 0.004 0 0.825 5 0.173 8 7.714 0.002 8 0.912 5 6 0.189 2 5.143 0.001 5 0.832 5 7 0.204 7 8.571 0.004 7 0.945

表5 测试样本点及代理模型得出的$X_{\rm HCW}$ Table 5 The $X_{\rm HCW}$ value computed by agent model corresponding to the test points

图13(Fig.13)

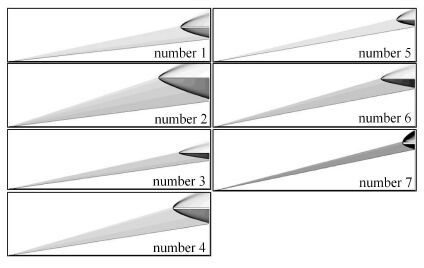
图13 测试样本点的压力分布云图 Fig.13 The pressure distribution of test points

基于上述多项式代理模型，对此构型的捕获翼设计位置与设计参数之间的关系进行了分析. 图14给出了设计空间内捕获翼位置$X_{\rm HCW}$与各设计变量的对应关系. 可以看出，随着机体压缩角、来流马赫数和钝化半径的增加，$X_{\rm HCW}$的数值也随之增加，即捕获翼的位置向后移动.图15给出了3个设计变量的单因素轮转法分析结果，即对3个设计变量每次固定两个参数，仅改变单个参数的取值.由于其他两个参数改变只会使$X_{\rm HCW}$曲线发生平移，故图15可以定性地分析$X_{\rm HCW}$与设计变量之间的变化规律. 从图中可知，机体压缩角、来流马赫数及钝化半径较小时，$X_{\rm HCW}$增长较快，随着变量值增加，$X_{\rm HCW}$趋于平缓，以缓慢趋势增加.

图14(Fig.14)

图14 $X_{\rm HCW}$与设计变量的关系 Fig.14 The relationship between $X_{\rm HCW}$ value and design variables

图15(Fig.15)

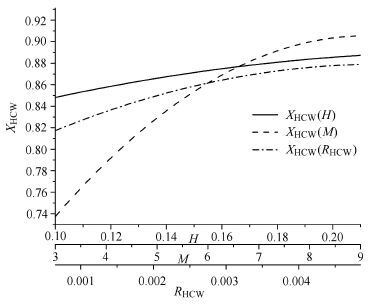
图15 $X_{\rm HCW}$与$H,M$和$R_{\rm HCW}$之间的关系 Fig.15 The relationship between the $X_{\rm HCW}$ and $H$,$M$,$R_{\rm HCW}$

对上述结果分析如下：当来流马赫数$M$和捕获翼钝化半径$R_{\rm HCW}$固定时，随着机体压缩角增加，压缩作用增强，机体压缩激波与机体距离减小. 为避免捕获翼激波反射于机体上，其设计位置必须向后移动.当机体压缩角进一步增大时，机体激波与机体距离以平缓趋势增加，因此，捕获翼位置的后移量逐渐减小.同样，当机体压缩角$H$和钝化半径$R_{\rm HCW}$固定时，捕获翼设计位置随马赫数变化趋势与其随压缩角的变化趋势一致.当固定机体压缩角$H$和来流马赫数$M$时，$X_{\rm HCW}$随捕获翼前缘钝化半径增加而增加，在上述捕获翼钝化半径的影响时已做详细分析，从图15可以看出，与前文分析规律一致.

本文针对高压捕获翼构型，根据高压捕获翼位置的基本设计准则，发展了一种确定捕获翼设计位置的有效方法，该方法在捕获翼设计位置参数分析的基础上，综合使用均匀实验设计、计算流体力学分析和代理模型方法，构建捕获翼设计位置与设计参数之间的映射关系. 锥体组合捕获翼构型的实例验证结果表明，该方法可以在较大设计范围内准确确定捕获翼的设计位置.

基于锥体组合捕获翼构型的分析可知，黏性效应及机体前缘钝化对捕获翼位置设计影响较小，锥体压缩角、来流马赫数和捕获翼钝化半径是决定捕获翼设计位置的关键参数，基于构建的代理模型结果可以看出，捕获翼设计位置与上述3个参数均呈单调正比关系.

虽然本文仅以圆锥形机体为例对所发展的方法进行验证及分析，但从该方法的流程可知，此方法具有较强的普适性，可推广至任意形状的机体构型. 由于捕获翼的位置仅与机体上表面相关，因此本文算例中所获得的基本结论亦可应用至类似构型，特别是上表面为锥体或锥柱组合体的构型. 此外，现有工作仅对捕获翼前缘点位置的设计方法进行研究，尚未考虑捕获翼长度选择、装配角选择以及前缘线型线变化等因素的影响，这些问题将在后续工作中逐步开展.

Li Guangli, Cui Kai, Xiao Yao, Xu Yingzhou