引言

射流破碎液滴的粒径分布和速度分布对液体射流的雾化具有重要的影响^{[1, 2, 3]}.

针对射流破碎液滴粒径与速度数量密度分布问题的研究，实验研究方法存在影响因素众多、准确度难以保证、实施比较困难等问题^{[4, 5, 6]}；理论研究方法仍然是目前射流破碎液滴粒径与速度数量密度分布问题研究的主要方法^{[7, 8]}. 最大熵原理方法是射流破碎液滴粒径与速度数量密度分布研究的重要理论方法之一，具有与实验结果吻合程度高、耗费时间短、研究成本低等特点^[9].

1948年，Shannon发表了一篇具有划时代意义的论文------通信的数学原理，从而奠定了现代信息理论的基础^[10].在这篇论文中，Shannon将概率理论与玻尔兹曼熵理论相结合，从数学上证明并定义了某一系统的信息熵 $$S_{\rm S}=-K\sum^n_{i=1} p_i \ln p_i$$ 其中，$S_{\rm S}$为系统的信息熵；$n$为系统可能出现状态的总数；$p_{i}$为微观状态$i$出现的概率.

当一个系统的微观状态具有概率密度$p(x)$时，系统的信息熵可以表示为 $$S_{\rm S}=-K\int^\infty_{-\infty} p(x) \ln p (x) d x$$

另外，文献^[10]还给出了多维度系统信息熵的定义. 从信息熵的定义中可以看到，一旦系统微观状态的概率分布得以确定，就可以得到系统的信息熵. 香农的信息熵能够反映一个宏观系统的微观状态的不确定性. 由于具有普适性的特点，信息熵已在许多领域中得到了非常广泛的应用.

1957年，Jaynes 在信息熵的基础上提出了最大熵原理(maximum entropy principle).最大熵原理的基本思想是：在某一系统各种微观状态概率分布不确定的条件下，对系统未知概率分布最合理的推断就是在已知的系统约束条件下，系统的信息熵最大；该推断是唯一可以做出的最客观的推断，任何其他的推断都会增加系统的约束或对未知概率分布的假设^{[11, 12]}.

对于某一系统来说，最大熵原理解决了系统的约束条件已知，而系统微观状态概率分布未知时，系统微观状态概率分布求解的问题. 最大熵原理可以被描述为一个最优化问题，如式(1)所示

\[\left. \begin{matrix} \text{max}{{S}_{\text{S}}}=-K\sum\limits_{i=1}^{n}{{{p}_{i}}}\ln {{p}_{i}} \\ \text{s}.\text{t}.\sum\limits_{i=1}^{n}{{{p}_{i}}}{{g}_{r,i}}=\langle {{g}_{r}}\rangle (r=1,2,\cdots ,m) \\ \sum\limits_{i=1}^{n}{{{p}_{i}}}=1({{p}_{i}}\ge 0,i=1,2,\cdots ,m) \\ \end{matrix} \right\}\]

(1)

其中，$p_{i}$为微观状态$i$发生的概率；$m$为系统约束的个数；$n$为微观状态的个数；$g_{r,i}$为微观状态$i$的函数；$p_{i}$为函数$g_{r,i}$发生的概率；$\langle g_{r} \rangle $是函数$g_{r,i}$在整个系统上的平均值.

对于式(1)形成的函数条件极值问题，可以使用拉格朗日乘数法进行求解. 拉格朗日方程如式(2)所示

\[\begin{align} & \Delta ({{p}_{i}})=\sum\limits_{i=1}^{n}{{{p}_{i}}}\ln {{p}_{i}}+{{\Delta }_{0}}(\sum\limits_{i=1}^{n}{{{p}_{i}}}-1)+ \\ & {{\Delta }_{r}}(\sum\limits_{i=1}^{n}{{{p}_{i}}}{{g}_{r,i}}-\langle {{g}_{r}}\rangle ) \\ \end{align}\]

(2)

对式(2)中的$p_{i}$求偏导数并令其为0，可以得到

\[\begin{align} & \frac{\partial }{\partial {{p}_{i}}}[\sum\limits_{i=1}^{n}{{{p}_{i}}}\ln {{p}_{i}}+{{\Lambda }_{0}}(\sum\limits_{i=1}^{n}{{{p}_{i}}}-1)+ \\ & {{\Delta }_{r}}(\sum\limits_{i=1}^{n}{{{p}_{i}}}{{g}_{r,i}}-\langle {{g}_{r}}\rangle )]=0 \\ \end{align}\]

(3)

对式(3)进行化简，得到

\[{{p}_{i}}=\exp [-1-{{\Lambda }_{0}}-{{\Lambda }_{r}}\langle {{g}_{r}}\rangle ]\]

(4)

其中，${{\Lambda }_{0}}$和${{\Lambda }_{r}}$满足式(1)中的约束条件.

将式(4)代入式(1)中的约束条件，可以得到

\[{{\Lambda }_{0}}=-1+\ln \sum\limits_{i=1}^{n}{\exp }(-\sum\limits_{r=1}^{n}{\text{ }{{\Lambda }_{r}}}{{g}_{r,i}})\]

(5)

\[\sum\limits_{i=1}^{n}{{{g}_{r,i}}}\exp [-1-{{\Lambda }_{0}}-{{\Lambda }_{r}}\langle {{g}_{r}}\rangle ]=\langle {{g}_{r}}\rangle \]

(6)

当${{\Lambda }_{r}}$确定后，${{\Lambda }_{0}}$可以由式(5)确定.

式(5)和式(6)是由$m$+1个方程组成的方程组，其中含有$m+1$个变量(拉格朗日乘数，${{\Lambda }_{0}}$和$\varLambda_{r}$，$r= 1,2,\cdots,m$). 未知量的个数与方程的个数相等,因此，拉格朗日乘数可以被唯一确定.

当拉格朗日乘数确定后，基于最大熵原理的概率$p_{i}$可以由式(4)得到.

上面给出的是离散型随机变量的最大熵原理. 类似地，连续型随机变量的最大熵原理如式(7)所示

\[\left. \begin{matrix} \text{max}{{S}_{\text{S}}}=-K\sum\limits_{-\infty }^{+\infty }{p}(x)\ln p(x)dx \\ \text{s}.\text{t}.\sum\limits_{-\infty }^{+\infty }{p}(x){{g}_{r}}(x)dx=\langle {{g}_{r}}\rangle (r=1,2,\cdots ,m) \\ \sum\limits_{-\infty }^{+\infty }{p}(x)dx=11.2cm(p(x)>0) \\ \end{matrix} \right\}\]

(7)

其中，$p$是连续型随机变量的概率密度函数.

上面给出的是最大熵原理在一维度系统中的情况，最大熵原理同样也可以应用于多维度系统.

采用最大熵原理对射流破碎液滴粒径与速度数量密度分布的研究始于20世纪80年代；经过30多年的研究，取得了很多研究成果.Sellens和Brzustowski^[13]对利用最大熵原理方法确定射流破碎液滴粒径和速度概率密度时的守恒约束条件进行了讨论.van derGdle和Vermeer^[14]，Cousin等^[15]对利用最大熵原理方法得到的破碎液滴粒径数量密度分布和体积密度分布进行了比较，认为数量密度分布更加准确. Chin等^[16]应用最大熵原理方法对双峰液滴数量密度分布进行了研究.Mitra和Li等^[17]首次将射流稳定性研究与最大熵原理方法相结合，计算得到了平面液体射流破碎液滴粒径和速度数量密度分布.Ahmadi和Sellens等^[18]在不考虑液滴速度概率密度分布的情况下，对最大熵原理方法的守恒约束条件进行了简化，包括质量守恒、表面能守恒等.文献^{[19, 20]}对采用最大熵原理对液体射流破碎液滴粒径与速度数量密度分布进行研究的理论基础及相关研究成果进行了较为详细的叙述.对于液体射流，研究者们往往将射流分类为平面液体射流、圆柱液体射流、圆环无旋转液体射流以及圆环旋转液体射流等，进行分类研究^{[21, 22, 23]}.采用最大熵原理对圆柱液体射流和平面液体射流破碎液滴粒径与速度数量密度分布的研究开展得较早^{[24, 25]}；对于圆环无旋转液体射流，研究者往往将其简化为平面液体射流进行研究^{[26, 27]}；对于圆环旋转黏性液体射流，研究者对其破碎液滴粒径数量密度分布和速度数量密度分布分别进行过研究^[28]，但对破碎液滴粒径数量密度分布与速度数量密度分布相关性的研究尚未见报道.

本文采用最大熵原理建立圆环旋转黏性液体射流破碎液滴粒径与速度数量密度联合概率密度函数，并在此基础上对圆环旋转黏性液体射流破碎液滴粒径数量密度分布与速度数量密度分布的相关性进行研究.

1 联合概率密度函数的建立及验证

根据最大熵原理，为了建立液体射流破碎液滴粒径与速度联合概率密度函数，首先需要确定射流系统的守恒约束条件. 液体射流满足质量守恒、动量守恒和能量守恒等基本守恒定律以及概率规范性等约束条件.

假设破碎液滴粒径数量密度分布和速度数量密度分布具有连续性，则无量纲化积分形式的约束条件可以表示为

\[\int_{{{D}_{\min }}}^{{{D}_{\max }}}{\int_{{{U}_{\min }}}^{{{U}_{\max }}}{f{{{\bar{D}}}^{3}}d\bar{U}d\bar{D}}}=1+{{\bar{S}}_{m}}\]

(8)

\[\int_{{{D}_{\min }}}^{{{D}_{\max }}}{\int_{{{U}_{\min }}}^{{{U}_{\max }}}{f\bar{U}{{{\bar{D}}}^{3}}d\bar{U}d\bar{D}}}=1+{{\bar{S}}_{mv}}\]

(9)

\[\int_{{{D}_{\min }}}^{{{D}_{\max }}}{\int_{{{U}_{\min }}}^{{{U}_{\max }}}{f\left( {{{\bar{D}}}^{3}}{{{\bar{U}}}^{2}}+G{{{\bar{D}}}^{2}} \right)}}d\bar{U}d\bar{D}=1+{{\bar{S}}_{e}}\]

(10)

\[\int_{{{D}_{\min }}}^{{{D}_{\max }}}{\int_{{{U}_{\min }}}^{{{U}_{\max }}}{f}}d\bar{U}d\bar{D}=1\]

(11)

其中，系数$G = 12\sigma / \rho _{\rm l} U_{\rm l}^2 D_{30} $，$D_{30}$为破碎液滴的质量平均粒径； $\bar {D}$和$\bar {U}$分别为破碎液滴的无量纲粒径和无量纲速度；$f$为破碎液滴粒径与速度的联合概率密度函数；各个守恒原项如下所示 $$\begin{align} & {{{\bar{S}}}_{m}}=0 \\ & {{{\bar{S}}}_{mv}}=Q{{\left( W-U_{\text{l}}^{*} \right)}^{2}}{{C}_{\text{D}}} \\ & {{{\bar{S}}}_{e}}=\frac{1}{2}Q{{\left( W-U_{\text{l}}^{*} \right)}^{3}}S{{C}_{\text{D}}} \\ \end{align}$$ 其中，$Q$为气液密度比；$W$为气液轴向速度比； $ U_{\rm l}^ * =\sqrt{1+(E(2A_{\rm h}+1)/2)^2}$为射流液体无量纲速度，$E$为射流旋转强度，$A_{\rm h}$为环形射流无量纲内半径；$S$为射流开始点到射流破碎点环形射流内外无量纲表面积；$C_{\rm D}$为曳力系数.

以射流系统的信息熵为目标函数建立最优化问题，进而可以求得最优化问题中随机变量的概率密度，即破碎液滴粒径与速度的联合概率密度函数，如式(12)所示

\[\begin{align} & f=\exp [-1-{{\Lambda }_{0}}-{{\Lambda }_{1}}{{{\bar{D}}}^{3}}-{{\Lambda }_{2}}{{{\bar{D}}}^{3}}\bar{U}- \\ & {{\Lambda }_{3}}\left( {{{\bar{D}}}^{3}}{{{\bar{U}}}^{2}}+G{{{\bar{D}}}^{2}} \right)] \\ \end{align}\]

(12)

式中的系数$\varLambda _0 $,$\varLambda _1 $,$\varLambda _2 $,$\varLambda _3 $以及$G$等皆与旋转强度$E$有关，因此，可以通过式(12)研究旋转强度$E$对联合概率密度函数变化的影响.

在速度维度上对式(12)进行积分，可以得到液滴粒径数量密度分布满足的方程

\[\begin{align} & \frac{dN}{d\bar{D}}=\int_{{{U}_{\min }}}^{{{U}_{\max }}}{f}d\bar{U}=\frac{\sqrt{\pi }}{2\sqrt{{{{\bar{D}}}^{3}}{{\Lambda }_{3}}}}\cdot \\ & \exp \left( -1-{{\Lambda }_{0}}-{{\Lambda }_{1}}{{{\bar{D}}}^{3}}+\frac{\Lambda _{2}^{2}}{4{{\Lambda }_{3}}\bar{D}}-{{\Lambda }_{3}}G{{{\bar{D}}}^{2}} \right)\cdot \\ & \left[ \text{erf}\left( {{X}_{\max 1}} \right)-\text{erf}\left( {{X}_{\min 1}} \right) \right] \\ \end{align}\]

(13)

其中，erf($X$) 表示变量$X$的误差函数；$N$表示液滴总数量；$X_{\max 1}$和$X_{\min 1}$分别为 $$\begin{align} & {{X}_{\max 1}}=\sqrt{{{\Lambda }_{3}}{{{\bar{D}}}^{3}}}({{{\bar{U}}}_{\max }}+\frac{{{\Lambda }_{2}}}{2{{\Lambda }_{3}}{{{\bar{D}}}^{2}}}) \\ & {{X}_{\min 1}}=\sqrt{{{\Lambda }_{3}}{{{\bar{D}}}^{3}}}({{{\bar{U}}}_{\min }}+\frac{{{\Lambda }_{2}}}{2{{\Lambda }_{3}}{{{\bar{D}}}^{2}}}) \\ \end{align}$$ 类似地，在液滴粒径维度上对式(12)进行积分，可以得到射流破碎液滴速度数量密度分布满足的方程

\[\frac{dN}{d\bar{U}}=\int_{{{D}_{\min }}}^{{{D}_{\max }}}{fd\bar{D}}\]

(14)

方程式(14)没有解析形式的解，但可以使用Mathematica软件通过数值方法进行求解.

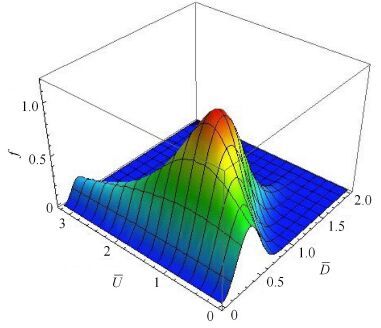
由式(12)可以计算得到圆环旋转黏性液体射流破碎液滴粒径与速度数量密度联合概率密度分布，如图1所示.

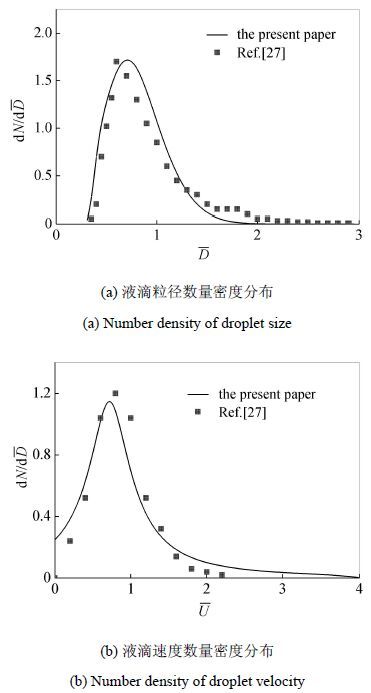
为了对建立的圆环旋转黏性液体射流破碎液滴粒径与速度的联合概率密度函数进行验证，图2给出了根据式(13)和式(14)计算得到的圆环旋转黏性液体射流破碎液滴粒径数量密度分布和速度数量密度分布与文献^[27]中的实验结果的对比.

从图2中可以看到，本文的计算结果与文献^[27]中的实验结果基本吻合，从一定角度证明了建立的圆环旋转黏性液体射流破碎液滴粒径与速度联合概率密度函数的正确性.

2 关于联合概率密度函数的讨论

有学者曾以质量守恒定律作为射流唯一守恒约束条件，采用基于最大熵原理的方法对射流破碎液滴粒径的数量分布特性进行过研究^{[16, 20]}，将射流破碎液滴粒径数量密度分布问题描述为^{[16, 20]}

\[\begin{align} & \\ & \left. \begin{matrix} \max {{S}_{\text{S}}}=-K\int_{{{D}_{\min }}}^{{{D}_{\max }}}{{{f}_{a}}}\ln {{f}_{a}}d\bar{D} \\ \text{s}.\text{t}.\int_{{{D}_{\min }}}^{{{D}_{\max }}}{{{f}_{a}}}{{{\bar{D}}}^{3}}d\bar{D}=1+{{{\bar{S}}}_{m}} \\ \int_{{{D}_{\min }}}^{{{D}_{\max }}}{{{f}_{a}}}d\bar{D}=1 \\ \end{matrix} \right\} \\ \end{align}\]

(15)

采用拉格朗日乘数法对式(15)描述的问题进行求解. 拉格朗日函数为

\[\begin{align} & \Lambda \left( \bar{D},{{\Lambda }_{0}},{{\Lambda }_{1}} \right)= \\ & \int_{{{D}_{\min }}}^{{{D}_{\max }}}{{{f}_{a}}\ln {{f}_{a}}d\bar{D}}+{{\Lambda }_{0}}\left( \int_{{{D}_{\min }}}^{{{D}_{\max }}}{{{f}_{a}}d\bar{D}}-1 \right)+ \\ & {{\Lambda }_{1}}\left( \int_{{{D}_{\min }}}^{{{D}_{\max }}}{{{f}_{a}}{{{\bar{D}}}^{3}}d\bar{D}}-{{{\bar{S}}}_{m}}-1 \right) \\ \end{align}\]

(16)

对式(16)中的$f_{a}$进行求导并令其为零，从而可以得到

\[\begin{align} & \frac{\partial }{\partial {{f}_{a}}}[\int_{{{D}_{\min }}}^{{{D}_{\max }}}{{{f}_{a}}\ln {{f}_{a}}d\bar{D}}+{{\Lambda }_{0}}\left( \int_{{{D}_{\min }}}^{{{D}_{\max }}}{{{f}_{a}}d\bar{D}}-1 \right)+ \\ & {{\Lambda }_{1}}\left( \int_{{{D}_{\min }}}^{{{D}_{\max }}}{{{f}_{a}}{{{\bar{D}}}^{3}}d\bar{D}}-{{{\bar{S}}}_{m}}-1 \right)]=0 \\ \end{align}\]

(17)

化简整理，得到破碎液滴粒径概率密度函数

\[{{f}_{a}}=\exp (-1-{{\Lambda }_{0}}-{{\Lambda }_{1}}{{\bar{D}}^{3}})\]

(18)

其中，${{\Lambda }_{0}}$和${{\Lambda }_{1}}$满足式(12)中的约束条件.

射流守恒约束条件中只有质量守恒定律时，研究的问题为一维随机变量(液滴粒径)的概率密度问题；只能够得到射流破碎液滴粒径数量密度分布的概率密度函数，无法得到液滴粒径与速度联合概率密度函数.

文献^[30]曾采用动量守恒定律作为唯一守恒约束条件，对射流破碎液滴粒径与速度联合概率密度函数进行过研究，给出的动量守恒约束条件为^[9]

\[\sum\limits_{i}{\sum\limits_{j}{{{p}_{i,j}}}}{{v}_{i}}u_{j}^{2}\dot{n}=AU_{0}^{3}\]

(19)

其中，$p_{i,j}$为体积为$v_{i}$、速度为$u_{j}$的液滴出现的概率；$\dot n$ 为单位时间内射流破碎产生液滴的总数量；$A$为喷嘴出口面积；$U_{0}$为喷嘴出口处液体速度.

在式(19)给出的动量守恒约束条件中，等式左端给出的是单位时间内产生的全部液滴单位质量动能的2倍，右端给出的是单位时间内单位质量液体动能的2倍；因此，式(19)实际上体现的是一种能量守恒关系.但是，如果从能量守恒角度来看，式(19)并未考虑到液滴的表面能.

尽管通过计算，文献^[30]给出了基本符合射流破碎液滴粒径与速度数量密度分布特点的液滴粒径与速度联合概率密度分布，如图3所示，但由于约束条件式(19)的合理性值得商榷，因此文献给出的粒径与速度联合概率密度函数是否能正确反映射流破碎液滴的粒径与速度数量密度分布，还有待进一步论证.

本文是在守恒约束条件中同时考虑质量守恒、动量守恒及能量守恒定律条件下，采用基于最大熵原理的方法得到了圆环旋转黏性液体射流破碎液滴粒径与速度的联合概率密度函数式.

如果在守恒约束条件中只考虑动量守恒定律或能量守恒定律时，射流破碎液滴粒径与速度数量密度分布问题则可分别用式(20)和式(21)描述为

\[\begin{align} & \\ & \left. \begin{matrix} \max {{S}_{\text{S}}}=-K\int_{{{D}_{\min }}}^{{{D}_{\max }}}{\int_{{{U}_{\min }}}^{{{U}_{\max }}}{{{f}_{b}}\ln {{f}_{b}}d\bar{U}d\bar{D}}} \\ \text{s}.\text{t}.\int_{{{D}_{\min }}}^{{{D}_{\max }}}{\int_{{{U}_{\min }}}^{{{U}_{\max }}}{{{f}_{b}}{{{\bar{D}}}^{3}}\bar{U}d\bar{U}d\bar{D}}}=1+{{{\bar{S}}}_{mv}} \\ \int_{{{D}_{\min }}}^{{{D}_{\max }}}{\int_{{{U}_{\min }}}^{{{U}_{\max }}}{{{f}_{b}}}}d\bar{U}d\bar{D}=1 \\ \end{matrix} \right\} \\ \end{align}\]

(20)

\[\left. \begin{matrix} \max {{S}_{\text{S}}}=-K\int_{{{D}_{\min }}}^{{{D}_{\max }}}{\int_{{{U}_{\min }}}^{{{U}_{\max }}}{{{f}_{c}}\ln fd\bar{U}d\bar{D}}} \\ \text{s}.\text{t}.\int_{{{D}_{\min }}}^{{{D}_{\max }}}{\int_{{{U}_{\min }}}^{{{U}_{\max }}}{{{f}_{c}}\left( {{{\bar{D}}}^{3}}{{{\bar{U}}}^{2}}+G{{{\bar{D}}}^{2}} \right)}}d\bar{U}d\bar{D}=1+{{{\bar{S}}}_{e}} \\ \int_{{{D}_{\min }}}^{{{D}_{\max }}}{\int_{{{U}_{\min }}}^{{{U}_{\max }}}{{{f}_{c}}}}d\bar{U}d\bar{D}=1 \\ \end{matrix} \right\}\]

(21)

采用拉格朗日乘数法对式(20)和式(21)描述的问题进行求解，得到守恒约束条件只有动量守恒定律或能量守恒定律的联合概率密度函数，分别如式(22)和式(23)所示.

\[{{f}_{b}}=\exp (-1-{{\Lambda }_{0}}-{{\Lambda }_{2}}{{\bar{D}}^{3}}\bar{U})\]

(22)

其中，${{\Lambda }_{0}}$和$\varLambda _{2}$满足式(20)中的约束条件.

\[{{f}_{c}}=\exp \left[ -1-{{\Lambda }_{0}}-{{\Lambda }_{3}}\left( {{{\bar{D}}}^{3}}{{{\bar{U}}}^{2}}+G{{{\bar{D}}}^{2}} \right) \right]\]

(23)

其中，${{\Lambda }_{0}}$和$\varLambda _{3}$满足式(21)中的约束条件.

为了便于比较，将守恒约束条件只有动量守恒定律、守恒约束条件只有能量守恒定律以及守恒约束条件中同时包括质量守恒定律、动量守恒定律和能量守恒定律的联合概率密度函数汇总如下

\[\begin{align} & \\ & \left. \begin{matrix} {{f}_{b}}=\exp \left( -1-{{\Lambda }_{0}}-{{\Lambda }_{2}}{{{\bar{D}}}^{3}}\bar{U} \right) \\ {{f}_{c}}=\exp \left[ -1-{{\Lambda }_{0}}-{{\Lambda }_{3}}\left( {{{\bar{D}}}^{3}}{{{\bar{U}}}^{2}}+G{{{\bar{D}}}^{2}} \right) \right] \\ {{f}_{d}}=\exp [-1-{{\Lambda }_{0}}-{{\Lambda }_{1}}{{{\bar{D}}}^{3}}-{{\Lambda }_{2}}{{{\bar{D}}}^{3}}\bar{U}- \\ {{\Lambda }_{3}}\left( {{{\bar{D}}}^{3}}{{{\bar{U}}}^{2}}+G{{{\bar{D}}}^{2}} \right)] \\ \end{matrix} \right\} \\ \end{align}\]

(24)

从式(24)中可以看到，满足不同守恒约束条件的圆环旋转黏性液体射流破碎液滴的粒径与速度联合概率密度函数存在较大差异；该差异体现了不同守恒定律在圆环旋转黏性液体射流破碎液滴粒径与速度联合概率密度函数中的作用.

为了进行比较，图4给出了在一定计算条件下，射流守恒约束条件分别只有动量守恒定律、只有能量守恒定律以及同时包括质量守恒定律、动量守恒定律和能量守恒定律时，圆环旋转黏性液体射流破碎液滴粒径与速度联合概率密度计算结果的比较.

从图4中可以看到，与守恒约束条件中同时包括质量守恒定律、动量守恒定律和能量守恒定律时相比，约束条件中只有动量守恒定律或只有能量守恒定律时，在无量纲速度较小或无量纲粒径较大情况下，不仅射流破碎液滴粒径与速度联合概率密度的具体数值差别很大，而且液滴粒径与速度联合概率密度随无量纲速度和无量纲粒径的分布也完全不同；在无量纲速度较大且无量纲粒径较小情况下，尽管射流破碎液滴粒径与速度联合概率密度随无量纲速度和无量纲粒径的分布规律类似，但液滴粒径与速度联合概率密度的具体数值差别很大.

由于没有给定速度先验分布，因此当守恒约束条件中只有动量守恒定律或只有能量守恒定律时，从图4(a)和图4(b)中可以看到，此时无量纲速度为0的破碎液滴数量最多，且随着无量纲速度的增加，破碎液滴的数量密度逐渐减小；射流破碎液滴速度数量密度随无量纲速度的这种变化规律与一般射流破碎液滴速度数量密度分布的特点不符.

根据文献^[25]和文献^[29]中的研究结果以及上述分析结果，射流守恒约束条件中只有质量守恒定律时，给不出联合概率密度函数；射流守恒约束条件中只有动量守恒定律或能量守恒定律时，联合概率密度函数不能正确反映射流破碎液滴粒径数量密度分布和速度数量密度分布.为了给出正确的圆环旋转黏性液体射流破碎液滴粒径与速度联合概率密度函数，射流守恒约束条件中必须同时包括质量守恒定律、动量守恒定律以及能量守恒定律.

3 破碎液滴粒径数量密度分布与速度数量密度分布相关性分析

在本文建立的圆环旋转黏性液体射流破碎液滴粒径与速度联合概率密度函数式(15)中，$\bar D^3 \bar U$项和$\bar D^3\bar U^2$ 项体现了破碎液滴粒径数量密度分布与速度数量密度分布之间的相关性.通过液滴粒径与速度联合概率密度函数，可以对破碎液滴粒径数量密度分布与速度数量密度分布的相关性进行分析.

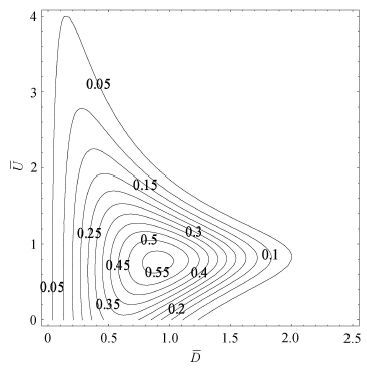
图5给出的是在一定的射流参数条件下，圆环旋转黏性液体射流破碎液滴粒径数量密度分布与速度数量密度分布的关系.

从图5中可以发现，对于无量纲粒径较小的破碎液滴，虽然破碎液滴的无量纲速度受无量纲粒径的影响仍然较大，但就同一无量纲粒径的破碎液滴来说，不同无量纲速度的破碎液滴的数量却几乎完全相同；只有对于无量纲粒径较大的破碎液滴，就某一无量纲粒径破碎液滴来说，无量纲速度的数量密度分布才呈现出比较明显的无量纲速度小和无量纲速度大的破碎液滴数量密度较小、无量纲速度处于中间位置附近的破碎液滴数量密度较大的特点.对于无量纲粒径较小的破碎液滴，速度数量密度的分布范围较宽；而对于无量纲粒径较大的破碎液滴，速度数量密度的分布范围则较窄，主要集中在某一无量纲速度附近.

从图5中还可以发现，对于无量纲速度较小和无量纲速度较大的破碎液滴，无量纲粒径数量密度分布的峰值较小，且主要出现在较小的无量纲粒径处，此时粒径数量密度的分布范围较窄；处于中间附近某一无量纲速度下的无量纲粒径数量密度的分布峰值达到最大，且出现在较大的无量纲粒径处，此时粒径数量密度的分布范围达到最宽.

从圆环旋转黏性液体射流的破碎雾化角度看，破碎液滴粒径的数量密度和速度数量密度分布处于图5左上角区域时，即破碎液滴整体平均粒径较小、整体平均速度较大时，比较有利于射流的破碎雾化.破碎液滴粒径的数量密度和速度数量密度分布处于图5左下角区域时，从破碎液滴粒径数量密度分布角度看，比较有利于射流的破碎雾化；而从破碎液滴速度数量密度分布角度看，则不利于射流的破碎雾化.破碎液滴粒径的数量密度和速度数量密度分布处于图5右半区域时，由于破碎液滴的整体平均粒径较大、整体平均速度一般，则不利于射流的破碎雾化.

射流旋转是本文研究的圆环旋转黏性液体射流的一个主要特点，对射流破碎液滴的粒径数量密度分布和速度数量密度分布会产生影响.图6给出的是在不同的射流旋转强度下，圆环旋转黏性液体射流破碎液滴粒径数量密度分布与速度数量密度分布的关系.

从图6中可以看到，射流旋转强度对破碎液滴粒径数量密度和速度数量密度的分布区域具有较大影响，对粒径数量密度与速度数量密度分布结构的影响不大. 随着射流旋转强度的增加，破碎液滴数量密度分布区域先向无量纲粒径较大的区域移动，然后快速向无量纲粒径较小的区域移动；在较大的射流旋转强度下，破碎液滴的数量密度主要集中在无量纲粒径较小的区域，此时速度数量密度分布与粒径数量密度分布体现出更强的相关性.

从图6中还可以看到，射流旋转强度对不同无量纲粒径下的无量纲速度数量密度的分布范围影响较大.随着旋转强度的增加，对于数量密度分布峰值所对应的无量纲粒径破碎液滴来说，无量纲速度数量密度的分布范围先减小后增加； 但对无量纲速度数量密度分布峰值所对应的无量纲速度则几乎没有影响.

从圆环旋转黏性液体射流破碎雾化角度看，在较大射流旋转强度下，数量密度范围集中在无量纲粒径较小的区域，这将有利于射流的破碎雾化.

4 结论

(1)采用最大熵原理方法建立了圆环旋转黏性液体射流破碎液滴粒径与速度联合概率密度函数，并对建立的粒径与速度联合概率密度函数进行了验证.

(2)为了给出正确的圆环旋转黏性液体射流破碎液滴粒径与速度联合概率密度函数，射流守恒约束条件中必须同时包括质量守恒定律、动量守恒定律以及能量守恒定律.

(3)破碎液滴粒径的数量密度分布与速度数量密度分布密切相关. 无量纲粒径较小液滴和无量纲粒径较大液滴的无量纲速度数量密度分布具有不同特点；不同无量纲速度液滴的无量纲粒径数量密度分布的特点也不同.

(4)射流旋转强度对破碎液滴粒径数量密度与速度数量密度分布结构的影响不大，对液滴粒径数量密度和速度数量密度的分布区域影响较大；在较大旋转强度下，液滴数量密度主要集中在无量纲粒径较小区域，且速度数量密度分布与粒径数量密度分布体现出更强的相关性.