雾爆发性增强,是指在很短时间内(一般小于30 min)雾突变为浓雾(能见度小于500 m),或浓雾跃增为强浓雾(能见度小于50 m)[1]. 过程中,地面气温持续下降,风向稳定,环境相对湿度逐渐升高. 此外,风速较小,湍流较弱,悬浮于空气中的大量气溶胶吸湿成为雾滴群,影响着人体健康、能见度以及大气辐射平衡[2, 3, 4, 5].
文献 [6]利用南京市北郊的外场观测数据,结合NCEP资料分析了雾的演变过程、微物理结构及边界层特征.颗粒的消光受到微物理参量的影响,即与颗粒尺度分布紧密相关.影响雾环境颗粒尺度分布的机制涉及颗粒的碰并、凝结、成核、沉积等动力学事件.在离散系统动力学演变领域,Wang等[7]将积分矩方法与计算流体力学结合,研究层流和湍流状态下的泰勒-库塔流中10 μm颗粒的凝并和破碎过程,取得了良好的研究成果.于明州、林建忠等[8]采用泰勒展开力矩(TEMOM)方法来处理颗粒布朗运动造成的凝并事件,得到颗粒的自保持分布和线性衰减定律.李瑞霞等[9]对$Re_{\lambda}$约为51均匀各向同性湍流内的有限惯性颗粒的碰撞行为进行了直接数值模拟,研究湍流对有限惯性颗粒碰撞的影响.
在诸如雾天这样的多相系统中,湍流作用于悬浮颗粒(雾滴、气溶胶)的动力学过程,后者又影响着大气能见度.查阅文献,将流场性质、 颗粒动力学、光辐射传输相耦合起来的研究鲜有报道.基于此,文中讨论大气环境雾滴湍流输运和颗粒局部聚集效应下颗粒间的碰并过程,数值分析湍流耗散率、颗粒尺度演化、系统散射的关系,揭示雾增强过程中雾滴与气溶胶碰并等导致谱拓宽、能见度降低的机制.
1 离散系统颗粒的动力学、光辐射传输模型与研究方法雾天爆发性增强,其本质上是雾滴爆发性增多增大. 其中颗粒的核化、凝结碰并作用活跃. 文中将重点关注悬浮颗粒经历的凝结碰并等动力学性质. 通过统计颗粒系统,得到粒子尺度分布函数的演变过程. 由于系统散射性质取决于其内部变量的分布函数,因此粒子尺度分布模型就成为研究颗粒系统的一个关键.
1.1 颗粒群平衡模拟颗粒群平衡模拟的特点是将离散系统视为一个服从统计学规律的整体,离散系统内每个动力学事件的发生服从一个概率模型(称核模型).
基于颗粒稀疏和分子混沌假设,在欧拉坐标体系下建立颗粒尺度分布的平衡方程[10, 11]
\[\begin{array}{l}
\frac{{\partial n(V,t)}}{{\partial t}} = \{ \frac{1}{2}\int_{{V_{\min }}}^V \beta (V - U,U,t)n(V - U,t)n(U,t)dU - \\
n(V,t)\int_{{V_{\min }}}^{{V_{\max }}} \beta (V,U,t)n(U,t)dU{\} _{{\rm{凝并}}}} + \\
\{ \int_V^{{V_{\max }}} \gamma (U,V,t)b(U,t)S(U,t)n(U,t)dU - \\
S(V,t)n(V,t){\} _{破碎}} - \{ {C_{{\rm{sur}}}}{D_{{\rm{sur}}}}(V - {V_0},t)n(V - {V_0},t) - \\
{C_{{\rm{sur}}}}{D_{{\rm{sur}}}}(V,t)n(V,t)\} 凝结/蒸发
\end{array}\]
(1)
颗粒凝并核模型十分复杂,引发的机理涉及重力、布朗扩散、热泳力、湍流曳力、范德华力、离心力、外加场力等[12]. 文中重点考虑的机理主要包括湍流作用和布朗扩散[13, 14, 15].
1.2 湍流扩散作用的碰撞凝并核模型
湍流是雾生成、发展的因素,它不仅对动量、热量和水汽的垂直输送起重要作用,也是雾滴碰并增长的关键条件. 大气环境,雾滴处于有限惯性颗粒的范畴[16]. 湍流对其碰撞凝并的影响涉及湍流输运和局部富集效应. 文中采取的有限惯性颗粒碰撞核函数如下
\[{\beta _t} = 2\pi {R^2}{\left( {\frac{2}{\pi }{{\left\langle {w_r^2} \right\rangle }_t}} \right)^{{\textstyle{1 \over 2}}}}g\left( R \right)\]
(2)
\[{\langle w_r^2\rangle _t} = {\langle w_r^2\rangle _{{\rm{shear}}}} + {\langle w_r^2\rangle _{{\rm{accel}}}} + {\langle w_r^2\rangle _{{\rm{coup}}}} + {\langle w_r^2\rangle _{{\rm{grav}}}}\]
(3)
\[\left. \begin{array}{*{35}{l}}
{{\langle w_{r}^{2}\rangle }_{\text{shear}}}=\frac{1}{15}{{R}^{2}}\frac{\varepsilon }{v} \\
{{\langle w_{r}^{2}\rangle }_{\text{coup}}}=2{{(1-\frac{{{\rho }_{\text{f}}}}{{{\rho }_{\text{p}}}})}^{2}}{{\tau }_{\text{pi}}}{{\tau }_{\text{pj}}}\langle {{(\frac{\text{D}u}{\text{D}t})}^{2}}\rangle \frac{{{R}^{2}}}{\lambda _{\text{D}}^{2}} \\
{{\langle w_{r}^{2}\rangle }_{\text{grav}}}=\frac{\pi }{8}{{(1-\frac{{{\rho }_{\text{f}}}}{{{\rho }_{\text{p}}}})}^{2}}{{({{\tau }_{\text{pi}}}-{{\tau }_{\text{pj}}})}^{2}}{{g}^{2}} \\
{{\langle w_{r}^{2}\rangle }_{\text{accel}}}={{C}_{\text{w}}}{{(1-b)}^{2}}u{{'}_{\text{f}}}^{2}\frac{\gamma }{\gamma -1}\cdot \\
\frac{{{({{\theta }_{i}}+{{\theta }_{j}})}^{2}}-4{{\theta }_{i}}{{\theta }_{j}}\sqrt{\frac{1+{{\theta }_{i}}+{{\theta }_{j}}}{(1+{{\theta }_{i}})(1+{{\theta }_{j}})}}}{{{\theta }_{i}}+{{\theta }_{j}}}. \\
[\frac{1}{(1+{{\theta }_{i}})(1+{{\theta }_{j}})}-\frac{1}{(1+\gamma {{\theta }_{i}})(1+\gamma {{\theta }_{j}})}] \\
\end{array} \right\}\]
(4)
\[\begin{array}{l}
\frac{{g(R) - 1}}{{R{e_\lambda }}} = \frac{{{y_0}(S{t_k})[1 - z_0^2(S{t_k})]}}{{R{e_\lambda }}} + \\
z_0^2(S{t_k})\{ {y_1}(S{t_k})[1 - {z_1}(S{t_k})] + \\
{y_2}(S{t_k}){z_1}(S{t_k}) + {y_3}(S{t_k}){z_2}(S{t_k})\}
\end{array}\]
(5)
雾中的多相体系能吸收和散射入射光,使波的能量发生衰减(消光效应). 基于此,文中结合求解球形粒子散射参数的Mie 理论[19],对于确定的入射波长和颗粒直径,计算出此颗粒的衰减效率因子、散射效率因子、吸收效率因子、散射和相函数以及不对称因子. 上述无量纲参数
\[{Q_{{\rm{ext}}}}(m,\chi ) = \frac{2}{{{\chi ^2}}}\sum\limits_{n = 1}^\infty {(2n + 1)} Re\left\{ {{a_n} + {b_n}} \right\}\]
(6)
\[{Q_{{\rm{sca}}}}(m,\chi ) = \frac{2}{{{\chi ^2}}}\sum\limits_{n = 1}^\infty {(2n + 1)} \left[ {{{\left| {{a_n}} \right|}^2} + {{\left| {{b_n}} \right|}^2}} \right]\]
(7)
\[{Q_{{\rm{abs}}}}(m,\chi ) = {Q_{{\rm{ext}}}}(m,\chi ) - {Q_{{\rm{sca}}}}(m,\chi )\]
(8)
\[\Phi (m,\chi ,\theta ) = \frac{1}{{{Q_{{\rm{sca}}}}{\chi ^2}}}\left[ {{{\left| {{S_1}} \right|}^2} + {{\left| {{S_2}} \right|}^2}} \right]\]
(9)
\[{a_n} = \frac{{{{\psi '}_n}\left( {m\chi } \right){\psi _n}(\chi ) - m{\psi _n}\left( {m\chi } \right){{\psi '}_n}(\chi )}}{{{{\psi '}_n}\left( {m\chi } \right){\xi _n}(\chi ) - m{\psi _n}\left( {m\chi } \right){{\xi '}_n}(\chi )}}\]
(10)
\[{b_n} = \frac{{m{{\psi '}_n}\left( {m\chi } \right){\psi _n}(\chi ) - {\psi _n}\left( {m\chi } \right){{\psi '}_n}(\chi )}}{{m{{\psi '}_n}\left( {m\chi } \right){\xi _n}(\chi ) - {\psi _n}\left( {m\chi } \right){{\xi '}_n}(\chi )}}\]
(11)
\[{S_1}\left( \theta \right) = \sum\limits_{n = 1}^\infty {\frac{{2n + 1}}{{n(n + 1)}}\left[ {{a_n}{\pi _n}\left( {\cos \theta } \right) + {b_n}{\tau _n}\left( {\cos \theta } \right)} \right]} \]
(12)
\[{S_2}\left( \theta \right) = \sum\limits_{n = 1}^\infty {\frac{{2n + 1}}{{n(n + 1)}}\left[ {{a_n}{\tau _n}\left( {\cos \theta } \right) + {b_n}{\pi _n}\left( {\cos \theta } \right)} \right]} \]
(13)
单个颗粒的散射性质是颗粒系统的基础,因此文中结合雾环境颗粒的相互作用、颗粒浓度及粒径分布等因素,建立雾环境颗粒系统的散射模型.
文中采用蒙特卡洛方法(Monte Carlo method,MC) [20, 21]. 它是以概率统计理论为指导的一类数值计算方法,可得到颗粒的轨道经历和历史效应,同时给出颗粒群内部变量时空演变信息(如颗粒尺度分布函数等).
(1) 颗粒系统碰撞凝并的动力学过程
在MC算法引入加权虚拟颗粒来代表数量众多的实际颗粒群,即采取异数目权值技术模拟颗粒群[13].为了验证,文中对颗粒碰撞凝并动力学过程采取常凝并核模型. 初始时刻,颗粒呈指数分布:$n(v,0) = N_0 / v_{g0}\times \exp ( - v / v_{g0} ) (N_0 $和$v_{g0} $分别为颗粒初始的数目浓度以及颗粒平均尺度[22]).在本文的数值模拟中,$A=6.405 \times 10^{-10}$ cm$^{3}$/s,虚拟颗粒数目为3 000,颗粒系统动力学演变的时间长度为$\tau_{\rm coag} / 2 \approx 1 561.3s(\tau _{\rm coag} = 2 /(AN_0 ))$.
颗粒尺度分布函数在$\tau _{\rm coag} / 8$和$\tau _{\rm coag} /2$时刻处的曲线分别如图1所示. 可以看到:加权MC数值模拟结果与理论分析解[23]吻合较好. 颗粒尺度分布曲线保持指数分布,与文献[24] 一致,反映了随时间演变的"自保持(self-preserving)"分布性质.

|
图1 颗粒尺度分布函数 Fig.1 Particle size distribution function |
(2) 颗粒系统的散射性质
MC方法在求解以辐射传输理论为基础的光分配问题中,将光束看作一系列经典粒子---光子. 然后将光子传播过程分解为发射、透射、反射、吸收独立的子过程[25],并把它们化成随机问题. 根据所建立的概率模型进行跟踪、统计,从而得到该单元辐射能量分配的统计结果. 基于此,文中根据Mie 理论和颗粒系统的分布情况(粒径、浓度等),由颗粒的折射率计算颗粒系统的散射参数.
为了验证模型和数值方法的正确性,文中开展颗粒系统散射性质的研究. 其中,颗粒采取四氯化碳(CCl$_{4}$),其初始粒径为1 μm,颗粒系统的体积浓度为5.0$\times$10$^{-5}$,颗粒系统的厚度为 1 cm. 模拟光束的光子数为1.0$\times$10$^{5}$个. 计算所得光子的运动轨迹见图2所示.
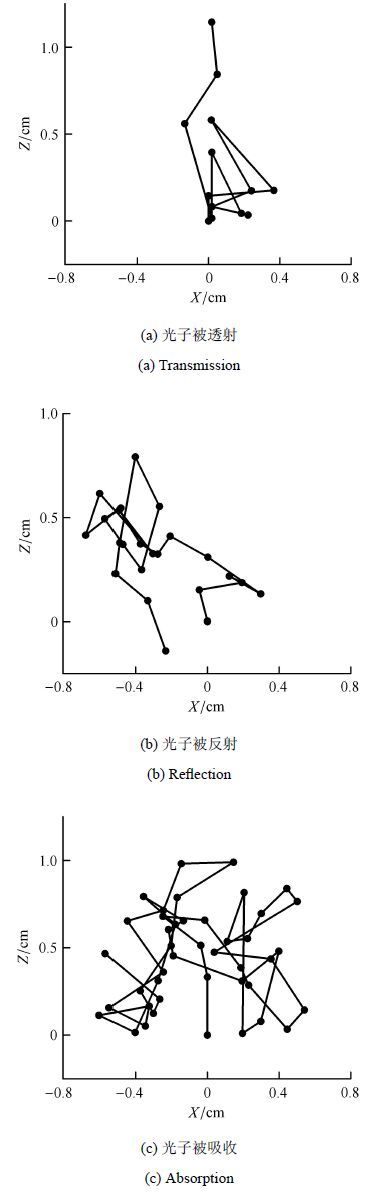
|
图2 光子的运动轨迹 Fig.2 The photon trajectories |
图3给出了计算所得的透过率光谱与文献[26]数据的比较,两者吻合较好. 说明文中所采用的 MC 方法对于计算具有一定辐射参数的颗粒系统的散射光谱具有较高的可靠性.
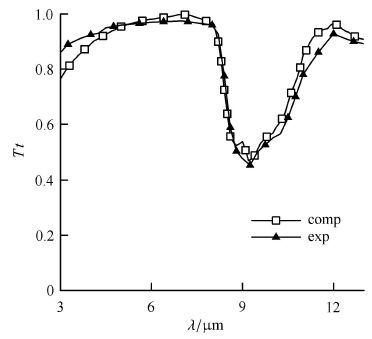
|
图3 CCl$_{4}$颗粒透过率的光谱图 Fig.3 Transmittance spectra of CCl$_{4}$ particles |
雾环境,在湍流输运及颗粒聚集效应的影响下,颗粒除发生复杂的碰撞凝并之外,还会发生破碎、蒸发、凝结等动力学过程[27]. 基于此,文中采取加权MC 方法[28]结合Mie理论,对颗粒系统的散射光谱进行模拟.
2.1 湍流的输运效应湍流动能耗散率代表了湍流扰动能量由大尺度向准平衡区尺度传输的速率. 文中采取湍流动能耗散率表征湍流的大小.在大气边界层范围内,湍流耗散率随高度的增加有递减的趋势.
主要考虑成分为水的雾滴系统. 初始时刻,流场雾滴取指数分布,平均粒径10 μm,颗粒的数目浓度为1.92 $\times$ 10$^{9}$ m$^{-3}$. 雾滴系统的厚度为 1 m.图4给出1 000 s时刻随着湍流耗散率的增加,雾滴尺度分布函数的变化情况. 显示湍流耗散率为1.0 ×10$^{-4}$ $\sim $ 1.0 × 10$^{- 2 }$ m$^{2}$/s$^{3}$,经过相同的时间,颗粒尺度变化较小.如流场的湍流耗散率1.0 × 10$^{ - 3}$m$^{2}$/s$^{3}$,颗粒无量纲尺度为0.075,其颗粒数目浓度峰值达到3.23 × 10$^{6}$ m$^{-3}$.但湍流耗散率进一步增大至1.0 × 10$^{-1}$m$^{2}$/s$^{3}$时,颗粒平均尺度增大为0.08,颗粒数目浓度降至2.72 × 10$^{6}$ m$^{-3}$.分析原因主要是,湍流耗散率越大,湍流越强,雾环境颗粒对径向相对速度增大,导致颗粒碰并效应增强. 此外,光谱计算结果显示:雾环境流场的性质及颗粒的碰并影响着系统的散射性能. 在波长0.4$\sim$ 0.76 μm的可见光范围内,雾滴组成的系统其透过率均呈现先下降再增大的趋势. 当湍流耗散率为1.0$\times$10$^{ - 3}$ m$^{2}$/s$^{3}$,对于0.55 μm的可见光,系统的透过率达到最低值0.46.
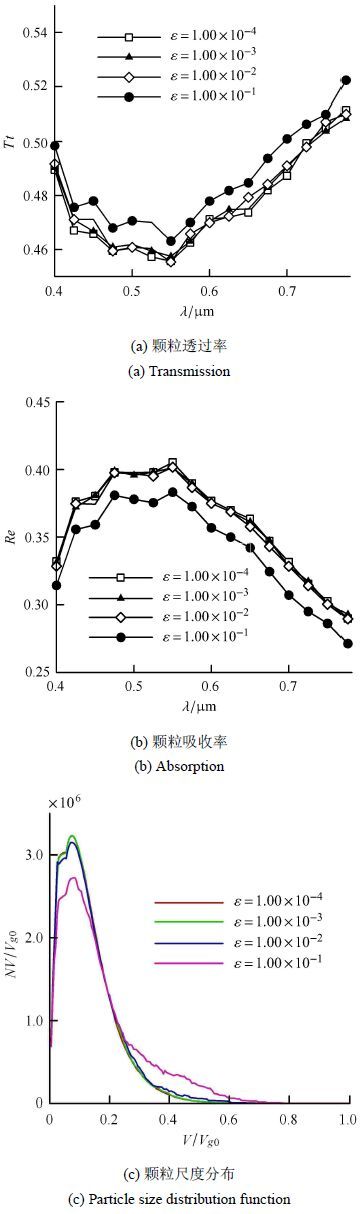
|
图4 颗粒尺度分布演化、系统透过率及吸收率图 Fig.4 The particle size evolution,transmittance and absorption rates of particle system |
基于可能发生碰撞的颗粒对径向相对速度的大小和分布来表征颗粒的碰并效应. 湍流耗散率、颗粒径向相对速度之间的关系见表1所示. 计算所得的颗粒对径向相对速度均为该参量与流场脉动速度的比值(无量纲量).
| 表1 湍流耗散率对颗粒对径向相对速度的影响 Table 1 Effects of turbulent dissipation rates on the dimensionless radial velocity of particles |
在影响颗粒径向速度的主要因素中,剪切项反映了颗粒因流体的剪切应力造成的碰撞.在文中讨论的范围,湍流耗散率越大,颗粒对径向相对速度也越大,影响因素中剪切项所占的比例也越大.如,对于湍流耗散率1.0×10$^{ -1}$ m$^{2}$/s$^{3}$,颗粒径向相对速度为0.159,剪切项所占了85.48%,远超过重力项所占的14.31%.
可见光范围内,湍流强度与颗粒动力学、散射性质的关系见图5所示.可以看到,随着流场湍流耗散率的增大,颗粒径向相对速度呈现先缓慢变化而后快速增大的趋势.1 000 s时刻,对于耗散率为1.0×10$^{ - 2}$ m$^{2}$/s$^{3}$,颗粒对径向相对速度为0.096 9;0.6 μm可见光条件下,雾环境颗粒系统的透过率为0.47.而对于耗散率为1.0×10$^{ - 1}$ m$^{2}$/s$^{3}$,颗粒对径向相对速度增大至0.159,系统的透过率增大为0.48.
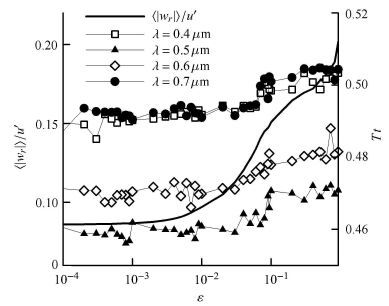
|
图5 湍流耗散率对颗粒对径向相对速度及系统透过率的影响 Fig.5 Effects of turbulent dissipation rates on radial velocity of particles,transmittance rates of particle system |
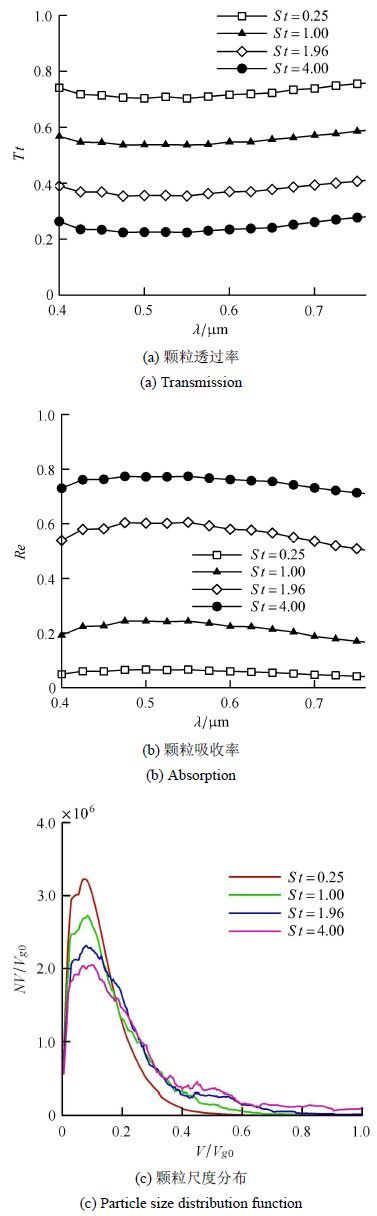
颗粒的局部富集效应描述了瞬时湍流场中颗粒在某一特定区域中的聚集现象.该现象反映了颗粒的瞬时浓度场与流场湍流结构的相关性,即短时间内与涡的作用有关.流场中,当颗粒的弛豫时间尺度与Kolmogorov时间尺度相当时,颗粒的数密度在湍流中表现出高度不均匀,流场中的涡旋将颗粒从涡旋的核心推向高应力的涡间区域. 表2给出了雾滴$St$ 与计算所得的径向分布函数$G(R)$关系.当$St$在1.0附近时,径向分布函数$G(R)$达到最大值,即7.514.
| 表2 颗粒$St$ 对颗粒径向分布函数的影响 Table 2 Effects of particles $St$ numbers on radial distribution function of particles |
图6显示了1 000 s时刻,不同$St$雾滴的尺度分布函数及系统透过率、吸收率的光谱图.
|
图6 雾滴尺度分布、系统透过率及吸收率光谱图 Fig.6 The fog particle size distribution,transmittance and absorption rates of particle system |
图7显示了雾发展中雾滴$St$与雾滴平均尺度、雾系统透过率之间的关系. 显示:当颗粒的$St \approx1.0$时,1 000 s时刻由于颗粒聚集效应较大,碰并颗粒的尺度急剧增加,而系统透过率加速降低.分析原因主要是,颗粒运动由各向同性湍流中的小涡结构控制.湍流涡团对颗粒的离心作用,使得颗粒聚集在高应变率区域,引起颗粒浓度的局部高浓度,导致颗粒碰撞显著增强. 因此,当颗粒$St$从0.81增大至1.0和1.44,颗粒平均体积从1.084 1增大至1.148 3和1.222 2,分别增大 5.92%和6.44%.同时,对于0.6 μm的可见光的辐射,在上述条件下系统透过率分别降低6.0%和11.58%.

|
图7 雾滴$St$与颗粒平均尺度、系统透过率的关系 Fig.7 Relation between fog particle $St$ and average size,and the transmission rates of system |
雾发展过程中,大气环境悬浮的气溶胶影响着雾的微物理结构.即细小气溶胶易吸湿成为雾滴,同时雾滴与气溶胶发生碰并[29].下面讨论中主要考虑成分为水的雾滴与成分为二氧化硅的气溶胶组成的多相系统,并与成分为水的雾滴系统进行比较.
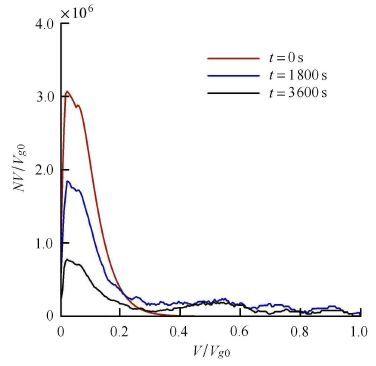
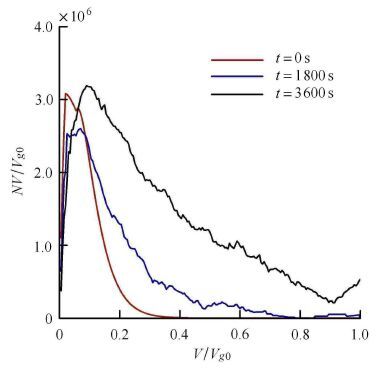
2.3.1 多相系统颗粒的动力学性质图8和图9显示了计算所得的气溶胶、雾滴随时间尺度的演化过程.其中,颗粒除发生破碎、蒸发、凝结效应外,湍流作用下有限惯性范畴的雾滴之间、布朗扩散的气溶胶之间,以及雾滴与气溶胶间的碰并效应十分活跃,生成大量复合粒子.气溶胶的数目浓度快速下降.
|
图8 气溶胶的尺度分布函数 Fig.8 Size distribution function of aerosol |
|
图9 雾滴的尺度分布函数 Fig.9 Size distribution function of fog |
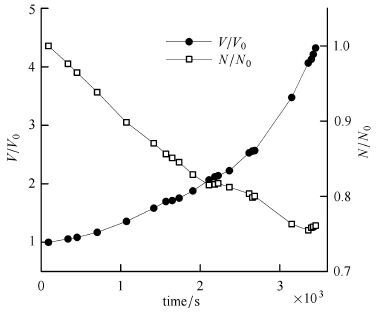
图10 给出多相系统颗粒平均体积和颗粒数目浓度随时间的变化情况.
|
图10 多相系统粒子平均尺度和数目浓度的变化 Fig.10 Average size and number concentration of multiphase system |
在雾爆发性增强时期,颗粒除凝结增长外,颗粒之间的碰并作用活跃,颗粒平均尺度增大,即产生了对含水量有主要贡献的大液滴,直接影响着系统对入射光的透过率.
图11给出雾滴、气溶胶组成的多相系统,其尺度和透过率随时间的演化.得出:相比于雾滴系统,多相系统粒子的平均体积增长速率慢. 当雾发展至1 687 s时刻,雾滴系统、多相系统颗粒的平均尺度分别为1.864和1.725,此时系统的透过率分别为0.502和0.487.即在相同条件下,多相系统的透过率较雾滴系统下降了2.99%,说明雾环境中由于形成大量的复合粒子,使得系统的透过率发生了变化.这也解释了近年来秋冬时期国内出现的雾增强天气,其能见度降低的原因.
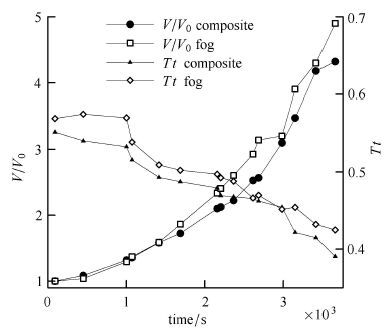
|
图11 多相系统与雾滴系统的比较 Fig.11 Comparison of multiphase and fog systems |
结合湍流性质、悬浮颗粒间碰并等效应及光辐射传输过程,文中利用加权MC方法,针对雾爆发性增强阶段物理量的演化展开数值研究. 得到:
(1)湍流输运和颗粒聚集效应对雾发展、能见度有较大的影响. 即湍流能提高雾滴的碰并效率,使雾滴谱拓宽,能见度降低.
在文中讨论的范围内,当湍流耗散率增大,雾环境颗粒对径向相对速度提高,颗粒碰并效应增强.当靠近地面的大气湍流耗散率进一步增大至1.0×10$^{ - 1}$m$^{2}$/s$^{3}$时,颗粒因流体的剪切应力造成的碰并占主导,碰并效应使得颗粒的平均尺度进一步增大.即1 000 s时刻,颗粒平均尺度(无量纲)可达到0.08. 此外,流场的湍流结构影响着颗粒的瞬时浓度场.当颗粒的$St$趋近于1.0时,1 000 s时刻由于颗粒受到涡的作用,聚集效应明显,颗粒的尺度急剧增加,而系统透过率降低.
(2)雾爆发性增强阶段,多相系统颗粒的动力学演化及散射性质不同于雾滴系统.
雾环境,气溶胶和雾滴的动力学演化呈现不同的规律. 气溶胶平均粒径小,通过碰并效应易与雾滴相结合产生大量的复合粒子,使得系统的透过率降低. 如1 687 s时刻,雾滴系统及多相系统颗粒的平均尺度分别为1.864和1.725,而系统的透过率分别为0.502和0.487. 相同条件下,多相系统较雾系统下降2.99%. 文中的研究结果解释了近年来国内出现的雾爆发性增强天气能见度降低的主要原因.
| [1] | 李子华,杨军,石春娥等.地区性浓雾物理.北京: 气象出版社,2008 (Li Zihua, Yang Jun, Shi Chune, et al. Regional Dense Fog Physics.Beijing: Meteorology Press, 2008 (in Chinese)) |
| [2] | Elias T, Haeffelin M, Drobinski P,et al. Particulate contribution to extinction of visible radiation: Pollution, haze, and fog. Atmospheric Research,2009,92:443-454 |
| [3] | 丁珏,王庆涛,刘义等. 雾环境二次气溶胶生长过程的数值研究,力学学报,2013, 45(2): 1-7 (Ding Jue, Wang Qingtao, Liu Yi, et al. Numerical study on the growth process of secondary aerosol in the fog. Chinese Journal of Theoretical and Applied Mechanics,2013,45(2): 1-7 (in Chinese)) |
| [4] | Ma N, Zhao CS, Chen J, et al. A novel method for distinguishing fog and haze based on PM2.5, visibility, and relative humidity. Science China, 2014,57(9): 2156-2164 |
| [5] | 崔桂香, 张兆顺, 许春晓等. 城市大气环境的大涡模拟研究进展. 力学进展, 2013, 43 (3): 295-328 (Cui Guixiangy, Zhang Zhaoshun, Xu Chunxiao, et al. Research advances in large eddy simulation of urban atmospheric environment. Advances in Mechanics, 2013, 43 (3): 295-328 (in Chinese)) |
| [6] | 刘霖蔚,牛杰生,刘端阳等. 南京冬季浓雾的演变特征及爆发性增强研究. 大气科学学报,2012, 35(1):103-112 (Liu Linwei, Niu Shengjie,Liu Duanyang,et al. Evolution characteristics and burst reinforcement of winter dense fog in Nanjing. Transactions of Atmospheric Sciences, 2012, 35(1):103-112(in Chinese)) |
| [7] | Wang LG, Vigil RD, Fox RO. CFD simulation of shear-induced aggregation and breakage in turbulent Taylor-Couette flow. Journal of Colloid and Interface Science, 2005, 285(1): 167-178 |
| [8] | Yu MZ, Lin JZ. Taylor-expansion moment method for agglomerate coagulation due to Brownian motion in the entire size regime. Aerosol Science, 2009 (40):549-562 |
| [9] | 李瑞霞,柳朝晖,贺铸等. 各向同性湍流内颗粒碰撞率的直接模拟研究. 力学学报,2006, 38(1):25-32 (Li Ruixia, Liu Zhaohui, He Zhu, et al. Direct numerical simulation of inertial particle collisions in isotropic turbulence. Chinese Journal of Theoretical and Applied Mechanics, 2006, 38(1): 25-32(in Chinese)) |
| [10] | Friedlander SK. Smoke, Dust and Haze: Fundamentals of Aerosol Behavior. New York: Wiley, 1997 |
| [11] | 李家骅,丁珏,翁培奋. 雾层两相耦合流场及气溶胶颗粒物的动力学性质. 力学季刊,2013, 34(1):8-15 (Li Jiahua, Ding Jue,Weng Peifen. Two-phase coupled flow and aerosols dynamical characteristics in the fog layer. Quarterly Journal of Mechanics, 2013, 34(1):8-15(in Chinese)) |
| [12] | Wang YM, Lin JZ. Collision efficiency of two nanoparticles with different diameters in Brownian coagulation. Applied Mathematics and Mechanics, 2011, 32(8): 1019-1028 |
| [13] | 赵海波, 郑楚光. 离散系统动力学演变过程的颗粒群平衡模拟. 北京: 科学出版社, 2008 (Zhao Haibo, Zheng Chuguang. Dynamics Balance Model on Evolution Process of Discrete System. Beijing: Science Press, 2008(in Chinese)) |
| [14] | Park SH. Evolution of particle size distributions due to turbulent and Brownian coagulation. Aerosol Science And Technology, 2002, 36:419-432 |
| [15] | Zaichik LI, Solovév AL. Collision and coagulation nuclei under conditions of brownian and turbulent motion of aerosol particles. High Temperature, 2002, 40(3): 422-427 |
| [16] | Chun J, Koch DL, Rani SL, et al. Clustering of aerosol particles in isotropic turbulence. Journal of Fluid Mechanics, 2005, 536: 219-251 |
| [17] | Wang LP,Wexler AS, Zhou Y. Statistical mechanical descriptions of turbulent coagulation. Phys Fluids,1998,10(10): 2647-2651 |
| [18] | Mcquarrie DA. Statistical Mechanics. New York: Harper & Row Publisher, 1976 |
| [19] | Mishchenko MI. Scattering Absorption and Emission of Light by Small Particles. New York: Cambridge University Press, 2002 |
| [20] | Howell JR, Perlmutter M. Monte carlo solution of thermal transfer through radiant media between gray walls. Journal of Heat Transfer- Transactions of the ASME, 1964, 86(1): 116-122 |
| [21] | Matthew S, Themis M. Constant-number Monte Carlo simulation of population balances. Chemical Engineering Science, 1998, 53 (9):1777-1786 |
| [22] | Zhao HB, Zheng CG, Xu MH. Multi-Monte Carlo method for coagulation and condensation/evaporation in dispersed systems. Journal of Colloid and Interface Science, 2005, 286: 195-208 |
| [23] | Williams MMR, Loyalka SK. Aerosol Science: Theory and Practice. New York: Pergamon Press, 1991 |
| [24] | Vemury S, Kusters KA, Pratsinis SE. Time-lag for attainment of the self-preserving particle size distribution by coagulation. Journal of Colloiscience and Interface , 1994, 165(1): 53-59 |
| [25] | Mishchenko MI, Travis LD, Lacis AA. Scattering, Absorption, and Emission of Light by Small Particles. Cambridge: Cambridge University. Press, 2002 |
| [26] | Self SA. Optical properties of fly ash. Quarterly Report, DOE/PC/79003-T19, 1994, 12 |
| [27] | 丁珏,刘义,李家骅. 雾天气向霾天气转化时气溶胶颗粒物的动力学特性. 气象与环境学报, 2012, 28(2): 91-96 (Ding Jue, Liu Yi, Li Jiahua. Dynamical characteristics of aerosol particles from fog to haze weather. Journal of Meteorology and Environment, 2012,28(2): 91-96(in Chinese)) |
| [28] | 裴鹿成,张孝泽. 蒙特卡罗方法及其在粒子输运问题中的应用. 北京:科学出版社,1980 (Pei Lucheng, Zhang Xiaoze. Application of Monte Carlo Method in Particle Transport Problems. Beijing: Science Press,1980(in Chinese)) |
| [29] | Yasmeen Z, Rasul G, Zahid M. Impact of aerosols on winter fog of Pakistan. Pakistan Journal of Meteorology, 2012, 8(16): 21-30 |
 2016, Vol. 48
2016, Vol. 48