作为交通工程建设中重要桥梁类型之一的斜拉桥,以其跨越能力强和施工方法成熟,在桥梁建设特别是大跨度桥梁建设中最具有竞争力.
自1955年世界首座现代斜拉桥斯特罗姆松德(Stromound)桥在挪威建成以来,斜拉桥在公路和铁路建设中一直发挥着重要作用.有关斜拉桥结构体系发展的问题可参阅文献[1].从1975年首座斜拉桥重庆云阳汤溪河桥建成,至2008年苏通大桥(主跨1 088 m)通车,斜拉桥在我国经历30多年的发展,主跨已迈入千米级时代.目前世界范围内已建成千米级的斜拉桥有昂船洲大桥(主跨1 018 m,中国)和海参崴跨海大桥(主跨1 104 m,俄罗斯).未来超大跨径斜拉桥的建设不仅将推动斜拉桥建造技术的进步,而且给相关学科特别是桥梁结构动力学的发展带来机遇和挑战.
斜拉桥作为高次超静定结构,虽然静力传递简明:通过上端锚固于桥塔的斜拉索向加劲梁/桥面体系提供弹性支撑,拉索对桥塔的水平分力自行平衡,竖向分力通过桥塔传递给基础.但是,由于斜拉桥跨度大,桥面梁和斜拉索相对于桥塔为柔性结构,在交通载荷、强风和地震等复杂环境载荷作用下,其动力学行为相当复杂.在一定条件下可能引发拉索的大幅振动,有时还激起桥面的振动及桥面和拉索的共振等危险情况,对桥梁安全构成严重威胁[2],关系我国社会经济可持续发展和国家安全.因此,针对大跨度斜拉桥的大幅振动问题,各国学者在斜拉索的空间大幅振动[3]、多模态耦合振动[4, 5]、斜拉索与梁的非线性耦合振动[6, 7]、车桥耦合振动[8]、风车桥之间的耦合振动[9]等问题上,从模型建立、分析方法和实验等方面已经开展了大量的研究,不仅揭示了斜拉桥的大幅振动机理,还为斜拉桥的减振和隔震提供技术支撑,促进了斜拉桥的发展.
虽然,对斜拉桥非线性振动问题的研究已经取得了阶段性成果,但由于斜拉桥结构体系自身的复杂性、新材料的应用、以及已有研究成果的局限性,将非线性振动理论的研究成果应用于实际工程还存在一定的距离,还有待进一步深入系统的研究. 关于斜拉桥的非线性振动问题的相关研究成果至今未见到有专著的出版. 因此,为促进非线性动力学理论和方法的发展,推动大跨度斜拉桥的建设及工程技术的进步,加快青年人才的培养,有必要对以往大跨度斜拉桥非线性建模理论及其动力学的研究成果进行归纳总结,使读者了解大跨度斜拉桥非线性振动问题的研究现状.
斜拉桥非线性动力学的研究,可归为两类问题的研究:一类为理想激励下基本单元结构的非线性动力学行为研究,另一类为非理想激励下的非线性振动研究. 前者研究斜拉桥局部单元(如:斜拉索和梁等)的振动,忽略了该构件对激励的影响,将激励考虑为简谐载荷等特定形式.非理想激励指在研究拉索的振动时,考虑自身振动对激励的影响,激励反过来又影响拉索自身振动,这个过程时时变化非常复杂.主要表现为桥面梁与拉索的耦合振动、拉索的风雨振动以及地基梁和桩基与土的相互作用等.基于以上考虑,本文将从索、梁简单构件的非线性振动问题到斜拉桥复杂体系(如:索梁模型)对斜拉桥非线性振动问题的研究进行评述.本文的结构如下:第1部分为斜拉索非线性动力学模型及理论与实验研究;第2部分为梁的非线性动力学模型及理论与实验研究;第3部分为斜拉桥整体非线性动力学模型及理论和实验研究;最后,对斜拉桥的非线性振动问题今后的发展方向进行了探讨和展望.
1 斜拉索的非线性振动斜拉索的动力学研究具有悠久的历史,远早于斜拉桥的诞生.斜拉索的动力学基本理论研究在20世纪已经取得了丰硕的成果,读者可从文献[10, 11, 12, 13]中查阅.这里我们仅从斜拉索的动力学模型、分析方法和实验研究3个方面回顾总结近10年来的最新研究成果.
斜拉索与悬索(如图1所示)主要区别于索的两端是否在同一水平面,以及两者的静态构形垂度的大小.通常斜拉索的垂度相对较小,静态构形常用抛物线模拟,而悬索的垂度较大,通常用悬链线模拟.在动力学建模方面,由于是在静平衡位置建立运动控制微分方程,其自由振动问题没有本质的区别.由于初始构形产生二次非线性对二者的影响有一定差异,导致表现出不同的动力学特性.对悬索非线性振动的研究主要集中在水平轴向激励引起的参数振动和横向强迫振动.对斜拉索的研究主要集中在强迫振动和参强振动(参数激励和强迫激励共同作用)的研究.

|
图1 斜拉索和悬索构形 Fig.1 Inclined cable and suspension cable |
力学模型是动力学研究的根基,对于同一研究对象(如:本节中的斜拉索),针对不同问题从不同角度建立的不同动力学模型,可揭示其独特的力学行为及其产生机理.
1.1.1 考虑弯曲刚度的斜拉索动力学模型
随着斜拉桥和悬索桥跨度的增大,无论是斜拉索还是悬索,直径变得越来越大,横向抗弯刚度对结构动力学特性特别是非线性振动行为的影响变得不可忽略.吴晓等[14]和赵跃宇等[15]推导得到了考虑弯曲刚度的斜拉索非线性运动控制微分方程
\[EA{\left[ {u' + y'v' + \frac{1}{2}\left( {{{v'}^2} + {{w'}^2}} \right)} \right]^\prime } + {P_u} - {\mu _u}\dot u = m\ddot u\]
(1)
\[\begin{array}{l}
{\left\{ {Hv' + EA\left( {y' + v'} \right)\left[ {u' + y'v' + \frac{1}{2}\left( {{{v'}^2} + {{w'}^2}} \right)} \right]} \right\}^\prime } + \\
{P_v} - {\mu _v}\dot v - EIv'''' = m\ddot v
\end{array}\]
(2)
\[\begin{array}{l}
{\left\{ {Hw' + EAw'\left[ {u' + y'v' + {\textstyle{1 \over 2}}\left( {{{v'}^2} + {{w'}^2}} \right)} \right]} \right\}^\prime } + \\
{P_w} - {\mu _w}\dot w - EIw'''' = m\ddot w
\end{array}\]
(3)
在考虑弯曲刚度影响的斜拉索动力学模型中,引入温度对初始张力和静平衡位置的影响,即
\[H = {H_0} - EA\alpha \Delta T\]
(4)
以考虑热应力的平衡状态为初始构形,建立考虑温度影响的斜拉索面内非线性动力学模型[17]
\[Hv{\rm{''}} + EAe(t)\left( {y{\rm{''}} + v{\rm{''}}} \right) = m\ddot v\]
(5)
\[e(t) = \frac{1}{L}\int_L {\left( {y'v' + {\textstyle{1 \over 2}}v{\rm{''}}} \right)} dx\]
(6)
该模型从本构关系中引入温度项,应用该理论通过研究温度对斜拉索频率的影响及索力对温度的敏感性分析[18],揭示了温度对斜拉索的基本动力学特性和非线性特性均有较大影响,特别是在成桥索力评估中考虑温度因素是很有必要的. 后期的研究,应注重斜拉索或斜拉桥温度的非均匀变化对结构行为影响的研究,在温度场中研究斜拉索的力学行为.
1.1.3 CFRP斜拉索动力学模型
碳纤维增强聚合物(carbon fiber reinforced polymer,CFRP)是一种增强型碳纤维复合材料,被广泛应用于航空航天、机械和土木工程等领域. CFRP斜拉索具有轻质(容重约为钢材的1/5)、高强(弹性模量最高可达1 000 GPa,抗拉强度可达2 700 MPa[19])和耐腐蚀等特点,能克服传统钢质拉索的锈蚀、疲劳、极限长度小、承载效率低等问题,近年来被用来取代钢质拉索建设CFRP斜拉桥. 对CFRP斜拉索的非线性动力学性能进行研究目前有两种理论,一类为基于各向同性理论的传统斜拉索非线性动力学理论,该理论认为CFRP索为细长索,横向各向异性表现并不明显[19]. 另一类为基于横观各向同性假设,建立CFRP斜拉索的非线性动力学模型[20]
\[{\left[ {{E_{11}}A(e + y{\rho _1} + z - y){T_{11}}} \right]^\prime } + {q_1} = m\ddot u + {c_1}\dot u\]
(7)
\[{\left[ {{E_{11}}A(e + y{\rho _1} + z - y){T_{12}}} \right]^\prime } + {q_2} = m\ddot v + {c_2}\dot v\]
(8)
\[{\left[ {{E_{11}}A(e + y{\rho _1} + z - y){T_{13}}} \right]^\prime } + {q_3} = m\ddot w + {c_3}\dot w\]
(9)
\[\begin{array}{l}
\{ {E_{11}}ye + [{G_{13}}{y^2} + {G_{12}}({z^2} - 2yz)]{\rho _{11}}\} ' - {E_{11}}ye{\rho _2} - \\
{E_{11}}ze{\rho _3} + {q_4} = J\ddot \varphi + {c_4}\dot \varphi
\end{array}\]
(10)
以上模型均以拉索两端固支或铰支作为边界条件,而未考虑支座运动的影响,属于理想激励模型,仅能研究强迫激励作用下斜拉索的动力学行为. 斜拉索在斜拉桥中并非独立的构件,它的力学行为受桥面梁和塔的影响不可忽略. 下面介绍的第四类斜拉索动力学模型中引入支座运动的影响,将斜拉索的动力学研究扩展到非理想激励.
1.1.4 考虑支座运动的斜拉索动力学模型
实际上,支座运动对斜拉索同时产生参数激励和强迫激励. 参数激励通过改变轴向应力应变关系,使斜拉索的频率不再固定不变,从而对斜拉索的非线性振动特性产生很大的影响[21, 22, 23, 24]. 有代表性的模型[25]为
\[\begin{array}{l}
mv + {c_2}v + EA{\left( {\frac{{mg}}{{{T_x}}}} \right)^2}\int_0^L {\frac{v}{L}} ds = \\
\left[ {\frac{{{T_x}}}{{\sin \alpha }} + \frac{{EA}}{L}({v_B}\cos \alpha - {u_A}\sin \alpha )} \right]\frac{{{\partial ^2}v}}{{\partial {s^2}}} + {f_v}
\end{array}\]
(11)
斜拉索的振动控制问题(图1(c))一直以来都是研究的热点,课题组基于以往研究成果,建立了考虑时滞及磁流变阻尼器的斜拉索动力学模型[27, 28]
\[\begin{array}{l}
\ddot v + {c_v}\dot v - \frac{{v{\rm{''}}}}{{{\pi ^2}}} - \frac{\alpha }{{{\pi ^2}}}(y{\rm{''}} + v{\rm{''}})\int_0^1 {\left[ {y'v' + \frac{1}{2}({{v'}^2} + {{w'}^2})} \right]} dx = \\
- {c_d}\dot v(t - \tau )\delta (x - a) + f
\end{array}\]
(12)
\[\begin{array}{l}
\ddot w + {c_w}\dot w - \frac{{w{\rm{''}}}}{{{\pi ^2}}} - \frac{\alpha }{{{\pi ^2}}}w{\rm{''}}\int_0^1 {\left[ {y'v' + \frac{1}{2}({{v'}^2} + {{w'}^2})} \right]} dx = \\
- {c_d}\dot w(t - \tau )\delta (x - a)
\end{array}\]
(13)
该模型可揭示斜拉索中时滞对振动控制系统的影响及振动行为产生的不同机制,评估控制系统的性能,以及如何利用或消除时滞的影响,具有重要的科学和工程意义.
1.2 研究方法斜拉索非线性振动问题的研究,主要采用数值方法、有限元法、近似求解和实验测试四种类型的方法.有限元法[29]主要集中在两类问题上:一类为直接应用大型通用有限元软件,采用不同的单元模拟斜拉索[30, 31],研究其非线性振动行为;一类集中在索单元的建立上,其中二节点单元[32, 33]的应用比较普遍,同时也有关于三节点单元[34]和五节点单元[35]的研究,可根据计算目的的不同采用不同单元进行计算分析.数值方法[36]应用于斜拉索的响应研究较为少见,近似求解方法和实验方法常被力学工作者应用于探索拉索的非线性动力学现象(分叉和混沌等).下面主要对多尺度法和实验研究进行概述.
1.2.1 多尺度法多尺度摄动方法是非线性动力学中应用最为广泛的近似分析方法,关于该方法的基本求解过程读者可参考非线性动力学专著[37, 38, 39, 40, 41, 42]. 在斜拉桥的整体模型和斜拉索模型的非线性振动研究中几乎均用多尺度摄动方法. 多尺度法中小参数$\varepsilon $选择的灵活性为求解各类问题提供方便. 在应用多尺度法时,一般将时间$t$通过小参数$\varepsilon$的不同次数定义为$\varepsilon^nt$,从而将时间分为不同尺度. 同时,为消除久期项,将运动方程中的阻尼项、非线性项和激励项定义为小参数$\varepsilon $的幂次项. 对于同时含有二次和三次非线性项的拉索运动控制微分方程(组),可将外激励通过小参数调整,灵活地求解超谐波共振、主共振、亚谐波共振时的周期解和准周期解等. 高俊[43]求解斜拉索轴向激励的参数振动时将运动方程中除线性刚度和惯性力项以外的部分引入小参数$\varepsilon $,从而得到其一阶近似解.
为求解得到拉索振动问题的二阶近似解,一般将解假设为[44]
\[\begin{array}{l}
{q_i} = \varepsilon {q_{i1}}({T_0},{T_1},{T_2}) + {\varepsilon ^2}{q_{i2}}({T_0},{T_1},{T_2}) + \\
{\varepsilon ^3}{q_{i3}}({T_0},{T_1},{T_2}) + \cdots
\end{array}\]
(14)
在将近似解设为式(14)的类型时,通过后面可解性条件的推导,通常会得出$\varepsilon
t$不出现的条件. 因此,李志江[20]在求解CFRP斜拉索的参数振动时,将解展开成$\varepsilon $和$\varepsilon ^3$形式,即
\[{q_i} = \varepsilon {q_{i1}}({T_0},{T_2}) + {\varepsilon ^3}{q_{i3}}({T_0},{T_2}) + \cdots \]
(15)
\[\begin{array}{l}
{q_i} = \varepsilon {q_{i1}}({T_0},{T_2}) + {\varepsilon ^2}{q_{i2}}({T_0},{T_2}) + \\
{\varepsilon ^3}{q_{i3}}({T_0},{T_2}) + \cdots
\end{array}\]
(16)
\[\begin{array}{l}
{q_i} = {q_{i1}}({T_0},{T_1},{T_2}) + {\varepsilon ^1}{q_{i2}}({T_0},{T_1},{T_2}) + \\
{\varepsilon ^2}{q_{i3}}({T_0},{T_1},{T_2}) + \cdots
\end{array}\]
(17)
由于多尺度法自身引入了小参数,致使其应用也受到一定的限制,大多应用于弱非线性系统,并且随着运动方程自由度的增加,多尺度法寻找久期项建立调谐方程(组)变得越来越复杂. 因此,如平均法[47]、同伦法[48]等其他近似方法在斜拉索的非线性振动问题的研究中也发挥了重要作用.
1.2.2 实验研究拉索的实验研究主要基于小型缩尺模型试验,由于桥梁结构的庞大和客观实际条件的问题,尚未见到针对实际桥梁中拉索的实验研究.
对索的实验研究,早期为对水平悬索非线性振动行为的实验研究. Nayfeh[49]研究了一端受参强激励的水平悬索的动力学行为,观察到了三模态共振行为.Rega等[13]通过两端竖向激励无初张力水平悬索,观察到了1:1,1:2及2:2:1:2等多种索的多模态内共振现象.Hu和Pai[50]实验研究了一端竖向激励下水平悬索的垂跨比对非线性振动行为的影响,试验观测到超谐波共振、亚谐波共振,以及悬索的1:1,2:2:1,1:2:2和2:4:2等多种内共振模式.上述实验研究主要集中在外激励对水平悬索的不同激励形式(如强迫激励、参强激励、一端或两端激励)、激励产生的共振形式(超谐波共振、主共振和亚谐波共振)和不同模态的内共振(面内两模态、三模态和多模态),并通过非线性动力学的研究方法观测到分叉现象、单周期和多周期运动、拟周期运动和混沌现象,从实验证实了水平悬索丰富的非线性动力学行为.
斜拉索非线性振动行为的实验研究. Berlioz 和 Lamarque [51, 52]通过在斜拉索上缠绕铜丝线进行配重,观测在拉索下端直接施加竖向激励时不同初始索力、不同激励频率及幅值对斜拉索的非线性动力学行为的影响. Rega 等 [53]实验研究了一根无初始张拉力斜拉索的自由振动和非线性强迫振动,观测到拉索不对称性引起的混合模态及由此产生的"频率避让"现象.陈丕华和王修勇等[54]试验研究了斜拉索受弦向位移激励的面内参数振动,观测到参数振动产生在一定的频率比范围内,斜拉索振幅与频率比关系曲线表现出非线性特性,系统阻尼使得斜拉索参数振动的激励幅值要超过一定的阀值才能出现.Gonzalez-Buelga 等[55]研究在面内竖向激励作用下拉索的面外振动稳定性,关注了模态间的 2:1内共振,得到其稳定边界. Macdonald 等[56]对下端竖向激励斜拉索的稳定区域进一步开展了研究,发现激励频率在一阶自然频率附近时,由于参强激励作用可以产生很大的二阶面内振动.上述斜拉索的非线性实验,基于研究斜拉桥中斜拉索的动力学问题的思路,无一例外地采用各种方式进行配重.虽然根据相似理论对斜拉索配重能够控制索的频率满足匹配关系,测试所得的非线性振动行为和理论研究成果一致性很好,但由于相似理论的局限性,只能从定性方面反映斜拉桥中斜拉索的非线性动力学行为.
拉索非线性振动行为控制的实验研究. Xu 等[57]试验研究了一根长3.2 m的拉索-油压阻尼器系统的线性和非线性振动特性,发现垂度会影响阻尼器的工作性能和通过调整阻尼的大小可得到拉索各阶振动模态阻尼比的极值.Gattulli 等[58]对悬索施加纵向反馈主动控制,有效控制了复杂动力学行为下的拉索的空间振动幅值. Faravelli 和Fuggini[59]采用形状记忆合金钢丝和敞口圈混合控制方式研究了拉索振动,表明该混合控制方法可有效地的控制拉索的对称及不对称振动.Jiang和Li等[60]采用被动控制策略对水平悬索振动行为进行控制,控制器主要由阻尼器和弹簧构成,使阻尼比达到2%.Alvarado 等[61]建立了阻尼主动控制系统,在实验室测试中可减小振幅达50%.在美国比较盛行将拉索进行横向连接形成索网结构对拉索的横向振动进行控制[62],但影响斜拉桥的整体美观.拉索振动控制的研究主要在阻尼器的种类(磁流变阻尼器[63]和油阻尼器等)和阻尼器的施加方式(横向或轴向)以及控制方式(主动控制、被动控制及两者结合)上有较多研究成果,但在控制理论及应用方面还需要有新的突破.另外,斜拉索振动产生的能量采集问题[64],可能在今后受到各国学者的青睐,特别是如何将能量采集与振动控制相结合,可能成为结构动力学与控制领域的研究热点.
2 梁的非线性振动梁是一种基本结构单元,应用于机械、航空航天、土木、生物等多个宏观和微观领域,这里仅对大跨度斜拉桥中梁相关动力学问题的研究进展进行总结.
随着新材料和新施工工艺的发展,斜拉桥中的主梁正朝着轻质和大跨方向发展,在环境载荷作用下结构的非线性动力学行为变得越来越复杂. 因此,对其非线性动力学行为的研究一直受到广大科技工作者的重视.由于斜拉桥中桥面梁主要由斜拉索支承,对桥面梁的动力学问题的研究,其动力学模型主要为离散弹性支承的欧拉-伯努利(Euler-Bernoulli)梁[65, 66]和连续弹性支承的欧拉-伯努利梁和铁木辛柯梁.前者主要应用于研究桥面梁的基本动力学性能及斜拉桥全局模态振动行为[67],后者主要应用于密索体系的桥面梁(悬索桥和斜拉桥)和桩基础[68, 69, 70]的动力学行为研究.
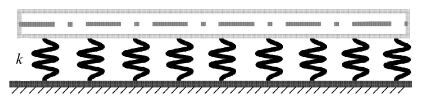
2.1 弹性地基梁动力响应研究弹性地基梁模型(图2所示)在土木工程中被广泛应用于模拟多种结构物的静动力响应问题[71],并且拓展应用到了碳纳米管的动力响应[72]研究中,已成为一类基本力学模型,在有介质或力支承的细长结构动力学研究方面具有普遍意义[73].
|
图2 弹性地基梁及地基模型 Fig.2 Beam on elastic foundation and its model |
作为土-结构相互作用问题的重要组成部分,国内外学者已对弹性地基梁的线性振动问题进行了广泛的研究.Valsangkar 和Pradhanang[74]运用双参数地基模型研究了弹性地基梁的固有频率. Lai等[75]则研究了弹性地基梁的固有频率及模态构型. Eisenberger[76]运用动力刚度方法探讨了单参数及双参数地基梁的固有频率. Morfidis[77]对三参数弹性地基铁木辛柯梁的动力响应问题进行了深入研究.随着工程实践的发展,为满足结构物在地震动激励或动力机器激励下的设计要求,需要在分析研究中考虑结构的非线性振动稳定问题.Pellicano和Mastroddi[78]运用规范型方法研究了非线性介质支承梁的非线性振动. Coskun和Engin[79] 研究了非线性无黏性文克勒 (Winkler)地基上梁的非线性动力响应. Zhu和Leung[80]针对双参数地基上变截面铁木辛柯梁的非线性振动问题进行了深入研究. Nayfeh[81] 及其合作者运用多尺度方法研究了非线性弹性地基上欧拉-伯努利梁的非线性模态和动力响应问题. 以上研究中,土-结构相互作用分析模型中多不考虑结构的几何非线性,通常仅假定地基为非线性或考虑上部结构的材料非线性. 王连华和马建军等[69, 71]将土-结构相互作用引起的二次弯矩效应引入到非线性动力学中,研究了土-结构相互作用效应对于弹性地基梁非线性动力响应特性的影响.并且,通过弹性地基梁非线性内共振响应研究发现,二次弯矩效应导致了连续系统保守特性的破坏.
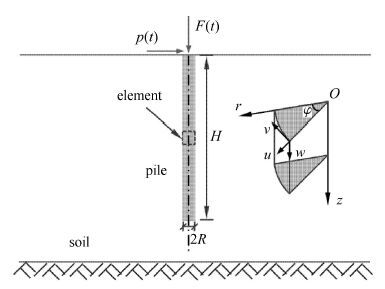
2.2 桩-土系统动力响应研究早期的桩主要承受竖向载荷,随着桩基应用的发展,水平受荷桩(图3所示)的应用也逐渐扩大[82],可将其归属于轴向受压梁的范畴.
|
图3 桩-土相互作用体系 Fig.3 Soil-pile interaction system |
丰富的试验及理论研究成果表明,外激励作用下桩-土相互作用响应具有明显的非线性特性.Naggar等[83]对瞬态动载荷或非谐和动激励作用下竖向或水平受荷单桩及桩群的非线性动力响应进行了研究,并得到了非线性动力响应系数.但是,该模型是通过离散等效土弹簧和阻尼器建立的,其求解过程是运用等效线性的方法.基于耦合系统运动为线性的假定,Rovithis等[84] 用3D有限元模型对土-桩-结构系统的地震动响应进行分析,提出土- 桩-结构系统的拟自然频率. 基于非线性文克勒地基梁假定,Soneji和Jangid[85]探讨了土-结构动力相互作用效应对于由刚性竖直群桩基础支撑的有基础隔震装置斜拉桥抗震性能的影响.随着研究的深入,桩-土系统非线性动力响应的基础理论研究逐渐受到重视. Chau和Yang[86]提出一种研究水平激励作用下有限厚度土场中的竖向圆桩的非线性动力响应的模型,该模型将桩周土场分为内外两个区域区别对待,重点考虑近桩土场的非线性.王连华和马建军等[87]将土-结构相互作用产生的二次弯矩效应引入到土-细长结构物的动力学建模中,分别利用牛顿定律和哈密尔顿原理建立了弹性地基梁的非线性动力学模型.研究了土-结构相互作用效应对于弹性地基梁非线性动力响应特性的影响.吕建根等[88]基于哈密尔顿变分原理推导了地震作用下非线性桩基的非线性控制方程,研究了桩的3次超谐波共振问题,当地震波频率约等于桩基固有频率的1/3时,容易激发桩的3次超谐波共振响应,其共振幅值较大.斜拉桥下部结构作为桥梁的支承体系,建立桩(群桩)-土系统的精细化动力学模型,对于研究斜拉桥的整体力学性能至关重要.
3 斜拉桥整体模型的非线性振动由于斜拉桥结构的复杂性以及非线性动力学研究方法对于多自由度问题的局限性,几乎没有见到基于斜拉桥整体模型非线性振动的相关研究工作.但是,为研究斜拉桥复杂的非线性动力学行为,广大学者基于斜拉桥的实地观察和实验研究,建立了能够揭示斜拉桥动力学行为产生机理的一些简单动力学模型.下面从索-梁组合模型(如图4)及索-质量块模型等对斜拉桥整体非线性动力学的研究进展进行总结.

|
图4 索-梁一般模型 Fig.4 Simple cable-stayed beam model |
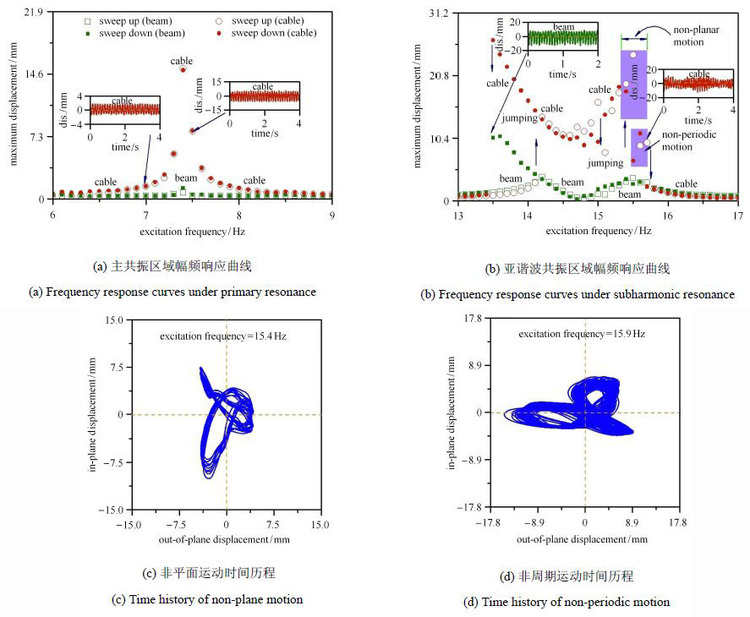
索-梁模型是Fujino和Warnitchait等[89]基于Gimsing[90]研究斜拉桥全桥振动时观察到全局模态和局部模态的研究成果提出的,被广泛应用于斜拉桥、塔式起重机、桅杆、悬索屋盖等结构的动力学研究.Fujino和Warnitchait用实验和理论研究了三自由度索-梁组合结构的自激参数共振.同时,将索-梁组合结构动力学模型由以前仅仅考虑整体振动改进为整体模态和局部模态作用,并观察到了由于整体模态和局部模态线性耦合的模态失真现象. 后来该课题组[91]研究发现梁在竖向随机激励下索与梁通过自激行为产生了横向振动. 与此同时,赵跃宇课题组[23,92, 93, 94]从连续介质力学出发,基于考虑弹性体与柔性体之间的耦合动力学特性,利用索-梁的连接条件和边界条件,建立了单索-梁、双索-梁、多索-梁及索-曲线梁的约化运动学控制方程,得到系统的多模态离散动力学方程,并对非线性动力学行为进行了系列理论和实验研究. Fung 等[95]基于哈密尔顿原理和有限元法推导了描述群索-梁耦合作用的非线性耦合微分方程组.Gattulli和Lepidi等[96]在索与梁的连续协调条件中引入非线性,研究了整体模态和局部模态之间1:2和2:1内共振时的能量传递. 周强课题组[97, 98]也对索与梁的响应、能量传递等进行了研究,发现索与梁在共振情况下存在较大的能量交换. Fung 等 [99]考虑索力和索长的时变特性,建立了索-梁组合结构动力学模型,发现张拉力不仅与索力相关,而且是横向和轴向位移的函数.Wei和Xiao 等[100, 101]研究索与梁同时受外载荷激励下索-梁组合结构的分岔、周期运动和混沌等非线性动力学行为. 为对索与梁的大幅振动行为进行控制,彭剑等[27]建立了时滞反馈作用下索-梁组合结构的运动控制微分方程,进而利用时滞反馈控制对索-梁组合结构的大幅振动进行控制,从而为索-梁组合结构的振动控制提供了一种方法.梁栋等[102]将主梁、索与阻尼器视为一个振动体系,进行了理论分析.同时,进行索梁模型试验,研究主梁振动对阻尼器减振效果的影响,发现主梁振动将降低阻尼器的减振效果.王志搴等[103]通过直接法和离散法研究了索-梁结构的非线性特性,发现索与梁的内共振行为可改变拉索的软硬动力学特性.赵珧冰[104]考虑温度效应对索-梁组合结构动力学行为的影响,发现温度的改变直接影响索与梁结构的固有频率,预示着索-梁结构的内共振特性受温度影响较大. 文献[105]中基于空间结构刚度受温度影响引起刚度非线性变化的情况,研究发现温度变化将可能引起索-梁结构的摆振.王涛和沈锐[106]基于非线性有限元法对多索-梁结构进行了数值分析,并提出了索与梁相关振动的概念. 后来,赵跃宇课题组[107]进一步对索-梁模型进行了实验研究,发现了索-梁组合结构在不同激励频率区间的多模态内共振、周期运动和非周期运动等复杂动力学行为(图5所示),以及跳跃现象经历的3个重要过程.本课题组[108, 109, 110]最近将索-梁模型进行了拓展,基于桥梁工程中的拱桥及斜拉拱桥的施工过程,建立了索-拱动力学模型,并应用于拱桥和斜拉拱桥的施工过程的动力学研究.
|
图5 索-梁模型的实测响应 Fig.5 Measured response of cable-beam |
以上研究,从索与梁不同的温度环境条件、到简谐或随机激励作用于索、梁或同时作用等激励方式,从索与梁固接或铰等连接条件,到悬臂直梁、简支直梁或曲梁等不同梁类型,从单索、双索、多索等不同数量的索-梁模型,到索与梁不同模态间的相互作用等方面对索-梁动力学模型的非线性振动及其控制开展了系统深入的理论和实验研究.
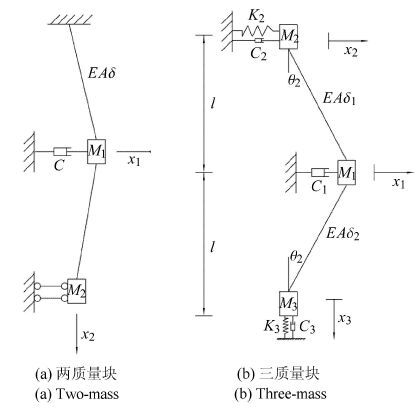
3.2 其他斜拉桥动力学模型及理论研究建立简单适用能揭示和反映斜拉桥非线性动力学本质问题的斜拉桥全桥动力学模型一直是广大学者的追求目标. 在过去的20年里,斜拉桥全桥非线性动力学研究在动力学模型方面可分为以下4类:(1)基于多质量块耦合模型的非线性振动研究(图6所示);(2)基于索-质量块的参数振动模型的动力学研究(图7所示);(3)基于索-质量块的参强激励模型的动力学研究(图8所示);(4)多体模型(图9所示)研究.
|
图6 斜拉桥的质量块模型 Fig.6 Multi-mass models of cable-stayed bridge |
|
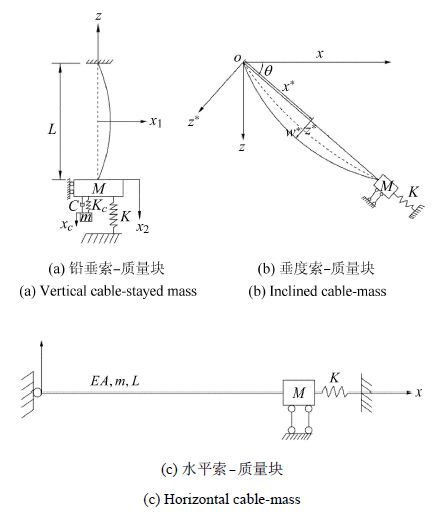
图7 索-质量块参数振动模型 Fig.7 Cable-mass model for parametric vibration of cable-stayed bridge |
|
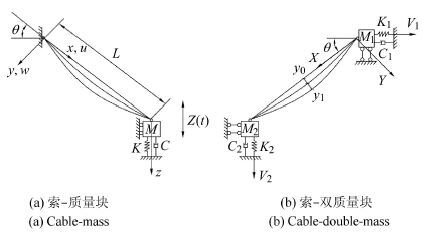
图8 索-质量块的参强激励模型 Fig.8 Cable-mass model for parametric and forced vibration of cable-stayed bridge |

|
图9 斜拉桥的多体模型 Fig.9 Multi-body model of cable-stayed bridge |
基于多质量块耦合模型的斜拉桥非线性振动研究.Virlogeux[111]最早将斜拉桥桥面简化为一质量块,同时也将斜拉索简化为一质量块,两质量块通过无质量拉索相连接,最后根据牛顿定律建立运动微分方程,重点研究了强迫振动,认为当索桥的固有频率很接近时,索端小的横向振动可以使索产生极大的振幅.后来,亢战和钟万勰[112]也建立了斜拉桥的两质量块模型(图6(a)所示),重点研究了索与桥面的参数振动问题.该研究发现,当拉索的局部自振频率与桥面的某一低阶自振频率的比值落在某一连续区间时将发生严重的参数共振现象.张妍等[113]在此基础上,考虑桥塔的影响,建立了斜拉桥拉索-桥面-桥塔的三质量块(图6(b)所示)三自由度耦合振动模型,通过对拉索-桥面-桥塔的1:2:1内共振的研究,揭示了斜拉桥三主要构件产生内共振的条件和存在能量传递的规律.
基于索-质量块参数振动模型的斜拉桥动力学研究.参数振动指外界激励不以外力形式作用于系统,通过系统内系数的周期性改变间接实现对系统的作用,系统控制方程为时变系数的偏微分方程.汪至刚和孙炳楠[114]用标准弦来模拟拉索,用弹簧来模拟桥面的刚度,建立了斜拉桥的索-质量块参数振动模型(图7(a)所示),对拉索在斜拉桥参数激励下引发的振动及由此采用的振动控制措施进行探讨.在此基础上,陈水生和孙炳楠[115]考虑索的垂度、几何非线性及桥面运动而导致的索内力变化等因素,建立了斜拉桥的索-质量块参数振动模型(图7(b)所示)及其控制微分方程,发现拉索的垂度在Irvine参数较大时对参数振动有较大影响.任淑淡[116]分别建立了不计拉索倾角和计入倾角影响,并同时考虑拉索第一和二阶模态的斜拉桥三自由度参数振动模型(图7(b)和图7(c)所示),研究发现倾角对共振的频率区间及共振出现的可能情况有较大的影响.周岱等[117]考虑空间结构-索-塔的联合作用,将空间结构和塔简化为弹簧质量块,建立了索-双质量块参数振动模型,研究发现当塔柱或者空间结构的固有频率约为拉索固有频率的2倍时,系统发生参数共振.
基于索-质量块的参强激励模型的斜拉桥非线性动力学研究.参强激励指作用于系统的外界激励同时给系统参数激励(引起系统的参数振动)和强迫激励(产生强迫振动).在斜拉桥的研究中,桥面对斜拉索的竖向激励或桥塔对斜拉索的水平激励均可将其分解为沿索轴向的参数激励和沿横向的强迫激励.谭长建和祝兵[118]为探讨大跨度斜拉桥拉索与桥面耦合振动特性,建立了拉索-质量块的参强激励动力学模型(图8(a)所示),揭示了桥面和拉索频率比为1:1、1:2和2:1时通过能量交换拉索产生大幅振动.郭翠翠[119]建立拉索-桥面-桥塔耦合振动模型(图8(b)所示),推导出三自由度非线性参数振动微分方程,研究发现当桥面、主塔频率为拉索频率二倍时,各拉索都将发生参数共振,并在此基础上增加了黏弹性阻尼器,对拉索的控制问题进行初步研究.
基于多体模型的斜拉桥非线性振动研究.前述不同类型斜拉桥动力学模型,从一些侧面揭示了斜拉桥动力学行为的产生机理,同时也反应斜拉桥动力学研究的复杂性,为更深入地研究斜拉桥的动力学特性,目前国内外学者逐渐在这方面开始了新的尝试.高骏[43]将桥塔视为质量块,将索与梁视为连续介质,建立了斜拉桥的桥面-拉索-桥塔耦合振动模型(图9(a)所示),研究发现桥塔刚度越大,斜拉索参数振动的振幅越大,说明塔的高度增加有利于减小斜拉索的振动幅度.在此基础上,彭然[120]进一步将桥塔用连续梁模型进行模拟,分别建立了斜拉桥的桥-索-塔三连续体的三自由度和四自由度动力学模型(图9(b)所示),研究发现若桥面激励频率和拉索面内频率不满足匹配关系,拉索面内、面外和桥面无明显的耦合作用. 在满足频率比匹配关系时,桥面激励引起的拉索面内振动可诱发拉索面外振动.汪峰等[121]进一步在塔模型的上端引入弹性支承,以模拟桥塔背索的作用,建立斜拉桥塔-索-桥面连续耦合振动模型,揭示了桥塔、斜拉索和桥面振动频率满足2:2:1时,振动能量在三者之间传递,存在强烈耦合振动现象.上述研究重点放在塔-索-桥面之间的能量传递上,而少有关于索与索间能量传递的研究.赵跃宇课题组[122]为此建立了斜拉桥的双索-质量块模型(图9(c)所示),得到了斜拉桥双索与桥面耦合的非线性振动方程,数值分析表明变动其中一根索的参数,另一根索的运动特性会受到较大影响,从时间历程可以看出双索间存明显的能量交换.
上述全桥动力学模型及理论研究揭示了斜拉桥部分非线性动力学行为的产生机理,但由于斜拉桥系统本身的复杂性,斜拉桥整桥的非线性动力学理论研究尚处于起步阶段,要建立斜拉桥整体大系统的动力学理论还需要深入系统地开展大量研究.
3.3 斜拉桥非线性动力学的实验研究斜拉桥的实验研究主要集中在斜拉桥建成后的验收阶段,大多针对斜拉桥整体的基本动力学问题:振动模态、频率和对应的各阶阻尼进行测试[123],关于斜拉桥的非线性振动行为和特性研究相对较少.Caetano等[124]通过对瓜迪亚纳 (Guadiana)桥大幅振动的现场测试,观测到了主梁纵向、横向和竖向运动及拉索摆动.魏晓军[125]对湛江海湾大桥进行了有限元分析和现场实测,测得了索-桥面的耦合振动.以上对实桥的测量验证了部分理论研究成果,但由于桥梁的运营和结构的庞大对其进行相应的实验研究相当困难,由此通过小型整体模型进行实验研究成为一种手段. Caetano等[126, 127]制作了珍岛 (Jindo) 桥(韩国)1:150的全桥模型,研究发现当几组拉索自然频率与整体结构的自然频率相近时将产生耦合现象,这时拉索将产生新的不同于非耦合状态的振动模态,而主梁和主塔的振动模态与非耦合状态较为相似.同时,通过振动台试验,发现斜拉索与整体振动的耦合可能减小主梁的响应,然而在狭窄的共振区某些拉索可能产生大幅振动,这种振动具有明显的非线性特性且可以激发高阶模态. Zuo 和 Li[128]制作了润扬长江大桥北汊桥全桥模型,测试了J13 号索在索-梁发生耦合时,记忆合金SMA 阻尼器能有效地控制拉索的振动,并减小加速度响应幅值.最近,El Ouni等[129]通过双悬臂试验模型研究了斜拉桥施工阶段,主梁和斜拉索的参数振动问题,研究发现索与主梁存在能量交换,特别是当激励幅值变大的时候,梁的响应变小而索的响应越来越大. 最后通过增加阻尼器的阻尼,有效减小拉索的振幅.赵跃宇课题组[107],最近制作了精细的斜拉桥全桥非线性振动试验模型(图10所示),观测到斜拉索、主梁和主塔间存在着丰富非线性耦合振动:不同激励频率下斜拉桥可发生整体、局部和全桥性耦合振动3种振动形式;相邻斜拉索耦合振动及索间的能量传递;共振时斜拉索、主梁和主塔均作大幅振动,且斜拉索两个响应频率之和正好等于激励频率;主梁和主塔大幅振动可改变某些斜拉索非线性振动特性,使其由"硬弹簧"变成"软弹簧"性质.

|
图10 斜拉桥实验模型 Fig.10 Bridge model |
实验研究越来越得到重视,但目前仍存在很多理论研究成果并未得到实验证实和一些新的实验现象及产生机理目前无法得到理论阐释这两类问题. 因此,斜拉桥全桥非线性振动的理论和实验研究还任重道远.
4 展望本文通过对近十年来国内外在斜拉桥非线性建模理论及动力学研究的总结,在该领域中,我们认为仍有诸多工作值得重视和进一步研究:
(1)考虑边界约束和弹性支承斜拉索的非线性振动问题
斜拉桥是一个高次超静定结构,在第一类问题的斜拉索非线性振动问题的研究中,几乎均以固定支撑或铰支为边界条件,少有涉及拉索对梁和塔刚度的影响以及梁和塔对拉索边界约束和弹性支承的考量,边界约束和弹性支承的刚度直接影响斜拉索的动力学特性,需要进行理论和实验研究.
(2)斜拉桥下部结构非线性振动
作为重要支承体系,斜拉桥下部结构所处场地土层特性多样、边界条件和受载情况复杂,而且动力响应中的桩-土耦合接触问题十分突出.克服现有土-结构动力相互作用和接触面弱化效应的理论局限性,建立桩(群桩)-$\!$土系统的精细化动力学模型,对于研究斜拉桥下部结构的非线性振动至关重要,同时将促进复杂载荷条件下斜拉桥大系统的动力学特性研究.
(3)斜拉桥大系统的非线性振动
近年来,国际国内学者对斜拉桥整桥非线性振动问题越来越重视,并建立各种各样的组合结构模型,据此开展了系列研究. 然而,通过模型实验研究和现场测试我们可以看到斜拉桥非线性振动行为的复杂性. 研究单根索与梁或塔间耦合振动问题并不能全面揭示斜拉桥的动力学行为. 斜拉桥中有多根对称拉索及相邻拉索的刚度是相等或相近的,从共振的角度看是相当复杂的. 因此,斜拉桥大系统的非线性振动问题有大量工作等待开展.
(4)高效有限元法
目前大型结构分析有限元商业软件发展迅速,但对于非线性问题的分析即使针对单个构件都相当困难,计算效率较低. 虽然我国计算机技术发展相当鼓舞人心,国内已建立三家国家级超级计算中心,但至今未见到针对斜拉桥全桥非线性振动问题的研究报道. 关键有两个问题没有很好解决:一是如何在计算中给定初始条件,初始条件是非线性振动响应计算的一个关键问题,另一个是如何提高超高自由度的计算效率.
(5)高维非线性动力学求解方法
高维非线性动力学求解方法问题不仅是斜拉桥动力学研究的瓶颈,也阻碍着大型旋转机械、高铁等其他工程问题的研究.动力学、振动与控制本身是力学的一个分支学科,虽然高维非线性动力学问题一直受到重视,除进行降维约化处理外,尚待有大的突破.
(6)斜拉桥大系统的随机振动
近年来虽有少数学者针对斜拉索及车-桥耦合振动等问题中的随机振动开展研究工作,工程实际中的环境激励大多可归结为随机振动问题,但针对斜拉桥的组合结构和全桥模型的随机振动问题研究并未见到相关报道,可以发展这方面的理论和进行相关的实验研究.
(7)斜拉桥振动能量采集与控制
目前,能量采集是世界范围内的热门课题,对于斜拉桥振动能量采集的研究才刚刚起步,如果将能量采集与振动控制相结合,将有利于大跨度斜拉桥的振动控制和超大跨度的桥梁发展.
| [1] | 埃尔莎·德·萨·卡埃塔诺. 斜拉桥的拉索振动与控制. 张德祥译. 北京:中国建筑工业出版社, 2012 (Caetano ETS. Cable Vibration in Cable-stayed Bridges. Zhang Dexiang, transl. Beijing: China Architecture & Building Press, 2012 (in Chinese)) |
| [2] | 王修勇, 陈政清, 倪一清. 斜拉桥拉索风雨振观测及其控制. 土木工程学报, 2003, 36(6): 53-59 (Wang Xiuyong, Chen Zhengqing, Ni Yiqing. Wind-rain induced vibration and its control on stay cables of cable-stayed bridges. China Civil Engineering Journal, 2003, 36(6):53-59 (in Chinese)) |
| [3] | Sofi A. Nonlinear in-plane vibrations of inclined cables carrying moving oscillators. Journal of Sound and Vibration, 2013, 332(7):1712-1724 |
| [4] | Tzanov VV, Krauskopf B, Neild SA. Vibration dynamics of an inclined cable excited near its second natural frequency. International Journal of Bifurcation and Chaos, 2014, 24(09): 1430024 |
| [5] | Lepidi M, Gattulli V. A parametric multi-body section model for modal interactions of cable-supported bridges. Journal of Sound and Vibration, 2014, 333(19): 4579-4596 |
| [6] | Wei M, Xiao Y, Liu H, et al. Nonlinear responses of a cable-beam coupled system under parametric and external excitations. Archive of Applied Mechanics, 2014, 84(2): 173-185 |
| [7] | Wang Z, Li T. Nonlinear dynamic analysis of parametrically excited space cable-beam structures due to thermal loads. Engineering Structures, 2015, 83: 50-61 |
| [8] | 夏禾, 张楠, 郭薇薇. 车桥耦合振动工程. 北京:科学出版社, 2014 (Xia He, Zhang Nan, Guo Weiwei. Coupling Vibration of Trainbridge System. Beijing: Science Press, 2014 (in Chinese)) |
| [9] | 李永乐, 赵凯, 吴梦雪等. 斜独塔混合梁斜拉桥风-汽车-桥梁系统耦合振动研究. 中国公路学报, 2012, 25(1): 47-54 (Li Yongle, Zhao Kai, Wu Mengxue, et al. Study of coupling vibration of windvehicle- bridge system for inclined single pylon cable-stayed bridge with hybrid girder. China Journal of Highway and Transport, 2012,25(1): 47-54 (in Chinese)) |
| [10] | Irvine HM. Cable Structures. The MIT Press, 1981 |
| [11] | 李国强,顾明,孙利民. 拉索振动、动力检测与振动控制理论. 北京: 科学出版社, 2014 (Li Guoqiang, Gu Ming, Sun Limin. Vibration, Dynamic Detection and Vibration Control Theory of Cable. Beijing: Science Press, 2014 (in Chinese)) |
| [12] | Rega G. Nonlinear vibrations of suspended cables-Part I: Modeling and analysis. Applied Mechanics Reviews, 2004, 57(6): 443-478 |
| [13] | Rega G. Nonlinear vibrations of suspended cables-part II: deterministic phenomena. Applied Mechanics Reviews, 2004, 57(6): 479-514 |
| [14] | 吴晓, 黎大志, 罗佑新. 斜拉索非线性固有振动特性分析. 振动与冲击, 2003, 22(3): 37-39 (Wu Xiao, Li Dazhi, Luo Youxin. Nonlinear natural vibration character analysis of stay cables. Journal of Vibration and Shock, 2003, 22(3): 37-39 (in Chinese)) |
| [15] | 赵跃宇, 周海兵, 金波等. 弯曲刚度对斜拉索非线性固有频率的影响. 工程力学, 2008, 25(1): 196-202 (Zhao Yueyu, Zhou Haibing, Jin Bo, et al. Influence of bending rigidity on nonlinear natural frequency of inclined cable. Engineering Mechanics, 2008, 25(1):196-202 (in Chinese)) |
| [16] | Kang HJ, Zhao YY, Zhu HP. Linear and nonlinear dynamics of suspended cable considering bending sti ness. Journal of Vibration and Control, 2015, 21(8): 1487-1505 |
| [17] | Lepidi M, Gattulli V. Static and dynamic response of elastic suspended cables with thermal e ects. International Journal of Solids and Structures, 2012, 49(9): 1103-1116 |
| [18] | 赵珧冰, 孙测世, 彭剑等. 不同初拉力拉索对温度变化的敏感性分析. 中南大学学报(自然科学版), 2014, 45(5): 1680-1685 (Zhao Yaobing, Sun Ceshi, Peng Jian, et al. Sensitivity analysis of di erent initial tension forces of suspended cable to temperature changes. Journal of Central South University (Science and Technology),2014, 45(5): 1680-1685 (in Chinese)) |
| [19] | 蔡东升. CFRP 索长大跨斜拉桥结构非线性动力学行为研究.[博士论文]. 镇江:江苏大学, 2013 (Cai Dongsheng. Research on nonlinear structural dynamic behaviors of long span cable-stayed bridge with CFRP cables. [PhD Thesis]. Zhengjiang: Jiangsu University,2014 (in Chinese)) |
| [20] | 李志江. 碳素纤维复合材料(CFRP) 斜拉索非线性振动特性和参数激励研究.[博士论文]. 武汉:华中科技大学, 2011 (Li Zhijiang. Study on nonlinear vibration properties and parametric excitations of CFRP stayed cables. [PhD Thesis]. Wuhan: Huazhong University of Science and Technology, 2011 (in Chinese)) |
| [21] | Wang LH, Zhao YY. Large amplitude motion mechanism and nonplanar vibration character of stay cables subject to the support motions. Journal of Sound and Vibration, 2009, 327(1-2): 121-133 |
| [22] | 孙测世, 王志搴, 赵珧冰等. 两端水平激励斜拉索面内非线性振动响应. 地震工程与工程振动, 2014, 34(6): 122-126(Sun Ceshi, Wang Zhiqian, Zhao Yaobing, et al. In-plane nonlinear vibrations of stayed cables under horizontal excitations. Earthquake Engineering and Engineering Dynamics, 2014, 34(6): 122-126 (in Chinese)) |
| [23] | 康厚军, 赵跃宇, 杨相展. 弯斜拉桥中拉索的主共振研究. 工程力学, 2008, 25(11): 68-91 (Kang Houjun, Zhao Yueyu, Yang Xiangzhan. Research on primary resonance of cables in curved cablestayed bridge. Engineering Mechanics, 2008, 25(11): 68-91 (in Chinese)) |
| [24] | 赵跃宇, 王涛, 康厚军. 斜拉索主参数共振的稳定性分析. 动力学与控制学报, 2008, 6(2): 112-117 (Zhao Yueyu, Wang Tao, Kang Houjun. Analysis of the stability of principal parametric resonance of stayed-cable. Journal of Dynamics and Control, 2008, 6(2): 112-117 (in Chinese)) |
| [25] | Ying ZG, Ni YQ, Ko JM. Parametrically excited instability of a cable under two support motions. International Journal of Structural Stability and Dynamics, 2006, 6(1): 43-58 |
| [26] | Tzanov VV, Krauskopf B, Neild SA. Vibration dynamics of an inclined cable excited near its second natural frequency. International Journal of Bifurcation and Chaos, 2014, 24(9):1430024 |
| [27] | 彭剑, 赵珧冰, 孙测世等. 磁流变阻尼器- 斜拉索控制系统中的时滞效应. 工程力学, 2014, 31(4): 155-159 (Peng Jian, Zhao Yaobing, Sun Ceshi, et al. Time delay e ects in MR amper-stay cable control systems. Engineering Mechanics, 2014, 31(4): 155-159 (in Chinese)) |
| [28] | 彭剑. 工程柔性结构振动控制中的时滞动力学研究.[博士论文]. 长沙:湖南大学, 2013 (Peng Jian. Time delay dynamics vibration control of flexible engineering structures. [PhD Thesis]. Changsha: Hunan University, 2013 (in Chinese)) |
| [29] | Gattulli V, Martinelli L, Perotti F, et al. Nonlinear oscillations of cables under harmonic loading using analytical and finite element models. Computer Methods in Applied Mechanics and Engineering,2004, 193(1): 69-85 |
| [30] | 王信. 索- 梁组合结构的建模与非线性有限元分析. [硕士论文]. 长沙:湖南大学, 2009(Wang Xin. Modeling and nonlinear analysis of cable-beam by finite element method. [Master Thesis]. Changsha: Hunan University, 2009 (in Chinese)) |
| [31] | 付英. 基础激励下桥梁斜拉索的非线性振动. 动力学与控制学报,2010, 8(1): 57-61 (Fu Ying. Nonlinear vibration of cables in cablestayed bridge under foundation excitation. Journal of Dynamics and Control, 2010, 8(1): 57-61 (in Chinese)) |
| [32] | Karoumi R. Some modeling aspects in the nonlinear finite element analysis of cable supported bridges. Computer and Structures, 1999,71(4): 397-412 |
| [33] | 胡建华, 王连华, 赵跃宇. 索结构几何非线性分析的悬链线索单元法. 湖南大学学报:自然科学版, 2007, 34(11): 29-32 (Hu Jianhua, Wang Lianhua, Zhao Yueyu. A catenary cable element for the nonlinear analysis of cable structures. Journal of Hunan University (Natural Sciences), 2007, 34(11): 29-32(in Chinese)) |
| [34] | 刘北辰. 工程计算力学理论与应用. 北京:机械工业出版社, 1994 (Liu Beichen. Theory and Application in Engineering Computational Mechanics. Beijing: China Machine Press, 1994 (in Chinese)) |
| [35] | Tang Jianmin, Shen Zuyan, Qian Ruojun. A nonlinear finite element method with five-node curved element for analysis of cable structures. In: Proceedings of IASS International Symposium, 1995, 2:929-935 |
| [36] | Vannemreddi S. Numerical modeling of stay cables and stay cable bridges. Northern Illinois University, 2010 |
| [37] | Nayfeh AH., Mook DT. Nonlinear Oscillations. JohnWiley & Sons,1979 |
| [38] | 陈予恕. 非线性动力学中的现代分析方法. 北京: 科学出版社,2000 (Chen Yushu. Modern Analysis Methods in Nonlinear Dynamics. Beijing: Science Press, 2000 (in Chinese)) |
| [39] | 胡海岩. 应用非线性动力学. 北京: 航空工业出版社,2000 (Hu Haiyan. Applied Nonlinear Dynamics. Beijing: Aviation Industry Press, 2000 (in Chinese)) |
| [40] | 刘延柱, 陈立群. 非线性振动. 北京:高等教育出版社, 2001 (Liu Yanzhu, Chen Liqun. Nonlinear Vibration. Beijing: Higher Education Press, 2001 (in Chinese)) |
| [41] | 王洪礼, 张琪昌, 郭树起等. 非线性动力学理论及其应用. 天津: 天津科学技术出版社, 2001 (Wang Hongli, Zhang Qichang, Guo Shuqi, et al. Nonlinear Dynamics Theory and its Application. Tianjing: Tianjin Science and Technology Press, 2001 (in Chinese)) |
| [42] | 张伟, 胡海岩. 非线性动力学理论与应用的新进展. 北京: 科学出版社, 2009 (Zhang Wei, Hu Haiyan. Advances of Research on Theory and Applications of Nonlin-ear Dynamics. Beijing: Science Press, 2009 (in Chinese)) |
| [43] | 高骏. 桥面激励下斜拉索的参数振动与减振研究. [硕士论文]. 哈尔滨:哈尔滨工业大学, 2012 (Gao Jun. Parametric vibration of stayd cable subjected to deck excitation and vibration reduction. [Master Thesis]. Harbin: Harbin Institute of Technology, 2012 (in Chinese)) |
| [44] | 康厚军, 赵跃宇. 索力对斜拉索动力特性的影响. 工程力学, 2010,27(6): 83-88 (Kang Houjun, Zhao Yueyu. E ects of initial tension ondynamic characteristics of stay cables. Engineering Mechanics,2010, 27(6): 83-88 (in Chinese)) |
| [45] | Kamel MM, Hamed YS. Nonlinear analysis of an elastic cable under harmonic excitation. Acta Mech, 2010, 214(3-4): 315-325 |
| [46] | 任爱娣, 张琪昌, 张良欣. 多尺度法的设解形式之探讨. 海军工程大学学报, 2006, 18(1): 11-14 (Ren Aidi, Zhang Qichang, Zhang Liangxin. Discussion of solutions supposed forms for method of multiple scales. Journal of Naval University of Engineering, 2006,18(1): 11-14 (in Chinese)) |
| [47] | Chen H, Xu Q. Bifurcations and chaos of an inclined cable. Nonlinear Dynamics, 2009, 57(1-2): 37-55 |
| [48] | Zhao YY, Sun CS, Wang ZQ, et al. Nonlinear in-plane free oscillations of suspended cable investigated by homotopy analysis method. Structural Engineering and Mechanics, 2015, 50(4): 487-500 |
| [49] | Nayfeh SA, Nayfeh AH, Mook DT. Nonlinear response of a taut string to longitudinal and transverse end excitation. Journal of Vibration and Control, 1995, 1(3): 307-334 |
| [50] | Hu J, Pai PF. Experimental study of resonant vibrations of suspended steel cables using a 3D motion analysis system. Journal of Engineering Mechanics, 2014, 138(6): 640-661 |
| [51] | Berlioz A, Lamarque CH. A non-linear model for the dynamics of an inclined cable. Journal of Sound and Vibration, 2005, 279(3):619-639 |
| [52] | Berlioz A, Lamarque CH. Nonlinear vibrations of an inclined cable. ASME Journal of Vibration and Acoustics, 2004, 127(4): 315-323 |
| [53] | Rega G, Srinil N, Alaggio R. Experimental and numerical studies of incl ined cables free and parametrically-forced vibrations. Journal of Theoretical and Applied Mechanics, 2008, 46(3): 621-640 |
| [54] | 陈丕华, 王修勇, 陈政清等. 斜拉索面内参数振动的理论和试验研究. 振动与冲击, 2010, 29(2): 50-53(Chen Pihua,Wang Xiuyong, Chen Zhengqing, et al. Theoretical and experimental study on planar parametric oscillations in a stayed-cable. Journal of Vibration and Shock, 2010, 29(2): 50-53 (in Chinese)) |
| [55] | Gonzalez-Buelga A, Neild S, Wagg D, et al. Modal stability of inclined cables subjected to vertical support excitation. Journal of Sound and Vibration, 2008, 318(3): 565-579 |
| [56] | Macdonald J, Dietz M, Neild S, et al. Generalised modal stability of inclined cables subjected to support excitations. Journal of Sound and Vibration, 2010, 329(21): 4515-4533 |
| [57] | Xu YL, Yu Z. Non-linear vibration of cable-damper systems part II: application and verification. Journal of Sound and Vibration, 1999,225(3): 465-481 |
| [58] | Gattulli V, Alaggio R, Potenza F. Analytical prediction and experimental validation for longitudinal control of cable oscillations. International Journal of Non-Linear Mechanics, 2008, 43(1): 36-52 |
| [59] | Faravelli L, Fuggini C, Ubertini F. Experimental study on hybrid control of multimodal cable vibrations. Meccanica , 2011, 46(5):1073-1084 |
| [60] | Jiang J, Li GQ, Lu Y. Vibration control of cables with damped flexible end restraint: Theoretical model and experimental verification. Journal of Sound and Vibration, 2013, 332(15): 3626-3645 |
| [61] | Alvarado CR, Carrion VF, Sarinana TA. Vibration reduction performance of an active damping control system for a scaled system of a cable-stayed bridge. International Journal of Structural Stability and Dynamics, 2015, 15(5): 1450077 |
| [62] | Ahmad J, Cheng SH. Analytical study on in-plane free vibration of a cable network with straight alignment rigid cross-ties. Journal of Vibration and Control, 2015, 21(7): 1299-1320 |
| [63] | Huang HW, Liu JY, Sun LM. Full-scale experimental verification on the vibration control of stay cable using optimally tuned MR damper. Smart Structures and Systems, An International Journal,2015, 16(6):1003-1021 |
| [64] | Grouthier C, Michelin S, Bourguet R, et al. On the e ciency of energy harvesting using vortex-induced vibrations of cables. Journal of Fluids and Structures, 2014, 49: 427-440 |
| [65] | 康厚军, 赵跃宇, 王连华. 斜拉桥中拉索对桥面动力特性的影响. 动力学与控制学报, 2007, 5(1): 44-49 (Kang Houjun, Zhao Yueyu, Wang Lianhua. Theoretical considerations for e ects of cables on deck of cable-stayed bridges. Journal of Dynamics and Control,2007, 5(1): 44-49 (in Chinese)) |
| [66] | Park NG, Lee S, Kim HK, et al. Vibration of initially stressed beam with discretely spaced multiple elastic supports. KSME International Journal, 2004, 18(5): 733-741 |
| [67] | Johansson C, Pacoste C, Karoumi R. Closed-form solution for the mode superposition analysis of the vibration in multi-span beam bridges caused by concentrated moving loads. Computers and Structures, 2013, 119: 85-94 |
| [68] | 赵跃宇, 马建军, 刘齐建等. 简谐横载荷作用下Winkler 地基上有限长梁1/3 次亚谐共振分析. 地震工程与工程振动, 2011, 31(3):148-153(Zhao Yueyu, Ma Jianjun, Liu Qijian, et al. 1/3 subharmonic resonance of finite-length beams on the Winkler foundation subjected to harmonic lateral loads. Journal of Earthquake Engineering and Engineering Vibration, 2011, 31(3): 148-153 (in Chinese)) |
| [69] | Wang LH, Ma JJ, Li LF, et al. Three-to-one resonant responses of inextensional beams on the elastic foundation. Journal of Vibration and Acoustics, 2013, 135(1): 48-65 |
| [70] | Mirghaderi R. Dynamic analysis of cable-stayed bridges. [PhD Thesis]. Purdue University, 1981 |
| [71] | Wang LH, Ma JJ, Peng J, et al. Large amplitude vibration and parametric instability of inextensional beams on the elastic foundation. International Journal of Mechanical Sciences, 2013, 67(1): 1-9 |
| [72] | Ouakad HM, Younis MI. Dynamic response of slacked singlewalled carbon nanotube resonators. Nonlinear Dynamics, 2012,67(2): 1419-1436 |
| [73] | 马建军. 土- 细长结构物相互作用的非线性动力学研究. [博士论文]. 长沙:湖南大学, 2012 (Ma Jianjun. Nonlinear dynamics response of the soil-slender structure system. [PhD Thesis]. Changsha: Hunan University, 2012 (in Chinese)) |
| [74] | Valsangkar AJ, Pradhanang R. Vibrations of beam-columns on twoparameter elastic foundations. Earthquake Engineering & Structural Dynamics, 1988, 16(2): 217-225 |
| [75] | Lai YC, Bing YT, Lee WS, et al. Dynamic response of beams on elastic foundation. Journal of Structural Engineering, 2014, 118(3):853-858 |
| [76] | Eisenberger M. Vibration frequencies for beams on variable oneand two-parameter elastic foundations. Journal of Sound and Vibration,1994, 176(5): 577-584 |
| [77] | Morfidis K. Vibration of Timoshenko beams on three-parameter elastic foundation. Computer and Structures, 2010, 88: 294-308 |
| [78] | Pellicano F, Vakakis AF. Normal Modes and Boundary Layers for a Slender Tensioned Beam on a Nonlinear Foundation. Springer Netherlands, 2001 |
| [79] | Coskun I, Engin H. Non-linear vibrations of a beam on an elastic foundation. Journal of Sound Vibration, 1999, 223(3): 335-354 |
| [80] | Zhu B, Leung AYT. Linear and nonlinear vibration of non-uniform beams on two-parameter foundations using p-elements. Computers & Geotechnics, 2009, 36(5): 743-750 |
| [81] | Nayfeh AH, Nayfeh SA. Nonlinear normal modes of a continuous system with quadratic nonlinearities. ASME Journal of Vibration and Acousttics, 1995, 117(2), 199-205 |
| [82] | Li R, Gong J. Analysis of laterally loaded pile in layered soils. Electronic Journal of Geotechnical Engineering, 2008, 13: 1-16 |
| [83] | Naggar MHE, Novak M. Nonlinear model for dynamic axial pile response. Journal of Geotechnical Engineering, 1994, 120(2): 308-329 |
| [84] | Rovithis EN, Pitilakis KD, Mylonakis GE. Seismic analysis of coupled soil-pile-structure systems leading to the definition of a pseudonatural SSI frequency. Soil Dynamics and Earthquake Engineering,2009, 29(6): 1005-1015 |
| [85] | Soneji BB, Jangid RS. Influence of soil-structure interaction on the response of seismically isolated cable-stayed bridge. Soil Dynamics & Earthquake Engineering, 2008, 28(4): 245-257 |
| [86] | Chau KT, Yang X. Nonlinear interaction of soil-pile in horizontal vibration. Journal of Engineering Mechanics, 2005, 131(8): 847-858 |
| [87] | Ma J, Peng J, Gao X, et al. Effect of soil-structure interaction on the nonlinear response of an inextensional beam on elastic foundation. Archive of Applied Mechanics, 2014, 85(2): 273-285 |
| [88] | 吕建根, 韩强, 王荣辉. 地震作用下非弹性地基桩的3次超谐波 共振. 动力学与控制学报, 2015, 13(4): 278-282 (Lü Jiangen, Han Qiang, Wang Ronghui. Super-harmonic resonance of pile foundation under earthquake action. Journal of Dynamics and Control,2015, 13(4): 278-282 (in Chinese)) |
| [89] | Fujino Y, Warnitchai P, Pacheco BM. An experimental and analytical study of autoparametric resonance in a 3DOF model of cablestayed- beam. Nonlinear Dynamics, 1993, 4(2): 111-138 |
| [90] | Gimsing NJ. Cable Supported Bridges. Wiley, 1983 |
| [91] | Xia Y, Fujino Y. Auto-parametric vibration of a cable-stayed-beam structure under random excitation. Journal of Engineering Mechanics,2006, 132(3): 279-286 |
| [92] | 赵跃宇. 大跨径斜拉桥非线性动力学的模型与理论研究. [博士 论文]. 长沙:湖南大学, 2000 (ZhaoYueyu.Study of the nonlinear dynamical modeling theory of long-span cable-stayed bridge. [PhD Thesis]. Changsha: Hunan University, 2000 (in Chinese)) |
| [93] | 赵跃宇, 蒋丽忠, 王连华等. 索-梁组合结构的动力学建模理论及 其内共振分析. 土木工程学报, 2004, 37(3): 69-72(Zhao Yueyu, Jiang Lizhong, Wang Lianhua, et al.The dynamical modeling theory and internal resonance of cable-beam composite structure. China Civil Engineering Journal,2004,37(3):69-72 (in Chinese)) |
| [94] | 周海兵. 索- 梁组合结构非线性动力学实验研究. [博士论文]. 长沙:湖南大学, 2007 (Zhou Haibin.The experimental investigation on nonlinear dynamics of cable-beam structure. [PhD Thesis]. Changsha: Hunan University, 2007 (in Chinese)) |
| [95] | Fung RF, Lu LY, Huang SC. Dynamic modelling and vibration analysis of a flexible cable-stayed beam structure. Journal of Sound and Vibration, 2002, 254(4): 717-726 |
| [96] | Gattulli V, Lepidi M. Nonlinear interactions in the planar dynamics of cable-stayed beam. International Journal of Solids and Structures,2003, 40(18): 4729-4748 |
| [97] | 周粉霞. 索- 梁结构面内面外非线性耦合振动分析. [硕士论 文]. 武汉: 武汉理工大学, 2008 (Zhou Fenxia. Nonlinear in-plane and out-of-plane coupled vibration analysis of cable-beam structure. [Master Thesis]. Wuhan: Wuhan University of Technology, 2008 (in Chinese)) |
| [98] | 郭少进. 索- 梁结构非线性振动分析. [硕士论文]. 武汉: 武汉理 工大学, 2007 (Guo Shaojin. Nonlinear vibration analysis of cablebeam structure. [Master Thesis]. Wuhan: Wuhan University of Technology, 2007 (in Chinese)) |
| [99] | Fung RF, Lu LY, Huang SC. Dynamic modelling and vibration analysis of a flexible cable-stayed beam structure. Journal of Sound and Vibration, 2002, 254(4): 717-726 |
| [100] | Wei MH, Xiao YQ, Liu HT. Bifurcation and chaos of a cable- beam coupled system under simultaneous internal and external resonances. Nonlinear Dynamics, 2012, 67(3): 1969-1984 |
| [101] | Wei MH, Xiao YQ, Liu HT, et al. Nonlinear responses of a cablebeam coupled system under parametric and external excitations. Archive of Applied Mechanics, 2014, 84(2): 173-185 |
| [102] | 梁栋, 孙利民, 程纬等. 斜拉桥主梁振动对拉索阻尼器减振效果 的影响. 力学学报, 2009, 41(4): 563-574 (Liang Dong, Sun Limin, Cheng Wei, et al. Effect of girder's vibration on performance of cable dampers for cable-stayed bridges. Chinese Journal of Theoretical and Applied Mechanics, 2009, 41(4): 563-574 (in Chinese)) |
| [103] | Wang ZQ, Sun CS, Zhao YY, et al. Modeling and nonlinear modal characteristics of the cable-stayed beam. European Journal of Mechanics -A/Solids, 2014, 47: 58-69 |
| [104] | 赵垗冰. 考虑温度效应的索梁结构建模及动力特性研究. [博士论 文]. 长沙:湖南大学, 2015 (Zhao Yaobing. Temperature effects on modeling and vibration properties of cable-stayed structures. [PhD Thesis]. Changsha: Hunan University, 2015 (in Chinese)) |
| [105] | Deng HQ, Li TJ, Xue BJ. Analysis of thermally induced vibration of cable-beam structures. Structural Engineering and Mechanics,2015, 53(3): 443-453 |
| [106] | 王涛, 沈锐利. 基于动力非线性有限元法的索-梁相关振动研究. 振动与冲击, 2015, 34(5): 159-167 (Wang Tao, Shen Ruili. Cablebeam vibration study with nonlinear dynamic FEM. Journal of Vibration and Shock. 2015, 34(5): 159-167 (in Chinese)) |
| [107] | 孙测世. 大跨度斜拉桥非线性振动试验研究. [博士论文]. 长沙: 湖南大学, 2015 (Sun Ceshi. Experimental study of nonlinear vibrations of long-span cable-stayed bridge. [PhD Thesis]. Changsha: Hunan University, 2015 (in Chinese)) |
| [108] | 吕建根, 赵跃宇, 王荣辉. 索拱组合结构的动力建模及其内共振 分析. 中南大学学报:自然科学版, 2010, 41(1): 316-321 (Lü Jiangen, Zhao Yueyu, Wang Ronghui. Dynamical modeling and internal resonance of cable-stayed arch structure. Journal of Central South University (Science and Technology),2010, 41(1): 316-321 (in Chinese)) |
| [109] | Kang HJ, Zhao YY, Zhu HP. Out-of-plane free vibration analysis of a cable-arch structure. Journal of Sound and Vibration, 2013,332(4): 907-921 |
| [110] | Zhao YY, Kang HJ. In-plane free vibration analysis of cable-arch structure. Journal of Sound and Vibration, 2008, 312(3): 363-379 |
| [111] | Virlogeux M. Cable vibration in cable-stayed bridges. Bridge Dynamics,1998, 56(2): 213-233 |
| [112] | 亢战, 钟万勰. 斜拉桥参数共振问题的数值研究. 土木工程学报,1998, 31(4): 14-22 (Kang Zhan, ZhongWanxie. Numerical study on parameteric resonance of cable in cable stayed bridge. China Civil Engineering Journal , 1998, 31(4): 14-22 (in Chinese)) |
| [113] | 张妍, 王怀磊, 杨杰. 斜拉桥索- 面- 塔三自由度非线性振动模 型及其1:2:1 内共振分析. 动力学与控制学报, 2010, 8(1): 62-66 (Zhang Yan, Wang Huailei, Yang Jie. Dynamics of a three degrees of freedom nonlinear vibration model of cables and bridge decks and towers with the frequency 1:2:1 internal resonance. Journal of Dynamics and Control, 2010, 8(1): 62-66 (in Chinese)) |
| [114] | 汪至刚, 孙炳楠. 斜拉桥参数振动引起的拉索大幅振动. 工程力 学, 2001, 18(1): 103-109 (Wang Zhigang, Sun Bingnan. Cable vibration for cable stayed bridge by parametric response. Engineering Mechanics, 2001, 18(1): 103-109 (in Chinese)) |
| [115] | 陈水生, 孙炳楠. 斜拉桥索- 桥耦合非线性参数振动数值研究. 土木工程学报, 2003, 36(4): 70-75 (Chen Shuisheng, Sun Bingnan. Numerical study on nonlinear parametric vibration of coupled cables and brid ge decks. China Civil Engineeringjournal, 2003,36(4): 70-75 (in Chinese)) |
| [116] | 任淑琰. 斜拉桥拉索参数振动研究. [博士论文]. 上海: 同济大学,2007 (Ren Shuyan. Parametric oscillation of cables in cable-stayed bridges. [PhD Thesis]. Shanghai:Tongji University, 2007 (in Chinese)) |
| [117] | 周岱, 柳杰, 郭军慧等. 轴向激励下斜拉索大幅振动分析. 工程力 学, 2007, 24(3): 34-41 (Zhou Dai, Liu Jie, Guo Junhui, et al. Vibration response of cables in cable-stayed spatial structures under axial excitation. Engineering Mechanics, 2007, 24(3): 34-41 (in Chinese)) |
| [118] | 谭长建, 祝兵. 大跨度斜拉桥索与桥面耦合振动分析. 西南交通 大学学报, 2007, 42(6): 726-731 (Tan Changjian, Zhu Bing. Coupled vibration analysis of bridge deck and cable of long-span cablestayed bridge. Journal of Southwest Jiaotong University, 2007,42(6): 726-731 (in Chinese)) |
| [119] | 郭翠翠. 斜拉索非线性参数振动与振动控制.[硕士论文]. 武汉: 华中科技大学, 2008 (Guo Cuicui. Nonlinear parametric vibration and vibration control of stay cables. [Master Thesis]. Wuhan: Huazhong University of Science and Technology, 2008 (in Chinese)) |
| [120] | 彭然. 桥面激励下斜拉索非线性耦合振动研究. [硕士论文]. 哈 尔滨:哈尔滨工业大学, 2013 (Peng Ran. A research on nonlinear vibration of stayed cable subjected to deck excitation. [Master Thesis]. Harbin: Harbin Institute of Technology, 2013 (in Chinese)) |
| [121] | 汪峰, 文晓旭, 刘章军. 斜拉桥塔- 索- 桥面连续耦合参数振动 特性分析. 应用力学学报, 2015, 32(2): 340-346 (Wang Feng, Wen Xiaoxu, Liu Zhangjun. Coupled vibration analysis of tower-cabledeck of long-span cable-stayed bridge. Chinese Journal of Applied Mechanics, 2015, 32(2): 340-346 (in Chinese)) |
| [122] | 赵跃宇, 王涛, 康厚军等. 斜拉桥双索与桥面耦合的非线性参数振 动特性分析. 湖南大学学报: 自然科学版, 2008, 35(10): 1-5 (Zhao Yueyu, Wang Tao,Kang Houjun,et al. Performance study of the nonlinear parametric vibration of coupled bridge decks and two cables. Journal of Hunan University(Natural Sciences), 2008, 35(10):1-5 (in Chinese)) |
| [123] | Ren WX, Peng XL, Lin YQ. Experimental and analytical studies on dynamic characteristics of a large span cable-stayed bridge. Engineering Structures , 2005, 27(4): 535-548 |
| [124] | Caetano E, Cunha A, Gattulli V, et al. Cable-deck dynamic interactions at the International Guadiana Bridge: On-site measurements and finite element modelling. Structural Control & Health Monitoring,2008, 15(3): 237-264 |
| [125] | 魏晓军. 大跨度斜拉桥索-桥耦合振动分析与实验. [硕士论文]. 长沙:中南大学, 2011 (Wei Xiaojun. Coupled vibration analysis and experiment of cable-bridge in large span cable-stayed bridge. [Master Thesis]. Changsha: Central South University, 2011 (in Chinese)) |
| [126] | Caetano E, Cunha A, Taylor CA. Investigation of dynamic cable interaction in a physical model of a cable-stayed bridge. Part I: modal analysis. Earthquake Engineering & Structural Dynamics, 2000,29(4): 481-498 |
| [127] | Caetano E, Cunha A, Taylor CA. Investigation of dynamic cabledeck interaction in a physical model of a cable-stayed bridge. Part II: seismic response. Earthquake Engineering & Structural Dynamics,2000, 29(4): 499-521 |
| [128] | Zuo XB, Li AQ. Numerical and experimental investigation on cable vibration mitigation using shape memory alloy damper. Structural Control & Health Monitoring, 2011, 18(1): 20-39 |
| [129] | Ouni MHE, Kahla NB, Preumont A. Numerical and experimental dynamic analysis and control of a cable stayed bridge under parametric excitation. Engineering Structures, 2012, 45: 244-256 |
 2016, Vol. 48
2016, Vol. 48