数字图像相关方法 [1] 已发展成为一种实用可靠的光学测量手段,在科研和工业领域广泛用于形貌和变形的全场测量 [2, 3, 4, 5, 6, 7]. 数字图像相关的基本原理是通过在参考图中选择子区,依据相关准则在目标图中获得精确的匹配位置,从而测量全场变形. 数字图像相关技术要求试件表面有足够的纹理特征,所以经常需要在试件表面制造散斑图案. 散斑图案对数字图像相关的计算精度有重要的影响. 通过优化散斑图案从而提高数字图像相关的计算精度是非常吸引人的想法,将优化的散斑图与水转印技术 [8] 的结合可以进一步提升数字图像相关技术的易用性,然而至今仍然没有统一的标准化散斑制作标准. 散斑制作标准的提出首先要依赖散斑质量评价体系的建立,而散斑质量评价体系则建立在对数字图像相关中误差深入分析的基础之上. 数字图像相关技术的典型位移测量精度在百分之几像素,测量误差受到诸多因素的影响,如图像噪声 [9]、形函数匹配 [10]、亚像素优化算法 [11]、相关计算策略 [12] 和插值精度 [13],插值在数字图像相关中起着关键性作用. 20 世纪八九十年代研究人员即在数字图像相关实验中观测到亚像素位移存在周期为 1 像素的类似于正弦形式的偏差可达百分之六个像素的周期性系统偏差 [14]. 其后 Schreier [13] 发现这种周期性系统偏差的原因是相关计算为了达到亚像素的测量精度,需要对图像亚像素位置进行灰度插值,由于插值不可能完全重构图像的原始信息,会引起相关计算亚像素位置测量的周期性系统偏差,称为插值偏差. Schreier 同时指出,可以通过图像亚像素平移的相关计算来估计插值偏差的量级. 此后,研究者们从各个方面提出减小插值偏差的手段,首先是提升插值算法,研究发现高阶的插值方法虽然通常具有更高的精度,但是计算时间更长,所以更好的手段是优化插值基函数,从而在引入很少额外计算量的情况下提高精度 [1],进一步的,改良 B 样条插值算法的引入进一步减小了插值偏差 [15, 16];另一方面,有学者 [17, 18] 提出对原始散斑图事先采用低通滤波处理,低通滤波可以将插值偏差急剧减小到可忽略的程度,但是遗憾的是图像细节的丢失会降低相关计算结果的空间分辨率;在图像处理领域,Rohde [19] 提出采用相关函数的积分形式代替求和形式,并通过随机积分方法近似相关函数的积分,取得了良好的效果.
虽然研究者提出了诸多减少插值偏差的手段,但插值偏差与散斑形状,插值算法的直接依赖关系至今仍然不清楚,插值偏差为什么随亚像素平移量呈正弦形式? 是否可以通过设计优化统计参数的散斑图,降低插值偏差,提高数字图像相关测量精度? 这些问题被研究者们共同关注 [20, 21]. 然而由于插值问题数学上较难处理,相关本质上又是非线性优化问题,所以定性讨论居多,定量研究比较少. 值得一提的是 Wang [22] 的工作,他基于最小平方距离准则,通过图像采样点的值估计了线性和三次多项式插值时图像平移的插值偏差,然而,Wang 的理论不适用于精度较高的 B 样条插值 [13] 和 OMOMS 插值 [15],由于包含亚像素位置灰度真实值与插值值之间的误差,故而其结果难以用于优化散斑形状,插值方法评判等问题的理论分析.
当前估计插值偏差的标准做法是采用模拟散斑图 [11],或者采用频谱平移 [13] 等数值方法生成一系列亚像素平移的散斑图,然后通过数字图像相关程序求出每一个阶段的插值偏差. 如果能从理论上找出插值偏差与散斑图样插值算法的关系,那么既能直观给出插值偏差的物理机制,又能简洁方便的估计偏差大小. 可以给出散斑图质量评估,给散斑图的设计带来方便.
类似的问题不仅出现在数字图像相关中,在图像处理 [19]、计算机视觉 [23]、卫星遥感测量 [24] 等领域对图像进行亚像素匹配的过程中,也发现插值偏差的存在. 虽然研究背景不同,采用的相关准则不同,但对于匹配过程非采样点的插值都会引入系统性偏差,这是一个具有一般性的问题.
值得注意的是形函数欠匹配也会引起系统误差 [10],但由于本文讨论平移情况,所以系统误差仅包括插值偏差. 以往数字图像相关中关于插值偏差的研究都是基于空域,考虑到插值偏差随亚像素平移量呈类似于正弦形式的变化,从频域入手可能是更好的手段. 本文针对亚像素插值偏差问题,基于频域傅里叶分析的方法,通过理论模拟和实验手段开展了图像平移情况下亚像素插值偏差的研究. 论文的结构如下:第 1 部分介绍数字图像相关和卷积型插值的基本原理,随后采用傅里叶分析,基于最小平方距离准则推导出一维情况插值偏差的具体形式,并通过一维模拟散斑的亚像素模拟平移验证了理论分析;第 2 部分,推导了高维插值偏差的解析形式,提出了一种通过散斑频谱快速估计插值偏差的算法,讨论了计算模板对估计精度的影响并通过模拟进行了验证;第 3 部分进行了讨论和总结.
1 一维插值偏差理论分析及模拟验证 1.1 数字图像相关的基本原理数字图像相关的基本原理是通过在参考图选择图像子区,采用 Newton–Raphson 或者 Levenberg–Marquardt 方法等非线性优化算法对相关准则进行最优化获得目标图像中的位置,来获得全场的变形. 相关准则通常有最大互相关准则 (CC) 和最小平方距离准则 (SSD) 两类,本文着重讨论 SSD 准则的运用.
1.2 卷积型插值插值是用已知函数 $f\left( x \right)$ 的采样值 $f\left[x \right]$,去构造函数 ${f_T}\left( x \right)$ 近似 $f\left( x \right)$ 的过程. 当前以采样定理为基础的卷积型插值,由于使用简便,性能优异而被广泛应用. 卷积型插值方法根据给定的插值基函数 $r\left( x \right)$,构造一组平移函数基 ${\rm{ }}\left\{ {r{\rm{ }}(x{\rm{ }}.{\rm{ }}k)|{\rm{ }}k{\rm{ }} \in Z} \right\}$,将 $f\left( x \right)$ 对这组基投影得到 ${f_T}\left( x \right)$
| ${f_T}\left( x \right) = \sum\limits_{k = - \infty }^\infty {{c_k}r\left( {x - k} \right)} $ | (1) |
其中插值系数 ${c_k}$ 选择满足 $f[n] = {f_T}(n)$. 式 (1) 也可以等价表述为
| ${f_T}\left( t \right) = \sum\limits_{n = - \infty }^\infty {f\left[k \right]\varphi \left( {t - k} \right)} $ | (2) |
$r(x)$ 和 $\varphi (x)$ 的关系参见文献 [25]. 被广泛采用的 Keys 插值,B 样条插值和 OMOMS 插值均属卷积型插值 [25],本文的研究也基于卷积型插值算法.
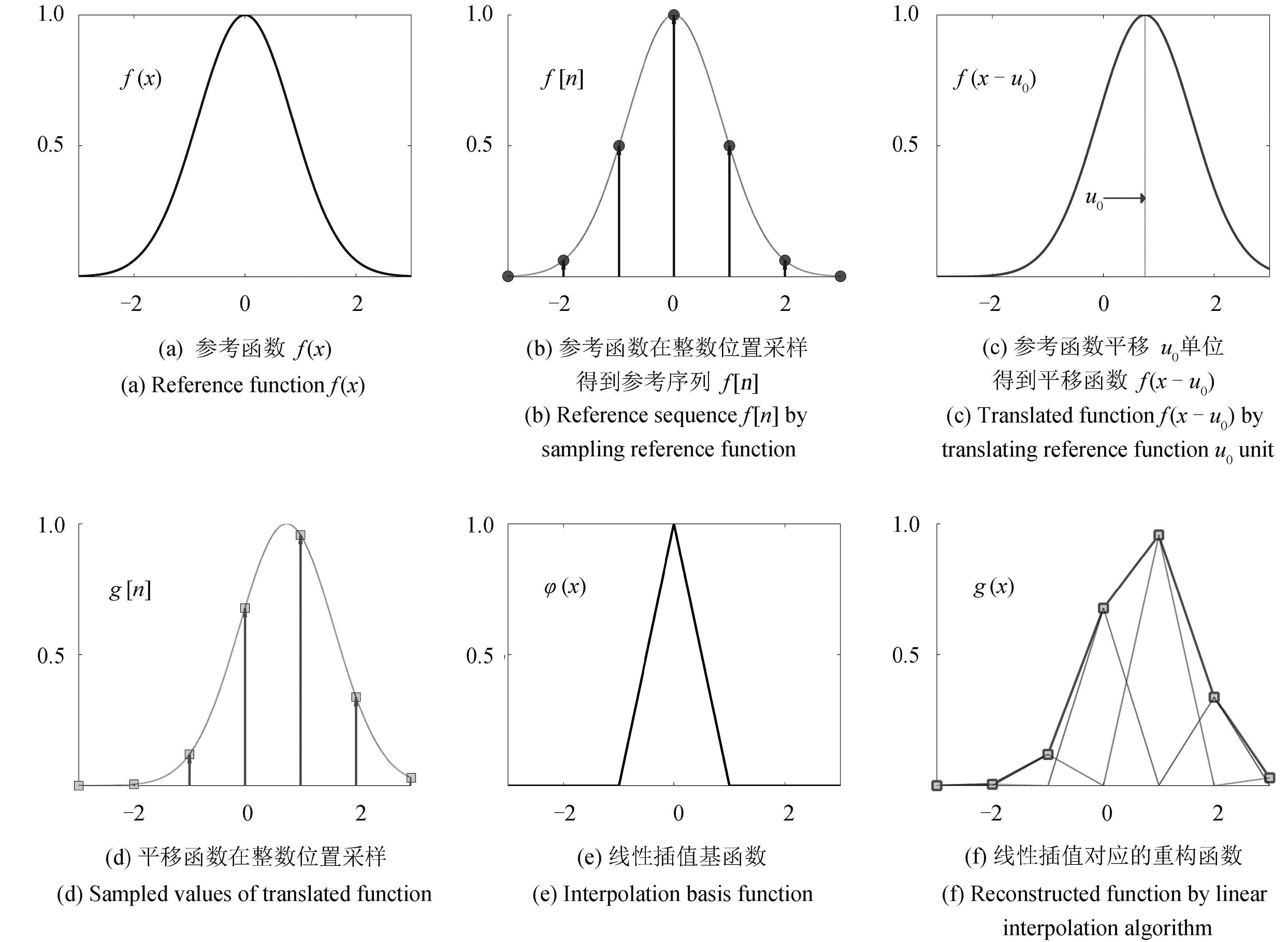
1.3 一维插值偏差的傅里叶分析图1(a) 描述了定义域为 $( - \infty ,\infty )$ 的一维连续函数 $f(x)$,称之为参考函数,对于有限定义域的函数可以通过补 0 延拓. $f(x)$ 采样 (图1(b)) 后得到参考序列 $f[n] = f(n)$,如图1(c) 所示将 $ f(x) $ 沿 $ x $ 轴正方向平移 $ {u_0} $ 单位得到平移函数 $ f(x - {u_0}) $,平移函数采样 (图1(d)) 得到目标序列 $ g[n] = f(n - {u_0}) $. 若插值基函数为 $ \varphi (x) $ (图1(e) 显示了线性插值的基函数),由式 (2) 重构的目标函数
|
图 1 模拟平移实验过程 Fig.1 Simulating translation |
| $g\left( x \right) = \sum\limits_{k = - \infty }^\infty {g\left[n \right]\varphi \left( {x - n} \right)} $ | (3) |
图1(f) 显示了线性插值对应的重构函数. 我们采用最小平方距离准则 (SSD),那么数字图像相关估计的位移 $ u $ 满足
| $u = {\rm{argmin}}\sum\limits_{n = - \infty }^\infty {{{\left[{f\left( n \right) - g\left( {n + u} \right)} \right]}^2}} $ | (4) |
由于插值缺陷 (图1(c) 和 1(f)),估计位移 $ u $ 包含插值偏差 $ {u_{\rm{e}}} $,给出 $ {u_{\rm{e}}} $ 与 $ f(x) $ 和 $ \varphi (x) $ 的依赖关系即是本节目标.
通过帕萨瓦尔定理 (Parseval’s theorem) 将式 (4) 化为频域的积分
| $\left. \matrix{ {\rm{ }}u = {\rm{argmin}}\int_{ - 1/2}^{1/2} {{{\left| {\hat F\left( \nu \right) - \hat G\left( \nu \right)} \right|}^2}{\rm{d}}\nu } \hfill \cr \hat F\left( \nu \right) = \sum\limits_{n = - \infty }^\infty {f\left( n \right){{\rm{e}}^{ - {\rm{j}}2\pi \nu n}}} \hfill \cr \hat G\left( \nu \right) = \sum\limits_{n = - \infty }^\infty {g\left( {n + u} \right){{\rm{e}}^{ - {\rm{j}}2\pi \nu n}}} \hfill \cr} \right\}$ | (5) |
其中,$\hat F\left( v \right)$ 和 $\hat G\left( v \right) $ 分别表示 $ f(x) $ 和 $ g(x) $ 的离散时间傅里叶变换 (discrete-time Fourier transform,DTFT). 设 $ f(x) $ 的傅里叶变换 $\;\hat f\left( v \right) = \int\limits_{ - \infty }^\infty {f\left( x \right){{\rm{e}}^{ - {\rm{j}}2\pi \nu x}}{\rm{d}}x} $,由泊松求和公式 (Poisson summation formula)
| $\hat F\left( \nu \right) = \sum\limits_{m = - \infty }^\infty {\hat f\left( {\nu - m} \right)} $ | (6) |
为了将 $\hat G\left( \nu \right)$ 用 $\; \hat f\left( \nu \right) $ 表示,需要 $\; \hat f\left( \nu \right) $ 与 $\hat g\left( \nu \right) = \displaystyle\int_{ - \infty }^\infty {g\left( x \right){{\rm{e}}^{ - {\rm{j}}2{\pi} \nu x}}{\rm{d}}x} $ 之间的关系. $ g(x) $ 由 $ f(x) $ 经平移,采样,插值而得,平移 (图1(c)) 对应于频域的相移,采样 (图1(d)) 对应于频谱的平移叠加,插值 (图1(f)) 对应于频域与插值传递函数 $\hat \varphi \left( \nu \right)$ 相乘,如果用 $\overset{\mathbb{F}}{\longleftrightarrow}$ 表示傅里叶变换对,上述过程可以表示为
| $\left. \begin{align} & f\left( x \right)\overset{\mathbb{F}}{\longleftrightarrow}\hat{f}\left( \nu \right) \\ & f\left( x-{{u}_{0}} \right)\overset{\mathbb{F}}{\longleftrightarrow}{{\text{e}}^{-\text{j}2\pi \nu {{u}_{0}}}}\hat{f}\left( \nu \right) \\ & f\left( x-{{u}_{0}} \right)\text{comb}\left( x \right)\overset{\mathbb{F}}{\longleftrightarrow}\sum\limits_{k=-\infty }^{\infty }{{{\text{e}}^{-\text{j}2\pi \left( \nu -k \right){{u}_{0}}}}\hat{f}\left( \nu -k \right)} \\ & g\left( x \right)=\varphi \left( x \right)*\left[ f\left( x-{{u}_{0}} \right)\text{comb}\left( x \right) \right]\overset{\mathbb{F}}{\longleftrightarrow} \\ & \quad \quad \hat{\varphi }\left( \nu \right)\sum\limits_{k=-\infty }^{\infty }{{{\text{e}}^{-\text{j}2\pi \left( \nu -k \right){{u}_{0}}}}\hat{f}\left( \nu -k \right)} \\ \end{align} \right\}$ | (7) |
其中 ${\mathop{\rm comb}\nolimits} \left( x \right) = \displaystyle\sum\limits_{k = - \infty }^\infty {\delta \left( {x - k} \right)} $ 表示梳状函数,再次使用泊松求和公式
| $\eqalign{ & \hat G\left( \nu \right) = \sum\limits_{m = - \infty }^\infty {{{\text{e}}^{{\text{j}}2\pi \left( {\nu - m} \right)u}}\hat \varphi \left( {\nu - m} \right)} \cdot \cr & \sum\limits_{k = - \infty }^\infty {{{\text{e}}^{ - {\text{j}}2\pi \left( {\nu - k} \right){u_0}}}\hat f\left( {\nu - k} \right)} \cr} $ | (8) |
将式 (6) 和 (8) 代入式 (5)
| $\left. \begin{align} & u=\text{argmin}\Gamma \left( u \right) \\ & \Gamma \left( u \right)=\int_{-1/2}^{1/2}{[-\sum\limits_{k=-\infty }^{\infty }{\hat{f}\left( \nu -k \right)}\cdot } \\ & \sum\limits_{n=-\infty }^{\infty }{{{\text{e}}^{\text{j}2\pi \left( \nu -n \right){{u}_{0}}}}{{{\hat{f}}}^{*}}\left( \nu -n \right)}\cdot \\ & \sum\limits_{n=-\infty }^{\infty }{{{\text{e}}^{-\text{j}2\pi \left( \nu -m \right)u}}{{{\hat{\varphi }}}^{*}}\left( \nu -m \right)}. \\ & \sum\limits_{n=-\infty }^{\infty }{{{\text{e}}^{-\text{j}2\pi \left( \nu -tn \right){{u}_{0}}}}\hat{f}\left( \nu -n \right)}\cdot \sum\limits_{m=-\infty }^{\infty }{{{\text{e}}^{\text{j}2\pi \left( \nu -m \right)u}}}\cdot \\ & \hat{\varphi }\left( \nu -m \right)+\sum\limits_{{{m}_{1}}=-\infty }^{\infty }{\sum\limits_{{{m}_{2}}=-\infty }^{\infty }{{{\text{e}}^{\text{j}2\pi \left( {{m}_{2}}-{{m}_{1}} \right)u}}}}\cdot \\ & \hat{\varphi }\left( \nu -{{m}_{1}} \right){{{\hat{\varphi }}}^{*}}\left( \nu -{{m}_{2}} \right)\cdot \\ & \sum\limits_{{{n}_{1}}=-\infty }^{\infty }{\sum\limits_{{{n}_{2}}=-\infty }^{\infty }{{{\text{e}}^{\text{j}2\pi \left( {{n}_{1}}-t{{n}_{2}} \right){{u}_{0}}}}}}\cdot \\ & \hat{f}\left( \nu -{{n}_{1}} \right){{{\hat{f}}}^{*}}\left( \nu -{{n}_{2}} \right)]\text{d}\nu \\ \end{align} \right\}$ | (9) |
式 (9) 是最小平方距离准则式 (4) 的频域表示,式 (9) 中积分函数前两项对应于空域的互相关 $ - 2\sum\limits_{k = - \infty }^\infty {f\left( n \right)g\left( {n + u} \right)} $,第三项对应 $\displaystyle\sum\limits_{n = - \infty }^\infty {{g^2}\left( {n + u} \right)} $.
如果 $ \Gamma (u) $ 足够光滑,估计位移 $ u $ 满足
| ${\Gamma ^\prime }\left( u \right) = 0$ | (10) |
估计位移 $ u = u{}_0 + {u_{\rm{e}}} $,考虑到插值偏差 $ {u_{\rm{e}}} $ 是小量,在一阶近似下
| ${\Gamma ^\prime }\left( {{u_0}} \right) + {\Gamma ^{\prime \prime }}\left( {{u_0}} \right){u_{\text{e}}} \approx 0$ | (11) |
可以得到插值偏差 $ {u_{\rm{e}}} $ 与参考函数频谱 $\hat f\left( \nu \right)$ 插值传递函数 $\; \hat \varphi \left( \nu \right)$ 之间的关系
| $\left. \matrix{ {u_{\rm{e}}} \approx - {{{\Gamma ^\prime }\left( {{u_0}} \right)} \over {{\Gamma ^{\prime \prime }}\left( {{u_0}} \right)}} \hfill \cr \Gamma '\left( {{u_0}} \right) = {\rm{j}}2\pi \mathop \smallint \nolimits_{ - 1/2}^{1/2} \left[ {\sum\limits_{k = - \infty }^\infty {\hat f\left( {\nu - k} \right)} \cdot } \right. \hfill \cr \sum\limits_{m = - \infty }^\infty {\sum\limits_{n = - \infty }^\infty {{{\rm{e}}^{{\rm{j}}2\pi \left( {m - tn} \right){u_0}}}} } \left( {\nu - m} \right){{\hat f}^*}\left( {\nu - n} \right) \cdot \hfill \cr {{\hat \varphi }^*}\left( {\nu - m} \right) - \sum\limits_{k = - \infty }^\infty {{{\hat f}^*}\left( {\nu - k} \right)} \cdot \hfill \cr \sum\limits_{m = - \infty }^\infty {\sum\limits_{n = - \infty }^\infty {{{\rm{e}}^{ - {\rm{j}}2\pi \left( {m - n} \right){u_0}}}\left( {\nu - m} \right)} } \cdot \hfill \cr \hat f\left( {\nu - n} \right)\hat \varphi \left( {\nu - m} \right) + \hfill \cr \sum\limits_{{n_1} = - \infty }^\infty {\sum\limits_{{n_2} = - \infty }^\infty {\sum\limits_{{m_1} = - \infty }^\infty {\mathop \sum \limits_{{m_2} = - \infty }^\infty } } } {{\rm{e}}^{{\rm{j}}2\pi \left( {{n_1} - {n_2} + {m_2} - {m_1}} \right){u_0}}} \cdot \hfill \cr \left( {{m_2} - {m_1}} \right)\hat f\left( {\nu - {n_1}} \right){{\hat f}^*}\left( {\nu - {n_2}} \right) \cdot \hfill \cr \left. {\hat \varphi \left( {\nu - {m_1}} \right){{\hat \varphi }^*}\left( {\nu - {m_2}} \right)} \right]{\rm{d}}\nu \hfill \cr \Gamma ''\left( {{u_0}} \right) = 4{\pi ^2}\int_{ - 1/2}^{1/2} {\mathop \sum \limits_{k = - \infty }^\infty } \hat f\left( {\nu - k} \right) \cdot \hfill \cr \sum\limits_{m = - \infty }^\infty {\sum\limits_{n = - \infty }^\infty {{{\rm{e}}^{{\rm{j}}2\pi \left( {m - n} \right){u_0}}}{{\left( {\nu - m} \right)}^2}{{\hat f}^*}\left( {\nu - n} \right)} } \cdot \hfill \cr {{\hat \varphi }^*}\left( {\nu - m} \right) + \sum\limits_{k = - \infty }^\infty {{{\hat f}^*}\left( {\nu - k} \right)} \cdot \hfill \cr \sum\limits_{m = - \infty }^\infty {\sum\limits_{n = - \infty }^\infty {{{\rm{e}}^{ - {\rm{j}}2\pi \left( {m - n} \right){u_0}}}{{\left( {\nu - m} \right)}^2}\hat f\left( {\nu - n} \right)} } \cdot \hfill \cr \hat \varphi \left( {\nu - m} \right) - \sum\limits_{{n_1} = - \infty }^\infty {\sum\limits_{{n_2} = - \infty }^\infty {\sum\limits_{{m_1} = - \infty }^\infty {\mathop \sum \limits_{{m_2} = - \infty }^\infty } } } \hfill \cr {{\rm{e}}^{{\rm{j}}2\pi \left( {{n_1} - t{n_2} + {m_2} - {m_1}} \right){u_0}}}{\left( {{m_2} - {m_1}} \right)^2} \hfill \cr \hat f\left( {\nu - {n_1}} \right){{\hat f}^*}\left( {\nu - {n_2}} \right)\hat \varphi \left( {\nu - {m_1}} \right) \cdot \hfill \cr \left. {{{\hat \varphi }^*}\left( {\nu - {m_2}} \right)} \right]{\rm{d}}\nu \hfill \cr} \right\}$ | (12) |
本文称式 (12) 为插值偏差的完全估计.
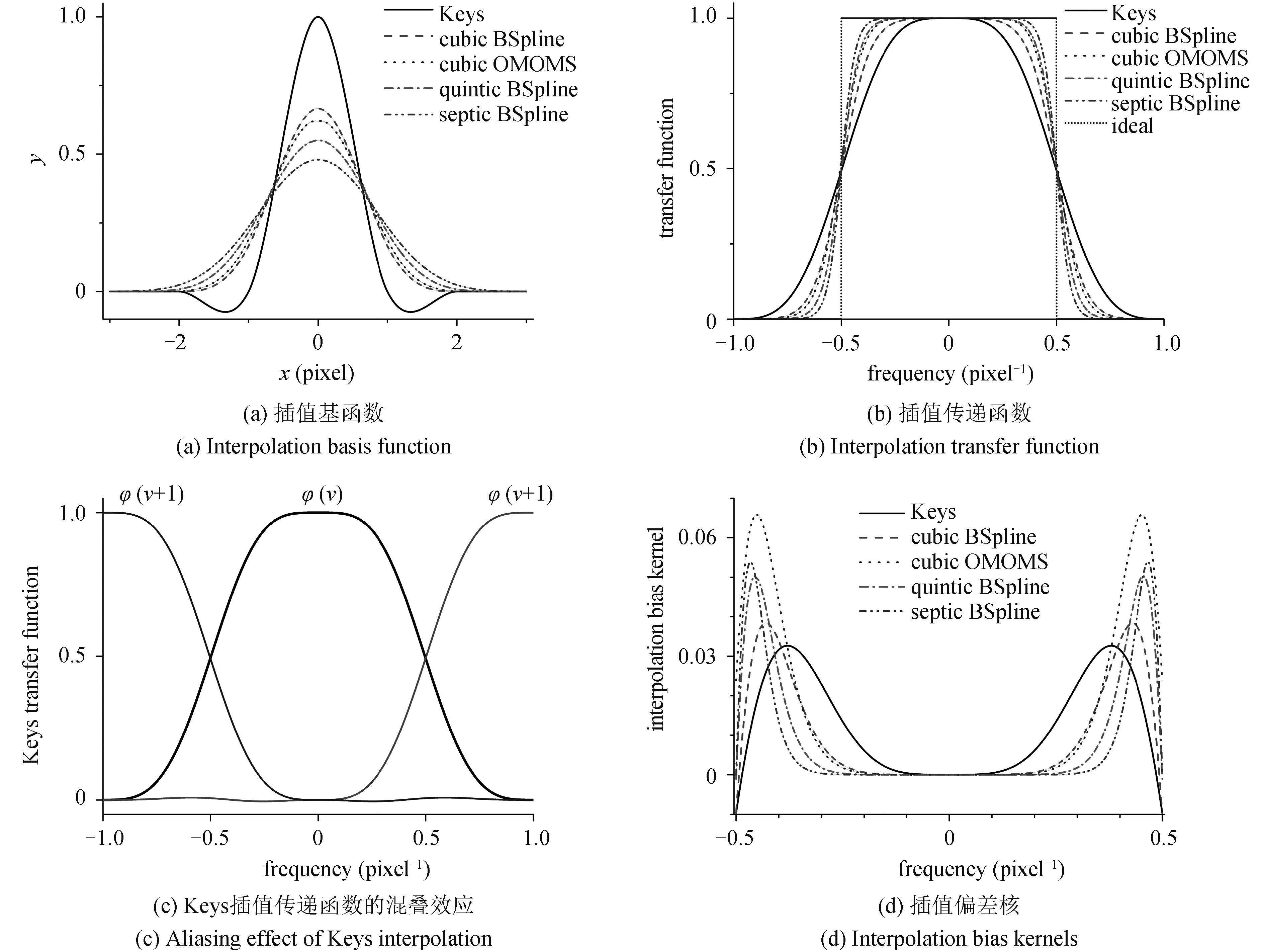
插值偏差的完全估计数学形式比较复杂,不便于计算也不便于物理意义的观察,我们致力于将式 (12) 进行简化. $\Gamma ''\left( {{u_0}} \right)$ 是周期为 1 的周期函数且包含直流分量,考虑到 $\hat \varphi \left( \nu \right)$ 是理想低通滤波的近似 (图2(b))
|
图 2 Fig.2 |
| \begin{equation} \Gamma ''\left( {{u_0}} \right) \approx 4{\pi ^2}\int_{ - 1/2}^{1/2} {{\nu ^2}\left( {\hat \varphi \left( \nu \right) + {{\hat \varphi }^*}\left( \nu \right)} \right){{\left| {\hat f\left( \nu \right)} \right|}^2}{\rm{d}}\nu } \end{equation} | (13) |
$\Gamma '\left( {{u_0}} \right) $ 也是周期为 1 的周期函数,然而即使进行傅里叶级数展开 $\Gamma '\left( {{u_0}} \right) = \displaystyle\sum\limits_{m = - \infty }^\infty {{a_m}{{\rm{e}}^{{\rm{j}}2\pi m{u_0}}}} $ 傅里叶系数仍然比较复杂,更好的策略应该是在一定条件下对其进行简化. 对于数字系统通常要求有足够的采样频率以满足采样定理,故而带限函数是常用的假设;实际使用中插值基函数均是偶函数,故而插值传递函数满足 $\hat \varphi \left( \nu \right) = {\hat \varphi ^*}\left( \nu \right)$. 基于带限函数假设和传递函数为实数的事实.
| $\left. \begin{align} & {{u}_{\text{e}}}\approx u-\frac{{\Gamma }'\left( {{u}_{0}} \right)}{{\Gamma }''\left( {{u}_{0}} \right)} \\ & {\Gamma }'\left( {{u}_{0}} \right)=-4\pi \int_{-1/2}^{1/2}{u}\left\{ \sum\limits_{m=-\infty }^{\infty }{\left( \nu -m \right)\hat{\varphi }\left( \nu -m \right)\cdot } \right. \\ & \sin \left( 2\pi m{{u}_{0}} \right)+\frac{1}{2}\sum\limits_{{{m}_{1}}=-\infty }^{\infty }{\underset{\text{ }{{m}_{2}}=-\infty }{\overset{\infty }{\mathop \sum }}\,} \\ & \left( {{m}_{2}}-{{m}_{1}} \right)\hat{\varphi }\left( \nu -{{m}_{1}} \right)\cdot \\ & \left. \hat{\varphi }\left( \nu -{{m}_{2}} \right)\sin \left[ 2\pi \left( {{m}_{2}}-{{m}_{1}} \right){{u}_{0}} \right] \right\} \\ & {\Gamma }''\left( {{u}_{0}} \right)\approx 8{{\pi }^{2}}\int_{-1/2}^{1/2}{{{\nu }^{2}}\hat{\varphi }\left( \nu \right){{\left| \hat{f}\left( \nu \right) \right|}^{2}}\text{d}\nu } \\ \end{align} \right\}$ | (14) |
本文称式 (14) 为插值偏差的带限近似. $\Gamma ''\left( {{u_0}} \right) $ 与灰度梯度平方和有关,$\Gamma '\left( {{u_0}} \right) $ 的积分表达式由两部分组成,第一部分 $\sum\limits_{m = - \infty }^\infty {\left( {\nu - m} \right)\hat \varphi \left( {\nu - m} \right)} \sin \left( {2\pi m{u_0}} \right) + \frac{1}{2}\sum\limits_{{m_1} = - \infty }^\infty {\sum\limits_{{m_2} = - \infty }^\infty {\left( {{m_2} - {m_1}} \right)} } \hat \varphi \left( {v - {m_1}} \right)\hat \varphi \left( {v - {m_2}} \right)\sin \left[{2\pi \left( {{m_2} + {m_1}} \right)} \right.{u_0}$ 由插值算法决定,是以亚像素平移 $ u{}_0 $ 为自变量的各阶正弦谐波叠加,而第二部分 ${\left| {\hat f\left( \nu \right)} \right|^2} $ 是参考函数的功率谱. 注意到插值传递函数 $\hat \varphi \left( \nu \right) $ 具有低通滤波的性质,而积分区域是能奎斯特频率 (Nyquist frequency) 决定的 [–0.5,0.5],可以仅考虑 $\hat \varphi \left( \nu \right)$ 和 $\hat \varphi \left( {\nu \pm 1} \right) $ 这 3 项的作用,同时我们只考虑基频的影响,那么
| $\left. \begin{align} & \text{ }{{u}_{\text{e}}}\approx C\sin 2\pi {{u}_{0}} \\ & C=\frac{1}{2\pi }\{\int\limits_{-1/2}^{1/2}{\left[ \left( \nu -1 \right)\hat{\varphi }\left( \nu -1 \right)-\left( \nu +1 \right) \right.} \\ & \left. \hat{\varphi }\left( \nu +1 \right)+\hat{\varphi }\left( \nu \right)\hat{\varphi }\left( \nu +1 \right)+\hat{\varphi }\left( \nu \right)\hat{\varphi }\left( \nu -1 \right) \right] \\ & {{\left| \hat{f}\left( \nu \right) \right|}^{2}}\text{d}\nu \}/\int_{-1/2}^{1/2}{{{\nu }^{2}}\hat{\varphi }\left( \nu \right){{\left| \hat{f}\left( \nu \right) \right|}^{2}}\text{d}\nu } \\ \end{align} \right\}$ | (15) |
式中,$ C $ 是仅由参考函数 $\; \hat f\left( \nu \right) $ 和插值算法 $\hat \varphi \left( \nu \right)$ 决定的常数,本文称式 (15) 为插值偏差的正弦近似.
插值偏差的正弦近似解释了众所周知的插值偏差 $ u{}_{\rm e} $ 随平移量 $ u{}_0 $ 呈正弦变化的现象 [13],直观给出了插值偏差振幅 $ C $ 与参考函数 $\hat f\left( \nu \right) $ 和插值算法 $\hat \varphi \left( \nu \right)$ 的直接依赖关系,${\left| {\hat f\left( \nu \right)} \right|^2}$ 给出了参考函数的功率谱,因子 $\left( {\nu - 1} \right)\hat \varphi \left( {\nu - 1} \right) - \left( {\nu + 1} \right)\hat \varphi \left( {\nu + 1} \right) + \hat \varphi \left( v \right)\hat \varphi \left( {\nu + 1} \right) + \hat \varphi \left( \nu \right)\hat \varphi \left( {\nu - 1} \right)$ 单纯由插值算法本身决定,表征了特定频率的插值偏差响应,本文称为插值偏差核 $ {E_{{\rm{ib}}}}(v) $.
| ${\text{ }}{E_{{\text{ib}}}}\left( \nu \right) = \left( {\nu - 1} \right)\hat \varphi \left( {\nu - 1} \right) - \left( {\nu + 1} \right)\hat \varphi \left( {\nu + 1} \right) + \hat \varphi \left( \nu \right)\hat \varphi \left( {\nu + 1} \right) + \hat \varphi \left( \nu \right)\hat \varphi \left( {\nu - 1} \right)$ | (16) |
图2 给出了 Keys 插值,三次 B 样条,三次 OMOMS,五次 B 样条,七次 B 样条等插值算法的插值基函数 (图2(a)),插值传递函数 $\hat \varphi \left( \nu \right)$ (图2(b)) 和插值偏差核 $ {E_{{\rm{ib}}}}(v) $ (图2(d)),由于考虑带限函数,$ {E_{{\rm{ib}}}}(v) $ 的频率范围为 –0.5 至 0.5 (频率 0.5 对应图像空间周期为两像素). $ {E_{{\rm{ib}}}}(v) $ 呈双峰对称分布,低频基本为 0,而后随着频率增大呈正相关,至特定频率达到极大值后减小,$ {E_{{\rm{ib}}}}(v) $ 的函数形式定量解释了学者观察到图像高频成分对插值偏差起主要贡献的现象 [13]. 不同的插值算法具有不同的插值偏差核 $ {E_{{\rm{ib}}}}(v) $,考虑到通常图像能量集中在低频,可以认为在低频附近 $ {E_{{\rm{ib}}}}(v) $ 越小,插值偏差通常也就越小. 比较同样是三次插值的 Keys 算法,B 样条和 OMOMS 算法,对于 $\left| v \right|$ < 0.394 的低频范围 $E_{{\rm{ib}}}^{{\rm{Keys}}}\left( \nu \right) > E_{{\rm{ib}}}^{{\rm{BSpline}}}\left( \nu \right)$,类似的当 $\left| v \right|$ < 0.349 时 $E_{{\rm{ib}}}^{{\rm{BSpline}}}\left( \nu \right) > E_{{\rm{ib}}}^{{\rm{OMOMS}}}$,故而研究者发现插值精度通常 OMOMS > BSpline > Keys[1, 15]. 提高 B 样条插值阶数可以使 $ {E_{{\rm{ib}}}}(v) $ 对于更宽广的低频范围具有几近为 0 的频率响应,从而具有更高的精度,这也与以往的研究结果一致 [13],插值偏差核的概念很好解释了以往学者关于插值精度的研究成果,表明了 $ {E_{{\rm{ib}}}}(v) $ 决定了插值算法用于相关匹配的优劣. 非理想插值往往包含低通滤波和混叠效应 (图2(b)),插值传递函数 $ \varphi (v) \ne 1,\left| {v} \right| < 0.5 $ 对应于低通滤波效应,$ \varphi (v) \ne 0,\left| {v} \right| > 0.5$ 对应于混叠效应. 考虑到对参考函数低通滤波可以有效减小插值偏差,插值偏差产生的原因为插值对采样引起的高频分量的混叠效应,从式 (15) 也可验证,图2(c) 给出了 Keys 插值算法的传递函数 $\hat \varphi \left( {v} \right) $ 以及对应的 $\hat \varphi \left( {v - 1} \right) $ 和 $\hat \varphi \left( {\nu + 1} \right) $,由于插值的混叠效应 $ \hat \varphi \left( {\nu - 1} \right)$ 和 $ \hat \varphi \left( {\nu + 1} \right)$ 在式 (15) 的积分区间 [–0.5,0.5] 之间不为 0,从而插值偏差核 $ {E_{{\rm{ib}}}}\left( v \right) \ne 0$ 引起插值偏差.
插值偏差的理论公式可以根据参考函数和插值算法直接估计插值偏差,免去了传统手段生成一系列亚像素位移散斑图和相关计算的繁琐. 插值偏差理论可以进一步优化插值算法,OMOMS 算法虽然在渐近意义上最优,然而并不意味最适用于数字图像相关,而且可以根据不同类型的散斑图优化不同的插值算法. 插值偏差理论可以解释低通滤波减小插值偏差 [17, 18] 的现象,对滤波模板的选取也能给予一定的指导意义. 插值偏差理论可以进一步用于散斑评价标准的建立和散斑图案设计.
1.4 一维模拟散斑验证本节通过一维散斑验证理论分析的准确性. 一维散斑的生成参见文献 [11],散斑颗粒为高斯散斑. 如果散斑的中心位置为 ${x_k}$,散斑半径为 $ r $,中心亮度为 $ {I_0} $,那么参考函数为
| $f\left( x \right) = \sum\limits_{k{\kern 1pt} = {\kern 1pt} 0}^N {{I_0}\exp \left[{ - \frac{{{{\left( {x - {x_k}} \right)}^2}}}{{{r^2}}}} \right]} $ | (17) |
其对应的频谱
| $\hat f\left( \nu \right) = {I_0}\sqrt \pi r{{\text{e}}^{ - {\pi ^2}{r^2}{\nu ^2}}}\sum\limits_{k{\kern 1pt} = {\kern 1pt} 0}^N {{{\text{e}}^{ - {\text{j}}2\pi \nu {x_k}}}} $ | (18) |
频谱的贡献分为两部分,一部分是高斯散斑基元 ${{\rm{e}}^{ - {x^2}/{r^2}}}$ 的傅里叶变换,另外一部分由散斑中心位置 ${x_k}$ 决定.
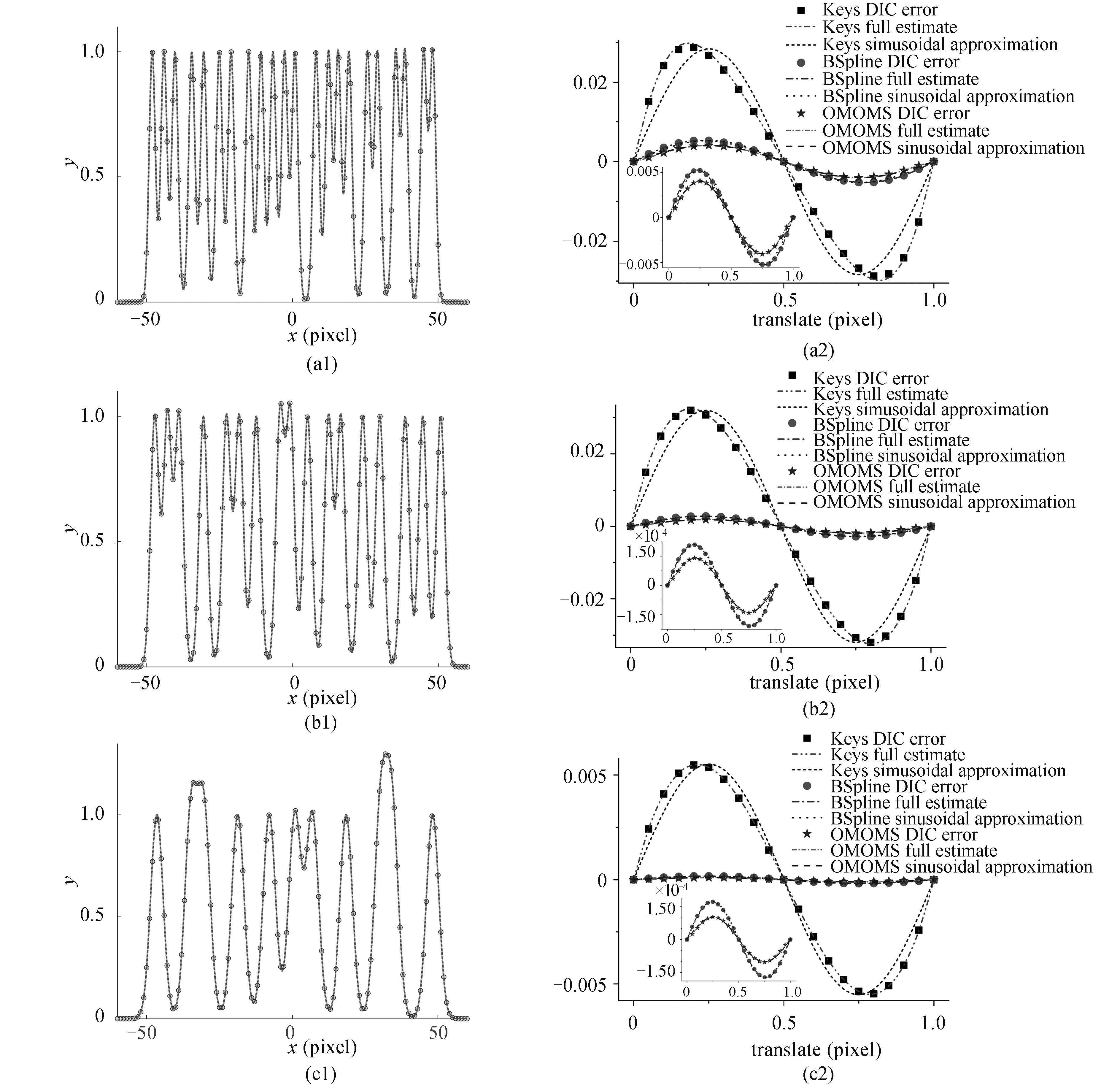
本文固定散斑中心亮度 ${I_0} = 1$,散斑随机分布在 (–50,50) 间,保证占空比为 65%,生成了半径分别为 1.5,2.0,3.0 的一维散斑,图3 (a1)(b1)(c1) 显示了参考函数 $f(x)$ 的形式及采样点的值,为了消除量化误差,整像素点采样值用浮点值表达的准确函数值;模拟平移每次将散斑中心 ${x_k}$ 向右平移 0.05,共移动 1 个像素;相关计算采用 0 阶形函数,依据最小平方距离准则通过正向高斯牛顿法 [26] 进行非线性优化,收敛准则要求相邻两次相关误差小于 1×10–10,相关模板选择为 [–60,60] 共 121 个点,插值分别采用 Keys 插值,三次 B 样条插值,三次 OMOMS 插值算法;偏差估计包含完全估计 (式 (12)) 和正弦近似 (式 (15)),完全估计中的无限求和取 –10 到 10 近似,积分采用增量步为 1×10–6 的梯形法做数值积分近似.
|
图 3 一维模拟散斑和插值偏差曲线,图(a1)(b1)(c1)分别显示了半径为1.5, 2.0, 3.0的一维模拟散斑,图(a2)(b2)(c2)给出了半径分别为1.5, 2.0, 3.0的模拟散斑采用Keys、三次B样条、三次OMOMS插值算法数字图像相关计算得到的插值偏差曲线以及采用完全估计(式12)和正弦近似(式15)的理论估计结果,由于Keys算法的插值偏差远大于其他两种,小图单独显示了B样条和OMOMS的插值偏差。 Fig.3 1-d synthetic speckle and interpolation bias. (a1)(b1)(c1) Speckle patterns of radius 1.5, 2.0, 3.0 respectively. (a2)(b2)(c2) Digital image correlation error, full estimate of interpolation bias (Eq. (12)) and sinusoidal approximation of interpolation bias (Eq. (15)) of speckle patterns with radius 1.5, 2.0, 3.0 respectively, the subfigures only show results of BSpline and OMOMS because the bias of Keys interpolation is much more significant. |
图3 (a2)(b2)(c2) 对于 Keys 插值,三次 B 样条插值和三次 OMOMS 插值,分别给出了数字图像相关计算结果,插值偏差完全估计结果 (式 (12)),以及插值偏差正弦近似 (式 (15)) 结果,由于 Keys 插值算法的插值偏差远大于三次 B 样条插值和三次 OMOMS 插值,在小图中将三次 B 样条和三次 OMOMS 算法的结果单独显示. Keys 插值算法插值偏差的完全估计与 DIC 的计算结果一致,正弦近似由于忽略了高频分量在细节上有所丢失,然而量级保持一致;三次 B 样条和 OMOMS 算法数字图像相关计算误差同样与理论上完全估计的结果完全吻合,且与正弦近似的结果保持高度一致,本文的估计理论与数字图像相关计算结果很好的吻合.
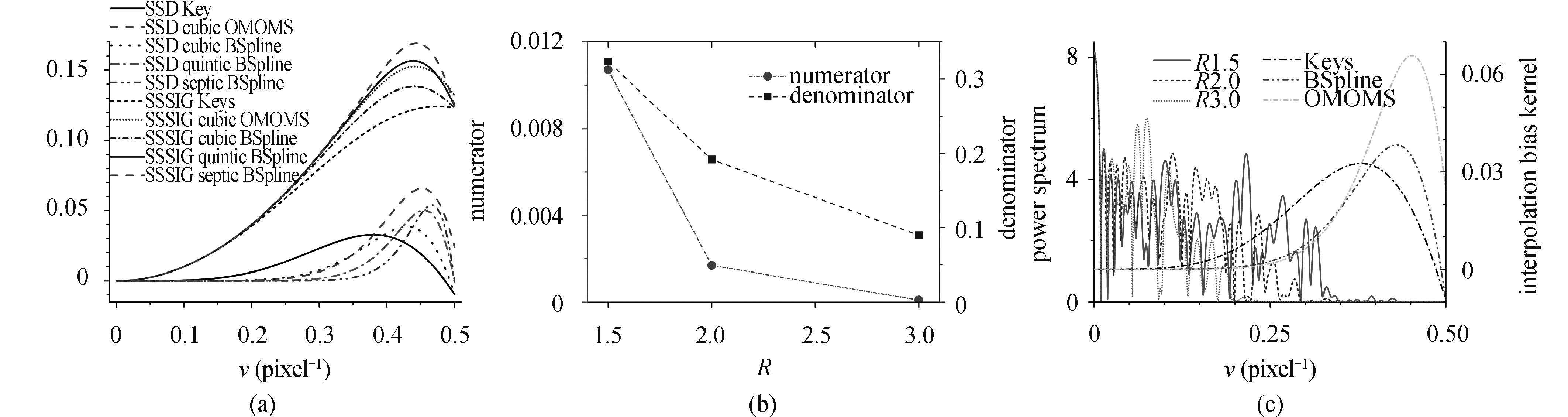
模拟结果表明插值偏差随散斑颗粒减小而增大,对相同的散斑插值偏差 Keys >> BSpline > OMOMS,上述现象可用插值偏差核 ${E_{{\rm{ib}}}}(v)$ 予以直观的解释. 式 (15) 中分子和分母对结果均有影响,图4(a) 绘制了分子和分母对于特定频率的响应,可见分母的数值远远大于分子,这与插值偏差通常是小量的观察是一致的. 虽然分母数值远远大于分子,但是如图4(b) 所示,分子的变化率是远远大于分母的,故而式 (15) 中分子取决定性作用,插值偏差可以看作主要由函数功率谱 ${\left| {\hat f\left( \nu \right)} \right|^2}$ 与插值偏差核 ${E_{{\rm{ib}}}}(v)$ 乘积的积分决定. 图4(c) 绘制了半径为 1.5,2.0,3.0 一维散斑的功率谱 (对数显示) 和 Keys 插值、三次 B 样条插值、三次 OMOMS 对应的插值偏差核 ${E_{{\rm{ib}}}}(v)$,由于对称性仅显示 [0,0.5] 区间. 散斑半径的减小对应于空间周期的收缩会引起频域的扩展,考虑到插值偏差核在高频响应比较大,故而引起插值误差的增大. 如图4(c) 所示,半径为 3.0 的散斑能量集中在 0.25 之下的低频部分,此时 B 样条和 OMOMS 插值偏差核基本为 0,所以采用 B 样条插值或者 OMOMS 算法插值误差仅有万分之一的量级 (如图3(c2) 局部放大图);半径为 2.0 的散斑在频域扩展,在 0.35 的频率处才趋于 0,此时插值偏差增大,B 样条和 OMOMS 插值偏差达到千分之一量级 (图3(b2)),而 Keys 算法达到 0.15 个像素 (图3(b2));对于散斑半径为 1.5 的情况,高频量更多,在 0.44 的频率都可以观察到具有能量分布,于是插值偏差进一步增大. 虽然当频率大于 0.35 的时候 OMOMS 插值方法对于 B 样条插值偏差核更大,然而由于绝大部分能量集中在低频域,而 OMOMS 在低频域具有更好的低频响应,所以 OMOMS 的插值算法仍然要优于 B 样条. 如果高频能量特别多,OMOMS 优于 B 样条优于 Keys 插值算法不一定成立,这需要具体问题具体分析.
|
图 4 (a) 式(15)中分子和分母的频率响应; (b) 式(15)中分子分母数值随散斑半径的变化;(c) 半径为1.5, 2.0, 3.0的模拟散斑的功率谱和Keys插值,三次B样条插值,三次OMOMS插值对应的插值偏差核,功率谱由对数表示。 Fig.4 (a) Frequency response of the numerator and denominator in Eq. (15); (b) The values of the numerator and denominator in Eq. (15) with respect to speckle radius; (c)Power spectrum (in logarithm scale) of speckle patterns with radius 1.5, 2.0, 3.0 and interpolation bias kernel. |
一维散斑的模拟证明,在函数频谱已知的情况下,采用本文的理论可以精确的估计插值偏差.
2 数字图像相关中插值偏差估计 2.1 高维情况插值偏差理论估计实际的数字图像相关和数字体相关是二维和三维情况,所以有必要将一维理论推广到高维. 在高维情况下,坐标和位移,频谱是向量,即一阶张量. 对于 $N$ 维空间,设参考函数为 $f( x)$,其对应的傅里叶变换为 $\; \hat f\left( { \nu } \right)$,真实位移为 ${ u}_0$,插值计算误差为 ${{ u}_{\rm{e}}}$,插值基函数为 $\varphi ( x)$,插值传递函数为 $\hat \varphi \left( { \nu} \right)$,采用类似于一维的推导思路,将求导化为变分,可以得到计算误差 ${{ u }_{\rm{e}}}$ 满足方程
| $\eqalign{ & \int_\Omega {[\sum\limits_k {\sum\limits_m {\sum\limits_n {{{\text{e}}^{{\text{j}}2\pi \left( {m - n} \right) \cdot {u_0}}}} {{\hat \varphi }^*}\left( {\nu - m} \right)} } } \cdot \cr & \hat f\left( {\nu - k} \right){{\hat f}^*}\left( {\nu - n} \right)\left( {\nu - m} \right) - \cr & \sum\limits_k {\sum\limits_m {\sum\limits_n {{{\text{e}}^{ - {\text{j}}2\pi \left( {m - n} \right) \cdot {u_0}}}} \hat \varphi \left( {\nu - m} \right)} } \cdot \cr & {{\hat f}^*}\left( {\nu - k} \right)\hat f\left( {\nu - n} \right)\left( {\nu - m} \right) + \cr & \sum\limits_{{n_1}} {\sum\limits_{{n_2}} {\sum\limits_{{m_1}} {\sum\limits_{{m_2}} {{{\text{e}}^{{\text{j}}2\pi \left( {{m_2} - {m_1} + t{n_1} - t{n_2}} \right) \cdot {u_0}}}} } } } \cr & \hat \varphi \left( {\nu - {m_1}} \right){{\hat \varphi }^*}\left( {\nu - {m_2}} \right)\hat f\left( {\nu - {n_1}} \right) \cdot \cr & {{\hat f}^*}\left( {\nu - {n_2}} \right)\left( {{m_2} - {m_1}} \right)]{\text{d}}\nu = \cr & {\text{j}}2\pi {\text{ }}\{ \int_\Omega {[\sum\limits_k {\sum\limits_m {\sum\limits_n {{{\text{e}}^{{\text{j}}2\pi \left( {m - tn} \right) \cdot {u_0}}}} {{\hat \varphi }^*}\left( {\nu - m} \right)} } } \cdot \cr & \hat f\left( {\nu - k} \right){{\hat f}^*}\left( {\nu - n} \right)\left( {\nu - m} \right) \otimes \left( {\nu - m} \right) - \cr & \sum\limits_k {\sum\limits_m {\sum\limits_n {{{\text{e}}^{ - {\text{j}}2\pi \left( {m - tn} \right) \cdot {u_0}}}} \hat \varphi \left( {\nu - m} \right)} } \cr & {{\hat f}^*}\left( {\nu - k} \right)\hat f\left( {\nu - n} \right)\left( {\nu - m} \right) \otimes \left( {\nu - m} \right) + \cr & \sum\limits_{{n_1}} {\sum\limits_{{n_2}} {\sum\limits_{{m_1}} {\sum\limits_{{m_2}} {{{\text{e}}^{{\text{j}}2\pi \left( {{m_2} - {m_1} + t{n_1} - t{n_2}} \right) \cdot {u_0}}}} \cdot } } } \cr & \hat \varphi \left( {\nu - {m_1}} \right){{\hat \varphi }^*}\left( {\nu - {m_2}} \right)\hat f\left( {\nu - {n_1}} \right) \cr & {{\hat f}^*}\left( {\nu - {n_2}} \right)\left( {{m_2} - {m_1}} \right) \otimes \left( {{m_2} - {m_1}} \right)]{\text{d}}\nu \} \cdot {u_{\text{e}}} \cr & \cr} $ | (19) |
其中 $ \otimes $ 表示张量的并矢,$\displaystyle\sum\limits_{k} {{f_{k}}} $ 表示在整个 $ {\mathbb {Z}^N}$ 空间中求和,积分区域 $\varOmega = {\left[{ - 1/2,1/2} \right]^N}$,高维的插值基函数可以由一维的组合而成. 式 (19) 等价于一个线性方程组,可以通过求解线性方程来获得插值偏差.
数字图像相关对应二维情况,将图像沿 $ x $ 方向平移,可以认为 $ y $ 方向的插值误差为 0,引入带限函数的假设和插值传递函数为实数,那么式 (19) 可以退化为类似式 (14) 的带限估计
| $\eqalign{ & {u_{\text{e}}} \approx {\mkern 1mu} \int_{ - 1/2}^{1/2} {\int_{ - 1/2}^{1/2} {\{ \sum\limits_{k = - \infty }^\infty {\sum\limits_{l = - \infty }^\infty {\left( {{\nu _x} - k} \right)} } } \cdot } \cr & \hat \varphi \left( {{\nu _x} - k,{\nu _y} - l} \right)\sin \left( {2\pi k{u_0}} \right) + \cr & \frac{1}{2}\sum\limits_{{k_1} = - \infty }^\infty {\sum\limits_{{k_2} = - \infty }^\infty {\sum\limits_{{l_1} = - \infty }^\infty {\sum\limits_{{l_2} = - \infty }^\infty {\left( {{k_2} - {k_1}} \right)} \cdot } } } \cr & \hat \varphi \left( {{\nu _x} - {k_1},{\nu _y} - {l_1}} \right)\hat \varphi \left( {{\nu _x} - {k_2},{\nu _y} - {l_2}} \right) \cdot \cr & \sin \left[{2\pi \left( {{k_2} - {k_1}} \right){u_0}} \right]\} {\left| {\hat f\left( {{\nu _x},{\nu _y}} \right)} \right|^2}{\text{d}}{\nu _x}{\text{d}}{\nu _y}/ \cr & \left[{2\pi \int_{ - 1/2}^{1/2} {\int_{ - 1/2}^{1/2} {\nu _x^2\hat \varphi \left( {{\nu _x},{\nu _y}} \right){{\left| {\hat f\left( {{\nu _x},{\nu _y}} \right)} \right|}^2}{\text{d}}{\nu _x}{\text{d}}{\nu _y}} } } \right] \cr} $ | (20) |
如果仅考虑基频分量
| $\eqalign{ & {u_{\text{e}}} \approx 1muC\sin \left( {2\pi {u_0}} \right) \cr & C = \left[ {\int_{ - 1/2}^{1/2} {\int_{ - 1/2}^{1/2} {{E_{{\text{ib}}}}\left( {{\nu _x},{\nu _y}} \right){{\left| {\hat f\left( {{\nu _x},{\nu _y}} \right)} \right|}^2}{\text{d}}{\nu _x}{\text{d}}{\nu _y}} } } \right]/ \cr & \left[ {\int_{ - 1/2}^{1/2} {\int_{ - 1/2}^{1/2} {\nu _x^2\hat \varphi \left( {{\nu _x},{\nu _y}} \right){{\left| {\hat f\left( {{\nu _x},{\nu _y}} \right)} \right|}^2}{\text{d}}{\nu _x}{\text{d}}{\nu _y}} } } \right] \cr & {E_{{\text{ib}}}}\left( {{\nu _x},{\nu _y}} \right) = \left( {{\nu _x} - 1} \right)\hat \varphi \left( {{\nu _x} - 1,{\nu _y}} \right) - \cr & \left( {{\nu _x} + 1} \right)\hat \varphi \left( {{\nu _x} + 1,{\nu _y}} \right) + \hat \varphi \left( {{\nu _x},{\nu _y}} \right) \cdot \cr & \hat \varphi \left( {{\nu _x} - 1,{\nu _y}} \right) + \hat \varphi \left( {{\nu _x},{\nu _y}} \right)\hat \varphi \left( {{\nu _x} + 1,{\nu _y}} \right) \cr} $ | (21) |
上式和一维情况是类似的,其中 ${E_{\rm{ib}}}\left( {{v _x},{v _y}} \right)$ 为插值偏差核,为了形式简单,我们忽略了 $ y $ 方向插值的混叠项 $ (l = {l_1} = {l_2} = 0) $,不过数值模拟证明 $ y $ 方向插值的混叠项影响较小.
2.2 实验散斑图模拟平移验证实验散斑图由相机采样量化得到,原始频谱未知. 本文提出通过计算模板的离散傅里叶变换作为参考函数的频谱近似,频谱估计的精度应与计算模板相关,本节分析了模板大小对插值偏差估计的影响,并与传统的插值偏差计算方法进行了比较分析.
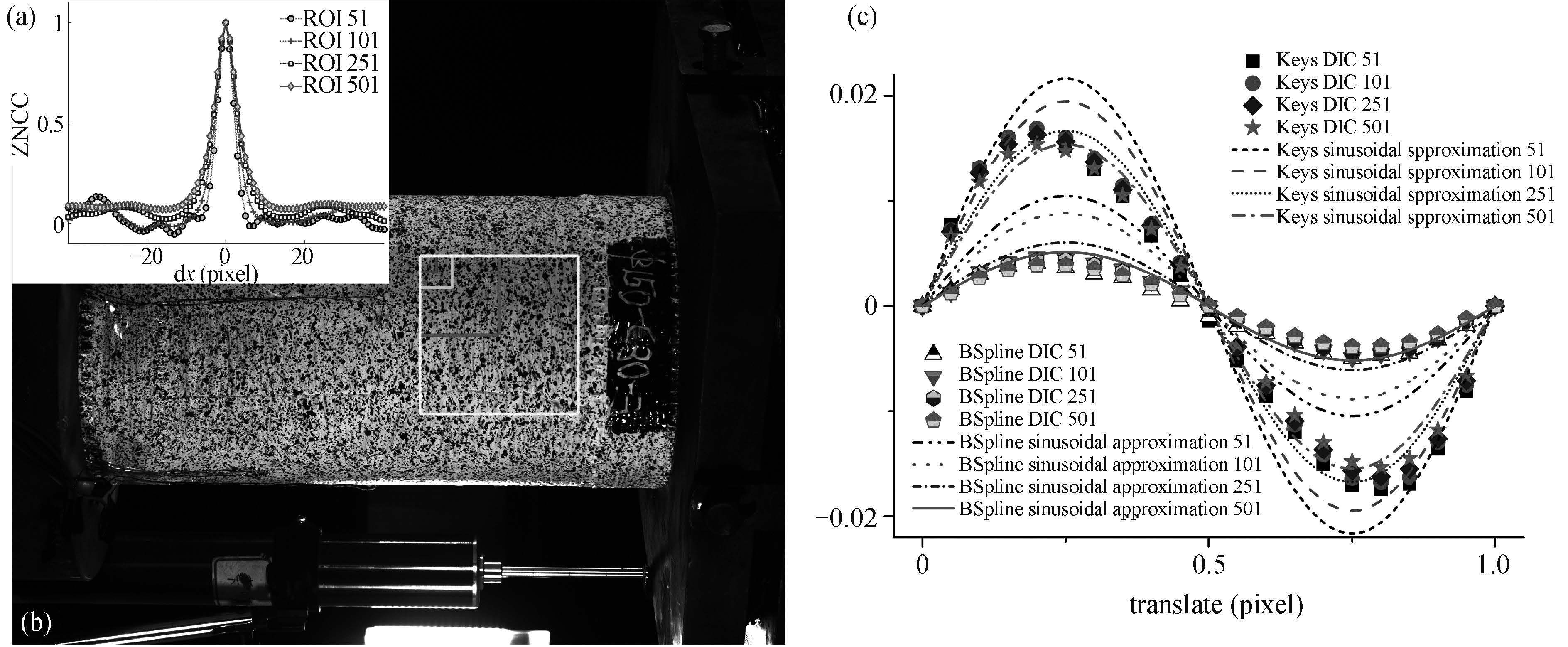
实验图片采用水泥柱压缩实验的散斑图片 [27],图片尺寸为 2 448×2 048,采用傅里叶分析方法将图片进行模拟平移,生成每次平移量为 0.05 像素,总计移动一个像素的一系列图片. 选择的计算模板如图5(b) 中所示,模板分别是边长为 51,101,251,501 的正方形区域,图6(a1) ~ 6(d1) 给出了各个模板的散斑图,为了显示方便,将其缩放到统一的大小,图5(a) 给出了不同模板的自相关曲线,可以观察到较大的模板相关峰附近波动比较小,而相关峰的宽度不受模板大小的影响;对图5(b) 所示的 4 个模板进行相关计算,相关程序采用 0 阶形函数的正向高斯牛顿法,使用了 Keys 和三次 B 样条插值算法,通过相关计算计算出插值偏差曲线; 插值偏差估计采用正弦近似 (式 (21)),通过 MATLAB 对选取的子区进行离散傅里叶变换近似参考图像的频谱,图6(a2) ~ 6(d2) 显示了不同模板大小散斑图案离散傅里叶变换的结果,公式中的积分通过 MATLAB 的数值积分函数 trapz 近似.
|
图 5 水泥柱压缩实验(a)不同模板大小散斑对应的自相关曲线;(b)实验散斑图和计算模板;(c)不同模板的数字图像相关计算偏差与估计偏差 Fig.5 Experiment of a compressed concrete cylinder. (a) autocorrelation functions of different subsets. (b) experiment speckle image and correlation subsets. (c) interpolation bias by digital image correlation and theoretical prediction by sinusoidal approximation (Eq. (21)) of different subsets |
通过图5(c) 可以观察到,数字图像相关计算的插值偏差基本不随着模板变化,而采用式 (21) 正弦近似的插值偏差估计值当模板选取较小要大于相关计算结果,随着计算模板的增大估计值与计算值之间的差距减小. 插值偏差估计值在大计算模板情况下更加精确的原因有两点,由图6(a2) ~ 6(d2),大模板对应的离散傅里叶变换结果更接近于原始的频率分布; 插值偏差的估计需要数值积分,大模板情况数值积分步长缩小,积分精度提高. 由于相关计算的插值偏差基本是与子区无关,为了提高理论估计的精度应该选取较大的子区,所以在下面的过程中,估计时都选取尽量大的子区. 对于子区比较小的情况,本文的理论估计值会大于数字图像相关的计算值,所以是一种安全的估计.

|
图 6 不同模板大小的散斑图和对应的频谱,为了显示起见,散斑图进行了放大,散斑图与图5(b)中线框显示部分一一对应。(a1) (b1)(c1)(d1)模板51,101,251,501散斑图;(a2)(b2)(c2)(d2)模板51,101,251,501的频谱。 Fig.6 Speckle patterns of different subsets and corresponding discrete Fourier transform, the speckle patterns are magnified to identical size for clarification. (a1)(b1)(c1)(d1) speckle patterns of subsets 51, 101, 251, 501. (a2)(b2)(c2)(d2) discrete Fourier transform of subsets 51, 101, 251, 501 |
本文提出的快速估计算法较之于生成一系列亚像素平移散斑图随后进行相关计算的传统方法具有计算速度的优势. 对于水泥柱压缩实验,生成 20 幅亚像素平移散斑图耗时 12.21 s,在模板为 501 的情况下采用三次 B 样条插值相关计算耗时 41.80 s,总计 54.01 s,而采用本文提出的算法使用 MATLAB 仅耗时 0.93 s,如果采用效率更高的 C++ 语言实现计算部分仅耗时 0.047 s,获得了近三个数量级的速度提升 (电脑配置为 Intel i5-3470 CPU @ 3.20GHz,Kingston 1600 MHz DDR3 8G RAM).
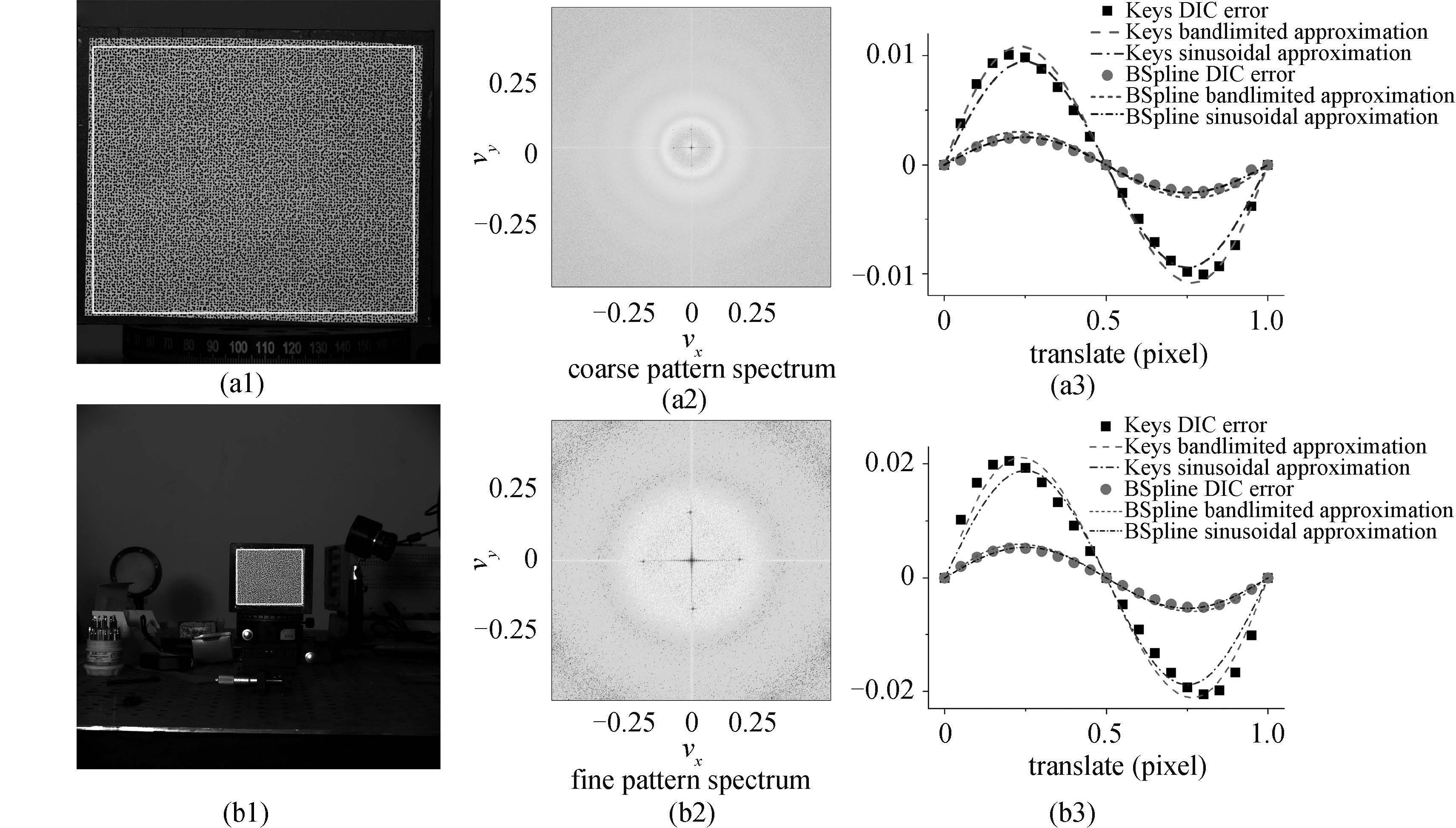
最近学者提出了由位置随机的圆斑组成的数字设计散斑,数字设计散斑更适应大视场的测量,而且采用高斯滤波可以同时减小计算偏差和随机误差 [28],本文采用数字设计散斑验证了这种设计散斑的插值偏差估计. 数字设计散斑采用自己编写的散斑生成程序生成,将散斑图样打印粘贴在平盘上,随后采用分辨率为 2 048×2 048 的 IDS 相机采集图片. 采集时为了调整散斑大小,分别距离较近和较远拍摄. 图7(a1),7(b1) 给出了相机拍摄图像,黄色线框表示了数字图像相关的计算区域. 图8(a1),8(b1) 给出了散斑图局部放大的结果,对于较大的散斑颗粒,散斑直径约为 10 个像素,对于较小的散斑,直径约为 4 个像素,两者的占空比为 65%,图8(a2),8(b2) 显示了计算模板的自相关曲线,观察发现自相关曲线相关峰至第一个波谷的距离基本为散斑的直径,散斑越小,自相关曲线越陡锐. 比较数字设计散斑的自相关 (图8(a2),8(b2)) 与传统散斑的自相关曲线 (图5(a)),数字设计散斑自相关曲线的波动更加的明显. 图7(a2),7 (b2) 给出了图7(a1),7 (b1) 中计算区域对应的频谱,可见对于数字设计散斑,其频谱呈带状的分布,这可以理解为圆域函数的傅里叶变换,这点与传统散斑也不同. 对于传统散斑的频谱 (图6(a2) ~ 6(d2)) 不存在这种带状的分布,这是由于传统散斑形状高度随机,不存在固定形状的散斑基元. 对于较大的散斑图,低频量较多,对于比较小的散斑图,空域的压缩相对于频域的扩展,高频分量增多.
|
图 7 二值化散斑,(a1)(b1)大散斑颗粒和小散斑颗粒时的散斑图和计算区域;(a2)(b2)大散斑和小散斑对应的频谱;(a3)(b3)大散斑和小散斑对应的计算偏差 Fig.7 Numerically-designed speckle pattern. (a1)(b1) speckle pattern and calculation subset of coarse and fine pattern. (a2)(b2) discrete Fourier transform of subsets of coarse and fine pattern. (a3)(b3) results of digital image correlation, band-limited approximation (Eq. (20)) and sinusoidal approximation (Eq. (21)) for coarse and fine pattern |

|
图 8 散斑局部放大图和自相关曲线(a1)(b1)大散斑和小散斑的局部放大图;(a2)(b2)大散斑和小散斑的自相关曲线 Fig.8 (a1)(b1) close up of coarse and fine pattern. (a2)(b2) autocorrelation of coarse and fine pattern |
图7(a3),7(b3) 给出了理论与数字图像相关计算的插值偏差模拟结果的比较,理论估计包括带限近似 (式 (20)) 和正弦近似 (式 (21)),结果显示高度一致. 与前面讨论一致的,小散斑高频成分多于大散斑 (图7 (a2),7(b2)),对应的插值偏差大于大散斑,例如对于 Keys 插值算法,对于图7 (a1) 的情况,插值偏差为 0.01 个像素,而当散斑颗粒的直径变小时,如图7 (b1) 所示的情况,插值偏差则达到 0.02 个像素; 对于 B 样条插值算法,插值偏差远远小于 Keys 插值算法,也是随着高频量的增大引起了插值偏差的增大. 在真实实验环境中存在图像噪声. 虽然大散斑颗粒对应的插值偏差小,然而其抗噪能力差从而随机误差大. 研究表明,当散斑尺寸在 2 ~ 4 个像素时,位移测量误差最小 [29].
3 结论为了研究散斑质量的标准评估方法,本文针对通过傅里叶分析手段给出散斑图插值偏差的一种安全估计方法,并通过数值模拟的亚像素平移实验进行了验证. 本文的工作结论如下:
(1) 基于最小平方距离准则获得了插值偏差与散斑图案,插值算法的直接关系,得到了只需要确定插值方法和散斑图就能方便得到插值偏差估计的理论公式,解释了插值偏差随亚像素平移呈类似于正弦形式变化的原因.
(2) 提出了插值偏差核的概念,插值偏差核表征了插值算法对散斑图特定频率的偏差响应,可以评价插值算法用于相关计算的优劣. 对插值偏差核的进一步研究表明图像高频成分对插值偏差起主要作用,插值偏差产生的原因是插值的混叠效应.
(3) 提出了通过插值方法传递函数和散斑图频谱估计插值偏差的算法,并通过数值模拟和实验进行了验证. 本文的估计方法计算简便有效,由于离散傅里叶变换和数值积分计算速度都非常快,故而较之于传统的生成一系列散斑图,做相关计算的方法具有明显的速度优势.
本文的工作可以进一步用于插值算法优化,滤波模板选取,建立散斑质量评估标准,设计制作优化的水转印标准散斑等方面.
| 1 | Sutton MA, Orteu JJ, Schreier H. Image Correlation for Shape, Motion and Deformation Measurements:Basic Concepts, Theory and Applications. Springer Science & Business Media, 2009 |
| 2 | Zhang QC, Jiang ZY, Jiang HF, et al. On the propagation and pulsation of Portevin-Le Chatelier deformation bands:An experimental study with digital speckle pattern metrology. International Journal of Plasticity, 2005, 21:2150-2173 |
| 3 | Zhang H, Fu DH, Song HP, et al. Damage and fracture investigation of three-point bending notched sandstone beams by DIC and AE techniques. Rock Mechanics and Rock Engineering, 2015, 48(3):1297-1303 |
| 4 | 戴云彤, 陈振宁, 朱飞鹏等. 小尺寸低碳钢试件吕德斯效应的三维数字图像相关测量. 力学学报, 2015, 47(1):119-126(Dai Yuntong, Chen Zhenning, Zhu Feipeng, et al. Measurement of Luders band in small size low carbon steel specimen by 3D digital image correlation method. Chinese Journal of Theoretical and Applied Mechanics, 2015, 47(1):119-126(in Chinese)) |
| 5 | 谢倍欣, 汤立群, 张晓阳等. 基于数字图像的分离式霍普金森压杆实验中试件应变及两端应力的同步测量法. 实验力学, 2014, 29(6):683-688(Xie Beixin, Tang Liqun, Zhang Xiaoyang, et al. On the synchronized measurement of specimen's strain and stress at both ends in SHPB tests based on digital image. Journal of Experimental Mechanics, 2014, 29(6):683-688(in Chinese)) |
| 6 | 蔡玉龙, 符师桦, 王玉辉等. 基于三维数字图像相关法的5456铝镁合金锯齿形屈服研究. 金属学报, 2014, 50(12):1491-1497(Cai Yulong, Fu Shihua, Wang Yuhui, et al. Serrated yielding of 5456 aluminium magnesium alloy based on three dimensional digital image correlation. Acta Metallurgica Sinica, 2014, 50(12):1491-1497(in Chinese)) |
| 7 | Cheng T, Xu XH, Cai YL, et al. Investigation of Portevin-Le Chatelier effect in 5456 Al-based alloy using digital image correlation. Optics and Lasers in Engineering, 2015, 65:89-92 |
| 8 | Chen ZN, Quan CG, Zhu FP, et al. A method to transfer speckle patterns for digital image correlation. Measurement Science and Technology, 2015, 26:095201 |
| 9 | Pan B, Xie HM, Wang ZY, et al. Study on subset size selection in digital image correlation for speckle patterns. Opt Express, 2008, 16:7037-7048 |
| 10 | 徐小海, 苏勇, 蔡玉龙等. 数字图像相关法测量局域变形场中形函数和模板尺寸的影响. 力学学报, 2015, 47(5):848-862(Xu Xiaohai, Su Yong, Cai Yulong, et al. Influence of shape functions and template size in digital image correlation method for highly inhomogeneous deformations. Chinese Journal of Theoretical and Applied Mechanics, 2015, 47(5):848-862(in Chinese)) |
| 11 | 潘兵, 谢惠民, 戴福隆. 数字图像相关中亚像素位移测量算法的研究. 力学学报, 2007, 39(2):245-252(Pan Bing, Xie Huimin, Dai Fulong. An investigation of sub-pixel displacements registration algorithms in digital image correlation. Chinese Journal of Theoretical and Applied Mechanics, 2007, 39(2):245-252(in Chinese)) |
| 12 | Shao XX, Dai XJ, He XY. Noise robustness and parallel computation of the inverse compositional Gauss-Newton algorithm in digital image correlation. Optics and Lasers in Engineering, 2015, 71:9-19 |
| 13 | Schreier HW, Braasch JR, Sutton MA. Systematic errors in digital image correlation caused by intensity interpolation. Opt Eng, 2000, 39:2915-2921 |
| 14 | Choi S, Shah SP. Measurement of deformations on concrete subjected to compression using image correlation. Experimental Mechanics, 1997, 37:307-313 |
| 15 | 王朝阳. 数字图像相关方法的准确度与速度增强. 实验力学, 2011, 26(5):632-638(Wang Zhaoyang. On the accuracy and speed enhancement of digital image correlation technique. Journal of Experimental Mechanics, 2011, 26(5):632-638(in Chinese)) |
| 16 | 任茂栋, 梁晋, 唐正宗等. 数字图像相关法中的优化插值滤波器. 西安交通大学学报, 2014, 48(7):65-70(Ren Maodong, Liang Jin, Tang Zhengzong, et al. Optimized interpolation filter for digital image correlation. Journal of Xi'an Jiaotong University, 2014, 48(7):65-70(in Chinese)) |
| 17 | Pan B. Bias error reduction of digital image correlation using Gaussian pre-filtering. Optics and Lasers in Engineering, 2013, 51:1161-1167 |
| 18 | Zhou YH, Sun C, Song YT, et al. Image pre-filtering for measurement error reduction in digital image correlation. Optics and Lasers in Engineering, 2015, 65:46-56 |
| 19 | Rohde GK, Aldroubi A, Healy DM. Interpolation artifacts in subpixel image registration. IEEE Transactions on Image Processing, 2009, 18:333-345 |
| 20 | 王志勇, 王磊, 郭伟等. 数字图像相关方法最优散斑尺寸. 天津大学学报, 2010, 43(8):674-678(Wang Zhiyong, Wang Lei, Guo Wei, et al. Optimal size of speckle spot in digital image correlation. Journal of Tianjin University, 2010, 43(8):674-678(in Chinese)) |
| 21 | 潘兵, 吴大方, 夏勇. 数字图像相关方法中散斑图的质量评价研究. 实验力学, 2010, 25(2):120-129(Pan Bing, Wu Dafang, Xia Yong. Study of speckle pattern quality assessment used in digital image correlation. Journal of Experimental Mechanics, 2010, 25(2):120-129(in Chinese)) |
| 22 | Wang YQ, Sutton MA, Bruck HA, et al. Quantitative error assessment in pattern matching:Effects of intensity pattern noise, interpolation, strain and image contrast on motion measurements. Strain, 2009, 45:160-178 |
| 23 | Shimizu M, Okutomi M. Sub-pixel estimation error cancellation on area-based matching. International Journal of Computer Vision,2005, 63:207-224 |
| 24 | Inglada J, Muron V, Pichard D, et al. Analysis of artifacts in subpixel remote sensing image registration. IEEE T. Geosci. Remote, 2007, 45:254-264 |
| 25 | Thevenaz P, Blu T, Unser M. Interpolation revisited. IEEE Transactions on Medical Imaging, 2000, 19:739-758 |
| 26 | 高越. 三维数字图像相关法的关键技术及应用研究.[博士论文]. 合肥:中国科学技术大学, 2014(Gao Yue. Research on key technologies and applications of three-dimensional digital image correlation.[PhD Thesis]. Hefei:University of Science and Technology of China, 2014(in Chinese)) |
| 27 | 刘聪, 陈振宁, 何小元. 3D-DIC在土木结构力学性能试验研究中的应用. 东南大学学报(自然科学版), 2014, 44(2):339-344(Liu Cong, Chen Zhenning, He Xiaoyuan. Application of 3D-DIC in experimental study on mechanical properties of civil structures. Journal of Southeast University(Natural Science Edition), 2014, 44(2):339-344(in Chinese)) |
| 28 | Mazzoleni P, Matta F, Zappa E, et al. Gaussian pre-filtering for uncertainty minimization in digital image correlation using numerically-designed speckle patterns. Optics and Lasers in Engineering, 2015, 66:19-33 |
| 29 | Hua T, Xie HM, Wang SN, et al. Evaluation of the quality of a speckle pattern in the digital image correlation method by mean subset fluctuation. Optics & Laser Technology, 2011, 43(1):9-13 |
 2016, Vol. 48
2016, Vol. 48