硬壳层通常是指由于载荷迁移、蒸发和风化等因素长期作用而在软土地表所形成的一层硬土[1],广泛分布于我国沿海和平原地区.硬壳层的厚度不一,厚者可达数米,但硬壳层的压缩性小、封水性好,与软土地基密切接触,能形成很好的承力体系,应充分利用天然或人造硬壳层的有利作用[2, 3],优化软土路堤填土高度设计与施工管理.目前对硬壳层软土地基研究较多的是按双层地基求其极限承载力[4, 5, 6, 7],但依此得到的填土高度常难满足路堤沉降标准.只要控制填土自重在软土地基的临塑/临界载荷范围内,路堤的沉降和稳定一般就都能达到要求,故硬壳层软土地基临塑/临界载荷的确定至关重要,尤其是软土在特定最大塑性区深度时所对应的硬壳层地基临界载荷,能较充分发挥地基的承载潜力和变形特性,常用于路堤填土高度计算. 代表性的研究有:王晓谋[8]假定软土侧压力系数$k_{\rm o}$为1.0,基于莫尔-库仑准则提出了考虑硬壳层厚度及强度影响的软土地基临塑载荷解答,并通过有限元模拟建议了应力扩散角的取值范围[9];问延煦等[10, 11]探究了硬壳层封闭作用的影响机理,并考虑硬壳层的应力扩散作用,推导了这两种作用下软土地基临塑载荷的莫尔-库仑公式,但同样假定侧压力系数$k_{\rm o}$为1.0. 上述侧压力数$k_{\rm o}$实为静止侧压力系数的简称,是指地基土在无侧向变形条件下水平有效应力与竖向有效应力的比值,用于表征地基土的初始应力场,广泛应用于静止土压力计算与基坑支护设计;地基土初始应力场中两个侧向的水平有效应力相等,但小于竖向自重有效应力,故侧压力数$k_{\rm o}$一般小于1.0且与中间有效主应力无关,工程应用时多将其视为常数. 侧压力系数$k_{\rm o}= 1.0$相当于地基土处于三向等压的静水应力场,与土体的实际应力状态明显不符,应考虑土体$k_{\rm o } e 1.0$的初始地应力状态.朱福等[12]依据统一强度理论建立的硬壳层软土地基上路堤的临塑/临界填土高度解析解,考虑了中间主应力和侧压力系数$k_{\rm o } e 1.0$的共同影响,但假定条形基础中心线下塑性区开展最深. 另外,问延煦[10]和朱福[12] 等所采用的应力扩散系数$\eta >1$,造成软硬土层交界面处应力集中,有悖于上硬下软地层的应力扩散规律,且硬壳层的封闭作用难以量化[13].
上述研究均没有考虑地基软土的实际非饱和状态,非饱和土分布十分广泛,干旱和半干旱地区的地基持力层多常年处于非饱和状态[14, 15, 16],上覆有渗透系数极小的硬壳层时更是如此,应考虑软土层的非饱和强度特性对路堤填土高度的影响,充分发挥地基土的真实强度潜能.非饱和土的总吸力通常由基质吸力和溶质吸力两部分组成,在土体溶质吸力不大即溶质浓度不高的前提下,可忽略溶质吸力的影响[17]. 另一方面,路堤下地基土处于三向不等应力作用的平面应变状态,其土体强度受中间主应力$\sigma_{2}$的影响显著[18, 19, 20],而由不考虑中间主应力 $\sigma_{2}$影响的莫尔-库仑准则得到的路堤填土高度过于保守,应采用能合理反映中间主应力 $\sigma_{2}$影响的非饱和土抗剪强度公式.张常光等[21, 22]建立的非饱和土平面应变抗剪强度统一解,可充分考虑中间主应力 $\sigma_{2}$对非饱和土强度的影响,同时结合吸力角双曲线模型可以反映非饱和土强度的非线性[22, 23],具有广阔的工程应用前景[24, 25, 26, 27].
因此,本文基于非饱和土平面应变抗剪强度统一解与吸力角双曲线模型,考虑硬壳层的应力扩散作用和自重反压护道作用,推导侧压力系数$k_{\rm o} e 1.0$时硬壳层非饱和软土地基的临塑/临界载荷计算公式,进而提出路堤临塑/临界填土高度的解析解,给出解析公式的适用条件及应用步骤,并进行可比性分析与对比验证,最后探讨硬壳层、侧压力系数、中间主应力和基质吸力等因素影响规律,所得结果可为硬壳层软土地基上的路堤填土设计和施工提供理论指导和优化建议.
1 非饱和土平面应变强度公式 1.1 抗剪强度统一解从非饱和土到饱和土,或从饱和土到非饱和土,应力状态及土体抗剪强度都应有平顺的过渡,基质吸力这一状态变量及其应力张量所发挥的作用至关重要 ?[14, 15, 16] ;当土体中的溶质吸力不大或溶质浓度不高时,基质吸力从大于零变为零,非饱和土的双应力状态变量则变为饱和土的单一有效应力,即非饱和土变为饱和土;相反,基质吸力从零变为大于零,则饱和土变为非饱和土. 张常光等[21, 22]依据俞茂宏统一强度理论[28]与非饱和土双应力状态变量强度理论[29],所建立的非饱和土平面应变抗剪强度统一解为 $${\tau _{\text{f}}} = {c'_{\text{t}}} + \left( {\sigma - {u_{\text{a}}}} \right)\tan {\phi '_{\text{t}}} + \left( {{u_{\text{a}}} - {u_{\text{w}}}} \right)\tan \phi _{\text{t}}^{\text{b}} = {c_{{\text{tt}}}} + \left( {\sigma - {u_{\text{a}}}} \right)\tan {\phi '_{\text{t}}}{\text{ = }} \tag{1}$$
$$\sin {\phi }'_{\rm t} = \dfrac{2\left( {1 + b} \right)\sin \phi '}{2 + b\left( {1 + \sin \phi '} \right)}$,${c}'_{\rm t} = \dfrac{2\left( {1 + b} \right)c'\cos \phi '}{2 + b\left( {1 + \sin \phi '} \right)}\dfrac{1}{\cos {\phi }'_{\rm t} }$$
$\sin \phi _{\rm t}^{\rm b} = \dfrac{2\left( {1 + b} \right)\sin \phi ^{\rm b}}{2 + b\left( {1 + \sin \phi ^{\rm b}} \right)}$,$c_{{\rm tt}} = {c}'_{\rm t} + \left( {u_{\rm a} - u_{\rm w} } \right)\tan \phi _{\rm t}^{\rm b} $
式中,$\tau_{\rm f}$为非饱和土的平面应变抗剪强度;$c'$和 $\phi' $为非饱和土对应饱和土时的有效黏聚力和有效内摩擦角,$c'_{\rm t} $和 $\phi'_{\rm t} $为统一有效黏聚力、统一有效内摩擦角;$u_{\rm a}$为孔隙气压,$u_{\rm w}$为孔隙水压,$u_{\rm a } -u_{\rm w}$为基质吸力; $\sigma $ 为总法向应力,$\sigma -u_{\rm a}$为净法向应力; $\phi^{\rm b}$为与基质吸力$u_{\rm a} -u_{\rm w}$有关的吸力角,$\phi_{\rm t}^{\rm b}$为统一吸力角,$c_{\rm tt}$为统一总黏聚力;$b$为统一强度理论参数,反映中间主应力对非饱和土强度的影响程度,也是选取不同强度准则的参数,取值范围为:$0 ≤ b ≤ 1$.
式(1)虽与非饱和土双应力状态变量抗剪强度公式的形式相同,但通过参数$b$可以反映中间主应力 $\sigma_{2}$效应和强度准则的选取,参数$b = 0$时式(1)退化为基于莫尔-库仑准则的双应力状态变量非饱和土抗剪强度公式[28],未考虑中间主应力的影响;参数$b = 1$时为基于双剪应力理论的非饱和土抗剪强度公式,参数0 < b < 1时为一系列新的非饱和土抗剪强度公式. 通过式(1)所代表的非饱和土抗剪强度直线和地基土体大主应力 $\sigma_{1}$、小主应力$\sigma_{3}$对应的最大莫尔圆相切,就可以建立能反映中间主应力$\sigma_{2}$影响的地基塑性区开展深度与承载力公式,进而确定路堤填土高度.
1.2 吸力角双曲线模型当基质吸力大于非饱和土的进气值($u_{\rm a} - u_{\rm w})_{\rm b}$时,吸力角 $\phi ^{\rm b}$则变为基质吸力$u_{\rm a} - u_{\rm w}$的非线性减函数[30, 31, 32, 33]. 文献[33]提出的吸力角 $\phi^{\rm b}$双曲线模型很有代表性,其表达式为 当$ u_{\rm a} - u_{\rm w} ≤ \left( { u_{\rm a} - u_{\rm w} } \right)_{\rm b} $时 $$ \phi ^{\rm b} = \phi ' \tag{2a}$$ 当$ u_{\rm a} - u_{\rm w} > \left( { u_{\rm a} - u_{\rm w} } \right)_{\rm b} $时 $$ \phi ^{\rm b} = \phi' - \dfrac{ u_{\rm a} - u_{\rm w} - \left( { u_{\rm a} - u_{\rm w} } \right)_{\rm b} }{m + n\left[{\left( { u_{\rm a} - u_{\rm w}} \right) - \left( { u_{\rm a} - u_{\rm w} } \right)_ {\rm b} } \right]} \tag{2b}$$ 式中,$m$和$n$分别为式(2b)变形直线方程后的截距和斜率.
由式(2)可知,当基质吸力处于不大于进气值 $(u_{\rm a} - u_{\rm w})_{\rm b}$的低吸力范围内时,吸力角 $\phi^{\rm b}$等于有效内摩擦角$\phi'$;而当基质吸力处于大于进气值($u_{\rm a} - u_{\rm w})_{\rm b}$的高吸力范围内时,吸力角 $\phi^{\rm b}$按双曲线模型不断减小并趋于稳定.同时,张常光等[22, 23]拟合了斜率倒数$1/ n$与有效内摩擦 $\phi'$之间的线性方程,即 $$ 1 / n = - 2.459 8 + 1.022 5\phi' \tag{3}$$ 因此,斜率$n$可根据有效内摩擦角 $\phi'$直接确定. 将式(2)和式(3)代入式(1),即可得到能考虑高基质吸力强度非线性影响的非饱和土平面应变抗剪强度统一解.
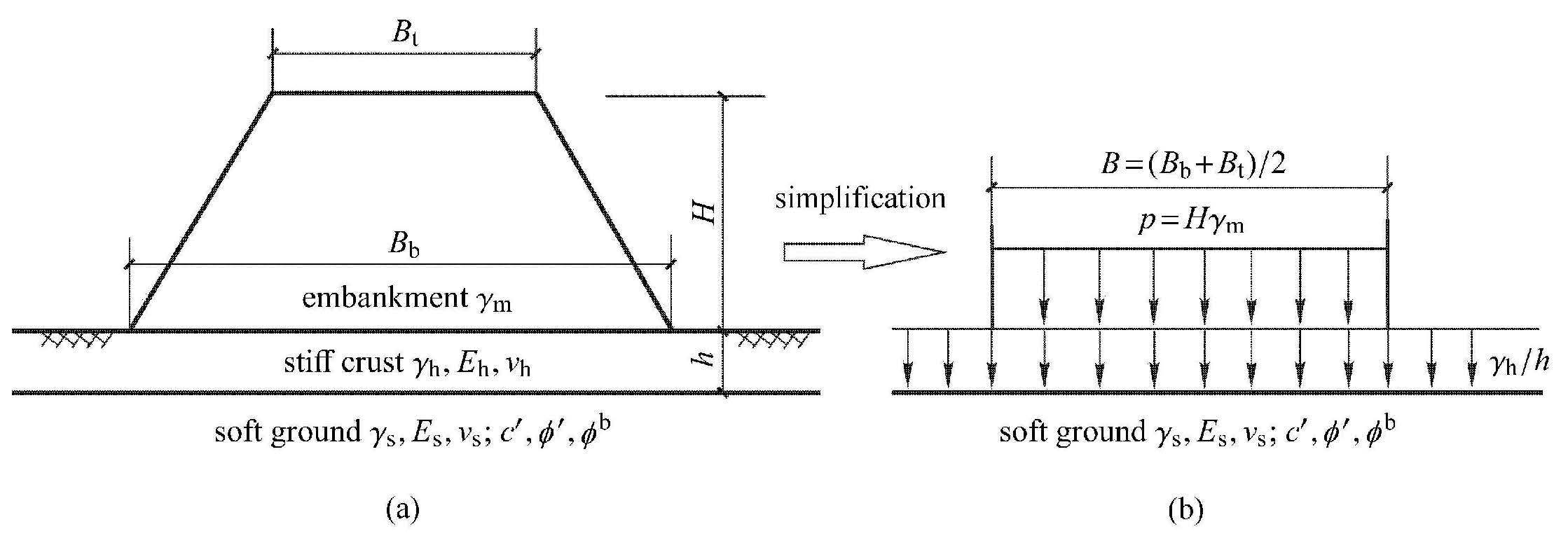
2 路堤填土高度常见硬壳层软土地基上的梯形路堤横断面及土体参数,如图1(a)所示,图中$H$为路堤填土高度,$B_{\rm t}$和$B_{\rm b}$分 别为路堤的上、下宽度,$\gamma_{\rm m}$为路堤填土的平均重度;$h$为硬壳层厚度,$\gamma_{\rm h}$,$E_{\rm h}$和 $u_{\rm h}$分别为硬壳层的重度、弹性模量和泊松比,$\gamma_{\rm s}$,$E_{\rm s}$和$u_{\rm s}$分别为地基软土的重度、弹性模量和泊松比;$c' $和$\phi'$为地基软土的有效黏聚力与有效内摩擦角,$\phi^{\rm b}$为地基软土的吸力角.不考虑路堤填土的逐层压实过程,采用等效宽度$B = (B_{\rm t}+B_{\rm b})/2$ 来代替路堤载荷的实际作用宽度(见图1(b));只考虑路堤填土的自重作用,等效路堤载荷$p = H\gamma_{\rm m}$ 以条形均布载荷,作用于均质各向同性的平面应变半无限硬壳层顶面.
|
图 1 上硬下软地基上的路堤模型 Fig.1 Embankment model on soft ground under stiff crust |
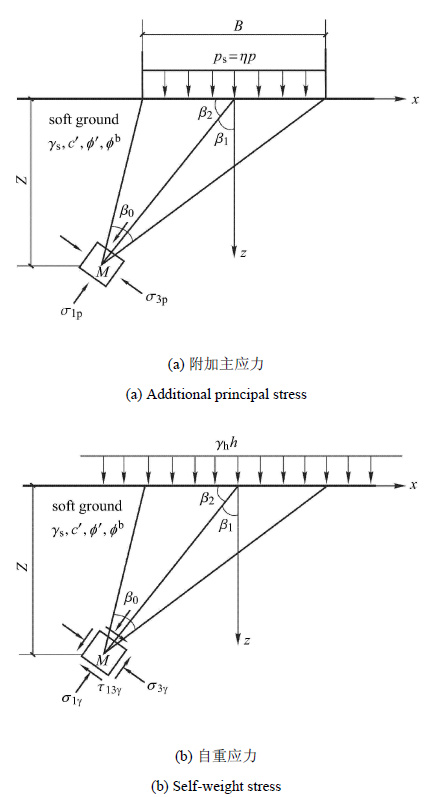
硬壳层通常具有应力扩散作用、自重反压护道作用、强度承载作用以及封闭作用等4种作用机理,但这4种作用机理并不是孤立无关的,而是相互关联的,只是各自的出发点略有不同.如:应力扩散作用和强度承载作用就是一对组合,只有硬壳层高承载作用的发挥,将上覆填土自重传递到路堤两侧更大范围的地基土内,才使其应力扩散作用得以显现,即二者是共存同发挥的、不应重复考虑,且强度完全承载时的填土高度常难以满足路堤沉降要求,故仅以硬壳层与软土层交界面处的应力扩散系数 $\eta $ 来概化这两种作用机理,将等效路堤载荷$p = H \gamma_{\rm m}$通过硬壳层应力扩散作用传至软土层顶面而变为$p_{\rm s }= \eta p = \eta H\gamma_{\rm m}$,如图2(a)所示;自重反压护道作用和封闭作用是另一对组合,自重反压护道作用是封闭作用得以实现的前提与表现,即二者也是共存同发挥的、不应同时考虑,且封闭作用难以量化,故仅以自重反压护道作用来考虑,将硬壳层自重$\gamma_{\rm h}h$作为大面积超载施加于软土层顶面,如图2(b)所示.对硬壳层作用的这2种处理,是符合尽量利用硬壳层弹性工作状态原则的[1].
|
图 2 地基M点应力分析 Fig.2 Stress analysis at point M of ground |
采用徐洋[13]通过有限元计算拟合的应力扩散系数$\eta $,其表达式为 $$ \left. \eta = \left( {d\sqrt {B / h} + e} \right) \left( {E'_{\rm s}/ E'_{\rm h} } \right)^{1/4} \\ E'_{\rm h} = \dfrac{E_{\rm h} }{1 - u _{\rm h}^{\rm 2} } ,E'_{\rm s} = \dfrac{E_{\rm s} }{1 - u _{\rm s}^{\rm 2} } \\ d = 0.146 1 \ln \left( {\dfrac{E'_{\rm h} }{E'_{\rm s} }} \right) + 0.001 8 \\ e = - 0.133 4 \ln \left( {\dfrac{E'_{\rm h} }{E'_{\rm s} }} \right) + 1.028 4 \!\!\right\} \tag{4}$$ 式中,$E'_{\rm h} $和$E'_{\rm s} $为弹性模量的中间参数;$d$和$e$为方程拟合参数.问延煦等[10]和朱福等[12]同样采用徐洋的应力扩散系数 $\eta $,但公式中遗漏($E'_{\rm s} /E'_{\rm h} )^{1 / 4}$项,以致应力扩散系数 $\eta $ 大于1,有违应力扩散作用的本质.
2.1 应力分析(1) 附加主应力
对于软土层顶面均布条形载荷$p_{\rm s}= \eta p$作用下的地基$M$点(见图2(a),$\beta _{0}$,$\beta_{1}$和$\beta_{2}$为图 中所示的夹角),根据弹性力学理论得该点的附加主应力为[34] $\sigma _{\rm 1p} = \dfrac{p_{\rm s} }{\pi}\left( {\beta _0 + \sin \beta _0 } \right) = \dfrac{\eta p}{\pi}\left( {\beta _0 + \sin \beta _0 } \right) \tag{5a}$ $\sigma _{\rm 3p} = \dfrac{p_{\rm s} }{\pi }\left( {\beta _0 - \sin \beta _0 } \right) = \dfrac{\eta p}{\pi }\left( {\beta _0 - \sin \beta _0 } \right) $ $\tau _{\rm 13p} = 0 \tag{5c}$
值得注意的是:地基$M$点的附加主应力即式(5)作用在夹角 $\beta_{0}$的平分线及其垂线上,是与$M$点的几何位置相关的.
(2) 自重应力
设地基$M$点距软土层顶面的距离即塑性区开展深度为$Z$,因大面积超载即硬壳层自重$\gamma_{\rm h}h$和地基软土自重$\gamma_{\rm s}Z$所引起的主应力作用在垂直方向和水平方向上,与条形载荷$p_{\rm s}$的附加主应力即式(5)的方向不同,故将自重主应力转换到附加主应力的方向(见图2(b)),得$M$点转换后的自重应力为[34] $ \sigma _{1\gamma } = \dfrac{\left( {\gamma _{\rm h} h + \gamma _{\rm s} Z} \right)\left( {1 + k_{\rm o} } \right)}{2} +\\ \dfrac{\left( {\gamma _{\rm h} h + \gamma _{\rm s} Z} \right)\left( {1 - k_{\rm o} } \right)}{2}\cos (2\beta _1) \tag{6a}$ $ \sigma _{3\gamma } = \dfrac{\left( {\gamma _{\rm h} h + \gamma _{\rm s} Z} \right)\left( {1 + k_{\rm o} } \right)}{2} -\\ \dfrac{\left( {\gamma _{\rm h} h + \gamma _{\rm s} Z} \right)\left( {1 - k_{\rm o} } \right)}{2}\cos (2\beta _1) \tag{6b}$ $ \tau _{13\gamma } = \dfrac{\left( {\gamma _{\rm h} h + \gamma _{\rm s} Z} \right)\left( {1 - k_{\rm o} } \right)}{2}\sin (2\beta _1) \tag{6c}$
(3) 地基$M$点的总应力
转换后的自重应力式(6)与附加主应力式(5)均作用在夹角 $\beta_{0}$的平分线及其垂线上,故叠加此二式得$M$点的总应力为 $ \sigma _{1{\rm t}} = \sigma _{\rm 1p} + \sigma _{\rm 1\gamma } = \dfrac{\eta p}{\pi}\beta _0 + \dfrac{\left( {\gamma _{\rm h} h + \gamma _{\rm s} Z} \right)\left( {1 + k_{\rm o} } \right)}{2} +$ $ \left[{\dfrac{\eta p}{ \pi }\sin \beta _0 + \dfrac{\left( {\gamma _{\rm h} h + \gamma _{\rm s} Z} \right)\left( {1 - k_{\rm o} } \right)}{2}\cos (2\beta _1) } \right] \tag{7a}$ $ \sigma _{3{\rm t}} = \sigma _{\rm 3p} + \sigma _{\rm 3\gamma } = \dfrac{\eta p}{\pi}\beta _0 + \dfrac{\left( {\gamma _{\rm h} h + \gamma _{\rm s} Z} \right)\left( {1 + k_{\rm o} } \right)}{2} -$ $ \left[{\dfrac{\eta p}{\pi}\sin \beta _0 + \dfrac{\left( {\gamma _{\rm h} h + \gamma _{\rm s} Z} \right)\left( {1 - k_{\rm o} } \right)}{2}\cos (2\beta _1) } \right] $ (7b) $\tau _{13{\rm t}} = \tau _{\rm 13p} + \tau _{\rm 13\gamma } = \dfrac{\left( {\gamma _{\rm h} h + \gamma _{\rm s} Z} \right)\left( {1 - k_{\rm o} } \right)}{2}\sin (2\beta _1) $ (7c)
2.2 填土高度当$M$点达到强度极限平衡时,其总应力式(7)满足非饱和土平面应变抗剪强度统一解式(1)所确定的莫尔圆几何关系,即 $$\dfrac{\sqrt {\left( {\sigma _{1{\rm t}} - \sigma _{3{\rm t}} } \right)^2 / 4 + \tau _{13{\rm t}}^2 } }{\left( {\sigma _{1{\rm t}} + \sigma _{3{\rm t}} } \right) / 2 + c_{{\rm tt}} \cot {\phi }'_{\rm t} } = \sin {\phi }'_{\rm t} \tag{8}$$ 因在路堤坡脚边缘下$B /4$深度范围内,其塑性区应力($\sigma _{\rm 1t } - \sigma_{\rm 3t})/2>\tau_{\rm 13t} >0$成立[22, 24, 34],满足数学近似公式$\sqrt {s^2 + t^2} \approx 1.0s + 0.38t$ [34]的使用条件(当$5t ≥ s > t > 0$时,相对误差小于7%;当$s > 5t> 0$时,相对误差小于5%)[35],进而简化式(8)得 $$ \dfrac{\sigma _{1{\rm t}} - \sigma _{3{\rm t}} }{2} + 0.38\tau _{13{\rm t}} = \dfrac{\sigma _{1{\rm t}} + \sigma _{3{\rm t}} }{2}\sin {\phi }'_{\rm t} +\\ \left[{c'_{\rm t} + \left( {u_{\rm a} - u_{\rm w} } \right)\tan \phi _{\rm t}^{\rm b} } \right]\cos {\phi }'_{\rm t} \tag{9}$$ 将式(7)代入式(9),整理得塑性区开展深度$Z$为
$ \left( {Z + \dfrac{\gamma _{\rm h} }{\gamma _{\rm s} }h} \right)\cdot \dfrac{ \pi \gamma _{\rm s} }{2} = $ $\quad \dfrac{\eta p\left( {\beta _0 \sin {\phi }'_{\rm t} - \sin \beta _0 } \right) + \pi \left[{c'_{\rm t} + \left( {u_{\rm a} - u_{\rm w} } \right)\tan \phi _{\rm t}^{\rm b} } \right]\cos {\phi }'_{\rm t} }{\left( {1 - k_{\rm o} } \right)\cos (2\beta _1) + 0.38\left( {1 - k_{\rm o} } \right)\sin (2\beta _1) - \left( {1 + k_{\rm o} } \right)\sin {\phi }'_{\rm t} } \tag{10}$
当硬壳层与地基非饱和软土的性质一定时,$Z$仅是夹角 $\beta_{0}$和$\beta_{1}$的函数.为求塑性区最大开展 深度$Z_{\max}$,由$\partial Z / \partial \beta _0 = 0$和$\partial Z / \partial \beta _1 = 0$得 $$ \beta _0 = \pi / 2 - {\phi }'_{\rm t} ,2\beta _1 \approx 21^\circ $$
将上述关系代入式(10),整理得塑性区最大开展深度$Z_{\max}$为 $$ \left[{Z_{\max } + \dfrac{\gamma _{\rm h} }{\gamma _{\rm s} }h} \right]\cdot \dfrac{{\pi }\gamma _{\rm s} }{2} = \\ \dfrac{\eta p\left[{\left( {{\pi } / 2 - {\phi }'_{\rm t} } \right)\tan {\phi }'_{\rm t} - 1} \right] + {\pi }\left[{c_{\rm t} ' + \left( {u_{\rm a} - u_{\rm w} } \right)\tan \phi _{\rm t}^{\rm b} } \right]}{1.07\left( {1 - k_{\rm o} } \right) / \cos {\phi }'_{\rm t} - \left( {1 + k_{\rm o} } \right)\tan {\phi }'_{\rm t} } \tag{11}$$
若塑性区最大开展深度$Z_{\max}$为0,即$Z_{\max }= 0$,则由式(11)得硬壳层非饱和软土地基的临塑载荷$p_{\rm cr}$为 $$ p_{{\rm cr}} = M_{\rm h} \gamma _{\rm h} h + M_{\rm C} \left[{c'_{\rm t} + \left( {u_{\rm a} - u_{\rm w} } \right)\tan \phi _{\rm t}^{\rm b} } \right] \tag{12}$$
若塑性区最大开展深度$Z_{\max}$为路堤等效宽度$B$的1/4,即$Z_{\max}=B /4$,则由式(11)得硬壳层非饱和软土地基的临界载荷$p_{1 / 4}$为 $$ p_{1 / 4} = M_{\rm B} \gamma _{\rm s} B + M_{\rm h} \gamma _{\rm h} h + M_{\rm C} \left[{c'_{\rm t} + \left( {u_{\rm a} - u_{\rm w} } \right)\tan \phi _{\rm t}^{\rm b} } \right] \tag{13}$$ 式中,$M_{\rm B}$,$M_{\rm h}$和$M_{\rm C}$为地基承载力系数,其表达式分别为 $$ \left.\!\! M_{\rm B} = \dfrac{{\pi }\left[{\left( {1 + k_{\rm o} } \right)\tan {\phi }'_{\rm t} - 1.07\left( {1 - k_{\rm o} } \right) / \cos {\phi }'_{\rm t} } \right]}{8\eta \left[{1 - \left( {\dfrac{{\pi }}{2} - {\phi }'_{\rm t} } \right)\tan {\phi }'_{\rm t} } \right]} \\ M_{\rm h} = 4M_{\rm B} ,M_{\rm C} = \dfrac{{\pi }}{\eta \left[{1 - \left( {\dfrac{{\pi }}{2} - {\phi }'_{\rm t} } \right)\tan {\phi }'_{\rm t} } \right]} \!\!\right\} \tag{14}$$
设路堤临塑填土高度为$H_{\rm cr}$,根据地基临塑载荷$p_{\rm cr}$是由路堤填土自重而引起的,即 $$ p_{{\rm cr}} = H_{{\rm cr}} \gamma _{\rm m} \tag{15}$$
将式(12)代入式(15),整理得硬壳层非饱和软土地基上路堤临塑填土高度$H_{\rm cr}$的解析解为 $$ H_{{\rm cr}} = \dfrac{M_{\rm h} \gamma _{\rm h} h + M_{\rm C} \left[{c'_{\rm t} + \left( {u_{\rm a} - u_{\rm w} } \right)\tan \phi _{\rm t}^{\rm b} } \right]}{\gamma _{\rm m} } \tag{16}$$
设路堤临界填土高度为$H_{1 / 4}$,同样根据地基临界载荷$p_{1 / 4}$是由路堤填土自重而引起的,即 $$ p_{1 / 4} = H_{1 / 4} \gamma _{\rm m} \tag{17}$$
将式(13)代入式(17),整理得硬壳层非饱和软土地基上路堤临界填土高度$H_{1 / 4}$的解析解为 $$ H_{1 / 4} = \dfrac{M_{\rm B} \gamma _{\rm s} B + M_{\rm h} \gamma _{\rm h} h + M_{\rm C}\left[{c'_{\rm t} + \left( {u_{\rm a} - u_{\rm w} } \right)\tan \phi_{\rm t}^{\rm b} } \right]}{\gamma _{\rm m} } \tag{18}$$
2.3 适用条件由2.2节可以看出:硬壳层非饱和软土的地基临塑载荷式(12)与路堤临塑填土高度式(16),都是有两项组成的:一项与硬壳层的自重 $\gamma_{\rm h}h$有关,另一项与地基土的统一总黏聚力$c_{\rm tt}$有关;而地基临界载荷式(13)与路堤临界填土高度式(18)都是有三项组成的,相比前者多了与地基土自重 $\gamma_{\rm s}B$有关的一项.不管是由两项还是三项组成,依据经典地基承载力的非负叠加原理[36],每项对地基承载力及路堤填土高度都应具有积极的正作用,即都应是非负的,进而得本文解析公式的适用条件为 $$ \left.\!\! M_{\rm B} = \dfrac{{\pi }\left[{\left( {1 + k_{\rm o} } \right)\tan {\phi }'_{\rm t} - 1.07\left( {1 - k_{\rm o} } \right) / \cos {\phi }'_{\rm t} } \right]}{8\eta \left[{1 - \left( {\dfrac{{\pi }}{2} - {\phi }'_{\rm t} } \right)\tan {\phi }'_{\rm t} } \right]} ≥ 0 \\ M_{\rm h} = 4M_{\rm B} ≥ 0 \\ M_{\rm C} = \dfrac{{\pi }}{\eta \left[{1 - \left( {\dfrac{{\pi }}{2} - {\phi }'_{\rm t} } \right)\tan {\phi }'_{\rm t} } \right]} ≥ 0 \!\!\right\} \tag{19}$$
同时结合上硬下软复合地层的应力扩散规律,整理得对应力扩散系数 $\eta $、地基土的有效内摩擦角$\phi' $及侧压力系数$k_{\rm o}$的要求分别为 $$ \left.\!\! 0 < \eta ≤ 1 \\ \left( {\dfrac{\pi }{2} - {\phi }'_{\rm t} } \right)\tan {\phi}'_{\rm t} <1 \\ k_{\rm o} ≥ \dfrac{1.07 - \sin {\phi }'_{\rm t} }{1.07 + \sin {\phi}'_{\rm t} } \!\!\right\} \tag{20}$$
由式(20)知,本文解析公式对侧压力系数$k_{\rm o}$有最小值要求,参数$b$即中间主应力$\sigma_{2}$效应不同,则对应要求的侧压力系数$k_{\rm o}$最小值亦不同;地基土有效内摩擦角 $\phi'$需满足隐式不等关系,应力扩散系数$\eta \in (0,1]$是对硬壳层应力扩散作用的保障.只有适用条件式(20)成立后,本文所得硬壳层非饱和软土地基的临塑载荷式(12)、临界载荷式(13)、路堤临塑填土高度式(16)与临界填土高度式(18)的计算结果才有效.
2.4 应用步骤针对某一具体的硬壳层非饱和软土路堤工程,需首先确定地基软土的物理力学指标、硬壳层厚度与变形等参数,进而利用式(20)对侧压力系数$k_{\rm o}$、有效内摩擦角 $\phi' $及应力扩散系数 $\eta $ 进行适用性验证,满足后依据式(14)确定地基承载力系数,继而由式(12)和式(13)可分别求出该地基的临塑载荷$p_{\rm cr}$与临界载荷$p_{1 / 4}$,最后由式(16)求得路堤临塑填土高度$H_{\rm cr}$、由式(18)求得路堤临界填土高度$H_{1/ 4}$. 在此求解过程中,可令某一个参数如硬壳层厚度$h$、硬壳层弹性模量$E_{\rm h}$、基质吸力$u_{\rm a } -u_{\rm w}$等,在其适用范围内变化而其他参数保持不变,从而建立路堤填土高度随该参数的变化关系,以进行影响特性分析并找出关键因素.
3 可比性分析及对比验证 3.1 可比性分析本文建立的硬壳层非饱和软土地基承载力即式(12)与式(13)、路堤填土高度即式(16)与式(18),考虑了硬壳层应力扩散作用即应力扩散系数 $\eta $、自重$\gamma_{\rm h}h$反压护道作用,非饱和强度特性即基质吸力$u_{\rm a} - u_{\rm w}$及高低吸力,中间主应力$\sigma _{2}$效应即参数$b$,以及地基土实际应力状态即侧压力系数$k_{\rm o } e1.0$等4种因素的综合影响,具有重要的理论意义与广泛的工程应用前景. 当 $\eta = 1$及 $\gamma_{\rm h } = 0$时,对应无硬壳层均一单层软土地基的解答;$u_{\rm a } - u_{\rm w } > 0$对应非饱和软土地基的解答,而$u_{\rm a } - u_{\rm w} = 0$则对应饱和软土地基的解答;参数$b =0$时为莫尔--库仑准则解答,参数$b = 1$时为双剪应力理论解答,$0 < b <1$时为一系列新的有序解答;当$k_{\rm o } = 1$时,对应地基土自重应力场如同静水压力时的解答.
对4种因素采取不同的组合时,本文解析公式可退化为众多已有解答,如:当 $\eta = 1$,$\gamma _{\rm h } = 0$,$k_{\rm o } = 1.0$,$b = 0$,$u_{\rm a }- u_{\rm w } = 0$时,对应单层饱和软土地基处于静水自重应力场时的莫尔-库仑解答[36];当 $\eta = 1$,$\gamma _{\rm h } = 0$,$b = 0$,$u_{\rm a } - u_{\rm w} = 0$时,对应单层饱和软土地基的莫尔--库仑解答[34];当$\eta = 1$,$\gamma _{\rm h } = 0$时,对应单层非饱和软土地基的统一强度理论解答?[22, 24];当$u_{\rm a } - u_{\rm w } = 0$时,对应硬壳层饱和软土地基的统一强度理论解答[12].因此,本文所得解析公式具有很好的可比性,同时还包含更多未见发表的新解答,可供实际工程根据具体情况做出合理选择,这也是对本文所得解析公式进行的必要性验证.
3.2 对比验证朱福等[12]基于统一强度理论建立了硬壳层饱和软土地基临塑载荷、临界载荷与路堤临塑填土高度、临界填土高度的解析解,考虑了中间主应力和侧压力系数$k_{\rm o } e 1.0$的影响,其分析思路及推导过程与本文有类似之处.用本文符号与参数表示的文献[12]路堤临界填土高度$H_{1 / 4}$为 $$ H_{1 / 4} = \dfrac{M_{\rm B} \gamma _{\rm s} B + M_{\rm h} \gamma _{\rm h} h + M_{\rm C} c'_{\rm t} } {\gamma _{\rm m} } \tag{21}$$
式(21)中的地基承载力系数$M_{\rm B}$,$M_{\rm h}$和$M_{\rm C}$以及应力扩散系数 $\eta $ 分别为 $ \left.\!\! M_{\rm B} = \dfrac{{ \pi}\left[{\left( {1 + k_{\rm o} } \right)\tan {\phi }'_{\rm t} - \left( {1 - k_{\rm o} } \right) / \cos {\phi }'_{\rm t} } \right]}{8\eta \left[{1 - \left( {\dfrac{{\pi }}{2} - {\phi }'_{\rm t} } \right)\tan {\phi }'_{\rm t} } \right]} \\ M_{\rm h} = 4M_{\rm B} \\ M_{\rm C} = \dfrac{{\pi }}{\eta \left[{1 - \left( {\dfrac{{\pi }}{2} - {\phi }'_{\rm t} } \right)\tan {\phi }'_{\rm t} } \right]} \\ \eta = d\sqrt {B / h} + e \!\!\right\} \tag{22}$
对比本文式(4)、式(14)、式(18)以及式(20)可以看出,本文与文献[12]的临界填土高度$H_{1 /4}$之间存在4点差异:一是本文采用的是非饱和土强度理论并考虑了基质吸力及高低吸力的不同影响;二是文献[12]的应力扩散系数$\eta $ 公式中遗漏($E'_{\rm s} /E'_{\rm h} )^{1 / 4}$项,导致应力扩散系数 $\eta $大于1;三是本文依据均布载荷作用下条形基础的地基塑性区发展规律,由两个偏导数为零求得塑性区最深处在基础两侧边缘下方,而不在基础中心线处,这体现在地基承载力系数$M_{\rm B}$和$M_{\rm h}$有所差异;四是本文给出了公式的适用条件,对应力扩散系数 $\eta $、地基土有效内摩擦角$\phi' $及侧压力系数$k_{\rm o}$的取值范围进行了限制.
假设地基软土处于完全饱和状态,仅以路堤临界填土高度$H_{1 / 4}$来比较后3点差异所造成的结果不同.某天然公路工程的梯形 路堤[8, 12]:路堤等效宽度$B = 12$ m,填土平均重度 $\gamma_{\rm m }=20$ kN/m$^{3}$;硬壳层的厚度$h = 3$ m、重度 $\gamma_{\rm h }= 18.4$ kN/m$^{3}$、弹性模量$E_{\rm h } =16$ MPa和泊松比$u _{\rm h } = 0.25$;地基软土的重度 $\gamma_{\rm s }= 17.4$ kN/m$^{3}$、弹性模量$E_{\rm s}= 3$ MPa和泊松比$u _{\rm s }= 0.42$,有效黏聚力$c' = 10$ kPa、有效内摩擦角 $\phi' = 8^{\rm o}$.表1给出了本文路堤临界填土高度式(18)与朱福等[12]、修正朱福等[12](应力扩散系数$\eta $中增加($E'_{\rm s}/E'_{\rm h} )^{1 / 4}$ 项)的计算结果比较,其中参数$b$取0,0.5和1.
由式(20)计算知:有效内摩擦角 $\phi'= 8^{\rm o}$满足本文公式适用条件,但侧压力系数$k_{\rm o}$应分别不小于0.77 ($b = 0$)、0.74 ($b= 0.5$)、0.72 ($b = 1.0$),因此侧压力系数$k_{\rm o } = 0.5$不满足公式适用条件,本文对此无解,相反文献[12]以及修正文献[12]给出的临界填土高度$H_{1 / 4}$为负或接近为零,这是因为$k_{\rm o}=0.5$时地基承载力系数$M_{\rm B}$与$M_{\rm h}$都是负的,与经典地基承载力的非负叠加理论有悖,也与类似工程及地基土依据施工经验所确定的填土高度相差甚远,可见本文给定公式适用条件的必要性和合理性.
当侧压力系数$k_{\rm o } =1.0$,0.8时,文献[12]的临界填土高度$H_{1 /4}$均小于修正文献[12]以及本文的,这主要是因为缺少($E'_{\rm s} /E'_{\rm h} )^{1 / 4}$项的应力扩散系数$\eta $大于1,与上硬下软双层地基的实际应力扩散规律不符,以致形成应力集中降低了地基土的承载力及填土高度;另外,即使增加了($E'_{\rm s} /E'_{\rm h} )^{1 / 4}$项改正应力扩散系数 $\eta $ 后,虽然$k_{\rm o } =1.0$时结果相同(此时本文地基承载力系数$M_{\rm B}$和$M_{\rm h}$与文献[12]的无差异),但是修正文献[12]的结果在$k_{\rm o} = 0.8$时却大于本文结果,且参数$b$越大,二者之间的差异越明显,这表明基础中心线处的地基塑性区发展深度并不是最大的,修正文献[12]的计算结果偏大,以此进行的路堤设计与施工偏于危险. 因此,本文解析公式采用了表达正确的应力扩散系数$\eta $,合理地考虑了地基土的塑性区实际发展情况,并给出了公式的适用条件及应用步骤,较文献[12]及修正文献[12]的解答均具有更大的优越性.
4 参数影响规律为探究硬壳层、侧压力系数、中间主应力以及基质吸力等4种因素对路堤临界填土高度$H_{1 / 4}$的影响规律,此处仍选择3.2节的公路路堤为分析对象,作为参数分析的共同基础.为弄清单个因素的影响特性且计算简单,在硬壳层、侧压力系数和中间主应力影响分析中,令基质吸力$u_{\rm a } - u_{\rm w}$为零即按完全饱和土地基进行求解;在基质吸力影响分析中,着重考察地基土的非饱和强度特性影响.
对公式适用条件式(20)的说明:有效内摩擦角 $\phi' = 8^{\rm o}$满足要求,但侧压力系数$k_{\rm o}$应分别不小于0.77($b = 0$)、0.74 ($b = 0.5$)、0.72 ($b = 1.0$). 因此,下文侧压力系数影响分析时$k_{\rm o}$从最小值开始取到1.0,中间主应力影响分析时$k_{\rm o}$取3个值(0.8,0.9和1.0),硬壳层及基质吸力影响分析时$k_{\rm o}$取0.85;由式(4)知,只有在硬壳层影响分析中,应力扩散系数 $\eta $才有变化,但均属于(0,1]区间,满足公式适用条件的要求.
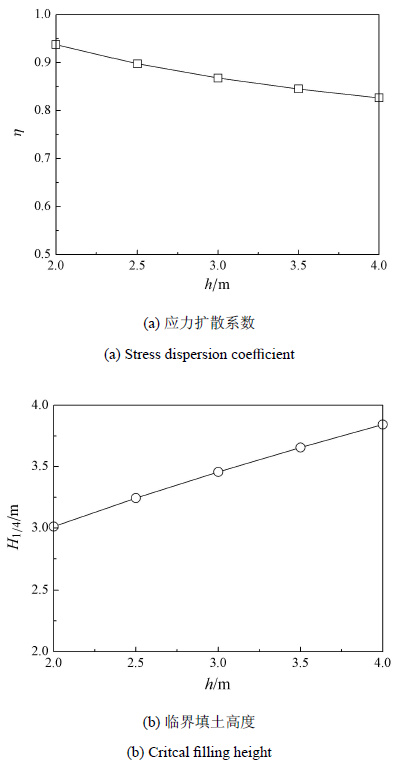
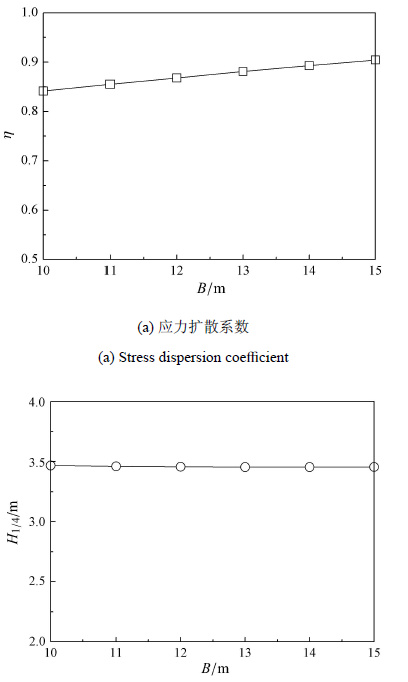
4.1 硬壳层硬壳层的厚度$h$、弹性模量$E_{\rm h}$以及路堤等效宽度$B$均会影响硬壳层的应力扩散程度即应力扩散系数 $\eta $,进而影响地 基应力分布及路堤填土高度. 图3 $\sim $图5分别给出了侧压力系数$k_{\rm o }= 0.85$、参数$b = 0.5$时,应力扩散系数 $\eta $、路堤临界填土高度$H_{1 / 4}$随硬壳层厚度$h$、弹性模量$E_{\rm h}$以及路堤等效宽度$B$的变化关系.
|
图3 硬壳层厚度的影响特性 Fig.3 Influence of the stiff crust thickness |
由图3和图4可以看出,随着硬壳层厚度$h$、弹性模量$E_{\rm h}$的增加,应力扩散系数 $\eta $逐渐减小,进而临界填土高 度$H_{1 / 4}$不断增大,即厚度$h$由2.0 m增加到4.0 m,$\eta $ 减小0.11,$H_{1 / 4}$相对增大27.6%;弹性模量$E_{\rm h}$由12 MPa增加到20 MPa,$\eta $ 减小0.06,$H_{1 /4}$相对增大6.6%,可见厚度$h$的影响较弹性模量$E_{\rm h}$更明显.若不考虑硬壳层影响按均一饱和软土地基进行分析,即令 $\eta = 1$,$\gamma _{\rm h } = 0$且$h = 3.0$ m,$E_{\rm h } = 16$ MPa,$b = 0.5$和$k_{\rm o } = 0.85$,可求得$H_{1 / 4}$ 仅为2.47 m,明显低于图3和图4中$H_{1 /4}$的变化范围,这说明硬壳层的影响是整体性的,需综合考虑厚度$h$和弹性模量$E_{\rm h}$的变化,并注意保护硬壳层的工程特性,合理利用其应力扩散和反压护道作用.
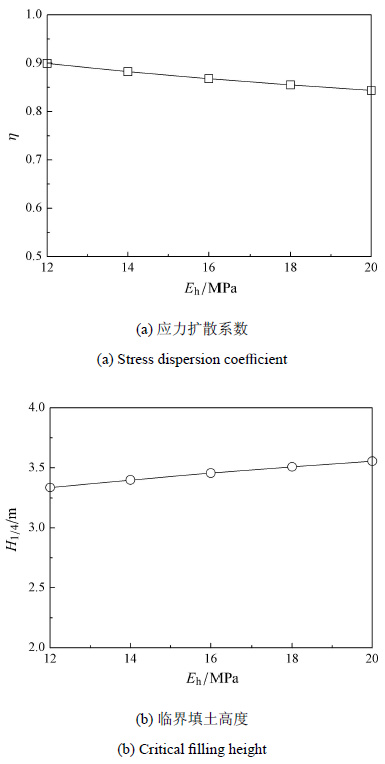
|
图4 硬壳层弹性模量的影响特性 Fig.4 Influence of the stiff crust Young’s modulus |
由图5可以看出,路堤等效宽度$B$对应力扩散系数 $\eta $ 的影响较大,但对临界填土高度$H_{1 /4}$的影响几乎可以忽略,这是因为宽度$B$对临界填土高度$H_{1 /4}$式(18)的分子和分母均有增加效果,且二者增加的速率相当,进而上下做比抵消,使得$H_{1 / 4}$呈水平直线而与宽度$B$无关.
|
图5 路堤等效宽度的影响特性 Fig.5 Influence of the embankment equivalent width |
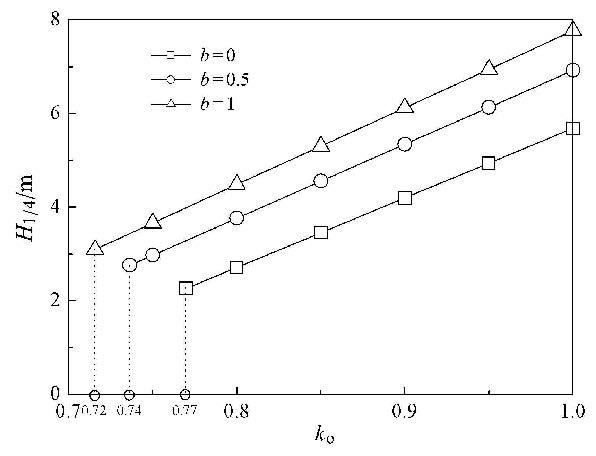
侧压力系数$k_{\rm o}$反映的是地基土的初始地应力情况,本文解析公式对其有最小值要求. 图6给出了参数$b $取0,0.5和1时,路 堤临界填土高度$H_{1 / 4}$随侧压力系数$k_{\rm o}$的变化关系.
|
图6 侧压力系数的影响特性 Fig.6 Influence of the lateral pressure coefficient |
由图6可以看出,在满足最小侧压力系数$k_{\rm o}$要求即本文公式适用条件式(20)成立后,临界填土高度$H_{1 /4}$随$k_{\rm o}$线性 显著增加,即$k_{\rm o}$对$H_{1 / 4}$具有重要影响,应合理测定地基土的真实$k_{\rm o}$,而不是人为地设定其恒为1.0,得到不切实际过大的填土高度;参数$b$即中间主应力$\sigma_{2}$效应越大,最小侧压力系数$k_{\rm o}$却越小,由0.77减小到0.72,表明本文解析公式的适用范围变的更广; 在不同参数$b$下,临界填土高度$H_{1 /4}$之间相互平行,且参数$b$越大,所对应的$H_{1 / 4}$亦越高.
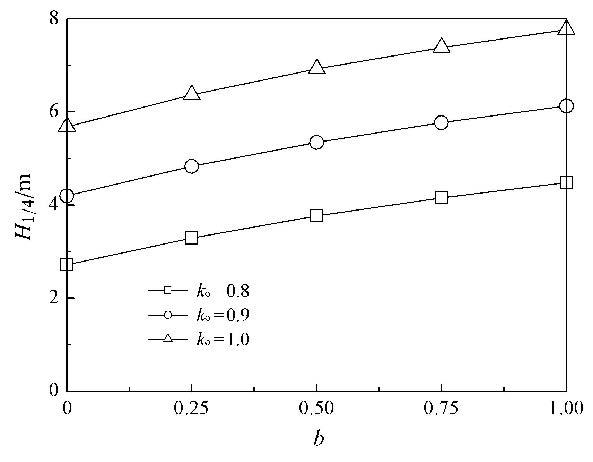
4.3 中间主应力平面应变状态下土体强度具有明显的中间主应力$\sigma_{2}$效应,且不同土体的$\sigma_{2}$效应不同,同时参数$b$也是不 同强度准则的选取参数.图7给出了侧压力系数$k_{\rm o }$为 0.8,0.9和1.0时,路堤临界填土高度$H_{1 / 4}$随参数$b$的变化关系.
|
图7 中间主应力的影响特性 Fig.7 Influence of the intermediate principal stress |
由图7可以看出,随着参数$b$的增加,临界填土高度$H_{1/4}$非线性增大,$b = 1$时的$H_{1/4}$比$b = 0$时分别相对增大了65.3% ($k_{\rm o } = 0.8$),45.9% ($k_{\rm o } = 0.9$),36.7% ($k_{\rm o } = 1.0$),表明临界填土高度$H_{1/4}$的强度理论效应显著,即采用不同强度准则计算得到的$H_{1/4}$差异显著,且侧压力系数$k_{\rm o}$越小,强度理论效应表现的越明显;由参数$b = 0$即不考虑中间主应力 $\sigma _{2}$影响的莫尔-库仑准则得到的$H_{1/4}$过于保守,应合理考虑土体强度的中间主应力$\sigma_{2}$效应,充分发挥地基土的强度潜能和自承载能力;不同侧压力系数$k_{\rm o}$下,临界填土高度$H_{1/ 4}$之间亦相互平行,且$k_{\rm o}$越大,所对应的$H_{1/4}$同样亦越高.
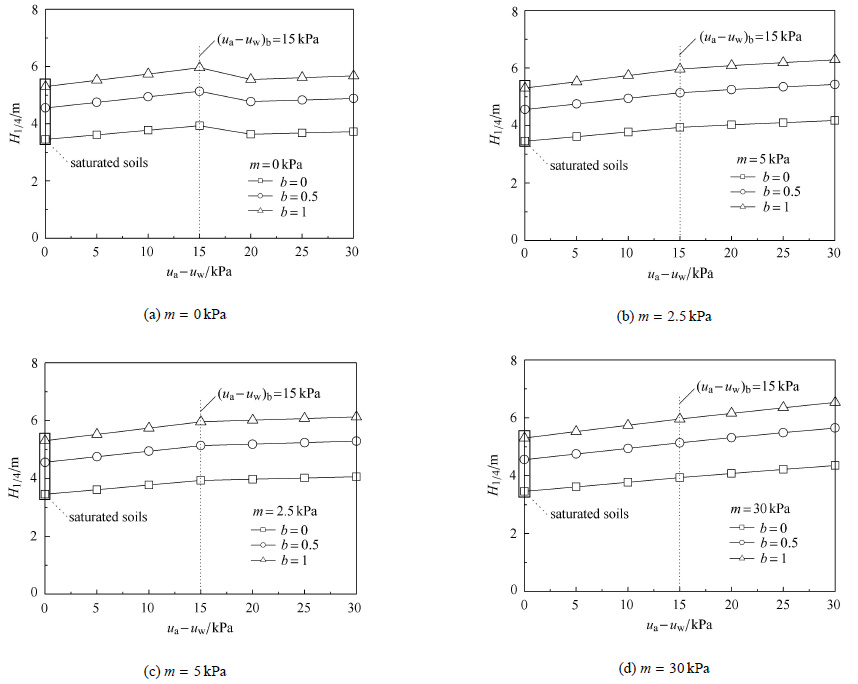
4.4 基质吸力当土体中溶质浓度不高即溶质吸力较小时[17],基质吸力成为非饱和土的基本属性,且单从非饱和土的抗剪强度组成式(1)来看,基质吸力为零则非饱和土变为完全饱和土;同时,高低吸力对非饱和土强度的影响特性不同.此处设定非饱和土的进气值($u_{\rm a } - u_{\rm w})_{\rm b } = 15$ kPa,进而由吸力角双曲线模型式(2)知:处于不大于15 kPa的低吸力范围时,$\phi^{\rm b }=\phi' = 8^{\circ}$;处于大于15 kPa的高吸力范围时,吸力角$\phi^{\rm b}$按双曲线模型式(2b)变化,且由式(3)求得斜率$n = 0.178 2$,截距$m$分别取0,2.5,5和30 kPa,以体现高吸力下吸力角 $\phi^{\rm b}$的不同变化速率.图8给出了当参数$b $为 0,0.5和1时,路堤临界填土高度$H_{1 / 4}$随基质吸力的变化关系.
|
图8 基质吸力的影响特性 Fig.8 Influence of the matric suction |
由图8可以看出,临界填土高度$H_{1 / 4}$在进气值($u_{\rm a } -u_{\rm w})_{\rm b } =15$ kPa处出现峰值(当$m=0$时)或转折(当$m>0$时),被分成变化规律明显不同的左右2段:左边的直线增加段对应低吸力情况,$H_{1 /4}$与截距$m$无关;而右边的区段则对应高吸力情况,$H_{1 / 4}$的变化与截距$m$密切相关. 图8(a)中截距$m = 0$即由式(2)和式(3)知:吸力角$\phi^{\rm b}$在整个高吸力范围内都恒为$\phi' - 1/n = 2.459 8 - 0.022 5\phi' \approx 2.3^{\circ}$,与低吸力时的8$^{\circ}$相差近2.5倍之多,因此$H_{1 /4}$才会出现峰值,且其后随基质吸力的增加先逐渐减小后缓慢增大;图8(b) $\sim $图8(d)中截距$m > 0$对应进气值处存在转折,说明左右两边$H_{1 /4}$的变化规律不同,但截距$m$越大,转折趋势就越不明显即两边的差异越小,截距$m = 30 $ kPa时已几乎看不出两边的差异. 另外,不同参数$b$所对应的$H_{1 / 4}$之间相互平行,且参数$b$大的$H_{1 /4}$亦越高.
实际上,图8中临界填土高度$H_{1 /4}$右段的变化反映的正是高吸力下非饱和土强度非线性的影响,即基质吸力对非饱和土强度具有双重影响:一是基质吸力对强度提高的效应,基质吸力越大,这种提高效应就越强;二是基质吸力通过减小吸力角 $\phi^{\rm b}$使强度降低的影响,基质吸力越大,这种降低影响也越强.这两种相反作用的相对大小决定了非饱和土的强度变化,进而影响高吸力下临界填土高度$H_{1 / 4}$的变化.图8可分为2种情况:(1) 当截距$m = 0$时,高吸力范围内$H_{1 / 4}$随基质吸力的增加先逐渐减小后缓慢增大,这是由于吸力角 $\phi^{\rm b } \approx 2.3^{\rm o}$使降低的影响已超过基质吸力提高的效应,但随着基质吸力的进一步增大,基质吸力提高的效应增加较快,并略超过吸力角$\phi^{\rm b}$降低的影响;(2) 当截距$m$为2.5,5和30 kPa时,高吸力范围内$H_{1 / 4}$随基质吸力的增加逐渐增大,只是增大的速率略有不同,这表明吸力角 $\phi^{\rm b}$降低的影响小于基质吸力提高的效应,基质吸力提高的效应占据主导地位,截距$m = 30 $ kPa时表现的最为明显. 因此,应深刻认识基质吸力对非饱和土强度的双 重影响特性,才能了解并掌握临界填土高度$H_{1 / 4}$ 的真实变化规律,进而利用非饱和土地基的$H_{1 /4}$明显高于饱和土的特点,优化路堤填土高度设计与 施工.
5 结 论(1)本文建立的硬壳层非饱和软土地基临塑/临界载荷、路堤临塑/临界填土高度的解析公式,综合考虑了硬壳层、基质吸力、中间主应力以及侧压力系数等4种因素影响,能退化为众多已有解答,同时还包含很多新解答,可适用于更多工程的具体情况,具有重要的理论意义与实际应用价值.
(2) 考虑硬壳层的应力扩散作用和自重反压护道作用,符合尽量利用硬壳层弹性工作状态的原则;经与文献[12]及修正文献[12]比较,验证了本文解析公式的正确性以及所给公式适用条件的必要性与合理性,同时也说明地基土的塑性区最深点不在条形基础中心线,本文解答具有更大的优越性.
(3)硬壳层的影响具有整体性,应同时考虑其厚度和弹性模量的变化,路堤等效宽度的影响可以忽略,需注意保护硬壳层的工程特性;侧压力系数$k_{\rm o}$对临界填土高度的影响明显,$k_{\rm o}=1.0$时的填土高度不切实际,应原位测试确定地基土的真实$k_{\rm o}$,同时应采用 满足解析公式适用条件的$k_{\rm o}$.
(4)临界填土高度的强度理论效应显著,莫尔-库仑准则的结果过于保守,应充分考虑中间主应力的影响;高、低吸力对临界填土高度的影响不同,低吸力时填土高度线性增加与截距无关,高吸力时受双重作用相对大小的控制,填土高度或先逐渐减小后缓慢增大、或逐渐增大,与截距密切相关.
| [1] | 郝传毅, 陈国靖. 硬壳层软土地基的工程特性. 中国公路学报, 1993, 6(2):68-74(Hao Chuanyi, Chen Guojing. Engineering features of soft subgrade with relatively hard clay shell. China Journal of Highway and Transport, 1993, 6(2):68-74(in Chinese)) |
| [2] | 董志良, 张功新, 周琦等. 天津滨海新区吹填造陆浅层超软土加固技术研发及应用. 岩石力学与工程学报, 2011, 30(5):1073-1080(Dong Zhiliang, Zhang Gongxin, Zhou Qi, et al. Research and application of improvement technology of shallow ultra-soft soil formed by hydraulic reclamation in Tianjin Binhai new area. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(5):1073-1080(in Chinese)) |
| [3] | 闫澍旺, 郭炳川, 孙立强等. 硬壳层在吹填土真空预压中的应用. 岩石力学与工程学报, 2013, 32(7):1497-1503(Yan Shuwang, Guo Bingchuan, Sun Liqiang, et al. Application of crust layer to vacuum preloading dredge fill. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(7):1497-1503(in Chinese)) |
| [4] | 杨果林. 硬壳层软土地基极限承载力研究. 湘潭矿业学院学报, 1995, 10(2):51-56(Yang Guolin. Study of ultimate bearing capacity of a soft soil foundation with a hard clay shell. Journal of Xiangtan Mining Institute, 1995, 10(2):51-56(in Chinese)) |
| [5] | 袁凡凡, 栾茂田, 闫澍旺等. 非均质介质破坏机制及承载力的有限元分析. 岩石力学与工程学报, 2005, 24(6):929-933(Yuan Fanfan, Luan Maotian, Yan Shuwang, et al. Finite element analysis on failure mechanism and bearing capacity behavior of inhomogeneous subsoil. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(6):929-933(in Chinese)) |
| [6] | 张其一, 栾茂田. 复合加载情况下双层地基极限承载力研究. 岩土力学, 2009, 30(4):1131-1136(Zhang Qiyi, Luan Maotian. Study of ultimate bearing capacity of two-layered subsoil under combined loading. Rock and Soil Mechanics, 2009, 30(4):1131-1136(in Chinese)) |
| [7] | Avesani-Neto JO, Bueno BS, Futai MM. A bearing capacity calculation method for soil reinforced with a geocell. Geosynthetics International, 2013, 20(3):129-142 |
| [8] | 王晓谋. 考虑硬壳层作用的软土地基临塑载荷计算. 岩土工程学报, 2002, 24(6):720-723(Wang Xiaomou. Calculation of proportional limit load for soft clay foundation involving the effect of dry crust. Chinese Journal of Geotechnical Engineering, 2002, 24(6):720-723(in Chinese)) |
| [9] | 王晓谋, 尉学勇, 魏进等. 硬壳层软土地基竖向附加应力扩散的数值分析. 长安大学学报(自然科学版), 2007, 27(3):37-41(Wang Xiaomou, Yu Xueyong,Wei Jin, et al. Numerical analysis of vertical additional stress spreading on soft clay foundation with dry crust. Journal of Chang'an University(Natural Science Edition), 2007, 27(3):37-41(in Chinese)) |
| [10] | 问延煦, 周健, 贾敏才. 考虑封闭作用和应力扩散的软土地基临塑载荷. 岩土力学, 2007, 28(8):1715-1718(Wen Yanxu, Zhou Jian, Jia Mincai. Critial edge pressure of soft clay foundation considering closure effect and stress dispersion of crust. Rock and Soil Mechanics, 2007, 28(8):1715-1718(in Chinese)) |
| [11] | 问延煦, 周健. 封闭作用对双层地基临塑载荷的影响. 岩土工程学报, 2008, 30(5):685-689(Wen Yanxu, Zhou Jian. Critical edge pressure analysis of two-layered ground considering closure effect. Chinese Journal of Geotechnical Engineering, 2008, 30(5):685-689(in Chinese)) |
| [12] | 朱福, 战高峰, 佴磊. 天然软土地基路堤临界高度一种计算方法研究. 岩土力学, 2013, 34(6):1738-1744(Zhu Fu, Zhan Gaofeng, Nie Lei. Study of a calculation method of critical height of embankment on natural soft soil foundation. Rock and Soil Mechanics, 2013, 34(6):1738-1744(in Chinese)) |
| [13] | 徐洋. 复合双层地基应力扩散效应研究.[学位论文]. 南京:河海大学, 2001(Xu Yang. Research on the effect of stress dispersion in compound two-layer foundation.[Dessertation]. Nanjing:Hohai University, 2001(in Chinese)) |
| [14] | Lu N, Likos WJ. Unsaturated Soil Mechanics. New York:John Wiley and Sons, lnc., 2004:3-40 |
| [15] | Fredlund DG, Rahardjo H, Fredlund MD. Unsaturated Soil Mechanics in Engineering Practices. New York:John Wiley and Sons, lnc., 2012 |
| [16] | 陈正汉. 非饱和土与特殊土力学的基本理论研究. 岩土工程学报, 2014, 36(2):201-272(Chen Zhenghan. On basic theories of unsaturated soils and special soils. Chinese Journal of Geotechnical Engineering, 2014, 36(2):201-272(in Chinese)) |
| [17] | 赵成刚, 韦昌富, 蔡国庆. 土力学理论的发展和面临的挑战. 岩土力学, 2011, 32(12):3521-3540(Zhao Chenggang, Wei Changfu, Cai Guoqing. Development and challenge for soil mechanics. Rock and Soil Mechanics, 2011, 32(12):3521-3540(in Chinese)) |
| [18] | Matsuoka H, Sun DA, Kogane A, et al. Stress-strain behaviour of unsaturated soil in true triaxial tests. Canadian Geotechnical Journal, 2002, 39(3):608-619 |
| [19] | Zhang CG, Chen XD, Fan W, et al. A new unified failure criterion for unsaturated soils. Environmental Earth Sciences, 2015, 74(4):3345-3356 |
| [20] | Nanda S, Patra NR. Determination of soil properties for plane strain condition from the triaxial tests results. International Journal for Numerical and Analytical Methods in Geomechanics, 2015, 39(9):1014-1026 |
| [21] | 张常光, 张庆贺, 赵均海. 非饱和土抗剪强度及土压力统一解. 岩土力学, 2010, 31(6):1871-1876(Zhang Changguang, Zhang Qinghe, Zhao Junhai. Unified solutions of shear strength and earth pressure for unsaturated soils. Rock and Soil Mechanics, 2010, 31(6):1871-1876(in Chinese)) |
| [22] | 张常光, 胡云世, 赵均海. 平面应变条件下非饱和土抗剪强度统一解及其应用. 岩土工程学报, 2011, 33(1):32-37(Zhang Changguang, Hu Yunshi, Zhao Junhai. Unified solution of shear strength for unsaturated soil under plane strain condition and its application. Chinese Journal of Geotechnical Engineering, 2011, 33(1):32-37(in Chinese)) |
| [23] | 张常光, 赵均海, 张冬芳. 非饱和土强度非线性及对被动土压力的影响. 广西大学学报(自然科学版), 2012, 37(4):797-802(Zhang Changguang, Zhao Junhai, Zhang Dongfang. Nonlinear strength of unsaturated soils and its influence on passive earth pressure. Journal of Guangxi University(Natural Science Edition), 2012, 37(4):797-802(in Chinese)) |
| [24] | 张常光, 曾开华, 赵均海. 非饱和土临界载荷和太沙基极限承载力解析解. 同济大学学报(自然科学版), 2010, 38(12):1736-1740(Zhang Changguang, Zeng Kaihua, Zhao Junhai. Analytical solutions of critical load and Terzaghi's ultimate bearing capacity for unsaturated soil. Journal of Tongji University(Natural Science), 2010, 38(12):1736-1740(in Chinese)) |
| [25] | 张常光, 赵均海, 朱倩. 非饱和土刚性挡墙抗倾覆临界嵌固深度研究. 岩石力学与工程学报, 2014, 33(11):2360-2369(Zhang Changguang, Zhao Junhai, Zhu Qian. Critical embedment depth of rigid retaining walls in foundation pit of unsaturated soils. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(11):2360-2369(in Chinese)) |
| [26] | 张常光, 孙珊珊, 殷佳. 考虑中间主应力的非饱和土刚性挡墙抗倾覆稳定性. 四川大学学报(工程科学版), 2014, 46(6):44-48, 62(Zhang Changguang, Sun Shanshan, Yin Jia. Anti-overturning stability of a rigid retaining wall in unsaturated soils considering the intermediate principal stress. Journal of Sichuan University(Engineering Science Edition), 2014, 46(6):44-48, 62(in Chinese)) |
| [27] | 张常光, 李艳, 朱倩. 考虑中间主应力的非饱和土边坡安全系数新解. 水利水电科技进展, 2014, 34(6):27-30(Zhang Changguang, Li Yan, Zhu Qian. New safety factor of slopes in unsaturated soils by considering the intermediate principal stress effect. Advances in Science and Technology of Water Resources, 2014, 34(6):27-30(in Chinese)) |
| [28] | 俞茂宏. 岩土类材料的统一强度理论及其应用. 岩土工程学报, 1994, 16(2):1-10(Yu Maohong. Unified strength theory for geomaterials and its applications. Chinese Journal of Geotechnical Engineering, 1994, 16(2):1-10(in Chinese)) |
| [29] | Fredlund DG, Morgenstem NR, Widger RA. The shear strength of unsaturated soils. Canadian Geotechnical Journal, 1978, 15(3):313-321. |
| [30] | Gan KJ, Frelund DG. Multistage direct Shear testing of unsaturated soils. Geotechnical Testing Journal, 1988, 11(2):132-138 |
| [31] | Rassam DW, Cook F. Predicting the shear strength envelope of unsaturated soils. Geotechnical Testing Journal, 2002, 25(2):215-220 |
| [32] | Lee IM, Sung SG, Cho GC. Effect of stress state on the unsaturated shear strength of a weathered granite. Canadian Geotechnical Journal, 2005, 42(2):624-631 |
| [33] | Houston SL, Perez-Garcia N, Houston WN. Shear strength and shear-induced volume change behavior of unsaturated soils from a triaxial test program. Journal of Geotechnical and Geoenvironmental Engineering, 2008, 134(11):1619-1632 |
| [34] | 赵树德. 地基弹塑性承载力K≠1:0 时的计算公式. 西安建筑科技大学学报, 1995, 27(3):294-298(Zhao Shude. Formulation of bearing capacity of subgrade with K≠1:0. Journal of Xi'an University of Architecture & Technology, 1995, 27(3):294-298(in Chinese)) |
| [35] | 现代工程数学手册编委会. 现代工程数学手册. 武汉:华中工学院出版社, 1985(Editorial Committee of Handbook of Modern Mathematics in Science and Engineering. Handbook of modern mathematics in science and engineering. Wuhan:Huazhong Institute of Technology Press, 1985(in Chinese)) |
| [36] | 高大钊. 土力学与基础工程. 北京:中国建筑工业出版社, 1998(Gao Dazhao. Soil Mechanics and Foundation Engineering. Beijing:China Architecture and Building Press, 1998(in Chinese)) |
 2016, Vol. 48
2016, Vol. 48