城市大气边界层内由建筑物所导致的独特湍流特征是影响城市环境的关键动力因素.近年来,相关研究受到了国内外学者的广泛关注[1, 2, 3, 4, 5, 6, 7, 8, 9].
由于海洋和陆地存在的热力差异,白天稳定的向岸风通过海岸带后,在下垫面热通量作用下,通常会在海岸带形成热力内边界层或泛称对流内边界层[10]. 内边界层从海岸线开始,逐步向内陆发展. 在海岸城市的上空,热力内边界层内的流动规律除了受海岸热力条件的控制外,还取决于特殊的城市下垫面特征. 大城市由于高层建筑和街道相间而成的过流环境,导致复杂大尺度涡旋的产生及其伴随的大气边界层在城市地区的高摩阻属性,使得海岸城市上空热力内边界层的发展特点有别于相同热力条件下自然开放的海岸带. Liu等[12]对海陆风下香港地区热力内边界层的研究表明,城市覆盖区的海岸边界层特点与非城市覆盖区存在明显的差异. 尽管如此,目前国内外对海岸城市热力内边界层的高精度研究仍然比较缺乏,特别是对城市建筑物与热条件的相互作用下,边界层内扩散特征与内边界层发展特点的研究更显不足.
与早期研究城市地区大气动力过程时将城市冠层假设成均匀冠层或均匀高粗糙度下垫面相比,近年来,随着实验条件和计算机计算能力的提高,学者们开始大量采用拟形化方法对城市地区大气边界层开展研究.在这些研究中,建筑物被视为一系列几何体,通过改变几何体的尺度、热力性质及分布,可达到精细模拟城市下垫面的目的.基于拟形化处理下垫面的研究可以给研究者提供更多城市内部大气流动的细节.Inagaki等[6, 13]建立了物理模型COSMO,通过观测一系列有序排放的混凝土立方块方阵内的湍流结构,来获取拟形城市边界层内的湍流特征.Castillo等[14]以COSMO物理模型为研究对象,采用直接数值模拟(DNS)方法,探究了大气湍流结构在城市冠层内部与外部的差异.Michioka等[15]利用大涡模拟(LES)技术系统地研究了城市构筑物形态特征对大气湍流结构的影响.Philips等[8]则利用大涡模拟技术对建筑物高度、角度不同的非均一的城市内边界层进行了数值模拟,发现外部风向对非均一城市内边界层中的污染物扩散具有至关重要的作用.
本文在之前学者研究的基础上,将城市冠层进行拟形化处理为一系列有序排列的立方体块,基于高精度大涡模拟方法获得的数值结果,分析海岸城市上空热力内边界层发展的基本规律.
2 数学模型 2.1 控制方程模型控制方程采用滤波后的N-S方程和热传导方程 $$\frac{{\partial \overline {{u_i}} }}{{\partial {x_i}}} = 0\tag{1}$$ $$ \dfrac{\partial \bar {u}_i }{\partial t} + \bar {u}_j \dfrac{\partial \bar {u}_i }{\partial x_j } = - \dfrac{\partial \bar {p}^\ast }{\partial x_i } - \dfrac{\partial \tau _{ij} }{\partial x_j } + \delta _{i3} g\dfrac{\left( {\bar {\theta } - \bar {\theta }_m } \right)}{\theta _0 } +\tag{2}$$ $$ f\varepsilon _{ij3} \bar {u}_j + F_i \tag{2}$$ $$\frac{{\partial \overline \theta }}{{\partial t}} + \frac{{\partial (\overline {{u_i}} \overline {\theta )} }}{{\partial {x_i}}} = \frac{{\partial {\pi _i}}}{{\partial {x_i}}}\tag{3}$$ 其中,"$\overline {} $"表示在空间网格尺度$\varDelta = \left( {\Delta x\Delta y\Delta z} \right)^{1/3}$的滤波,向量和张量采用下标表示法,下标$i,j = 1,2,3$,$x_{i }$表示笛卡尔坐标,$t$为时间,$u_{i}$为速度,$p^\ast $为动压强,$g$为重力加速度,$F_{i}$为附加质量力,$f$为科里奥利参数,$\theta $ 为位温,$\theta_0 $为参考表面位温,$\bar {\theta }_{\rm m} $是水平方向的平均位温,$\delta _{i3} $为克罗内克函数,$\varepsilon _{ij3} $为变换单位张量. $\tau _{ij} $和$\pi _i $分别为亚格子应力与亚格子热通量.根据Smagorinsky理论,亚格子应力和亚格子热通量可以表示为 $${{\tau }_{ij}}=-2{{({{c}_{s}}\Delta )}^{2}}\overline{\left| s \right|}{{\overline{s}}_{_{ij}}}\tag{4}$$ $${\pi _i} = \frac{{{{\left( {{c_{s\Delta }}} \right)}^2}\overline {\left| s \right|} }}{{{p_r}}}\frac{{\partial \overline \theta }}{{\partial {x_i}}}\tag{5}$$ 式中,$\bar {S}_{ij} = \left( {{\partial \bar {u}_i }/{\partial x_j } + {\partial \bar {u}_j } / {\partial x_i }} \right) /2$为大尺度流动的应变率张量,$\bar {S} = \left( {2\bar {S}_{ij} \bar {S}_{ij} } \right)^{1/2}$,Smagorinsky参数$c_{\rm s}$在不同的流动条件下取不同的值,$Pr $为亚格子湍流普朗特数. 考虑到海岸城市边界层内流场具有显著的各向异性,本文采用Bou-Zeid等提出的拉格朗日尺度依赖动力学模型(LASD) [16]来确定$c_{\rm s}$,即令 $$ c_{\rm s,\varDelta}^2 = \dfrac{{\varsigma _{LM} }/{\varsigma _{MM} }}{\max \left( {{\varsigma _{QN} \varsigma _{MM} } / {\varsigma_{NN} \varsigma _{LM} },1 / 8} \right)} \tag{6}$$ 其中,$c_{\rm s,\varDelta } $为网格尺度为$\varDelta $的Smagorinsky参数,且规定 $$ \varsigma _{AB} = \int_{ - \infty }^t {A_{ij} B_{ij} \left[{ { x} \left( {t}' \right),{t}'} \right]W\left( {t - {t}'} \right)d{t}'} \tag{7}$$ 其中,$W(t) = {\rm e}^{ - t / T}/T$是一个指数权重函数,$T$为时间尺度,根据DNS的结果和一致性原则可知,$T = 1.5\varDelta \left( {\varsigma _{LM} \varsigma _{MM} } \right)^{ - 1 / 8}$. 此外,${ x}\left( {t}' \right)$表示流体质点在先前${t}'$时刻的空间位置,$\zeta $的两个下标分别和式(7)右边被积函数中所含的两个张量相对应,张量$A_{ij} $和$B_{ij} $指代张量$L_{ij} $,$M_{ij} $,$Q_{ij} $和 $N_{ij} $中的某一个,被指代的张量定义为 $$L_{ij} =\widetilde{\overline{u}_i \overline{u}_j } -\tilde {\overline{u}}_i \tilde {\overline {u}}_j \tag{8}$$ $$M_{ij} = 2\varDelta ^2\left[{\widetilde{\left| \overline{S} \right|\overline{S}_{ij} } - 4\beta \left| \tilde {\overline{S}} \right|\tilde {\overline{S}}_{ij} } \right] \tag{9}$$ $$Q_{ij} = \widehat{\overline{u}_i \overline{u}_j } - \hat {\overline{u}}_i \hat {\overline {u}}_j \tag{10}$$ $$N_{ij} = 2\varDelta ^2\left[{\widehat{\left| \overline{S} \right|\overline{S}_{ij} } - 16\beta \left| \hat {\overline{S}} \right|\hat {\overline{S}}_{ij} } \right] \tag{11}$$ 式中,"$\sim $"和"$\hat{ }$"分别表示在尺度为2$\varDelta $和4$\varDelta $的网格上进行的滤波运算. 假设$\beta = {c_{{\rm s},2\varDelta }^2 }/ {c_{{\rm s},\varDelta }^2 } = {c_{{\rm s},4\varDelta }^2 } /{c_{{\rm s},2\varDelta }^2 }$,即 $\beta $ 不依赖于滤波尺度.LASD模型的相关细节见Bou-Zeid等[16]的论文.
控制方程的离散在水平方向上采用拟谱方法,在垂直方向上采用中心差分格式,时间递进采用二阶Adams-Bashforth格式.
2.2 对象问题的设置及边界条件本文模拟海风恒定向岸吹送的情况. 在海岸线往内陆方向200 m至1 700 m的范围内均布12$\times $7的立方形建筑物阵列(图1).计算域在垂直于海岸线方向取4 km,在平行海岸线方向取0.84 km,在垂直方向上取800 m.入风边界至海岸线的距离为1.5 km,下垫面为海域,海岸至出风边界的距离为2.1 km,下垫面为陆域.对象问题模拟北纬37°附近的典型中性层结海岸边界层,边界层高度为500 m,边界层上部为一个强度为8 K/km的逆温层.为了描述方便,本文将坐标原点设置于海岸线上,$x$轴垂直于海岸线并指向内陆,$y$轴平行于海岸线,$z$轴垂直于海岸线向上.考虑未扰动风场为地转风的理想情况.本文考虑中性条件和对流条件下的海岸城市内边界层以及对流条件下的自然海岸(没城市冠层的开阔海岸)边界层的3种情况,以便对比研究热力与城市摩阻共同与分别单独作用下的海岸边界层特征.根据之前学者建议[17, 18],在两个热力内边界层的算例中,我们在陆域上施加向上大小为0.15 K$\cdot$ms$^{-1}$的热通量来模拟白天海岸带加热过程. 考虑到数值计算稳定性的要求,模拟时间步长取0.05 s.计算总时步240 000步,约合时间过程3.33 h. 模拟计算采取Xeon E7-4830处理器16核并行处理,单例计算时间约20 d.模拟计算的其他参数见表1.
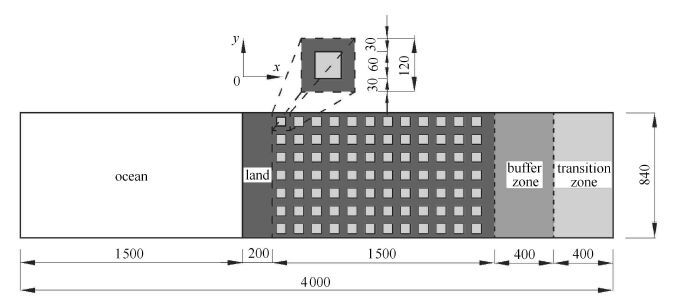
|
图1 计算域(单位:m) Fig.1 Definition of domain (unit: m) |
| 表1 模拟计算参数表 Table 1 Parameters used in computations |
由于采用快速傅里叶变换在水平方向上进行谱分解,计算模型的4个侧边界限于周期性边界条件.数值模型的周期性边界条件和对 象问题显然是不匹配的.为了解决这个矛盾,采用了Chester等[19]建议的方法,即首先对满足周期性假设的海洋大气边界层进行长时间的模拟计算并得到稳定的流场,当流场稳定后我们继续进行模拟并记录每一个时步$x$轴侧边界上的流场信息.此后,在对不满足周期性边界条件的海岸大气边界层进行模拟的算例中,稳定流场被用做初始条件,并于每时步在$x$轴侧边界上施加记录的入流信息. 为了使流场在出流边界上能够满足周期性条件,把$x$轴出流边界前的40个网格设置为过渡区.在过渡区内,流场通过一个余弦函数进行平滑处理,使陆域的流场可以逐渐过渡到出流边界上海洋边界层的流场.为了减小过渡区数值处理对上游流场的影响,过渡区前40个网格设置为缓冲区. 缓冲区内的流场信息不计入计算结果.
本研究采用浸入边界法处理城市拟形化后的下垫面条件.浸入边界法是将边界上复杂凸起对流动的影响模化为N-S方程中的体积力的作用进行处理的方法,可极大地提高计算效率[20].Tseng和Ferziger [21, 22]对浸入边界法进行了改进,提出了虚拟网格浸入边界法并将其用于单个建筑物问题的大涡模拟之中.该方法的思路是利用楼体周边的流场信息,通过一个拉普拉斯平滑函数在楼体内插值出一个虚拟的连续速度场,并将此用于真实大气的速度场在水平方向求导,以克服在大涡模拟中采用拟谱方法离散时,因为楼体与大气间速度不连续所导致的吉布斯效应.Bou-Zeid等[5]进一步研究了此方法对建筑群附近流场特征求解的适用性,认为在单个构筑物内网格点少于4$^{3}$时,建筑群内流场特征无法得到很好的反映,而当单个建筑物内网格点多于6$^{3}$时,用此方法求得的流场与实际观测结果吻合良好.本研究采用虚拟网格浸入边界法,构筑物内部采用6×6×8个网格点,以确保流场计算的精度.
本文假设块体表面热通量为零,壁面处的动量通量采用壁面模型进行计算,以块体水平面处的动量通量计算为例,相应的计算公式为 $$ \left( {\tau _{xz} } \right)_{i,j,1} = - u_\ast ^2 \left[{\dfrac{\bar {u}_{i,j,1} }{\sqrt {\bar {u}_{i,j,1}^2 + \bar {v}_{i,j,1}^2 } }} \right] \tag{12}$$ 其中,$u_{i,j,1} $和$v_{i,j,1} $为块体表面之上第一层网格中心处的流速分量,摩阻流速$u_\ast $用下式计算 $$ u_\ast = \dfrac{\kappa \sqrt {\bar {u}_{i,j,1}^2 + \bar {v}_{i,j,1}^2 } }{\ln \left( { {z_1 }/{z_0 }} \right)} \tag{13}$$ 其中,$\kappa $为卡门常数,$z_1 $为第一层网格中心点到块体表面的距离,$z_0 $为块体表面摩阻高度. 块体内的虚拟应力通过文献 [22]提出的拉普拉斯平滑算子计算得到.
3 结果与讨论 3.1 平均流场取模拟结束前半个小时内的数据进行平均化处理后作为计算结果. 由于海洋上的风场是恒定的,按照文献中的建议,取海域等价摩阻高度为0.18 mm时,对应的海面摩阻流速$u_\ast =0.23$ m/s. 用$u_{\ast }$与边界层高$z_{i} =500$ m对结果进行无量纲化,平均后的流速分布与水平流速剖面参见图2. 从图中可以清晰地看出,海风登陆后,低空近地处的水平流速会受到下垫面摩阻突增的影响而减小. 当风传播到城市建筑 物冠层时,受到建筑物阻碍水平流速进一步减小. 在城市建筑物冠层迎风边缘,有强烈的垂直向上气流产生,而在建筑物后方的街谷内,出现顺时针方向环流.

|
图2 平均流速分布 Fig.2 Distribution of averaged velocity |
通过对图2的观察还可以发现,在建筑物冠层顶之上,气流会因为构筑物的摩阻效应产生城市摩阻边界层,此边界层向内陆逐步发展.此外,还可以看到,城市摩阻边界层上方的水平流速$u$较冠层前略有升高,这可能是由于本文计算中逆温层上部边界条件采用了刚盖假设 的缘故.
3.2 边界层内的湍流特征和温度分布这里我们考察内边界层中的温度分布和湍流特征. 反映湍流特征的几个主要参数是
(1)速度分量标准差 $$ \sigma _{u_i } = \sqrt {\left\langle {\bar {u}_i \bar {u}_i } \right\rangle - \left\langle {\bar {u}_i } \right\rangle ^2 + \left\langle {\tau _{ii} } \right\rangle } $$
(2)雷诺应力 $$ R_{ij} = \left\langle {\bar {u}_i \bar {u}_j } \right\rangle - \left\langle {\bar {u}_i } \right\rangle \left\langle {\bar {u}_j } \right\rangle + \left\langle {\tau _{ij} } \right\rangle $$
(3)速度分量间相关系数 $$ r_{u_i u_j } = {R_{ij} } /{\sigma _{u_i } \sigma _{u_j } } $$ 式中,$\left\langle \right\rangle $表示雷诺平均,各湍流参数定义中涉及到的速度分量的脉动值为瞬时值和雷诺平均值之差,包括大涡值偏离雷诺平均值的部分和亚格子分量两个部分.
从图3中可以清晰地看出,海岸热力内边界层中的各湍流特征值在街谷尺度上的分布皆具有非常明显的空间差异性.(1)登陆风主流向速 度$u$的紊动在建筑物屋顶上方最为强烈,其强度随着离屋顶高度的增加而逐渐减弱.(2)水平侧方向速度$v$紊动最强烈的部位处于街谷底部,前建筑物屋顶的后沿和后方建筑物墙面前.(3)垂向速度$w$和侧向速度$v$的紊动分布规律基本相似,只不过在街谷顶部出口处,大气的垂向紊动强度也十分大.(4)雷诺应力最大的位置出现在街谷顶部出口,而街谷后端处呈现反方向的动量传输. (5)图3(e)给出的$u$和$w$的相关系数的空间分布,表征了湍流对动量传输的有效率.可以看出,街谷顶部出口是湍流对动量传播最有效的区域,比建筑物顶上要更为明显,最大的传输有效率约为0.7.而在顺流方向上街谷的后端或建筑物的前端,由于顺时针环流的作用使得街谷内的动量具有向地面方向传输的趋势,最大有效传输率仅为0.2左右.

|
图3 海岸城市热力内边界层内湍流特征量和温度场的空间分布(单位:K) Fig.3 Spatial distribution of turbulence and temperature in coastal urban thermal internal boundary layer (unit: K |
从图3(f)中可以看出,由于街谷内顺时针环流的存在,顺流方向上街谷的后部或建筑物之前位置处的大气向地面方向运动会使得此处街谷底部热量集聚,而在街谷前方建筑物后面气流的向上运动使得该处热量向上扩散较快.总的来看,城市冠层的存在如同一个"罩子",减弱了其中的风速,从而使得从地面产生的热量很难向下风方向传输,而更多地弥留在其中.街谷环流中向上传输的气流将热量带到冠层顶部,并最终由冠层顶部的强烈的紊动传输进入到冠层上部的大气层中.
为了进一步分析海岸城市热力内边界层内的湍流特征,图4中给出了湍流特征量在$x =1.28$ km处街谷剖面上的垂直分布.此处 边界层发展较为充分便于对紊动特征的研究.通过比较这些紊动量的分布特征可以发现:(1)海岸城市热力内边界层和中性的海岸城市边界层湍流特征在垂直方向上分布规律是相同的,它们具有相似的垂直剖面形式.(2)在热力作用下,不论在海岸城市冠层之内或之外,其紊动强度都会在中性基础上有所增加,在本文的算例中增加了约0.3倍.(3)可以看出海岸城市在热力作用下,大气的湍流强度比纯热力和纯建筑物摩阻的线性叠加结果更大.城市冠层的存在削减了近地处的流速使得海岸带产生的热量弥留在冠层中从而使冠层内温度快速升高,对流作用加强.因此,海岸城市在热力影响下,其紊动强度比周边自然海岸带要强得多,建筑物的摩阻作用和热力作用从宏观上来看起到了相互促进的效果.(4)在两种不同层结的海岸城市街谷中,相关系数$r_{uw}$基本相同且绝对值比天然的海岸热力内边界层小,说明街谷中湍流对动量的传输受到抑制. 本文中,由于逆温层上部边界条件采用了刚盖假定的缘故,因此在高出城市冠层的部分,登陆海风的动量增加(参见图2(c)),湍流对动量的有效传输也明显提高.
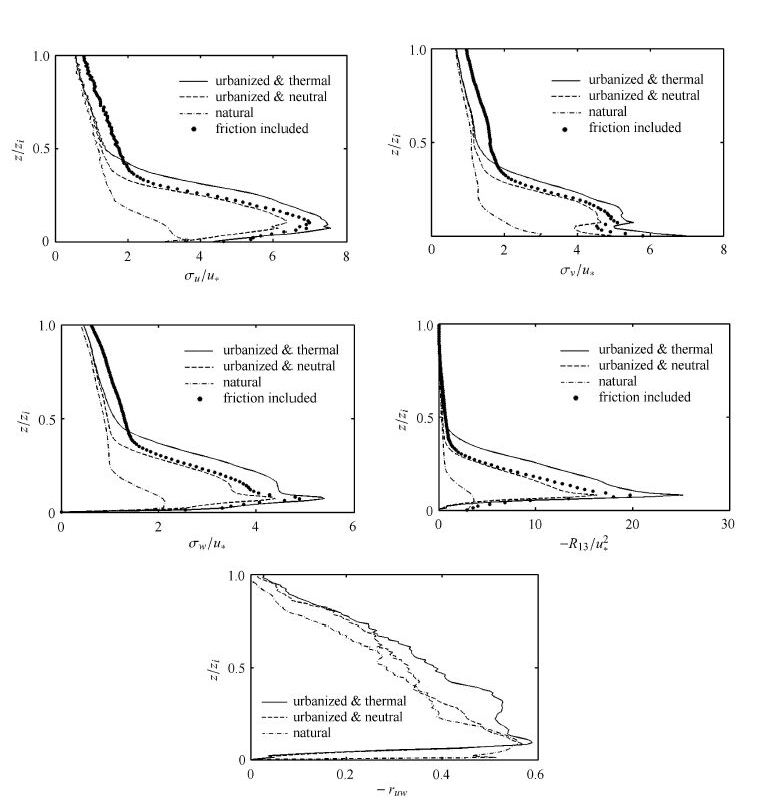
|
图4 海岸城市热力内边界层内的湍流特征(x = 1:28 km 处)(续) Fig.4 Turbulent quantities in coastal urban thermal internal boundary layer (at x = 1:28 km)(continued) |
目前学术界对热力内边界层高度$\delta _{\rm c} $有诸多的定义[23-25],本文为了简便起见,令边界层外缘位置满足条件$\left| {\bar {\theta }_\delta - \bar {\theta }_0 } \right|= \varepsilon $,其中$\bar {\theta }_\delta $为内边界层外缘处的位温,$\bar {\theta }_0$为此处原未受扰动的位温,$\varepsilon $为一个小量,本文 取0.05 K. 图5表示热力内边界层高度$\delta _{\rm c}$的发展规律.通过比较海岸城市热力内边界层和天然海岸热力内边界层高度的不同,可以发现:由于海岸城市冠层极大削弱了冠层内的平均水平流速从而减少了热量向下游的传递,相同热力条件下,城市冠层内热量的积累更为快速,热力内边界层发展也更快.
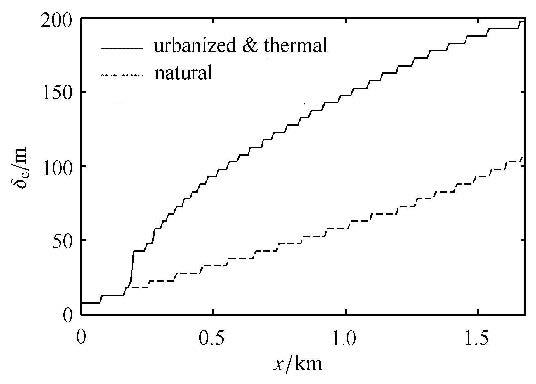
|
图5 海岸热力内边界层高度 Fig.5 Coastal thermal internal boundary layer thickness |
值得注意的是,两个算例中热力内边界层高度在到达城市冠层之前的发展规律是相同的,但是在城市冠层的边缘处,热力内边界层突然快速发展,边界层高度快速超越城市构筑物顶高$h =40$ m. 在城市冠层之前,登陆风的平均流速与其在天然海岸带是一致的,热量的传输与扩散规律也都相同. 如3.2节中所述,城市冠层的存在使得海岸城市冠层内形成一个相对独立的系统,新生热量弥留在街谷内快速升高城市内部温度,使得城市冠层形成类似于热岛效应的"保温"效果. 如图2所示,在城市冠层迎风边缘,会由于建筑物对登陆风的阻碍作用在此处产生较大的垂向向上气流. 此外,由于"边缘效应",在城市冠层的前端,风场的紊动变得异常强烈,特别是垂向的湍流动量输送和湍流热输送都大幅增加,最终使得对流内边界层高度在城市冠层边缘处发生激增.
城市冠层上方的热力内边界层高随进岸距离增加的增长规律明显与自然海岸热力内边界层不同. 在自然海岸带,其热力内边界层高发展与进岸距离$x$成正比,而在海岸城市上方,热力内边界层高的发展更接近与$x$的1/2次方呈现正相关规律. Hara等通过风洞和DNS试验分别对稳定层结和中性层结海岸带上形成的热力内边界层发展规律进行研究的结果也表明,强稳定条件下(初始边界层内${\partial \theta } / {\partial z}$较大)生成的热力内边界层,其高与进岸距离$x$的1/2次方呈正比. 相反地,在中性条件下生成的海岸热力内边界层高更像是与$x$呈正比关系[26],本文在初始中性条件下计算得到的热力自然海岸边界层发展规律与此相符合. 由此可见,城市冠层内的建筑物阵列使得建筑物上方气团的速度梯度和切应力出现显著的增加,导致层结切变流混合过程中气团位能的增量与动能损失比变小,即机械湍能产生率与热力湍能产生率的比值提高,故而大气的稳定度在实际上得到提高. 因此,热力内边界层的发展规律在城市上方更接近稳定层结下的规律.
4 结 论本文基于对建筑物冠层的拟形化处理,采用大涡模拟的方法对热力作用下海岸城市热力内边界层进行了研究.讨论了在海岸带、城市建筑物和热力作用共同影响下,边界层内平均流场的特征、流场的湍流特征以及内边界层发展的规律等.
研究结果表明:(1)海风在到达海岸城市边缘时,受边缘效应的影响,产生较大的上升气流,在城市冠层顶部产生城市摩阻内边界层并逐步向内陆方向发展,而在街谷内产生相应的环流. (2)在街谷尺度下,海岸城市热力内边界层中紊动特征量的分布在空间上呈现有规律的差异性. 海岸城市在受到热力条件影响时,其内边界层内紊动强度高于中性城市边界层和相同热力的条件自然海岸热力边界层紊动线性叠加的结果. 建筑物的摩阻作用和热力作用从宏观上来看起到了相互促进的效果. (3)在海岸城市冠层与热力作用的共同作用下,热力内边界层高度很快高于城市冠层,且其发展会明显快于天然海岸带热力内边界层. (4)与天然海岸的热力内边界层相比,海岸城市热力内边界层的发展与进岸距离之间的关系发生显著变化.
| 1 | Xie ZT, Castro IP. Large-eddy simulation for flow and dispersion in urban streets. Atmospheric Environment, 2009, 43(13):2174-2185 |
| 2 | Li XX, Britter RE, Norford LK, et al. Flow and pollutant transport in urban street canyons of different aspect ratios with ground heating:large-eddy simulation. Boundary-Layer Meteorology, 2010, 142(2):289-304 |
| 3 | Yaghoobian N, Kleissl J, Paw UKT. An improved three-dimensional simulation of the diurnally varying street-canyon flow. Boundary-Layer Meteorology, 2014, 153(2):251-276 |
| 4 | 桑建国,刘辉志,王保民等. 街谷环流和热力结构的数值模拟. 应用气象学报, 2002, 13(S):69-81 |
| 5 | Bou-Zeid E, Overney J, Rogers BD, et al. The effects of building representation and clustering in large-eddy simulations of flow in urban canopies. Boundary-Layer Meterology, 2009, 132(3):415-436 |
| 6 | Inagaki A, Kanda M. Turbulent flow similarity over an array of cubes in near-neutrally stratified atmospheric flow. Journal of Fluid Mechanics, 2008, 615:101-120 |
| 7 | Coceal O, Dobre A, Thomas TG, et al. Structure of turbulent flow over regular arrays of cubical roughness. Journal of Fluid Mechanics, 2007, 589:375-409 |
| 8 | Philips DA, Rossi R, Iaccarino G. Large-eddy simulation of passive scalar dispersion in an urban-like canopy. Journal of Fluid Mechanics, 2013, 723:404-428 |
| 9 | Freitas ED, Rozoff CM, Cotton CW, et al. Interactions of an urban heat island and sea-breeze circulations during winter over the metropolitan area of São Paulo, Brazil. Boundary-Layer Meteorology, 2007, 122(1):43-65 |
| 10 | Mahrt L. Surface heterogeneity and vertical structure of the boundary layer. Boundary-Layer Meteorology, 2002, 96(1-2):33-62 |
| 11 | Jones JA.The fifth report of a working group on atmospheric dispersion:models to allow for the effects of coastal sites, plume rise and buildings on dispersion of radionuclides and guidance on the balue of deposition velocity and washout coefficients. 1983 |
| 12 | Liu HP, Chan JC, Cheng AY. Internal boundary layer structure under sea-breeze conditions in Hong Kong. Atmospheric Environment, 2001, 35(4):683-692 |
| 13 | Inagaki A, Kanda M. Organized structure of active turbulence over an array of cubes within the logarithmic layer of atmospheric flow. Boundary-Layer Meteorology, 2010, 135(2):209-228 |
| 14 | Castillo MC, Inagaki A, Kanda M. The effects of inner-and outerlayer turbulence in a convective boundary layer on the near-neutral inertial sublayer over an urban-like surface. Boundary-Layer Meteorology, 2011, 140(3):435-469 |
| 15 | Michioka T, Takimoto H, Sato A. Large-eddy simulation of pollutant removal from a three-dimensional street canyon. Boundary-Layer Meteorology, 2014, 150(2):259-275 |
| 16 | Bou-Zeid E, Meneveau C, Parlange MB. A scale-dependent Lagrangian dynamic model for large eddy simulation of complex turbulent flows. Physics of Fluids, 2005,17(2):025105 |
| 17 | Antonelli N, Rotunno R. Large-eddy simulation of the onset of the sea breeze. Journal of the Atmospheric Science, 2007, 64(12):4445-4457 |
| 18 | Crosman ET, Horel JT. Idealized large-eddy simulations of sea and lake breezes:sensitivity to lake diameter, heat flux and stability. Boundary-Layer Meteorology, 2012, 144(3):309-328 |
| 19 | Chester S, Meneveau C, Parlange MB. Modeling turbulent flow over fractal trees with renormalized numerical simulation. Computational Physics, 2007, 225(1):427-448 |
| 20 | 宫兆新,鲁传敬,黄华雄. 浸入边界法及其应用. 力学季刊, 2007, 28(3):353-361 |
| 21 | Tseng YH, Ferziger JH. A ghost-cell immersed boundary method for flow in complex geometry. Journal of Computational Physics, 2003, 192(2):593-623 |
| 22 | Tseng YH, Meneveau, Parlange MB. Modeling flow around bluff bodies and predicting urban dispersion using large eddy simulation. Environmental Science & Technology, 2006, 40(8):2653-2662 |
| 23 | Venkatram A. A model of internal boundary-layer development. Boundary-Layer Meteorology, 1977, 11(4):419-437 |
| 24 | Raynor GS, Sethuraman S, Brown RM. Formation and characteristics of coastal internal boundary layers during onshore flows. Boundary-Layer Meteorology, 1979, 16(4):487-514 |
| 25 | Kleissl J, Kumar V, Meneveau C, et al. Numerical study of dynamic Smagorinsky models in large-eddy simulation of the atmospheric boundary layer:validation in stable and unstable conditions. Water Resource Research, 2006, 42(6):376-389 |
| 26 | Hara T, Ohya Y, Uchida T, et al. Wind-tunnel and numerical simulations of the coastal thermal internal boundary layer. Boundary-Layer Meteorology, 2009, 130(3):365-381 |
| 27 | Kumar V, Kleissl J, Meneveau C, et al. Large-eddy simulation of a diurnal cycle of the atmospheric boundary layer:atmospheric stability and scaling issues. Water Resource Research, 2006, 42(6):650-664 |
| 28 | Mason PJ. Large-eddy simulation of the convective atmospheric boundary layer. Journal of Atmospheric Science, 1989, 46(11):1492-1516 |
| 29 | Cheng WC, Pote-Agel F. Adjustment of a turbulent boundary layer flow to idealized urban surfaces:A large-eddy simulation study. Boundary-Layer Meteorology, 2015, 115:249-270 |
| 30 | 崔桂香, 史瑞丰, 王志石等. 城市大气微环境大涡模拟研究. 中国科学, 2008, 6(6):626-636 |
| 31 | Sang Jianguo, Liu huizhi, Wang Bomin, et al. Numerical simulation of the flow field and thermal structure over a street canyon. Journal of Applied Meteorology Science, 2002, 13(S):69-81(in Chinese) |
| 32 | Gong Zhaoxin, Lu Chuanjing, Huang Huaxiong. Immersed boundary method and its application. Chinese Quarterly of Mechanics, 2007, 28(3):353-361(in Chinese) |
| 33 | Cui Guixiang, Shi Ruifeng, Wang Zhishi, et al. Large-eddy simulation of urban micro-atmospheric environment. Science China G, 2008, 6(6):626-636(in Chinese)) |
 2016, Vol. 48
2016, Vol. 48
