致密气属于三大非常规天然气之一，资源量丰富，开发潜力大.致密气藏具有低渗、低压、低丰度等特点，气井自然生产能力低，需要经过储层改造措施后才具有工业开采价值.目前长庆致密气藏的开采普遍采用多段压裂水平井技术. 试井测试是评价压裂效果获取压后裂缝参数和储层参数的重要手段.致密气井的试井测试常常伴随着一定的产水量，产水量从几方到几十方不等.由于产水的原因，使得井筒流体的流动为气液两相流，增加了井筒流体的流动阻力，同时也加大了井筒流体流动对水平井试井的影响，造成压裂水平井试井曲线难拟合、解释结果不准确等问题.

目前国内外对常规压裂水平井试井模型的研究有不少^{[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12]}，针对致密气藏渗流特征的压裂水平井试井模型研究也有一部分^{[13, 14, 15]}，对井筒多相流压力损失的计算方法有多种^{[16, 17, 18, 19, 20, 21, 22]}，将地层渗流与井筒管流耦合的模型也比较常见^{[23, 24, 25, 26, 27]}，但大部分的模型仅考虑的是井筒单相流，并且主要针对油气井产能分析.目前在已有压裂水平井试井模型的文献中考虑井筒两相流或多相流的试井模型还很少，大部分压裂水平井试井模型忽略了水平井筒流体的流动阻力，即假设水平井筒具有无限大导流能力.

井筒多相流压力损失的计算方法主要有Duns-Ros方法^[16]、Hagedron-Brown方法^[17]、Orkiszewski方法^[18]、Aziz方 法^[19]、Beggs-Brill方法^{[20, 21]}、Ansari方法^[22]、OLGAS方法等.Lawson和Vohra等^{[28, 29]}利用726口井的数据和流体物性参数评价了9种常用方法的精度，从气液比、管径、液相折算速度等多个方面来比较误差，结果表明Hagedron-Brown方法与Beggs-Brill方法适用范围广、精度高.最近，Ruiz 等^[30]评价了8种多相流计算模型的流型预测精度和压力损失计算精度，结果发现Beggs-Brill方法预测流型精度最高，Hagedron-Brown方法与Beggs-Brill方法计算压力损失误差最小.由于Hagedron-Brown方法只能用于直井，而Beggs-Brill方法在直井、斜井及水平井均适用，因此本文采用Beggs-Brill方法进行井筒气液两相流流型预测及流动阻力计算.

为了明确致密气藏压裂水平井井筒气液两相流对试井测试的影响，建立一种井筒气液两相流与地层渗流耦合的试井模型，模型考虑致密气藏的应力敏感特征，采用数值方法进行求解，获得考虑井筒气液两相流的致密气压裂水平井试井理论曲线、压力场分布及各裂缝产量分布.对比忽略气液两相流的计算结果，明确井筒气液两相流对压裂水平井试井曲线、压力场扩散及裂缝产量分布等的影响，为产水致密气压裂水平井的试井解释提供理论指导.

在压裂水平井中忽略井筒气液两相流的影响，会对试井解释造成以下两方面的误差：

(1)水平井筒无限大导流能力假设的误差

虽然管流的流动阻力相比于低渗透储层的渗流阻力来说比较小，但是由于水平井筒长度比较大，通常有1 000$\sim $2 000 m，再加上水平井筒为气液两相流时的流动阻力会加大，所以总的井筒流动阻力并不小，此外较小的井筒流动阻力都会对裂缝产量分布产生不小的影响，因此水平井筒假设为无限大导流能力可能会造成不小的误差.

(2)测试点压力看作(或折算)到入窗点压力的误差

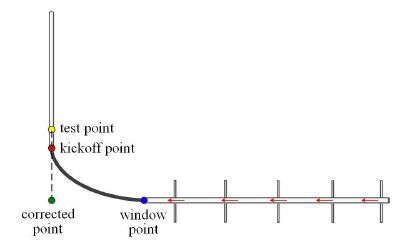
在水平井试井测试中，压力计通常无法下入到储层深度，只能下入到造斜点以上位置，如图1所示.然而，在试井解释过程中，目前常 将压力计测试得到的数据直接用于试井解释，即忽略测试点与入窗点之间的压差.虽然在产能评价上可根据造斜点以上的流压梯度折算得到井底流压，但由于造斜段的流压梯度跟垂直段流压梯度相差较大，这种折算方法也可能会造成较大误差.

图1(Fig.1)

图1 压裂水平井试井测试示意图 Fig.1 Well test of the fractured horizontal well

建立考虑井筒气液两相流的压裂水平井试井解释模型可将地层渗流与井筒两相流耦合计算，不仅考虑了水平井筒的流动阻力，还可计算得到压力计下入位置的压力值，将其与该点的实测压力进行拟合分析，从而可以很好地解决以上两个因素造成试井解释误差的问题.

为了建立压裂水平井井筒两相流与地层渗流的试井数学模型，需基于下列假设：

(1) 储层非均质且渗透率各向异性，储层非均质情况根据测井结果来设定.测试过程中储层以气体为主，地层水为束缚水，水仅影响气 体的渗透率，地层中仅考虑单相气的渗流.

(2)原始致密储层具有应力敏感效应，引入渗透率模量的概念来描述应力敏感对渗透率的影响.

(3)气体为可压缩气体，在地层中的流动为层流状态，满足达西定律，在裂缝中的流动速度较大，考虑高速非达西效应，引入惯性-湍流表皮系数来计算.

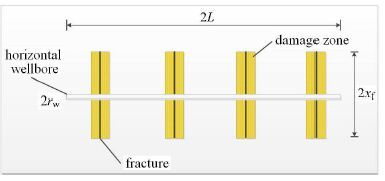
(4) 多级分段压裂后产生多段裂缝，裂缝为有限导流裂缝，裂缝可设置为不等长，不等距.考虑压裂液对地层的污染，采用矩形污染区来代 替，流体在裂缝中的流动为二维流动，如图2所示.

图2(Fig.2)

图2 压裂水平井物理模型示意图 Fig.2 Physical model of the fractured horizontal well

(5) 采用Beggs-Brill方法计算井筒气液两相流的流动阻力，考虑真实的井眼轨迹以及井内管柱结构变化.

将压裂水平井计算区域划分3个区域：地层、裂缝、井筒. 井筒气液两相流与地层裂缝渗流在水平井筒边界处关联耦合，为此联立渗流压力方程与两相流压力方程，建立的耦合数学模型如下：

地层 $$ \begin{align} & {{K}_{x\text{D}}}\frac{{{\partial }^{2}}{{p}_{\text{DR}}}}{\partial x_{\text{D}}^{2}}+{{K}_{y\text{D}}}\frac{{{\partial }^{2}}{{p}_{\text{DR}}}}{\partial y_{\text{D}}^{2}}+{{K}_{z\text{D}}}\frac{{{\partial }^{2}}{{p}_{\text{DR}}}}{\partial z_{\text{D}}^{2}}- \\ & {{K}_{x\text{D}}}{{\gamma }_{\text{D}}}{{\left( \frac{\partial {{p}_{\text{DR}}}}{\partial {{x}_{\text{D}}}} \right)}^{2}}-{{K}_{y\text{D}}}{{\gamma }_{\text{D}}}{{\left( \frac{\partial {{p}_{\text{DR}}}}{\partial {{y}_{\text{D}}}} \right)}^{2}}- \\ & {{K}_{z\text{D}}}{{\gamma }_{\text{D}}}{{\left( \frac{\partial {{p}_{\text{DR}}}}{\partial {{z}_{\text{D}}}} \right)}^{2}}=\frac{{{e}^{{{\gamma }_{\text{D}}}{{p}_{\text{DR}}}}}}{{{K}_{\text{lD}}}}\frac{\partial {{p}_{\text{DR}}}}{\partial {{t}_{\text{D}}}} \\ \end{align} \tag{1}$$

裂缝 $$ \dfrac{\partial ^2p_{\rm Df} }{\partial r_{\rm D}^2 } + \dfrac{\partial ^2p_{\rm Df} }{\partial z_{\rm D}^2 } = \dfrac{1}{K_{f{\rm D}} }\dfrac{\partial p_{\rm Df} }{\partial t_{\rm D} } \tag{2}$$

井筒 $$ - \dfrac{d p_{\rm w} }{d Z} = \dfrac{\left[{\rho _{\rm l} H_{\rm L} + \rho _{\rm g} \left( {1 - H_{\rm L} } \right)} \right] \sin \theta + \dfrac{\lambda Gv_{\rm m} }{2AD}}{1 - {\left\{ {\left[{\rho _{\rm l} H_{\rm L} + \rho _{\rm g} \left( {1 - H_{\rm L} } \right)} \right]v_{\rm m} v_{\rm sg} } \right\}}/ p} \tag{3}$$

其中，持液率$H_{\rm L}$和摩擦阻力系数$\lambda $根据实际生产数据、井眼轨迹和管柱结构等数据采用Beggs-Brill方法计算得到.

初始条件 $$ p_D \left( {x,y,z,0} \right) = 0 \tag{4}$$

内边界条件

$$\left. {\sum_{j = 1}^N A_{j{\rm D}} K_{ j{\rm D} } {\rm e}^{ - \gamma _{\rm D} p_{j{\rm D}} } \left( {\dfrac{\partial p_{j{\rm D}} }{\partial n'}} \right) } \right|_{\Gamma_{\rm in} } = 2\pi h_{\rm D} \left( {1 - C_{\rm D} \dfrac{d p_{\rm wD} }{d t_{\rm D} }} \right) \tag{5}$$

$$p_{\rm wD} \left( {t_{\rm D} } \right) = p_{j{\rm D}} - S_t \dfrac{\sum_{j = 1}^N {A_{j{\rm D}} K_{ j{\rm D} } {\rm e}^{ - \gamma _{\rm D} p_{j{\rm D}} }} }{2\pi h_{\rm D} }\left( {\dfrac{\partial p_{j{\rm D}} }{\partial n'}} \right) - MP_{j{\rm D}} \tag{6}$$

外边界条件

封闭 $$ \left. {\dfrac{\partial p_{\rm D} }{\partial n'}} \right|_{\Gamma _{\rm out} } = 0 \tag{7}$$

定压 $$ {{\left. {{p}_{\text{D}}} \right|}_{{{\Gamma }_{\text{out}}}}}=0 \tag{8}$$

耦合条件

地层与井筒交接面 $$ \left. {p_{i\rm DR} } \right|_{\Gamma _{\rm in} } = p_{\rm wD} + MP_{iD} \tag{9}$$

裂缝与井筒交接面 $$ \left. {p_{j\rm Df} } \right|_{\Gamma _{\rm in} } = p_{\rm wD} + MP_{j\rm D} \tag{10}$$

无量纲量的定义 $$\begin{align} {{p}_{\text{D}}}=\frac{784.9\sqrt{{{K}_{x}}{{K}_{y}}}h\left( {{\psi }_{i}}-\psi \right)}{{{Q}_{\text{sc}}}T},{{C}_{\text{D}}}=\frac{0.1592C}{\phi h{{c}_{\text{t}}}{{L}^{2}}} \\ {{t}_{\text{D}}}=\frac{3.6\times {{10}^{-3}}\sqrt{{{K}_{x}}{{K}_{y}}}t}{\phi \mu {{c}_{\text{t}}}{{L}^{2}}},38;{{K}_{x\text{D}}}=\frac{{{K}_{x}}}{\sqrt{{{K}_{x}}{{K}_{y}}}} \\ {{K}_{y\text{D}}}=\frac{{{K}_{y}}}{\sqrt{{{K}_{x}}{{K}_{y}}}},{{K}_{z\text{D}}}=\frac{{{K}_{z}}}{\sqrt{{{K}_{x}}{{K}_{y}}}},{{K}_{f\text{D}}}=\frac{{{K}_{f}}}{\sqrt{{{K}_{x}}{{K}_{y}}}} \\ {{\gamma }_{\text{D}}}=\frac{{{Q}_{\text{sc}}}T\gamma }{784.9Kh},\psi =2\int_{{{p}_{m}}}^{p}{\frac{p}{\mu Z}}dp \\ \end{align}$$

其中，$p_{\rm D}$为无量纲压力,$t_{\rm D}$为无量纲时间,$C_{\rm D}$为无量纲井筒储存系数,$K_{x\rm D}$为$x$方向无量纲渗透率,$K_{y\rm D}$为$y$方向无量纲渗透率,$K_{z\rm D}$为$z$方向无量纲渗透率,$K_{f\rm D}$为无量纲裂缝渗透率,$K_{\rm lD}$为区域的无量纲渗透率,$h_{\rm D}$为无量纲储层厚度,$\gamma_{\rm D}$为无量纲渗透率模量,$p_{\rm wD}$为第一条裂缝与井筒交点处的无量纲压力,$MP_{i\rm D}$为$i$点无量纲压力与$p_{\rm wD}$之间的差值，由式(3)数值计算得到,$H_{\rm L}$为持液率,$\lambda $为摩擦阻力系数. $K_{x}$为$x$方向的渗透率，mD；$K_{y}$为$y$方向的渗透率，mD；$K_{z}$为$z$方向的渗透率，mD；$K_{\rm f}$为裂缝渗 透率，mD；$K_{\rm l}$为区域渗透率，mD； $\psi $ 为拟压力，MPa$^{2}$/(mPa$\cdot $s)；$h$为储层有效厚度，m；$Q_{\rm sc}$为标准状况下气体产量，m$^{3}$/d；$T$为储层温度，K；$t$为测试时间，h； $\phi $ 为有效孔隙度； $\mu $ 为气体黏度，mPa$\cdot $s；$c_{\rm t}$为综合压缩系数，1/MPa；$L$为水平井半长，m；$Z$为气体偏差因子； $\gamma $ 为渗透率 模量，mPa$\cdot $s/MPa$^{2}$；$\rho _{\rm L}$为液体密度，kg/m$^{3}$；$\rho _{\rm g}$为气体密度，kg/m$^{3}$；$G$为气液混合物质量流量，kg/s；$v_{\rm m}$为混合物流动速度，m/s；$v_{\rm sg}$为气体表观流速，m/s；$A$为井筒油管截面积，m$^{2}$；$D$为油管内径，m.

由于渗流模型与井筒两相流模型在控制方程上具有较大差异，另外井筒两相流模型的计算方法是基于经验公式来计算的，因此两者无法直接通过联立方程组的方式进行耦合求解.

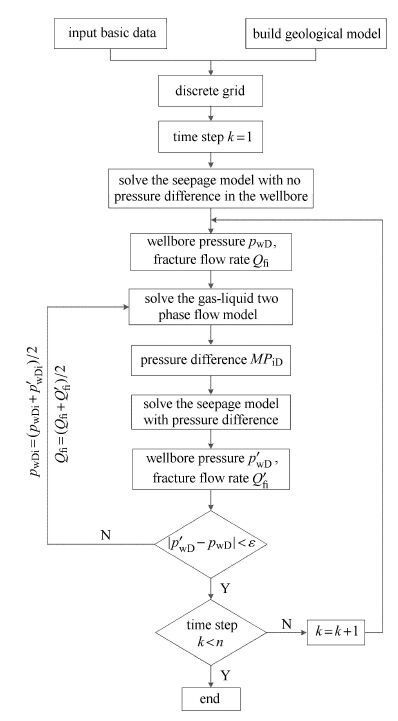
首先利用有限元方法对渗流方程进行求解(具体计算方法可参考文献 ^{[31, 32, 33]})，根据渗流方程计算得到的流量值和压力值，再将井筒划分为若干个微元段进行井筒两相流计算，计算得到的井筒压差分布带回到渗流方程，反复迭代，最终要求两迭代步计算的压力值 的差别小于一个小量，再进入下一个时间步的计算，即每个时间步迭代结束的条件是计算结果既满足渗流模型又满足井筒两相流计算模型，如图3所示的计算流程图.

图3(Fig.3)

图3 耦合模型求解的计算流程图 Fig.3 Solving process of the coupling model

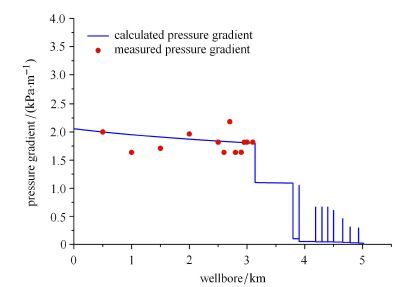
为了验证模型计算的准确性，将某口井修正等时试井中延续期所测得的井筒流压梯度与耦合模型所计算得到的流压梯度进行对比.已知该井延续期平均日产气1×10$^5$ m$^{3}$/d，日产水约2 m$^{3}$/d，流温流压测试时井底压力为28.8 MPa，井底温度114.8$℃，井口压力为23.1 MPa，井口温度36.7$℃.根据气液流量、实际井眼轨迹、井内管柱结构以及压力温度数据采用耦合模型计算得到的井筒压力梯度与实际测试得到的结果对比，如图4所示. 该井0$\sim $3 140 m为直井段，3 140 m$\sim $3 796 m为造斜段，3 796 m$\sim$5 062 m为水平段，由于测试压力计只能下入到造斜点，因此实际测试仅得到了直井段的流压梯度.受水力喷枪管径缩小的影响，计算得到压裂位置上的压力梯度较大.由图中结果对比可知，理论计算结果与实测结果基本一致，验证了所建立模型的正确性.

图4(Fig.4)

图4 井筒压力梯度的结果对比图 Fig.4 Comparison of wellbore pressure gradient values

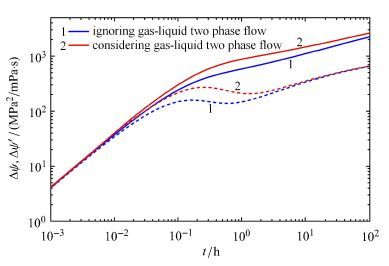
采用如表1中所给出的基础参数，计算得到考虑井筒两相流和不考虑井筒两相流条件下的试井曲线对比如图5所示.

表1(Table 1)

表1 计算的基础参数表Table 1 Basic parameters used in calculation Parameters Value Parameters Value gas flow rate/(10$^{4}$m$^{3}$$\cdot$d$^{-1}$) 5 Permeability/mD 0.2 liquid flow rate/(m$^{3}$$\cdot$d$^{-1}$) 10 porosity 0.05 formation thickness/m 10 temperature/$℃ 80 initial pressure/MPa 25 fracture number 7 fracture conductivity $F_{\rm CD}$ 4 fracture spacing/m 200 permeability ratio $K_{y}/K_{x}$ 1 fracture skin 0.01 Wellbore storage/(m$^{3}$$\cdot$MPa$^{-1}$) 6 permeability modulus/(mPa$\cdot $s$\cdot$MPa$^{-2}$) 10$^{ - 5}$

表1 计算的基础参数表 Table 1 Basic parameters used in calculation

图5(Fig.5)

图5 考虑井筒两相流的压裂水平井试井曲线 Fig.5 Well test type curves of the fractured horizontal well considering the wellbore two-phase flow

由图5可知，传统模型假设水平井筒无限大导流能力会影响双对数曲线的特征,尤其是在曲线早期阶段.考虑井筒两相流的试井曲线要高于不考虑井筒两相流的试井曲线，因为井筒两相流会增加流动阻力，所以造成相同流量条件下，所需的压降更大.从曲线型态可以看到，井筒两相流的影响有些类似于表皮系数的影响，即增加井筒存储阶段的时间，加大表皮过渡阶段的驼峰的幅值，增加后期压力曲线与压力导数曲线的张开大小.

与表皮系数不同的是井筒两相流还会影响储层压力的扩散方式.图6为时间$t=100$ h时考虑井筒两相流的压力场分布，其中储层 渗透率为0.5 mD，其余计算参数与上节相同.由图可知，第一条裂缝压力扩散的范围最大，越远离入窗点的裂缝压力扩散的范围越小，从图可以看到第一条裂缝与第二条裂缝已经产生了干扰，而其余裂缝间还未产生干扰. 由此说明，压力场分布受井筒两相流的影响比较大，不仅是试井过程，生产过程也是如此.

图6(Fig.6)

图6 考虑井筒两相流的压力场分布 Fig.6 Pressure field in consideration of the wellbore two-phase flow

图7为考虑井筒两相流的裂缝产量分布图.从图7(a)可知，考虑井筒两相流的裂缝产量分布差异非常明显，距离入窗点越近的裂缝，裂缝产量越大，这是因为考虑井筒两相流流动阻力后，第一条裂缝处的井筒压力最小，与储层压差最大，而最后一条裂缝的井筒压力值最大，与储层压差最小.

图7(Fig.7)

图7 考虑井筒两相流的裂缝产量分布图 Fig.7 Flow rate of fractures considering the wellbore two-phase flow

井筒两相流对裂缝产量分布的影响程度在裂缝产生干扰后会有一定的减弱，如图7(b)所示.由于裂缝发生干扰的强度不同，中间裂缝的产量下降，两端的裂缝产量增加，但井筒两相流造成的产量差别依然比较明显，对比第2条与第6条的产量差别可知，100 h时相差约1 700 m$^{3}$/d，1 000 h时相差约1 000 m$^{3}$/d，差值有一定的减小.井筒两相流对生产的影响始终存在，对早期的影响最大.

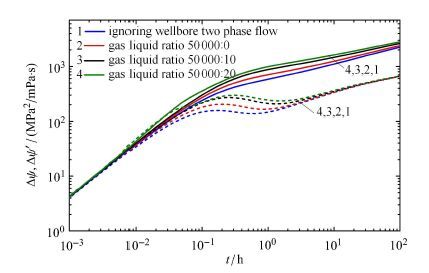
图8为不同产水量条件下的试井曲线，曲线1为不考虑井筒流动阻力的试井曲线，曲线2中气流量为5×10$^4$ m$^{3}$/d，而水流量为0，考虑的是气体单相的流动阻力，曲线3$\sim $4为气流量为5×10$^4$ m$^{3}$/d，而水流量分别为10 m$^{3}$/d和20 m$^{3}$/d.根据曲线1和曲线2的对比可知，单相气流动同样会影响试井曲线，说明即使是没有产水的情况，井筒流动阻力同样应该考虑.对比曲线1 $\sim $曲线3可知，随着水流量的增加，压力曲线值越高，这是由于流动阻力增加的原因造成的.曲线4的水含量很大，造成早期试井曲线有类似于变井储的特征.由此说明在相同储层条件下，产水量越大(气液比越小)，井筒两相流对试井曲线的影响越大.

图8(Fig.8)

图8 不同产液量对试井曲线的影响 Fig.8 Effect of water rate on well test type curves

利用所建立的井筒两相流和地层渗流耦合的试井模型对长庆苏里格气田的多口压裂水平井进行了试井解释，以其中一口为例.该井在 修正等时试井测试时水产量范围为2$\sim $5 m$^{3}$/d，根据各流动段记录的水流量数据进行两相流流动阻力计算.压力计下入的位置为3 140 m，而入窗点为3 796 m.

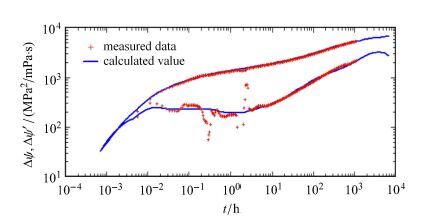
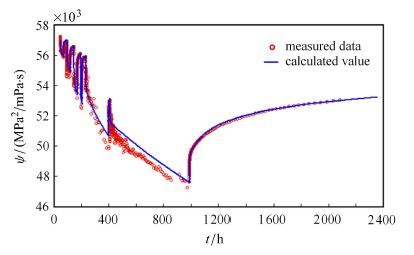
试井解释得到的结果见表2所示，拟合曲线图见图9和图10所示，由图可知曲线拟合程度较高.解释得到的渗透率为0.30 mD，测井得到 的水平井段平均渗透率为0.32 mD.若采用的试井模型不考虑井筒两相流，而其余因素均考虑，在双对数曲线拟合上通过增加裂缝表皮系数同样可以拟合的较好，但是全历史曲线拟合的程度要差些，究其原因主要是因为井筒两相流对双对数曲线的影响类似于增加了表皮系数，而井筒两相流对全历史曲线的影响无法通过修改表皮系数来代替，因为测试过程中开关井造成测试点与水平段之间压差不是一个定值，而是随着气液流量的变化而变化，考虑井筒两相流的模型在解释过程中根据实测气液产量计算了该压差的动态变化，因此能够得到较好的解释.

表2(Table 2)

表2 苏里格某井试井解释结果Table 2 Well test interpretation results of a well in Sulige gas field Parameters Value Parameters Value permeability/mD 0.303 7 fracture length/m 109.5 permeability ratio 1.156 fracture permeability/D 32.06 fracture skin 0.195 3 initial pressure/MPa 32.83 wellbore storag (m$^{3}$$\cdot$MPa$^{-1}$) 1.586 permeability modulus (mpa$\cdot$s/(MPa$^{-2}$) 9.1×10$^{-6}$ damage zone thickness=m 2.172 inertia-turbulence coefficient/(d$\cdot$m$^{-3}$) 1.1×10$^{-7}$

表2 苏里格某井试井解释结果 Table 2 Well test interpretation results of a well in Sulige gas field

图9(Fig.9)

图9 苏里格某井的双对数曲线拟合图 Fig.9 Log-Log type curves matching of a well in Sulige gas field

图10(Fig.10)

图10 苏里格某井的的全历史压力拟合图 Fig.10 The whole history pressure curves matching of a well in Sulige gas field

不考虑井筒两相流解释得到的裂缝表皮系数为0.3950，原始地层压力为32.21 MPa，而考虑井筒两相流后的裂缝表皮系数为0.195 3，原始地层压力为32.83 MPa.对比结果可知，传统不考虑井筒两相流的模型会造成解释得到的裂缝表皮系数偏大，而原始地层压力值偏小，其中裂缝表皮系数偏大的原因主要是传统模型假设水平井筒为无限大导流所引起的，而原始地层压力偏小的原因主要是因为传统模型中将测试点压力看作为入窗点压力所导致的.不考虑井筒两相流所引起的裂缝表皮系数误差大小主要由气液比、储层渗透率、裂缝参数、水平井长等参数决定，而原始地层压力的误差大小主要由测试点离入窗点距离以及气液比决定.

(1)基于井筒两相流计算方法和压裂水平井试井模型，建立了一种耦合井筒气液两相流和地层渗流的致密气藏压裂水平井试井模型，采用数值迭代方法对耦合模型进行求解，获得了考虑井筒两相流流动阻力的致密气藏压裂水平井试井曲线、储层压力场以及裂缝产量分布等结果.

(2)井筒气液两相流对试井的影响有些类似于表皮系数，但又不同于表皮系数. 井筒两相流会造成试井曲线中压力和压力导数值变大，对试井曲线形态的改变主要在测试早期，即增加井筒储集阶段持续时间，加大表皮影响阶段的"驼峰". 井筒两相流流动阻力会造成靠近入窗点的压力扩散要快于远离入窗点的压力扩散. 井筒两相流还会造成裂缝产量分布不均匀，靠近入窗点的裂缝产量大，远离入窗点的裂缝产量小. 产水量越大，井筒两相流流动阻力越大，井筒两相流对试井的影响也越大.

(3)不考虑井筒气液两相流可能会造成产水压裂水平井试井曲线拟合困难，拟合得到的参数存在较大误差的现象，主要表现为常规水平井筒假设为无限大导流能力会使得拟合得到的表皮系数偏大，将测试点视为入窗点会使得拟合得到的原始地层压力偏小. 本文所建立的考虑井筒气液两相流的压裂水平井试井模型为产水致密气井试井资料的正确解释提供了重要技术保障.

Ouyang Weiping, Zhang Mian, Sun Hu