工程实际中,很多时候结构在服役环境下所受的外部激励不仅随时间变化,而且表现出明显的不确定性,这使得结构响应也具有时变或动态不确定性,如大气湍流引起的飞机颤振、风载荷引起的高层建筑振动、波浪引起的海洋平台振动等.传统的随机过程理论是处理时变不确定性的主要数学工具,随机过程可理解为随时间变化的随机变量,按其概率结构分有泊松过程、独立增量过程、马尔可夫过程和平稳随机过程等[1].基于随机过程模型,目前已发展出了一套求解随机激励下结构动态响应的有效计算方法,即随机振动理论,并已在工程领域得到大量应用.20世纪50年代,发展出了线性体系随机反应分析方法,其主要是基于均方微积分理论的随机微分方程求解及解过程统计矩计算的方法[2, 3].随后,谱分析被引进随机振动中并建立起了结构随机响应等基本概念[4].有人提出了处理线性多自由度系统随机振动问题的反应谱方法[5],有人提出的虚拟激励法则有效提高了线性随机振动问题的计算效率[6],使大型复杂结构的随机响应分析成为可能,已被应用于实际工程问题[7, 8].至今线性系统的随机振动分析已发展得相对成熟,非线性系统的随机振动问题已成为近些年的研究重点.由伊藤随机微分方程及其解过程的马尔可夫性的应用,FPK方程法发展成为非线性体系随机振动分析的精确方法[9, 10].但由于FPK方程的解析解一般难以获得,针对一般的非线性随机振动问题,又发展出了其它的近似分析方法.有人研究了针对弱非线性系统随机振动的摄动法[11],还有些人对随机平均法在随机振动中的应用和进展进行了全面的总结[12, 13, 14].文献[15]使用等效线性化方法分析了非线性系统受非平稳随机载荷作用的振动问题.文献[16]归纳了用于强非线性问题的渐进方法的最新进展.除了随机响应分析,基于随机过程理论的结构时变和动态可靠性问题也是近年来大家关注的一个重点.有学者提出了计算跨越率和时变可靠度简化计算的PHI2方法[17];研究了非线性振子在随机激励下的首次超越方法[18];考虑了随机载荷过程穿越随机界限的可靠性计算问题[19].有学者基于两种状态马尔可夫过程,估计了具有条件跨越率的时变可靠性[20],还有一些学者提出了针对随机结构动力响应分析和动态可靠度分析的概率密度演化方法[21, 22].文献 [23]提出了一种基于随机过程离散时变可靠性分析方法(TRPD).
在上述随机振动与动态可靠性分析中,首先需建立不确定性激励的随机过程模型,而随机过程精确概率分布特征的获取需基于大量的时间历程实验样本. 而在实际工程问题中,很多时候因为试验条件或成本的限制难以获得充足的样本,如地震工程中,由于客观条件的限制,我们能得到的外部激励的样本信息非常有限. 因此,在实际的随机振动或结构动态可靠性分析中,很多时候不得不对激励随机过程模型的概率分布做出一些假设. 然而,研究表明即使概率分布参数相对于真实值的微小偏差都可能导致结构不确定性分析的很大误差[24]. 为此,在我们近期研究中,发展出了一种新的时变不确定性分析模型,即"非概率凸模型过程"[25],其在每一时间点使用区间而非精确概率分布来描述参数的不确定性,而在整个时间历程上通过两条边界描述参数的时变不确定性,可很大程度上降低对样本量的依赖性,从而为信息量缺乏的结构时变或动态不确定性分析提供了一种有效的数学工具.
本文在先前研究的基础上[25, 26, 27],将凸模型过程与传统振动理论相结合,构建了一种非随机振动分析方法,为实验信息相对缺乏的不确定性振动分析提供了一种潜在方法.需要指出的是,在我们最近工作[27]中已经提出了"非随机振动"的基本概念,然而本文在理论的两个关键地方,即不确定性激励的建模及动态响应边界的数值计算上使用和建立了不同的分析方法.如在不确定性激励的建模方面,本文采用了非概率凸模型过程,在不同时间点多维不确定域的构建、相关性函数的建立等方面与论文[27]中的非随机过程有很大不同,从而从不同的角度揭示振动系统在不确定性激励下的动态响应特征,为非随机振动理论后续在实际工程问题中的应用奠定了更好的理论基础.文章剩余部分安排如下:第2节介绍了非概率凸模型过程的基本概念;第3节建立了单、多自由度系统非随机振动分析算法,并给出了其蒙特卡罗仿真方法;第4节通过3个数值算例验证了本文方法的有效性.
1 非概率凸模型过程基本原理[25]在传统的随机过程理论中,不确定过程$X(t)$在任意时刻$t$被视为一随机变量,任意时刻变量间的相关性由自相关函数描述. 而在非概率凸模型过程中,用一个有界闭区间来表示任意时刻变量的不确定性,两个时刻变量之间的相关性通过定义相应的相关函数来描述.
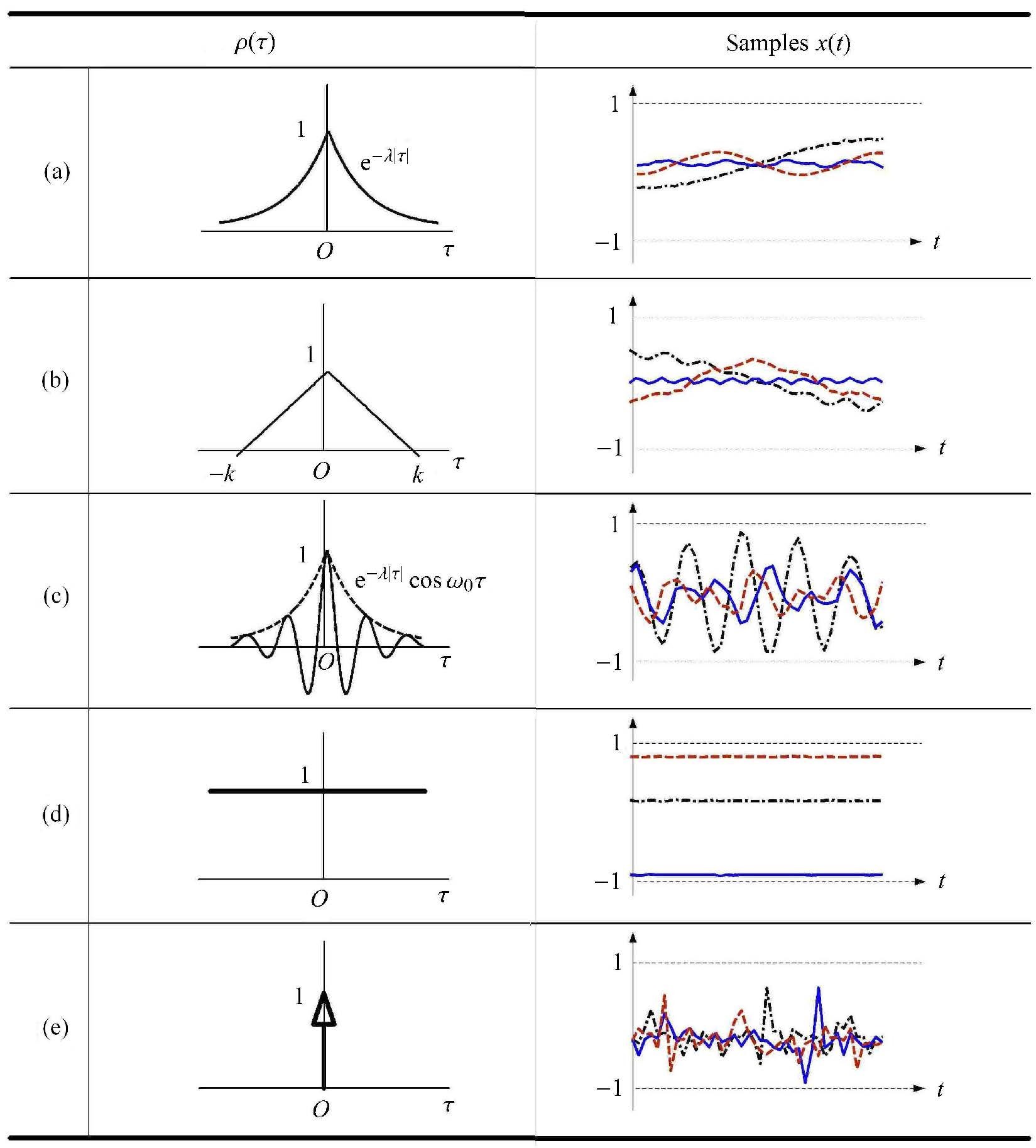
对于不确定过程$\left\{ {X(t);t \in T} \right\}$,$T$是参数$t$的集合. 如图1所示,如果对于任意时刻$t_i (i = 1,2,\cdots,n)$,$X(t_i )$的所有可能的值都在区间$\left[{X^{\rm L}(t_i ),X^{\rm U}(t_i )} \right]$内,且对于任意正整数$n$,$(X(t_1 ),X(t_2 ),\cdots,X(t_n ))$的联合分布区域为一个凸集,则将该过程称为非概率凸模型过程,简称凸模型过程,通常记为$X^I(t)$. 本文利用多维椭球模型[24, 28, 29]来描述凸模型过程的有限维分布域,即把$(X(t_1 ),X(t_2 ),\cdots,X(t_n ))$的不确定域表示为一个$n$维超椭球包含的区域 $$ ({ X} - { X}^{\rm c})^{\rm T}{ G} ({ X} - { X}^c) ≤ 1 \tag{1}$$ 其中${ X} = \left[{X\left( {t_1 } \right),X\left( {t_2 } \right),\cdots,X\left( {t_n } \right)} \right]^{\rm T}$,${ X}^{\rm c}$是区间向量${ X}$的中值向量,${ G}$为一对称正定矩阵,称为椭球模型的特征矩阵,它确定了椭球体的大小和形状,也反映了各个时间点参数的相关性.关于如何通过实验样本构建该多维椭球可参考作者先前的工作[25, 26].如图1所示,不确定过程$X(t)$所有可能的类型和形状都将包含在上边界和下边界组成的"带"内.为表述方便,本文也将将$X(t_i )$写成$X_i $,$X^{\rm I}(t_i )$写成$X_i^{\rm I} $. 另外,如$X_1^{\rm I} (t),X_2^{\rm I} (t),\cdots ,X_m^{\rm I} (t)$ 均为凸模型过程,则称 ${ X}^{\rm I} (t) = \left( {X_1^{\rm I} (t),X_2^{\rm I} (t),\cdots,X_m^{\rm I} (t)} \right)$ 为$m$ 维凸模型过程矢量.
|
图1 凸模型过程 Fig.1 Convex model process |
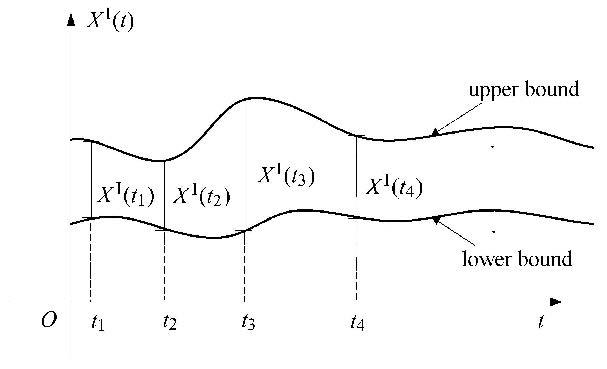
对于凸模型过程$X^{\rm I} (t)$,将其上边界函数和下边界函数分别记为$X^{\rm U} (t)$和$X^{\rm L} (t)$,则该凸模型过程的中值函数$X^{\rm c} (t)$定义为 $$ X^{\rm c}(t) = \dfrac{X^{\rm U}(t) + X^{\rm L}(t)}{2} \tag{2}$$ 凸模型过程$X^{\rm I}(t)$的方差函数$D_X (t)$定义为 $$ D_X (t) = \left( {\dfrac{X^{\rm U}(t) - X^{\rm L}(t)}{2}} \right)^2 \tag{3}$$ 对任意时刻$t_i $和$t_j $,凸模型过程$X^{\rm I}(t)$的自协方差函数定义为 $$ Cov\left( {X_i ,X_j } \right) = \sin \theta \cos \theta \left( {r_1^2 - r_2^2 } \right) \tag{4}$$ 如图2所示为一包络$t_i $和$t_j $时刻$X^{\rm I}(t)$样本的椭圆,$X_i^{\rm I} $和$X_j^{\rm I} $分别为两时刻参数变化的边缘区间,$\theta $为相关角,$r_1 $和$r_2 $分别为椭圆的两个半轴长度. 另外,定义$X_i $和$X_j $之间的自相关系数为 $$\rho _{X_i X_j } = \dfrac{Cov(X_i ,X_j )}{\sqrt {D(X_i )} \sqrt {D(X_j )} } \tag{5}$$ 相关系数的大小反映变量之间线性相关的程度. 当$\left| \rho \right| = 1$时,椭圆退化成一条线段,表明两变量完全线性相关. 实际使用中,式(1)中多维椭球域的特征矩阵可通过协方差矩阵${\Omega }_X $获得[25, 26] $$ { G }= { \Omega}_X^{ - 1} =\\ \left[\!\! \begin{array}{cccc} {D(X_1 )} & {Cov(X_1 ,X_2 )} & \cdots & {Cov(X_1 ,X_n )} \\ {Cov(X_2 ,X_1 )} & {D(X_2 )} & \cdots & {Cov(X_2 ,X_n )} \\ \vdots & \vdots & \ddots & \vdots \\ {Cov(X_n ,X_1 )} & {Cov(X_n ,X_2 )} & \cdots & {D(X_n )} \\ \end{array} \!\! \right]^{ - 1} \tag{6}$$
|
图2 任意两时刻区间变量的相关性定义 Fig.2 Definition of correlation between interval variables at two time points |
对于二维凸模型过程$\left( {X^{\rm I}(t),Y^{\rm I}(t)} \right)$,对任意整数$n,m$及任意的$t_1 ,t_2 ,\cdots,t_n \in T$,${t}'_1 ,{t}'_2 ,\cdots,{t}'_m \in T$,$n + m$维向量$(X(t_1 ),X(t_2 ),\cdots,X(t_n ), Y({t}'_1 ),Y({t}'_2 ),\cdots,Y({t}'_m ))$的不确定域可表示为 $$ ({ V} - { V}^{\rm c})^{\rm T}{\Omega}_V ^{ - 1}({ V} - { V}^{\rm c}) ≤ 1 \\ {\Omega}_V = \left[\!\!\begin{array}{cc} {{\Omega}_X } & {{\Omega}_{XY} } \\ {{\Omega}_{YX} } & {{\Omega}_Y } \end{array}\!\!\right] \tag{7}$$ 其中${ V} = \left[{X_1 ,X_2 ,\cdots,X_n ,{Y}'_1 ,{Y}'_2 ,\cdots,{Y}'_m } \right]^{\rm T}$,${Y}'_i ,i = 1,2,\cdots,m$为$Y({t}'_i )$的简写. 协方差矩阵 ${\Omega}_V $中的子矩阵如下 $$ \left.\!\! {\Omega}_X = \left[\!\! \begin{array}{cccc} {D(X_1 )} & {Cov(X_1 ,X_2 )} & \cdots & {Cov(X_1 ,X_n )} \\ {Cov(X_2 ,X_1 )} & {D(X_2 )} & \cdots & {Cov(X_2 ,X_n )} \\ \vdots & \vdots & \ddots & \vdots \\ {Cov(X_n ,X_1 )} & {Cov(X_n ,X_2 )} & \cdots & {D(X_n )} \end{array} \!\! \right]_{n\times n} \\ {\Omega}_Y = \left[\!\! \begin{array}{cccc} {D({Y}'_1 )} & {Cov({Y}'_1 ,{Y}'_2 )} & \cdots & {Cov({Y}'_1 ,{Y}'_m )} \\ {Cov({Y}'_2 ,{Y}'_1 )} & {D({Y}'_2 )} & \cdots & {Cov({Y}'_2 ,{Y}'_m )} \\ \vdots & \vdots & \ddots & \vdots \\ {Cov({Y}'_m ,{Y}'_1 )} & {Cov({Y}'_m ,{Y}'_2 )} & \cdots & {D({Y}'_m )} \end{array} \!\! \right]_{m\times m} \\ {\Omega}_{XY} ={\Omega}_{YX}^{\rm T} = \left[\!\! \begin{array}{cccc} {Cov(X_1 ,{Y}'_1 )} & {Cov(X_1 ,{Y}'_2 )} & \cdots & {Cov(X_1 ,{Y}'_m )} \\ {Cov(X_2 ,{Y}'_1 )} & {Cov(X_2 ,{Y}'_2 )} & \cdots & {Cov(X_2 ,{Y}'_m )} \\ \vdots & \vdots & \ddots & \vdots \\ {Cov(X_n ,{Y}'_1 )} & {Cov(X_n ,{Y}'_2 )} & \cdots & {Cov(X_n ,{Y}'_m )} \end{array} \!\! \right]_{n\times m} \right\} \tag{8}$$ 其中$X^{\rm I}(t)$与$Y^{\rm I}(t)$的互协方差函数定义与式(4)类似.同时,它们的互相关系数函数的定义也与式(5)类似.高于二维的凸模型过程矢量的多维不确定域构建可在上述二维情况的基础上拓展得到.
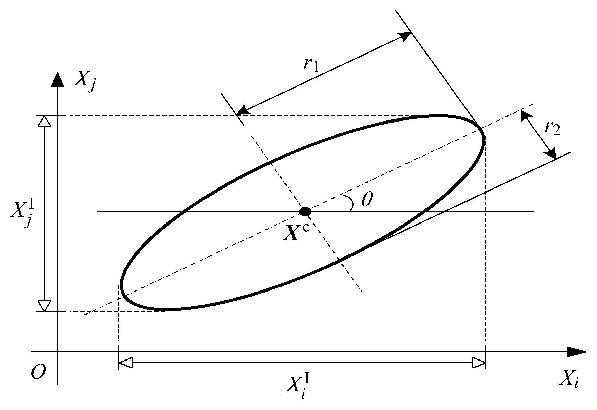
1.2 平稳凸模型过程如果某一凸模型过程$X^{\rm I} (t)$的边界函数$X^{\rm L} (t)$与$X^{\rm U} (t)$均为常数,自协方差函数与自相关系数函数只与时间间隔$\tau = t_2 - t_1 $相关而与时刻$t_1 $和$t_2 $无关,即 $$X^{\rm L}(t) = X^{\rm L} \tag{9}$$ $$X^{\rm U}(t) = X^{\rm U} \tag{10}$$ $$Cov(X_1 ,X_2 ) = C(\tau ) \tag{11}$$ $$\rho _{X_1 X_2 } = \rho (\tau ) \tag{12}$$ 其中,$X^{\rm L}$与$X^{\rm U}$是常数,$C(\tau )$和$\rho (\tau )$都是关于$\tau $的函数,则$X^{\rm I}(t)$称为平稳凸模型过程. 如图3所示为一平稳凸模型过程,其中值函数和边界函数都不随时间变化.如传统的随机过程理论,我们定义了几类典型的平稳凸模型过程的自相关系数函数,如附表所示.
|
图3 平稳凸模型过程 Fig.3 Stationary convex model process |
在传统的随机振动分析中,通常用随机过程描述不确定性激励,则结构的响应也为一随机过程,目前在该领域已提出很多方法来求解结构响应的随机分布特征[2-3,5- 6,9-16]. 而在非随机振动分析中,用非概率凸模型过程描述不确定性激励,则结构的响应也为一凸模型过程,即结构可能的最大响应和最小响应组成的两条时间历程边界. 而实际工程问题中,上述响应边界对于结构或产品的安全性评估及可靠性设计具有重要的工程意义;而且响应边界的概念及可靠性设计方式易于工程人员理解,尤其是在可靠度要求较高的结构安全性设计问题上具有很大应用潜力. 下面,本文将分别针对单自由度和多自由度系统,建立相应的非随机振动分析方法,以求解振动系统在不确定性激励下的动态响应区间;另外,本文也将给出其蒙特卡罗仿真方法,为非随机振动提供一种最为一般的分析工具,同时也为各类非随机振动分析算法的开发提供精度验证.
2.1 单自由度系统考虑如下的单自由度振动系统 $$ m\ddot {x}(t) + c\dot {x}(t) + kx(t) = f(t) \tag{13}$$ 其中,$m$,$c$和 $k$分别为系统的质量,阻尼和刚度,$x(t)$为位移响应,$f(t)$为系统所受激励. 首先考虑$f(t)$为确定性载荷的情况,对于式(13)目前已有多种有效数值求解算法,如纽马克法[30],威尔逊 $\theta $ 法[31],中心差分法[32]等. 本文基于纽马克法进行分析,其计算过程可简述如下
(1) 选择合适的步长$\Delta t$,参数$\alpha $和$\delta $,并计算下列积分常数$a_i ,i = 1,2,\cdots,7$ $$ a_0 = \dfrac{1}{\alpha (\Delta t)^2} ,a_1 = \dfrac{\delta }{\alpha \Delta t} ,a_2 = \dfrac{1}{\alpha \Delta t} ,a_3 = \dfrac{1}{2\alpha } - 1 \\ a_4 = \dfrac{\delta }{\alpha } - 1 ,a_5 = \dfrac{\Delta t}{2}\Big(\dfrac{\delta }{\alpha } - 2\Big) ,a_6 = \Delta t(1 - \delta ) \\ a_7 = \delta \Delta t $$
(2) 计算等效刚度 $$ \hat {k} = k + a_0 m + a_1 c \tag{14}$$
(3) 假定系统在$t_k $时刻的响应(位移、速度和加速度)已知,则$t_{k + 1} $时刻的响应计算如下
$t_{k + 1}$ 时刻的等效力 $$ \hat {f}_{k + 1} = f_{k + 1} + m(a_0 x_k + a_2 \dot {x}_k + a_3 \ddot {x}_k ) +\\ c(a_1 x_k + a_4 \dot {x}_k + a_5 \ddot {x}_k ) \tag{15}$$
$t_{k + 1}$ 时刻的位移响应 $$ x_{k + 1} = \dfrac{\hat {f}_{k + 1} }{\hat {k}} \tag{16}$$
$t_{k + 1}$ 时刻的加速度、速度响应 $$ \ddot {x}_{k + 1} = a_0 (x_{k + 1} - x_k ) - a_2 \dot {x}_k - a_3 \ddot {x}_k \tag{17}$$ $$ \dot {x}_{k + 1} = \dot {x}_k + a_6 \ddot {x}_k + a_7 \ddot {x}_{k + 1} \tag{18}$$ 其中,$\Delta t = t_{k + 1} - t_k $,$x_{k + 1} = x(t_{k + 1} )$,$\dot {x}_{k + 1} = \dot {x}(t_{k + 1} )$,$\ddot {x}_{k + 1} = \ddot {x}(t_{k + 1} )$,$f_{k + 1} = f(t_{k + 1} )$. 针对时间间隔$\Delta t$内加速度的不同描述形式,纽马克法具有三种常用的计算形式:常加速度法,常平均加速度法和线性加速度法.本文采用常平均加速度法,$\delta $与$\alpha $为算法中的两个参数,常平均加速度法中取$\delta = 0.5$,$\alpha = 0.25$. 可将式(15) $\sim$式(18)写成矩阵形式,并通过递推,将$t_{k + 1} $时刻响应表示成激励时间序列与初始条件的线性组合 $$ x_{k + 1} = \left( { { H}_x } \right)_1 { x} + \left( {{ H}_f } \right)_1 { f} \tag{19}$$ $$ \dot {x}_{k + 1} = \left( {{ H}_x } \right)_2 { x} + \left( {{ H}_f } \right)_2 { f} \tag{20}$$ $$ \ddot {x}_{k + 1} = \left( {{ H}_x } \right)_3 { x} + \left( {{ H}_f } \right)_3 { f} \tag{21}$$ 其中,$\left( \cdot \right)_i (i = 1,2,3)$表示矩阵第$i$行向量,${ x} = \left[{x_1 ,\dot {x}_1 } \right]^{\rm T}$为初始条件,${ f} = [f_1 ,f_2 ,\cdots,f_{k + 1}]^{\rm T}$表示激励的时间序列,${ H}_x $和${ H}_f $的形式见附录A.
其次,考虑$f(t)$为动态不确定性激励的情况,在非随机振动分析中,使用凸模型过程$f^{\rm I}(t)$来表征该激励,则式(13)可表述为 $$ m\ddot {x}(t) + c\dot {x}(t) + kx(t) = f^{\rm I}(t) \tag{22}$$ 式中,激励$f(t)$所有可能的形式都被限定在两条随时间变化的上、下边界曲线之内,则系统的响应也将属于一随时间变化的区间,即响应也为一凸模型过程$x^{\rm I}(t)$. 下面,将给出相应方法计算该响应边界.
根据凸模型过程理论[25],激励$f^{\rm I}(t)$的时间序列向量${ f} = [f_1 ,f_2 ,\cdots,f_{k + 1}]^{\rm T}$的不确定域为 $$ ({ f} - { f}^{\rm c})^{\rm T}{\Omega}_f ^{ - 1}({ f} - { f}^{\rm c}) ≤ 1 \tag{23}$$ 其中${ f}^{\rm c}$为区间中值向量,${\Omega}_f $为$f^I(t)$中$k + 1$个时间点区间变量的协方差矩阵 $$ {\Omega}_f = \left[\!\!\begin{array}{cccc} {D(f_1 )} & {Cov(f_1 ,f_2 )} & \!\!\cdots\!\! & {Cov(f_1 ,f_{k + 1} )} \\ {Cov(f_2 ,f_1 )} & {D(f_2 )} & \!\!\cdots\!\! & {Cov(f_2 ,f_{k + 1} )} \\ \vdots & \vdots & \!\!\ddots\!\! & \!\!\vdots\!\! \\ {Cov(f_{k + 1} ,f_1 )} & {Cov(f_{k + 1} ,f_2 )} & \!\!\cdots\!\! & {D(f_{k + 1} )} \end{array} \!\! \right] \tag{24}$$
由式(19)和(23)可知,求解不确定位移响应$x_{k + 1} $的上、下边界即可转化为如下最优化问题 $$ \max x_{k + 1} = \left( { { H}_x } \right)_1 { x} + \left( {{ H}_f } \right)_1 { f} \\ {\rm s.t.} ({ f} - { f}^{\rm c})^{\rm T}{\Omega}_f ^{ - 1}({ f} - { f}^{\rm c}) ≤ 1 \tag{25}$$ 和 $$ \max x_{k + 1} = \left( { { H}_x } \right)_1 { x} + \left( {{ H}_f } \right)_1 { f} \\ {\rm s.t.} ({ f} - { f}^{\rm c})^{\rm T}{\Omega}_f ^{ - 1}({ f} - { f}^{\rm c}) ≤ 1 \tag{26}$$ 其中,${ f}$为优化向量. 上述优化问题中,目标函数为线性函数,约束条件为凸集,则由优化理论可知,该问题的最优解将在凸集(多维椭球体)的边界上取得,故不等式约束可等效为等式约束,即最优点处$({ f} - { f}^{\rm c})^{\rm T} {\Omega}_f^{ - 1} ({ f} - { f}^{\rm c}) = 1$成立. 则可使用拉格朗日乘子法[33]求解该优化问题,首先构建拉格朗日函数$L$ $$ L = \mu [({ f}- { f}^{\rm c})^{\rm T}{\Omega} _f^{ - 1} ({ f} - { f}^{\rm c}) - 1] +\\ \left( { { H}_x } \right)_1 { x} + \left( {{ H}_f } \right)_1 { f} \tag{27}$$ 其中,$\mu $为拉格朗日乘子. 令$\dfrac{\partial L}{\partial { f}} ={\bf 0}$,得到 $$ { f} - { f}^{\rm c} = - \dfrac{1}{2\mu }{\Omega}_f \left( {{ H}_f } \right)_1^{\rm T} \tag{28}$$ 将上式代入等式约束得到 $$ \mu = \pm \dfrac{\sqrt {\left( {{ H}_f } \right)_1 {\Omega}_f \left( {{ H}_f } \right)_1^{\rm T} } }{2} \tag{29}$$ 得到最优解为 $$ { f} ={ f}^{\rm c}\pm \dfrac{{\Omega}_f \left( {{ H}_f } \right)_1^{\rm T} }{\sqrt {\left( {{ H}_f } \right)_1 {\Omega}_f \left( {{ H}_f } \right)_1^{\rm T} } } \tag{30}$$ 从而得到位移响应$x_{k + 1} $的上边界$x_{k + 1}^U $和下边界$x_{k + 1}^L $分别为
$ x_{k + 1}^{\rm U} = \left( { { H}_f } \right)_1 { f}^{\rm c }+ \dfrac{\left( {{ H}_f } \right)_1 {\Omega}_f \left( {{ H}_f } \right)_1^{\rm T} }{\sqrt {\left( {{ H}_f } \right)_1 {\Omega}_f \left( {{ H}_f } \right)_1^{\rm T} } } + \left( {{ H}_x } \right)_1 { x} =$ $$ \left( {{ H}_x } \right)_1 { x} + \left( {{ H}_f } \right)_1 { f}^{\rm c }+ \sqrt {\left( {{ H}_f } \right)_1{\Omega}_f \left( {{ H}_f } \right)_1^{\rm T} } \tag{31}$$ $ x_{k + 1}^{\rm L} = \left( {{ H}_f } \right)_1 { f}^{\rm c} - \dfrac{\left( {{ H}_f } \right)_1 {\Omega}_f \left( {{ H}_f } \right)_1^{\rm T} }{\sqrt {\left( {{ H}_f } \right)_1 {\Omega}_f \left( {{ H}_f } \right)_1^{\rm T} } } + \left( {{ H}_x } \right)_1 { x} =$ $$ \left( {{ H}_x } \right)_1 { x} + \left( {{ H}_f } \right)_1 { f}^{\rm c} - \sqrt {\left( {{ H}_f } \right)_1 {\Omega}_f \left( {{ H}_f } \right)_1^{\rm T} } \tag{32}$$ 通过上式求出各个时间点的响应区间,则可获得单自由度振动系统在不确定性激励下随时间变化的位移响应边界. 类似地,还可以求得速度和加速度的响应边界.
2.2 多自由度系统考虑$l$维的多自由度振动系统 $$ { M}\ddot { X}(t) +{ C}\dot{ X} (t) + { K}{ X} (t) = { F}(t) \tag{33}$$ 其中,${ M}$,${ C}$和${ K}$分别为质量矩阵,阻尼矩阵和刚度矩阵; ${ F}(t) = \left[{f_1 (t),f_2 (t),\cdots,f_l (t)} \right]^{\rm T}$为$l$维的激励向量,${ X}(t) = \left[{x_1 (t),x_2 (t),\cdots, x_l (t)} \right]^{\rm T}$为$l$维的位移响应向量. 首先考虑${ F}(t)$为确定性激励的情况,仍然使用纽马克法求解式(33),其计算过程简述如下:
(1) 选择合适的步长$\Delta t$,并计算下列积分常数$a_i ,i = 1,2,\cdots,7$ $$ \begin{array}{l} a_0 = \dfrac{1}{\alpha (\Delta t)^2} ,a_1 = \dfrac{\delta }{\alpha \Delta t} ,a_2 = \dfrac{1}{\alpha \Delta t} ,a_3 = \dfrac{1}{2\alpha } - 1 \\ a_4 = \dfrac{\delta }{\alpha } - 1 ,a_5 = \dfrac{\Delta t}{2}(\dfrac{\delta }{\alpha } - 2) ,a_6 = \Delta t(1 - \delta ) \\ a_7 = \delta \Delta t \end{array} $$ 其中参数$\alpha $和$\delta $的取值和单自由度系统一致.
(2) 计算等效刚度 $$ \hat { K} = { K}+ a_0 { M} + a_1 { C} \tag{34}$$
(3) 假定系统在$t_k $时刻的响应(位移、速度和加速度)已知,则$t_{k + 1} $时刻的响应计算如下:
$t_{k + 1}$ 时刻的等效力 $$ \hat { F}_{k + 1} = { F}_{k + 1} +{ M}(a_0{ X}_k + a_2 \dot{ X}_k + a_3 \ddot { X}_k ) +\\ { C}(a_1{ X}_k + a_4 \dot{ X}_k + a_5 \ddot{ X}_k ) \tag{35}$$
$t_{k + 1}$时刻的位移响应 $$ { X}_{k + 1} = \hat{ K}^{ - 1}\hat{ F}_{k + 1} \tag{36}$$
$t_{k + 1}$ 时刻的加速度、速度向量 $$\ddot{ X}_{k + 1} = a_0 ({ X}_{k + 1} - { X}_k ) - a_2 \dot{ X}_k - a_3 \ddot { X}_k \tag{37}$$ $\dot{ X}_{k + 1} = \dot{ X}_k + a_6 \ddot{ X}_k + a_7 \ddot{ X}_{k + 1} \tag{38}$ 其中${ X}_{k + 1} = { X} (t_{k + 1} )$,$\dot{ X}_{k + 1} = \dot { X} (t_{k + 1} )$,$\ddot{ X}_{k + 1} = \ddot{ X} (t_{k + 1} )$,${ F}_{k + 1} = { F} (t_{k + 1} )$.将式(35) $\sim$式(38)写成矩阵的形式,并通过递推,将$t_{k + 1} $时刻响应表示成激励时间序列与初始条件的线性组合 $$ \left[\!\! \begin{array}{c} {{ X}_{k + 1} } \\ {\dot{ X}_{k + 1} } \\ {\ddot{ X}_{k + 1} } \end{array} \!\! \right] = \hat { H}_X \left[\!\! \begin{array}{c} {{ X}_1 } \\ {\dot { X}_1 } \\ \end{array} \!\! \right] + \hat { H}_F { F} \tag{39}$$ 其中,${ X}_1 $,$\dot{ X}_1 $为初始位移和速度,$\hat { H}_X $和$\hat { H}_F $的形式见附录B.${ F}$表示$l$维激励的时间序列 $$ { F}= \left[ {\left( {{ F}_1 } \right)^{\rm T}} {\left( {{ F}_2 } \right)^{\rm T}} \cdots {\left( {{ F}_{k + 1} } \right)^{\rm T}} \right]^{\rm T} \tag{40} $$ 其中 $$ { F}_i = \left[ {f_1 (t_i )} {f_2 (t_i )} \cdots {f_l (t_i )} \right]^{\rm T} ,i = 1,2,\cdots,k + 1 \tag{41}$$ 为方便分析,将${ F}$中元素重新排列得到新的激励序列${ F}'$ $$ { F}' = \left[ {\left( {{ F}'_1 } \right)^{\rm T}} {\left( {{ F}'_2 } \right)^{\rm T}} \cdots {\left( {{ F}'_l } \right)^{\rm T}} \right]^{\rm T} \tag{42}$$ 其中 $$ { F}'_i = \left[ {f_i (t_1 )} {f_i (t_2 )} \cdots {f_i (t_{k + 1} )} \right]^{\rm T} , i = 1,2,\cdots,l \tag{43}$$ 相应地,$\hat { H}_F $ 中的元素也要重新排列,式(39)可以改写为 $$ \left[\begin{array}{c} {{ X}_{k + 1} } \\ {\dot { X}_{k + 1} } \\ {\ddot { X}_{k + 1} } \end{array} \right] = \hat{ H}_X \left[\begin{array}{c} {{ X}_1 } \\ {\dot { X}_1 } \\ \end{array} \right] + {\hat { H}}'_F { F}' \tag{44}$$ 其中,${\hat { H}}'_F $ 是$\hat{ H}_F $经过重新排列后得到的矩阵.
其次,考虑${ F} (t)$为动态不确定性激励的情况,在非随机振动分析中,使用$l$维凸模型过程向量${ F}^{\rm I}(t)$来表征该激励,则式(33)可表述为 $$ { M}\ddot{ X}(t) + { C}\dot{ X}(t) + { K}{ X}(t) ={ F}^{\rm I} (t) \tag{45}$$ 下面,将给出相关方法计算上式中多维动态响应的边界.
激励时间序列向量${ F}'$的不确定域可描述为 $$ ({ F}' - { F}'^{\rm c})^{\rm T}{\Omega}'^{ - 1}_{F} ({ F}' - { F}'^{\rm c}) ≤ 1 \tag{46} $$ 其中${ F}'^{\rm c}$是区间向量${ F}'$的中值向量,${\Omega} _{F'} $是${ F}'$中变量的协方差矩阵,可划分为$l\times l$个分块矩阵,即 $$ {\Omega}_{F'} = \left[\!\! \begin{array}{cccc} {{\Omega}_{F'_1 } } & {{\Omega}_{F'_1 F'_2 } } & \cdots & {{\Omega}_{F'_1 F'_l } } \\ {{\Omega}_{F'_2 F'_1 } } & {{\Omega}_{F'_2 } } & \cdots & {{\Omega}_{F'_2 F'_l } } \\ \vdots & \vdots & \ddots & \vdots \\ {{\Omega}_{F'_l F'_1 } } & {{\Omega}_{F'_l F'_2 } } & \cdots & {{\Omega}_{F'_l } } \\ \end{array} \!\! \right] \tag{47}$$ 其中 $\left.\!\!\begin{array}{l} {\Omega} _{F'_i } = \left[\!\! \begin{array}{cccc} {D(f_i (t_1 ))} & {Cov(f_i (t_1 ),f_i (t_2 ))} & \cdots & {Cov(f_i (t_1 ),f_i (t_{k + 1} ))} \\ {Cov(f_i (t_2 ),f_i (t_1 ))} & {D(f_i (t_2 ))} & \cdots & {Cov(f_i (t_2 ),f_i (t_{k + 1} ))} \\ \vdots & \vdots & \ddots & \vdots \\ {Cov(f_i (t_{k + 1} ),f_i (t_1 ))} & {Cov(f_i (t_{k + 1} ),f_i (t_2 ))} & \cdots & {D(f_i (t_{k + 1} ))} \end{array} \!\! \right] i= 1,2,\cdots,l \\ {\Omega}_{F'_i F'_j } = \left[\!\! \begin{array}{cccc} {Cov(f_i (t_1 ),f_j (t_1 ))} & {Cov(f_i (t_1 ),f_j (t_2 ))} & \cdots & {Cov(f_i (t_1 ),f_j (t_{k + 1} ))} \\ {Cov(f_i (t_2 ),f_j (t_1 ))} & {Cov(f_i (t_2 ),f_j (t_2 ))} & \cdots & {Cov(f_i (t_2 ),f_j (t_{k + 1} ))} \\ \vdots & \vdots & \ddots & \vdots \\ {Cov(f_i (t_{k + 1} ),f_j (t_1 ))} & {Cov(f_i (t_{k + 1} ),f_j (t_2 ))} & \cdots & {Cov(f_i (t_{k + 1} ),f_j (t_{k + 1} ))} \end{array} \right] i e j \end{array} \!\! \right\} \tag{48}$
由式(44)和式(46)可得,求解位移响应$x_j (t_{k + 1} )$(第$j$个自由度在$t_{k + 1} $时刻位移)的上、下边界可转化为如下最优化问题 $$ \max x_j (t_{k + 1} ) = \left( {\hat { H}_X } \right)_j \left[ \!\!\begin{array}{c} {{ X}_1 } \\ {\dot{ X}_1 } \end{array} \!\! \right] + \left( { \hat{ H}'_F } \right)_j { F}' \\ {\rm s.t.} ({ F}' - { F}'^{\rm c})^{\rm T}{\Omega} _{ F'}^{ - 1} ({ F}' - { F}'^{\rm c}) ≤ 1 \tag{49}$$ 和 $$\min {x_j}({t_{k + 1}}) = {\left( {{{\hat H}_X}} \right)_j}\left[ {\matrix{ {{X_1}} \cr {{{\dot X}_1}} \cr } } \right] + {\left( {{{\hat H'}_F}} \right)_j}F'{\rm{s}}.{\rm{t}}.{(F' - {F'^{\rm{c}}})^{\rm{T}}}\Omega _{F'}^{ - 1}(F' - {F'^{\rm{c}}}) \le 1 \tag{50}$$ 其中$\left( \cdot \right)_j (1 ≤ j ≤ l)$表示括号内矩阵的第$j$行向量. 同样运用拉格朗日乘子法求解该优化问题,得到位移响应$x_j (t_{k + 1} )$的上边界$x_j^{\rm U} (t_{k + 1} )$和下边界$x_j^{\rm L} (t_{k + 1} )$ $x_j^{\rm U} (t_{k + 1} ) = \left( {\hat{ H}_X } \right)_j \left[\!\! \begin{array}{c} {{ X}_1 } \\ {\dot{ X}_1 } \end{array} \!\! \right] + \left( { \hat{ H}'_F } \right)_j { F}'^{\rm c} + \sqrt {\left( { \hat{ H}'_F } \right)_j {\Omega}_{F'} \left( { \hat{ H}'_F } \right)_j^{\rm T} } \tag{51}$
$x_j^L (t_{k + 1} ) = \left( {\hat{ H}_X } \right)_j \left[\!\! \begin{array}{c} {{ X}_1 } \\ {\dot{ X}_1 } \end{array} \!\! \right] + \left( { \hat{ H}'_F } \right)_j { F}'^{\rm c} - \sqrt {\left( { \hat{ H}'_F } \right)_j {\Omega} _{F'} \left( { \hat{ H}'_F } \right)_j^{\rm T}} \tag{52}$ 最终可获得各自由度随时间变化的位移响应边界. 类似地,还可以求得速度和加速度的响应边界.
2.3 蒙特卡罗仿真本文还提出一种蒙特卡罗仿真方法来计算动态响应的上下边界,虽然效率较低,但是可为非随机振动提供一种最为一般的分析工具,同时也为各类分析算法的开发提供精度验证.针对单自由度系统,蒙特卡罗仿真的计算流程如下: (1) 对于凸模型过程$f^{\rm I}(t)$,采用文献[25]中的方法进行采样,获得$M$个载荷样本;每一个载荷样本都为一$N$维的时间序列$\left( {f\left( {t_1 } \right),f\left( {t_2 } \right),\cdots,f\left( {t_N } \right)} \right)$,用以描述其动态特性.
(2) 针对任一载荷样本$\left( {f\left( {t_1 } \right),f\left( {t_2 } \right),\cdots,f\left( {t_N } \right)} \right)$,进行式(13)所示的振动分析,获得相应的系统动态响应$\left( {x\left( {t_1 } \right),x\left( {t_2 } \right),\cdots,x\left( {t_n } \right)} \right)$;$M$个载荷样本将对应$M$个位移响应样本.
(3)在任意时间点,从$M$个位移响应样本中选出最大值和最小值,分别作为响应上界和下界;综合所有时间点数据,即可获得随时间变化的系统动态位移响应边界.
(4)基于所有响应样本,也可使用文献[26]中方法计算位移响应凸模型过程$x^{\rm I}(t)$的自协方差函数和自相关系数函数.
对于多自由度系统,其蒙特卡罗仿真可由单自由度振动系统的蒙特卡罗仿真拓展得到,此处不再赘述.
3 算例 3.1 单自由度系统考虑一单自由度振动系统,其质量为$m = 1$,阻尼系数为$c = 2\pi $,刚度为$k = 4\pi ^2$,初始条件为$x(0) = \dot {x}(0) = 0$. 考虑外部激励$f(t)$是一个平稳凸模型过程,在任意时刻$t_i $,变量$f(t_i )$的区间为$\left[{ - 3,3} \right]$,自相关系数函数为$\rho _f (\tau )$.
首先,选取$\rho _f (\tau ) = {\rm e}^{ - \left| \tau \right|}$,图4给出了由本文方法计算得到位移响应$x(t)$的上、下边界(实线)及经蒙特卡罗法得到的10 000条响应样本曲线(虚线).从图中可以看到计算得到的$x(t)$边界完全包络了这些样本曲线,说明本文建立的非随机振动分析算法能较好地保证计算结果的安全性. 图5给出系统阻尼$c$分别为$2\pi $,$0.2\pi $,0时计算得到的响应边界.从图中可以看出,响应在起始阶段是非平稳的,位移响应区间随时间变化;经过一段时间的过渡后,响应区间趋于恒定,即进入平稳阶段. 从非平稳到平稳阶段过渡时间的长短与系统阻尼大小有关,阻尼越小,过渡时间越长;当阻尼为0时,响应区间将具有逐渐变大趋势,达不到平稳响应状态. 图6给出了激励自相关系数函数为$\rho _f \left( \tau \right) ={\rm e}^{ - \lambda \left| \tau \right|}$的情况下,$\lambda $取不同值时的动态响应结果. 从结果可以看出,随着$\lambda $增大,系统平稳响应阶段的区间将变小,$\lambda $取1时稳态响应区间为$\left[{ - 0.075 2,0.075 2} \right]$,而$\lambda $取10时其缩小为$[- 0.055 5,0.055 5]$,说明在激励区间不变的情况下其自相关系数函数对响应区间可以有显著影响.
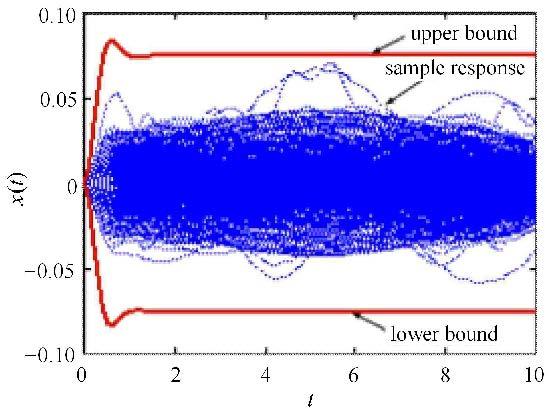
|
图4 单自由度系统的动态位移响应边界 Fig.4 Dynamic displacement response bounds of the SDOF system |
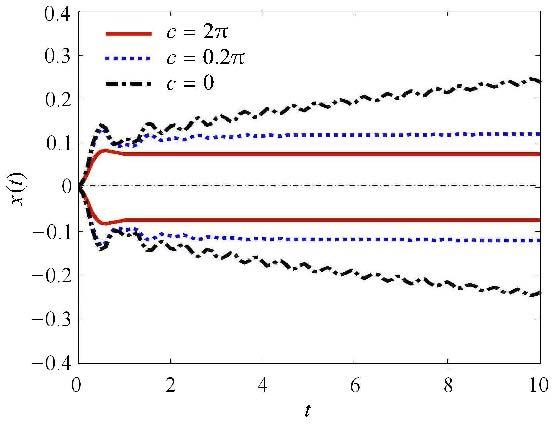
|
图5 单自由度系统不同阻尼系数下的动态位移响应边界 Fig.5 Dynamic displacement response bounds under different damping coefficients of the SODF system |
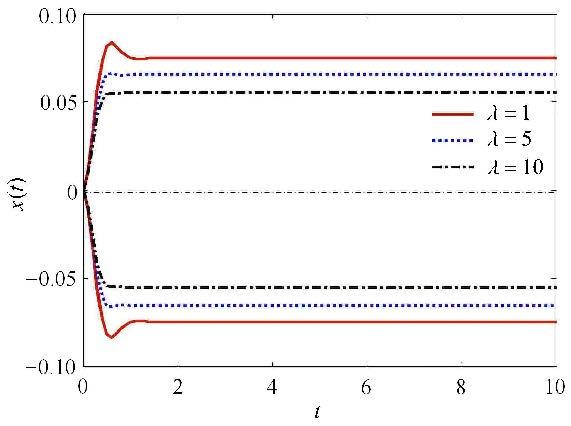
|
图6 单自由度系统在不同参数$\lambda $下的动态位移响应边界 Fig.6 Dynamic displacement response bounds under different $\lambda $ of the SODF system |
另外,如图7所示,考虑激励$f(t)$为非平稳凸模型过程的情况,对任意时刻$t$,其区间为$[- 2 - \sin (2\pi t),2 + \sin (2\pi t)]$. 对任意时刻$t_1 ,t_2 $,假设$f(t_1 )$与$f(t_2 )$的相关系数为$\rho _{f_1 f_2 } ={\rm e}^{ - \left| {t_2 - t_1 } \right|}$,图8给出了计算得到的响应上下边界曲线.由结果可知,若激励是非平稳凸模型过程,则位移响应在时间历程内也将是非平稳的,响应边界将随时间变化.
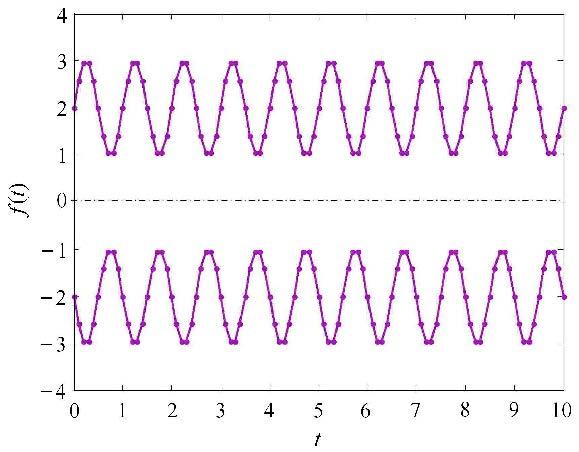
|
图7 非平稳凸模型过程$f(t)$ Fig.7 The non-stationary convex model process $f(t)$ |
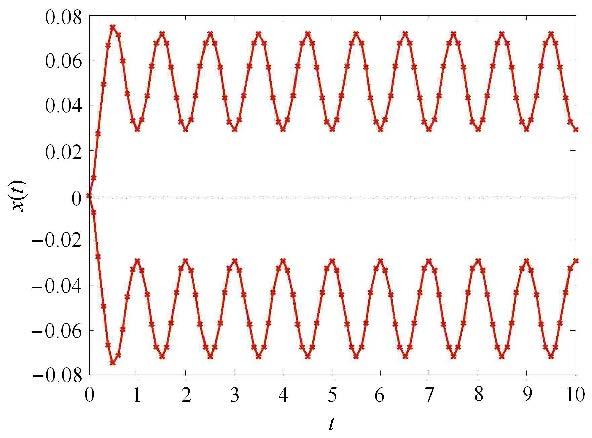
|
图8 非平稳凸模型过程$f (t)$ 作用下的动态位移响应边界 Fig.8 Dynamic displacement bounds under the non-stationary convex model process $f (t)$ |
考虑二自由度振动系统受二维激励,其质量矩阵、阻尼矩阵和刚度矩阵分别为 $${ M} = \left[\!\! \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \!\! \right] \tag{53}$$ $$C = \left[ {\matrix{ {20} & { - 10} \cr { - 10} & {10} \cr } } \right]{\rm{ }} \tag{54}$$ $${ K} = \left[\!\! \begin{array}{cc} {30} & { - 10} \\ { - 10} & {10} \end{array} \!\! \right] \tag{55}$$ 振动初始条件为${ X}(0) = \dot{ X} (0) = {\bf 0}$;激励$f_1 (t)$和$f_2 (t)$为二维平稳凸模型过程,$f_1 (t),f_2 (t)$的区间分别为$\left[{ - 3,3} \right]$,$\left[{ - 6,6} \right]$,其自相关系数函数分别为$\rho _1 (\tau )$,$\rho _2 (\tau )$,互相关系数函数为$\rho _{12} (\tau )$. 采用本文方法对系统动态位移响应进行分析.
设$\rho _1 (\tau ) = {\rm e}^{ - \left| \tau \right|}\cos (2\tau )$,$\rho _2 (\tau ) = {\rm e}^{ - 2\left| \tau \right|}\cos (2\tau )$,$\rho _{12} (\tau ) = \cos (2\tau + \pi / 6)$.图9给出了由本文方法计算得到的动态位移响应边界及由蒙特卡罗仿真获得的10 000条位移样本曲线. 由结果可知,$x_1 (t)$和$x_2 (t)$的边界都很好地包络了各自的样本曲线,说明本文方法针对该二自由度系统不确定振动的响应边界计算结果同样是可靠的.令$\rho _1 \left( \tau \right) = {\rm e}^{ - \lambda _1 \left| \tau \right|}\cos (2\tau )$,$\rho _2 \left( \tau \right) = {\rm e}^{ - \lambda _2 \left| \tau \right|}\cos (2\tau )$,$\rho _{12} (\tau ) = \cos (\lambda _3 \tau + \pi / 6)$,可以通过变化$\lambda _1 $,$\lambda _2 $和$\lambda _3 $来改变$\rho _1 \left( \tau \right)$,$\rho _2 \left( \tau \right)$和$\rho _{12} (\tau )$,以此分析激励的相关系数函数对响应区间的影响,设两响应在平稳阶段的区间半径分别为$R_{x_1 } $ 和$R_{x_2 } $.为描述方便,每一次分析中$\lambda _1 $,$\lambda _2 $和$\lambda _3 $中的两个保持恒定,另外一个连续变化,其计算结果如图10所示. 由图可知,任意一个相关系数函数改变对$R_{x_1 } $和$R_{x_2 } $的值都有影响,并且影响程度不同. 在本算例中,$R_{x_1 } $和$R_{x_2 } $对$\lambda _2 $和$\lambda _3 $的敏感性较$\lambda _1 $要强.因此,在对实际的多维系统进行非随机振动分析时,应更好地保证敏感性较强的非随机过程的相关性函数的建模精度.
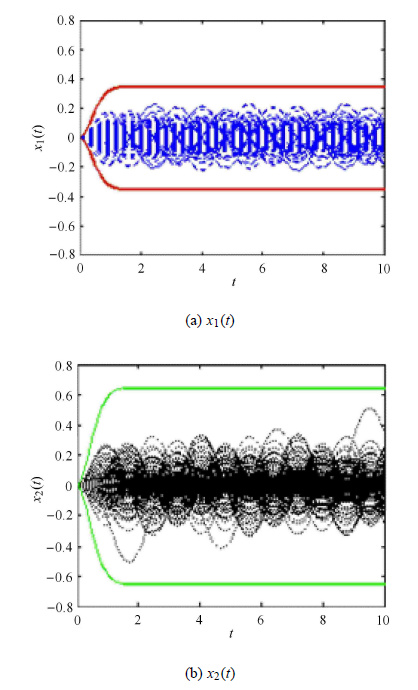
|
图9 二自由度系统的动态位移响应边界 Fig.9 Dynamic displacement response bounds of the two-degree-of-freedom system |
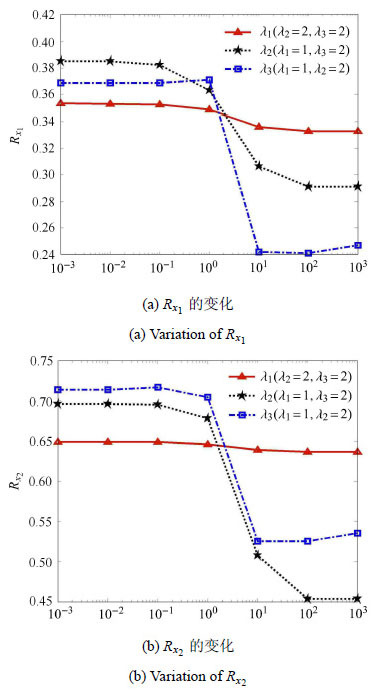
|
图10 二自由度系统中激励相关性对动态响应区间的影响 Fig.10 Effects of the excitations' correlations on the dynamic response bounds of the two-degree-of-freedom system |
车辆振动不仅会引起车上乘员不适和货物受损,而且会使整车零部件过早磨损和疲劳破坏[34]. 为了更好地保证乘员舒适性和行车安全性,需要对车辆的振动响应进行分析.在本算例中,我们考虑如图11所示的8自由度车辆振动问题[35],系统的主要参数如表1所示.假定汽车从静止状态以速度$v = 20$ m/s开始匀速前进. 该振动系统的动力学方程为 $$ { M}\ddot { Z} + { C}\dot { Z} + { K}{ Z} = { K}_t { Q }\tag{56}$$ 其中${ M}$,${ C}$和${ K}$均为$8\times 8$的矩阵,矩阵中各项元素的具体形式可参见文献 [35]. 轮胎的刚度矩阵为 $$ { K}_{\rm t} = \left[\!\! \begin{array}{cccc} {k_{\rm tf} } & 0 & 0 & 0 \\ 0 & {k_{\rm tr} } & 0 & 0 \\ 0 & 0 & {k_{\rm tf} } & 0 \\ 0 & 0 & 0 & {k_{\rm tr} } \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{array} \!\! \right] \tag{57}$$ 路面激励向量为 $$ { Q} = \left[ {q_{\rm fL} } {q_{\rm rL} } {q_{\rm fR} } {q_{\rm rR} } \right]^{\rm T} \tag{58}$$ 响应向量为 $$ { Z} = \left[{Z_{\rm fL} } {Z_{\rm rL} } {Z_{\rm fR} } {Z_{\rm rR} } {Z_{\rm b} } {\theta _x } {\theta _y } {Z_{\rm c} } \right]^{\rm T} \tag{59}$$
| 表1 八自由度车辆振动模型参 Table 1 Parameters of the eight-degree-of-freedom vibration model of vehicle |
将4个轮上的不确定性路面激励均处理为平稳凸模型过程,其区间均为$\left[{ - 5,5} \right]$ cm,自相关系数函数均为$\rho _{\rm q} \left( \tau \right) ={\rm e}^{ - v^2\tau ^2}$.由于同一侧前后轮行驶经过同样的路面轨迹,且前轮的激励过程比后轮领先$\Delta t = \dfrac{l_{\rm f} + l_{\rm r} }{v}$,则可以得到$q_{\rm fL} (t) = q_{\rm rL} (t + \Delta t)$,$q_{\rm fR} (t) = q_{\rm rR} (t + \Delta t)$.因此可以得到同一侧前后轮激励的互相关系数函数为 $ \rho _{q_{\rm fL} q_{\rm rL} } (\tau ) = \rho (q_{\rm fL} (t_i ),q_{\rm rL} (t_i + \tau )) =$ $$ \rho (q_{\rm fL} (t_i ),q_{\rm fL} (t_i + \tau - \Delta t)) = \rho _{\rm q } (\tau - \Delta t) \tag{60}$$ $$\rho _{q_{\rm fR} q_{\rm rR} } (\tau ) = \rho _{\rm q} (\tau - \Delta t) \tag{61}$$ 设左右轮上的路面激励独立,则左轮激励与右轮激励之间的互相关系数均为0,即有 $$ \rho _{q_{\rm fL} q_{\rm fR} } (\tau ) = \rho _{q_{\rm fL} q_{\rm rR} } (\tau ) = \rho _{q_{\rm rL} q_{\rm fR} } (\tau ) = \rho _{q_{\rm rL} q_{\rm rR} } (\tau ) = 0 $$ 由本文方法得到各响应的边界曲线如图12所示,可以看到各响应量均在经历了起始的非平稳阶段后逐渐达到稳态. 其中,4个轮胎的垂向位移$Z_{\rm fL} (t)$,$Z_{\rm rL} (t)$,$Z_{\rm fR} (t)$和$Z_{\rm rR} (t)$最快达到平稳,其非平稳阶段均在1 s以内. 而其余4个响应量则在开始运动$4 \sim 6$ s后逐渐进入平稳状态.
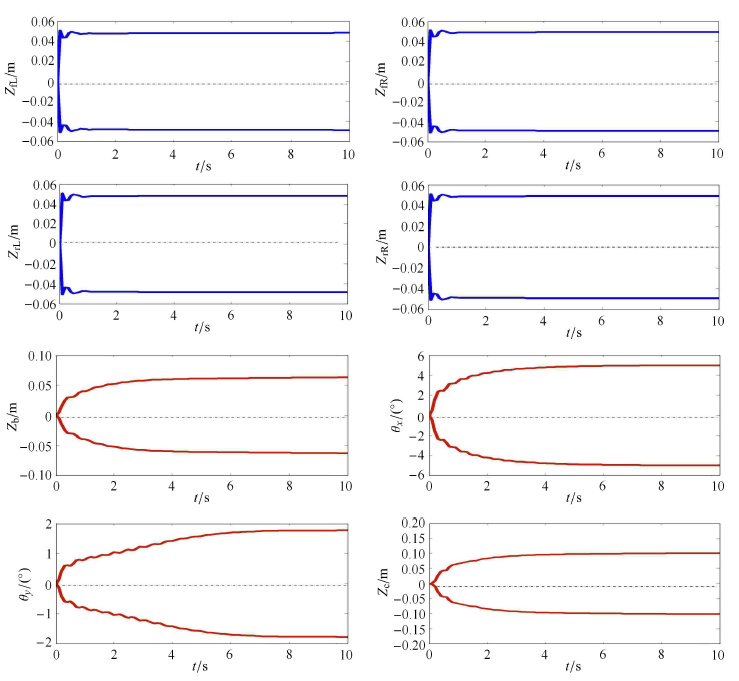
|
图12 八自由度车辆振动模型的动态响应边界 Fig.12 Dynamic displacement response bounds of the eight-degree-of-freedom vibration model of vehicle |
表2为各响应在稳态时的区间,可以看到四个轮胎垂向位移的区间大致相同,而车身垂向位移$Z_{\rm b} (t)$,车身俯仰角位移$\theta _x (t)$及驾驶座垂向位移$Z_{\rm c} (t)$的稳态区间分别为$\left[{ -6.32,6.32} \right]$ cm,$[- 5.00^ \circ ,5.00^ \circ]$,$\left[{ - 10.19,10.19} \right]$ cm,这意味着在车辆行驶过程中,这3个响应量可能达到的最大振幅分别为6.32 cm,$5.00^\circ $,10.19 cm. 车身侧倾角位移$\theta _y (t)$的区间仅为$[- 1.78^ \circ,1.78^ \circ ]$,表明行驶过程中车辆的侧倾角运动并不明显.
| 表2 八自由度车辆振动系统各响应稳态时的区间 Table 2 The stationary response intervals of the eight-degree-of-freedom vibration model of vehicle |
本文提出了一种非随机振动分析方法,可以给出振动系统在不确定性激励下的动态响应边界,从而为复杂结构或系统的可靠性设计提供一种潜在的分析工具.非随机振动分析中,使用随时间变化的区间变量而非依赖于精确概率分布的随机过程模型来描述不确定性激励,一定程度上避免了对大实验样本量的依赖性.另外,系统的动态响应边界在概念上易于工程人员理解,在实际的结构可靠性设计中也方便使用,尤其是对于高可靠性问题具有更好的适用性.非随机振动分析方法可以作为传统随机振动理论的补充,在工程不确定性结构动力学分析及设计领域发挥一定作用.作为一新的工具,非随机振动分析方法未来可扩展至更多自由度的结构问题、非线性振动、结构动态可靠性设计等诸多领域.
附录A将式(15) ~ 式(18) 写成矩阵形式并递推得 $$\eqalign{ & \left[ {\matrix{ {{x_{k + 1}}} \cr {{{\dot x}_{k + 1}}} \cr {{{\ddot x}_{k + 1}}} \cr } } \right] = \left[ {\matrix{ {1/\hat k\left( {{a_0}m + {a_1}c} \right)} & {1/\hat k\left( {{a_2}m + {a_4}c} \right)} & {1/\hat k\left( {{a_3}m + {a_5}c} \right)} & {1/\hat k} \cr {{a_0}{a_7}\left[ {1/\hat k\left( {{a_0}m + {a_1}c} \right) - 1} \right]} & {{a_7}{a_0}1/\hat k\left( {{a_2}m + {a_4}c} \right) + (1 - {a_7}{a_2})} & {{a_7}{a_0}1/\hat k\left( {{a_3}m + {a_5}c} \right) + \left( {{a_6} - {a_7}{a_3}} \right)} & {{a_7}{a_0}1/\hat k} \cr {{a_0}\left[ {1/\hat k\left( {{a_0}m + {a_1}c} \right) - 1} \right]} & {{a_0}1/\hat k\left( {{a_2}m + {a_4}c} \right) - {a_2}} & {{a_0}1/\hat k\left( {{a_3}m + {a_5}c} \right) - {a_3}} & {{a_0}1/\hat k} \cr } } \right] \cdot \cr & } $$ $$\left[ {\matrix{ {{x_k}} \cr {{{\dot x}_k}} \cr {{{\ddot x}_k}} \cr {{f_{k + 1}}} \cr } } \right] = {H_k}\left[ {\matrix{ {{x_k}} \cr {{{\dot x}_k}} \cr {{{\ddot x}_k}} \cr {{f_{k + 1}}} \cr } } \right]$$ $$\left[ \matrix{ {x_k} \hfill \cr {{\dot x}_k} \hfill \cr {{\ddot x}_k} \hfill \cr {f_{k + 1}} \hfill \cr} \right] = \left[ {\matrix{ {1/\hat k\left( {{a_0}m + {a_1}c} \right)} & {1/\hat k\left( {{a_2}m + {a_4}c} \right)} & {1/\hat k\left( {{a_3}m + {a_5}c} \right)} & {1/\hat k} & 0 \cr {{a_0}{a_7}\left[ {1/\hat k\left( {{a_0}m + {a_1}c} \right) - 1} \right]} & {{a_0}{a_7}1/\hat k\left( {{a_2}m + {a_4}c} \right) + \left( {1 - {a_7}{a_2}} \right)} & {{a_0}{a_7}1/\hat k\left( {{a_3}m + {a_5}c} \right) + \left( {{a_6} - {a_3}{a_7}} \right)} & {{a_0}{a_7}1/\hat k} & 0 \cr {{a_0}\left[ {1/\hat k\left( {{a_0}m + {a_1}c} \right) - 1} \right]} & {{a_0}1/\hat k\left( {{a_2}m + {a_4}c} \right) - {a_2}} & {{a_0}1/\hat k\left( {{a_3}m + {a_5}c} \right) - {a_3}} & {{a_0}1/\hat k} & 0 \cr 0 & 0 & 0 & 0 & 1 \cr } } \right]$$ $$\left[ {\matrix{ {{x_{k - 1}}} \cr {{{\dot x}_{k - 1}}} \cr {{{\ddot x}_{k - 1}}} \cr {{f_k}} \cr {{f_{k + 1}}} \cr } } \right] = {H_{k - 1}}\left[ {\matrix{ {{x_{k - 1}}} \cr {{{\dot x}_{k - 1}}} \cr {{{\ddot x}_{k - 1}}} \cr {{f_k}} \cr {{f_{k + 1}}} \cr } } \right] \tag{A1}$$ $$\eqalign{ & \cr & \left[ {\matrix{ {{x_2}} \cr {{{\dot x}_2}} \cr {{{\ddot x}_2}} \cr {{f_3}} \cr \vdots \cr {{f_k}} \cr {{f_{k + 1}}} \cr } } \right] = \left[ {\matrix{ {1/\hat k\left( {{a_0}m + {a_1}c} \right)} & {1/\hat k\left( {{a_2}m + {a_4}c} \right)} & {1/\hat k\left( {{a_3}m + {a_5}c} \right)} & {1/\hat k} & 0 & 0 & 0 \cr {{a_0}{a_7}\left[ {1/\hat k\left( {{a_0}m + {a_1}c} \right) - 1} \right]} & {{a_0}{a_7}1/\hat k\left( {{a_2}m + {a_4}c} \right) + (1 - {a_7}{a_2})} & {{a_0}{a_7}1/\hat k\left( {{a_3}m + {a_5}c} \right) + \left( {{a_6} - {a_3}{a_7}} \right)} & {{a_0}{a_7}1/\hat k} & 0 & 0 & 0 \cr {{a_0}\left[ {1/\hat k\left( {{a_0}m + {a_1}c} \right) - 1} \right]} & {{a_0}1/\hat k\left( {{a_2}m + {a_4}c} \right) - {a_2}} & {{a_0}1/\hat k\left( {{a_3}m + {a_5}c} \right) - {a_3}} & {{a_0}1/\hat k} & 0 & 0 & 0 \cr 0 & 0 & 0 & 0 & 1 & 0 & 0 \cr 0 & 0 & 0 & 0 & 0 & \ddots & 0 \cr 0 & 0 & 0 & 0 & 0 & 0 & 1 \cr } } \right] \cr & \cr} $$ $$\left[ {\matrix{ {{x_1}} \cr {{{\dot x}_1}} \cr {{{\ddot x}_1}} \cr {{f_2}} \cr \vdots \cr {{f_k}} \cr {{f_{k + 1}}} \cr } } \right] = {H_1}\left[ {\matrix{ {{x_1}} \cr {{{\dot x}_1}} \cr {{{\ddot x}_1}} \cr {{f_2}} \cr \vdots \cr {{f_k}} \cr {{f_{k + 1}}} \cr } } \right]$$
令$t_1 = 0$,由方程式(13)得 $\ddot {x}_1 = \dfrac{1}{m}\left( {f_1 - c\dot {x}_1 - kx_1 } \right) \tag{A2}$
因此又有 $$\left[ {\matrix{ {{x_1}} \cr {{{\dot x}_1}} \cr {{{\ddot x}_1}} \cr {{f_2}} \cr \vdots \cr {{f_k}} \cr {{f_{k + 1}}} \cr } } \right] = \left[ {\matrix{ {\matrix{ 1 & 0 & 0 \cr 0 & 1 & 0 \cr { - {k \over m}} & { - {c \over m}} & {{1 \over m}} \cr } } & 0 \cr 0 & I \cr } } \right]\left[ {\matrix{ {{x_1}} \cr {{{\dot x}_1}} \cr {{{\ddot x}_1}} \cr {{f_2}} \cr \vdots \cr {{f_k}} \cr {{f_{k + 1}}} \cr } } \right] = \Gamma \left[ {\matrix{ {{x_1}} \cr {{{\dot x}_1}} \cr {{{\ddot x}_1}} \cr {{f_2}} \cr \vdots \cr {{f_k}} \cr {{f_{k + 1}}} \cr } } \right] \tag{A3}$$
从而得到 $$\left[\!\! \begin{array}{c} {x_{k + 1} } \\ {\dot {x}_{k + 1} } \\ {\ddot {x}_{k + 1} } \end{array} \!\! \right] = {\pmb H}_k {\pmb H}_{k - 1} \cdots {\pmb H}_1 {\pmb \varGamma }\left[\!\! \begin{array}{c} {x_1 } \\ {\dot {x}_1 } \\ {f_1 } \\ {f_2 } \\ \vdots \\ {f_k } \\ {f_{k + 1} } \end{array} \!\! \right] = {\pmb H}\left[\!\! \begin{array}{c} {x_1 } \\ {\dot {x}_1 } \\ {f_1 } \\ {f_2 } \\ \vdots \\ {f_k } \\ {f_{k + 1} } \end{array} \!\! \right] \tag{A4}$$ 其中${\pmb H}_k {\pmb H}_{k - 1} \cdots {\pmb H}_1 {\pmb \varGamma }$. 令 $${\pmb H} = \left[ {{\pmb H}_x } \ \ {{\pmb H}_f } \right]\,, \ \ \left[\!\! \begin{array}{c} {x_1 } \\ {\dot {x}_1 } \\ {f_1 } \\ {f_2 } \\ \vdots \\ {f_k } \\ {f_{k + 1} } \end{array} \!\! \right] = \left[\!\! \begin{array}{c} {\pmb x} \\ {\pmb f} \end{array} \!\! \right] \tag{A5}$$
由式(A4)即得 $$x_{k + 1} = \left( {{\pmb H}_x } \right)_1 {\pmb x} + \left( {{\pmb H}_f } \right)_1 {\pmb f} \tag{A6}$$ $$\dot {x}_{k + 1} = \left( {{\pmb H}_x } \right)_2 {\pmb x} + \left( {{\pmb H}_f } \right)_2 {\pmb f} \tag{A7}$$ $$\ddot {x}_{k + 1} = \left( {{\pmb H}_x } \right)_3 {\pmb x} + \left( {{\pmb H}_f } \right)_3 {\pmb f} \tag{A8}$$ 其中$\left( \cdot \right)_i \ (i = 1,2,3)$表示矩阵的第$i$行向量.
附录B将式(35) $\sim$式(38)写成矩阵的形式并递推得 $$\eqalign{ & \cr & \left[ {\matrix{ {{X_{k + 1}}} \cr {{{\dot X}_{k + 1}}} \cr {{{\ddot X}_{k + 1}}} \cr } } \right] = \left[ {\matrix{ {{{\hat K}^{ - 1}}\left( {{a_0}M + {a_1}C} \right)} & {{{\hat K}^{ - 1}}\left( {{a_2}M + {a_4}C} \right)} & {{{\hat K}^{ - 1}}\left( {{a_3}M + {a_5}C} \right)} & {{{\hat K}^{ - 1}}} \cr {{a_7}{a_0}\left[ {{{\hat K}^{ - 1}}\left( {{a_0}M + {a_1}C} \right) - I} \right]} & {{a_7}{a_0}{{\hat K}^{ - 1}}\left( {{a_2}M + {a_4}C} \right) + \left( {1 - {a_7}{a_2}} \right)I} & {{a_7}{a_0}{{\hat K}^{ - 1}}\left( {{a_3}M + {a_5}C} \right) + \left( {{a_6} - {a_7}{a_3}} \right)I} & {{a_7}{a_0}{{\hat K}^{ - 1}}} \cr {{a_0}\left[ {{{\hat K}^{ - 1}}\left( {{a_0}M + {a_1}C} \right) - I} \right]} & {{a_0}{{\hat K}^{ - 1}}\left( {{a_2}M + {a_4}C} \right) - {a_2}I} & {{a_0}{{\hat K}^{ - 1}}\left( {{a_3}M + {a_5}C} \right) - {a_3}I} & {{a_0}{{\hat K}^{ - 1}}} \cr } } \right]. \cr} $$ $$\left[ {\matrix{ {{X_k}} \cr {{{\dot X}_k}} \cr {{{\ddot X}_k}} \cr {{F_{k + 1}}} \cr } } \right] = {\hat H_k}\left[ {\matrix{ {{X_k}} \cr {{{\dot X}_k}} \cr {{{\ddot X}_k}} \cr {{F_{k + 1}}} \cr } } \right]$$ $$\left[ {\matrix{ {{X_k}} \cr {{{\dot X}_k}} \cr {{{\ddot X}_k}} \cr {{F_{k + 1}}} \cr } } \right] = \left[ {\matrix{ {{{\hat K}^{ - 1}}\left( {{a_0}M + {a_1}C} \right)} & {{{\hat K}^{ - 1}}\left( {{a_2}M + {a_4}C} \right)} & {{{\hat K}^{ - 1}}\left( {{a_3}M + {a_5}C} \right)} & {{{\hat K}^{ - 1}}} & 0 \cr {{a_7}{a_0}\left[ {{{\hat K}^{ - 1}}\left( {{a_0}M + {a_1}C} \right) - I} \right]} & {{a_7}{a_0}{{\hat K}^{ - 1}}\left( {{a_2}M + {a_4}C} \right) + \left( {1 - {a_7}{a_2}} \right)I} & {{a_7}{a_0}{{\hat K}^{ - 1}}\left( {{a_3}M + {a_5}C} \right) + \left( {{a_6} - {a_7}{a_3}} \right)I} & {{a_7}{a_0}{{\hat K}^{ - 1}}} & 0 \cr {{a_0}\left[ {{{\hat K}^{ - 1}}\left( {{a_0}M + {a_1}C} \right) - I} \right]} & {{a_0}{{\hat K}^{ - 1}}\left( {{a_2}M + {a_4}C} \right) - {a_2}I} & {{a_0}{{\hat K}^{ - 1}}\left( {{a_3}M + {a_5}C} \right) - {a_3}I} & {{a_0}{{\hat K}^{ - 1}}} & 0 \cr 0 & 0 & 0 & 0 & I \cr } } \right]. \tag{B1}$$ $$\left[ {\matrix{ {{X_{k - 1}}} \cr {{{\dot X}_{k - 1}}} \cr {{{\ddot X}_{k - 1}}} \cr {{F_k}} \cr {{F_{k + 1}}} \cr } } \right] = {\hat H_{k - 1}}\left[ {\matrix{ {{X_{k - 1}}} \cr {{{\dot X}_{k - 1}}} \cr {{{\ddot X}_{k - 1}}} \cr {{F_k}} \cr {{F_{k + 1}}} \cr } } \right]{\rm{ }}$$ $$ \vdots $$ $ \left[\!\! \begin{array}{c} {{\pmb X}_2 } \\ {\dot {\pmb X}_2 } \\ {\ddot {\pmb X}_2 } \\ {{\pmb F}_3 } \\ \vdots \\ {{\pmb F}_k } \\ {{\pmb F}_{k + 1} } \end{array} \!\! \right] = \left[\!\! \begin{array}{ccccccc} {\hat {\pmb K}^{ - 1}\left( {a_0 {\pmb M }+ a_1 {\pmb C}} \right)} & {\hat {\pmb K}^{ - 1}\left( {a_2 {\pmb M} + a_4 {\pmb C}} \right)} & {\hat{\pmb K}^{ - 1}\left( {a_3 {\pmb M} + a_5 {\pmb C}} \right)} & {\hat {\pmb K}^{ - 1}} & & & \\ {a_7 a_0 \left[ {\hat {\pmb K}^{ - 1}\left( {a_0 {\pmb M }+ a_1 {\pmb C}} \right) - {\pmb I}} \right]} & {a_7 a_0 \hat {\pmb K}^{ - 1}\left( {a_2 {\pmb M} + a_4 {\pmb C}} \right) + \left( {1 - a_7 a_2 } \right) {\pmb I}} & {a_7 a_0 \hat {\pmb K}^{ - 1}\left( {a_3 {\pmb M} + a_5 {\pmb C}} \right) + \left( {a_6 - a_7 a_3 } \right){\pmb I}} & {a_7 a_0 \hat {\pmb K}^{ - 1}} & & & \\ {a_0 \left[ {\hat{\pmb K}^{ - 1}\left( {a_0 {\pmb M} + a_1 {\pmb C}} \right) - {\pmb I}} \right]} & {a_0 \hat {\pmb K}^{ - 1}\left( {a_2 {\pmb M} + a_4 {\pmb C}} \right) - a_2 {\pmb I}} & {a_0 \hat {\pmb K}^{ - 1}\left( {a_3{\pmb M} + a_5 {\pmb C}} \right) - a_3 {\pmb I}} & {a_0 \hat {\pmb K}^{ - 1}} & & & \\ & & & & \!\!{\pmb I}\!\! & & \\ & & & & & \!\ddots\! & \\ & & & & & & \!{\pmb I}\! \end{array} \!\! \right]\cdot $ $$\left[ {\matrix{ {{X_1}} \cr {{{\dot X}_1}} \cr {{{\ddot X}_1}} \cr {{F_2}} \cr \vdots \cr {{F_k}} \cr {{F_{k + 1}}} \cr } } \right] = {\hat H_1}\left[ {\matrix{ {{X_1}} \cr {{{\dot X}_1}} \cr {{{\ddot X}_1}} \cr {{F_2}} \cr \vdots \cr {{F_k}} \cr {{F_{k + 1}}} \cr } } \right]$$ 令$t_1 = 0$,由式(33)有 $$\ddot{ X}_1 ={ M}^{ - 1}({ F}_1 - { C}\dot { X}_1 -{ K}{ X}_1 ) \tag{B2}$$ 因此有 $$\left[ {\matrix{ {{X_1}} \cr {{{\dot X}_1}} \cr {{{\ddot X}_1}} \cr {{F_2}} \cr \vdots \cr {{F_k}} \cr {{F_{k + 1}}} \cr } } \right] = \left[ {\matrix{ I & {} & {} & {} & {} & {} \cr {} & I & {} & {} & {} & {} \cr { - {M^{ - 1}}K} & { - {M^{ - 1}}C} & {{M^{ - 1}}} & {} & {} & {} \cr {} & {} & {} & I & {} & {} \cr {} & {} & {} & {} & \ddots & {} \cr {} & {} & {} & {} & {} & I \cr } } \right]\left[ {\matrix{ {{X_1}} \cr {{{\dot X}_1}} \cr {{F_1}} \cr \vdots \cr {{F_k}} \cr {{F_{k + 1}}} \cr } } \right] = \hat \Gamma \left[ {\matrix{ {{X_1}} \cr {{{\dot X}_1}} \cr {{F_1}} \cr \vdots \cr {{F_k}} \cr {{F_{k + 1}}} \cr } } \right] \tag{B3}$$ 从而得到 $$\left[ {\matrix{ \matrix{ {X_{k + 1}} \hfill \cr {{\dot X}_{k + 1}} \hfill \cr {{\ddot X}_{k + 1}} \hfill \cr} \cr } } \right] = {\hat H_k}{\hat H_{k - 1}} \cdots {\hat H_1}\hat \Gamma \left[ {\matrix{ \matrix{ {X_1} \hfill \cr {{\dot X}_1} \hfill \cr {F_1} \hfill \cr \vdots \hfill \cr {F_k} \hfill \cr {F_{k + 1}} \hfill \cr} \cr } } \right] \tag{B4} $$ 令 $$\hat H = \left( {\mathop \Pi \limits_{j = 1}^k {{\hat H}_j}} \right)\widehat {{\text{ }}\Gamma }{\mkern 1mu} ,F = {\left[ {F_1^{\text{T}}\;\;F_2^{\text{T}}\;\; \cdots \;\;F_{k + 1}^{\text{T}}} \right]^{\text{T}}} \tag{B5}$$ 则式(B4)可以写为 $$\left[ {\matrix{ \matrix{ {X_{k + 1}} \hfill \cr {{\dot X}_{k + 1}} \hfill \cr {{\ddot X}_{k + 1}} \hfill \cr} \cr } } \right] = \hat H\left[ {\matrix{ \matrix{ {X_1} \hfill \cr {{\dot X}_1} \hfill \cr F \hfill \cr} \cr } } \right] \tag{B6}$$ 通过将$\hat{ H}$分块,即 $\hat{ H} = \left[ {\hat { H}_X } \ \ {\hat { H}_F } \right]$,上式可以写为 $$\left[ {\matrix{ \matrix{ {X_{k + 1}} \hfill \cr {{\dot X}_{k + 1}} \hfill \cr {{\ddot X}_{k + 1}} \hfill \cr} \cr } } \right] = {\hat H_X}\left[ {\matrix{ \matrix{ {X_1} \hfill \cr {{\dot X}_1} \hfill \cr} \cr } } \right] + {\hat H_F}F \tag{B7}$$
| 附表 几种典型的平稳凸模型过程的相关系数函数[25] Attached Table Several typical correlation coefficient functions for stationary convex model process[25] |
| 1 | 徐全智. 随机过程及应用. 北京:高等教育出版社, 2013. 6(Xu Quanzhi. Stochastical Process and Applications. Beijing:Higher Education Press, 2013. 6(in Chinese)) |
| 2 | Crandall SH. Random Vibration. Cambridge:The MIT Press, 1958 |
| 3 | Lin YK. Probabilistic Theory of Structural Dynamics. New York:McGraw-Hill, 1967 |
| 4 | Morrow CT, Muchmore RB. Shortcomings of present methods of measuring and simulating vibration environments. ASME J Appl Mech, 1955, 22:367-371 |
| 5 | Kiureghian AD. A response spectrum method for random vibration analysis of MDF systems. Earthquake Engineering & Structural Dynamics, 1981, 9(5):419-435 |
| 6 | 林家浩, 张亚辉. 随机振动的虚拟激励法. 北京:科学出版社,2004(Lin Jiahao, Zhang Yahui. Pseudo Excitation Method of Random Vibration. Beijing:Science Press, 2004(in Chinese)) |
| 7 | Caprani CC. Application of the pseudo-excitation method to assessment of walking variability on footbridge vibration. Comput Struct, 2014, 132:43-54 |
| 8 | Zhang YW, Zhao Y, Zhang YH, et al. Riding comfort optimization of railway trains based on pseudo-excitation method and symplectic method. J Sound Vib, 2013, 332(21):5255-5270 |
| 9 | Caughey TK. Derivation and application of the Fokker-Planck equation to discrete nonlinear dynamic systems subjected to white random excitation. Journal of the Acoustical Society of America, 1963, 35(11):1683 |
| 10 | Fuller AT. Analysis of nonlinear stochastic systems by means of the Fokker-Planck equation. International Journal of Control, 1969, 9(6):603-655 |
| 11 | Crandall SH. Perturbation techniques for random vibration of nonlinear systems. J Acoust Soc Am, 1963, 35(11):1700-1705 |
| 12 | Roberts JB, Spanos PD. Stochastic averaging:an approximate method of solving random vibration problems. International Journal of Non-Linear Mechanics, 1986, 21(2):111-134. |
| 13 | Zhu WQ. Stochastic averaging methods in random vibration. Appl.Mech.Rev, 1988, 41(5):189-199. |
| 14 | Zhu WQ. Recent developments and applications of the stochastic averaging method in random vibration. Appl Mech Rev, 1996, 49(10S):S72-S80 |
| 15 | Iwan WD, Mason AB. Equivalent linearization for systems subjected to non-stationary random excitation. International Journal of Non-Linear Mechanics, 1980, 15(2):71-82. |
| 16 | He JH. Some asympotic methods for strongly nonlinear equations. International Journal of Modern Physics B, 2012, 20(10):1141-1199 |
| 17 | Andrieu-Renaud C, Sudret B, Lemaire M. The PHI2 method:a way to compute time-variant reliability. Reliab Eng Syst Safety, 2004, 84(1):75-86 |
| 18 | Zhang YW, Wen BC, Liu QL. First passage of uncertain single degree-of-freedom nonlinear oscillators. Comput Meth Appl Mech Eng, 1998, 165(1):223-231 |
| 19 | Beck AT. The random barrier-crossing problem. Probabilist Eng Mech, 2008, 23:134-145 |
| 20 | Conte JP, Peng BF. Fully nonstationary analytical earthquake ground-motion model. ASCE J Engng Mech, 1997, 123:15-24 |
| 21 | 李杰, 陈建兵. 随机结构动力反应分析的概率密度演化方法. 力学学报, 2003, 35(4):437-442(Li Jie, Chen Jianbing. The probability density evolution method for the analysis of stochastic structural dynamic response. Chinese Journal of Theoretical and Applied Mechanics, 2003, 35(4):437-442(in Chinese)) |
| 22 | 李杰, 陈建兵. 随机结构动力可靠度分析的概率密度演化方法. 振动工程学报, 2004, 17(2):121-125(Li Jie, Chen Jianbing. The probability density evolution method for the analysis of stochastic structural dynamic reliability. Journal of Vibration Engineering, 2004, 17(2):121-125(in Chinese)) |
| 23 | Jiang C, Huang XP, Han X, et al. A time-variant reliability analysis method based on stochastic process discretization. Journal of Mechanical Design, 2014, 136(9):543-552 |
| 24 | Ben-Haim Y, Elishakoff I. Convex Models of Uncertainties in Applied Mechanics. Amsterdam:Elsevier Science Publisher, 1990 |
| 25 | Jiang C, Ni BY, Han X, et al. Non-probabilistic convex model process:A new method of time-variant uncertainty analysis and its application to structural dynamic reliability problems. Comput Methods Appl Mech Engrg, 2014, 268:656-676 |
| 26 | Jiang C, Han X, Lu GY, et al. Correlation analysis of nonprobabilistic convex model and corresponding structural reliability technique. Comput Methods Appl Mech Engrg, 2011, 200(33-36):2528-2546 |
| 27 | Jiang C, Ni BY, Liu NY, et al. A non-random vibration analysis method based on an interval process model, submitted |
| 28 | Wang XJ, Wang L, Elishakoff I, et al. Probability and convexity concepts are not antagonistic. Acta Mech, 2011, 219:45-64 |
| 29 | Kang Z, Luo YJ. Non-probabilistic reliability-based topology optimization of geometrically nonlinear structures using convex model. Computer Methods in Applied Mechanics & Engineering, 2009, 198:3228-3238 |
| 30 | Newmark NM. A method of computation for structural dynamics. Journal of the Engineering Mechanics Division, 1959, 85(3):67-94 |
| 31 | Bathe KJ, Wilson EL. Stability and accuracy analysis of direct integration methods. Earthquake Engineering & Structural Dynamics, 1972, 1(3):283-291 |
| 32 | Bathe KJ, Wilson EL. Numerical Methods in Finite Element Analysis. New Jersey:New Jersey Prentice Hall, 1976 |
| 33 | Everett Iii H. Generalized lagrange multiplier method for solving problems of optimum allocation of resources. Operations Research, 1963, 11(3):399-417 |
| 34 | 余志生. 汽车理论(第二版). 北京:机械工业出版社, 1989:169-215(Yu Zhisheng. Automobile Theory(2nd edn). Beijing:China Machine Press, 1989:169-215(in Chinese)) |
| 35 | Long XY, Elishakoff I, Jiang C, et al. Notes on random vibration of a vehicle model and other discrete systems possessing repeated natural frequencies. Archive of Applied Mechanics, 2014, 84(8):1091-1101 |
 2016, Vol. 48
2016, Vol. 48