引力辅助技术(gravity-assist)通过借助天体引力来实现飞行器变轨,不仅可以有效减少燃料消耗而且可以降低任务所需的发射能量[1],因而是一种受到广泛关注的星际航行节能技术.
自从1988年布鲁克[2]对引力辅助的开创性研究以来,经过一系列后续的发展,目前对引力辅助的机理研究已比较完备.当飞行器轨道与借力天体轨道共面时,为二维引力辅助.有人分别基于圆型与椭圆型限制性三体问题对二维引力辅助进行了研究[3, 4].当飞行器轨道与借力天体轨道不共面时,为三维引力辅助.有人基于限制性三体问题对三维引力辅助进行了研究[5, 6, 7, 8].文献[5, 6]分析了引力辅助参数对飞行器轨道的影响;文献[7, 8]将三维引力辅助轨道划分为16种类型,讨论了引力辅助参数对轨道类型、轨道能量和轨道倾角的影响.基于限制性三体问题导出的动力学方程不存在解析解,因此必须通过数值积分方法进行分析;而如果采用二体问题进行建模,虽然精度稍差但可以得到解析公式.有学者基于二体问题,推导了三维引力辅助变轨前后飞行器速度、能量、角动量和轨道倾角与引力辅助参数之间的解析公式[9, 10].
目前已经有多个任务利用引力辅助技术设计了行星际探测轨道,如水手10号、旅行者1号、旅行者2号、伽利略号、卡西尼号等[11]. 除了利用行星之外,还可以利用天然卫星进行引力辅助变轨,文献[12]通过木卫一引力辅助变轨进入木卫二的绕飞轨道,文献[13]利用伽利略卫星的引力辅助变轨来实现木星俘获或逃逸,文献[14]利用月球引力辅助变轨使得小行星被地月系统俘获.
然而,仅仅通过引力辅助,飞行器相对于借力天体的速度和能量的改变都是有限的,常常不能满足实际任务的需求,尤其难以满足轨道拼接的C3匹配原则等较强的约束条件.针对这一问题,在引力辅助技术的基础发展出了其他的变轨方式,如小推力引力辅助[15, 16, 17]、气动引力辅助[18, 19, 20]和带脉冲的引力辅助等变轨技术.带脉冲的引力辅助变轨,即通过在引力辅助过程中对飞行器施加脉冲,改善引力辅助效果,以满足轨道拼接的C3匹配原则和其他的任务要求,可以显著提高引力辅助轨道设计的灵活性.
有学者研究了在近拱点施加共面脉冲的二维引力辅助,采用10个参数对模型进行描述,给出了飞行器速度、能量和角动量的改变量与参数之间的解析方程[21].但上述10个参数并不是相互独立的,实际上只需5个参数就足够了;而且假设引力辅助过程所持续的时间为零,借力天体的位置和速度在引力辅助前后都是不变的,而实际上引力辅助变轨需要一小段时间,而在此过程中,借力天体的位置和速度都是变化的.
还有人研究了带共面脉冲的二维引力辅助变轨的参数优化问题[22],分析了参数变化对飞行器能量变化的影响,指出优化问题中的关键参数是脉冲的大小、脉冲与飞行器速度之间的夹角和飞越借力天体时的最小高度.
有些学者基于限制性三体问题,采用对动力学方程进行数值积分的方法,分析了二维引力辅助中施加脉冲的最优方向[23, 24].
文献[25]对带脉冲的三维引力辅助进行了研究,推导过程中进行了一系列假设与近似,给出的分析只适用于小脉冲,只有当脉冲小于飞行器轨道速度的1%时才近似成立. 当脉冲较大时,假设与近似不能成立,无法进行分析.
对于在三维引力辅助过程中施加任意大小和方向的脉冲,目前尚无文献进行分析,使得在目前的轨道设计中[26, 27, 28, 29, 30],一般仅能运用二维引力辅助,并只能施加共面脉冲. 而实际情况中,飞行器轨道与借力天体轨道往往并不共面,而施加非共面脉冲可以在改变飞行器能量的同时改变轨道倾角,因此分析带脉冲的三维引力辅助具有重要意义.
本文研究在近拱点施加任意大小和方向的脉冲的三维引力辅助变轨. 首先采用8个独立参数对模型进行描述;然后建立分析问题的一组坐标系,推导飞行器的位置矢量和速度矢量与上述8个参数的解析公式;之后验证公式的有效性;最后分析施加脉冲的最优策略.
1 问题描述如图1所示,${M}_{2} $绕${M}_{1} $的质心以圆轨道运动. $M_2$为借力天体,飞行器${M}_{3} $从$A$点进入${M}_{2}$的影响球(如果不施加脉冲,飞行器将沿双曲线轨道$\mathop{AB}\limits^{\frown}$运动),经过近拱点$P$时施加一个任意脉冲(大小方向均无限制),之后飞行器沿轨道$\mathop{PC}\limits^{\frown}$运动从$C$点离开${M}_{2} $的影响球.
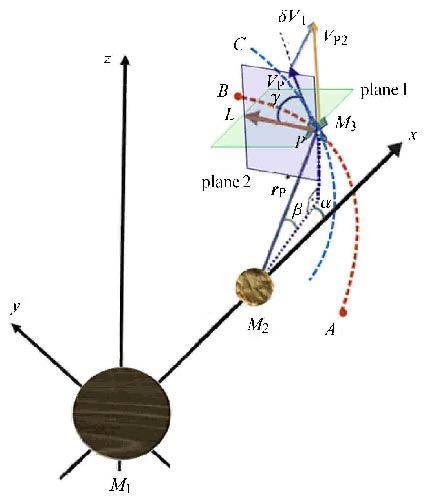
|
图1 带任意脉冲的三维引力辅助示意图 Fig.1 Powered gravity assist in three dimensions |
由于引力辅助变轨需要一段时间,在此期间借力天体的位置和速度会发生变化,因此需要对 $M_2$的运动进行描述.
1.1 带脉冲的三维引力辅助模型在本文中,带脉冲的三维引力辅助可以通过8个独立参数来描述:(1) ${ V}_{\rm P1} $:施加脉冲之前,${M}_{3}$在${P}$点时相对于${M}_{2} $的速度(${P}$点为轨道$\mathop{AB}\limits^{\frown}$的近拱点);(2) $\alpha $,$\beta $:表征近拱点的方向;$\alpha$为$P$与$M_2$ 质心的连线在$xy$平面的投影与$x$轴的夹角,$\beta$为$P$与$M_2$质心的连线与 $xy$平面的夹角; (3) ${ r}_{\rm P} $:近拱点${P}$的位置矢量;(4) $\gamma _1 $:速度${ V}_{\rm P1} $与${ L}$的夹角(记过${P}$点平行于$xy$的平面为平面1,记过${P}$点、向量${ V}_{\rm P1}$并且垂直于${ r}_{\rm P} $的平面为平面2,${ L}$为平面1与平面2的交线); (5) $\delta { V}$:施加脉冲的大小;(6) $\xi $和$\eta $:表征施加脉冲的方向,$\xi $为$\delta { V}$与平面2的夹角;$\eta $为$\delta { V}$在平面2的投影与 ${ V}_{\rm P1}$之间的夹角.
$\alpha$,$\beta$,$\gamma _1$, $\xi$ 和$\eta $的取值范围为: $\alpha \in [0^ \circ ,360^ \circ )$,$\beta \in [- 90^ \circ ,90^ \circ]$,$\gamma _1 \in [0^ \circ ,180^ \circ]$, $\xi \in [- 90^ \circ ,90^ \circ]$, $\eta \in [- 180^ \circ ,180^ \circ]$.
1.2 坐标系的建立借力天体的轨道、轨道$\mathop{AP}\limits^{\frown}$、轨道$\mathop{PC}\limits^{\frown}$处于不同平面内,为了方便,需要在不同的坐标系中描述. 本文建立的坐标系如图2所示.
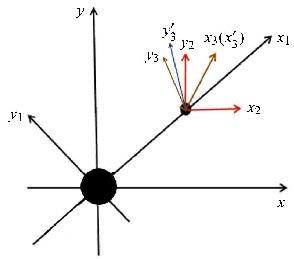
|
图2 本文定义的5个坐标系 Fig.2 Five coordinate systems defined in this paper |
坐标系1:惯性坐标系$xyz$ . 以${M}_{1} $的质心为原点;$x$轴为$t = 0$时刻(${M}_{3} $到达${P}$点时刻)${M}_{1} $和${M}_{2} $的连线;$xy$平面位于${M}_{2} $的运动平面.
坐标系2:旋转坐标系$x_1 y_1 z_1 $. 以${M}_{1} $的质心为原点;$x_1 $轴为任意时刻${M}_{1} $和${M}_{2} $的连线;$x_1 y_1 $平面位于${M}_{2} $的运动平面. $z_1 $轴符合右手定则.
坐标系3:直角坐标系$x_2 y_2 z_2 $. 以${M}_{2} $质心为原点;$x_2 $轴,$y_2 $轴,$z_2 $轴始终与$x$轴,$y$轴,$z$轴平行.
坐标系4:直角坐标系$x_3 y_3 z_3 $. 以${M}_{2} $质心为原点;$x_3 $轴、$y_3 $轴分别与${ r}_{\rm P},{ V}_{\rm P1}$平行,$z_3 $轴符合右手定则. 于是,轨道$\mathop{AP}\limits^{\frown}$位于 $x_3 y_3 $平面内.
坐标系5:直角坐标系${x}'_3 {y}'_3 {z}'_3 $. 以${M}_{2} $质心为原点;${x}'_3 $轴、${y}'_3 $轴分别与${ r}_{\rm P}$,${ V}_{2}$ (${ V}_2 $为施加脉冲之后的飞行器速度在平面2中的投影)平行,${z}'_3 $轴符合右手定则. 于是,轨道$\mathop{PC}\limits^{\frown}$位于 ${x}'_3 {y}'_3 $平面内.
下面推导飞行器在$A$和$C$点的位置矢量和速度矢量与8个引力辅助参数之间的解析公式.
2 带脉冲的三维引力辅助的解析公式 2.1 计算飞行器在$A$点的速度和矢径当${M}_{3} $处于${M}_{2} $影响球内时,由于本文基于二体问题,由轨道动力学可知轨道$\mathop{AP}\limits^{\frown}$为双曲线,并且处于${ r}_{\rm P}$和 ${ V}_{\rm P1}$所确定的平面内,即$x_3y_3$平面内. 如图3所示.

|
图3 前半段轨道$\mathop{AP}\limits^{\frown}$示意图 Fig.3 The first section of orbit |
飞行器在$A$点的绝对速度为相对于$M_2$的速度与牵连速度的矢量和,因此首先需要求出相对于$M_2$的速度.
2.1.1 计算在坐标系 $x_3 y_3 z_3 $下表示的飞行器在$A$点相对于${M}_{2} $的位置矢量和速度矢量${ v}_{\rm in}$为飞行器进入${ M}_{2}$ 影响球时相对于 ${ M}_{2}$ 的速度,用$v_{\infty 1}$表示其大小.${ v}_{\rm in}$ 与双曲线渐近线共线,记${ v}_{\rm in}$与${ V}_{\rm P1}$ 的夹角为$\delta _1$, 于是${ v}_{\rm in}$可表示为 $$ { v}_{\rm in} = (v_{\infty 1} \sin \delta _1 ,v_{\infty 1} \cos \delta _1 ) \tag{1}$$ 其中 $$ v_{\infty 1}^2 = V_{\rm P1}^2 - 2\mu _2 / r_{\rm P} \\ \sin \delta _1 = 1 / \left( {1 + r_{\rm P} v_{\infty 1}^2 / \mu _2 } \right) = 1 / \left( {r_{\rm P} V_{\rm P1}^2 / \mu _2 - 1} \right) $$ 式中$\mu _2 $为${M}_{2}$ 的引力参数.
由轨道力学知 $$ r = h_1^2 / \left[{\mu _2 \left( {1 + e_1 \cos \theta _1 } \right)} \right] \\ v_{\infty 1} = \mu _2 \sqrt {e_1^2 - 1} / h_1 ,\ e_1 = 1 / \sin \delta _1 $$ 其中,$r$为飞行器与${M}_{2} $的距离,$h_1 $为单位相对角动量,$e_1 $为双曲线轨道的偏心率,$\theta _1 $为$A$点的真近点角.可得 $$ \cos \theta _1 = \left( { - \mu _2 r + r_{\rm P}^2 V_{\rm P 1}^2 } \right) / \left[{r\left( {r_{\rm P} V_{\rm P 1}^2 - \mu _2 } \right)} \right] \tag{2}$$ 记${M}_{2} $的影响球半径为$r_{\rm SOI } $,则$A$处$r = r_{\rm SOI} $,得 $$ \cos \theta _1 = \left( { - \mu _2 r_{\rm SOI} + r_{\rm P}^2 V_{\rm P 1}^2 } \right) / \left[{r_{\rm SOI } \left( {r_{\rm P} V_{\rm P 1}^2 - \mu _2 } \right)} \right] \tag{3}$$
于是得到:$A$点矢径${ r}_{\rm in} $在直角坐标系$x_3 y_3 z_3 $中的表示为 $$ { r}_{\rm in} = (r_{\rm SOI} \cos \theta _1 ,- r_{\rm SOI} \sin \theta _1 ,0) \tag{4}$$
2.1.2 计算在坐标系 $x_2 y_2 z_2 $ 下表示的飞行器在$A$点相对于 ${M}_{2} $ 的位置矢量和速度矢量直角坐标系$x_3 y_3 z_3 $可由直角坐标系$x_2 y_2 z_2 $先绕$z_2 $轴旋转$\alpha $角、再绕$y_2 $轴旋转$ - \beta $角、最后绕$x_2 $轴旋转$\gamma _1 $角得到. 由此可得到$\left( {x_2 ,y_2 ,z_2 } \right)$和$\left( {x_3 ,y_3 ,z_3 } \right)$之间的转换矩阵,进而可求得${ v}_{\rm in}$和${ r}_{\rm in}$ 在直角坐标系$x_2 y_2 z_2 $中的坐标表示[8].
2.1.3 计算在惯性坐标系中表示的飞行器在$A$点处的绝对速度矢量和位置矢量${M}_{2}$ 的位置与速度是随时间改变的,如图4所示. 记$A$点时刻为:$t = - t_1 $. $t_1 $可由式(5)计算得到 $$ t_1 = \dfrac{\mu _2 }{\left( {V_{P1}^2 - 2\mu _2 / r_{\rm p} } \right)^{3 / 2}}\left\{ {\dfrac{e_1 \sqrt {e_1^2 - 1} \sin \theta _1 }{1 + e_1 \cos \theta _1 }- }\right. \\ \left.{ \ln \left[{\dfrac{\sqrt {e_1 + 1} + \sqrt {e_1 - 1} \tan (\dfrac{\theta _1 }{2})}{\sqrt {e_1 + 1} - \sqrt {e_1 - 1} \tan \Big(\dfrac{\theta _1 }{2}\Big )} } \right]} \right\} \tag{5}$$

|
图4 不同时刻$M_2$位置示意图 Fig.4 Different locations of $M_{2}$ at various times |
此时${M}_{2} $在惯性坐标系中的矢径${ r}_{\rm 2in}$为 $${ r}_{\rm 2in} = \left( {d\cos (\omega t_1) - d\sin \omega (t_1 ,0)} \right) \tag{6}$$ 速度向量${ v}_{\rm 2in} $为 $$ { v}_{\rm 2in} = {\omega} \times { r}_{\rm 2in} \tag{7}$$ 其中,$d$为${M}_{2} $到原点的距离,${ \omega} $为${ M}_{2} $绕原点转动的角速度.
由复合运动可知,飞行器在$A$点,相对于惯性坐标系的绝对速度${ v}_{\rm i} $和矢径${ r}_{\rm i} $分别为 $$ { v}_{\rm i} = { v}_{\rm in} + { v}_{\rm 2in } ,\ { r}_{\rm i} = { r}_{\rm in} + { r}_{\rm 2 in } \tag{8}$$ 可得 $${ v}_{\rm i} = \left[\!\! \begin{array}{c} {v_{\infty 1} \cos \alpha \cos \beta \sin \delta _1 - v_{\infty 1} \cos \delta _1 (\sin \alpha \cos \gamma _1 + \cos \alpha \sin \beta \sin \gamma _1 ) + \\ d\omega \sin (\omega t_1 )} \\ {v_{\infty 1} \sin \alpha \cos \beta \sin \delta _1 + v_{\infty 1} \cos \delta _1 (\cos \alpha \cos \gamma _1 - \sin \alpha \sin \beta \sin \gamma _1 ) + \\ d\omega \cos (\omega t_1 )} \\ {v_{\infty 1} \sin \beta \sin \delta _1 + v_{\infty 1} \cos \delta \cos \beta \sin \gamma _1 } \end{array} \!\! \right] \tag{9}$$ $${r_i} = \left[ \begin{gathered} {r_{{\text{SOI}}}}\cos \alpha \cos \beta \cos {\theta _1} + {r_{{\text{SOI}}}}\sin {\theta _1}(\sin \alpha \cos {\gamma _1} + \\ \cos \alpha \sin \beta \sin {\gamma _1}) + d\cos (\omega {t_1}) \hfill \\ {r_{{\text{SOI}}}}\sin \alpha \cos \beta \cos {\theta _1} - {r_{{\text{SOI}}}}\sin {\theta _1}(\cos \alpha \cos {\gamma _1} - \\ \sin \alpha \sin \beta \sin {\gamma _1}) - d\sin (\omega {t_1}) \hfill \\ {r_{{\text{SOI}}}}\sin \beta \cos {\theta _1} - {r_{{\text{SOI}}}}\sin {\theta _1}\cos \beta \sin {\gamma _1} \hfill \\ \end{gathered} \right] \tag{10}$$
2.2 计算飞行器在$C$点的速度和矢径 2.2.1 计算施加脉冲之后的近拱点速度施加脉冲之前,飞行器在近拱点$P$的速度为${ V}_{\rm P 1} $,施加脉冲$\delta { V}$之后,记飞行器的速度为${ V}_{\rm P2} $. 如图5所示,平面2为过$P$点和向量${ V}_{\rm P 1} $并且垂直于${ r}_{\rm P} $的平面. $\delta { V}$在${ r}_{\rm P} $方向的投影为$\delta { V}_{1} $,在平面2的投影为$\delta { V}_{2} $. $\xi $为$\delta { V}$与平面2的夹角;$\eta $为$\delta { V}_{2} $与${ V}_{\rm P 1} $的夹角. ${ V}_2 $为${ V}_{\rm P2} $ 在平面2中的投影. 记${ V}_2 $与${ V}_{\rm P 1} $的夹角为$\lambda $,与${ L}$的夹角为$\gamma _2 $. 平面2内各矢量的关系如图6所示.
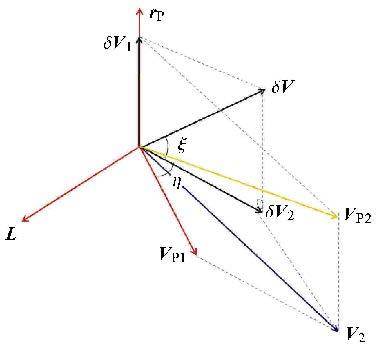
|
图5 施加脉冲之后的近拱点速度示意图 Fig.5 The velocity of the spacecraft at the periapsis after the impulse is applied |
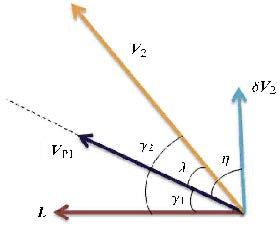
|
图6 平面2中各矢量的夹角关系 Fig.6 Vectors in the plane 2 |
于是可得 $$ \left.\!\! \delta V_{1} =\delta V\sin \xi ,\delta V_{2} =\delta V\cos \xi \\ V_{\rm P 2} = \sqrt {V_{\rm P 1}^2 + \delta V^2 + 2V_{\rm P 1} \delta V\cos \xi \cos \eta } \!\!\right\} \tag{11}$$ ${ V}_2$ 为${ V}_{\rm P2}$在平面2中的投影 $$ V_2 = \sqrt {V_{\rm P 1}^2 + \delta V_{2}^{2} + 2V_{\rm P 1} \delta V_{2} \cos \eta } \tag{12}$$ ${ V}_2$ 与${ V}_{\rm P1}$的夹角为$\lambda $满足 $$ \cos \lambda = \left( {V_{\rm P 1} { + }\delta V_{2} \cos \eta } \right) / V_2 $$ 得 $$ \lambda =\pm {\rm arccos}\left[{\left( {V_{\rm P 1} + \delta V_{2} \cos \eta } \right) / V_2 } \right] \tag{13}$$ $\lambda $的正负选择由以下规则决定:若$\sin \eta > 0$,则 $$ \lambda ={\rm arccos}\left[{\left( {V_{\rm P1} +\delta V_{2} \cos \eta } \right) / V_2 } \right] $$ 若$\sin \eta < 0$,则 $$ \lambda = - {\rm arccos}\left[{\left( {V_{\rm P1} { + }\delta V_{2} \cos \eta } \right) / V_2 } \right] $$ 可得${ V}_2$与${ L}$的夹角 $\gamma _2 = \gamma _1 + \lambda $
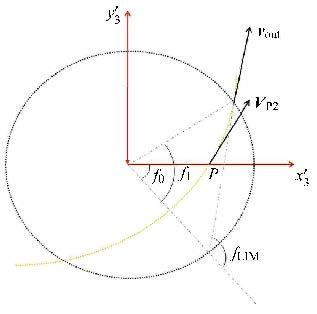
2.2.2 计算在坐标系${x}'_3 {y}'_3 {z}'_3 $ 下表示的飞行器在$C$点相对于 ${M}_{2} $ 的位置矢量和速度矢量由轨道动力学可知后半段轨道$\mathop{PC}\limits^{\frown}$ 为双曲线的一部分,整个变轨过程处于${ r}_{\rm P} $和${ V}_{\rm P2}$ 所确定的平面内,即$x'_3y'_3$平面内. 如图7所示.
|
图7 后半段轨道$\mathop{PC}\limits^{\frown}$示意图 Fig.7 The second section of orbit |
计算飞行器在$C$点相对于$M_2$的位置矢量和速度矢量,推导步骤如下
第1步:${ v}_{\rm out} $的大小记为$v_{\infty 2} $,计算$v_{\infty 2} $ $$ v_{\infty 2} = \sqrt {V_{\rm P 2}^2 - 2\mu _2 / r_{\rm P} } \tag{14}$$
第2步:计算后半段双曲线半长轴$a$ $$ a = \mu _2 / v_{\infty 2}^2 \tag{15}$$
第3步:计算角动量$h$、半正交弦$p$、偏心率$e_2 $. 公式为 $$ \left.\!\! h = \left| { { r}_{\rm P} \times { V}_{\rm P2} } \right| = r_{\rm P} V_2 \\ p = h^2 / \mu _2 ,e_2 = \sqrt {1 + p / a} \!\!\right\} \tag{16}$$
第4步:计算施加脉冲之后的双曲线轨道中飞行器的真近点角$f_0 $. 公式为 $$ f_0 = \pm \arccos \left[\left( p / r_{\rm P} - 1 \right)/e_2 \right] \tag{17}$$ $f_0$ 的正负选取规则:若$0^ \circ < \xi <180^ \circ$,则径向速度增加,意味着飞行器正在逃逸,因此飞行器已经经过近拱点,所以真近点角为正;若$ - 180^ \circ < \xi <0^ \circ $,则径向速度减小,意味着飞行器正接近次要天体,因此飞行器正飞向近拱点,所以真近点角为负.
第5步:由$e_2 $计算$f_{\rm LIM} $(后半段双曲线轨道渐近线和近拱点方向的夹角). 公式为 $$ f_{\rm LIM} = \arccos ( - 1 / e_2 ) \tag{18}$$
第6步:于是得到${ v}_{\rm out}$ $$ { v}_{\rm out} = \left[{v_{\rm out} \cos ( f_{\rm LIM} - f_0 ) ,v_{\rm out} \sin( f_{\rm LIM} - f_0 ) ,0 } \right] \tag{19} $$
第7步:计算$f_1 $ $$ \cos f_1 =\left( {\dfrac{h^2}{\mu _2 r_{\rm SOI} } - 1} \right) / e_2 \tag{20}$$
第8步:于是得到${ r}_{\rm out} $ $$ { r}_{\rm out} = \left[{r_{\rm SOI} \cos ( f_1 - f_0 ) ,r_{\rm SOI} \sin ( f_1 - f_0 ) ,0} \right] \tag{21} $$
记 $\delta _2 =f_{\rm LIM} - f_0 $,$\theta _2 =f_1 - f_0 $,式(19)和式(21)可以表示为 $$ { v}_{\rm out} = \left[{v_{\rm out} \cos \delta _2 ,v_{\rm out} {\sin}\delta _2 ,0} \right] \tag{22}$$ $$ { r}_{\rm out} = \left[{r_{\rm SOI} \cos \theta _2 ,r_{\rm SOI} \sin \theta _2 ,0} \right] \tag{23}$$
2.2.3 计算在坐标系 $x_2 y_2 z_2 $ 下表示的飞行器在$C$点相对于 ${M}_{2} $ 的位置矢量和速度矢量直角坐标系${x}'_3 {y}'_3 {z}'_3 $可由直角坐标系$x_2 y_2 z_2 $先绕$z_2 $轴旋转$\alpha $角、再绕$y_2 $轴旋转$ - \beta $角、最后绕$x_2 $轴旋转$\gamma _2 $角得到. 由此可得到$(x_2,y_2,z_2 )$和$\left( {{x}'_3,{y}'_3 ,{z}'_3 } \right)$之间的转换矩阵[8],进而可求得${ v}_{\rm out}$,${ r}_{\rm out}$ 在直角坐标系$x_2 y_2 z_2$中的坐标表示.
2.2.4 计算在惯性坐标系中表示的飞行器在$C$点处的绝对位置矢量和速度矢量记飞行器离开${M}_{2} $影响球的时刻为:$t = t_2 $. $t_2 $可由式(24)计算得到 $$ t_2 = \dfrac{h^3}{\mu _2^2 \left( {e_2^2 - 1} \right)^{3 / 2}}\left\{ {\dfrac{e_2 \sqrt {e_2^2 - 1} \sin f_1 }{1 + e_2 \cos f_1 } - }\right. \\ \left.{ \ln \left[ {\dfrac{\sqrt {e_2 + 1} + \sqrt {e_2 - 1} \tan \Big(\dfrac{f_1 }{2}\Big)}{\sqrt {e_2 + 1} - \sqrt {e_2 - 1} \tan \Big(\dfrac{f_1 }{2}\Big)}} \right]} \right\} -\\ \dfrac{h^3}{\mu _2^2 \left( {e_2^2 - 1} \right)^{3 / 2}}\left\{ {\dfrac{e_2 \sqrt {e_2^2 - 1} \sin f_0 }{1 + e_2 \cos f_0 } - }\right. \\ \left.{\ln \left[ {\dfrac{\sqrt {e_2 + 1} + \sqrt {e_2 - 1} \tan \Big(\dfrac{f_0 }{2}\Big)}{\sqrt {e_2 + 1} - \sqrt {e_2 - 1} \tan \Big(\dfrac{f_0 }{2}\Big)}} \right]} \right\} \tag{24}$$
$t = t_2$ 时刻${M}_{2}$ 在惯性坐标系中的矢径${ r}_{\rm 2out} $和速度向量 ${ v}_{\rm 2out}$表达式分别为 $$ { r}_{\rm 2out} = \left( {d\cos (\omega t_2) ,d\sin (\omega t_2) ,0 } \right) ,\quad { v}_{\rm 2out} ={ \omega} \times { r}_{\rm 2out} \tag{25}$$
由复合运动可知,飞行器离开${ M}_{2} $影响球时,相对于惯性坐标系的绝对速度 ${ v}_{\rm o} $和矢径${ r}_{\rm o} $为 $$ { v}_{\rm o} = { v}_{\rm out} + { v}_{\rm 2out} ,\quad { r}_{\rm o} = { r}_{\rm out} +{ r}_{\rm 2out} \tag{26}$$ 可得 ${ v}_{\rm o} = \left[\!\! \begin{array}{c} { - v_{\infty 2} \cos \alpha \cos \beta \sin \delta _2 - \\ v_{\infty 2} \cos \delta _2 (\sin \alpha \cos \gamma _2 + \cos \alpha \sin \beta \sin \gamma _2 ) - d\omega \sin (\omega t_2)} \\ { - v_{\infty 2} \sin \alpha \cos \beta \sin \delta _2 + \\ v_{\infty 2} \cos \delta _2 (\cos \alpha \cos \gamma _2 - \sin \alpha \sin \beta \sin \gamma _2 ) + d\omega \cos (\omega t_2)} \\ { - v_{\infty 2} \sin \beta \sin \delta _2 + v_{\infty 2} \cos \delta _2 \cos \beta \sin \gamma _2 } \end{array} \!\! \right] \tag{27}$ ${ r}_{\rm o} = \left[\!\!\begin{array}{c} {r_{\rm SOI} \cos \alpha \cos \beta \cos \theta _2 - \\ r_{\rm SOI} \sin \theta _2 (\sin \alpha \cos \gamma _2 + \cos \alpha \sin \beta \sin \gamma _2 ) + d\cos (\omega t_2 )} \\ {r_{\rm SOI} \sin \alpha \cos \beta \cos \theta _2 + \\ r_{\rm SOI}\sin \theta _2 (\cos \alpha \cos \gamma _2 - \sin \alpha \sin \beta \sin \gamma _2 ) + d\sin (\omega t_2) } \\ {r_{\rm SOI} \sin \beta \cos \theta _2 + r_{\rm SOI}\sin \theta _2 \cos \beta \sin \gamma _2 } \end{array}\!\! \right] \tag{28}$
2.3 各物理量的计算引力辅助变轨之后飞行器速度变化为 $$ \Delta { v} = { v}_{\rm o} - { v}_{\rm i} \tag{29}$$ 飞行器能量变化为 $$ \Delta E = \dfrac{1}{2}\left| {{ v}_{\rm o} } \right|^2 - \dfrac{1}{2}\left| {{ v}_{\rm i} } \right|^2 \tag{30}$$ 飞行器进入和离开$M_{2} $影响球时的角动量分别为 $$ { C}_{\rm i} = { r}_{\rm i} \times { v}_{\rm i} ,\quad { C}_{\rm o} = { r}_{\rm o} \times { v}_{\rm o} $$ 飞行器角动量改变为 $$ \Delta { C} = { C}_{\rm o} - { C}_{\rm i} \tag{31}$$
飞行器进入和离开${M}_{2} $影响球时的轨道倾角分别为 $$ i_{i} = \arccos \left( {C_{{\rm i}z} / C_{\rm i} } \right) ,i_{\rm o} = \arccos \left( {C_{{\rm o}z} / C_{\rm o} } \right)$$ 飞行器轨道倾角改变为 $ \Delta i = i_{\rm o} - i_{\rm i} \tag{32}$ 将式(9)、式(10)、式(27)、式(28) 代入式(29) ~ 式(32)可以得到完整但非常复杂的表达形式,篇幅所限此处不再展开.
指定借力天体之后,$\mu _2 $,$r_{\rm SOI} $,$\omega $可通过查找天文数据得到.只要给8个引力辅助参数赋值,就可由上述公式计算飞行器的速度、能量、角动量、轨道倾角的改变量.
3 解析公式的数值验证以上推导是基于二体问题,为了验证解析公式的有效性,与基于圆型限制性三体问题的数值积分方法进行对比. 圆型限制性三体问题的无量纲化表述与数值计算方法在文献[3, 4, 5, 6, 7, 8]中已有系统详细的论述.
以在太阳-木星系统中借助木星引力辅助变轨为例,则$\mu _2 = 9.538 4\times 10^{ - 4}$,$r_{\rm SOI} = 6.198 6\times 10^{ - 2}$,令$r_{\rm P} = 1.375 95\times 10^{ - 4}$,$V_{\rm P 1} = 4.0$.表1将解析公式计算的结果与数值仿真结果进行了对比.
| 表1 本文结果与数值仿真结果的对比 Table 1 Comparison between the results predicted by the analytical equations and the results computed by the numerical method |
可以看到,各项绝对误差均小于0.01,相对误差为千分之一量级. 表明本文公式可以满足轨道设计的需要,从而可以避免进行数值积分.
4 研究脉冲大小和方向对引力辅助效果的影响应用本文给出的公式,可以分析施加脉冲对引力辅助效果的影响. 仍以太阳-木星系统为例. 设置飞越木星的条件:$r_{\rm P} = 1.375 95\times 10^{ - 4}$,$V_{\rm P 1} = 4.0$. 此外还有6个参数,$\alpha $,$\beta $和$\gamma _1 $表征是否三维引力辅助,$\delta V$,$\eta $和$\xi $表征施加脉冲的大小和方向.
4.1 脉冲大小和方向对飞行器能量的影响 4.1.1 二维引力辅助施加共面脉冲二维引力辅助意味着参数 $\beta = 0$,$\gamma _1 = 0$,施加共面脉冲意味着参数$\eta = 0$.
4.1.1.1 $\alpha $对施加脉冲的最优方向的影响对于不带脉冲的引力辅助,有经典结论:前向飞越使飞行器能量减少,后向飞越使飞行器能量增加,即当$\alpha \in (0^ \circ ,180^\circ )$时$\Delta E <0$,当$\alpha \in (180^ \circ ,360^ \circ )$时$\Delta E > 0$.对于带脉冲的引力辅助,$\alpha $仍为重要参数,此外脉冲方向$\xi $也为关键参数,因此首先分析$\alpha $和$\xi$对飞行器能量的影响. 设置参数$\delta V = 1.0 $和$\xi \in [- 90^ \circ ,90^ \circ]$.
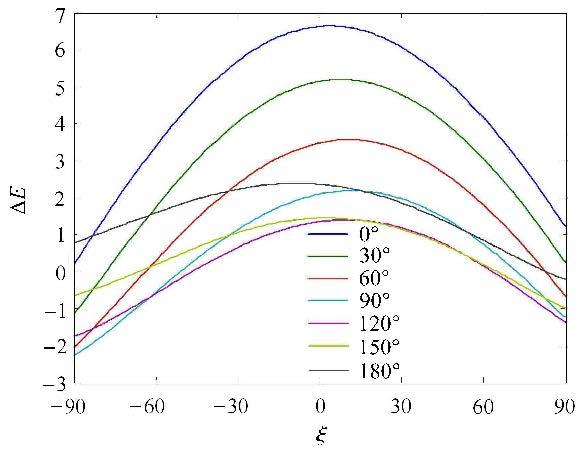
图8所示是$\alpha $分别为0°,30°,60°,90°,120°,150°和 180°时$\Delta E$与$\xi $的关系图.
|
图8 $\Delta E$与$\xi $的关系图 ($\alpha \in [0^ \circ ,180^ \circ])$ Fig.8 Variation in energy ($\alpha \in [0^ \circ ,180^ \circ]$) |
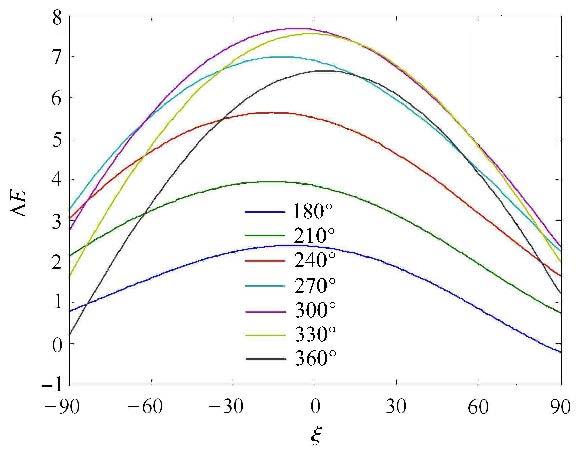
图9所示是$\alpha $分别为180°,210°,240°,270°,300°,330°和360°时,$\Delta E$与$\xi $的关系图.
|
图9 $\Delta E$与$\xi $的关系图($\alpha \in [180^ \circ ,360^ \circ])$ Fig.9 Variation in energy ($\alpha \in [180^ \circ ,360^ \circ])$ |
由图8和图9可得到以下结论:
结论1:前向飞越使飞行器能量减少、后向飞越使飞行器能量增加的结论只对不带脉冲的引力辅助成立,对带脉冲的引力辅助不成立.
结论2:对于施加共面脉冲的二维引力辅助,以最大能量改变为优化目标,施加脉冲的最优方向与$\alpha $显著相关. 当$\alpha \in [0^\circ ,180^ \circ]$时,最优方向大于0°,约为10°左右;当$\alpha \in [180^ \circ ,360^ \circ]$,最优方向小于0°,约为 $-10$° 左右.
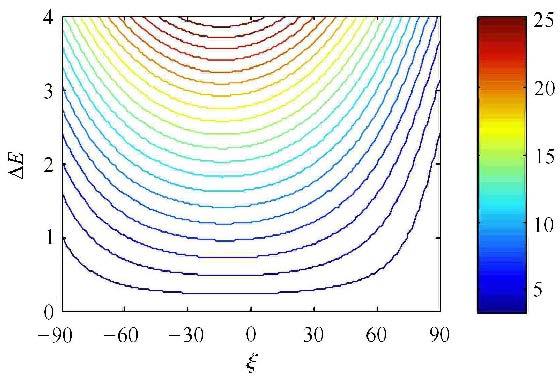
4.1.1.2 脉冲大小$\delta V$对施加脉冲的最优方向的影响施加脉冲的最优方向除与$\alpha $相关外,也会受到脉冲大小$\delta V$的影响. 仍取$\beta = 0$,$\gamma _1 = 0$,$\eta = 0$. $\xi \in [- 90^ \circ ,90^ \circ]$,$\delta V \in [0,4.0]$. 图10所示为$\alpha = 270^ \circ $时,$\Delta E$关于$\xi $与$\delta V$的等高线图;图11所示为$\alpha = 90^ \circ $时,$\Delta E$关于$\xi $与$\delta V$的等高线图.
|
图10 $\alpha = 270^ \circ $时,$\Delta E$关于$\xi $与$\delta V$的等高线图 Fig.10 Variation in energy $(\alpha = 270^ \circ)$ |

|
图11 $\alpha = 270^ \circ $时,$\Delta E$关于$\xi $与$\delta V$的等高线图 Fig.11 Variation in energy ($\alpha = 270^ \circ$) |
由图10和图11可知以下结论:
结论3:施加脉冲方向一定的情况下,$\Delta E$与$\delta V$正相关;
结论4:当$\alpha = 270^ \circ $时,施加脉冲的最优方向小于0°,并随$\delta V$的增大而略有减小;当$\alpha = 90^ \circ $时,施加脉冲的最优方向大于0°,并随$\delta V$的增大而略有增大. 总的来说,施加脉冲的最优方向对脉冲大小$\delta V$不敏感,而主要由参数$\alpha $决定.
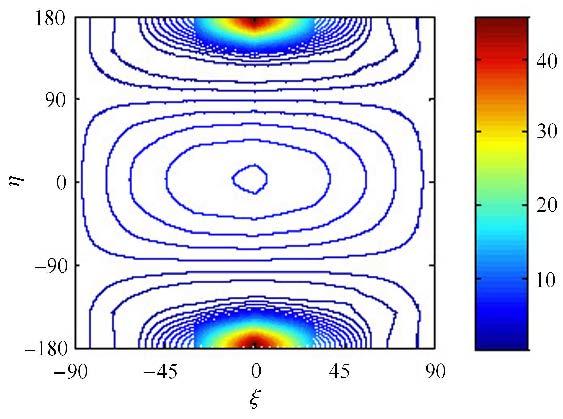
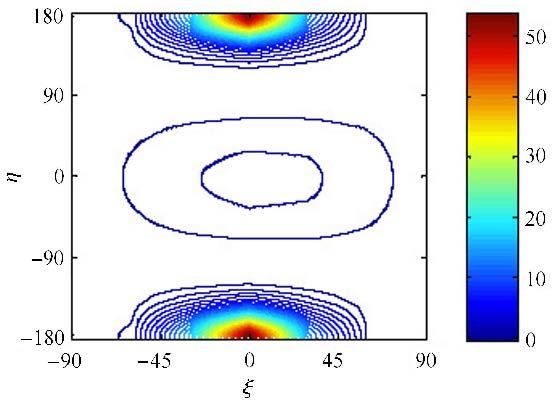
4.1.2 带任意脉冲的三维引力辅助图12所示为$\alpha = 270^ \circ$,$\beta = 45^ \circ $,$\gamma _1 = 60^ \circ $和$\delta V = 1.0$时,$\Delta E$关于$\xi $与$\eta $的等高线图. 图13所示为$\alpha = 90^ \circ$,$\beta = 45^ \circ $,$\gamma _1 = 60^ \circ $和$\delta V = 1.0$时,$\Delta E$关于$\xi $与$\eta $的等高线图.
|
图12 $\Delta E$关于$\xi $与$\eta $的等高线图 Fig.12 Variation in energy |
|
图13 $\Delta E$关于$\xi $与$\eta $的等高线图 Fig.13 Variation in energy |
由图12和图13可得
结论5:$\Delta E$出现两个尖点,表明施加脉冲与${ V}_{\rm P 1} $方向基本一致时,效果最为明显.
4.2 脉冲大小和方向对飞行器轨道倾角的影响施加脉冲之后,飞行器的轨道能量改变的同时,轨道倾角也发生变化.
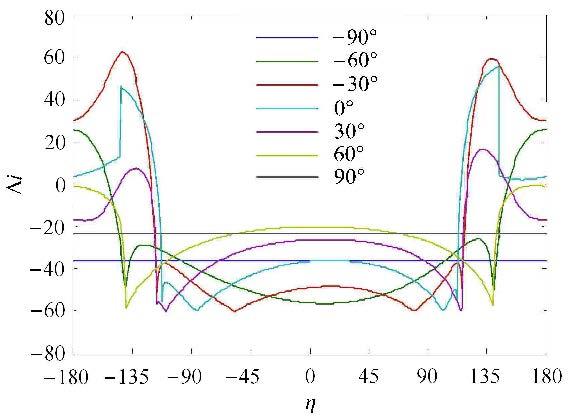
三维引力辅助施加任意脉冲.设置参数$\alpha = 270^ \circ$,$\beta = 45^ \circ $,$\gamma _1 = 60^ \circ $和$\delta V = 2.0$,图14所示是$\xi $分别为$-90$°,$-60$°,$-30$°,0°,30°,60°,90°时,$\Delta i$与$\eta $的关系图.
|
图14 $\Delta i$与$\eta $的关系图 Fig.14 Variation in inclination |
图中两条直线分别对应$\xi = - 90^ \circ $与$\xi = 90^ \circ $时情况,此时$\Delta i$为特定值,与$\eta $无关.从其他几条曲线可以看到,曲线关于$\eta = 0$对称,一般具有两个极大值和两个极小值,且极小值位于极大值内侧.$\Delta i$对脉冲方向$\xi $和$\eta $都非常敏感,因此,对于具体问题需要进行具体分析.
5 结论本文采用8个参数对带任意脉冲的三维引力辅助问题进行了描述,提出了一套分析方法,推导了飞行器的位置矢量和速度矢量关于上述8个参数的解析公式,进而求得能量和轨道倾角的改变量.
应用导出的解析公式分析了施加脉冲的大小和方向对飞行器轨道能量和轨道倾角的影响,讨论了施加脉冲的最优方向. 研究结果表明:
(1)脉冲方向一定的情况下,飞行器的能量变化与脉冲的大小正相关;
(2)以最大能量改变为优化目标,施加脉冲的最优方向与该点的速度方向一般并不重合而是有一个小的夹角;
(3)施加脉冲的最优方向与参数$\alpha$显著相关,而对脉冲大小不敏感;
(4)施加脉冲的方向对轨道倾角的影响显著.
| 1 | Strange NJ, Longuski JM. Graphical methods for gravity-assist trajectory design. Journal of Spacecraft and Rockets, 2002, 39(1):9-16 |
| 2 | Broucke RA. The celestial mechanics of the gravity assist. In:Proc. of AIAA/AAS Astrodynamics Conference. Washington. D C:American Institute of Aeronautics and Astronautics, 1988:69-78 |
| 3 | Campagnola S, Skerritt P, Russell RP. Flybys in the planar, circular, restricted, three-body problem. Celestial Mechanics and Dynamical Astronomy, 2012, 113:343-368 |
| 4 | Prado AFBA. Close-approach trajectories in the elliptic Restricted problem. Journal of Guidance, Control and Dynamics, 1997, 20(4):797-802 |
| 5 | 乔栋,崔平远,崔祜涛. 基于圆型限制性三体模型的借力飞行机理研究. 宇航学报,2009, 30(1):82-87(Qiao Dong, Cui Pingyuan, Cui Hutao. Research on gravity-assist mechanism in circular restricted three-body model. Journal of Astronautics, 2009, 30(1):82-87(in Chinese)) |
| 6 | 乔栋,崔平远,尚海滨. 基于椭圆型限制性三体模型的借力飞行机理研究. 宇航学报,2010, 31(1):36-43(Qiao Dong, Cui Pingyuan, Shang Haibin. Research on gravity-assist mechanism in elliptic restricted three-body model. Journal of Astronautics, 2010,31(1):36-43(in Chinese)) |
| 7 | Felipe G, Prado AFBA. Classification of out-of-plane swing-by trajectories. Journal of Guidance, Control and Dynamics, 1999, 22(5):643-649 |
| 8 | 贾建华,王琪. 三维引力辅助机理分析. 北京航空航天大学学报, 2012, 38(7):981-986(Jia Jianhua, Wang Qi. Research on gravityassist mechanism based on three-dimension elliptic restricted threebody model. Journal of Beijing University of Aeronautics and Astronautics, 2012, 38(7):981-986(in Chinese)) |
| 9 | 贾建华, 王琪. 三维引力辅助解析分析方法研究. 力学学报, 2013, 45(3):412-420(Jia Jianhua, Wang Qi. An analytical study of gravity assist in three dimensions. Chinese Journal of Theoretical and Applied Mechanics, 2013, 45(3):412-420(in Chinese)) |
| 10 | Formiga JKS. Souza dos S, Denilson P. An analytical description of the three-dimensional swing-by. Computational & Applied Mathematics, 2015, 34(2):491-506 |
| 11 | Curtis HD. 轨道力学. 北京:科学出版社,2009:308-309(Curtis HD. Orbital Mechanics for Engineering Students. Beijing:Science Press,2009:308-309(in Chinese)) |
| 12 | Kloster KW, Petropoulos AE, Longuski JM. Europa Orbiter tour design with Io gravity assists. Acta Astronautica, 2011, 68:931-946 |
| 13 | Prado AFBA, Gomes VM. Searching for capture and escape trajectories around Jupiter using its Galilean satellites. Computational & Applied Mathematics, 2015, 34(2):451-460 |
| 14 | Gong SP, Li JF. Asteroid capture using lunar flyby. Advances in Space Research, 2015, 56(5):848-858 |
| 15 | Cai XS, Li JF, Gong SP. Solar sailing trajectory optimization with planetary gravity assist. Sci China-Phys Mech Astron, 2015, 58:014501 |
| 16 | Cai X, Chen Y, Li J. Low-thrust trajectory optimization in a fullephemeris model. Acta Mech Sin, 2014, 30(5):615-627 |
| 17 | Shen HX, Zhou JP, Peng QB, et al. Multi-objective interplanetary trajectory optimization combining low-thrust propulsion and gravity-assistmaneuvers. Sci China Tech Sci, 2012, 55:841-847 |
| 18 | Armellin R, Lavagna M, Ercoli-Finzi A. Aero-gravity assist maneuvers:controlled dynamics modeling and optimization. Celestial Mechanics and Dynamical Astronomy, 2006, 95:391-405 |
| 19 | Jordi C, Daniel L. Mission design of guided aero-gravity assist trajectories at Titan. Advances in the Astronautical Sciences, 2010, 135:2149-2168 |
| 20 | 张万里, 王常虹, 夏红伟等. 气动-引力辅助轨道机动轨迹优化方法. 西南交通大学学报,2011, 46(1):167-174(ZhangWanli,Wang Changhong, Xia Hongwei. et al. Trajectory optimization method of aero-gravity assist orbital maneuver. Journal of Southwest Jiaotong University, 2011, 46(1):167-174(in Chinese)) |
| 21 | Prado AFBA. Powered swingby. Journal of Guidance, Control and Dynamic, 1996, 19(5):1142-1147 |
| 22 | Casalino L, Colasurdo G, Pastrone D. Simpe strategy for powered swingby. Journal of Guidance, Control and Dynamic, 1999, 22(1):156-159 |
| 23 | Ferreira AFS, Prado AFBA. Optimal impulsive control in a powered swingby.//AIAA Guidance, Navigation, and Control(GNC) Conference, Boston USA, 2013 |
| 24 | Ferreira AFS, Prado AFBA. Powered swing-by in the elliptic restricted problem. In:Proc. of SpaceOps 2014 Conference, Pasadena USA, 2014 |
| 25 | Prado AFBA., Felipe G. An analytical study of the powered swingby to perform orbital maneuvers. Advances in Space Research, 2007, 40:102-112 |
| 26 | 侯艳伟, 岳晓奎, 张莹. 基于脉冲机动的引力辅助深空探测轨道设计. 西北工业大学学报, 2012, 30(4):491-496(Hou Yanwei, Yue Xiaokui,Zhang Ying. Design of gravity-assist trajectory based impulsive maneuver. Journal of Northwestern Polytechnical University, 2012, 30(4):491-496(in Chinese)) |
| 27 | 陈杨, 宝音贺西, 李俊峰. 我国小行星探测目标分析与电推进轨道设计. 中国科学:物理学力学天文学, 2011, 41:1104-1111(Chen Yang, Baoyin Hexi, Li Junfeng. Target analysis and low-thrust trajectory design of Chinese asteroid exploration mission. Sci Sin Phys Mech Astron, 2011, 41:1104-1111(in Chinese)) |
| 28 | Zhu KJ, Li JF, Baoyin HX. Multi-swingby optimization of mission to saturn using global. Acta Mech Sin, 2009, 25:839-845 |
| 29 | Cui PY, Qiao D, Cui HT, et al. Target selection and transfer trajectories design for exploring asteroid mission. Sci China Tech Sci, 2010, 53:1150-1158 |
| 30 | Ferreira AFS, Prado AFBA, Winter OC. A numerical study of powered swing-bys around the Moon. Advances in Space Research, 2015, 56:252-272 |
 2016, Vol. 48
2016, Vol. 48