在日趋成熟的现代控制理论中,人们发现利用现代控制理论进行控制器设计时,需要有精确的过程模型.但在实际应用中,系统建模不可避免地要忽略一些因素从而造成模型误差,如模型高阶项的忽略、外干扰的不确定性、模型参数的误差等,系统矩阵的确定往往并不是非常精确.学者们对不确定系统的控制器设计进行了全面研究,一种是假设过程的参数是未知的,如自校正控制器[1]和模型参考自适应控制器[2]方案;另一种途径是假设系统是不确定的,如鲁棒控制理论方法[3, 4, 5].鲁棒控制理论为了弥补现代控制理论这种不足,在控制器设计过程中考虑被控对象所存在的各种不确定性因素,基于不确定性的非精确模型来设计控制器. 因此,研究控制器的鲁棒性能显得尤为重要.
从20世纪80年代初开始,控制系统的鲁棒稳定性问题受到了重视和研究,如鲁棒自适应的研究?[6, 7, 8]. 鲁棒控制理论发展的突出的标志是$H_{\infty }$控制理论. $H_{\infty }$控制方法在工程中应用很多,它以$H_{\infty }$范数作为性能指标,在可能发生最坏扰动情况下,使系统的误差达到极小,将干扰问题转化为闭环系统稳定性的问题[9].谢立敏等[10]研究了漂浮基柔性空间机器人的鲁棒控制及振动抑制.经学者在理论与试验方面的不断研究,在线性系统$H_\infty $控制方面取得了很大的发展,如线性矩阵不等式方法[11, 12, 13]、微分对策法[14, 15]、$\mu $分析、$\mu $综合等方法[16, 17, 18].但这些成果应用到实际中,却存在求解过程繁琐、系统的保守性不强、结构复杂和控制器阶数较高等问题.钟万勰从一个新的角度设计$H_{\infty }$鲁棒控制器[19, 20, 21, 22, 23, 24],通过引入区段混合能的概念,采用精细积分和扩展的威廉姆斯(W-W)算法求解导引模临界值$\gamma _{\rm cr}^{ - 2} $,并理论上证明了其解可以达到计算机精度.
运用计算结构力学与最优控制相模拟的理论,导引模就是结构力学中的本征值问题,即弹性稳定的欧拉临界力[25].$H_{\infty }$控制需要全状态信息,并且需要计算复杂的黎卡提(Riccati)方程,具有在线计算时间长等缺点.基于市场机制的控制(market-based control,MBC)策略模拟自由市场机制,通过模拟市场行为完成控制系统中有限能量的最优分配.基于市场机制的控制策略只需离散点的状态信息,具有在线计算时间短和参数选取简便等优点.本文针对多高层剪切型结构,将扩展的威廉姆斯(W-W)算法和精细积分法应用到结构基于市场机制的控制策略中,提出了线性结构基于市场机制的鲁棒控制.以20层基准(Benchmark)模型进行数值模拟,将提出的线性结构基于市场机制的鲁棒控制策略和$H_{\infty }$鲁棒控制的效果进行了比较,验证了本文方法的有效性.
1 基于市场机制的控制策略基于市场机制的控制算法将控制系统中的能量源系统和受控系统分别比作虚拟市场中的销售商和消费者,在这个虚拟市场中受控结构对控制能量的需求和能量源对控制能量的供给都与市场价格有关.在每一个时间点需求函数和供给函数相交的点即为市场中控制能量在这一时刻的平衡价格,也意味着控制能量得到最合理的分配.当价格确定后,每个受控结构以市场价格购买一定数量的控制能量,并以控制力形式施加到结构上.本文采用作者提出的线性供给-指数需求模型(linear-supply & exponential-demand model,LEM) [25, 26, 27, 28, 29, 30]验证模拟结果,即供给函数为 $${ Q}_{{\rm S},j} = {\eta}_j \cdot p \tag{1}$$ 和需求函数 $${ Q}_{{\rm D},i} ={ W}_i \cdot | { \alpha}_i { x}_{{\rm d},i} + {\beta}_i \dot { x}_{{\rm d},i} | \cdot {\rm e}^{ - cp} \tag{2}$$
当市场达到均衡时 $$\sum_j { Q}_{{\rm S},j} = \sum_i { Q}_{{\rm D},i} \tag{3}$$ 通过平衡价格$p$可求得正比与需求能量的控制力 $${ U}_i = - K \cdot { W}_i \cdot ({\alpha}_i { x}_{{\rm d},i} + {\beta} _i \dot {x}_{{\rm d},i} ) \cdot {\rm e}^{ - cp} \tag{4}$$ 式中,${ W}_i ≥ {\bf 0}$表示各买方的虚拟财富值;${ c}$为需求调节系数,一般可取为1;${\eta }_j $为反映能量源供给的常数;${\alpha}_i ≥ {\bf 0}$,${\beta}_i > {\bf 0}$为相应的权系数; ${ x}_{{\rm d},i} $和$\dot { x}_{{\rm d},i} $分别表示单个买方代表的结构的层间相对位移和层间相对速度,$K > 0$为控制力增益系数,可按所要达到的控制效果进行选取.
2 基于市场机制的鲁棒控制器设计本节第一部分运用结构力学与最优控制相模拟的理论,根据扩展的威廉姆斯(W-W)算法[24],应用精细积分法计算临界参数$\gamma_{\rm cr}^{ - 2} $,设计了鲁棒控制系统;在确定临界参数后,第二部分给出了基于市场机制的控制力中其余参数的确定方法.
2.1 鲁棒控制系统系统矩阵${ A}$是被控对象运动规律的反映,在实际应用中,不可避免地有许多抽象,这些抽象都将带来误差. 鲁棒控制要考虑的是在给定范围内任意可能的变动$\Delta{ A}$阵,并选取最不利的变动阵. 将这一因素考虑进去,则结构系统的动力方程和输出方程将成为 $$\dot{ Z} (t) = { A Z}(t) + (\Delta { A Z} + { B}_{\rm w}{ w}) + { B}_{\rm u} { U}(t) \tag{5}$$ $${ Y}={ C}_Z { Z}+{ D}_{12}{ U} \tag{6}$$
其中,${ Z}(t) = \left\{ \!\!\begin{array}{c} { { x} (t)} \\ \dot { x}(t)\end{array}\!\! \right\}$,${ A }= \left[\!\! \begin{array}{cc} {\bf 0} & { I} \\ - { M}^{ - 1}{ K } & - { M}^{ - 1}{ C} \end{array}\!\! \right]$,${ B}_{\rm u} = \left[\!\! \begin{array}{c} {\bf 0} \\ { M}^{ - 1}{ B}_{\rm s} \end{array} \!\! \right]$,${ B}_{\rm w} = \left[\!\! \begin{array}{c} {\bf 0} \\ - { I} \end{array} \!\!\right]$,${ M}$,${ C}$ 和 ${ K}$ 分别为结构质量、阻尼和刚度矩阵;${ U}(t)$为控制力向量;${ B}_{\rm s} $为相应的位置矩阵;${ x}(t)$,$\dot { x}(t)$和$\ddot { x}(t)$分别为结构$n$维位移、速度和加速度向量;${ w} $是具有给定统计特性的白噪声向量;${ C}_Z $和${ D}_{12} $分别为输出矩阵和传递矩阵.
并且通过变换可得[7] $${ D}_{12}^{\rm T} { D}_{12} ={ I}_m \tag{7}$$
鲁棒控制在数学上的精确表达可通过引入导引模$\gamma ^2$阐述. 式(5)中将$\Delta { A }$项并入干扰项,考虑系统鲁棒性的要求,尽量考虑对系统性能最不利的干扰选择. 当${ B}_{\rm w}{ w}=0$,即外干扰全部是由$\Delta { A}$项产生的,按式(10)可确定一个临界值$\gamma _{\rm cr}^2 $,即系统不需外界激励而自己就激励起来所求的临界值. 当$\gamma ^2$超过$\gamma_{\rm cr}^2 $时,系统就不会因自激励的${ w}$而失稳,也就说此时系统可承受外界干扰,系统是稳定的.对于$Y$的度量可以用模来表示,即 $$ \left\| { Y} \right\| = \int_t^{t_{\rm f} } { Y}^{\rm T}{ Y} /2 \tau + { Z}_{\rm f}^{\rm T}{ S}_{\rm f}{ Z}_{\rm f } /2,\mathop {\min }\limits_U \left\| { Y} \right\| \tag{8}$$
激励${ w}$度量为 $$ \left\| { w} \right\| = \int_t^{t_{\rm f} } { w}^{\rm T}{ w} /(2 \tau) \tag{9}$$
激励${ w}$应该考虑最不利的干扰,其选择的原则是使$\left\| { Y} \right\|$为最大 $$ \gamma ^2 = \left\| { Y} \right\| / \left\| { w} \right\| ,\mathop {\max }\limits_w \mathop {\min }\limits_U \gamma ^2 = \gamma _{\rm cr}^2 \tag{10}$$
导引模取极值是一个变分问题. 由动力方程与输出方程仍应满足,因此是条件变分. 可先将方程改写为 $$J_{\rm c} = \int_t^{t_{\rm f} } ({ Y}^{\rm T}{ Y} / 2-\gamma ^2{ w}^{\rm T}{ w}/ 2) \tau + \\ { Z}_{\rm f}^{\rm T} { S}_{\rm f} { Z}_{\rm f} / 2,\mathop {\max }\limits_w \mathop {\min }\limits_U J_{\rm c} \tag{11}$$
将式(6)代入式(11),并对其引入拉格朗日(Lagrange)参数向量${ \lambda}$,有 $$\eqalign{ & {J_{{\text{cA}}}} = \int_t^{{t_{\text{f}}}} {{\lambda ^{\text{T}}}} (\dot Z - AZ - {B_{\text{w}}}w - {B_{\text{u}}}U) + \cr & {U^{\text{T}}}U/2 + {U^{\text{T}}}D_{12}^{\text{T}}{C_z}Z + {Z^{\text{T}}}C_z^{\text{T}}{C_z}Z/2 - \cr & {\gamma ^2}{w^{\text{T}}}w/2)\tau + Z_{\text{f}}^{\text{T}}{S_{\text{f}}}{Z_{\text{f}}}/2,\delta {J_{{\text{cA}}}} = 0 \cr} \tag{12}$$
$J_{\rm cA}$是扩展了的指标泛函,其中有4类变量. 对$J_{\rm cA}$完成对${ w}$取最大、对${ U}$取最小,有 $${ w} = - \gamma ^2{ B}_{\rm w}^{\rm T}{ \lambda } \tag{13}$$ $${\lambda}= ({ B}_{\rm u}^{\rm T} )^{ - 1}({ U} +{ D}_{12}^{\rm T} { C}_z { Z}) \tag{14}$$
式(12)中$J_{\rm cA} $对$\lambda $取驻值,并将上式代入可得 $$ \dot{ Z}(t) = \tilde { A}{ Z}(t) + \tilde { B}{ U}(t) \tag{15}$$ 其中 $$ \tilde{ A} ={ A} - \gamma ^{-2}{ B}_{\rm w}{ B}_{\rm w}^{\rm T} ({ B}_{\rm u}^{\rm T} )^{ - 1}{ D}_{12}^{\rm T}{ C}_z \\ \tilde{ B} ={ B}_{\rm u} - \gamma ^{ - 2}{ B}_{\rm w}{ B}_{\rm w}^{\rm T}({ B}_{\rm u}^{\rm T} )^{ - 1} $$
现在系统矩阵中多了$\gamma ^{ - 2}$一项,这正是鲁棒控制的特点. 当$\gamma ^{ - 2}$趋于零时,就是结构基于市场机制的控制算法. 外干扰全部是由$\Delta { A}$引起的,即为研究${ A}$阵偏离引起的自干扰下的稳定性. 当$\gamma^{ - 2}$增加表示$\Delta { A}$的作用越大,但不能无限制的增大,增长到临界值$\gamma _{\rm cr}^{ - 2} $时,系统将会失稳. 因此,很重要的是讨论$\gamma _{\rm cr}^{ - 2} $值.
运用结构力学与最优控制相模拟的理论,导引模$\gamma ^2$就是结构力学中的本征值问题,即弹性稳定的欧拉临界力或结构振动的本征频率[24]. 根据扩展的威廉姆斯(W-W)算法[25],应用精细积分法计算临界参数$\gamma _{\rm cr}^{ - 2} $. 首先,引入区段混合能,一般形式可写为 $$ V({ Z}_{\rm a} ,{ \lambda}_{\rm b} ) = { \lambda }_{\rm b}^{\rm T} { F}{ Z}_{\rm a} + { \lambda}_{\rm b}^{\rm T} { G}{ \lambda}_{\rm b} /2 - { Z}_{\rm a}^{\rm T} { Q}{ Z}_{\rm a} /2 \tag{16}$$
相连的两个区段可以合并为一个区段,其合并公式为 $${ Q}_{\rm c} = { Q}_1 + { F}_1^T ({ Q}_2^{ - 1} + { G}_1 )^{ - 1}{ F}_1 \tag{17}$$ $${ G}_{\rm c} = { G}_2 + { F}_2 ({ G}_1^{ - 1} + { Q}_2 )^{ - 1}{ F}_1 \tag{18}$$ $${ F}_{\rm c} = { F}_2 ({ I} + { G}_1 { Q}_2 )^{ - 1}{ F}_1 \tag{19}$$
文献[24]指出,对于给定的参数$\gamma _\# ^{ - 2} = \omega _\# ^2 $ ,用$J_{\rm R}(\omega _\# ^2 )$表示区段($t_{\rm a}$,$t_{\rm b})$在其两端分别为给定左端位移为零和右端力为0的条件下,区段内部本征值$\omega^2 < \omega _\# ^2 $的计数,即$\gamma _{\rm cr}^{ - 2} < \gamma _\# ^{ - 2} $的本征值计数 $$ J_{\rm Rc} (\omega _\# ^2 ) = J_{\rm R1} (\omega _\# ^2 ) + J_{\rm R2} (\omega _\# ^2 ) - s\left\{ { Q}_2 \right\} + s\left\{ { G}_1 +{ Q}_2^{ - 1} \right\} \tag{20}$$ 其中,$J_{\rm R1} $和$J_{\rm R2} $分别为区段1和区段2小于$\omega _\# ^2 $的本征值计数;$J_{\rm Rc}$为区段1和区段2合并后小于$\omega _\# ^2 $的本征值计数. $s\left\{ { M} \right\}$为将对称阵${ M}$分解为${ M} = { L D L}^{\rm T}$三角化形式,对角阵${ D}$中出现负值的个数.
整个区段本征值计数可表示为 $$ J_{\rm Rf} = J_{\rm R} - s\left\{ { { S}_{\rm f} } \right\} + s\left\{ { { G} + { S}_{\rm f}^{ - 1} } \right\} \tag{21}$$
此时,$J_{\rm Rf} = 0$就表明$\gamma _\# ^{ - 2} $是次优参数,即在整个区段中没有奇点. 对$\gamma _\# ^{ - 2} $运用搜索法,便可找到本征值$\gamma _{\rm cr}^{ - 2}$任意指定的精度. 混合能中的区段矩阵${ F}$,${ G}$和${ Q}$可采用精细积分计算,具体的表达形式可参见文献[24].
2.2 控制器参数确定方法现在控制系统矩阵中多了$\gamma ^{ - 2}$一项,设计的线性结构基于市场机制的鲁棒控制的稳定性需要进一步研究. 控制系统的稳定性是指控制系统在平衡状态下受外部扰动后恢复到平衡状态的趋势或能力[31]. 文献[26]给出了线性基于市场机制的控制策略的稳定性及参数的确定方法,但考虑鲁棒控制时,参数的形式会发生改变. 采用结构控制系统极值点位置来判断系统的稳定性. 假设式(4)中参数满足 $$ \dfrac{\alpha _1 }{\beta _1 } = \dfrac{\alpha _2 }{\beta _2 } = \cdots = \dfrac{\alpha _m }{\beta _m } = \xi ≥ 0 \tag{22}$$ 则式(4)写成整体矩阵的形式为[29] $$ { U }(t) = - \mu { W } \cdot { \beta } \cdot { B}_{\rm u}^{\rm T} \cdot { Q} \cdot { Z} (t) \tag{23}$$ 其中 $$ \mu = K \cdot {\rm e}^{ - cp} ,\ { W} = {\rm diag} ([W_1 ,W_2,\cdots ,W_m]) \\ { \beta } ={\rm diag} ([\beta _1 ,\beta _2 \cdots ,\beta _m ]) \\ { Q} = { Q}^{\rm T} = \left[\!\!\begin{array}{cc} { K} & \xi { M} \\ \xi { M} & { M} \end{array}\!\!\right] > 0 $$
将式(23)代入式(15)可得 $$ \dot{ Z}(t) = (\tilde{ A} - \tilde{ B} \cdot \mu { W} \cdot { \beta } \cdot { B}_{\rm u}^{\rm T} \cdot { Q} ) \cdot { Z} (t) \tag{24}$$
取下式作为李雅普诺夫函数 $$ \upsilon ({ Z} ) = { Z }^{\rm T}{ Q Z} ≥ 0 \tag{25}$$
根据李雅普诺夫直接法[32],要使控制系统保持稳定,矩阵${ Q}$应满足 $$ \dfrac{\upsilon ({ Z})}{{ Z}} = { Z}^{\rm T} \cdot (\tilde{ A}^{\rm T}{ Q} + { Q}\tilde { A}) \cdot { Z} - \\ { Z}^{\rm T} \cdot (2{ Q}\tilde { B} \cdot \xi { W} \cdot { \beta } \cdot { B}_{\rm u}^{\rm T} { Q} ) \cdot { Z} ≤ 0 \tag{26}$$
对于式(26),右边第2项是恒成立的;欲使式(26)恒成立,则必须有 $$ { Z }^{\rm T} \cdot (\tilde{ A}^{\rm T}{ Q} + { Q}\tilde { A}) \cdot { Z} ≤ 0 \tag{27}$$ 恒成立,则矩阵$(\tilde{ A}^{\rm T}{ Q} + { Q}\tilde { A})$应为半负定矩阵,其特征根应在复平面虚轴左侧,即${\rm Re} (\lambda (\tilde{ A}^{\rm T}{ Q} + { Q}\tilde { A})) ≤ 0$.
当$\xi = 0$时,可知$(\tilde{ A}^{\rm T}{ Q} + { Q}\tilde { A})$恒为半负定矩阵,控制系统恒稳定. 当$\xi > 0$时,可取得一个较小的$\xi $值保证${\rm Re} ({\lambda} (\tilde{ A}^{\rm T} { Q} + { Q}\tilde { A})) ≤ 0$,控制系统也是稳定的.这样可以先确定$\xi $值,然后根据式(22)可求得$\alpha $和$\beta $值,再使得控制效果最优的前提下求得增益系数$K$.
综上,求解线性结构基于市场机制的控制系统中的参数如下:(1)根据2.1节中的方法确定临界参数,进而确定导引模$\gamma ^{ - 2}$;(2)选取多条与场地土匹配的地震波,按设防要求对结构进行无控工况下的分析,得到多条地震动作用下无控结构相应层层间位移与层间速度的峰值平均值;(3)确定$\mu $值,保证矩阵$(\tilde{ A}^{\rm T}{ Q} + { Q}\tilde { A})$的特征值的实部均不大于0;(4)针对各层最大层间反应下的供需进行"归1化"处理,确定相应的加权系数${\alpha } $与${\beta} $;(5) 根据控制装置的出力范围及特性来选择控制力增益系数$K$.
3 数算例及分析为了验证本文提出控制策略的有效性,将该策略应用到一座20层钢框架结构,结构参数如表1中所示. 结构前两阶的阻尼比皆为0.02. 为了节省篇幅,地震记录只选取地震波"El Centro (NS,May 18,1940)",峰值加速度调整为4 m/s$^{2}$. 控制装置分别在结构第1$\sim $5层每层设置5个磁流变阻尼器,第8$\sim $12层各层设置4个,第15$\sim $19层每层设置3个. 为了衡量提出的线性结构基于市场机制的鲁棒控制系统的性能,本文选取$H_{\infty }$鲁棒控制[24]和无控系统与之对比.
| 表 1 结构主要参数 Table 1 Main parameters of the structure |
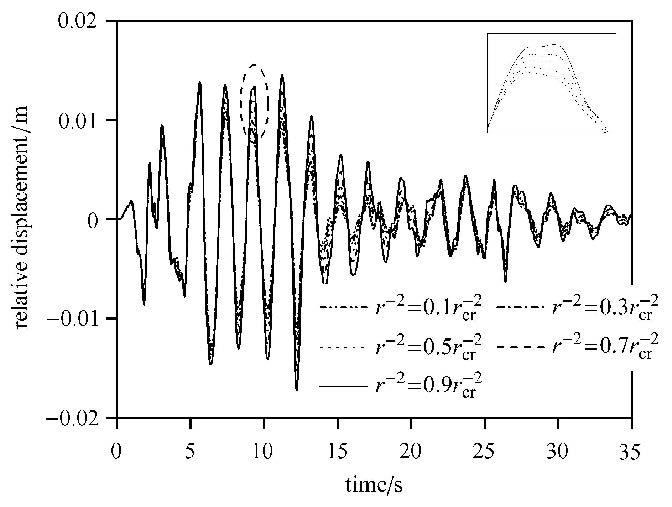
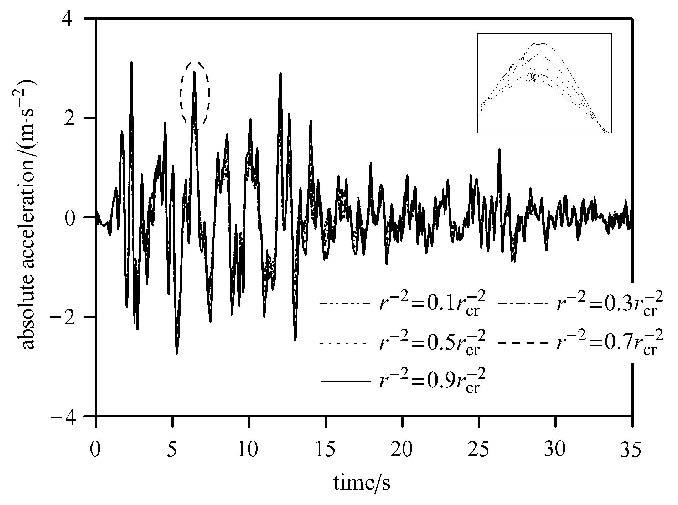
图1和图2分别为不同参数$\gamma $下结构第10层层间位移响应和加速度响应. 从图中可以看出,当参数$\gamma ^{ - 2}$接近临界值时,干扰抑制效果越差,并且所需的控制力会增大. 在实际计算时,导引模不能取到临界值,否则会导致控制输入趋于无穷大,这与文献[10]中的结论一致.
|
图1 不同参数$\gamma $结构第10层位移响应 Fig.1 Time history of relative displacement for the 10th floor under different $\gamma $ |
|
图2 不同参数$\gamma $结构第10层加速度响应 Fig.2 Time history of absolute acceleration for the 10th floor under different $\gamma $ |
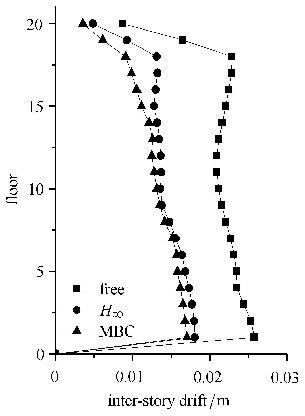
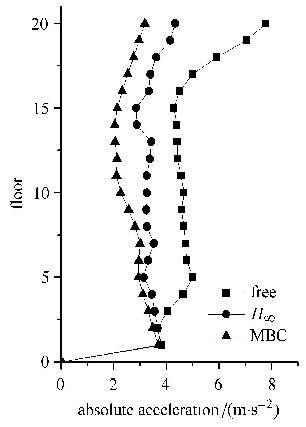
图3为各层层间相对位移反应峰值,从图中可以看出,基于市场机制的控制策略对于结构加速度的控制效果要好于$H_{\infty }$控制. 其中,结构第18层的相对位移峰值基于市场机制的控制策略要好于$H_{\infty }$控制约42.1%左右.图4为各层绝对加速度峰值. 从图中可以看出,基于市场机制的控制策略对于结构加速度的控制效果要好于$H_{\infty }$控制. 其中,结构第10层的绝对加速度峰值基于市场机制的控制策略要好于$H_{\infty }$控制约29.3%左右.
经计算,基于市场机制的控制策略和$H_{\infty }$控制在整个时程中所消耗的时间分别为9.12 s和12.44 s,即前者比后者快26.7%. 主要原因是基于市场机制的控制策略在计算增益矩阵时只需简单的乘法运算,而$H_{\infty }$控制需要迭代复杂的黎卡提方程.
|
图3 各层层间相对位移反应峰值 Fig.3 The maximum inter-story drift of each story |
|
图4 各层绝对加速度峰值 Fig.4 The maximum absolute acceleration of each story |
综上,基于市场机制的控制策略和$H_{\infty }$控制采用了相同的方法考虑系统的不确定性,前者的控制效果要好于后者的主要原因是,基于市场机制的控制策略模拟自由市场,在这个虚拟的市场中,即使系统出现不确定性,也可以通过虚拟市场的价格反映出来,价格决定供需函数,进而确定控制力,具有很强的适应性. 而$H_{\infty }$控制属于定常系统,一旦参数确定就不会变动,缺少灵活性.
4 结论本文针对大型工程结构振动控制系统建模时存在不确定性问题,提出了线性结构基于市场机制的鲁棒控制策略. 运用计算结构力学与最优控制相模拟的理论,将精细积分的思想和扩展的威廉姆斯算法应用到基于市场机制的控制器的设计中,这样设计的策略不需要求解复杂的黎卡提方程,并且基于市场机制的控制算法本身只需离散点的状态信息,从而大大节省了在线计算时间. 另外,该控制器中参数选取简便,为实际工程实现带来可能. 从仿真的结果可以看出,结构基于市场机制的鲁棒控制效果要好于$H_{\infty }$控制,并且具有很强的应变能力,能较好地适用于高层和多维结构.
| 1 | Ioannou PA, Sun J. Robust adaptive control. International Journal of Control, 1991, 54(1):241-256 |
| 2 | 赵国良, 姜仁锋. 自适应控制技术与应用. 北京:人民交通出版社,1991(Zhao Guoliang, Jiang Renfeng. Adaptive Control Technology and Application. Beijing:People's Communications Press, 1991(in Chinese)) |
| 3 | Feintuch A. Robust Control Theory. Berlin:Springer, 2012 |
| 4 | Surhone LM, Tennoe MT, Henssonow SF, et al. Robust control. Advances in Industrial Control, 2010, 121(2):S1-S2 |
| 5 | Xiao H, Zhao L. Robust passive control of uncertain switched timedelay systems:A sliding mode control design. Journal of Control Theory and Applications, 2013, 11(1):96-102 |
| 6 | 朱宏平, 张源. 基于自适应BP 神经网络的结构损伤检测. 力学学报, 2003, 1(1):110-116(Zhu Hongping, Zhang Yuan. Application of self-adaptive be neural networks to the detection of structural damage. Chinese Journal of Theoretical and Applied Mechanics, 2003, 1(1):110-116(in Chinese)) |
| 7 | 朱永红. 非线性不确定系统鲁棒自适应控制研究.[硕士论文]. 南京:南京航空航天大学, 2003(Zhu Yonghong. Research on robust adaptive control for nonlinear uncertain systems.[Master Thesis]. Nanjing:Nanjing University of Aeronautics and Astronautics, 2003(in Chinese)) |
| 8 | 韩曾晋. 自适应控制. 北京:清华大学出版社, 1994(Han Zengji. Adaptive Control. Beijing:Tsinghua University Press, 1994(in Chinese)) |
| 9 | Feng CC, Yin LP, Chang EC. Robust control design based on integral. Sliding Modal Control, 2013, 284(5):2301-2304 |
| 10 | 谢立敏, 陈力. 漂浮基柔性空间机器人的鲁棒控制及振动抑制. 力学学报, 2012, 46(6):1057-1065(Xie Limin, Chen Li. Robust control and vibration suppression of free-floating flexible space robot. Chinese Journal of Theoretical and Applied Mechanics, 2012, 46(6):1057-1065(in Chinese)) |
| 11 | 王鹏, 宋鹏云, 张继业. 基于向量Lyapunov 函数和LMI 的大系统分散镇定. 动力学与控制学报, 2013, 11(2):109-113(Wang Peng, Song Pengyun, Zhang Jiye. Decentralized stabilization of largerscale system based on vector Lyapunov function and LMI. Journal of Dynamics and Control, 2013, 11(2):109-113(in Chinese)) |
| 12 | 王露健, 周星德, 秦飞马等. 基于观测器的LMI 振动控制算法. 河海大学学报:自然科学版, 2014, 42(4):342-345(Wang Lujian, Zhou Xingde, Qin Feima, et al. Observer-based LMI vibration control algorithm. Journal of Hohai University(Natural Sciences), 2014, 42(4):342-345(in Chinese)) |
| 13 | 富饶, 黄琳. 基于LMI 的μ方法及其在电力系统中的应用. 自动化学报, 2002, 22(10):496-506(Fu Rao, Huang Lin. Optimized LMI algorithm for μ analysis and synthesis with application in power system. Acta Automatica Sinica, 2002, 22(10):496-506(in Chinese)) |
| 14 | 徐自祥, 周德云, 邓子辰. 基于Hamilton 体系和辛算法的微分对策数值法. 应用数学和力学, 2006, 27(3):305-310(Xu Zixiang, Zhou Deyun, Deng Zichen. Numerical method based on hamilton system and symplectic algorithm to differential games. Applied Mathematics and Mechanics, 2006, 27(3):305-310(in Chinese)) |
| 15 | 王长青, 史晓丽, 王新民等. 基于LQ 微分对策的最优规避策略与决策算法. 计算机仿真, 2008, 25(9):74-78(Wang Changqing, Shi Xiaoli, Wang Xinmin, et al. Optimal evasive strategies based on LQ differential games. Computer Simulation, 2008, 25(9):74-78(in Chinese)) |
| 16 | Ehsan Omidi, Nima Mahmoodi S. Sensitivity analysis of the nonlinear integral positive position feedback and integral resonant controllers on vibration suppression of nonlinear oscillatory systems. Commun. Nonlinear Sci. Numer. Simulat., 2015, 22(3):149-166 |
| 17 | 孙涛, 喻凡, 柳江等. 基于混合不确定建模的主动悬架鲁棒μ综合控制分析. 上海交通大学学报, 2006, 40(6):936-941(Sun Tao, Yu Fan, Liu Jiang, et al. The mixed-uncertainty modeling and control for active suspension based on robust μ-synthesis. Journal of Shanghai Jiaotong University, 2006, 40(6):936-941(in Chinese)) |
| 18 | 何朕, 姜晓明, 孟范伟等. μ综合中的D-K 迭代算法. 电机与控制学报, 2010, 14(9):31-35(He Zhen, Jiang Xiaoming, Meng Fanwei, et al. D-K iteration algorithm for μ-synthesis. Electric Machines and Control, 2010, 14(9):31-35(in Chinese)) |
| 19 | Li MW, Peng HJ, Zhong WX. A symplectic sequence iteration approach for nonlinear optimal control problems with state-control constraints. Journal of the Franklin Institute, 2015, 352(6):2381-2406 |
| 20 | 钟万勰, 张洪斌, 吴承伟. 参变量变分原理及其在工程中的应用. 北京:科学出版社, 1997(Zhong Wanxie, Zhang Hongbin, Wu Chengwei. Parametric Variational Principle and its Application in Engineering. Beijing:Science press, 1997(in Chinese)) |
| 21 | Peng HJ, Wu ZG, Zhong WX. H∞ norm computation of linear continuous-time periodic systems by a structure-preserving algorithm. International Journal of Control, 2014, 87(1):131-142 |
| 22 | Zhong Wanxie. Duality System in Applied Mechanics and Optimal Control. Kluwer Academic Publishers, 2004 |
| 23 | Peng HJ, Cao Q, Wu ZG. Efficient sparse approach for solving receding-horizon control problems. Journal of Guidance Control & Dynamics, 2013, 36(6):1864-1872 |
| 24 | 钟万勰, 吴志刚, 谭述君.状态空间控制理论与计算. 北京:科学出版社, 2007(Zhong Wanxie, Wu Zhigang, Tan Shujun. The State Space Control Theory and Calculated. Beijing:Science Press, 2007(in Chinese)) |
| 25 | 钟万勰. 应用力学对偶体系. 北京:科学出版社, 2002(Zhong Wanxie. Duality System in Applied Mechanics. Beijing:Science Press, 2002(in Chinese)) |
| 26 | 李宏男, 李瀛. MBC 策略供需函数模型研究. 计算力学学报, 2010,27(1):28-34(Li Hongnan, Li Ying. Study on supply-demand function models of MBC strategy. Chinese Journal of Computational Mechanics, 2010, 27(1):28-34(in Chinese)) |
| 27 | 李宏男, 李学涛, 霍林生. 基于市场机制结构控制策略的研究和应用进展. 世界地震工程, 2005, 21(4):1-9(Li Hongnan, Li Xuetao, HuoLinsheng. Research and application progress of structure control strategy based on market-based control. Earthquake Engineering, 2005, 21(4):1-9(in Chinese)) |
| 28 | 霍林生, 李宏男. 基于市场机制的TLCD 半主动控制方案. 应用力学学报, 2005, 22(1):71-75(Huo Linsheng, Li Hongnan. Control law for market-based semi-active timed liquid column dampers. Journal of Applied Mechanics, 2005, 22(1):71-75(in Chinese)) |
| 29 | 李瀛. 应用MBC 策略的建筑结构振动控制.[硕士论文]. 大连:大连理工大学, 2007(Li Ying. Structural vibration control using MBC strategy.[Master Thesis]. Dalian:Dalian University of Technology,2007(in Chinese)) |
| 30 | 李宏男,李学涛,霍林生. 多维结构振动的改进MBC 控制策略. 振动工程学报,2007,20(4):317-323(Li Hongnan,Li Xuetao, Huo Linsheng. Advanced market-based control applied in eccentric structure. Journal of Vibration Engineering, 2007, 20(4):317-323(in Chinese)) |
| 31 | 胡寿松. 自动控制原理(第四版). 北京:科学出版社, 2002(Hu Shousong. Automatic Control Theory(Fourth Edition). Beijing:Science Press, 2003(in Chinese)) |
| 32 | 欧进萍. 结构振动控制——主动、半主动和智能控制. 北京:科学出版社, 2003(Ou Jinping. Structural Vibration Active, Semi-Active and Intelligent Control. Beijing:Science Press, 2003(in Chinese)) |
 2016, Vol. 48
2016, Vol. 48