由于主动振动控制具有良好的控制效果以及对不同结构的适应能力,因此得到了广泛的应用[1]. 其中,比例--积分--微分控制策略算法简单、可靠性高,尤其是利用各种智能算法以及模糊数学理论对比例--积分--微分控制的参数进行整定与优化后,可以取得较好的控制效果,已广泛应用于柔性机械臂振动控制[2]、建筑结构振动控制[3]、旋转梁振动控制[4]、车辆悬架振动控制[5]等领域.
分数阶微积分理论的发展已有300多年的历史,近年来分数阶微积分的应用研究得到迅速发展[6, 7, 8, 9, 10, 11, 12, 13],同时分数阶微积分的数值计算方法以及计算机硬件技术的发展也促进了分数阶微积分理论的研究发展.由于很多工程问题可以用分数阶微分或积分方程建立比传统整数阶微积分方程更准确的模型[14],因此分数阶微积分在工程中的应用越来越广泛.另一个重要的应用领域就是在控制系统中引入闭环分数阶比例-积分-微分控制器,利用分数阶反馈的鲁棒性好、抗噪声能力强等优点,提高系统的控制效果[15, 16, 17, 18, 19].赵春娜等[20]利用位置伺服系统对分数阶比例-积分-微分控制器与整数阶比例-积分-微分控制器进行了比较,发现分数阶比例-积分-微分控制器可以更好地提高控制系统的稳定性与鲁棒性.目前学者们对分数阶比例-积分-微分控制的研究,主要集中在控制器的设计方法、稳定性分析以及最优化控制等方面[21, 22, 23].
达芬方程能体现很多非线性本质现象[24],在机械动力学、物理学、结构动力学等领域中得到了广泛应用,尤其是系统的动力学分析吸引了许多学者进行研究[25, 26]. 在振动控制研究中,位移和速度反馈控制常用来控制振动系统的大幅振动. 同时,基于速度反馈进行控制在振动控制中应用非常广泛,例如,文献[27]研究了基于速度反馈的柔性结构振动控制和实验;石秀东等[28]研究了基于加速度和速度反馈的半主动减振控制策略;文献[29]研究了基于速度反馈的柔性梁振动控制.
本文以一个基于速度反馈分数阶比例-积分-微分控制的达芬振子为例,利用平均法得到了系统的近似解析解.通过等效线性刚度、等效质量和3个等效线性阻尼参数表示了速度反馈分数阶比例-积分-微分控制的参数对系统动力学性能的影响,并通过数值解验证了结果的正确性.建立了主共振幅频响应方程的解析表达式,对定常解的稳定性进行了分析.最后分析了分数阶比例-积分-微分控制器的系数$K_{\rm p}$,$K_{\rm i}$,$K_{\rm d}$以及分数阶阶次 $\lambda $ 和 $\delta $ 变化时,对系统主共振幅频响应的影响.
1 近似解析解分数阶比例-积分-微分控制器的时域数学模型为[18] $$ u(t) = K_{\rm p} e(t) + K_{\rm i} {\rm D}_t^{ - \lambda } e(t) + K_{\rm d} {\rm D}_t^\delta e(t) \tag{1}$$ 其中,$u(t)$为控制器的输出量,$e(t)$为控制器的输入量,$K_{\rm p}$,$K_{\rm i}$,$K_{\rm d}$分别为比例、积分、微分环节的可调常数,$\lambda $ 和 $\delta $ 分别为积分环节和微分环节的分数阶阶次. 分数阶微积分算子${\rm D}_t^r $的定义为 $$ {\rm D}_t^r = \left\{ \begin{array}{ll} \dfrac{d^r}{d t^r} , & {\rm Re} (r) > 0 \\ 1 , & {\rm Re} (r) = 0 \\ \int_0^t (d\tau )^{ - r} , & {\rm Re} (r) <0 \end{array}\right. \tag{2}$$ 其中,$r$为分数阶微分和积分的阶次,此处$r$为实数,分数阶积分算子以0为积分下限,以$t$为积分上限.
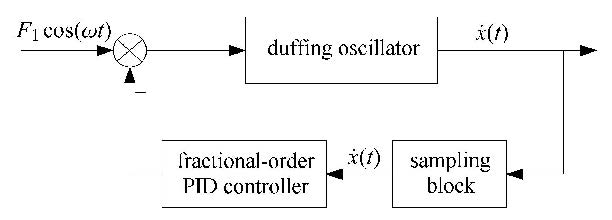
研究含有速度反馈的分数阶比例-积分-微分控制的达芬振子,其系统结构如图1所示.
|
图1 闭环反馈分数阶比例-积分-微分控制系统 Fig.1 Closed-loop feedback of fractional-order PID control system |
以系统的输出速度作为反馈量,含有分数阶比例-积分-微分控制的达芬振子的运动方程如下 $$ m\ddot {x}(t) + kx(t) + c\dot {x}(t) + \alpha _1 x^3(t) + K_{\rm p} \dot {x}(t) + $$ $$ K_{\rm i} {\rm D}_{t}^{ - \lambda } [\dot {x}(t)] + K_{\rm d} {\rm D}_{t}^\delta [\dot {x}(t)] = F_1 \cos (\omega t) \tag{3}$$ 其中,$m$为系统质量,$k$为线性刚度,$c$为线性阻尼系数,$\alpha_{1}$为非线性刚度系数,$0 ≤ \lambda ≤ 1$,$0 ≤ \delta ≤ 1$,$F_1 $为简谐激励的幅值,$\omega $为简谐激励的频率. 分数阶微积分的定义有多种形式,它们在一定条件下是等价的,这里采用卡普托定义,其形式为 $${\rm D}_t^\delta [\dot {x}(t)] = {\rm D}_t^{1 + \delta } [x(t)] = \dfrac{1}{\Gamma (1 - \delta )}\int_0^t \dfrac{{x}"(\tau )}{(t - \tau )^\delta } d\tau \tag{4}$$ $${\rm D}_t^{ - \lambda } [\dot {x}(t)] = {\rm D}_t^{1 - \lambda } [x(t)] = \dfrac{1}{\Gamma (\lambda )}\int_0^t \dfrac{{x}'(\tau )}{(t - \tau )^{1 - \lambda }} d\tau \tag{5}$$ 其中$\Gamma (z)$为伽马函数,满足$\Gamma (z + 1) = z\Gamma (z)$.
令$\omega _0 = \sqrt {\dfrac{k}{m}} $,$2\varepsilon \mu = \dfrac{c + K_{\rm p} }{m}$,$\varepsilon \alpha = \dfrac{\alpha _1 }{m}$,$\varepsilon k_{\rm i} = \dfrac{K_{\rm i} }{m}$,$\varepsilon k_{\rm d} = \dfrac{K_{\rm d} }{m}$,$\varepsilon f = \dfrac{F_1 }{m}$,式(3)可化简为
$$ \ddot {x}(t) + \omega _0^2 x(t) + 2\varepsilon \mu \dot {x}(t) + \varepsilon \alpha x^3(t) + $$ $$ \varepsilon k_{\rm i}{\rm D}_{\rm t}^{1 - \lambda } [x(t)] + \varepsilon k_{\rm d} {\rm D}_{\rm t}^{1 + \delta } [x(t)] = \varepsilon f\cos (\omega t) \tag{6}$$ 式(6)从形式上满足了平均法求解的要求.
研究系统的主共振问题,即外激励频率 $\omega $ 接近系统固有频率 $\omega_{0}$时的共振,并引入$\omega^2 = \omega _0^2 + \varepsilon \sigma $ ($\sigma $为调谐参数)定量表示两个频率之间的接近程度,则式(6)可整理为 $$ \ddot {x}(t) + \omega ^2x(t) = \varepsilon \left( {f\cos (\omega t) + \sigma x(t) - 2\mu \dot {x}(t)} \right) +$$ $$ \varepsilon \left( { - \alpha x^3(t) - k_{\rm i} {\rm D}_t^{1 - \lambda } [x(t)] - k_{\rm d} {\rm D}_t^{1 + \delta } [x(t)]} \right) \tag{7}$$ 利用平均法求其一次近似解. 设式(7)的解满足 $$ x = a(t)\cos \varphi ,\dot {x} = - \omega a(t)\sin \varphi \tag{8}$$ 其中$\varphi = \omega t + \theta $,则根据平均法可以得到 $$ \left.\!\!\begin{array}{l} \dot {a}(t) = - \dfrac{\varepsilon }{\omega }\left({P_1 \left[ {a(t),\theta } \right] + P_2 \left[{a(t),\theta } \right] + } \right. \\ \left. { P_3 \left[{a(t),\theta } \right]} \right) \sin \varphi \\ a(t)\dot {\theta } = - \dfrac{\varepsilon }{\omega }\left( {P_1 \left[ {a(t),\theta } \right] + P_2 \left[{a(t),\theta } \right] +} \right. \\ \left. { P_3 \left[{a(t),\theta } \right]} \right) \cos \varphi \end{array}\!\!\right\} \tag{9}$$ 其中 $$ P_1 \left[{a(t),\theta } \right] = f\cos (\varphi - \theta ) + \sigma a(t)\cos \varphi +\\ 2\mu \omega a(t)\sin \varphi - \alpha a^3(t)\cos ^3\varphi \\ P_2 \left[{a(t),\theta } \right] = - k_{\rm i} {\rm D}_{\rm t}^{1 - \lambda } [a(t)\cos \varphi]\\ P_3 \left[{a(t),\theta } \right] = - k_{\rm d} {\rm D}_{\rm t}^{1 + \delta } [a(t)\cos \varphi] $$
振幅$a$和相位$\theta $是随时间变化的$\varepsilon $的同阶小量,与$\varphi $相比,它们变化缓慢.利用平均法,可以将式(9)在区间$[0,T]$之间进行积分平均,得到振幅$a$和相位$\theta $的近似值. 将式(9)改写为 $$ \dot {a}(t) = - \dfrac{\varepsilon }{T\omega }\int_0^T \left( {P_1 \left[ {a(t),\theta } \right] + P_2 \left[{a(t),\theta } \right] +} \right. \\ \left. { P_3 \left[{a(t),\theta } \right]} \right) \sin \varphi d\varphi \tag{10a}$$ $$ a(t)\dot {\theta } = - \dfrac{\varepsilon }{T\omega }\int_0^T \left( {P_1 \left[{a(t),\theta } \right] + P_2 \left[{a(t),\theta } \right] +} \right.\\ \left. { P_3 \left[{a(t),\theta } \right]} \right) \cos \varphi d\varphi \tag{10b}$$ 如果$P_i \left[{a(t),\theta } \right] (i = 1,2,3)$为周期函数,那么积分终止时间$T$可以取为$T = 2\pi $;如果$P_i \left[{a(t),\theta } \right] (i = 1,2,3)$为非周期函数,那么积分终止时间$T$可以取为 $T = \infty $. 这样,式(10)中的第1部分积分为 $$ \left. \begin{align} & {{{\dot{a}}}_{1}}(t)=-\frac{\varepsilon }{2\pi \omega }\int_{0}^{2\pi }{{{P}_{1}}\left[ a(t),\theta \right]\sin \varphi }d\varphi = \\ & -\frac{\varepsilon f}{2\omega }\sin \theta -\varepsilon \mu a(t) \\ & a(t){{{\dot{\theta }}}_{1}}=-\frac{\varepsilon }{2\pi \omega }\int_{0}^{2\pi }{{{P}_{1}}\left[ a(t),\theta \right]\cos \varphi }\text{d}\varphi = \\ & \frac{3\varepsilon \alpha {{a}^{3}}(t)}{8\omega }-\frac{\varepsilon f}{2\omega }\cos \theta -\frac{\varepsilon \sigma a(t)}{2\omega } \\ \end{align} \right\} \tag{11}$$
为了计算式(10)中的其他部分,引入两个基本公式 $$ \left. \!\! \begin{array}{l} B_1 = \mathop {\lim }\limits_{T \to \infty } \int_0^T {\dfrac{\sin (\omega t)}{t^p}} d t = \omega ^{p - 1}\Gamma (1 - p)\cos \Big(\dfrac{p\pi }{2}\Big) \\ B_2 = \mathop {\lim }\limits_{T \to \infty } \int_0^T {\dfrac{\cos (\omega t)}{t^p}} d t = \omega ^{p - 1}\Gamma (1 - p)\sin \Big (\dfrac{p\pi }{2}\Big) \end{array}\!\!\right\} \tag{12}$$ 这两个公式的求解过程可参见文献[30].
研究式(10a)的第2部分 $$ \dot {a}_2 (t) = - \mathop {\lim }\limits_{T \to \infty } \dfrac{\varepsilon }{T\omega }\int_0^T {P_2 \left[{a(t),\theta } \right]\sin \varphi } d\varphi =\\ - \dfrac{\varepsilon k_{\rm i} a(t)}{2}\omega ^{-\lambda }\sin \Big (\dfrac{1 - \lambda }{2}\pi \Big ) \tag{13a}$$ 利用同样的方法可以得到 $$ a(t)\dot {\theta }_2 = - \mathop {\lim }\limits_{T \to \infty } \dfrac{\varepsilon }{T\omega }\int_0^T P_2 \left[{a(t),\theta } \right]\cos \varphi d\varphi =\\ \dfrac{\varepsilon k_{\rm i} a(t)}{2}\omega ^{ - \lambda }\cos \Big (\dfrac{1 - \lambda }{2}\pi\Big ) \tag{13b}$$
对于式(10a)的第3部分,也可以得到 $$ \dot {a}_3 (t) = - \mathop {\lim }\limits_{T \to \infty } \dfrac{\varepsilon }{T\omega }\int_0^T P_3 \left[{a(t),\theta } \right]\sin \varphi d\varphi =\\ - \dfrac{\varepsilon k_{\rm d} a(t)}{2}\omega ^\delta \cos \Big (\dfrac{\delta }{2}\pi \Big) \tag{14a}$$ $$ a(t)\dot {\theta }_3 = - \mathop {\lim }\limits_{T \to \infty } \dfrac{\varepsilon }{T\omega }\int_0^T P_3 \left[{a(t),\theta } \right]\cos \varphi d\varphi =\\ - \dfrac{\varepsilon k_{\rm d} a(t)}{2}\omega ^\delta \sin \Big( \dfrac{\delta }{2}\pi \Big) \tag{14b}$$
将式(11),式(13)和式(14)联合起来,则有 $$ \left. \begin{align} & \dot{a}(t)=-\frac{\varepsilon f}{2\omega }\sin \theta -\frac{\varepsilon {{k}_{\text{i}}}a(t)}{2}{{\omega }^{-\lambda }}\sin (\frac{1-\lambda }{2}\pi )- \\ & \varepsilon \mu a(t)-\frac{\varepsilon {{k}_{\text{d}}}a(t)}{2}{{\omega }^{\delta }}\cos (\frac{\delta }{2}\pi ) \\ & a(t)\dot{\theta }=\frac{3\varepsilon \alpha {{a}^{3}}(t)}{8\omega }+\frac{\varepsilon {{k}_{\text{i}}}a(t)}{2}{{\omega }^{-\lambda }}\cos (\frac{1-\lambda }{2}\pi )- \\ & \frac{\varepsilon f}{2\omega }\cos \theta -\frac{\varepsilon \sigma a(t)}{2\omega }-\frac{\varepsilon {{k}_{\text{d}}}a(t)}{2}{{\omega }^{\delta }}\sin (\frac{\delta }{2}\pi ) \\ \end{align} \right\} \tag{15}$$
将原系统参数代入式(15),则得到 $$ \left. \!\! \begin{array}{l} \dot {a}(t) = - \dfrac{F_1 }{2m\omega }\sin \theta - \dfrac{a(t)}{2m}\left( {c + C(P) + } \right. \\ \left. { C(I) + C(D)} \right) \\ \dot {\theta } = - \dfrac{F_1 }{2m\omega a(t)}\cos \theta + \dfrac{3\alpha _1 a^2(t)}{8m\omega } - \dfrac{\omega }{2} +\\ \dfrac{1}{2\omega }\left( {\dfrac{k}{m} + \dfrac{K(I)}{m} - \dfrac{M(D)}{m}\omega ^2} \right) \end{array} \!\! \right\} \tag{16}$$ 其中,5个新的参数为 $$ \left. \!\! \begin{array}{l} C(P) = K_{\rm p} \\ C(I) = K_{\rm i} \omega ^{ - \lambda }\cos \Big (\dfrac{\lambda }{2}\pi \Big) \\ C(D) = K_{\rm d} \omega ^\delta \cos \Big (\dfrac{\delta }{2}\pi\Big ) \\ K(I) = K_{\rm i} \omega ^{1 - \lambda }\sin \Big (\dfrac{\lambda }{2}\pi \Big) \\ M(D) = K_{\rm d} \omega ^{\delta - 1}\sin \Big (\dfrac{\delta }{2}\pi \Big) \end{array}\!\! \right\} \tag{17}$$
这样就得到了系统的近似解析解.式(16)表明,在系统(3)中,分数阶比例-积分-微分控制通过参数$C(P),C(I), C(D)$增大了系统的阻尼,可以将参数$C(P),C(I), C(D)$分别定义为比例环节、积分环节、微分环节引起的等效线性阻尼;通过参数$K(I)$增大了系统的线性刚度,可以将参数$K(I)$定义为等效线性刚度;通过参数$M(D)$增大了系统的质量,可以将参数$M(D)$定义为等效质量.分数阶比例--积分--微分控制器的比例环节系数$K_{\rm p}$增大了系统的线性阻尼;积分环节不但通过$K_{\rm i } \omega ^{ - \lambda }\cos ( \lambda \pi /2)$增大了系统的线性阻尼,还通过$K_{\rm i } \omega ^{1 - \lambda }\sin ( \lambda \pi /2)$增大了系统的线性刚度及固有频率;微分环节不但通过$K_{\rm d } \omega ^\delta \cos ( \delta \pi/2 )$增大了系统的阻尼,还通过$K_{\rm d }\omega ^{\delta - 1}\sin ( \delta \pi/2 )$增大了系统的质量,降低了系统的固有频率.
分数阶比例--积分--微分控制器所起的作用不仅与控制器的输入量有关,还取决于系数$K_{\rm p}$,$K_{\rm i}$,$K_{\rm d}$以及分数阶阶次 $\lambda $ 和 $\delta $. 比例环节通过$K_{\rm p}$调节系统的线性阻尼. 积分环节通过$K_{\rm i}$和 $\lambda $ 调节系统的动力学特性:当$\lambda = 0$时,积分环节退化为线性阻尼$K_{\rm i}$,不影响系统的固有频率;当$\lambda $从0增大到1的过程,积分环节逐渐过渡为线性刚度;当$\lambda = 1$时,积分环节不再影响系统的阻尼,仅增大系统的固有频率. 微分环节通过$K_{\rm d}$和 $\delta $ 调节系统的动力学特性:当$\delta = 0$时,微分环节退化为线性阻尼$K_{\rm d}$,不影响系统的固有频率;当 $\delta $ 从0变为1的过程,微分环节逐渐过渡为线性质量;当$\delta = 1$时,不再影响系统的阻尼,仅降低系统的固有频率.
2 定常解和稳定性分析为了确定系统对应稳态运动的定常解振幅$\bar {a}$和相位$\bar {\theta }$,令式(16)中的$\dot {a}(t) = 0$和$\dot {\theta } = 0$,则有
$$\bar {a}\left( {c + C(P) + C(I) + C(D)} \right) = - \dfrac{F_1 }{\omega }\sin \bar {\theta } \tag{18a}$$
$$\bar {a}\left( {\dfrac{3\alpha _1 \bar {a}^2}{4\omega } - m\omega + \dfrac{k}{\omega } + \dfrac{K(I)}{\omega } - M(D)\omega } \right) =$$$$ \dfrac{F_1 }{\omega }\cos \bar {\theta } \tag{18b}$$ 式(18a)和(18b)两式平方后相加,得到幅频响应方程
$$ \bar {a}^2\left( {\dfrac{3\alpha _1 \bar {a}^2}{4\omega } - m\omega + \dfrac{k}{\omega } + \dfrac{K(I)}{\omega } - M(D)\omega } \right)^2 +$$ $$ \bar {a}^2\left( {c + C(P) + C(I) + C(D)} \right)^2 = \Big(\dfrac{F_1 }{\omega }\Big)^2 \tag{19}$$ 以及相频响应方程 $$ \bar {\theta } = {\rm arc} \tan \left( { - \dfrac{c + C(P) + C(I) + C(D)}{\dfrac{3\alpha _1 \bar {a}^2}{4\omega } - m\omega + \dfrac{k}{\omega } + \dfrac{K(I)}{\omega } - M(D)\omega }} \right) \tag{20}$$ 稳态振幅的最大值为 $$ \bar {a}_{\max } = \left| {\dfrac{F_1 }{\omega \left( {c + C(P) + C(I) + C(D)} \right)}} \right| \tag{21}$$ 该值与激励振幅、稳态振幅出现峰值的激励频率(即共振频率)、系统的线性阻尼和比例环节、积分环节以及微分环节的等效线性阻尼有关. 由式(19)得到 $$ \omega = \sqrt {\dfrac{3\alpha _1 \bar {a}^2 + 4m\omega _0^2 + 4K(I)}{4m + 4M(D)}} \tag{22}$$ 该式确定的曲线称为主共振的骨架线,将式(21)中的$\bar {a}_{\max } $代入式(22)就可以确定出现峰值的激励频率,显然与非线性因素有关,而且与积分环节的等效线性刚度及微分环节的等效质量有关.
下面对定常解的稳定性进行分析,引入$a(t) = \bar {a} + \Delta a$和$\theta = \bar {\theta } + \Delta \theta $,代入式(16),进行线性化处理,得到 $$ \dfrac{d\Delta a}{d t} = - \dfrac{c + C(P) + C(I) + C(D)}{2m}\Delta a -$$ $$ \dfrac{F_1 }{2m\omega }\cos \bar {\theta } \Delta \theta \tag{23a}$$ $$ \dfrac{d\Delta \theta }{d t} = \left( {\dfrac{3\alpha _1 \bar {a}}{4m\omega } + \dfrac{F_1 }{2m\omega \bar {a}^2}\cos \bar {\theta } } \right)\Delta a +$$ $$ \dfrac{F_1 \sin \bar {\theta } }{2m\omega \bar {a}}\Delta \theta \tag{23b}$$ 利用式(18)消去上式中的$\bar {\theta }$,得到特征行列式 $$ \det \left[\begin{array}{ll} - \dfrac{C}{2m} - \lambda & - \dfrac{\bar {a}}{2m}A \\ \dfrac{B}{2m\bar {a}} & - \dfrac{C}{2m} - \lambda \end{array} \right] = 0 \tag{24}$$ 其中 $$ C = c + C(P) + C(I) + C(D) \\ A = \dfrac{3\alpha _1 \bar {a} ^2}{4\omega } - m\omega + \dfrac{k}{\omega } + \dfrac{K(I)}{\omega } - M(D)\omega \\ B = \dfrac{9\alpha _1 \bar {a} ^2}{4\omega } - m\omega + \dfrac{k}{\omega } + \dfrac{K(I)}{\omega } - M(D)\omega $$ 展开式(24),得到特征方程 $$ \lambda ^2 + \dfrac{C}{m}\lambda + Q = 0 \tag{25}$$ 其中,$Q = \dfrac{C^2}{4m^2} + \dfrac{AB}{4m^2}$. 由于$C > 0$,因此定常解的稳定条件为 $$ Q > 0 \tag{26}$$ 该条件表明,当幅频曲线方程存在3个定常解时,中间的一支解是不稳定的.
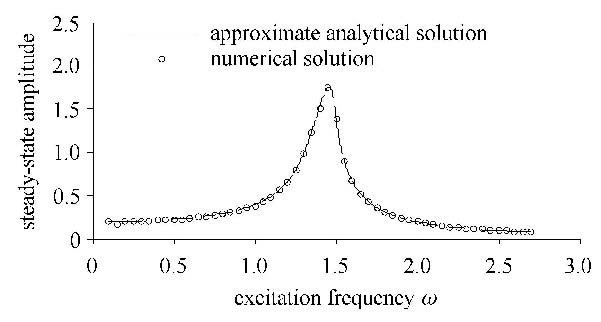
3 近似解析解和数值解的比较研究系统(3),选取一组基本参数,$m = 5$,$k = 10$,$c = 0.3$,$\alpha _1 = 0.3$,$K_{\rm p} = 0.2$,$K_{\rm i} = 0.2$,$K_{\rm d} = 0.2$,$\lambda = 0.6$,$\delta = 0.4$,$F_1 = 2$,根据式(19)可以画出系统的主共振幅频响应曲线,如图2中实线所示,图中横轴为激励频率 $\omega $,纵轴为响应振幅$a$. 为了进行比较,本文采用文献[6]中介绍的幂级数法计算系统(3),其计算公式为 $$ {\rm D}^p[y(t_n )] \approx h^{ - p}\sum_{j = 0}^n {C_j^p y(t_{n - j} )} \tag{27}$$ 其中$t_n = n\ast h$为时间采样点,$h$为时间步长,$C_j^p $为分数阶二项式系数,并且具有下述递推关系 $$ C_0^p = 1 ,C_j^p = \left( {1 - \dfrac{1 + p}{j}} \right)C_{j - 1}^p \tag{28}$$ 根据式(27)和(28),系统(3)可以表示为 $$x(t_n ) = y(t_{n - 1} )h - \sum_{j = 1}^n {C_j^1 x(t_{n - j} )} \tag{29a}$$ $$ y(t_n ) = \Big [F_1 \cos (\omega t_n ) - \alpha _1 x^3(t_n ) - kx(t_n ) - $$ $$ (c + K_{\rm p} )y(t_{n - 1} ) - K_{\rm i} z_1 (t_{n - 1} ) -$$ $$ K_{\rm d} z_2 (t_{n - 1} ) \Big]\dfrac{h}{m} - \sum_{j = 1}^n {C_j^1 y(t_{n - j} )} \tag{29b}$$ $$z_1 (t_n ) = \left[{y(t_n )} \right]h^\lambda - \sum_{j = 1}^n {C_j^\lambda z_1 (t_{n - j} )} \tag{29c}$$ $$ z_2 (t_n ) = \Big [F_1 \cos (\omega t_n ) - \alpha _1 x^3(t_n ) - kx(t_n ) -$$ $$ (c + K_{\rm p} )y(t_n ) - K_{\rm i} z_1 (t_n ) -$$ $$ K_{\rm d} z_2 (t_{n - 1} ) \Big]\dfrac{h^{1 - \delta }}{m} - \sum_{j = 1}^n {C_j^{1 - \delta } z_2 (t_{n - j} )} \tag{29d}$$ 计算过程中时间步长$h = 0.005$,分数阶项的初值设定如下[31] $$ \left.\!\!\begin{array}{l} {\rm D}_t^{1 - \lambda } [x(0)] = a_0 \cos \Big (\dfrac{1 - \lambda }{2}\pi \Big) \\ {\rm D}_t^{1 + \delta } [x(0)] = a_0 \cos \Big (\dfrac{1 + \delta }{2}\pi\Big ) \end{array}\!\!\right\} \tag{30}$$ 计算时间为150 s,并取后60 s响应的最大值作为响应振幅,所得数值计算结果也显示在图2中,以圆圈表示.由图2可见,数值解和近似解析解二者具有较高的符合度.
|
图2 数值解和近似解析解比较 Fig.2 Comparison of numerical solution and approximate analytical solution |
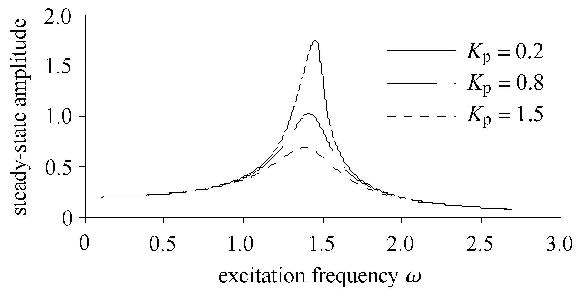
下面分别分析分数阶比例-积分-微分控制器的系数$K_{\rm p}$,$K_{\rm i}$,$K_{\rm d}$以及分数阶阶次 $\lambda $ 和 $\delta $ 变化时,对主共振振幅的影响.在系统(3)中,分数阶比例-积分-微分控制器的比例环节系数$K_{\rm p}$分别取0.2,0.8,1.5时,系统的幅频响应曲线如图3所示.
|
图3 $K_{\rm p}$变化时的幅频曲线 Fig.3 Amplitude-frequency curves with different $K_{\rm p}$ |
从图3中可以看出,随着$K_{\rm p}$的增大,系统(3)的最大响应幅值即共振振幅逐渐减小,共振频率略有减小,说明系统(3)的线性阻尼增大了.因此,增大比例系数$K_{\rm p}$可以增大系统的线性阻尼,减小系统的共振振幅.
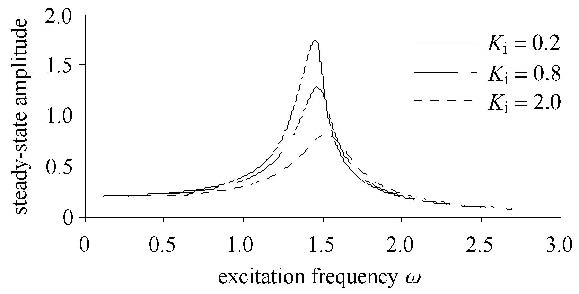
在系统(3)中,积分环节系数$K_{\rm i}$分别取0.2,0.8,2时,系统的幅频响应曲线如图4所示. 从图4中可以看出,随着$K_{\rm i}$的增大,系统(3)的共振频率略有增大,共振振幅逐渐减小.在系统(3)的质量保持不变的情况下,说明系统(3)的线性刚度增大了;系统(3)的共振振幅逐渐减小,说明系统(3)的共振频率或线性阻尼增大了. 由式(16)可知,系统(3)的线性阻尼和线性刚度同时增大了. 因此,增大积分环节系数$K_{\rm i}$可以同时增大系统的线性刚度和线性阻尼,减小系统的共振振幅.
|
图4 $K_{\rm i}$变化时的幅频响应曲线 Fig.4 Amplitude-frequency curves with different $K_{\rm i}$ |
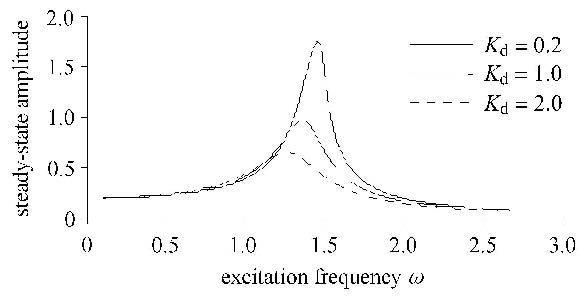
在系统(3)中,微分环节系数$K_{\rm d}$分别取0.2,1,2时,系统的幅频响应曲线如图5所示. 从图5中可以看出,随着$K_{\rm d}$的增大,系统(3)的共振频率逐渐减小. 由式(16)和(22)可知,系统(3)的质量增大了,非线性因素的作用减小了,从而导致共振频率减小了;系统(3)的共振振幅逐渐减小,说明系统(3)的线性阻尼增大了. 可见,增大微分环节系数$K_{\rm d}$降低了系统的共振频率,但同时增大了系统的线性阻尼,从而减小了系统的共振振幅.
|
图5 $K_{\rm d}$变化时的幅频响应曲线 Fig.5 Amplitude-frequency curves with different $K_{\rm d}$ |
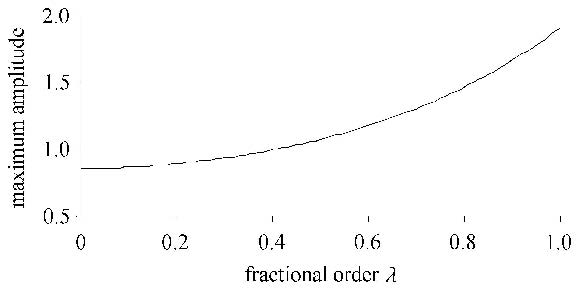
在系统(3)中,根据式(16)可知,积分环节的分数阶阶次 $\lambda $ 和系数$K_{\rm i}$将共同调节积分环节的作用. 为了更直观的分析 $\lambda $ 的作用,令$K_{\rm i} =1$,分数阶阶次 $\lambda $ 从0到1变化时得到系统的最大响应振幅如图6所示. 从图6中可以看出,随着 $\lambda $ 的增大,系统(3)的共振振幅逐渐增大. 由式(16)和(22)可知,系统(3)的共振频率略有增大,线性阻尼逐渐减小.可见,积分环节分数阶阶次 $\lambda $ 调整了积分环节的作用,同时会影响积分环节系数$K_{\rm i}$的作用;减小 $\lambda $ 虽然减小了系统的共振频率,但同时增大了系统的线性阻尼,从而减小了系统的共振振幅.
|
图6 $\lambda $ 变化时的最大响应振幅曲线 Fig.6 Maximum response amplitude curve with $\lambda $ |
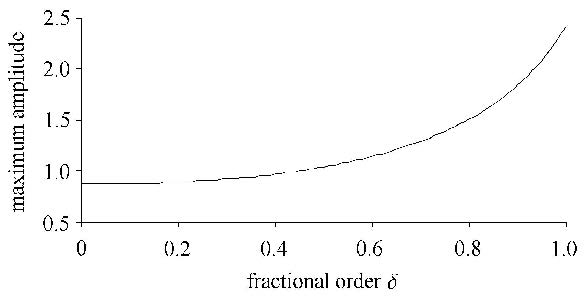
在系统(3)中,根据式(16)可知,微分环节的分数阶阶次 $\delta $ 和系数$K_{\rm d}$将共同调节微分环节的作用. 为了更直观地分析 $\delta $ 的作用,令$K_{\rm d} =1$,分数阶阶次 $\delta $ 从0到1变化时得到系统的最大响应振幅曲线如图7所示. 从图7中可以看出,随着 $\delta $ 的增大,系统(3)的共振振幅逐渐增大.由式(16)和(22)可知,系统(3)的共振频率先逐渐减小后略有增大,线性阻尼逐渐减小. 可见,微分环节分数阶阶次 $\delta $ 调整了微分环节的作用,同时会影响微分环节系数$K_{\rm d}$的作用;减小 $\delta $ 可以增大系统的线性阻尼并调整共振频率,减小系统的共振振幅.
|
图7 $\delta $ 变化时的最大响应振幅曲线 Fig.7 Maximum response amplitude curve with $\delta $ |
经过对分数阶比例-积分-微分控制器的控制参数分析,发现当仅以衰减共振振幅为控制目标时,取$\lambda = 0$和$\delta = 0$,分数阶比例-积分-微分控制器退化成包含3个比例环节的基于速度反馈的比例控制器,而且可以达到较好的控制效果.但是基于速度反馈的比例控制器增大了系统的阻尼比,随着阻尼比的增大,单独使用比例控制器可能会使系统的响应速度变慢.若综合考虑系统响应的快速性与准确性,控制器应包含积分环节与微分环节.下面对相同系数的分数阶与整数阶比例-积分-微分控制的效果进行比较. 取$K_{\rm p} = 0.2$,$K_{\rm i} = 0.2$,$K_{\rm d} = 0.2$,当 $\lambda = 1$,$\delta = 1$时,分数阶比例-积分-微分控制器转变为传统的整数阶比例-积分-微分控制器;分数阶比例-积分-微分控制器的阶次取$\lambda = 0.5$,$\delta = 0.5$,系统的幅频响应曲线如图8所示.从图8中可以看出,分数阶比例-积分-微分控制对达芬振子主共振振幅的控制效果要好于整数阶比例-积分-微分控制.

|
图8 分数阶与整数阶比例-积分-微分的控制效果比较 Fig.8 Comparison between the control performances of FOPID with integer-order PID |
本文研究了基于速度反馈分数阶比例-积分-微分控制的达芬振子的主共振,从理论上分析了基于速度反馈的分数阶比例-积分-微分控制对系统动力学的影响.由于平均法可以分别求解系统的线性项、非线线项和分数阶微积分项的近似解析解,因此本文得到的分数阶比例-积分-微分控制的解析表达式可以直接应用到其它基于速度反馈分数阶比例-积分-微分控制系统的主共振分析中.详细分析了分数阶比例-积分-微分控制的系数$K_{\rm p}$,$K_{\rm i}$,$K_{\rm d}$以及分数阶阶次 $\lambda $ 和 $\delta $ 变化时,对系统主共振振幅的影响,为基于速度反馈的分数阶比例-积分-微分控制对达芬振子的主共振进行控制时,控制器的参数整定提供了理论依据,同时为类似非线性系统的主共振振动控制提供了参考.对分数阶比例-积分-微分控制和传统整数阶比例-积分-微分控制的控制效果进行了比较,发现当控制器的系数$K_{\rm p}$,$K_{\rm i}$,$K_{\rm d}$相同时,基于速度反馈的分数阶比例-积分-微分控制对达芬振子主共振振幅的控制效果要优于传统整数阶比例-积分-微分控制.
| 1 | 李海斌, 毕世华, 方远等. 振动主动控制技术现状及发展. 振动与冲击, 1998, 17(3):38-42(Li Haibin, Bi Shihua, Fang Yuanqiao, et al. An overview and assessment on active vibration control. Journal of Shock and Vibration, 1998, 17(3):38-42(in Chinese)) |
| 2 | 曹青松, 洪芸芸, 周继惠等. 基于PSO 自整定PID 控制器的柔性臂振动控制. 振动、测试与诊断, 2014, 34(6):1045-1049(Cao Qingsong, Hong Yunyun, Zhou Jihui, et al. Vibration control of flexible manipulator based on self-tuning PID controller by PSO. Journal of Vibration,Measurement & Diagnosis, 2014, 34(6):1045-1049(in Chinese)) |
| 3 | Thenozhi S, Yu W. Stability analysis of active vibration control of building structures using PD/PID control. Engineering Structures, 2014, 81:208-218 |
| 4 | Zhou LW, Chen GP. Intelligent vibration control for high-speed spinning beam based on fuzzy self-tuning PID controller. Shock and Vibration, 2015, ID:617038 |
| 5 | 周兵, 赵保华. 汽车主动悬架自适应模糊PID 控制仿真研究. 湖南大学学报(自然科学版), 2009, 32(16):27-30(Zhou Bing, Zhao Baohua. Simulation study of self-adaptive fuzzy-PID control of active suspension. Journal of Hunan University, 2009, 32(16):27-30(in Chinese)) |
| 6 | Petras I. Fractional-Order Nonlinear Systems. Beijing:Higher Education Press, 2011 |
| 7 | Podlubny I. Fractional Differential Equations, Mathematics in Science and Engineering. New York:Academic Press, 1999 |
| 8 | Shen YJ, Yang SP, Xing HJ, et al. Primary resonance of Duffing oscillator with fractional-order derivative. Communication in Nonlinear Science and Numerical Simulation, 2012, 17(7):3092-3100 |
| 9 | 申永军, 杨绍普, 邢海军. 分数阶Duffing 振子的超谐共振. 力学学报, 2012, 44(4):762-767(Shen Yongjun, Yang Shaopu, Xing Haijun. Super-harmonic response of fractional-order Duffing oscillator. Chinese Journal of Theoretical and Applied Mechanics, 2012, 44(4):762-767(in Chinese)) |
| 10 | Yang SP, Shen YJ. Recent advances in dynamics and control of hysteretic nonlinear systems. Chaos Solitons and Fractals, 2009, 40(4):1808-1822 |
| 11 | Li CP, Deng WH. Remarks on fractional derivatives. Applied Mathematics and Computation, 2007, 187(1):777-784 |
| 12 | Chen LC, Zhu WQ. Stochastic jump and bifurcation of Duffing oscillator with fractional derivative damping under combined harmonic and white noise excitations. International Journal of Non-Linear Mechanics, 2011, 46(10):1324-1329 |
| 13 | 曹建雄, 丁恒飞, 李常品. 分数阶扩散方程的隐差分格式. 应用数学与计算数学学报, 2013, 27(1):61-74(Cao Jianxiong, Ding Hengfei, Li Changpin. Implicit difference schemes for fractional diffusion equations. Communication on Applied Mathematics and Computation, 2013, 27(1):61-74(in Chinese)) |
| 14 | Agrawal OP. A quadratic numerical scheme for fractional optimal control problems. Journal of Dynamic Systems Measurement and Control, Transactions of the ASME, 2008, 130(1):011010.1-011010.6 |
| 15 | Chen JH, Chen WC. Chaotic dynamics of the fractionally damped van der Pol equation. Chaos, Solitons and Fractals, 2008, 35(1):188-198 |
| 16 | 吴光强, 黄焕军, 叶光湖. 基于分数阶微积分的汽车空气悬架半主动控制. 农业机械学报, 2014, 45(7):19-24(Wu Guangqiang, Huang Huanjun, Ye Guanghu. Semi-active control of automotive air suspension based on fractional calculus. Transactions of the Chinese Society for Agricultural Machinery, 2014, 45(7):19-24(in Chinese)) |
| 17 | 李媛萍, 张卫, 欧阳东. 具有分数导数本构关系的粘弹性浅拱的非线性动力学行为. 振动工程学报, 2012, 25(3):342-350(Li Yuanping, Zhang Wei, Ouyang Dong. Nonlinear dynamic behaviors of viscoelastic shallow arch with fractional derivative constitutive relationship. Journal of Vibration Engineering, 2012, 25(3):342-350(in Chinese)) |
| 18 | Podlubny I. Fractional-order systems and PIλDμ-controllers. IEEE Transactions on Automatic Control, 1999, 44(1):208-214 |
| 19 | 陈宁, 陈南, 王乃洲等. 基于分数阶参考模型的车辆悬架自适应控制. 南京林业大学学报, 2009, 33(3):247-253(Chen Ning, Chen Nan, Wang Naizhou, et al. Adaptive control of vehicle suspension using fractional order reference models. Journal of Nanjing Forestry University, 2009, 33(3):116-120(in Chinese)) |
| 20 | 赵春娜, 赵雨, 张祥德等. 分数阶控制器与整数阶控制器仿真研究. 系统仿真学报, 2009, 21(3):768-775(Zhao Chunna, Zhao Yu, Zhang Xiangde, et al. Simulation research on fractional order controllers with integer order controllers. Journal of System Simulation, 2009, 21(3):768-775(in Chinese)) |
| 21 | Chen YQ, Petras I, Xue DY. Fractional order control-a tutorial.2009 Conference on American Control Conference, 2009 American Control Conference, St. Louis, MO, USA, 2009-6-10-12. Piscataway:IEEE Press, 2009. 1397-1411 |
| 22 | Ostalczyk PW, Duch P, Brzeziski DW, et al. Order functions selection in the variable-, fractional-order PID controller. Advances in Modelling and Control of Non-integer Order Systems, 6th Conference on Non-integer Order Calculus and Its Applications, Opole, Poland, 2014-11-6-6. New York:Springer Verlag, 2015. 159-170 |
| 23 | 薛定宇, 赵春娜. 分数阶系统的分数阶PID 控制器设计. 控制理论与应用, 2007, 24(5):771-775(Xue Dingyu, Zhao Chunna. Fractional order PID controller design for fractional order system. Control Theory & Applications, 2007, 24(5):771-775(in Chinese)) |
| 24 | 曹军义, 谢航, 蒋庄德. 分数阶阻尼Duffing 系统的非线性动力学特性. 西安交通大学学报, 2009, 43(3):50-53(Cao Junyi, Xie Hang, Jiang Zhuangde. Nonlinear dynamics of Duffing system with fractional order damping. Journal of Xi'An Jiaotong University, 2009, 43(3):50-53(in Chinese)) |
| 25 | 黄建亮, 黄惠仪, 陈恒等. 梁的强非线性超、次谐波共振. 振动与冲击, 2004, 23(1):1-3(Huang Jianliang, Huang Huiyi, Chen Heng, et al. Superharmonic and subharmonic resonances of strongly nonlinear vibration of beams. Journal of Shock and Vibration, 2004, 23(1):1-3(in Chinese)) |
| 26 | 刘灿昌, 裘进浩, 孙慧玉等. 悬臂梁智能结构主共振响应的最优化控制. 中国机械工程, 2013, 24(12):1600-1604(Liu Canchang, Qiu Jinhao, Sun Huiyu, et al. Optimal control of primary resonance of smart structures of cantilever beams. China Mechanical Engineering, 2013, 24(12):1600-1604(in Chinese)) |
| 27 | Zillettia M, Elliotta SJ, Gardoniob P, et al. Experimental implementation of a self-tuning control system for decentralised velocity feedback. Journal of Sound and Vibration, 2012, 331(1-2):1-14 |
| 28 | 石秀东, 钱林方, 陈龙淼. 基于加速度和速度反馈的半主动减振系统控制策略研究. 南京理工大学学报(自然科学版), 2005, 29(5):556-559(Shi Xiudong, Qian Linfang, Chen Longmiao. Semi-active vibration control strategy based on acceleration and velocity feedback. Journal of Nanjing University of Science and Technology, 2005, 29(5):556-559(in Chinese)) |
| 29 | Zhang T, Li HG, Cai GP, et al. Experimental verifications of vibration suppression for a smart cantilever beam with a modified velocity feedback controller. Shock and Vibration, 2014:172570 |
| 30 | 申永军, 杨绍普, 邢海军. 含分数阶微分的线性单自由度振子的动力学分析. 物理学报, 2012, 61(11):110505(Shen Yongjun, Yang Shaopu, Xing Haijun. Dynamical analysis of linear single degreeof-freedom oscillator with fractional-order derivative. Acta Physica Sinica, 2012, 61(11):110505(in Chinese)) |
| 31 | Shen YJ, Yang SP, Sui CY. Analysis on limit cycle of fractionalorder van der Pol oscillator. Chaos, Solitons & Fractals, 2014, 67:94-102 |
 2016, Vol. 48
2016, Vol. 48