随机性作为一种客观实在,普遍存在于各种物理和力学系统之中. 对于随机动力系统的分析,是现代力学研究的一个重要分支. 如何处理多维复杂非线性随机动力系统,是研究中的热点问题.
近年来,李杰、陈建兵从概率守恒的基本原理出发,发展了概率密度演化分析理论,建立了广义概率密度演化方程(GDEE),为复杂非线性随机动力系统的分析提供了一条可行的途径[1, 2, 3, 4, 5]. 已有的工作证明,这一新的分析理论在线性与非线性系统的随机动力反应分析[6]、结构动力可靠度计算[7, 8]、结构随机最优控制[9]等方面均可获得高效、准确的分析结果.
经过十余年的研究,已逐步形成了一套完整的基于概率空间剖分和有限差分方法的广义概率密度演化方程数值求解理论体系[10, 11]. 在这一背景下,为了将这一分析理论推广到更为一般的随机动力系统,使之适用于更为广泛的物理系统乃至化学、生物系统,就有必要继续深入地研究广义概率密度演化方程的解析解,从而为更加广阔的研究奠定基础. 为此,本文试图对一些典型的随机动力系统,采用李群分析方法,得出若干典型随机物理系统的概率密度解析解,为进一步发展随机动力系统分析方法提供统一的校核标准和依据.
1 广义概率密度演化方程不失一般性,考察随机动力系统 $$ \dot { X} ={ G}({ X},{\varTheta},t) ,\dot{ X}(t_0 ) = { x}_0 \tag{1} $$ 式中,${ X} = ({X}_1 ,{X}_2 ,\cdots ,{X}_{n} )^ {\rm T}$,$ {n}$是物理系统的维数;${ G}( \cdot )$为一般非线性系统,${\varTheta} = ({\varTheta }_1 ,{\varTheta }_2 ,\cdots ,{\varTheta }_{s} )^{\rm T}$,其联合概率密度函数为${p}_\varTheta ({\theta})$,${s}$是系统中随机变量的总个数;${ x}_0 = ({x}_1 ,{x}_2 ,\cdots ,{x}_{n} )^{\rm T}$是系统的初始条件.
通常,对于适定的动力学系统,方程(1)的解答存在、唯一且连续地依赖于初始条件. 即对于给定的初始条件,式(1)的解可以写为 $$ { X}={ H}({ \varTheta},{t}) \tag{2} $$ 在实际问题中,所关心的物理量可能是${ X}$和$\dot { X}$的函数. 一般地,它们可以表达为 $$ { Z} ={ H}_Z ({\varTheta},{t}) \tag{3} $$ 其时间变化率为 $$ \dot{ Z} = \dfrac{\partial { H}_Z ({\varTheta},{t})}{\partial {t}} = { h}_Z ({\varTheta},{t}) \tag{4} $$
对于保守的随机动力系统,由概率守恒原理可得[3] $$ \dfrac{{\rm D}}{{\rm D}t}\int_{\Omega _t \times \Omega _\varTheta } p_{Z\varTheta } ({ z},{\theta },t) d { z} d {\theta} = 0 \tag{5} $$ 式中$p_{Z\varTheta } ({ z},{\theta},t)$是$({ Z}(t),{\varTheta } )$的联合概率密度函数,$\Omega _t \times \Omega _\varTheta $表示在初始时刻区域$\Omega _{t_0 } \times \Omega _\varTheta $经时间$t$后所到达的区域. 由式(5)可导出如下广义概率密度演化方程[1, 3] $$ \dfrac{\partial p_{Z\varTheta } ({ z},{\theta},t)}{\partial t} + \sum_{j = 1}^m \dot {Z}_j ({\theta},t)\dfrac{\partial p_{Z\varTheta } ({ z},{\theta},t)}{\partial z_j } = 0 \tag{6} $$ 其初始条件为 $$ p_{Z\varTheta } ({ z},{\theta},t_0 ) = \delta ({ z} -{ H}_Z ({\theta},t_0 ))p_\varTheta ({\theta} ) \tag{7} $$
对于由式(6)和式(7)组成的偏微分方程,可以采用特征线法将其转换为沿着特征线的常微分方程求解[12]. 即有 $$ p_{Z\varTheta } ({ z},{\theta},t_0 ) = \delta ({ z} - { H}_Z ({\theta},t_0 )) \cdot p_\varTheta ({\theta} ) \tag{8} $$ 对式(8)关于随机变量积分,即可得${ Z}$的概率密度函数 $$ p_{Z\varTheta } ({ z},t) = \int_{\Omega _\varTheta } \delta ({ z} -{ H}_Z ({\theta},t)) \cdot p_\varTheta ({\theta} ) d{\theta} \tag{9} $$ 结合复合Dirac函数的转化法则和Dirac函数的筛选性质[13],式(9)可进一步转化为 $$ p_{Z\varTheta } ({ z},t) = \sum_{i = 1}^{N_{\rm sol} } \left| { J} \right|^{-1} p_\varTheta (\tilde {\theta }_j ({ z},t)) \tag{10} $$ 式中,${ J}$为雅克比矩阵,$\tilde {\theta }_j ({ z},t)$为${ z} -{ H}_Z ({\theta},t) = 0$的根轨迹,$N_{\rm sol} $为${ z}-{ H}_Z ({\theta} ,t) = 0$的根轨迹个数,$\Omega_{\varTheta _i } $为$\Omega _\varTheta $区域中对应于$i$的不同积分域.
2 求解非线性系统解析解的李群方法显然,根据式(10),求解广义概率密度演化方程解析解的一个重要基础是首先求取对应物理系统的解析解.
对于非线性微分方程的解析求解,自19世纪30年代泊松(Poisson)提出摄动法的基本思想以来,已取得了一系列卓有成效的进展,先后提出了平均法[14]、KBM法[15]、多尺度法[16]等求解方法[17]. 然而,上述方法均将非线性因素作为对线性系统的一种摄动,从而在线性系统解的基础上求得非线性系统的近似解. 因此,其研究对象多局限于非线性项为小量的弱非线性系统,属于近似解析方法.
李群方法(Lie group method) 是现代非线性微分方程研究的核心. 大量的证据表明,群理论是求解非线性微分方程解析解的通用和有效的方法[18]. 根据李群理论,只要常微分方程接受一个李群,则该方程便可通过坐标变换降低一阶,甚至将非线性微分方程变换为线性微分方程,从而求得其解析解. 使用李群方法求解非线性微分方程可遵循下列步骤[19].
(1) 寻找方程的无穷小生成元以计算二阶方程 $$ {y}" = f({x},{y},{y}') \tag{11} $$ 的无穷小生成元为例. 方程(11)所容许的无穷小生成元 $$ {\rm X} = {\xi }({x},{y})\dfrac{\partial }{\partial {x}} + {\eta }({x},{y})\dfrac{\partial }{\partial {y}} \tag{12} $$ 可以从下列称为决定方程的方程得到 $$ {X}({y}" -{f}({x},{y},{y}')) |_{y"=f} \equiv \\ ( {\zeta }_2 - {\zeta }_1 {f}_{{y}'} - \xi f_{x} - \eta f_{y} )|_{{y}" =f} = 0 \tag{13} $$ 式中符号$ |_{{y}" =f} $是指${y}"$在对应的表达式中被方程(11)的右边取代,而式中${\zeta }_1 $和${\zeta }_2 $则由延拓方程决定 $$ \left.\!\! {\zeta }_1 = {D}_{x} ({\eta }) - {{y}'D}_{x} ({\xi }) =\\ {\eta }_{x} + ({\eta }_{y} - {\xi }_{x} ) {y}' - {\xi }_{y} {y}'^2 \\ {\zeta }_2 = {D}_{x} ({\zeta }_1 ) - {y}"D_{x} ({\xi }) =\\ {\eta }_{ xx} + (2{\eta }_{ xy} - {\xi }_{ xx } ) {y}' + ({\eta }_{ yy } - 2{\xi }_{ xy } ){ y}'^2 -\\ {\xi }_{{yy}} {{y}'}^3 + ({\eta }_{y} - 2{\xi }_{x} - 3{\xi }_{y} {y}'){y}" \!\!\right\} \tag{14} $$ 将式(14)代入决定方程(13)中,得到 $$ {\eta }_{xx} + (2{\eta }_{xy} - {\xi }_{xx} ){y}' + ({\eta }_{yy} - 2{\xi }_{xy} ){y}'^2 -\\ {\xi }_{yy} {y}'^3 - \xi f_{x} - \eta f_{y} + ({\eta }_{y} - 2{\xi }_{x} - 3{\xi }_{y} {y}'){f} -\\ [{\eta }_{x} + ({\eta }_{y} - {\xi }_{x} ){y}'- {y}'^2{\xi }_{y}]{f}_{y'} = 0 \tag{15} $$ 上式包含所有3个变量${x}$,${y}$和${y}'$,但是${y}'$并不出现在${\xi }$和${\eta }$中. 因此,决定方程(15)可以分解成几个方程从而转换为对未知函数${\xi }$和${\eta }$的超静定微分方程组. 求解这个方程组即可得到方程(11)的所有无穷小生成元.
(2) 将无穷小生成元转换为典型变量对方程所容许的无穷小生成元 $$ {\rm X}_{i} = {\xi }_{i} ({x},{y})\dfrac{\partial }{\partial {x}} + {\eta }_{i} ({x},{y})\dfrac{\partial }{\partial {y}} \tag{16} $$ 使用李括号进行计算,将结果代入4种标准形式组成的表格中进行匹配,可判断其所属类型. 将无穷小生成元代入所属类型下的方程组,可解得典型变量 $$ {t} = {t}({x},{y}) ,{u} = {u}({x},{y}) \tag{17} $$
(3) 根据典型变量求解非线性方程根据典型变量(17)对原方程(11)进行变量替换使其转化为可积形式 $$ \dfrac{d^2{u}}{d{t}^2} = g(t)\dfrac{d{u}}{d{t}} \tag{18} $$ 求解方程(18),将求得的解通过典型变量(17)返回原始变量取得到原方程的解.
以下,将利用李群方法和广义概率密度演化方程的特征线解(10),求取若干典型随机动力系统的解析解.
3 Van der Pol振子 3.1 物理系统解Van der Pol振子是非线性系统的经典模型之一. 它起源于范德波尔对电子电路中三极管的振荡效应的研究[20]. 这一模型在物理学、生物学、神经学甚至经济学中都有着广泛的应用[21, 22, 23]. 考虑一维Van der Pol方程 $$ \ddot {x} + {x} + {\theta x}^2{\dot {x}} = 0 \tag{19} $$ 假定系统的非线性阻尼${\theta }$是一个相对小量,对上式进行对称性分析[24],可知其存在2个对称群 $$ {\rm X}_1 = \dfrac{\partial }{\partial {t}},\;\;\;{\rm X}_2 = {x}\dfrac{\partial }{\partial {x}} - 2{\theta }\dfrac{\partial }{\partial {\theta }} \tag{20} $$ 由 $$[{\rm X}_1 ,{\rm X}_2] ={\bf 0} \tag{21} $$ 可知,算子${\rm X}_1 ,{\rm X}_2 $提供了一个二维李代数${L}_2 $的基,且此李代数属于类型I [17]. 因此,可用于式(19)的解析求解. 首先,将对称群${\rm X}_1 = \dfrac{\partial }{\partial {t}}$的典型变量 $$ {x}' = {y}({x}) \tag{22} $$ 分别代入式(19)和式(20),可得 $$ {y}' + \dfrac{x}{y} + {\theta x}^2 = 0 \tag{23} $$ $$ {\rm X}_2 = {x}\dfrac{\partial }{\partial {x}} + {y}\dfrac{\partial }{\partial {y}} - 2{\theta }\dfrac{\partial }{\partial {\theta }} \tag{24} $$ 由于${\theta }$是一个相对小量,可由求解类型I的近似方程[24] $$ {\rm X}_2 {\tau }({x},{y},{\theta }) \approx 0 ,{\rm X}_2 {z}({x},{y},{\theta }) \approx 1 \tag{25} $$ 得到对称群(24)的典型变量 $$ {\tau } = \dfrac{x}{y} ,{z} = \ln {x} \tag{26} $$ 将式(26)代入式(23),可得 $$ {z}' = \dfrac{1}{{\tau } + {\tau }^3} - {\theta }\dfrac{{\tau }^2}{({\tau } + {\tau }^3)} {\rm e}^{2z} \tag{27} $$ 当${\theta } = 0$时,上式的解为${z} = \ln \dfrac{{C}_1 {\tau }}{\sqrt {1 + {\tau }^2} }$. 因此,可假设式(27)的解的形式为 $$ {z} \approx \ln \dfrac{{C}_1 {\tau }}{\sqrt {1 + {\tau }^2} } + {\theta w}({\tau }) \tag{28} $$ 将式(28)代入式(27)中,可得 $$ {w}' = - \dfrac{{C}_1^2 {\tau }^2}{(1 + {\tau }^2)^3} \tag{29} $$ 对上式使用分离变量法求解,可得 $$ {w} = {C}_1^2 \Bigg(\dfrac{{\tau }}{4(1 + {\tau }^2)^2} - \dfrac{{\tau }}{8(1 + {\tau }^2)} - \dfrac{1}{8}\arctan {\tau } \Bigg ) \tag{30} $$ 将其返回原始变量,可得一阶微分方程 $$ \dot{x} = \sqrt {{C}_1^2 - {x}^2} - {\theta } \Bigg (\dfrac{{x}^3}{4} - \dfrac{{x}}{8}{C}_1^2 + \dfrac{{C}_1^4 }{8\sqrt {{C}_1^2 - {x}^2} } \arctan \dfrac{x}{\sqrt {{C}_1^2 - {x}^2} } \Bigg) \tag{31} $$ 采用与式(27)同样的方法对其求解,最终得到 $$ {x} \approx {C}_1 \sin ({t} + {C}_2 ) - \\ {\theta }\left( {\dfrac{{C}_1^3 }{8}\cos ^3({t} + {C}_2 ) + \dfrac{{C}_1^3 }{8}{t}\sin ^3({t} + {C}_2 )} \right) \tag{32} $$ 式中${C}_1 $为任意常数.
3.2 概率密度解令${\theta }$为随机参数,其概率密度函数为${p}_\varTheta ({\theta })$,初始条件为${x} |_{t = 0} = 1$,$\dot {x} |_{t = 0} = 0$. 将其代入式(32)可得 $$ x \approx \cos {t} - \dfrac{1}{8}t\theta \cos ^3{t} + \dfrac{1}{8}\theta \sin ^3{t} \tag{33} $$ 将式(33)代入式(10)中,可得位移的概率密度函数为 $$ {p}_{X\varTheta } (x,t) = \Bigg ( p_\varTheta \dfrac{8\left( {\cos t - x} \right)}{t\cos ^3t - \sin ^3t} \Bigg ) \Bigg/ \\ \left| { - \dfrac{1}{8}t\cos ^3t + \dfrac{\sin ^3t}{8} } \right| \tag{34} $$ 同理可得速度的概率密度函数为
$ {p}_{X\varTheta } (\dot {x},{t}) = $
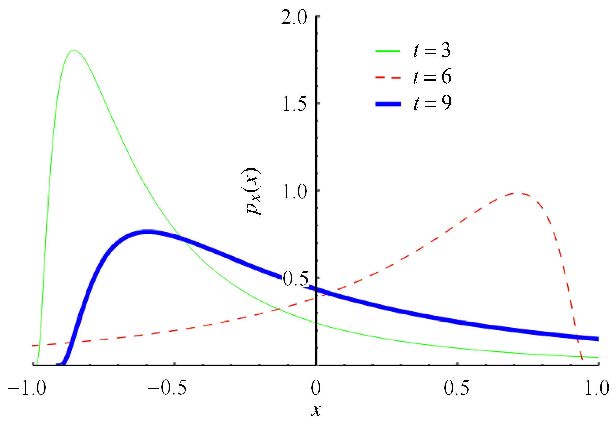
$ \Bigg ( {p}_\varTheta \dfrac{8{\rm sec} t\left( {x + \sin t} \right)}{ - \cos ^2t + 3t\cos t\sin t + 3\sin ^2t} \Bigg ) \Bigg / $ $ \left| { - \dfrac{1}{8}\cos ^3t + \dfrac{3}{8}t\cos ^2t\sin t + \dfrac{3}{8}\cos t\sin ^2t} \right| \tag{35}$$ 图1和图2分别给出了当${\theta }$分别服从对数正态分布
${p}_\varTheta (\theta) = \dfrac{{\rm e}^{ - \tfrac{1}{2}\left( {\ln {\theta }} \right)^2}}{\sqrt {2\pi } {\theta }}$和${p}_\varTheta ({\theta }) = \dfrac{{\rm e}^{ - \tfrac{1}{2}\left( {1 + \ln {\theta }} \right)^2}}{\sqrt {2\pi } {\theta }}$ 时,典型时刻的响应的概率密度函数. 由这些结果,可以清晰看到系统响应的随机跃迁和概率密度的变化.
|
图1 服从第1个对数正态分布时Van der Pol方程概率密度解 Fig.1 PDFs of Van der Pol oscillator when $\theta$ is lognormally distributed |

|
图2 服从第2个对数正态分布时Van der Pol方程概率密度解 Fig.2 PDFs of Van der Pol oscillator when $\theta$ is lognormally distributed |
KL散度(Kullback--Leibler divergence),又称相对熵(relative entropy),是描述两个概率分布$P$和$Q$差异的一种指标. 为验证解析结果的正确性,表1计算了Van der Pol振子响应概率密度的解析解与10 000次Monte Carlo模拟的数值结果的相对熵,如表1所示.
| 表1 Van der Pol振子解析解与数值解的相对熵 Table 1 K-L distance between and numerical solution for Van der Pol oscillator |
需要提醒的是,由于在前面推导中假定了非线性项为一个相对小量. 因此,在${\theta }$的变异性较小时解的精度较高. 表1的结果也验证了这一结论.
4 Riccati方程 4.1 物理系统解作为控制理论中的重要方程,Riccati方程涉及了线性二次调节器问题、Kalman 滤波、$H - \infty $控制、完全最小二乘问题、两点边值问题以及模型简化等诸多问题[25, 26].
考虑一维Riccati方程 $$ \dot {x} = {a}(t){x}^2 + {b}(t){x} + {c}(t) ,{a}(t) e 0 \tag{36} $$ 并采用非局部李群方法对式(36)求解.
首先,式(36)可由对称群${\rm X}_1 = {y}\dfrac{\partial }{\partial {y}}$的典型变量 $$ t = \tau ,x = - \dfrac{1}{a(t)}\dfrac{{y}'}{y} \tag{37} $$ 转换为二阶线性齐次常微分方程 $$ \ddot {y} - \left( {\dfrac{{a}'(\tau)}{a(\tau)} + {b}(\tau)} \right)\dot {y} + {c}(\tau ){a}(\tau ){y} = 0 \tag{38} $$
对式(38)进行对称性分析[27],可得式(38)的另一个对称群为${\rm X}_2 = {h}(\tau )\dfrac{\partial }{\partial y}$,其中${h}$是式(38)的一个群.
进一步计算可得 $$[- {\rm X}_1 ,{\rm X}_2] = {\rm X}_2 \tag{39} $$ 式中$[\cdot]$表示李括号算符[17].
由式(39)可知,算子${\rm X}_1 ,{\rm X}_2 $提供了一个二维李代数${L}_2 $的基,即${L}_2 $是一个由${\rm X}_1 ,{\rm X}_2 $生成的李群. 而式(38)可通过对称群${\rm X}_1 $化简为Riccati方程(36),此时生成元${\rm X}_2 $即为式(36)的非局部对称群 $$ \tilde {\rm X}_2 = \exp \Bigg(\int {a}(t) \cdot {x}d {t} \Bigg) \Bigg(x \cdot {h}(t) + \dfrac{ h'(t)}{a(t)} \Bigg)\dfrac{\partial }{\partial {x}} \tag{40} $$ 由于 $$ {\rm X}_1 = [{y} / {h}({\tau })]{\rm X}_2 \tag{41} $$ 根据非局部对称理论[28],存在变换 $$ T = {t} ,X = - {a}({t}){x} - \dfrac{h'(t)}{h(t)} \tag{42} $$ 将式(42)代入式(36),可得到如下Bernoulli方程 $$ \dfrac{d X}{d T} = \left( { b(T) + \dfrac{a'(T)}{a(T)} - 2\dfrac{h'(T)}{h(T)} } \right)X - X^2 \tag{43} $$ 对一阶Bernoulli方程的求解可在任一高等数学教材中找到,此处不再赘述.
4.2 概率密度解在式(36)中,令${a}(t) = - {\theta }$,${b}(t) = 1$,${c}(t) = 0$,假定${\theta }$为线性系统控制问题中的随机质量,其概率密度函数为${p}_\varTheta (\theta)$,初始条件为${x}\left| {_{{t} = 0} = {x}_0 } \right.$.
将上述条件代入式(38)和式(43),可得 $$ \left. \!\!\begin{array}{l} \ddot {y} - \dot {y} = 0 \\ \dfrac{d X}{d T} = \left( {1 - 2\dfrac{h'(T)}{h(T)}} \right)X -X^2 \end{array} \!\! \right \} \tag{44} $$ 求解式(44),并将所得结果按式(42)进行变量替换,可得 $$ {x} = \dfrac{{\rm e}^t{x}_0 }{1 + {\theta }\left( { - 1 + {\rm e}^t} \right){x}_0 } \tag{45} $$ 将上式代入式(10)中,可得 $$ {p}_{X\Theta } ({x},{t}) = \Bigg ( {p}_\varTheta \dfrac{ - x + {\rm e}^t{x}_0 }{\left( { - 1 + {\rm e}^t} \right)x{x}_0 } {\rm e}^{t} \Bigg ) \Bigg / \\ \left| {\left( { - 1 + {\rm e}^t} \right)x^2} \right| \tag{46} $$
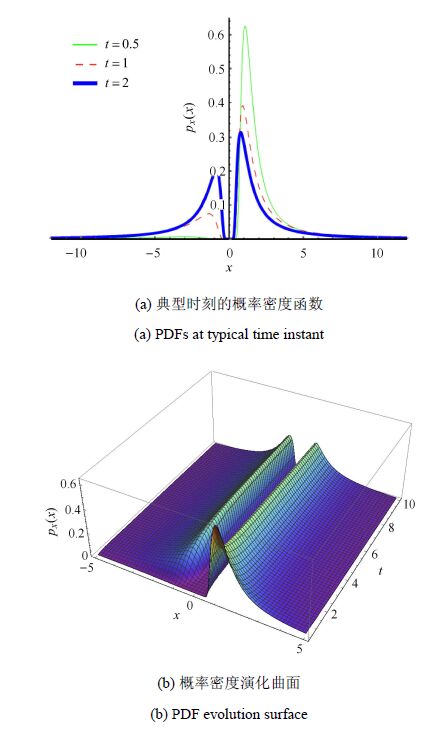
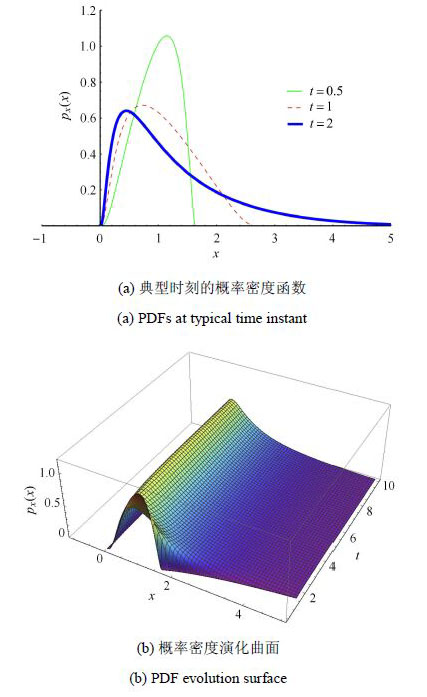
图3和图4分别给出了当${x}_0 = 1$,${\theta }$分别服从标准正态分布${p}_\varTheta ({\theta }) = \dfrac{1}{\sqrt {2\pi } }{\rm e}^{ - \tfrac{{\theta }^2}{2}}$和标准对数正态分布${p}_\varTheta ({\theta }) = \dfrac{{\rm e}^{ - \tfrac{1}{2}\ln ^2\left( {\theta } \right)}}{\sqrt {2\pi } {\theta }}$时,典型时刻系统响应的概率密度函数及其时间演化的曲面. 同样地,表2计算了Riccati方程响应概率密度的解析解与10 000次Monte Carlo模拟的数值结果的相对熵.
| 表2 Riccati方程解析解与数值解的相对熵 Table 2 K-L distance between and numerical solution for Riccati system |
观察图3可见,系统响应的概率密度函数随时间经历了由单峰到双峰,最后再到单峰的过程. 这种随机演化的现象反映了 Riccati系统由于参数的随机性所表现出两种截然不同、发散和收敛相互竞争的物理过程. 而当基本随机变量服从对数正态分布时,系统演化过程变得平缓、相应概率密度仅有分布区域上的变化,而未出现大幅度的形态变化.
|
图3 ${\theta }$服从正态分布时的Riccati方程的概率密度解 Fig.3 PDFs of Riccati system when ${\theta }$ is normally distributed |
|
图4 服从对数正态分布时的Riccati方程的概率密度解 Fig.4 PDFs of Riccati system when ${\theta }$ is lognormally distributed |
Helmholtz振子起源于亥姆霍兹在19世纪50年代对声学中的频率和音高的研究[29]. 它广泛地应用于结构在风致载荷下的空气动力学特性、船舶在海浪激励下的倾覆问题、弹性力学中的薄膜振动问题[30, 31, 32, 33]等研究领域.
考察一维Helmholtz振子 $$ \ddot {x} + 2{\dot {x}} + \dfrac{24}{25}{x} - {\theta x}^2 = 0 \tag{47} $$ 对上式进行对称性分析[34],可知其存在两个对称群 $$ {\rm X}_1 = \dfrac{\partial }{\partial {t}} ,{\rm X}_2 = - \dfrac{5}{4}{\rm e}^{\tfrac{2}{5}{t}}\dfrac{\partial }{\partial {t}} + {x}{\rm e}^{\tfrac{2}{5}{t}}\dfrac{\partial }{\partial {x}} \tag{48} $$ 进而,由 $$[{\rm X}_1 ,{\rm X}_2] = \dfrac{2}{5}{\rm X}_2 \tag{49} $$ 可知,算子${\rm X}_1 ,{\rm X}_2 $提供了一个二维李代数${L}_2 $的基,且此李代数属于类型III [17]. 且由此可知存在对称群${\rm X}_1,{\rm X}_2 $的典型变量 $$ {y} = \dfrac{25{\theta }}{24}{x}{\rm e}^{ - \tfrac{2}{5}{t}} ,{\tau } ={\rm e}^{ - \tfrac{2}{5}{t}} \tag{50} $$ 将式(50)代入式(47),可得 $$ {y}'^2 = 4{y}^3 - {C} \tag{51} $$
式(51)的解是Weierstrass函数,其解处处连续而处处不可导. 按${C}_1 $的值对式(51)分类求解,并返回原始变量,可得当${C} = 0$时 $$ {x} = \dfrac{24}{25{\theta }}\left( {1 + {C}_2 {\rm e}^{\tfrac{2}{5}{t}}} \right)^{ - 2} \tag{52} $$ 当${C} > 0$时 $$ {x} = \dfrac{6}{25{\theta }}{C}_1^2 \cdot \\ \left[{\dfrac{1}{\sqrt 3 } + \dfrac{1 + cn({C}_1 {\rm e}^{ - \tfrac{2}{5}{t}} + 0.067{C}_2 )}{1 - cn({C}_1 {\rm e}^{ - \tfrac{2}{5}{t}} + 0.067{C}_2)}} \right] {\rm e}^{ - \tfrac{4}{5}{t}} \tag{53} $$ 当${C} <0$时 $$ {x} = \dfrac{6}{25{\theta }}{C}_1^2 \cdot \\ \left[{\dfrac{1}{\sqrt 3 } + \dfrac{1 + cn({C}_1 {\rm e}^{ - \tfrac{2}{5}{t}} + 0.933{C}_2 )}{1 - cn({C}_1 {\rm e}^{ - \tfrac{2}{5}{t}} + 0.933{C}_2 )}} \right] {\rm e}^{ - \tfrac{4}{5}{t}} \tag{54} $$ 式中${C}_1 $,${C}_2 $为任意常数.
5.2 概率密度解令${C} = 0$,假定${\theta }$为薄膜振动问题中的随机初始条件,其概率密度函数为${p}_\varTheta (\theta)$,初始条件为${x}\left| {_{{t} = 0} = \dfrac{6}{25{\theta }}\;} \right.$,${\dot {x}}\left| {_{{t} = 0} = - \dfrac{12}{125{\theta }}} \right.$. 将此条件代入式(52)中,可得 $$ {x} = \dfrac{24}{25{\theta }}\left( {1 + {\rm e}^{\tfrac{2}{5}{t}}} \right)^{ - 2} \tag{55} $$ 将式(55)代入式(10)中,可得位移的概率密度函数为 $$ {p}_{X\varTheta } (x,t) =\Bigg ( {p}_\varTheta \dfrac{24}{25\left( {1 + {\rm e}^{\tfrac{2}{5}{t}}} \right)^2x} \Bigg ) \Bigg / \\ \left| { - \dfrac{25}{24}\left( {1 + {\rm e}^{\tfrac{2}{5}{t}}} \right)^2x^2} \right| \tag{56} $$ 同理,速度的概率密度函数为 $$ {p}_{X\varTheta } (\dot {x},{t}) = \Bigg ( -{p}_\varTheta \dfrac{96e^{\tfrac{2}{5}{t}}}{125 (1 + {\rm e}^{\tfrac{2}{5}{t}})^3\dot{x}} \Bigg ) \Bigg / \\ \Bigg [\dfrac{125}{96}{\rm e}^{ -\tfrac{2}{5}{t}}\left| {\left( {1 + {\rm e}^{\tfrac{2}{5}{t}}} \right)^3 \dot{x}^2} \right| \Bigg] \tag{57} $$
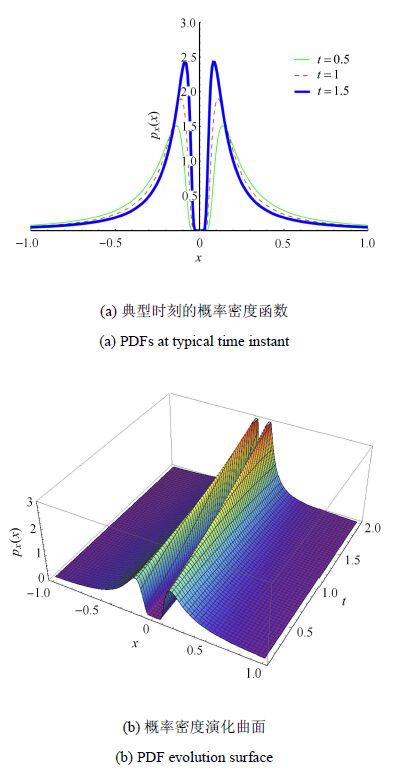
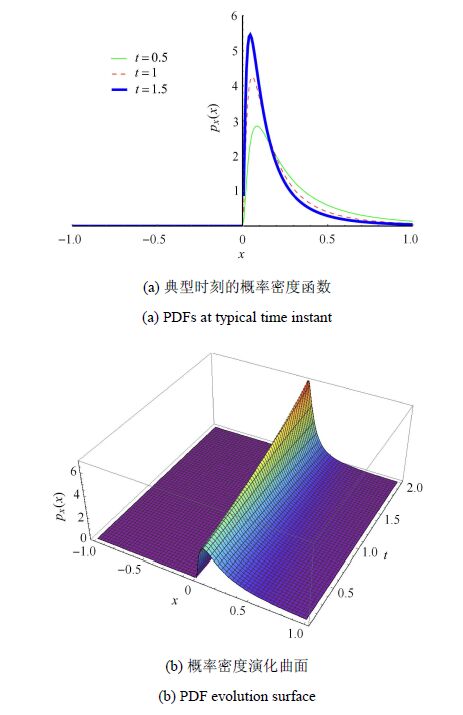
图5和图6 分别给出了当${\theta }$分别服从标准正态分布${p}_\varTheta ( \theta ) = \dfrac{1}{\sqrt {2\pi } }{\rm e}^{ - \tfrac{{\theta }^2}{2}}$和标准对数正态分布${p}_\varTheta ({\theta }) = \dfrac{{\rm e}^{ - \tfrac{1}{2}\ln ^2\left( {\theta } \right)}}{\sqrt {2\pi } {\theta }}$时典型时刻系统响应的概率密度函数和随时间改变的概率密度演化曲面. 表3计算了Helmholtz振子响应概率密度的解析解与10 000次Monte Carlo模拟的数值结果的相对熵.
| 表3 Helmholtz振子解析解与数值解的相对熵 Table 3 K-L distance between and numerical solution for Helmholtz oscillator |
从图5可以看出:系统响应的概率密度函数的2个峰值随着时间推移峰值不断变高,反映了Helmholtz系统的吸引子使得系统响应分布表现出逐步演化的趋势. 而图6则表明,当随机变量的概率密度分布从正态分布变为对数正态分布时,系统响应的概率密度函数的形态由双峰变为单峰.
|
图5 ${\theta }$服从正态分布时Helmholtz振子的概率密度解 Fig.5 PDFs of Helmholtz oscillator when ${\theta }$ is normally distributed |
|
图6 ${\theta }$服从对数正态分布时Helmholtz振子的概率密度解 Fig.6 PDFs of Helmholtz oscillator when $\theta$ is lognormally distributed |
广义概率密度演化方程的解析解在随机动力系统分析中具有重要的意义,其价值不仅在于可以用于检验数值解的准确性、收敛性、 稳定性等,也可以用它来研究并构造各种新的数值算法格式.
本文引入李群方法对若干典型随机非线性系统及其相应的广义密度演化方程进行了解析求解. 所获取的解答不仅可作为研究相应物理系统时所开发的近似数值算法的校核标准,也有助于进一步深入研究和剖析随机动力系统中随机性与非线性的耦合机制.
值得提醒的是,李群方法的使用前提是非线性微分方程含有某种对称性. 对于具有足够对称性的非线性微分方程,可以用统一的方法进行约化和求解,但这并不意味着所有的非线性微分方程均可通过李群方法求解. 事实上,能够通过李群方法获取解析解的非线性微分方程仍极为有限[27].
| 1 | 李杰,陈建兵. 随机结构非线性动力响应概率密度演化分析. 力学学报, 2003, 35(6):716-722(Li Jie, Chen Jianbin. The probability density evolution method for analysis of dynamic nonlinear response of stochastic structures. Chinese Journal of Theoretical and Applied Mechanic, 2003, 35(6):716-722(in Chinese)) |
| 2 | 李杰,陈建兵. 随机系统分析中的广义密度演化方程. 自然科学进展, 2006, 16(6):712-719(Li Jie, Chen Jianbin. Generalized density evolution equation in stochastic dynamical system. Progress in Natural Science, 2006, 16(6):712-719(in Chinese)) |
| 3 | Li J, Chen JB. The principle of preservation of probability and the generalized density evolution equation. Structural Safety, 2008, 30:65-77 |
| 4 | Chen JB, Li J. A note on the principle of preservation of probability and probability density evolution equation. Probability Engineering Mechanics, 2009, 24(1):51-59 |
| 5 | Li J,Chen JB. Stochastic Dynamics of Structures. John Wiley & Sons, 2009 |
| 6 | Li J, Chen JB. The probability density evolution method for dynamic response analysis of non-linear stochastic structures. International Journal for Numerical Methods in Engineering, 2006, 65:882-903 |
| 7 | Li J,Chen JB,Fan WL. The equivalent extreme-value event and evaluation of the structural system reliability. Structural Safety, 2007, 29(2):112-131 |
| 8 | Chen JB,Li J. The extreme value distribution and dynamic reliability analysis of nonlinear structures with uncertain parameters. Structural Safety, 2007, 29(2):77-93 |
| 9 | Li J,Peng YB,Chen JB. A physical approach to structural stochastic optimal controls. Probabilistic Engineering Mechanics, 2010, 25(1):127-141 |
| 10 | 陈建兵,李杰. 随机结构静力反应概率密度演化方程的差分方法. 力学季刊, 2004, 25(1):21-28(Chen Jianbin, Li Jie. Difference method for probability density evolution eqaution of stochastic structural response. Chinese Quarterly of Mechanics, 2004, 25(1):21-28(in Chinese)) |
| 11 | Li J, Chen JB. The number theoretical method in response analysis of nonlinear stochastic structures. Computational Mechanics, 2007, 39(6):693-708 |
| 12 | Farlow SJ. Partial Differential Equations for Scientists and Engineers. Courier Dover Publications, 2012 |
| 13 | 刘延柱,陈立群. 非线性振动. 北京:高等敎育出版社, 2001(Liu Yanzhu, Chen Liqun. Nonlinear Vibration. Beijing:Higher Education Press, 2001(in Chinese)) |
| 14 | 陈立群,吴哲民. 多自由度非线性振动分析的平均法. 振动与冲击, 2002, 21(3):63-64(Chen Liqun, Wu Zhemin. Study on the precession of vibrating shape for circular cylindrical shell. Journal of Vibration and Shock, 2002, 21(3):63-64(in Chinese)) |
| 15 | 李骊. 强非线性振动系统的定性理论与定量方法. 北京:科学出版社, 1997(Li Li. The qualitative theory and quantitative methods of strong nonlinear vibration system. Beijing:Science Press, 1997(in Chinese)) |
| 16 | Nayfeh AH. Perturbation Methods. New York:John Wiley & Sons, 2008 |
| 17 | Ibragimov NH. Classical and new methods, nonlinear mathematical models, symmetry and invariance principles.//A Practical Course in Differential Equations and Mathematical Modelling. World Scientific, 2010 |
| 18 | Olver PJ. Applications of Lie Groups to Differential Equations. Berlin:Springer, 2000 |
| 19 | Ibragimov NH. 微分方程与数学物理问题. 北京:高等教育出版社, 2013(Ibragimov NH. A Practical Course in Differential Equations and Mathematical Modelling. Beijing:Higher Education Press, 2013(in Chinese)) |
| 20 | Van der Pol B. On "relaxation-oscillations". The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 1926, 2(11):978-992 |
| 21 | Samuelson PA. Generalized predator-prey oscillations in ecological and economic equilibrium.//Proceedings of the National Academy of Sciences, 1971, 68(5):980-983 |
| 22 | Athans M,Dertouzos ML,Spann RN, et al. Systems, Networks, and Computation. New York:McGraw-Hill, 1974 |
| 23 | Guckenheimer J. Dynamics of the van der Pol equation. Circuits and Systems, IEEE Transactions on, 1980, 27(11):983-989 |
| 24 | Gazizov RK,Khalique CM. Approximate transformations for van der Pol-type equations. Mathematical Problems in Engineering, 2006, ID 68753 |
| 25 | 卢琳璋. 两类代数黎卡提方程数值解法的研究进展. 厦门大学学报(自然科学版),2001, 40(2):182-186(Lu Linzhang. Study progress of numerical methods for solutions of two classes of algebraic riccati equations. Journal of Xiamen University(Natural Science), 2001, 40(2):182-186(in Chinese)) |
| 26 | Anderson BDO,Moore JB. Linear Optimal Control. New Jersey:Prentice-hall Englewood Cliffs, 1971 |
| 27 | Cantwell B. Introduction to Symmetry Analysis with CD-ROM. Cambridge:Cambridge University Press, 2002 |
| 28 | Adam AA,Mahomed FM. Non-local symmetries of first-order equations. IMA Journal of Applied Mathematics, 1998, 60(2):187-198 |
| 29 | Helmholtz HLF. On the Sensations of Tone as a Physiological Basis for the Theory of Music. Cambridge:Cambridge University Press, 2009 |
| 30 | Kang IS. Dynamics of a conducting drop in a time-periodic electric field. Journal of Fluid Mechanics, 1993, 257:229-264 |
| 31 | Lochner JPA. Utilization of wave motion. U.S. Patent, 1925, 1531:169 |
| 32 | Morel T. Jet-driven Helmholtz fluid oscillator. U.S. Patent, 1977, 4041:984 |
| 33 | Morel T. Experimental study of a jet-driven Helmholtz oscillator. Journal of Fluids Engineering, 1979, 101(3):383-390 |
| 34 | Almendral JA,Sanjuán MAF. Integrability and symmetries for the Helmholtz oscillator with friction. Journal of Physics A:Mathematical and General, 2003, 36(3):695-698 |
 2016, Vol. 48
2016, Vol. 48
