2. 上海交通大学数学系, 上海 200240;
3. 上海第二工业大学理学院, 上海 201209
辛性质是哈密顿系统重要的性质,有人[1, 2, 3]针对哈密顿系统提出了辛积分方法.辛算法的优异的稳定性和长时间跟踪能力有着重要的应用前景, 许多计算领域, 如:分子电子计算、经典力学、流体力学等.辛算法解决了在长期计算过程中幅值误差的积累问题,但相位误差积累问题仍然存在. 还有人[4, 5, 6]给出了辛算法误差分析和修正,文中的方法是一种后验误差修正,根据单步辛算法的误差进行时间修正,并得到:相位误差不影响系统的能量而只影响位移和速度等物理量的幅值变化规律和跟踪精度的结论.陈璐等[7]对几种常见的保结构方法(AVF、Padé对角逼近、生成函数法)的相位误差及修正给出详尽的分析,但是文中对缺乏对哈密顿函数守恒性的讨论,文中的算例显示12阶相位误差的算法能量误差仅有$O(10^{-6})$.
近年来,辛方法相位误差现象越来越引起国内外学者关注,RKN方法[8, 9]和SPRK方法[10, 11, 12],都是通过泰勒展开研究相位误差,推导出很多相位误差较小的计算格式,这些方法需要优化求解出合适的参数使得相位误差最小, 所得参数也比较复杂.刘晓梅等[13]提出FSJS方法,该方法巧妙的利用向前和向后差分方法引起的相位误差分别是正方向和负方向的性质,提出分数步计算方案,该方法极大的减小了相位误差,但是每一步计算过程中都要计算分数步数步,从而增加了计算量.颜娜[14]则对引起辛算法的漂移的原因,以及几种传递矩阵的相位误差进行了分析.
文献[15]指出时间有限元方法求解ODE在有些情况下和有限差分方法是等价的,论文同时指出C-TFE求解哈密顿系统可以保证哈密顿函数的守恒.陈传淼等[16, 17, 18]提出有限元方法求解哈密顿系统,该方法显示对线性哈密顿系统连续有限元方法可以保证哈密顿系统的辛结构以及哈密顿函数的守恒.有限元方法求解哈密顿系统有着保能量守恒和保辛结构的优势,但是对有限元方法求解哈密顿系统的相位误差,尚没有文章进行分析.
钟万勰[19, 20]提出精细积分方法通过积累计算小量的技巧,有效地避免了计算机实现的过程中"大数吃小数"现象.曾进等[21]针对哈密顿系统提出精细辛几何算法,该克服了算法对积分时间步长的依赖性,同时保证哈密顿系统的性质.徐明毅等[22]则对精细辛几何算法的误差进行详尽分析.
本文提出的求解哈密顿系统精细辛有限元方法,这种方法结合有限元方法和精细方法的特点.不增加计算工作量就能保证哈密顿系统的性质(辛结构和哈密顿函数守恒)同时极大的减少相位误差.对高低混频和刚性系统在大步长下实现对高频信号的精确仿真. 数值结果令人满意.
1 哈密顿系统考虑如下哈密顿正则方程 $$ \left. \begin{align} & \dot{x}=y \\ & \dot{y}=-{{\omega }^{2}}x \\ \end{align} \right\} \tag{1}$$ 给定初始条$x ( 0 ) = x_0, y(0) = y_0 $.
方程(1)对应的哈密顿函数 $$ H\left( { Z} \right) = \dfrac{1}{2}{ Z}^{\rm T} { C Z} $$ 式中,$Z = \left[ {\begin{array}{*{20}{c}} x\\ y \end{array}} \right]$,${ C} = \left[\!\!\begin{array}{cc} {\omega ^2} & 0 \\ 0 & 1 \end{array}\!\!\right]$.
式(1)可以化为 $$ \dfrac{d { Z}}{d t} ={ J}^{ - 1}{ C Z} \tag{2}$$ 式中,$ { J} = \left[\!\! \begin{array}{cc} 0 & 1 \\ { - 1} & 0 \end{array} \!\! \right]$.
方程(1)对应的解析解为 $$ \left[\!\!\begin{array}{c} x \\ y \end{array}\!\! \right] = \left[\!\!\begin{array}{cc} {\cos \omega t} & {\dfrac{1}{\omega}\sin \omega t} \\ { - \omega\sin \omega t} & {\cos \omega t} \end{array}\!\! \right]\left[\!\!\begin{array}{c} {x_0 } \\ {y_0 } \end{array}\!\! \right] $$
2 时间有限元的精细辛积分方法 2.1 时间有限元方法的保辛和保能量特性利用时间有限元方法求解,线性哈密顿系统(2)正则方程及初始条件 $$ \left. \!\!\begin{array}{l} \dfrac{d { Z}}{d t} = { J}^{ - 1}{ C}{ Z} \\ { Z}(0) ={ Z}_0 \end{array} \!\! \right\} \tag{3}$$ 将计算域$ {I} = \left[{0, T } \right]$作一致剖分$0 = t_1 < t_2 \cdots < t_N = T$, $ { I}_n = \left( {t_n , t_{n + 1} } \right)$, $h_n = t_{n + 1} - t_n $.
相应的有限元空间 $$ S^h = \left\{ w |w \in \mathbb{P}^k ( {I}_n ) \right\} $$ 其中$\mathbb{P}^k\left( {I}_n \right)$是次数不超过$k$ 的多项式空间.
方程(3)的Galerkin变分 $$ \begin{array}{l} \int_{t_n }^{t_{n + 1}} \left( {\dfrac{d { Z}}{d t}-{ B Z} } \right)v\left( t \right)d t = 0 \\ { Z}(0) ={ Z}_0 \\ { Z} \in \mathbb{P}^k\left( {I}_n \right) , v\left( t \right) \in \mathbb{P}^{k - 1}\left( {I}_n \right) \end{array} $$ 式中,${ B} = { J}^{ - 1}{ C}$.
连续一次元和二次元. 得到[16] $$ { Z}_{j + 1} = \Bigg ({ E} + \dfrac{h{ B}}{2}\Bigg ) \Bigg / \Bigg ({ E}- \dfrac{h{ B}}{2} \Bigg ) { Z}_j \tag{4}$$ $$ { Z}_{j+1} = \dfrac{12{ E} + 6h{ B} + h^2{ B}^2}{12{ E} - 6h{ B} + h^2{ B}^2} { Z}_j \tag{5}$$ 式中,${ E}$为单位矩阵.
雅可比矩阵$\Bigg ({ E} + \dfrac{h{ B}}{2}\Bigg ) \Bigg / \Bigg (E - \dfrac{h{ B}}{2}\Bigg )$和$\dfrac{12{ E} + 6h{ B} + h^2{ B}^2}{12{ E} - 6h{ B} + h^2 { B}^2}$为辛矩阵,因此可以很好的控制幅值误差[4, 5, 6, 7, 13].
同时,连续时间有限元方法同时可以保证能量守恒[15, 16].
2.2 精细辛有限元方法的相位误差及辛特性时间有限元方法求解(2),能够保持系统原有的辛性质,因而在长期定量计算中显示出传统算法不可比拟的优点:守恒性和长期跟踪能力.但时间有限元方法都不可避免的产生相位误差. 虽然系统守恒性得到保持,但是,长时间的计算相位误差仍旧不理想.为了进一步提高计算精度,减少相位误差,可以将精细辛积分方法[21]引入时间有限元的计算格式中.
以较复杂的二次时间有限元为例 $$ { Z}_{j + 1} = \Bigg ({ E} + \dfrac{h{ B}}{2}+\dfrac{h^2{ B}^2}{12} \Bigg ) \Bigg / \Bigg ({ E}- \dfrac{h{ B}}{2}+ \dfrac{h^2{ B}^2}{12}\Bigg ) { Z}_j $$ 式中,$h$为有限元单元步长. 为了提高精度,将$h$细分为$2^N$等分$\tau = \dfrac{h}{2^N}$,则精细算法为 $$ { Z}_{j + 1} = \left( \dfrac{{ E} + \dfrac{\tau { B}}{2} + \dfrac{\tau ^2{ B}^2}{12}}{{ E} - \dfrac{\tau { B}}{2} + \dfrac{\tau ^2{ B}^2}{12}}\right )^{2^N}{ Z}_j \tag{6}$$ 令 $ { T}_1 = \dfrac{\tau { B}}{2}$, ${ T}_2 = \dfrac{\tau ^2{ B}^2}{12}$. 则式(5)变为 $$ { Z}_{j + 1} = \left( {\dfrac{{ E} + { T}_1 +{ T}_2 }{{ E} - { T}_1 + { T}_2 }} \right)^{2^N}{ Z}_j $$ 对传递矩阵 $\left( {\dfrac{{ E} + { T}_1 + { T}_2 }{{ E} - { T}_1 + { T}_2 }} \right)^{2^N}$ 分子分母同时用精细积分方法. 计算过程如下
(1) ${ T}_{e} = { T}_1 + { T}_2 $
${ T}_{n} = - { T}_1 + { T}_2$
$N=0$, $N_{\max}=30 $
(2) Repeat $(N< N_{\max})$
$N = N+1$
${ T}_{n} = { T}_{n}{ T}_{n} + 2{ T}_{n} $
${ T}_e = { T}_e { T}_e + 2{ T}_e $
(3) ${ T} = \dfrac{{ E} + { T}_{e} }{{ E} -{ T}_n }$
同理可得一次精细辛有限元方法 $$ { Z}_{j + 1} = \left( {\dfrac{{ E}+ \dfrac{\tau { B}}{2}}{{ E}- \dfrac{\tau { B}}{2}}} \right)^{2^N}{ Z}_j \tag{7}$$
定理1 一次、两次精细有限元辛方法的相位误差随着精细化参数的增大趋于0.
证明:
系统(1)一次时间有限元方法得到的传递矩阵${ A}$为 $$ { A} = \left[\begin{array}{cc} {\Gamma }_{11} & \tau {\Gamma }_{12} \\ -\tau { \Gamma }_{12} & {\Gamma }_{22} \end{array} \right] $$ 其中 $$ {\Gamma }_{11} = \dfrac{4 - \tau ^2}{\tau ^2w^2 + 2} \\ {\Gamma }_{22} = \dfrac{2 - 2w^4\tau ^2}{\tau ^2w^2 + 2} \\ {\Gamma }_{12} = \dfrac{2w^2 + 1}{\tau ^2w^2 + 2} $$ 传递矩阵${ A}$特征值为 $$ \lambda _{1, 2} = - \dfrac{\tau ^2 + \tau ^2w^4 - 8}{2\left( {\tau ^2w^2 + 4} \right)}\pm \dfrac{\alpha + \beta }{2\left( {\tau ^2w^2 + 4} \right)} $$ 其中 $$ \begin{array}{l} \alpha = \tau w^2\sqrt { - \left( { - \tau w^2 + \tau + 4} \right)\left( {\tau w^2 - \tau + 4} \right)} \\ \beta = \tau \sqrt { - \left( { - \tau w^2 + \tau + 4} \right)\left( {\tau w^2 - \tau + 4} \right)} \end{array} $$ 可得 $\mathop {\lim }\limits_{\tau \to 0} \lambda _{1, 2} = 1$.即,$ \tau $趋于0,系统的相位误差趋于0.
同理,可以证明二次精细辛有限元方法的相位误差随着精细化参数的增大趋于0.
定理2 时间有限元的精细积分方法是辛方法
证明:
由式(4)可知
单步时间连续有限元方法是辛方法[15, 16], 即 $$ \left( {\dfrac{ { E} + \dfrac{\tau { B}}{2}}{{ E} - \dfrac{\tau { B}}{2}}} \right) \in {\rm Sp}\left( {2n} \right) , \quad \left( {\dfrac{{ E}+ \dfrac{\tau { B}}{2} + \dfrac{\tau ^2B^2}{12}}{{ E} - \dfrac{\tau { B}}{2} + \dfrac{\tau ^2B{ B}^2}{12}}} \right) \in {\rm Sp}\left( {2n} \right)$$ 同时,精细积分方法将计算域${ I}_n$再次剖分,得递推公式(5).
两个辛矩阵的乘积仍然是辛矩阵. 故 $$ \left( {\dfrac{{ E} + \dfrac{\tau { B}}{2}}{{ E} - \dfrac{\tau { B}}{2}}} \right)^{2^N} \in {\rm Sp}\left( {2n} \right) , \quad \left( {\dfrac{{ E} + \dfrac{\tau { B}}{2} + \dfrac{\tau ^2{ B}^2}{12}}{{ E} - \dfrac{\tau { B}}{2} + \dfrac{\tau ^2{ B}^2}{12}}} \right)^{2^N} \in {\rm Sp}\left( {2n} \right)$$ 即,时间有限元的精细积分方法是辛方法.
为了表述方便, 记, 时间一次元、二次元分别为TFE1和TFE2; 本文提出的精细化时间有限元分别为HPD-FEM1和HPD-FEM2.
3 数值算例 3.1 椭圆型哈密顿系统考察$H = \dfrac{1}{2}\left( {p^2 + 4q^2} \right)$, 对应的正则方程为${p}'=-4q$, $q'=p$, 初始条件为$p(0) = 0$, $q(0) = 0.6 $, 精确解为 $ p\left( t \right) = - 1.2\sin \left( {2t} \right) , q \left( 0 \right) = 0.6\cos \left( {2t} \right) $. 计算时间域为$\left[{0, 1 000s} \right]$.
因为算例的精确解是个周期函数,单纯的比较指定时刻的误差值,比较片面. 表1 和表2 所列误差均是指在$\left[ {0, 1 000 s} \right]$内所有单元节点误差绝对值的最大值.
| 表1 $h = 0.5$单元总数2 000, 精细化参数$m =25$的计算结果比较 Table 1 Compare the result with parameter $h=0.5$ number of node 2 000, and $m=25$ |
| 表2 $h = 0.2$单元总数5 000, 精细化参数$m =50$的计算结果比较 Table 2 Compare the result with parameter $h=0.2$, number of node 5 000, and $m =50$ |
从表1和表2可以看出本文提出的TFE1-HPD, TFE2-HPD和TFE[16]方法一样可以保持哈密顿系统的能量守恒,但本文的方法具有极高的点态数值精度,即,漂移误差极小. 相较FSJS[13], RKN[8, 9]和SPRK[12]等设计的纠漂或者相位误差极小化的方法,本文方法的相位误差更小,而且本文算法克服了纠漂方法FSJS, RKN以及SPRK方法不能保证哈密顿系统的能量守恒的弱点.
3.2 高低混频哈密顿系统对于高低混频系统,文献[23]指出数值方法的计算步长和系统频率之间必须满足CFL条件,即$hw \approx 1$. 这意味着对于高频信号的仿真,数值上必须采用极小的步长.
考察哈密顿函数 $$ H\left( {p_1 , q_1 , p_2 , q_2 } \right) =\\ \dfrac{1}{2}\left( {50p_1^2 + \dfrac{1}{50}p_2^2 + 200q_1^2 + \dfrac{4}{50}q_2^2 } \right) $$ 正则方程组为 $$ \begin{array}{l} p'_1 = - 200q_1 \\ p'_2 = - 4 q_2/ 50 \\ q'_1 = 50p_1\\ q'_2 = p_2/50 \end{array} $$ 初值 $$ \begin{array}{l} p_1 (0) = 2 , p_2 (0) = 2 \\ q_1 (0) = 0 , q_2 (0) = 0 \end{array} $$ 解析解为 $$ \begin{array}{l} p_1 = 2\cos \left( {100t} \right) , q_1 = \sin \left( {100 t} \right) \\ p_2 = 2\cos \left( {\dfrac{t}{25}} \right) , q_2 = \sin \left( {\dfrac{t}{25}} \right) \end{array} $$ 采用FSJS3[13], RKN[8], SPRK[12],其步长分别是$h = 0.000 1$,$h = 0.001$,$h = 0.000 01$以及HPD-FEM方法,步长$h = 0.5$,精细化参数$N = 60$.
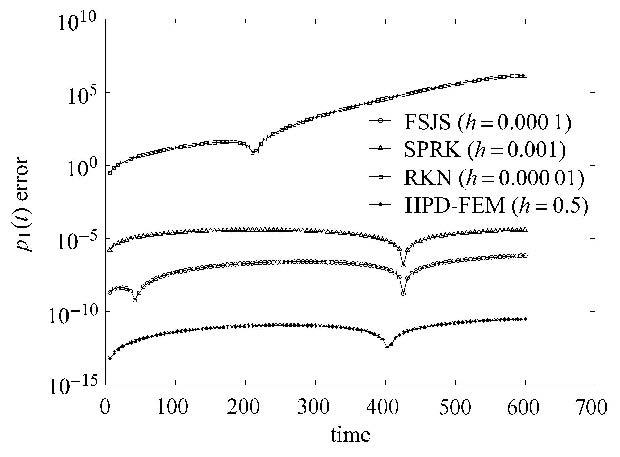
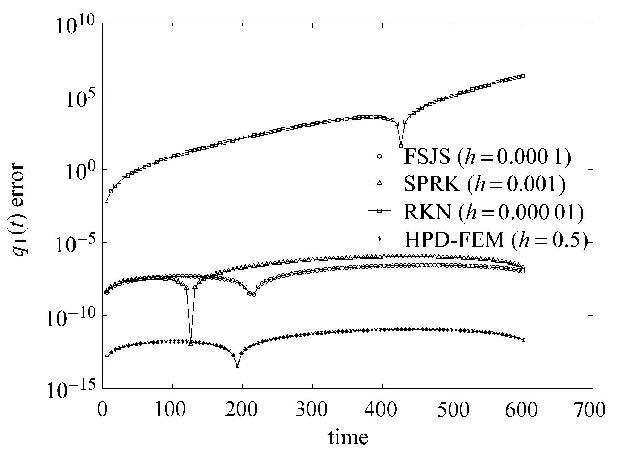
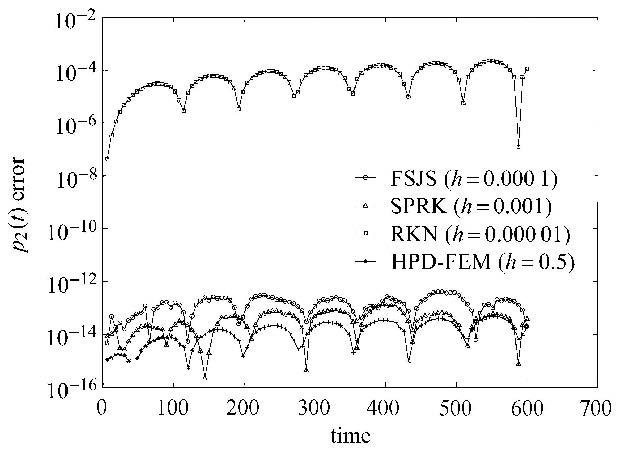
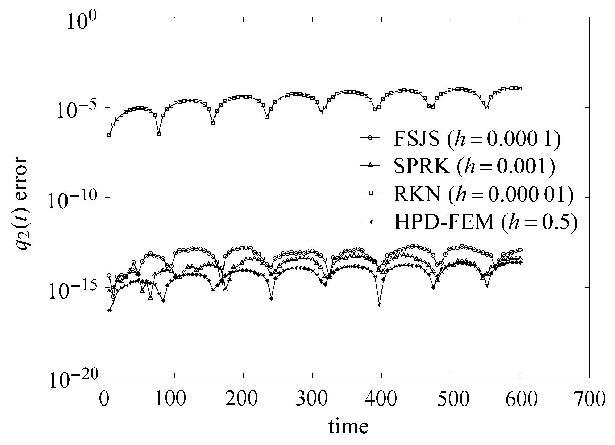
图1 和图2是高频信号的计算误差图,图3和图4是低频信号误差图.从时域误差图可以看出HPD-FEM在大步长下同时对高频和低频信号的精确仿真,计算误差均在$10^{ - 12}$以下.这是现有方法所无法比拟的. 图5是哈密顿函数的误差图,HPD-FEM方法同样可以在大步长的情况下,实现算法的保能量特性.
|
图1 不同时间的$p_1 \left( t \right)$误差 Fig.1 The error of $p_1 \left( t \right)$ at different times |
|
图2 不同时间的$q_1 \left( t \right)$误差 Fig.2 The error of $q_1 \left( t \right)$ at different times |
|
图3 不同时间的$p_2 \left( t \right)$误差 Fig.3 The error of $p_2 \left( t \right)$ at different times |
|
图4 不同时间的$q_2 \left( t \right)$误差 Fig.4 The error of $q_2 \left( t \right)$ at different times |

|
图5 不同时间的哈密顿函数误差 Fig.5 The error of Hamiltonian at different times |
精细化参数$N$, 是HPD-FEM方法设计过程中引入的参量. 图6是不同的精细化参数,时域上计算误差最大值. 从图6,对于高频信号$p_1 - q_1 $, 较小的参数$N$,对于计算精度提高不大. 可以看出参数$N$越大,计算的精度越高,但$N > 60$,$N$的增加对计算误差的影响极小. 同时较大的参数也会引入计算机舍入误差以及较多的计算量.所以,在计算过程中,需要选择合适的$N$. 根据计算经验,参数$N$和系统的刚性有关,刚性越大,$N$就越大.
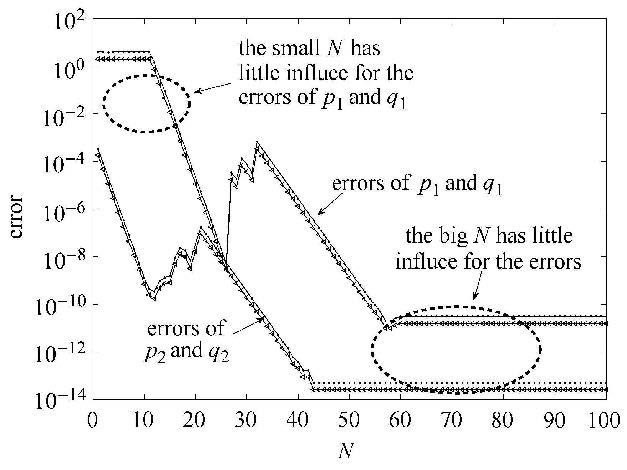
|
图6 不同精细参数计算误差 Fig.6 Different parameter of HPD-FEM |
文献[24]给出弹簧振子的算例,该算例是个刚性系统. 物理模型如图7.
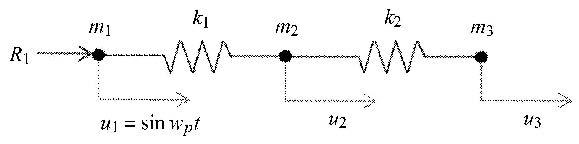
|
图7 三自由度弹簧振子物理模型 Fig.7 Model problem of three degrees of freedom spring system |
系数分别为$k_1=10^7$, $k_2=1$, $w_p=2$ $$ \left [\!\! \begin{array}{ccc} u_1 \\ u_2 \\ u_3 \end{array} \!\!\right] + \left[\!\! \begin{array}{ccc} {10^7} & { - 10^7} & 0 \\ { - 10^7} & {10^7 + 1} & { - 1} \\ 0 & { - 1} & 1 \end{array} \!\! \right]\left[\!\! \begin{array}{c} {u_1 } \\ {u_2 } \\ {u_3 } \end{array} \!\! \right] = \left[\!\! \begin{array}{c} {r_1 } \\ 0 \\ 0 \end{array} \!\! \right] \tag{8}$$ 其中$r_1 $是左边振子的受力. 由于$u_1 $是已知的,式(8)可以写成 $$ \left[\!\! \begin{array}{c} u_2 \\ u_3 \end{array} \!\!\right] + \left[\!\! \begin{array}{cc} {10^7 + 1} & { - 1} \\ { - 1} & 1 \end{array} \!\! \right]\left[\!\! \begin{array}{c} {u_2 } \\ {u_3 } \end{array} \!\! \right] = \left[\!\! \begin{array}{c} {10^7\sin (2t)} \\ 0 \end{array} \!\! \right] \tag{9}$$ 利用齐次扩容技术[25, 26, 27, 28, 29, 30],方程(9)可以改写成齐次常微分方程. 分别用Newmark-$ \alpha$ ($\alpha=0.25$), $\beta=0.5$, Wilson-$\theta$ ($\theta = 1.4 $), 步长为$h = 0.000 5$, 和HPD-FEM ($N=40$), 步长为$h = 0.5$.
| 表3 不同方法计算误差 Table 3 The errors by different methods |
表3 可以看出HPD-FEM 方法可以在大步长下实现对刚性系统的精确仿真. 这是其他方法所没有的特性.
4 结论精细辛有限元方法继承了有限元方法在求解哈密顿系统中保辛和保能量的优良特性,同时,极大的减少相位漂移误差,几乎达到机器精度. 对于高低混频或者刚性系统,HPD-FEM方法可以在较大步长下实现对高低频信号的精确仿真.数值结果令人满意,具有广泛的工程实践价值.
| 1 | Feng K. Difference schemes for Hamiltonian formalism and symplectic geometry. Journal of Computational Mathematics, 1986,4(3):279-289 |
| 2 | Feng K, Qin M. Symplectic Geometric Algorithms for Hamiltonian Systems. Heidelberg, Dordrecht, London, New-York:Springer, 2010 |
| 3 | Calvo MP. Numerical Hamiltonian Problems. CRC Press, 1994 |
| 4 | Brusa L, Nigro L. A one-step method for direct integration of structural dynamic equations. International Journal for Numerical Methods in Engineering, 1980, 15(5):685-699 |
| 5 | 邢誉峰, 杨蓉. 单步辛算法的相位误差分析及修正. 力学学报, 2007, 39(5):668-671(Xing Yufeng, Yang Rong. Phase errors and their correction in symplectic implicit single-step algorithm. Chinese Journal of Theoretical and Applied Mechanics, 2007, 39(5):668-671(in Chinese)) |
| 6 | 邢誉峰, 冯伟. 李级数算法和显式辛算法的相位分析. 计算力学学报, 2009, 26(2):167-171(Xing Yufeng, Feng Wei. Phase analysis of Lie series algorithm and explicit symplectic algorithm. Chinese Journal of Computational Mechanics, 2009, 26(2):167-171(in Chinese)) |
| 7 | 陈璐, 王雨顺. 保结构算法的相位误差分析及其修正. 计算数学, 2014,(3):271-290(Chen Lu, Wang Yushun. Phase error analysis and correction of structure preserving algorithms. Mathematica Numerica Sinica, 2014,(3):271-290(in Chinese)) |
| 8 | Vyver HVD. A symplectic Runge-Kutta-Nystrom method with minimal phase-lag. Physics Letters A, 2007, 367(1):16-24 |
| 9 | Monovasilis T, Kalogiratou Z, Simos TE. Exponentially fitted symplectic Runge-Kutta-Nyström methods. Appl Math Inf Sci, 2013, 7(1):81-85 |
| 10 | Monovasilis T, Kalogiratou Z, Simos TE. Symplectic partitioned Runge-Kutta methods with minimal phase-lag. Computer Physics Communications, 2010, 181(7):1251-1254 |
| 11 | Simos TE. A two-step method with vanished phase-lag and its first two derivatives for the numerical solution of the Schrödinger equation. Journal of Mathematical Chemistry, 2011, 49(10):2486-2518 |
| 12 | Monovasilis T, Kalogiratou Z, Simos TE. Two new phase-fitted symplectic partitioned Runge-Kutta methods. International Journal of Modern Physics C, 2011, 22(12):1343-1355 |
| 13 | 刘晓梅, 周钢, 王永泓等. 辛算法的纠飘研究. 北京航空航天大学学报, 2013, 39(1):22-26(Liu Xiaomei, Zhou Gang, Wang Yonghong. Rectifying drifts of symplectic algorithm. Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(1):22-26(in Chinese)) |
| 14 | 颜娜. 辛算法及其相位飘移性质的研究. 上海交通大学, 2010(Yan Na. The study on phase shift properties based on symplectic algorithm.[Master Thesis]. Shanghai:Shanghai Jiao Tong University,2010(in Chinese)) |
| 15 | Tang W, Sun Y. Time finite element methods:A unified framework for numerical discretizations of ODEs. Applied Mathematics & Computation, 2012, 219(4):2158-2179 |
| 16 | 汤琼, 陈传淼. 哈密顿系统的连续有限元法. 应用数学和力学, 2007, 28(8):958-966(Tang Qiong, Chen Chuanmiao. Continuous finite element methods of hamiltonian systems. Applied Mathematics and Mechanics, 2007, 28(8):958-966(in Chinese)) |
| 17 | 陈传淼, 汤琼. 哈密顿系统的有限元研究. 数学物理学报:A 辑, 2011, 31(1):18-33(Chen Chuanmiao, Tang Qiong. Study of finite element for Hamiltonian systems. Acta Mathematica Scientia, 2011, 31(1):18-33(in Chinese)) |
| 18 | Hu SF, Chen CM. Runge-Kutta method, finite element method, and regular algorithms for Hamiltonian system. Applied Mathematics & Mechanics:English Edition, 2013, 34(6):747-760 |
| 19 | 钟万勰. 结构动力方程的精细时程积分法. 大连理工大学学报, 1994,(2):131-136(Zhong Wanxie. On precise time-integration method for structural dynamics. Journal of Dalian University of Technology, 1994,(2):131-136(in Chinese)) |
| 20 | Zheng Z, Yao WX. Time domain FEM and symplectic conservation. Journal of Mechanical Strength, 2005, 2:008 |
| 21 | 曾进, 周钢. 精细辛算法. 上海交通大学学报, 1997,(9):31-33(Zeng Jin, Zhou Gang. Precise symplectic algorithm. Journal of Shanghai Jiao Tong University, 1997,(9):31-33(in Chinese)) |
| 22 | 徐明毅, 张勇传. 精细辛几何算法的误差估计. 数学物理学报, 2006, 26(2):314-320(Xu Mingyi, Zhang Yongchuan. Accuracy estimation of precise symplectic integration method. Acta Mathematica Scientia, 2006, 26(2):314-320(in Chinese)) |
| 23 | Cohen D, Hairer E, Lubich Ch. Numerical energy conservation for multi-frequency oscillatory differential equations. BIT Numerical Mathematics, 2005, 45(2):287-305 |
| 24 | Klaus-Jürgen Bathe, Gunwoo Noh. Insight into an implicit time integration scheme for structural dynamics. Computers & Structures, 2012, 98:1-6 |
| 25 | Wang YX, Tian XD, Zhou G. Homogenized high precision direct integration scheme and its applications in engineering. Communications in Numerical Methods in Engineering, 2002, 18(6):429-439 |
| 26 | 王跃先, 周钢, 陈军等. 齐次扩容精细算法. 计算力学学报, 2001, 18(3):339-344(Wang Yuexian, Zhou Gang, Chen Jun, et al. Homogenized high precision direct integration scheme. Chinese Journal of Computational Mechanics, 2001, 18(3):339-344(in Chinese)) |
| 27 | 周钢, 王跃先, 贾国庆等. 一种基于Taylor 级数的齐次扩容精细算法. 上海交通大学学报, 2001,(12):1916-1919(Zhou Gang, Wang Yuexian, Jia Guoqing, et al. A homogenized high precise direct integration based on Taylor serials. Journal of Shanghai Jiao Tong University, 2001,(12):1916-1919(in Chinese)) |
| 28 | 时小红, 周钢, 付召华. 基于Legendre 多项式函数系的齐次扩容精细算法. 计算力学学报, 2005,(3):335-338(Shi Xiaohong, Zhou Gang, Fu Shaohua. A homogenized high precise direct integration based on Legendre serials. Chinese Journal of Computational Mechanics, 2005,(3):335-338(in Chinese)) |
| 29 | 王龙, 周钢. 具有任意激励的非齐次线性自治系统的齐次扩容精细算法. 上海理工大学学报, 2006,(2):128-132(Wang Long, Zhou Gang. New homogenized high precision direct integration to solve nonhomogeneous autonomy system with arbitrary stimulus. J University of Shanghai for Science and Technology, 2006,(2):128-132(in Chinese)) |
| 30 | 付召华, 周钢, 罗顺等. 基于Chebyshev 多项式函数系的齐次扩容精细算法. 东华大学学报(自然科学版), 2006,(2):46-49(Fu Shaohua, Zhou Gang, Luo Shun, et al. Homogenized high precision direct integration based on Chebyshev polynomial series. Journal of Donghua University, 2006,(2):46-49(in Chinese)) |
2. Department of Mathematics, Shanghai Jiao Tong University, Shanghai 200240, China;
3. Department of Mathematics, Shanghai Second Polytechnic University, Shanghai 201209, China
 2016, Vol. 48
2016, Vol. 48