随着航空航天、电子、医疗、机械等领域技术的发展，各领域对所用材料的强度、耐久性等力学性能的要求越来越高.而传统的单质材料很难满足这样的力学要求，但是如复合材料、合金等非均质材料既可以发挥各种单质材料的优点，又可以使各组分之间取长补短，相互协同，形成优于单质材料的功能特性.然而用常规有限元法求解非均质材料的相关力学行为时，为保证计算精度，必须使网格的尺寸小于等于材料的最小的特征尺寸，这样会耗费大量的计算时间和计算资源，有时候可能还无法求得正确的结果.因此，寻求既可以节省计算资源，又可以保证计算精度的多尺度数值计算方法已经成为近年来研究的热点^{[1, 2]}.

多尺度有限元法(multiscale finite element method,MsFEM)的原始思想来源于巴布萨卡 ^{[3, 4]}.侯天耀等^{[5, 6]}和Efendiev等 ^{[7, 8, 9]}对该方法的发展做出了重要的贡献.多尺度有限元的基本原理是通过在每个宏观单元上求解子问题，利用一定的数值方法构造出能有效捕捉材料非均质特性的多尺度基函数，使其在粗网格尺度上对原问题进行求解时能得到较高的精度^[10]；张洪武等^[11]通过分别构造固相变形场和液相压力场基函数的方法将多尺度有限元法用于求解饱和多孔介质的固结问题，并考虑多维矢量场不同方向的耦合作用，在基函数中引入耦合附加项，提出了扩展多尺度有限元法(EMsFEM)^{[12, 13]}.

扩展多尺度有限元法的数值基函数是在子网格域上通过求解静力平衡方程得到的，故它只能反映微观材料的刚度特性，无法反映材料的惯性效应^[14]，因此将扩展多尺度有限元法直接用到多尺度动力问题计算当中会导致较大的计算误差.对于动力问题，为了考虑子网格上材料的惯性效应，张洪武等^[12]在宏观单元的多尺度数值基函数中引入模态基函数，而模态基函数一般是通过在子网格域上求解广义特征值方程得到，这在一定程度上增加了计算量.

不同于扩展多尺度有限元法，本文所提出的广义多尺度有限元法构造基函数不必通过在子网格域施加指定边界约束对静力方程多次进行求解得到^[15]，可以直接通过矩阵运算得到，因此可以提高计算效率.另外，由于广义多尺度有限元法的宏观节点可分布在宏观单元的内部，故其能更准确地模拟具有缺陷^[16]、裂纹等^{[17, 18]}复杂几何的非均质单胞^[19]的变形情况.和其它典型的多尺度方法(如计算多尺度均匀化方法^{[20, 21]}、非均质多尺度法^{[22, 23]}、广义有限元法^[24]、多尺度本征元法^{[25, 26]}等)不同，本文提出的广义有限元法在获得宏观尺度上的解后，可以再次利用所构造的多尺度基函数进行降尺度计算，很容易获得微观尺度上的应力应变等信息.

本文分4部分，第1部分介绍了广义多尺度有限元法计算的一般过程；第2部分详细介绍了广义多尺度有限元法构造基函数的构造过程；第3部分为数值验证，通过静力问题，广义特征值问题和瞬态响应分析的算例来证明该多尺度方法的有效性以及适用性；第4部分是本文工作的总结.

多尺度有限元法的基本思想是通过求解在粗网格内部要满足特定边界条件下的平衡方程来数值构造多尺度基函数 $$ \left.\!\!\begin{array}{lc} { L}{ N}_{i} = {O} , & {\rm in} { K} \\ { N}_{i} {(x)} , & {\rm affined on} \partial { K} \\ {i} = 1,2,3,4,\cdots & \end{array} \right\} \tag{1}$$ 式中,${ L}$为微分算子，满足${ L u} = {\rm div} [{ D} :\dfrac{ 1}{2} (\nabla { u} + (\nabla { u} )^{\rm T} )]$；${ K}$为粗网格的内部域，${ K} \subset { \Omega }$，${ \Omega }$为求解域；${ N}_{i} $为粗网格节点$i$的基函数，满足${ N}_{i} |_{j} = { N}_{i} ({ x}_{j},{ y}_{j} ) = \delta _{ij} $ ($i,j=1,2,3,\cdots,m$), $\delta $为克罗内克(Kronecker)符号；$m$为粗网格的节点个数.

根据不同的边界条件求得位移基函数后，得到等效刚度矩阵以及等效外力向量如下 $${ K}_{\rm c} = { N}^{\rm T}{ K}_{\rm s} { N} \tag{2}$$ $${ F}_{\rm c} = { N}^{\rm T}{ F}_{\rm s} \tag{3}$$ 式中，${ K}_{\rm s} $是与宏观单元相对应的子网格的总体刚度矩阵，它可以由常规有限元法计算得到； ${ F}_{\rm s} $是子网格上的外力向量. ${ K}_{\rm c} $和${ F}_{\rm c} $为宏观单元的等效刚度矩阵和等效外力向量.同样可以得到等效质量矩阵为 $$ { M }_{\rm c} = { N }^{\rm T}{ M }_{\rm s} { N} \tag{4}$$ 式中，${ M}_{\rm s} $是与宏观单元相对应的子网格的总体质量矩阵，它可以由常规有限元法计算得到；${ M}_{\rm c} $为宏观单元的等效质量矩阵.

得到单个宏观单元的等效刚度和等效质量矩阵后，通过对每个宏观单元进行集成得到整个结构的宏观等效刚度矩阵和宏观等效质量矩阵，即 $${ K}_{\rm C} = { A}_{ c= 1}^{N_{c} } { K} \tag{5}$$ $${ M }_{C} = { A }_{ c= 1}^{ N_{c} } { M }_{c} \tag{6}$$ 式中，${ A }_{ c= 1}^{{N}_{c}} $是一个矩阵(或者向量)集成算子；${N}_{c} $表示粗网格中宏观单元的个数. 形成了宏观尺度上的等效刚度和等效质量矩阵之后，就可以在宏观尺度上对非均质材料进行求解. 然后，利用多尺度的数值基函数，可以很容易地由粗网格宏观尺度上的解得到子网格上微观尺度的解.

本文的宏观单元采用两种宏观节点，V节点和O节点，其中V节点表示与其他宏观单元相连的节点，O节点表示不和其他宏观单元相连接的宏观节点.V节点和O节点的分布可以由如下方法得到，根据结构的几何特征，先对结构整体进行粗网格尺度上的划分，然后在粗网格进行细尺度上的划分.在子网格上，根据粗网格划分的特征，选择非均质单胞的角点或者与常规有限元网格的交点处作为V节点；选择可以描述单胞内部几何边界或者材料信息的位置作为O节点. 如图1所示.

图1(Fig.1)

图1 广义多尺度有限元法示意图 Fig.1 Schematic description of the multi-node GMFEM

子网格上的线弹性问题的常规有限元离散方程写成矩阵形式为 $$ { K }_{\rm s} { u }_{\rm s} = { F }_{\rm s} \tag{7}$$ 式中${ u }_{\rm s} $表示子网格上的位移. 将子网格内部的自由度通过静态凝聚法^[27]凝聚到宏观节点上，得到 $$ \left[\!\!\begin{array}{cccc} { K}_{{\rm ii}} & { K}_{{\rm ib}} & { K}_{{\rm io}} & { K}_{{\rm iv}} \\ { K}_{{\rm bi}} & { K}_{{\rm bb}} & { K}_{{\rm bo}} & { K}_{{\rm bv}} \\ { K}_{{\rm oi}} & { K}_{{\rm ob}} & { K}_{{\rm oo}} & { K}_{{\rm ov}} \\ { K}_{{\rm vi}} & { K}_{{\rm vb}} & { K}_{{\rm vo}} & { K}_{{\rm vv}} \end{array}\!\!\right]\left\{ \!\!\begin{array}{c} { u}_{\rm i} \\ { u}_{\rm b} \\ { u}_{\rm o} \\ { u}_{\rm v} \end{array}\!\! \right\} = \left\{ \!\!\begin{array}{c} {\bf 0 }\\ {\bf 0 }\\ { F }_{\rm o} \\ { F }_{\rm v} \end{array}\!\! \right\} \tag{8}$$ 其中i,b,o,v分别代表子网格的内部自由度、边界自由度、不和其他宏观单元相连接的宏观节点自由度、与其他宏观单元相连接的宏观节点自由度.

利用罚函数法^{[28, 29]}，将与其他宏观单元相邻的子网格边界节点绑定到邻近的宏观V节点上，使相邻的宏观单元之间满足位移协调.$$ { u }_{{\rm bi}} = \alpha _{i} { u }_{{\rm v}j} + (1 -\alpha _{i} ){ u }_{{\rm v}(j + 1)} \tag{9}$$ 其中${ u }_{{\rm bi}} $表示子网格边界点上位移，${ U }_{{{\rm v}j}} $和${ u }_{{\rm v}(j + 1)} $表示和$b$节点最近的两个V节点的位移，$\alpha _i $为比例因子. 可以得到 $$ { u }_{\rm b} = { C }_{{\rm bv}} { u }_{\rm v} \tag{10}$$ 其中${ C }_{{\rm bv}} $表示V节点和b节点的关系矩阵.应用式(8)和式(10)，可以导出子网格节点位移与宏观节点位移之间的关系矩阵，即多尺度单元的形函数矩阵，具体过程如下，首先得到子网格内部的势能方程 $$ \varPi = \dfrac{ 1 }{ 2 }{ u }^{\rm T}{ K }_{\rm s} { u } - { u }_{\rm o}^{\rm T} { F }_{\rm o} - { u }_{\rm v}^{\rm T} { F }_{\rm v} \tag{11}$$ 应用拉格朗日乘数法将约束条件式(10)代入式(11) 得到含约束的势能泛函 $$ \varPi^\ast = \varPi + { \lambda }^{\rm T} ( { u}_{\rm b} - { C }_{{\rm bv}} { u }_{\rm v} ) \tag{12}$$ 将式(12)对5个变量分别进行变分，经过运算可得 $$ \left[\!\!\begin{array}{ccccc} { K}_{{\rm ii}} & { K}_{{\rm ib}} & { K}_{{\rm io}} & { K}_{{\rm iv}} & {\bf 0} \\ { K}_{{\rm bi}} & { K}_{{\rm bb}} & { K}_{{\rm bo}} & { K}_{{\rm bv}} & { I }_{{\rm bb}} \\ { K}_{{\rm oi}} & { K}_{{\rm ob}} & { K}_{{\rm oo}} & { K}_{{\rm ov}} & {\bf 0} \\ { K}_{{\rm vi}} & { K}_{{\rm vb}} & { K}_{{\rm vo}} & { K}_{{\rm vv}} & - { C }_{{\rm bv}}^{\rm T} \\ {\bf 0 } & { I }_{{\rm bb}} & {\bf 0} & - { C }_{{\rm bv}} & {\bf 0 } \end{array} \!\! \right]\left\{ \!\! \begin{array}{c} { u}_{\rm i} \\ { u}_{\rm b} \\ { u}_{\rm o} \\ { u}_{\rm v} \\ { \lambda } \end{array}\!\!\right\} = \left\{ \!\!\begin{array}{c} {\bf 0} \\ {\bf 0} \\ { F}_{\rm o} \\ { F}_{\rm v} \\ {\bf 0} \end{array} \!\! \right\} \tag{13}$$ 由式(13)中的第一个方程组可得子网格内部节点位移和宏观节点位移之间的联系 $$ { u }_{\rm i} = - { K }_{{\rm ii}}^{-1 } [{ K }_{{\rm io}} { u }_{\rm o} + ( { K }_{{\rm io}} { u }_{\rm o} + ( { K }_{{\rm iv}} { C }_{{\rm bv}} ) { u }_{\rm v} )] \tag{14}$$ 进一步可得多尺度单元的子网格节点位移和宏观节点位移之间的关系为 $$ \left\{ \!\!\begin{array}{c} {{ u }_{\rm v} }\\ {{ u }_{\rm o} }\\ {{ u }_{\rm i} }\\ {{ u }_{\rm b} } \end{array} \!\! \right\} = \left[\!\! \begin{array}{cc} { I }_{{\rm vv}} & {\bf 0} \\ {\bf0} & { I }_{{oo}} \\ { N }_{{\rm iv}} & { N }_{{\rm io}} \\ { N }_{{\rm bv}} & { N }_{{\rm bo}} \end{array} \!\! \right]\left\{ \!\! \begin{array}{c} { u }_{\rm v} \\ { u }_{\rm o} \end{array}\!\! \right\} \tag{15}$$ 式中 $$ \left. \begin{align} & {{N}_{\text{iv}}}=-K_{\text{ii}}^{-1}({{K}_{\text{iv}}}+{{K}_{\text{ib}}}{{C}_{\text{bv}}}),{{N}_{\text{io}}}=-K_{\text{ii}}^{-1}{{K}_{\text{io}}} \\ & {{N}_{\text{bv}}}={{C}_{\text{bv}}},{{N}_{\text{bo}}}=\mathbf{0} \\ \end{align} \right\} \tag{16}$$ 可简写为 $$ { u } = { N U } \tag{17}$$ 其中，${ u}$表示子网格节点上的位移，${ U}$表示宏观节点上的位移.$$ { N} = \left[\!\! \begin{array}{cc} { I }_{{\rm vv}} & {\bf 0} \\ { 0 } & { I }_{{\rm oo}} \\ { N }_{{\rm iv}} & { N }_{{\rm io}}\\ { N }_{{\rm bv}} & { N }_{{\rm bo}} \end{array} \!\! \right] \tag{18}$$

将式(18)代入式(2) $\sim $式(4) 中可以得到等效刚度矩阵${ K }_{\rm c} $，等效质量矩阵${ M }_{\rm c}$.

本节分别进行了静力分析，广义特征值分析和瞬态响应分析，并将计算结果与常规有限元的结果进行对比，验证该广义多尺度有限元算法的有效性和准确性. 其中，"FEM"表示传统有限元在细尺度上的解，作为参考解.

算例1 如图2所示，悬臂梁长为1.2，宽为0.24，左边为固定端，在右边边界上施加大小为20 kN/m 的均布力. 每个宏观单元的尺寸为0.06×0.06，横截面积为1.弹性模量的分布如图2(b)所示，每个宏观单元中间圆形夹杂区域的弹性模量在1×10$^{8}\sim $1×10$^{9}$之间随机变化，泊松比$\mu =0.3$；圆形夹杂外部的弹性模量为$E =1 \times 10^{8}$，泊松比$\mu =0.3$. 宏观单元的宏观节点分布如图3所示.

图2(Fig.2)

图2 计算模型 Fig.2 Computation

图3(Fig.3)

图3 3种不同的宏观单元节点分布 Fig.3 Three different kinds of coarse cells nodes distribution

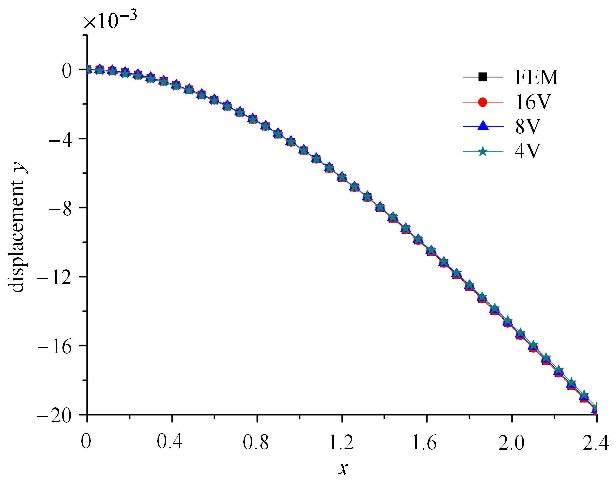
悬臂梁中性轴上$y$方向的位移值如图4所示，4个V节点，8个V节点以及16个V节点的位移曲线与传统有限元的解基本上是重合的，说明多尺度有限元计算的结果与传统有限元的计算结果吻合得很好.由图5可以发现，宏观单元中V节点个数的增加，多尺度有限元计算的结果越精确，相对误差最大的4个V节点的宏观单元与传统有限元的计算结果误差也是在2%以内，而16个V节点的宏观单元计算结果和传统有限元的计算结果几乎是相同的.由于该结构不是周期性的非均质材料分布，因此需要对每个宏观单元进行数值基函数的求解，再集成宏观单元.但从表1中可以看出，相比于常规有限元，多尺度有限元的计算效率有着显著的提高.

图4(Fig.4)

图4 中性轴$y$方向上的位移值 Fig.4 Displacement at neutral axis in the $y$ direction

图5(Fig.5)

图5 $y$方向的相对误差 Fig.5 Relative errors of the displacement $y$

表1(Table 1)

表1 悬臂梁静力分析计算效率比较Table 1 Comparisons of the computational efficiency for the static analysis of cantilever beam $N_{\rm DOF}$ Time/s FEM 115 778 13 315.6 16V 1 314 324.8 8V 578 300.5 4V 210 321.0

表1 悬臂梁静力分析计算效率比较 Table 1 Comparisons of the computational efficiency for the static analysis of cantilever beam

算例2 如图6所示，带孔悬臂梁包含20×4个宏观单元，悬臂梁的长为1.2，宽为0.24，左边边界$x$方向固定，左边边界的中点$y$方向固定. 每个宏观单元的尺寸为0.6×0.6，横截面积为1.弹性模量$E$为10$^{7}$，泊松比$\mu $为0.3. 其中V节点和O节点的分布如图7所示.

图6(Fig.6)

图6 计算模型 Fig.6 Computation

图7(Fig.7)

图7 5种不同的宏观单元节点分布 Fig.7 Five different kinds of coarse cells nodes distribution

粗网格下的广义特征值方程为 $$ { K }_{\rm C} { U }_{\rm C}^{i} = {\omega }_{i}^{2} { M }_{\rm C} { U }_{\rm C}^{i} \tag{19}$$ 其中，${ K }_{\rm C}$和${ M }_{\rm C}$是结构宏观尺度下的整体刚度矩阵和整体质量矩阵，$\omega_i$是结构的第$i$阶的圆频率，${ U}_{\rm C}^{i}$ 是与第$i$阶的圆频率相对应的广义未知量向量.

从图8当中可以看出，16个V节点的宏观单元得到的前50阶频率与传统有限元的解基本上是一致的. 而在低阶模态下，4个V节点和8个V节点的宏观单元也与传统有限元的解相近.但是随着模态阶数的增加，4个V节点和8个V节点相对于传统有限元解的误差也越来越大.由表1中可以看出，V节点的个数从4个增加到16个，第50阶频率的相对误差由19.39%减小到只有2.71%.而从图9可以看到，随着O节点个数的增加，多尺度算法求得的结果就越接近传统有限元的结果.从中可以看出宏观单元节点个数对计算精度有着显著的影响.本算例的计算效率如表2所示，可以看出多尺度计算方法比常规有限元法具有更高的计算效率.

图8(Fig.8)

图8 前50阶频率 Fig.8 The first 50 order frequencies

表2(Table 2)

表2 悬臂梁广义特征值分析的计算效率比较Table 2 Comparisons of the computational efficiency for the generalized eigenvalue analysis of cantilever beam $N_{\rm elem}$ $N_{\rm DOF}$ $\omega_{50}$/Hz Error of $\omega_{50}$/% Time/s FEM 23 040 50 338 8 594 --- 2 634 4V 80 210 10 260 19.39 74.2 8V 80 578 9 321 8.47 75.4 16V 80 1 354 8 828 2.71 73.2 16V4O 80 1 954 8 803 2.43 72.9 16V8O 80 2 594 8 782 2.18 133.3

表2 悬臂梁广义特征值分析的计算效率比较 Table 2 Comparisons of the computational efficiency for the generalized eigenvalue analysis of cantilever beam

图9(Fig.9)

图9 前50阶频率的相对误差 Fig.9 Relative errors of the first 50 frequencies

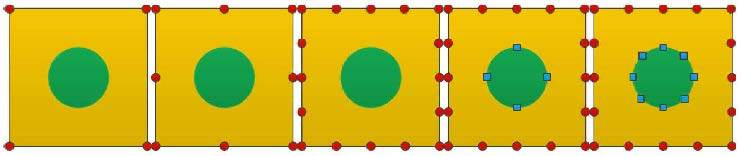
算例3 如图10所示，长为2.4，宽为1.92的非均质长方形平板，粗尺度网格划分如图10(a)所示，子网格如图10(b)所示，每个子网格的尺寸为0.24×0.24. 宏观单元上V节点和O节点的分布如图11所示. 其中${E}_{1} = 10^5$,$\mu _1 = 0.3$，$\rho _1 = 1$；${E}_{2} = 10^6$，$\mu _2 = 0.3$，$\rho _2 = 1$. 左右边界固定 $x$方向上的位移，底部固定$y$方向上的位移. 外力 $q(t)$从$x = 0$到$x = 0.96$均匀地分布在顶边界，$q(t)$可以表达为 $${q(t)} = {P(t) / 3.6} \tag{20}$$ $${P(t)} = \left\{ \!\! \begin{array}{ll} {8}\times {10}^{5}{t} , & {0} < {t} ≤ {0.025s} \\ {2}\times {10}^{4} , & {0.025s} < {t} ≤ {0.1s} \end{array} \right. \tag{21}$$ 结构的初始位移和初始速度均为零. 宏观尺度上的动力响应方程为 $$ { M}_{\rm C} \ddot{ U}_{\rm C} {(t)} + { K}_{\rm C} { U}{(t)} = { F}_{\rm C} {(t)} \tag{22}$$ 其中，$t$表示时间,${ M}_{\rm C} $和${ K}_{\rm C} $可以由式(2)和式(4)得到，初始时刻的外力向量${ F }_{\rm C}^{0} $由施加的荷载决定.这样，动力响应方程就可以用数值积分的方法来求解，这里采用比较常见的(逐步积分法) Newmark 算法^[30]来计算结构的动力瞬态响应. 在本算例中时间步长为$5\times 10^{ - 5}$，总计算时间为0.1 s.

图10(Fig.10)

图10 计算模型 Fig.10 Computation model

图11(Fig.11)

图11 5种不同的宏观单元节点分布 Fig.11 Five different nodes distributions of coarse element

$C$点和$D$点的$y$方向的位移响应如图12和图13所示. 随着V节点个数的增加，广义多尺度算法的位移响应曲线和传统有限元的曲线越接近. 当V节点增加到16个的时候，几乎是与传统有限元的解的曲线重合.对比16V，16V4O，16V8O三条曲线，可以看出O节点对于计算结果的精度有所提高.16V8O的曲线可以认为与传统有限元的曲线重合.

图12(Fig.12)

图12 $C$点$y$方向的位移响应曲线 Fig.12 Displacement response in the $y$-direction of point $C$

图13(Fig.13)

图13 $D$点$y$方向的位移响应曲线 Fig.13 Displacement response in the $y$-direction of point $D$

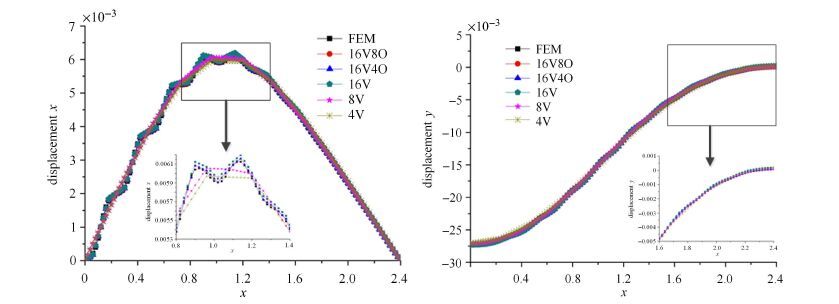
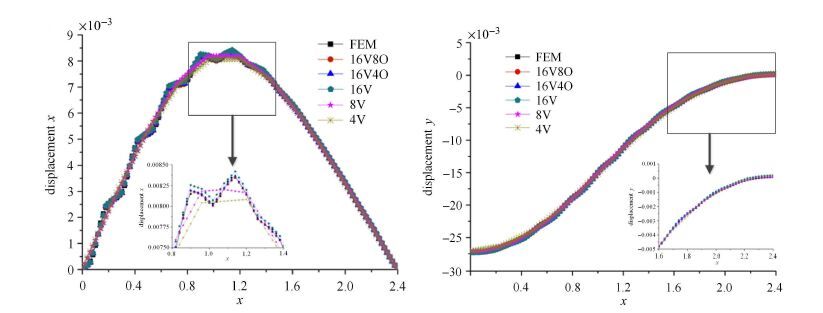
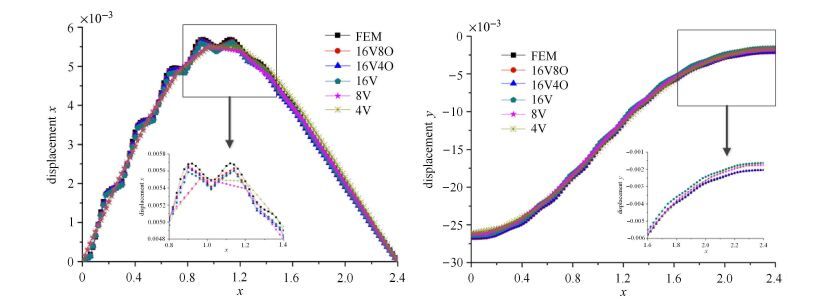
图14，图15和图16分别为直线$AB$上的点在$t=0.025$ s，$t=0.05$ s，$t=0.1$ s时刻的位移.可以看到，16个V节点的宏观单元的计算结果比4个V节点和8个V节点的计算结果更接近传统有限元的解.对比含有16个V节点的宏观单元和含有16个V节点和4个O节点的宏观单元的曲线，含有O节点的宏观单元的解得到的曲线更接近传统有限元的解，基本上可以认为与传统有限元的解重合.为了进一步说明广义多尺度有限元法的效率，对结构的总的自由度和计算时间与参考解做了比较，如表3所示，与传统有限元的解相比，广义多尺度有限元法的计算量和计算时间都大大减少，该多尺度方法极大地提高了计算效率.

图14(Fig.14)

图14 在$t = 0.025$ s $x$时刻$AB$直线在$x$方向和$y$方向的位移 Fig.14 Displacements at line $AB$ in the $x $ and $y $ directions at $t=0.025$ s

图15(Fig.15)

图15 在$t = 0.05$ s时刻$AB$直线在$x$方向和$y$方向的位移 Fig.15 Displacements at line $AB$ in the $x $ and $y $ directions at $t=0.05$ s

图16(Fig.16)

图16 在$t = 0.1$ s时刻$AB$直线在$x$方向和$y$方向的位移 Fig.16 Displacements at line $AB$ in the $x $ and $y $ directions at $t=0.1$ s

表3(Table 3)

表3 结构瞬态分析的计算效率比较Table 3 Comparison of computational efficiency for structural transient analysis $N_{\rm DOFEL}$ $N_{\rm ELEM}$ $N_{\rm DOF}$ Time/min FEM 8 57 600 115 634 276.8 4V 8 80 198 5.15 8V 16 80 554 5.18 16V 32 80 1 266 5.07 16V4O 40 80 1 906 5.31 16V8O 48 80 2 546 5.24

表3 结构瞬态分析的计算效率比较 Table 3 Comparison of computational efficiency for structural transient analysis

本文利用凝聚法和罚函数法，针对非均质材料的动力响应问题，发展了一种新的广义多尺度有限元法. 与传统扩展多尺度有限元相比，该方法中的多尺度基函数可直接通过矩阵运算得到，而不需要通过在子网格域上多次求解静力方程得到，且可以描述具有更加复杂边界的非均质单胞的变形情况，是对扩展多尺度有限元法的一种拓展.文中提出了一类含有两种不同宏观节点的宏观单元，详细阐述了该单元数值基函数的构造过程.并简明地给出了广义多尺度有限元法的计算流程.通过静力分析以及广义特征值和瞬态响应分析可知，与传统有限元方法相比，该方法具有较高的准确性和计算效率.

Zhuo Xiaoxiang, Liu Hui, Chu Xihua, Xu Yuanjie