连续纤维增强陶瓷基复合材料(CMCs)在高温环境下具有优异的抗氧化烧蚀性能和力学性能[1, 2],使其在高性能航空发动机[3]和高超声速飞行器热防护系统[4]等重要航空航天领域具有广阔的应用前景.作为一种新型的正交各向异性材料,面内剪切性能是其重要特性,目前也是其基本力学行为研究方面的薄弱环节.了解和掌握材料的剪切力学行为是推动其工程应用的必备工作.
至今为止,关于2D-SiC/SiC和2D-C/SiC复合材料的研究工作主要集中在轴向拉伸力学行为方面.在剪滞理论框架下,结合基体随机开裂和纤维随机断裂模型,材料的拉伸力学行为研究日趋完善[5, 6, 7, 8, 9, 10].相比于拉伸力学行为,材料的剪切力学行为研究还不多见.现有的研究成果表明,材料的剪切损伤失效机制主要包括基体开裂、分层、界面脱粘、纤维和纤维束的断裂和拔出[11, 12].在面内剪切载荷作用下,材料内部的基体开裂方向与纤维轴向夹角主要呈0°/90°和45° [13, 14].基体开裂和纵向基体碎块的刚体位移是材料表现出显著的非线性应力-应变行为和产生较大剪切塑性变形的主要原因[15, 16, 17],纤维与基体间的界面性能是控制材料剪切力学行为的主要因素[18].上述研究工作确认了材料的多种剪切细观损伤机制并阐明了材料的宏观剪切应力-应变行为特点[11, 19],但是在材料细观组份的承载机制和对应力-应变行为的影响机制方面,还有在材料的剪切细观损伤演化进程表征和模型建立等方面的研究工作还有待进一步开展和深入.
本文通过对2D-SiC/SiC和2D-C/SiC复合材料面内剪切力学行为进行研究,从材料细观结构和损伤机制入手,提出了纤维弯曲承载机制和表征材料细观损伤的变量,揭示了材料内部细观组份间剪切载荷的传递和分配机制,得到了不同细观损伤模式的演化规律.上述工作为后续进一步研究材料的损伤耦合效应和建立材料的细观损伤本构方程打下了基础.
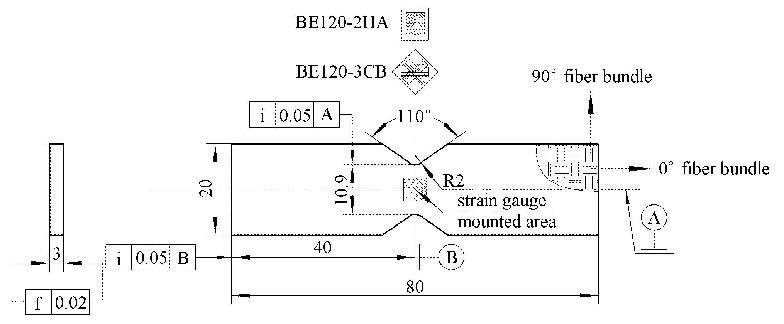
1 剪切试件和试验2D-SiC/SiC和2D-C/SiC复合材料分别由碳纤维和碳化硅纤维预制体通过化学气相渗透(CVI)工艺沉积碳化硅基体制备而成,纤维与基体间制有厚度约为200 nm的热解碳界面层.两种材料的纤维体积含量和孔隙率均为40%和19%左右,平均密度分别为2.4 g/cm$^{3}$和2.0 g/cm$^{3}$,常温下两种材料的热残余应力分别约为19 MPa[20]和130 MPa[21]. 试验采用约西佩斯库(Iosipescu)双边对称V型缺口试件.试验过程中通过在试件表面粘贴两种类型的应变片(BE120-2HA和BE120-3CB,中航工业电测仪器股份有限公司)分别获取剪切应变以及与0°纤维束呈0°和$\pm $45°夹角方向上的线应变. 试件加工尺寸和应变片粘贴细节如图1所示.
|
图1 约西佩斯库试件尺寸和应变片粘贴细节 Fig.1 Configuration of Iosipescu specimen and mounted details of strain gauges |
为方便进行循环加卸载,试验采用了如图2所示的勺型反对称加载装置,配合"Instron 8801"液压伺服试验机在室温下(25 ℃)进行剪切试验,加载速率为0.1 mm/min.试验过程中利用DH3820静态应变测试系统同步采集应变片所测应变数据.

|
图2 试件加持示意图 Fig.2 Photographs of a specimen within test fixture |
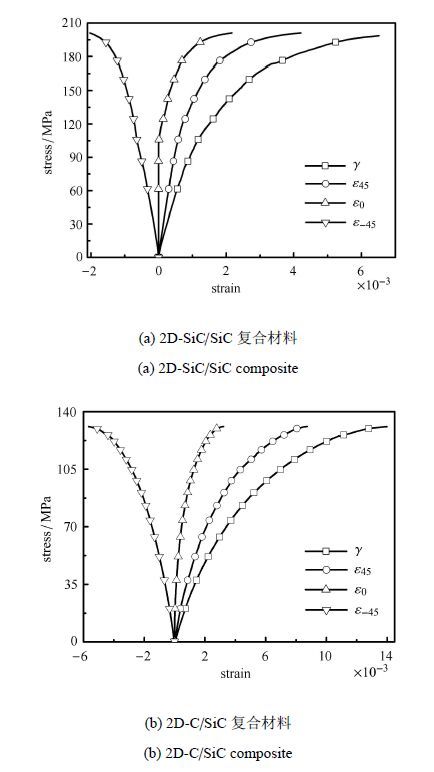
图3和图4分别给出了2D-SiC/SiC和2D-C/SiC复合材料在单调和循环加卸载过程中的剪切应力-应变曲线,其中$\gamma $,$\varepsilon _{45}$,$\varepsilon _{0}$和$\varepsilon _{ -45}$分别为剪切应变和与0°纤维束呈45°,0°和$-45$°方向上的线应变. 两种材料的剪切应力-应变行为均表现出显著的非线性. 较低应力水平下$\varepsilon _{45}$ 和$\varepsilon _{ - 45}$相差不大,而高应力水平下$\varepsilon_{45}$数值明显超出$\varepsilon _{ - 45}$. 这是因为剪切应力在$\pm $45° 方向上分别表现为拉伸和压缩应力,导致材料在45° 方向上产生更多的基体裂纹. 所以高应力水平下材料的剪切应变主要由$\varepsilon _{45}$贡献. 对比发现,2D-SiC/SiC复合材料对应应力-应变曲线具有明显的初始线性段(0$\sim $30 MPa),并且整体应变数值也较小;而2D-C/SiC复合材料没有明显的线性段且对应应变数值较大,这是材料内部较大的热残余应力所导致的.
|
图3 单调加载面内剪切应力-应变曲线 Fig.3 In-plane shear stress-strain curves of specimen under monotonic loading |
|
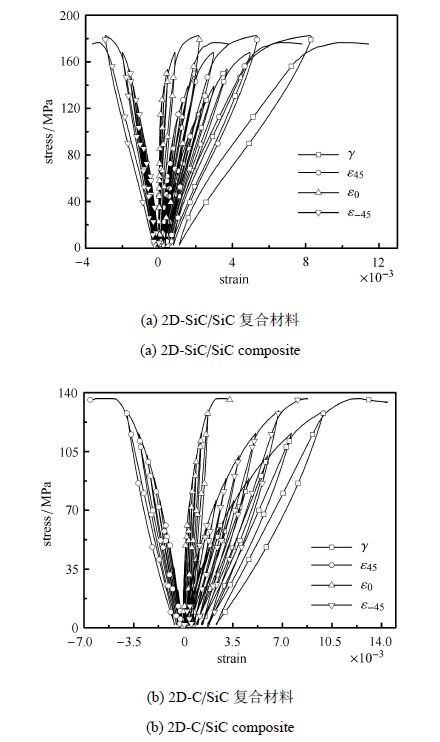
图4 循环加载面内剪切应力-应变曲线 Fig.4 In-plane shear stress-strain curves of specimen under cyclic loading |
在循环加卸载过程中,材料的四组应力-应变曲线都表现出显著的迟滞行为. 随着卸载峰值应力$\sigma_{\rm p} $的不断增大,曲线迟滞环宽度$L_{\rm h }$和残余应变$\varepsilon _0 $数值也不断增加;表明材料损伤随$\sigma _{\rm p }$增大而不断加剧. 通过观察$L_{\rm h} $和$\varepsilon _0 $随$\sigma _{\rm p} $的增长规律发现,2D-SiC/SiC复合材料的剪切损伤速率在$\sigma _{\rm p } $达到120 MPa之前很慢,而后快速增加;而2D-C/SiC复合材料的剪切损伤速率在整个加卸载过程中基本恒定.此外,低应力水平下2D-SiC/SiC复合材料对应曲线出现了明显的裂纹闭合现象,而后者无明显迹象.裂纹闭合效应的差异也主要是由于2D-C/SiC复合材料具有较大的热残余应力造成的.
2.2 剪切损伤失效模式为了解材料的剪切损伤模式和失效机制,通过扫描电镜对试件断口进行观察,得到的断口照片如图5所示. 由图5(a)可见,断面上0°纤维束发生横向折断,纤维全部断裂并伴有较短拔出;90°纤维束发生纵向劈裂,内部纤维与基体剥离严重,大部分纤维保持完好.由图5(b)看到,材料基体裂纹主要分布在与0°纤维束呈90°和45°夹角方向上,此外0°纤维束内部界面脱粘等轴向损伤和90°纤维束横向开裂损伤等可以看作是0° 夹角方向上的裂纹损伤.图5(c)和图5(d)是对0°纤维束断裂面的特征放大,可见纤维束内部发生严重的界面脱粘损伤,纤维与基体间出现大量缝隙;纤维的断面形貌和断裂位置的台阶状分布形态说明0°纤维束是在弯剪载荷作用下发生断裂破坏的.

|
图5 试件破坏断口电镜照片 Fig.5 The SEM photographs of fracture surface of 2D-SiC/SiC composite specimen |
综上所述,在剪切载荷作用下,材料基体裂纹主要分布在与0°纤维束呈0°/90°和45°夹角方向上;对比0°/90°纤维束的损伤形貌可知,材料的剪切应力-应变行为主要受0°纤维束损伤进程影响;当0°纤维束受弯剪载荷作用下发生断裂时,试件整体发生剪切失效破坏. 由于2D-C/SiC和2D-SiC/SiC复合材料具有相同的剪切损伤失效机制[11],在此不再赘述.
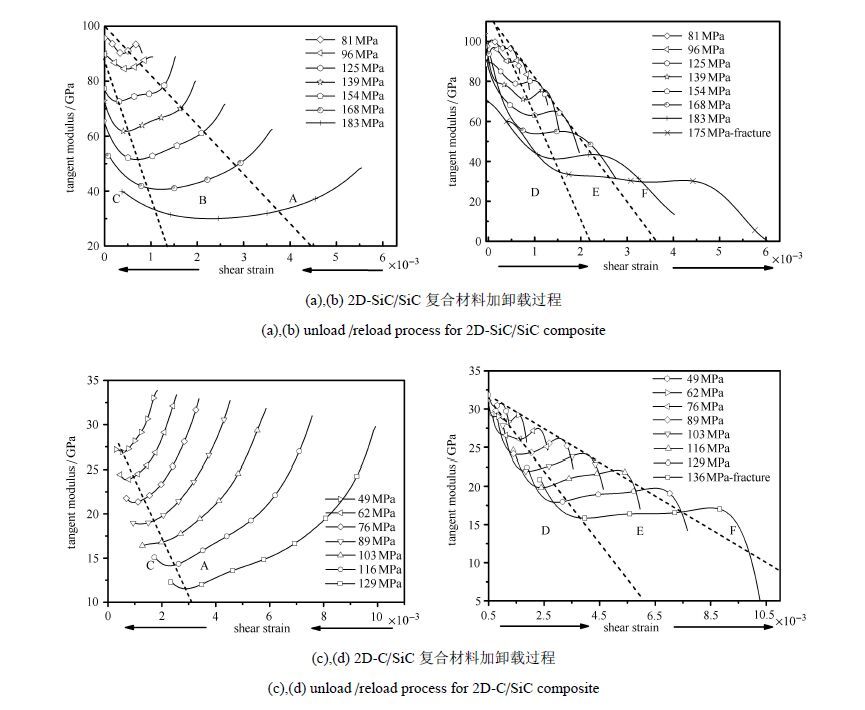
3 纤维弯曲承载机制通过将剪切应力-应变曲线($\tau -\gamma$)对$\gamma $求一阶导数分别得到了卸载和重加载过程中剪切切线模量随应变的变化曲线,如图6所示. 依据数值变化特点,可以将上述曲线大致划分为下述区域:下降区域A,D和F,上升区域C和E,以及过渡区域B.与轴向拉伸相同,材料的剪切迟滞环形状也是由材料内部损伤情况和材料细观组份间载荷传递分配机制决定的[20].分析发现,加卸载过程中材料剪切切线模量的上述变化特征是由基体裂纹闭合效应和纤维弯曲承载机制共同导致的.
|
图6 加卸载过程中材料剪切切线模量随剪切应变变化曲线 Fig.6 Relation curves between tangent shear modulus and shear strain under cyclic loading |
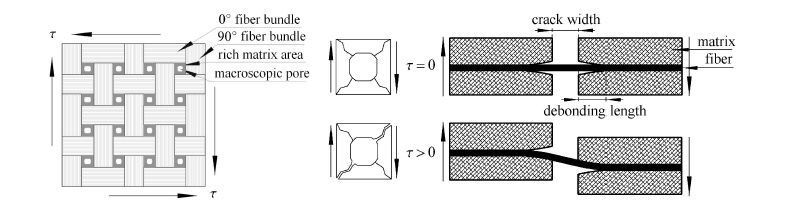
由于化学气相渗透制备工艺的特点,材料内部纤维束间存在大量的富基体区域和宏观孔洞,如图7中左图所示.复杂的孔洞形状会引起严重的应力集中现象,再加上热残余应力影响,富基体区域材料将率先在薄弱处开裂.随着载荷的增加,上述裂纹不断扩展并进入纤维束,当遇到纤维与基体间界面时,裂纹发生偏转沿界面层继续扩展.在纤维束内部基体裂纹两侧,将伴随发生界面脱粘和滑移. 受拉伸应力分量和热残余应力释放的影响,纤维束内部基体裂纹不会完全闭合;在剪切载荷作用下,相邻裂纹面间发生相互错动.裂纹间起到桥连作用的纤维将会发生弯曲变形并承担和传递剪切载荷.
|
图7 材料内部几何结构及纤维弯曲承载机制示意图 Fig.7 The sketch of geometric structure within composite and bearing mechanism of bending fiber |
加卸载过程中,基体裂纹和纤维束内桥连纤维随剪切载荷的形态变化如图7中右图所示.基体裂纹的张开和扩展会使材料整体的剪切模量下降,而低应力水平下发生的裂纹闭合会使模量上升.桥连纤维的弯曲刚度同材料剪切模量也呈正比关系,其大小具有如下关系 $$ R \propto \dfrac{rE_{\rm f} }{L_{\rm c} + L_{\rm d} } \tag{1}$$ 式中,$R$为桥连纤维弯曲刚度,$r$为纤维半径,$E_{\rm f }$为纤维弹性模量,$L_{\rm c } $和$L_{\rm d} $分别为图7中所示裂纹宽度和界面脱粘长度. 可见,在不同加卸载循环内,$L_{\rm c} $和$L_{\rm d} $会随$\sigma _{\rm p} $的增加而增加,并导致$R$值不断下降;同时桥连纤维的弯曲变形能力不断增强,即材料可以产生更大的剪切变形.需要指出的是,同一循环内随着施加载荷和桥连纤维弯曲变形的增加,脱粘区域基体对纤维的接触约束增强,也会增加其弯曲刚度,但是上述影响随着$\sigma_{\rm p} $的增加而逐渐减弱.在剪切受载状态下,界面性能和热残余应力等材料特性将通过影响裂纹宽度和界面脱粘长度进而影响材料的剪切应力-应变行为.
基于上述分析可知,图6中材料剪切切线模量上升区域C和下降区域D是由基体裂纹闭合效应造成的;下降区域A和上升区域E主要由桥连纤维弯曲刚度与施加应力的变化关系所控制;过渡区域B是裂纹闭合效应与纤维弯曲承载机制共同作用的结果;最后下降区域F是由新高应力水平下材料产生新的剪切损伤所造成的. 观察发现,随着$\sigma _{\rm p} $的增大,不同循环对应曲线在区域A和E内的数值变化速率不断减小而趋于平缓,区域对应应变范围不断增大.这是因为裂纹宽度和脱粘长度随$\sigma _{\rm p} $的增大不断增加,而桥连纤维弯曲刚度受接触约束增强影响不断减弱所导致的.由于2D-C/SiC复合材料在低应力水平下表现出很弱的裂纹闭合效应,最终造成了其卸载过程对应关系曲线不具有B区域特征.
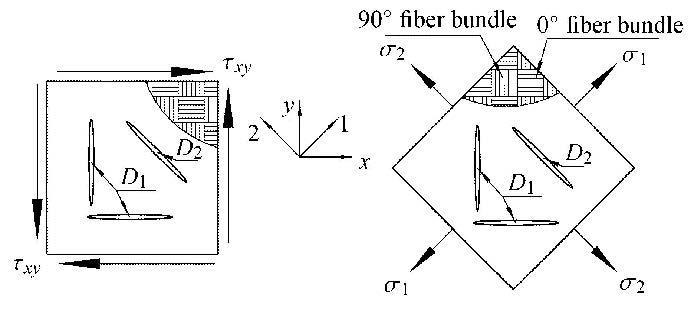
4 剪切损伤进程表征加载过程中材料内部的微裂纹主要集中在与0°纤维束呈0°/90°和45°夹角方向上,而在试件发生剪切断裂前纤维基本保持完好. 所以可以依据上述微裂纹的演化规律进而表征材料整体的剪切损伤演化规律.其中0°/90°方向裂纹主要造成了纤维束弹性性能的下降,下降程度记为$D_1 $;45°方向裂纹主要造成基体弹性性能的下降,记为$D_2 $.建立如图8所示的材料平面应力单胞模型进行分析,可以利用$D_1 $和$D_2 $ 两个损伤变量对材料的剪切损伤失效进程进行表征和分析.
|
图8 材料平面应力单胞模型示意图 Fig.8 The unit cell of composite under plane stress state |
首先将剪切应力$\tau _{xy} $由材料主方向坐标系($x-y$)转换到主应力坐标系(1--2)中,由应力转轴公式可得 $$ \sigma _1 = \tau _{xy} ,\sigma _2 = - \tau _{xy} ,\tau _{12} = 0 \tag{2}$$ 当材料发生损伤并产生微裂纹后,在1--2坐标系中材料仍可以近似认为是正交各向异性材料[13]. 那么在式(2)所描述应力状态下则有 $$ \varepsilon _1 = \sigma_1 / E_{11} ,\varepsilon _2 = \sigma_2 / E_{22} ,\gamma _{12} = 0 \tag{3}$$ 其中$E_{11} $和$E_{22} $分别为发生损伤后材料1和2方向上实时拉伸和压缩模量.由于基体裂纹具有细长形状,只会造成与其走向垂直方向上材料弹性性能的下降. 基于此定义损伤变量$D_1 $和$D_2 $的形式如下 $$ E_{11} = E_{11}^0 (1 - D_1 )(1 - D_2 ) ,E_{22} = E_{22}^0 (1 - D_1 )\tag{4}$$ 其中$E_{11}^0 $和$E_{22}^0 $分别为材料在1和2方向上的初始拉伸和压缩模量. 由应变转轴公式可得 $$ \varepsilon _x = \dfrac{1}{2}(\varepsilon _1 + \varepsilon _2 ) - \dfrac{\gamma _{12} }{2} \tag{5}$$ 综合式(2)$\sim $式(5)可得 $$ \varepsilon _x = \dfrac{\tau _{xy} }{2(1 - D_1 )}\Big (\dfrac{1}{E_{11}^0 (1 - D_2 )} - \dfrac{1}{E_{22}^0 } \Big) \tag{6}$$ 由剪切应变的计算公式并结合式(2) $\sim $式(4)可得 $$ \gamma _{xy} = \varepsilon _1 - \varepsilon _2 = \dfrac{\tau _{xy} }{1 - D_1 }\Big (\dfrac{1}{E_{11}^0 (1 - D_2 )} + \dfrac{1}{E_{22}^0 }\Big)\tag{7}$$ 连列式(6)和式(7)可求得$D_1 $和$D_2 $表达式如下 $$ D_1 = 1 - \dfrac{2\tau }{E_{22}^0 (\gamma _{xy} - 2\varepsilon _x )} ,D_2 = 1 - \dfrac{E_{22}^0 (\gamma _{xy} - 2\varepsilon _x )}{E_{11}^0 (\gamma _{xy} + 2\varepsilon _x )} \tag{8}$$
通过45°偏轴拉伸和压缩试验得到材料1和2方向上的初始拉伸和压缩模量$E_{11}^0 $和$E_{22}^0 $;并将单调面内剪切试验数据代入式(8),其中$\gamma $和$\varepsilon _0 $分别对应$\gamma _{xy} $和$\varepsilon _x $,得到加载过程中损伤变量$D_1 $和$D_2 $随施加剪切应力$\tau $的变化关系如图9所示.利用多项式可以很好地拟合上述变化关系,具体形式如下 $$ D_i = A_i + B_i \tau + C_i \tau ^2 + D_i \tau ^3 + E_i \tau ^4 + F_i \tau ^5 \tag{9}$$ 式中,$i = 1,2$. 各项系数具体数值统一在表1中列出.

|
图9 剪切加载过程中损伤变量$D_1 $和$D_2 $随施加应力的数值变化曲线 Fig.9 The variation of $D_1 $ and $D_2 $ with applied stress during in-plane shear loading process |
| 表1 式(9)中各项系数数值汇总 Table 1 Values of the coefficients in Eq.(9) |
由图9可以看到,2D-SiC/SiC复合材料45°方向裂纹的起裂应力约为100 MPa,明显大于0°/90°方向裂纹的起裂应力(35 MPa),而2D-C/SiC复合材料45°方向裂纹的起裂应力接近于0,明显小于0°/90°方向裂纹的起裂应力(35 MPa). 上述差异主要是由材料内部具有不同热残余应力所造成的. 此外,两种材料对应的基体开裂速率(曲线切线模量)随施加应力的变化规律也表现出不同特征,这与材料内部不同方向裂纹的相互作用机制和纤维性能参数有关. 利用损伤变量$D_1 $和$D_2 $随施加剪切应力的变化关系,可以反向对材料的剪切应力-应变行为进行预测和模拟. 需要指出,由于上述两种材料的损伤力学行为受环境温度影响显著,所以本文的研究结果只适用于材料的室温损伤力学行为分析.
5 结论(1)通过对平纹编织SiC/SiC和C/SiC复合材料面内剪切损伤力学行为的试验研究,表明高应力水平下材料的剪切应变主要由45°方向拉伸线应变贡献;材料的剪切损伤演化规律受热残余应力影响严重. 受剪状态下材料内部微裂纹主要集中在与纤维束呈0°/90°和45°方向上;0°纤维束内部桥连纤维承受显著的弯曲载荷和变形.
(2)基于桥连纤维的受约束形式、载荷承担和传递方式,提出的纤维弯曲承载机制,合理地解释了材料的剪切迟滞环形状.结果表明材料剪切迟滞应力-应变行为主要由裂纹闭合和纤维弯曲承载两大机制共同控制.
(3)基于材料内部微裂纹取向规律提出的两个细观损伤变量,直观地表征了材料内部剪切微裂纹随施加应力的损伤演化规律,以及热残余应力对上述规律的影响. 上述研究结论为后续进一步研究平纹编织陶瓷基材料的损伤耦合效应和建立材料的细观损伤本构方程打下了基础.
| 1 | Hallett SR, Green BG, Jiang WG, et al. An experimental and numerical investigation into the damage mechanisms in notched composites. Composites:Part A, 2009, 40:613-624 |
| 2 | Schmidt S, Beyer S, Knabe H, et al. Advanced ceramic matrix composite materials for current and future propulsion technology applications. Acta Astronaut, 2004, 55(3-9):409-420 |
| 3 | 张鹏, 朱强, 秦鹤勇等. 航空发动机用耐高温材料的研究进展. 材料导报, 2014, 28(11):27-31(Zhang Peng, Zhu Qiang, Qin Heyong, et al. Research progress of high temperature materials for aeroengines. Materials Review, 2014, 28(11):27-31(in Chinese)) |
| 4 | 鲁芹, 胡龙飞, 罗晓光等. 高超声速飞行器陶瓷基复合材料与热结构技术研究进展. 硅酸盐学报, 2013, 41(2):251-260(Lu Qin, Hu Longfei, Luo Xiaoguang, et al. Development of ceramic composite and hot structures for hypersonic vehicles. Journal of the Chinese Ceramics Society, 2013, 41(2):251-260(in Chinese)) |
| 5 | Vagaggini E, Domergue JM, Evans AG. Relationship between hysteresis measurements and the constituent properties of ceramic matrix composites:I, Theory. J Am Ceram Soc, 1995, 78(10):2709-2720 |
| 6 | Ahn BK, Curtin WA. Strain and hysteresis by stochastic matrix cracking in ceramic matrix composites. J Mech Phys Solids, 1996, 45(2):177-209 |
| 7 | Pryce AW, Smith PA. Matrix cracking in ceramic matrix composites under quasi-static tensile loading. Acta Metal Mater, 1993, 41:1269-1281 |
| 8 | Li LB, Song YD. An approach to estimate interface shear stress of ceramic matrix composites from hysteresis loop. Appl Compos Mater, 2010, 17:309-328 |
| 9 | Wang YQ, Zhang LT, Cheng LF, et al. Characterization of tensile behavior of a two-dimensional woven carbon/silicon carbide composite fabricated by chemical vapor infiltration. Material Science and Engineering A, 2008, 497:295-300 |
| 10 | 杨成鹏, 矫桂琼, 王波. 2D-C/SiC 复合材料的单轴拉伸力学行为及其强度. 力学学报, 2011, 43(2):330-337(Yang Chengpeng, Jiao Guiqiong, Wang Bo. Uniaxial tensile stress-strain behavior and strength of plain woven C/SiC composite. Chinese Journal of Theoretical and Applied Mechanics, 2011, 43(2):330-337(in Chinese)) |
| 11 | 管国阳, 矫桂琼, 张增光. 平纹编织C/SiC 复合材料剪切性能. 机械科学与技术, 2005, 24(5):515-517(Guan Guoyang, Jiao Guiqiong, Zhang Zengguang. In-plane shear fracture characteristics of plain-woven C/SiC composite. Mechanical Science and Technilogy, 2005, 24(5):515-517(in Chinese)) |
| 12 | Yan KF, Zhang CY, Qiao SR, et al. Failure and strength of 2D-C/SiC composite under in-plane shear loading at elevated temperature. Materials and Design, 2011, 33:3504-3508 |
| 13 | Weigel N, Kroplin B, Drinkler D. Micromechanical modeling of damage and failure mechanisms in C/C-SiC. Computational Materials Science, 1999, 16:120-132 |
| 14 | Weigel N, Dinkler D, Kroplin B. Micromechanically based continuum damage mechanics material laws for fiber-reinforced ceramics. Computers and Structures, 2001, 79:2277-2286 |
| 15 | Povl B, Heredia FE, Evans AG. In-plane shear properties of 2-D ceramic matrix composites. J. Am. Ceram. Soc., 1994, 77(10):2569-2574 |
| 16 | Keith WP, Kedward KT. The stress-strain behavior of a porous unidirectional ceramic matrix composite. Composites, 1995, 26(3):163-174 |
| 17 | Wang YQ, Zhang LT, Cheng LF. Comparison of in-plane shear behaviors of 2D plain woven C/SiC composites. Ceramic-Silikaty, 2012, 54:26-30 |
| 18 | Keith WP, Kedward KT. Shear damage mechanisms in a woven, nicalon-reinforced ceramic-matrix composite. J Am Ceram Soc, 1997, 80(2):357-364 |
| 19 | 李潘, 王波, 甄文强等. 二维编织SiC/SiC 复合材料的剪切性能. 机械强度, 2014, 36(5):691-693(Li Pan,Wang Bo, ZhenWenqiang, et al. In-plane shear properties of plane-woven SiC/SiC composites. Journal of Mechanical Strength, 2014, 36(5):691-693(in Chinese)) |
| 20 | 郭洪宝, 贾普荣, 王波等. 基于迟滞行为的2D-SiC/SiC 复合材料组份力学性能分析. 力学学报, 2015, 47(2):260-269(Guo Hongbao, Jia Purong, Wang Bo, et al. Study on constituent properties of a 2D-SiC/SiC composite by hysteresis measurments. Chinese Journal of Theoretical and Applied Mechanics, 2015, 47(2):260-269(in Chinese)) |
| 21 | 杨成鹏. 陶瓷基复合材料的力学特性和氧化损伤模拟研究.[博士论文]. 西安:西北工业大学,2011(Yang Chengpeng. Mechanical characterization and oxidation damage modeling of ceramic matrix composites. Xi'an:Northwestern Polytechnical University, 2011(in Chinese)) |
 2016, Vol. 48
2016, Vol. 48