固体表面被液体润湿以及液体经过表面时的运动机理是表面物理化学中非常重要的内容[1]. 许多工业生产过程,如机械润滑、喷雾冷却、喷涂印刷以及各种自清洁表面的制备[2, 3, 4, 5],都与液体的铺展与润湿特性有关.
在杨[6]和文策尔[7]分别建立了液滴在光滑和粗糙表面上的润湿模型之后,大量关于润湿过程的唯现象学研究也随之展开[8, 9, 10],主要探讨固体表面粗糙度对液滴的浸润深度以及固体壁面润湿性的影响. 拉菲马[8]通过总结前人的研究,推测液滴在粗糙表面上存在除凯西和文策尔模型外的第三种状态,这种状态下液滴部分浸入了粗糙表面的微槽内. 研究者发现,通过控制粗糙表面上织构的类型以及织构分辨率等几何参数,能够有效的改善液滴在固体表面上的铺展与润湿特性[9, 10].
近年来随着数值模拟方法和高速摄像技术的发展,国内外研究学者对液体在粗糙壁面上的微观运动细节进行了大量研究[11, 12, 13, 14, 15, 16].赵亚溥课题组[11, 12, 13]利用高速摄影技术和分子动力学模拟方法对亲水柱状阵列表面液滴的润湿过程展开了多尺度的研究,研究结果对理解液滴铺展的动力学特性具有重要的作用.陈石等[14]通过数学建模从理论上得到了液滴静态平壁铺展半径与液滴物性参数以及接触角之间的数学表达式,研究结果可用于分析计算液滴在水平壁面上的静态铺展半径和静态高度,但仅限于光滑固体壁面.李春曦等[15]利用数值计算方法研究了二维柱状阵列壁面上活性剂液滴的铺展特征,研究结果表明增大凹槽深度和宽度可加速活性剂液滴的铺展和液膜表面的振动幅度.宋云超等[16]利用数值模拟方法分析了液滴以不同速度撞击润湿壁面后的运动形态及运动机制,指出撞击速度和壁面液体层厚度共同决定了液滴的分离形态、飞溅速度等物理量.
在探究固体表面粗糙度对液滴铺展影响的过程中,三相接触线处的钉扎-去钉扎效应是不可忽视的重要因素[17, 18, 19, 20, 21, 22].当系统的尺度变小时,液体的表面积与体积比将会增大,这使得固-液间的浸润性显著影响液体的运动特性[17].液滴在实际粗糙表面上的微观接触角总是在一定范围内发生变化,而固-液接触面积却保持不变,安德雷德[18]将这种由于表面粗糙度引起的接触角变化归结为热动力学所导致的接触角滞后.拉奥等[19]认为接触线的钉扎效应是液滴在表面上流动时能量损耗的度量. 王晓东等[20],魏明锐等[5]以及曹晓平等[21]则从接触线上的受力情况出发,提出钉扎效应的静摩擦力模型,能够合理的解释由于表面粗糙度引起的接触角变化.周建臣等[22]研究了固着液滴的振动特性,指出在低频率范围内液滴与基底的接触线出现显著的固着-移动现象,接触线的震荡行为与液滴对外界驱动的效应密切相关.
已有的研究表明:表面粗糙度对液滴的铺展过程以及壁面润湿性有重要的影响,接触线处的钉扎-去钉扎转变也与表面粗糙度的大小密切相关.但是真实固体基面的表面形貌往往是一个随机变量,粗糙度与壁面润湿性间的关系缺少参数化表征.另外,目前对表面粗糙度对液滴铺展过程影响的研究大多是针对单一的织构类型进行分析和探讨[11, 12, 13],而对于织构的几何特性以及液滴铺展过程中接触线的力学特性研究较少.针对这一问题,本文以亲水表面为基底,采用数值模拟与润湿性实验相结合的方法,观察不同类型的离散型织构表面上液滴的铺展过程,引入织构润湿因子$\theta^{\ast }$,探究不同类型的离散型织构对表面润湿性以及液滴铺展特性的影响程度,同时分析表面粗糙度在液滴铺展过程以及接触线钉扎-去钉扎转变中的作用机理,以期为通过构造表面织构类型控制其润湿性提供一定指导.
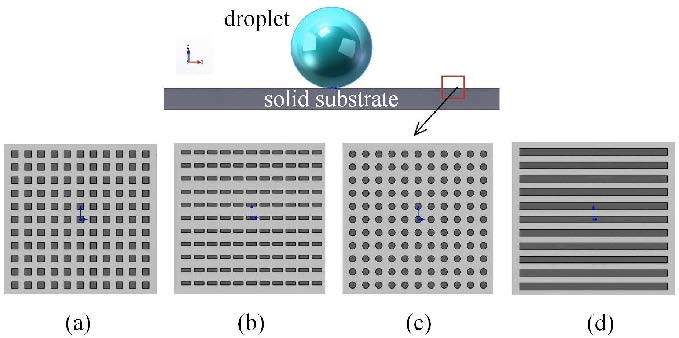
1 数值模型计算 1.1 模型结构基于三维建模软件 Solidworks,本文建立了4种不同类型的离散型织构表面,分别为正方形、矩形、圆形和槽状织构,如图1所示. 根据实际液滴的体积大小和铺展范围,确定织构区域面积为10 mm × 10 mm,织构的相关参数如表1所示. 液滴初始位置定义在微织构区域中央,$z$方向上液滴的下端刚接触到织构表面.
|
图1 离散型织构表面示意图 Fig.1 Sketch of the surfaces with different discrete texture |
| 表1 离散型织构相关参数 Table 1 Control parameters of discrete textures |
本文采用45钢、水以及空气作为固液 气三相的模拟工质. 水为不可压缩的黏性流体,密度1 000 kg/m$^{3}$,黏度0.001 Pa$\cdot $s,表面张力 $\gamma_{\rm lv}$为0.072 N/m, 重力加速度${ g}$为9.8 m/s$^{2}$,水在45钢表面的杨氏接触角为80$^{\circ}$.杨氏接触角为不考虑固体表面粗糙度影响的理想接触角,由润湿基本方程所定义 $$ \cos \theta = \dfrac{\gamma _{\rm sv} - \gamma _{\rm sl} }{\gamma _{\rm lv} } $$
根据离散型织构的区域面积建立流域的计算模型,由于液滴初始轮廓为球体,以经过液滴球心的直径为$z$轴,液滴在$x$方向上的铺展具有对称性,如图2右所示. 为了减小计算量,节约计算时间,故对液滴的1/2进行网格划分.另外,由于固体表面存在尺寸较小的离散型织构,为了提高计算精度,对织构处的网格进行局部加密.整个计算模型的网格数约为55万,计算模型如图2所示.

|
图2 计算模型及1/2的网格模型 Fig.2 Computational model and 1/2 mesh model |
考虑水为不可压缩黏性流体,则描述其铺展过程的动量和连续性方程可写为 $$\dfrac{\partial {P}}{\partial {x}} + \rho \cdot {G}_{x} = \mu \cdot \Big ( \dfrac{\partial ^2{u}}{\partial {x}^2} + \dfrac{\partial ^2{u}}{\partial {z}^2} \Big ) \nabla^2 u \tag{1}$$ $$\dfrac{\partial {P}}{\partial {z}} + \rho \cdot {G}_{x} = \mu \cdot \Big ( \dfrac{\partial ^2{w}}{\partial {x}^2} + \dfrac{\partial ^2{w}}{\partial {z}^2} \Big )\nabla^2 w \tag{2}$$ $$\dfrac{\partial {u}}{\partial {x}} + \dfrac{\partial {w}}{\partial {z}} = 0 \tag{3}$$ 其中,$u$和$w$分别为$x$和$z$方向上的速度分量,$\rho $是液体密度,$\eta $ 是液滴的运动黏度,$\triangledown^{2}$ 为二维拉普拉斯算子,$P$为压强,$G_{x}$和$G_{z}$分别是重力沿$x$和$z$方向上的加速度.
依据润滑近似假设,奥朗等[23]推导了液滴沿光滑壁面铺展过程中的膜厚演化方程.而在液滴的实际铺展过程中,由于受到表面粗糙度和外界条件的影响,液滴的实际铺展尺度不可能满足润滑近似条件,但拉尔森等[24]指出,无论薄膜是在大方向尺寸上的流动,还是在小方向尺寸上的流动,利用润滑近似计算的结果与实验结果都非常相似.因此,液滴在粗糙固体壁面上铺展运动过程也可采用润滑近似下的控制方程.
本文采用流体体积函数方法(VOF)进行数值模拟.流体体积函数法利用单元格流体体积计算自由液面的位置和形状,可以很好地确定接触线的铺展半径、速度分布以及液气界面的变形,这些参数的变化规律为接触线的移动机制理论的建立奠定了基础.
流体沿固体壁面流动时,传统的边界条件为无滑移边界条件. 根据设定的坐标系方向,液滴沿$z_{\min}$重力方向铺展,因此边界条件设置墙,其余5个方向选择默认边界条件.
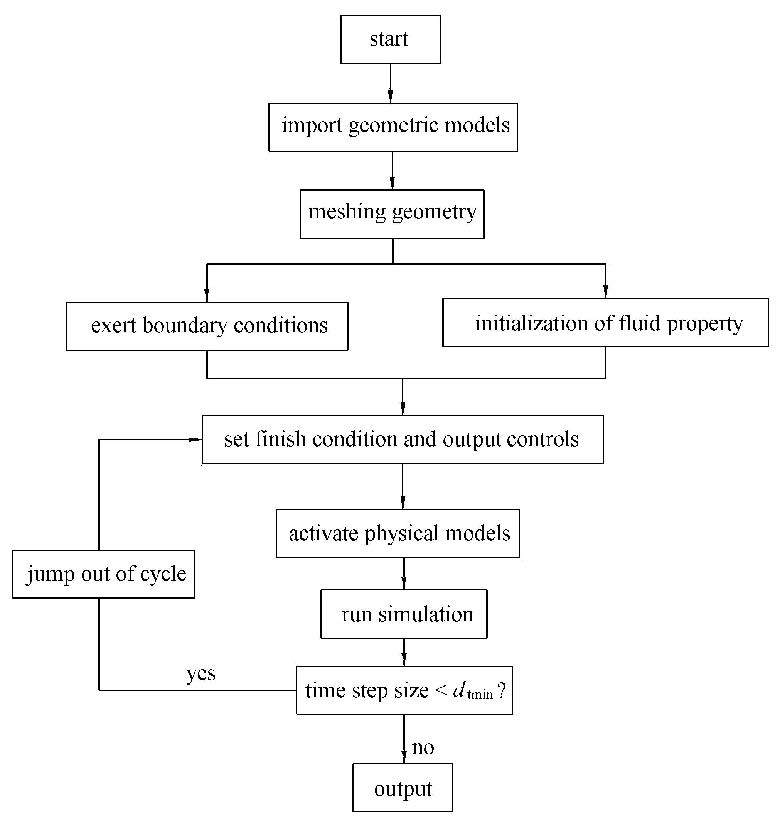
1.4 数值求解流程液滴在固体表面上的铺展过程是一个典型的气液两相流动与固壁相互作用的耦合过程. 本文采用 Flow-3D 软件进行数值模拟计算,求解流程如图3所示. 需要注意的是,模拟计算开始之前需要设置最小时间步长$d_{\rm t\min}$,以保证计算过程的收敛性.
|
图3 数值仿真流程图 Fig.3 Simulation flow chart |
由于 Flow-3D 采用变步长计算,当液滴铺展至某一时刻计算步长小于$d_{\rm t\min}$时,系统将自动跳出循环,此时需要重新设置输出参数与结束条件.
2 润湿性试验方法为了验证数值仿真结果的有效性,采用激光微造型技术,以45钢为固体基底材料,制备图1所示的4种不同类型的离散型织构表面.随后在SL200KS界面张力仪上进行接触角测量实验,利用张力仪摄像系统对室温条件下的水滴壁面铺展过程进行了动态记录. 表2给出了接触角测量时的相关参数.
| 表2 试验条件参数 Table 2 Parameters of experimental conditions |
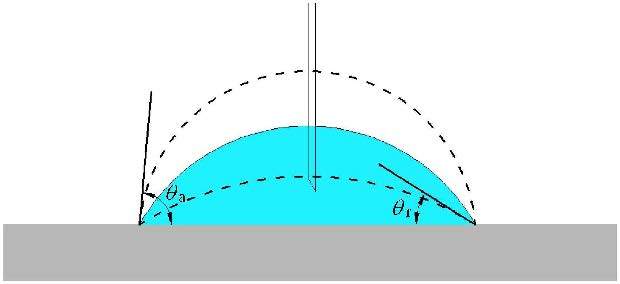
当液滴铺展至平衡位置时,如果继续向液滴内部添加液体,可以观察到三相接触线被钉扎在固体表面,液滴的平衡接触角不断增大. 当液滴的体积增大到一定程度时,接触线又开始移动,平衡接触角减小.接触线的这种钉扎-去钉扎效应与接触角滞后的大小密切相关,通常用上限值 $\theta_{\rm a}$与下限值 $\theta_{\rm r}$之差表示接触角滞后的大小,该数值的大小可以看做是黏附和摩擦的度量指标[19].如图4所示,本文将采用增减体积法分别测量液滴在不同离散型织构表面上的滞后性大小,并与未织构表面作对比,进而分析表面粗糙度对接触线钉扎-去钉扎效应的作用机理.
|
图4 增减体积法 Fig.4 Add/remove volume method |
随着对表面润湿研究的深入,液滴铺展过程的动态特性以及表面粗糙度的影响规律已经无法通过一个静态接触角值直接反映.假设液滴在固体基面上的杨氏接触角为 $\theta_{\rm y}$,在离散型织构表面上的表观接触角为 $\theta_{\rm a}$,引入如下无量纲参数 $$ \theta ^ * = \dfrac{{cos}\theta _{\rm a} - \cos \theta _{\rm y} }{\cos \theta _{\rm y}} \tag{4}$$ 其中,$\theta^{\ast }$为织构润湿因子,表征不同类型的离散型织构对表面润湿性的影响程度.接触线的动态铺展半径为$R$,最终铺展半径为$R_{\rm f}$,铺展速度$v$,铺展时间$t$.
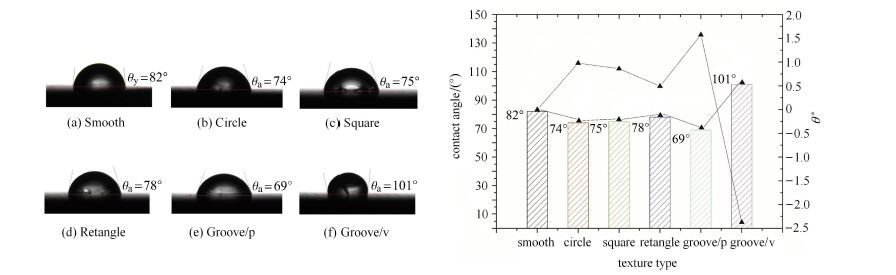
3.1.1 织构类型对表面润湿性的影响图5(a) $\sim $图5(e)为SL200KS界面张力仪所测得的液滴在不同离散型织构表面的平衡接触角,实验结果显示相较于未织构的光滑表面,4种离散型织构表面上的平衡接触角均变小,铺展半径增大,表面润湿性得到改善. 另外,织构润湿因子 $\theta^{\ast }$的变化规律表明槽状离散型织构对表面润湿性的影响程度最大,液滴在其上的平衡接触角最小,铺展特性最优.图6(a)为液滴铺展过程的数值模拟结果.为了验证其有效性,本文对比了赵亚溥课题组分子动力学模拟过程[11],如图6(b).两组数值模拟结果均表明表面粗糙度对液滴的平壁铺展过程具有促进作用,通过合理的微织构设计可以使固体表面的润湿特性得到改善.
|
图5 液滴在不同离散型织构表面上的平衡接触角 Fig.5 Contact angle and $\theta^{\ast }$ on the textured surfaces |
|
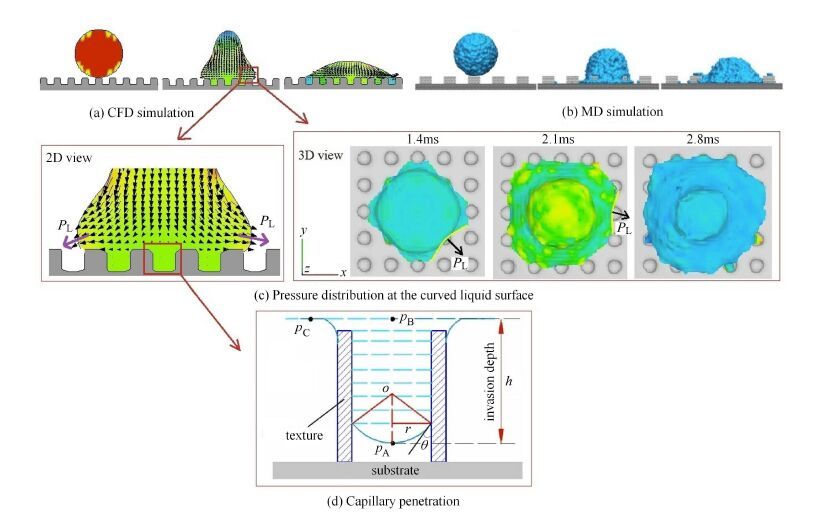
图6 流体动力学仿真和分子动力学仿真[11]结果示意图 Fig.6 CFD and MD simulations of a droplet spreading on the textured surfaces[11] |
如图6(d)所示,当液滴沿固体表面铺展时,最靠近固体表面的液体分子在毛细力作用下率先向前加速并进入微织构内部,固液接触面积随之增大. 此后,位于上端的液体(体区液体)在前驱膜[12]的基础上向四周铺展,从二维铺展示意图中可以看到,液滴内部的拉普拉斯压力差是促进液体铺展的主要驱动力.随着铺展时间的推移,位于铺展前沿的液体分子部分浸润织构内部,导致液面曲率增大,液滴内部的拉普拉斯压力上升.增大的$P_{\rm L}$为相邻离散型织构间的液体提供了额外的驱动力和能量,使得接触线的铺展速度加快,接触角不断减小.从三维示意图可以看到,由于离散型织构的存在,$P_{\rm L}$由圆心指向四周,加速了铺展过程.赵亚溥等人通过数值计算得到弯曲液面处的$P_{\rm L}$量级,与惯性力作用相比,发现接触线处的拉普拉斯压力是促使液滴铺展特性变优的主要原因[13],本文的研究结果与其有较好的一致性.
根据流体体积函数方法,选取$j=45,k=5$,$1<i<87$ (坐标为$y=0.3,z=0.05, 0<x<0.6$)所在的流体截面进行内部压力分析. 图7为液滴在圆形织构表面铺展时不同时刻的内部压力分布图.通过观察可以发现,流体在任意铺展时刻的压力分布近似满足两端大中间小的分布规律,铺展两端压力大的原因是由于铺展前沿的液体分子在毛细作用下逐渐浸润了织构内部,弯曲液面处的曲率突然增大,从而导致液体内部的拉普拉斯压力变大.

|
图7 液滴在不同铺展时刻的内部压力分布图 Fig.7 Pressure distribution inside the droplet at different spreading time |
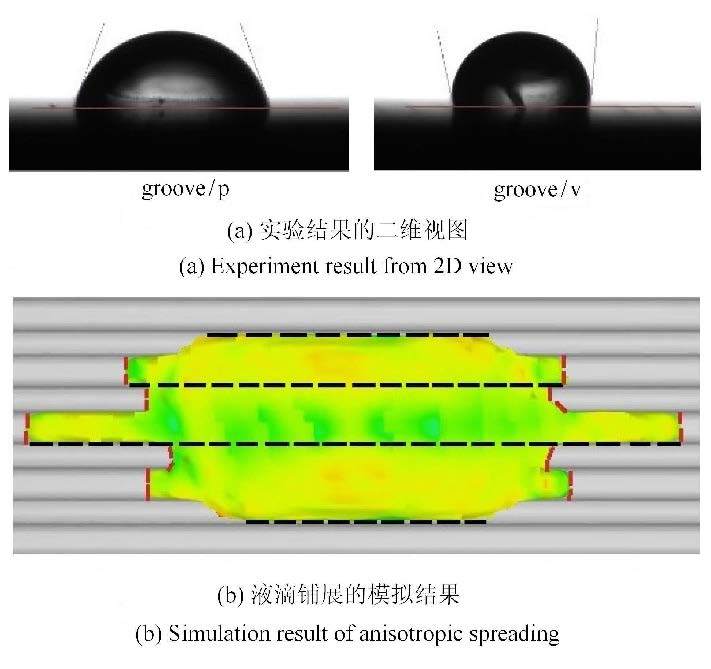
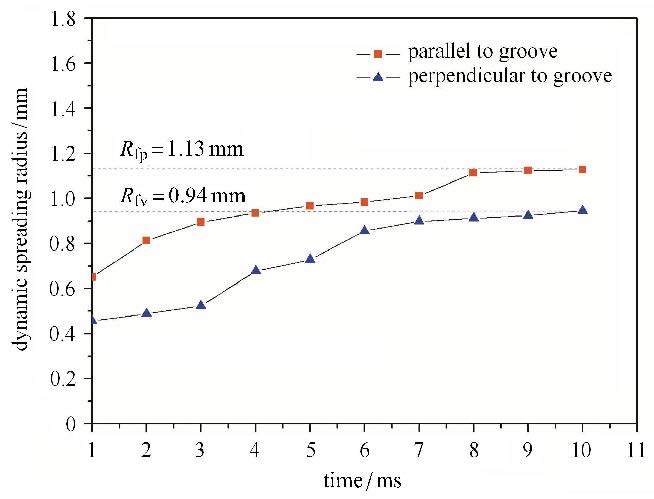
在槽状织构表面进行接触角测量实验时,液滴在平衡位置呈现出两种截然不同接触角形态,如图8(a)所示. 平行于槽织构方向(groove/p)的接触角较小,在所有的表面中润湿因子最大,液滴铺展效果最优;而垂直于槽织构方向(groove/v)的接触角较大,织构润湿因子小于0,液滴铺展特性反而变差. 数值模拟过程同样观察到了这种现象,结果如图8(b)所示.液滴的这种各向异性铺展特性与粗糙表面的织构类型有关. 本文所设计的4种离散型织构中槽状织构属于各向异性纹理,当液滴在槽状织构表面铺展时,平行于槽织构方向的固液气三相接触线连续好,能量势垒低,液滴铺展速度快,铺展半径大,如图8(b)标注的黑色虚线;垂直于槽织构方向的移动接触线被离散型织构阻断,液滴跨越相邻织构所需克服的能量势垒大,因而铺展特性差,如图8(b)标注的红色虚线. 图9分别给出了液滴在平行和垂直于槽两个方向上的铺展半径随时间的变化关系图.很明显可以看到平行于沟槽方向的液滴铺展速度更快,最终铺展半径更大,而垂直于沟槽方向的液滴铺展特性较差,润湿接触角较大.液滴在各向异性织构表面上的铺展特性对许多基于异性材料的光学和磁学器件以及化学生物传感器的进一步实际应用具有非常重要的意义[25],本节从接触线的连续性角度分析了液滴在各向异性织构表面上的铺展机理,以期为特殊润湿性能的表面形貌设计提供了一定指导.
|
图8 液滴铺展过程的各向异性特性 Fig.8 Anisotropic property of the droplet spreading process |
|
图9 动态铺展半径随时间的变化关系图 Fig.9 Dynamic spreading radius $R$ as a function of time $T$ |
由于表面粗糙度、表面多级结构以及外界污染等因素的存在,处于平衡铺展位置下的液滴若想继续沿固体壁面铺展,需要克服基底对接触线的钉扎作用.在3.1.2中,本文分析了液滴铺展过程中接触线的力学特性,得到弯曲液面处的拉普拉斯压力是主导液滴铺展的主要动力.
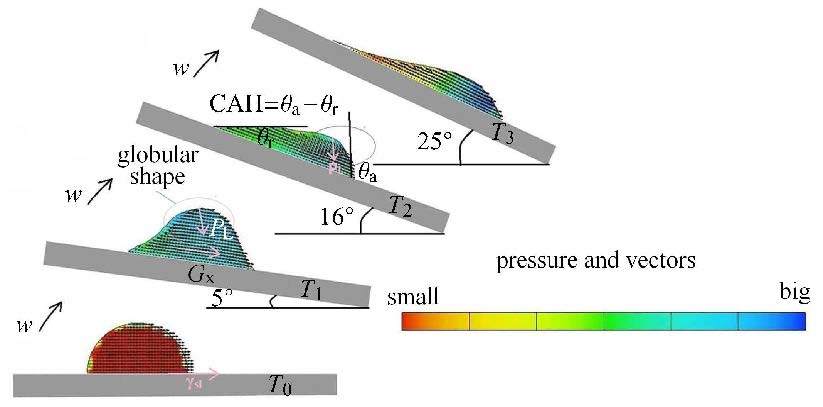
图10为数值仿真得到的液滴沿倾斜壁面铺展时接触线附近流体压力分布图,模拟过程采用倾斜平板法.研究结果表明:弯曲液面处的拉普拉斯压力和液滴自身重力所引起的下滑力与表面粗糙度所引起的黏滞阻力之间的动态平衡,是接触线发生钉扎-去钉扎转变的主要原因.$T_{0}$至$T_{1}$初始铺展阶段,表面张力起主导作用,三相接触线沿固体基面向下移动,固液接触面积逐渐增大,液滴表面能也逐渐增大;$T_{1}$至$T_{2}$接触角滞后阶段,位于液滴上层的流体在拉普拉斯压力$P_{L}$和重力引起的下滑力$G$的共同作用下继续向前铺展,而位于固液接触面处的最下层流体,由于表面粗糙度引起的黏性阻力作用,钉扎在倾斜表面的凹坑中停滞不前,使得前沿接触角逐渐增大,后沿接触角逐渐减小,即接触角发生滞后;$T_{2}$至$T_{3}$铺展至平衡阶段,随着前沿接触角的不断增大,弯曲液面处的曲率不断增大,拉普拉斯压力也随之不断增大,当$P_{L}$和$G$引起的下滑力大于黏滞阻力时,三相接触线又继续沿倾斜表面铺展,并最终以稳定的铺展速度沿斜面向下滑动.
|
图10 接触线附近流体压力分布图 Fig.10 Distribution of Laplace pressure and gravity at different rolling angle |
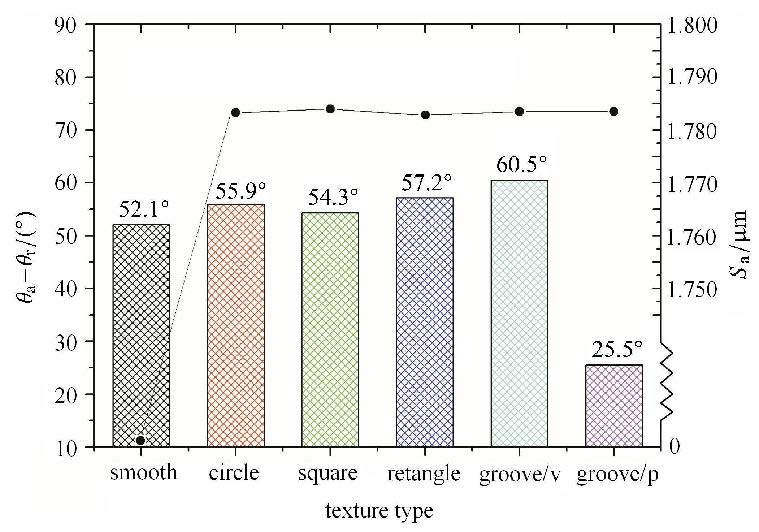
图11是在SL200KS界面张力仪上利用增减体积法测得的液滴在不同离散型织构表面的接触角滞后大小. 离散型织构的表面粗糙度$S_{\rm a}$利用三维光学轮廓仪(Talysulf CCI Lite)测得,$S_{\rm a}$越大,表面越粗糙. 可以看到未织构的原始光滑表面接触角滞后最小,经过激光微织构后的固体表面粗糙度增大,接触角滞后也明显增大. 这是因为液滴在粗糙表面铺展至平衡位置后,铺展前沿的三相接触线浸润了离散型织构内部,导致固液真实接触面积增大,原本连续的三相接触线被离散型织构所阻断,阻碍了液滴的继续铺展.
|
图11 不同离散型织构表面的接触角滞后大小 Fig.11 Contact angle hysteresis on the textured surfaces |
另外,槽状织构表面上的钉扎效应还表现出了方向性. 如图11所示,平行于槽纹理方向的的接触角滞后为25.5°,在所有的表面中滞后效应最小,表明液滴沿固体壁面继续铺展需要跨越的能量势垒低,因而铺展特性好;垂直于槽纹理方向的的接触角滞后为60.5°,滞后效应最明显,铺展特性最差.
4 结论(1)液滴在离散型织构表面铺展时,液滴内部的拉普拉斯压力差是促进液滴铺展的主要驱动力. 随着铺展时间的推移,位于铺展前沿的液体分子部分浸润织构内部,导致液面曲率增大,液滴内部的拉普拉斯压力上升. $P_{\rm L}$增大为相邻离散型织构间的液体提供了额外的驱动力和能量,接触线的铺展速度加快,接触角不断减小,从而铺展特性变优.
(2)在所设计的4种离散型织构表面中,槽状织构对表面润湿性的影响程度最大,通过比较织构润湿因子$\theta^{\ast}$的大小,发现液滴在其上的铺展过程具有各向异性特性,平行于槽织构方向的三相接触线连续,能量势垒低,液滴铺展速度快,铺展半径大;垂直于槽织构方向的移动接触线被离散型织构阻断,液滴跨越相邻织构所需克服的能量势垒大,因而铺展特性差.
(3)弯曲液面处的拉普拉斯压力和液滴自身重力所引起的下滑力与表面粗糙度所引起的黏滞阻力之间的动态平衡,是接触线发生钉扎-去钉扎转变的力学作用机制.另外,接触线的钉扎效应与固体表面粗糙度的大小和微织构类型密切相关,表面粗糙度越大,钉扎效应越明显,其中槽状织构对接触线的钉扎作用还具有方向性.
| 1 | 赵亚溥. 表面与界面物理力学. 北京:科学出版社,2012(Zhao Yapu. Physical Mechanics of Surfaces and Interfaces. Beijing:Science Press, 2012(in Chinese)) |
| 2 | 杨淑燕,郭峰,马冲. 固液润湿性对流体动压润滑薄膜的影响. 摩擦学学报,2010,30(2):203-208(Yang Shuyan, Guo Feng, Ma Chong. Influences of the liquid/solid wettability on thin hydrodynamic lubrication films. Tribology, 2010, 30(2):203-208(in Chinese)) |
| 3 | 胡海豹,鲍路瑶,黄苏和. 不同润湿性纳米通道内库埃特流动的模拟. 力学学报,2013,45(7):507-514(Hu Haibao, Bao Luyao, Huang Suhe. Simulation of the liquid couette flow in a nano-channel with different wettability. Chinese Journal of Theoretical and Applied Mechanics, 2013, 45(7):507-514(in Chinese)) |
| 4 | Zhao HY,Wen L, Guo GP. A new model for thermodynamic analysis on wetting behavior of superhydrophobic surfaces. Applied Surface Science, 2012, 258:2707-2716 |
| 5 | 魏明锐,刘明嘉,颜伏伍等. 液滴平壁铺展过程分析. 内燃机学报,2012,30(6):539-543(Wei Mingrui, Liu Mingjia, Yan Fuwu, et al. Analysis of spreading process of droplet on flat surface. Transaction of Csice, 2012,30(6):539-543(in Chinese)) |
| 6 | Young T. An essay on the cohesion of fluids. Philosophical Transactions of the Royal Society of London, 1805, 95:65-87 |
| 7 | Wenzel RN. Resistance of solid surfaces to wetting by water. Industrial Engineering Chemistry, 1936, 28:988-994 |
| 8 | Lafuma A, Quéré D. Superhydrophobic states. Nature Materials, 2003, 2:457-460 |
| 9 | 程帅,董云开,张向军. 规则粗糙固体表面液体浸润性对表观接触角影响的研究. 机械科学与技术,2007,26(7):822-827(Cheng Shuai, Dong Yunkai, Zhang Xiangjun. Study of the influence of apparent contact angle on regular rough surface considering liquid wetting properties. Mechanical Science and Technology for Aerospace Engineering, 2007,26(7):822-827(in Chinese)) |
| 10 | 杨常卫,何枫,郝鹏飞. 微结构疏水表面上液滴的表观接触角. 中国科学:化学, 2010, 40(10):1545-1549(Yang Changwei, He Feng, Hao Pengfei. The apparent contact angle on hydrophobic surface with micro-texture. Scientia Sinica Chimica, 2010, 40(10):1545-1549(in Chinese)) |
| 11 | Yuan QZ, Zhao YP. Multiscale dynamic wetting of a droplet on a lyophilic pillar-arrayed surface. Journal of Fluid Mechanics, 2013, 716:171-188 |
| 12 | Yuan QZ, Zhao YP. Wetting on flexible hydrophilic pillar-arrays. Scientific Reports, 2013, 3:1944 |
| 13 | Yuan QZ, Huang XF, Zhao YP. Dynamic spreading on pillar-arrayed surfaces:viscous resistance versus molecular friction. Physics of Fluids, 2014, 26:092104 |
| 14 | 陈石,陶英,沈胜强等. 平壁液滴静态铺展影响因素的研究. 力学学报,2014,46(3):330-335(Chen Shi, Tao Ying, Shen Shengqiang, et al. Static spreading of droplet impact on solid surface:influence factor. Chinese Journal of Theoretical and Applied Mechanics, 2014,46(3):330-335(in Chinese)) |
| 15 | 李春曦, 杨保才, 叶学民. 分离压对波状基底上活性剂液滴铺展过程的影响. 力学学报,2015,47(1):71-81(Li Chunxi, Yang Baocai, Ye Xuemin. Effect of disjoining pressure on spreading of liquid droplet containing surfactant over corrugated topography surface. Chinese Journal of Theoretical and Applied Mechanics, 2015, 47(1):71-81(in Chinese)) |
| 16 | 宋云超,宁智,孙春华等. 液滴撞击湿润壁面的运动形态及飞溅运动机制. 力学学报,2013,45(6):834-842(Song Yunchao, Ning Zhi, Sun Chunhua, et al. Movement and splashing of a droplet impacting on a wet wall. Chinese Journal of Theoretical and Applied Mechanics, 2013, 45(6):834-842(in Chinese)) |
| 17 | 张明焜,陈硕,尚智. 带凹槽的微通道中液滴运动数值模拟. 物理学报,2012,61(3):034701(Zhang Mingkun, Chen shuo, Shang zhi. Numerical simulation of a droplet motion in a grooved microchannel. Acta Physica Sincia, 2012, 61(3):034701(in Chinese)) |
| 18 | Andrade JD, Smith LM, Gregonis DE. The contact angle and interface energetic//Andrade JD ed. Surface and Interfacial Aspects of Biomedical Polymers, Volume 1. New York:Plenum Press, 1985 |
| 19 | Rao DN. The concept, characterization, concerns and consequences of contact angles in solid-liquid-liquid systems//Mittal KL ed. Contact Angle, Wettability and Adhesion. Utrecht:VSP. 2003, 3:191-210 |
| 20 | 王晓东,彭晓峰,李笃中. 粗糙表面上的移动接触线和动态接触角. 化工学报,2004,55(3):403-407(Wang Xiaodong, Peng Xiaofeng, Li Duzhong. Moving contact line and dynamic contact angle on rough solid surfaces. Journal of Chemical Industry and Engineering,2004,55(3):403-407(in Chinese)) |
| 21 | 曹晓平,蒋亦民. 浸润接触线的摩擦性质与固体表面张力的Wenzel 行为. 物理学报,2005,54(5):2203-2205(Cao Xiaoping, Jiang Yiming. The frictional property of wetting line andWenzel behavior of surface tension. Acta Physica Sincia, 2005,54(5):2203-2205(in Chinese)) |
| 22 | 周建臣,耿兴国,林可君等. 微液滴在超疏水表面的受迫振动及其接触线的固着-移动转变. 物理学报,2014,63(21):216801(Zhou Jianchen, Geng Xingguo, Lin Kejun, et al. Stick-slip transition of a water droplet vibrated on a superhydrophobic surface. Acta Physica Sincia, 2014,63(21):216801(in Chinese)) |
| 23 | Oran A, Davis SH, Bankoff SG. Long-scale evolution of thin liquid films. Reviews of Modern Physics, 1997, 69:931-980 |
| 24 | Stillwagon LE, Larson RG. Leveling of thin films over uneven substrates during spin coating. Physics of Fluids A:Fluid Dynamics, 1990, 2(11):1937-1944 |
| 25 | 王铁强. 不对称微结构的构筑以及各向异性性质的研究.[博士论文]. 吉林:吉林大学,2013(Wang Tieqiang. Fabrication of asymmetric microstructures and investigation of their anisotropic properties.[PhD Thesis]. Jilin:Jilin University, 2013(in Chinese)) |
 2016, Vol. 48
2016, Vol. 48