现今高性能计算机的发展，使计算流体力学工作者有给出高精度计算数据的可能，于是，学术界一方面在研究提高计算出发的流动物理模型(如湍流模型)的精度，另一方面，在关注发展高精度的计算方法. 关于后者，引起了学术界的广泛重视.

1983年，Harten 提出了总变差减小(TVD)格式^[1]，后来又发展了本质无波动(ENO)和加权本质无波动(WENO)等高阶精度格式^{[2, 3, 4]}. 张涵信根据修正方程和熵增等物理原则，提出了无波动、无自由参数的耗散差分格式(NND)格式^{[5, 6]}，后来，又提出了三阶、四阶和五阶精度本质无波动无自由参数(ENN)格式^{[7, 8, 9]}.傅德薰和马延文^{[10, 11, 12, 13, 14]}根据耗散比拟和群速度控制，提出了迎风紧致格式和超紧致格式等高阶格式.沈孟育等^{[15, 16]}根据物理原则提出了广义紧致格式. 这些格式都是与本质无波动格式独立进行的.2000年，在莱勒(Lele)半点型线性紧致格式^[17]基础上，采用加权本质无波动格式的插值方法^[4]，通过对守恒型变量进行加权插值，邓小刚和张涵信^[18]发展了五阶精度的加权紧致非线性格式(WCNS)，张树海等^[19]采用加权本质无波动格式的插值方法，发展了通量型高阶精度加权紧致格式(WCOMP)，针对气动声学特别是激波噪声计算的需求，刘旭亮等^{[20, 21]}发展了具有谱分辨率的紧致格式.

加权本质无波动格式是国外常用的格式，加权型紧致格式和加权本质无波动格式有紧密的关系，这促使我们研究、比较这两种格式的关系和应用情况，有无进一步研究改进之处，这就是本文的目的.

为便于讨论数值格式的构造方法，考虑如下一维非线性双曲守恒方程 $$ \dfrac{\partial u}{\partial t} + \dfrac{\partial f(u)}{\partial x} = 0 \tag{1}$$

设计高阶精度捕捉激波的数值格式的主要任务就是设计非线性导数$\dfrac{\partial f(u)}{\partial x}$的离散方法，使得数值解在激波附近不存在非物理波动，同时具有高阶精度.

方程(1)可以写成如下守恒型半离散格式 $$ \dfrac{\partial u}{\partial t} = - \dfrac{\hat {f}_{i + 1 / 2} - \hat {f}_{i - 1 / 2} }{\Delta x} \tag{2}$$ 这里，$\hat {f}_{i + 1 / 2} $是数值通量，它以高阶精度逼近$h_{i + 1 / 2} = h(x_{i + 1 / 2} )$. 函数$h(x)$的定义是 $$ f(u(x)) = \dfrac{1}{\Delta x}\int_{x - \Delta x / 2}^{x + \Delta x / 2} h(\xi ) d\xi \tag{3}$$

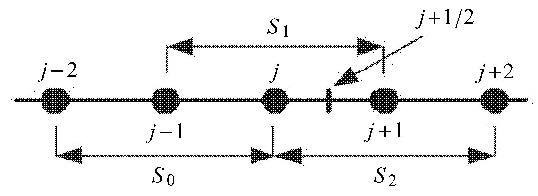
加权本质无波动格式的设计思想是采用包括$2r - 1$个节点的模板$S^{2r - 1} = (x_{i - r + 1} , \cdots, x_{i + r - 1} )$，重构$2r - 1$阶(此模板上可构造的最高阶精度)线性数值通量$\hat {f}_{i + 1 / 2} $如下 $$ \hat {f}_{i + 1 / 2}^L = q^{2r - 1}(f_{i - r + 1} , \cdots , f_{i + r - 1} )\tag{4}$$ 包括$2r - 1$个节点的模板$S^{2r - 1}$可以分解成$r$个子模板$S_0 $, $S_1 $, $\cdots$, $S_{r - 1} $如图1所示，在每个子模板上，可以重构一个$r$阶数值通量 $$ \hat {f}_{i + \tfrac{1}{2}}^{(k)} = q_k^r (f_{i + k - r + 1} , \cdots, f_{i + k} ) , k = 0, 1, \cdots , r-1 \tag{5a}$$ 其中 $$ q_k^r (g_0 , g_1, \cdots, g_{r - 1} ) = \sum_{l = 0}^{r - 1} a_{k, l}^r g_l \tag{5b}$$ 简单的数学推导可知，$\hat {f}_{i + 1 / 2}^L $可以由$\hat {f}_{i + 1/2}^{(k)} $的线性组合得到 $$ \hat {f}_{i + 1 / 2}^L = \sum_{k = 0}^{r - 1} d_k^r f_{i + 1 / 2}^{(k)} \tag{6}$$ 其中$d_k^r $是线性权. 由于线性权无法捕捉强激波，按照加权本质无波动格式的思想，采用非线性权$\omega _k^r $替代线性权$d_k^r $，得到非线性数值通量 $$ \hat {f}_{i + 1 / 2} = \sum_{k = 0}^{r - 1} {\omega _k^r } f_{i + 1 / 2}^{(k)} \tag{7}$$ 其中 $$ \omega _k^r = \dfrac{d_k^r }{(\varepsilon + IS_k^r )^p} \tag{8}$$ $IS_k^r $是光滑测试因子，由下式给出^[4] $$ IS_k^r = \sum_{l = 0}^{r - 1} \int_{x_{i - 1 / 2} }^{x_{i + 1 / 2} } {\Delta x^{2l - 1}} \left(\dfrac{\partial ^l\hat {f}^{(k)}(x)}{\partial ^lx } \right)^2 d x \tag{9}$$

图1(Fig.1)

图1 五阶加权本质无波动格式的设计模板和子模板 Fig.1 The stencil and substencils of the fifth order WENO scheme

只要非线性权与线性权之间满足一定的精度条件^{[4, 22]}，加权本质无波动格式在光滑区可以达到最优格式精度，而在激波区，保持了本质无波动的特性.

为便于比较，下面给出五阶加权本质无波动格式的具体数值通量 $$ \hat {f}_{i + 1 / 2} = \omega _0 \hat {f}_{i + 1 / 2}^{(0)} + \omega _1 \hat {f}_{i + 1 / 2}^{(1)} + \omega _2 \hat {f}_{i + 1 / 2}^{(2)} \tag{10}$$

在3个子模板上的三阶数值通量是 $$\hat {f}_{i + 1 / 2}^{(0)} = \dfrac{1}{3}f_{i - 2} - \dfrac{7}{6}f_{i - 1} + \dfrac{11}{6}f_i \tag{11a}$$ $$\hat {f}_{i + 1 / 2}^{(1)} = - \dfrac{1}{6}f_{i - 1} + \dfrac{5}{6}f_i + \dfrac{1}{3}f_{i + 1} \tag{11b}$$ $$\hat {f}_{i + 1 / 2}^{(2)} = \dfrac{1}{3}f_i + \dfrac{5}{6}f_{i + 1} - \dfrac{1}{6}f_{i + 2} \tag{11c}$$

线性权是 $$ d_0 = 0.1 , d_1 = 0.6 , d_2 = 0.3 \tag{12}$$ 光滑测试因子为

$$IS_0 = \dfrac{13}{12}(f_{i - 2} - 2f_{i - 1} + f_i )^2 + \dfrac{1}{4}(f_{i - 2} - 4f_{i - 1} + 3f_i )^2 \tag{13a}$$

$$IS_1 = \dfrac{13}{12}(f_{i - 1} - 2f_i + f_{i + 1} )^2 + \dfrac{1}{4}(f_{i - 1} - f_{i + 1} )^2 \tag{13b}$$

$$IS_2 = \dfrac{13}{12}(f_i - 2f_{i + 1} + f_{i + 2} )^2 + \dfrac{1}{4}(3f_i - 4f_{i + 1} + f_{i + 2} )^2 \tag{13c}$$

详见文献^[4].

加权型紧致格式是基于莱勒的半点型线性紧致格式^[17]和加权本质无波动格式^[4]的捕捉激波思想设计的.1992年，莱勒^[17]提出了半点型线性紧致格式 $$ \beta {f}'_{i - 2} + \alpha {f}'_{i - 1} + {f}'_i + \alpha {f}'_{i + 1} + \beta {f}'_{i + 2} = \\ a\dfrac{f_{i + 1/2} - f_{i - 1/2} }{\Delta x} + b\dfrac{f_{i + 3/2} - f_{i - 3/2} }{3\Delta x} + c\dfrac{f_{i + 5/2} - f_{i -5/2} }{5\Delta x} \tag{14}$$

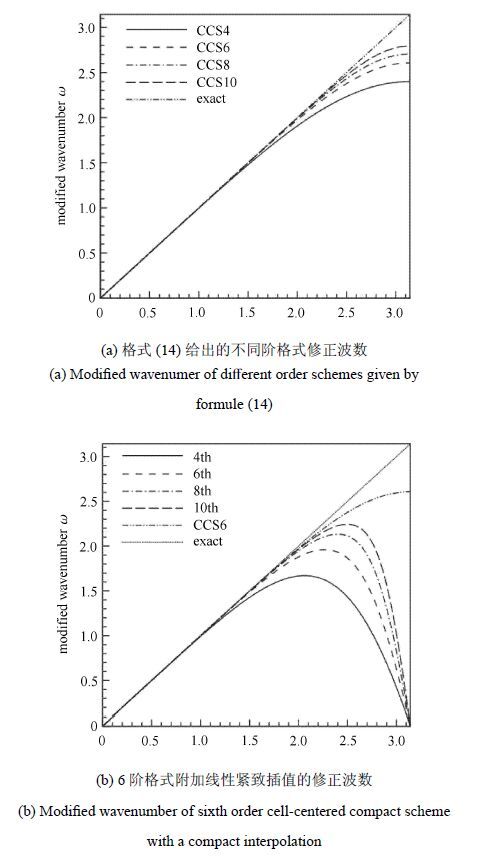
该格式左端是网格点上的函数导数值，右端是半点的函数值，它最大的优点是分辨率非常高，接近谱方法分辨率，如图2所示.但是，右端半点的函数值是未知的，莱勒^[17]设计了线性紧致插值的方法求得半点的值.

特别地，如果$\beta = 0$和$c = 0$，格式(14)可以简化为三对角型格式 $$ \alpha {f}'_{i - 1} + {f}'_i + \alpha {f}'_{i + 1} = \\ a\dfrac{f_{i + 1/2} - f_{i-1/2} }{\Delta x} + b\dfrac{f_{i + 3/2} - f_{i-3/2} }{3\Delta x} \tag{15}$$ 如果$\alpha = \dfrac{1}{22}$，格式进一步简化为 $$ \alpha {f}'_{i - 1} + {f}'_i + \alpha {f}'_{i + 1} = a\dfrac{f_{i + 1/2} - f_{i -1/2} }{\Delta x} \tag{16}$$

图2(Fig.2)

图2 线性紧致格式的修正波数 Fig.2 Modified wavenumber of the cell-centered compact scheme

如果$\alpha = \beta = 0$，可以得到显式格式 $$ {f}'_i = a\dfrac{f_{i + 1/2} - f_{i-1/2} }{\Delta x} + b\dfrac{f_{i + 3/2} - f_{i-3/2} }{3\Delta x} + c\dfrac{f_{i + 5/2} -f_{i-5/2} }{5\Delta x} \tag{17}$$

线性紧致格式具有高阶精度、高分辨率和低耗散的特性，是计算多尺度流动比较好的数值格式.但是，线性紧致格式无法捕捉流场中的强激波，为了达到捕捉激波的效果，引入加权本质无波动格式^[4]捕捉激波的思想，对式(14)右端半点值进行加权插值.

仍采用图1所示的加权本质无波动格式构造模板，在$S^{2r - 1}$上可以设计$2r-1$阶精度的插值函数 $$ \hat {f}^{2r - 1}(x) = f_i + \sum_{l = 1}^{2(r - 1)} {a_l } (x - x_i )^l \tag{18}$$ 该插值函数在$x_{i + 1/2} $处取值，得到半点处的$2r-1$阶线性插值公式 $$ \hat {f}_{i + 1 / 2}^L = q^{2r - 1}(f_{i - r + 1} , \cdots , f_{i + r - 1} ) \tag{19}$$ 在每个子模板$S_k ^{2r - 1}$上，可以得到$r$阶插值函数和半点$x_{i + 1/2} $处的$r$阶插值公式 $$ \hat {f}_{i + 1/2}^{(k)} = q_k^r (f_{i + k - r + 1} , \cdots, f_{i + k} ) \tag{20a}$$ 其中 $$ q_k^r (g_0 , \cdots, g_{r - 1} ) = \sum_{l = 0}^{r - 1} {a_{k, l}^r } g_l \tag{20b}$$ $\hat {f}_{i + 1 / 2}^L $可以由$\hat {f}_{i + 1/2}^{(k)} $线性组合得到 $$ \hat {f}_{i + 1 / 2}^L = \sum_{k = 0}^{r - 1} {d_k^r } f_{i + 1 / 2}^{(k)} \tag{21}$$ 其中$d_k^r $是线性权. 由于线性权无法捕捉强激波，按照加权本质无波动的思想，采用非线性权 $$ \hat {f}^W_{i +1/2} = \sum_{k = 0}^{r - 1} {\omega _k^r \hat {f}_{i + 1/2}^{(k)} } \tag{22}$$ 其中$\omega _k^r = \dfrac{d_k^r }{(\varepsilon + IS_k^r )^p}$ . 这里，$IS_k^r $是光滑测试因子，按照加权本质无波动格式计算方法的式(9)计算.

将式(22)得到的半点的通量值代入到线性紧致格式(14)的右端，就得到一定精度的加权型紧致格式.

2008年，张树海等^[19]将加权本质无波动格式重构过程复制到对通量进行插值，发展了通量型高阶精度加权紧致格式. 我们以五阶精度格式$r = 3$为例予以说明，其插值公式为 $$ \hat {f}_{i + 1 / 2}^L = \dfrac{1}{128}(3f_{i - 2} - 20f_{i - 1} + 90f_i + 60f_{i + 1} - 5f_{i + 2} )\tag{23}$$ 在3个子模板上的三阶插值公式是 $$\hat {f}_{i + 1/2}^{(0)} = \dfrac{1}{8}(3f_{i - 2} - 10f_{i - 1} + 15f_i ) \tag{24a}$$ $$\hat {f}_{i +1/2}^{(1)} = \dfrac{1}{8}( - f_{i - 1} + 6f_i + 3f_{i + 1} ) \tag{24b}$$ $$\hat {f}_{i + 1/2}^{(2)} = \dfrac{1}{8}(3f_i + 6f_{i + 1} - f_{i + 2} ) \tag{24c}$$ 线性权是 $$ d_0 = \dfrac{1}{16} , d_1 = \dfrac{10}{16} , d_2 = \dfrac{5}{16} \tag{25}$$ 光滑测试因子与五阶加权本质无波动格式的光滑测试因子完全一致. 详见文献^[19].

对比加权本质无波动格式和加权紧致格式，我们看到，加权紧致格式采用了加权本质无波动的加权插值过程^[4]，而加权本质无波动格式采用的重构过程，两者在加权过程中公式具有相同的形式，只是系数不同，因此，程序完全可拷贝，只是修改相应的系数即可.

邓小刚和张涵信^[18]采用加权本质无波动加权插值思想，对欧拉方程的特征变量$Q$进行加权插值，发展了四阶和五阶的加权紧致非线性格式. $Q$的定义是：$Q = LU$. $L$和$R$是雅克比矩阵$A = \dfrac{d F(U)}{d U}$的左右特征矩阵.

邓小刚和张涵信^[18]给出的插值公式是 $$\tilde {Q}_{L, i + 1 / 2} = Q_i + \dfrac{\Delta x}{2}t_i + \dfrac{\Delta x^2}{8}s_i \tag{26a}$$ $$\tilde {Q}_{R, i + 1 / 2} = Q_i - \dfrac{\Delta x}{2}t_i + \dfrac{\Delta x^2}{8}s_i \tag{26b}$$ $t_i $和$s_i $是$Q$的一阶导数和二阶导数的近似值. $Q_{i + 1 / 2} $ 插值公式的模板与图1所示加权本质无波动格式的模板一致，在五阶插值公式的模板 $S^5$的3个子模板$S_0$, $S_1 $和$S_2 $上，其计算公式是 $$t_i^{(0)} = \dfrac{1}{2\Delta x}(Q_{i - 2} - 4Q_{i - 1} + 3Q_i ) \tag{27a}$$ $$t_i^{(1)} = \dfrac{1}{2\Delta x}(Q_{i + 1} - Q_{i - 1} ) \tag{27b}$$ $$t_i^{(2)} = \dfrac{1}{2\Delta x}( - 3Q_i + 4Q_{i + 1} - Q_{i + 2} ) \tag{27c}$$ 和 $$s_i^{(0)} = \dfrac{1}{\Delta x^2}(Q_{i - 2} - 2Q_{i - 1} + Q_i ) \tag{28a}$$ $$s_i^{(1)} = \dfrac{1}{\Delta x^2}(Q_{i - 1} - 2Q_i + Q_{i + 1} ) \tag{28b}$$ $$s_i^{(2)} = \dfrac{1}{\Delta x^2}(Q_i - 2Q_{i + 1} + Q_{i + 2} ) \tag{28c}$$ 在3个子模板上，得到3个三阶精度插值公式，进行加权得到五阶插值公式 $$\tilde {Q}_{L, i + 1 / 2}^w = \sum_{k = 0}^2 {\omega _{L, k} \tilde {Q}_{L, i + 1 / 2}^{(k)} } \tag{29a}$$ $$\tilde {Q}_{R, i + 1 / 2}^w = \sum_{k = 0}^2 {\omega _{R, k} \tilde {Q}_{R, i + 1 / 2}^{(k)} } \tag{29b}$$

邓小刚和张涵信^[18]采用与加权本质无波动格式相同的非线性权计算公式(8)，光滑测试因子的计算公式略有不同，具体如下 $$ IS_k = (\Delta xt^{(k)})^2 + (\Delta x^2s^{(k)})^2 \tag{30}$$ 具体形式是 $$ \left.\!\!\begin{array}{l} IS_0 = \dfrac{1}{4}(Q_{i - 2} - 4Q_{i - 1} + 3Q_i )^2 + (Q_{i - 2} - 2Q_{i - 1} + Q_i )^2 \\ IS_1 = \dfrac{1}{4}(Q_{i + 1} - Q_{i - 1} )^2 + (Q_{i - 1} - 2Q_i + Q_{i + 1} )^2 \\ IS_2 = \dfrac{1}{4}( - 3Q_i + 4Q_{i + 1} - Q_{i + 2} )^2 + (Q_i - 2Q_{i + 1} + Q_{i + 2} )^2 \end{array} \!\! \right \} \tag{31}$$

得到特征量的值之后，经过如下计算 $$\tilde {U}_{L, i + 1 / 2} = R\tilde {Q}_{L, i + 1 / 2}^w \tag{32a}$$ $$\tilde {U}_{R, i + 1 / 2} = R\tilde {Q}_{R, i + 1 / 2}^w \tag{32b}$$

可以得到守恒量的值，之后，采用罗(Roe)方法计算通量$f_{i + 1 / 2} $的近似值如下 $$ \tilde {F}_{i + 1 / 2}^{\rm Roe} = \dfrac{1}{2}\Big[F(\tilde {U}_{L, i + 1 / 2} ) + F(\tilde {U}_{R, i + 1 / 2} ) -\\ \vert \tilde {A}\vert (\tilde {U}_{R, i + 1 / 2} - \tilde {U}_{L, i + 1 / 2} )\Big] \tag{33}$$ 特别的，把这种对守恒变量的加权插值应用于方程(17)，邓小刚给出了一种五阶显式加权紧致非线性格式(WCNS-E-5)，具体如下 $$ {f}'_i = \dfrac{75}{64}\dfrac{f_{i + 1/2} - f_{i-1/2} }{\Delta x} - \dfrac{25}{384}\dfrac{f_{i + 3/2} - f_{i - 3/2} }{\Delta x} + \\ \dfrac{3}{640}\dfrac{f_{i + 5/2} - f_{i - 5/2} }{\Delta x} \tag{34}$$

数值分析和数值试验表明，前面提到的加权紧致格式与加权本质无波动格式相比，并没有明显的优势. 为提高高阶精度格式的分辨率，以满足激波噪声的计算需求，我们发展了具有谱分辨率的紧致格式(CCSSR)，这种格式包括线性格式和非线性格式.

式(14)给出的莱勒的半点型线性紧致格式有两个缺点：(1)设计模板包括了整点和半点的函数值，但莱勒格式要么仅用整点的值，要么仅用半点的值，格式没有达到该模板上的最优精度，(2)半点上的值需要插值方法求得，任何插值方法都存在传递误差，导致格式对高波数的分辨率大幅度下降. 我们采取两种方法，克服了莱勒格式的缺点. 第一，格式包括模板上所有信息，格式精度可以达到最优；第二，采用同样的格式，求得半点和整点的值，避免了插值过程引起的传递误差. 具体如下 $$ \begin{array}{l} \beta {{f'}_{i - 2}} + \alpha {{f'}_{i - 1}} + {{f'}_i} + \alpha {{f'}_{i + 1}} + \beta {{f'}_{i + 2}} = \\ a\frac{{{f_{i + 1/2}} - {f_{i - 1/2}}}}{{\Delta x}} + b\frac{{{f_{i + 1}} - {f_{i - 1}}}}{{2\Delta x}} + c\frac{{{f_{i + 3/2}} - {f_{i - 3/2}}}}{{3\Delta x}} + \\ d\frac{{{f_{i + 2}} - {f_{i - 2}}}}{{4\Delta x}} + e\frac{{{f_{i + 5/2}} - {f_{i - 5/2}}}}{{5\Delta x}} \end{array} \tag{35a}$$ $$ \begin{array}{l} \beta {{f'}_{i - 5/2}} + \alpha {{f'}_{i - 3/2}} + {{f'}_{i - 1/2}} + \alpha {{f'}_{i + 1/2}} + \beta {{f'}_{i + 3/2}} = \\ a\frac{{{f_i} - {f_{i - 1}}}}{{\Delta x}} + b\frac{{{f_{i + 1/2}} - {f_{i - 3/2}}}}{{2\Delta x}} + c\frac{{{f_{i + 1}} - {f_{i - 2}}}}{{3\Delta x}} + \\ d\frac{{{f_{i + 3/2}} - {f_{i - 5/2}}}}{{4\Delta x}} + e\frac{{{f_{i + 2}} - {f_{i - 3}}}}{{5\Delta x}} \end{array} \tag{35b}$$

求得网格点和半点处的一阶导数之后，通过求解相应的控制方程，即可求得下一时刻的网格点和半点处函数值.

与莱勒的格式相比，式(35)给出的数值格式有两个优点：第一，格式的精度有一定的提高，莱勒格式最高达到十阶精度，此格式可以达到十四阶；第二，网格点和半点上的函数值都是通过同一格式计算得到，消除了原格式紧致插值引起的传递误差，保证了计算过程的精度和分辨率. 与莱勒格式的比较，我们改进格式的修正波数与精确值相差无几. 详见文献^[20].

将前面的加权插值技术代入到式(35)，就可以得到具有谱分辨率的非线性紧致格式.但是，正如我们前面设计的加权紧致格式一样，所得到的格式耗散性仍比较高.事实上，模拟强激波问题需要一定的耗散，而计算流场中的噪声希望耗散尽可能的小，这本身是一个矛盾.我们的设计思想就是希望格式的捕捉激波能力与耗散能够达到一种平衡，为了能够更好地计算流场中的声波，甚至可以牺牲一些捕捉激波的鲁棒性. 达到这一目的并非易事，现在仍在研究之中.此处，我们仅列出一种我们刚刚设计的混合插值技术得到的格式具有谱分辨率的紧致非线性(CCSSR-HW)^[21].

由于加权本质无波动格式的模板$S^{2r - 1}$具有迎风特性，得到的数值格式具有较强的耗散特性，为降低格式的耗散特性，扩展一个节点，采用对称模板$S^{2r}$设计插值.以五阶插值为例，该模板可以分为4个子模板，前3个子模板与五阶加权本质无波动格式的子模板完全一样，第4个子模板上的插值是 $$ \hat {f}_{i + 1/2}^{(3)} = \dfrac{1}{8}(15f_{i + 1} - 10f_{i + 2} + 3f_{i + 3} )\tag{36}$$ 在模板$S^{2r}$我们既可以设计五阶迎风插值，也可以设计六阶中心插值.

$$\hat {f}_{i + 1/2}^U = \dfrac{1}{128} (3 f_{i - 2} - 20f_{i - 1} + 90f_i + 60f_{i + 1} - 5f_{i + 2} ) \tag{37a}$$

$$\begin{array}{l} \hat f_{i + 1/2}^C = \frac{1}{{256}}(3{f_{i - 2}} - 25{f_{i - 1}} + 150{f_i} + 150{f_{i + 1}} - \\ 25{f_{i + 2}} + 3{f_{i + 3}}) \end{array} \tag{37b}$$ 为平衡捕捉激波的鲁棒性和格式的耗散性，我们采取如下混合插值 $$ \hat {f}_{i + 1/2}^H = \left( {1 - \sigma } \right)\hat {f}_{i + 1/2}^U + \sigma \hat {f}_{i + 1/2}^C = \sum_{r = 0}^3 {d_r } \hat {f}_{i + 1/2}^{(r)} \tag{38}$$ 或 $$ \hat {f}_{i + 1/2}^H = \dfrac{3d_0 }{8}f_{i - 2} - \dfrac{10d_0 + d_1 }{8}f_{i - 1} + \dfrac{15d_0 + 6d_1 + 3d_2 }{8}f_i +\\ \dfrac{3d_1 + 6d_2 + 15d_3 }{8}f_{i + 1} - \dfrac{d_2 + 10d_3 }{8}f_{i + 2} + \dfrac{3d_3 }{8}f_{i + 3} \tag{39}$$ 这里$d_0 $, $d_1 $, $d_2 $和$d_3 $是线性权，如下 $$ \left. \begin{align} & {{d}_{0}}=\frac{2-\sigma }{32},{{d}_{1}}=\frac{5\left( 4-\sigma \right)}{32} \\ & {{d}_{2}}=\frac{5\left( 2+\sigma \right)}{32},{{d}_{3}}=\frac{\sigma }{32} \\ \end{align} \right\} \tag{40}$$ $\sigma $是混合插值参数，定义如下 $$\sigma = \min \left( {1, \:\dfrac{r_{i + 1/2} }{r_{\rm c} }} \right) \tag{41a}$$ $$r_{i + 1/2} = \min \left( {r_i , r_{i + 1} } \right) \tag{41b}$$ $$r_i = \dfrac{\left| {2\left( {f_{i + 1} - f_i } \right)\left( {f_i - f_{i - 1} } \right)} \right| + \delta }{\left( {f_{i + 1} - f_i } \right)^2 + \left( {f_i - f_{i - 1} } \right)^2 + \delta } \tag{41c}$$ $$\delta = \dfrac{0.9r_{\rm c} }{1 - 0.9r_{\rm c} }\times 10^{ - 6} \tag{41d}$$ 详见文献^[21].

加权型紧致格式采用了加权本质无波动格式的插值方法，因此，包括格式的捕捉激波能力、精度、分辨率、耗散和收敛性等都保留了加权本质无波动格式的属性.本节我们将对五阶加权紧致格式(WCOMP5)^[19]、五阶显式加权紧致非线性格式(WCNS-E-5)^[18]和五阶加权本质无波动格式(WENO5)^[4]进行比较全面比较.

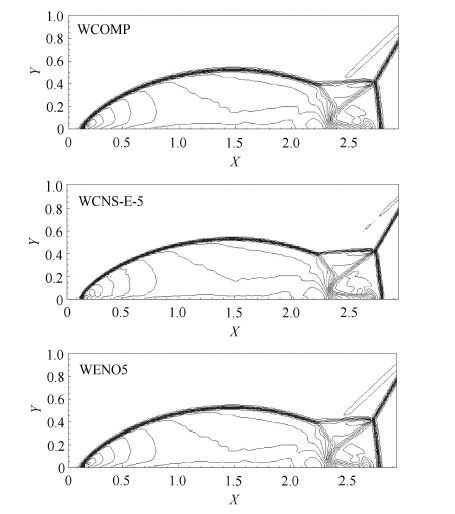
为了测试格式的捕捉激波能力，我们计算了两个问题，一个是马赫数为10的激波绕一斜坡的马赫反射问题^[19]，计算区域为[0, 4]×[0, 1]，采用240×60均匀网格.图3是计算得到的密度等值线，可以看到，不同格式的数值结果虽有些微弱的差别，但结果基本相当.

图3(Fig.3)

图3 3种格式计算双马赫反射问题的密度等值线. 密度变化区间[1.731, 20.92]和30条等值线 Fig.3 Density contours of double mach reflection problem, 30 contour lines between [1.731, 20.92]

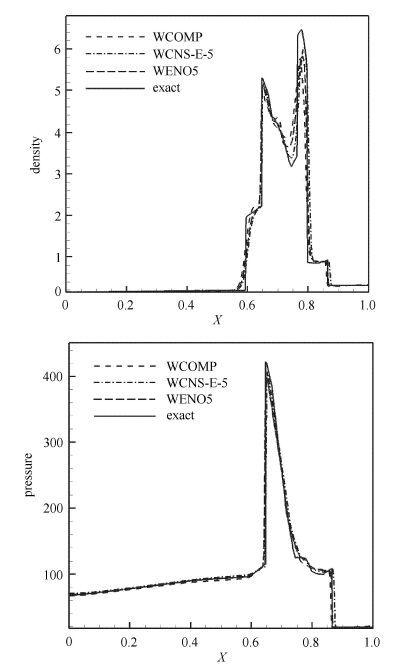
第2个问题是两个爆炸波碰撞问题，其条件为 $$ U(x, 0) = \left\{ \begin{array}{ll} U_{\rm L} , & 0 < x <0.1 \\ U_{\rm M} , & 0.1 < x < 0.9 \\ U_{\rm R} , & 0.9 < x <1.0 \end{array} \right. \tag{42}$$ $\rho _{\rm L} = \rho _{\rm M }= \rho _{\rm R} = 1$，$u_{\rm L} = u_{\rm M} = u_{\rm R} = 1$，$p_{\rm L} = 1\times 10^3$，$p_{\rm M} = 1\times 10^{ - 2}$，$p_{\rm R} = 1\times 10^2$.这是一个包含强间断的问题，左区和中间区域初始压力分布的比值达到$10^{5}$量级，很多格式都难以顺利计算.在计算过程中，五阶加权本质无波动格式可以顺利得到计算结果，五阶加权紧致格式和五阶显式加权紧致非线性格式需要进行熵修正才能使计算得以进行.图4是采用400均匀网格的计算结果及其比较，结果基本一致，其"精确解"是五阶加权本质无波动格式和20 000空间网格点的计算结果.

图4(Fig.4)

图4 两个爆炸波相碰撞模型问题的数值结果及其比较 Fig.4 Comparison of numerical results of two blasting waves

我们知道，加权本质无波动格式的精度是有条件的，以五阶加权本质无波动格式为例，它达到设计精度的充要条件是^[22] $$ \left. \begin{array}{l} \sum\limits_{k = 0}^2 {({\omega _k} - {d_k})} = O(\Delta {x^6})\\ 3\omega _1^{( + )} - 3\omega _1^{( - )} - \omega _2^{( + )} + \omega _2^{( - )} + \omega _3^{( + )} - \omega _3^{( - )} = O(\Delta {x^3})\\ {\omega _k} - {d_k} = O(\Delta {x^2}) \end{array} \right\} \tag{43}$$ 其中$\omega _k $为第$k$个模板上的权因子，$\omega _k^{(\pm )} $ 的上标$(\pm )$分别对应$x_{i\pm 1/2} $处的通量.

亨里克(Henrick)等^[22]证明，原始加权本质无波动格式并不能满足上述条件，导致格式在极值点附近降阶，并给出了改善极值点精度的映射方法.

加权型紧致格式是采用加权本质无波动插值技术构造的，其精度与加权本质无波动格式相似，在极值点附近也降阶.我们以五阶显式加权紧致非线性格式为例予以说明. 该格式达到设计精度(五阶)需满足如下条件 $$ \left. \begin{align} & \sum\limits_{k=0}^{2}{({{\omega }_{k,m}}-{{d}_{k}})=O(\Delta {{x}^{6}})} \\ & \sum\limits_{m=1}^{6}{{{c}_{m}}}\sum\limits_{k=0}^{2}{({{\omega }_{k,m}}-{{d}_{k}}){{l}_{k}}=O(\Delta {{x}^{3}})} \\ & {{\omega }_{k,m}}-{{d}_{k}}=O\left( \Delta {{x}^{2}} \right) \\ \end{align} \right\} \tag{44}$$ 其中，下标$m$取$1, 2, \cdots , 6$，依次对应$i - \dfrac{5}{2}$, $i - \dfrac{3}{2}, \cdots , i + \dfrac{5}{2}$处的插值，下标$k$表示该处插值中第$k$个模板；$c_1 = - c_6 = - \dfrac{3}{640}$，$c_2 = - c_5 = \dfrac{25}{384}$，$c_3 = - c_4 = - \dfrac{75}{64}$，$l_1 = - \dfrac{5}{16}$，$l_2 = - l_3 = \dfrac{1}{16}$.该要求与五阶加权本质无波动格式对精度的要求非常相似，在正常点($u' \ne 0$和$u" \ne 0)$附近，格式能达到五阶精度；在一阶极值点($u' = 0$，$u" \ne 0)$附近，格式降为三阶精度； 在二阶极值点($u' = u" = 0$)附近，格式降为二阶精度.

为了考核并比较各个格式的精度，我们计算一维标量方程 $$ \left. \begin{array}{l} {u_t} + {u_x} = 0, - 1 \le x \le 1\\ u(x,0) = {u^0}(x) \end{array} \right\} \tag{45}$$ 边界为周期条件，选择两种初值$u^0(x) = \sin (\pi x)$和$\sin ^4(\pi x)$，分别计算到无量纲时间$t=1$和$t=10$，结果分别列于表1和表2，我们看到，对第一个初值问题，计算很快收敛到设计精度，而对于含有高阶极值点的第二个初值问题，3种格式精度都难以收敛到设计精度，就误差的量来对比，五阶加权紧致格式的误差明显小于五阶显式加权紧致非线性格式的误差，五阶显式加权紧致非线性格式的误差明显小于五阶加权本质无波动格式的误差.

表1(Table 1)

表1 一维标量方程(45)和初始值$\sin (\pi x)$的数值误差和精度及其比较Table 1 Comparison of different schemes, numerical error and convergence accuracy for advection problem with initial value $\sin (\pi x)$ Method Grid $L_1$ error $L_1$ order $L_\infty $ error $L_\infty $ order 10 1.42×10$^{-2}$ 2.58×10$^{-2}$ 20 6.20×10$^{-4}$ 4.52 1.22×10$^{-3}$ 4.40 WCOMP 40 1.84×10$^{-5}$ 5.07 3.73×10$^{-5}$ 5.03 80 5.63×10$^{-7}$ 5.03 1.20×10$^{-6}$ 4.95 160 1.76×10$^{-8}$ 5.00 3.63×10$^{-8}$ 5.05 10 1.41×10$^{-2}$ 2.53×10$^{-2}$ 20 6.05×10$^{-4}$ 4.54 1.19×10$^{-3}$ 4.41 WCNS-E-5 40 1.82×10$^{-5}$ 5.05 3.67×10$^{-5}$ 5.01 80 5.63×10$^{-7}$ 5.02 1.19×10$^{-6}$ 4.95 160 1.76×10$^{-8}$ 5.00 3.54×10$^{-8}$ 5.07 10 1.72×10$^{-2}$ 2.98×10$^{-2}$ 20 7.75×10$^{-4}$ 4.48 1.49×10$^{-3}$ 4 .33 WENO5 40 2.34×10$^{-5}$ 5.05 4 .70×10$^{-5}$ 4 .98 80 7.23×10$^{-7}$ 5.01 1.52×10$^{-6}$ 4 .96 160 2.26×10$^{-8}$ 5.00 4 .53×10$^{-8}$ 5.06

表1 一维标量方程(45)和初始值$\sin (\pi x)$的数值误差和精度及其比较 Table 1 Comparison of different schemes, numerical error and convergence accuracy for advection problem with initial value $\sin (\pi x)$

表2(Table 2)

表2 一维标量方程(45)和初值为$\sin ^4(\pi x)$的数值误差和精度及其比较 Table 2 Comparison of different schemes, numerical error and convergence accuracy for advection problem with initial value $\sin ^4(\pi x)$ Method Grid $L_1$ error $L_1$ order $L_\infty $ error $L_\infty $ order 10 3.55×10$^{-1}$ 4.63×10$^{-1}$ 20 9.18×10$^{-2}$ 1.95 2.09×10$^{-1}$ 3.91 WCOMP 40 7.18×10$^{-3}$ 3.68 1.16×10$^{-3}$ 3.58 80 3.05×10$^{-4}$ 4.56 5.64×10$^{-6}$ 7.69 160 1.13×10$^{-6}$ 8.07 1.44×10$^{-7}$ 5.30 10 3.56×10$^{-1}$ 4.47×10$^{-1}$ 20 1.36×10$^{-1}$ 1.39 3.03×10$^{-1}$ 0.56 WCNS-E-5 40 2.29×10$^{-2}$ 2.57 5.42×10$^{-2}$ 2.48 80 2.22×10$^{-3}$ 3.37 4.45×10$^{-3}$ 3.60 160 1.15×10$^{-4}$ 4.26 4.47×10$^{-4}$ 3.32 10 3.55×10$^{-1}$ 4 .44×10$^{-1}$ 20 1.53×10$^{-1}$ 1.21 3.30×10$^{-1}$ 0.43 WENO5 40 2 .88×10$^{-2}$ 2 .41 6.66×10$^{-2}$ 2 .31 80 2 .45×10$^{-3}$ 3.55 4 .67×10$^{-3}$ 3.83 160 1 .87×10$^{-4}$ 3 .71 8.16×10$^{-4}$ 2 .52

表2 一维标量方程(45)和初值为$\sin ^4(\pi x)$的数值误差和精度及其比较 Table 2 Comparison of different schemes, numerical error and convergence accuracy for advection problem with initial value $\sin ^4(\pi x)$

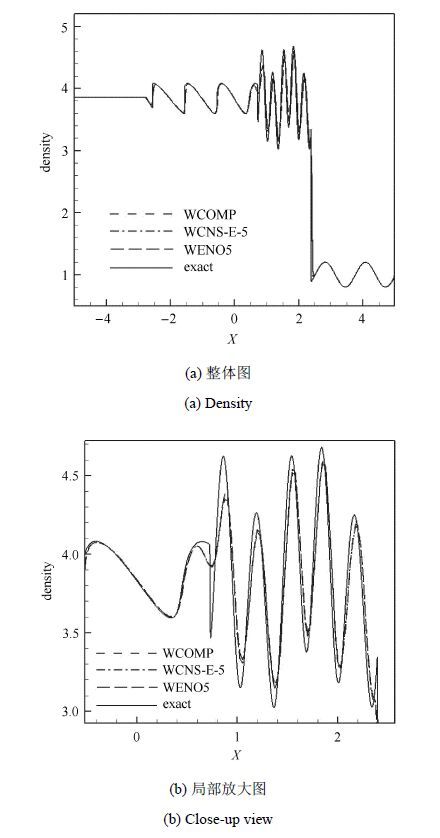
图5是3种格式采用400均匀网格计算舒-奥舍(Shu-Osher)问题的结果比较，其中，"精确解"是五阶加权本质无波动格式和20 000个空间网格点的计算结果.这是几乎所有高阶精度格式设计时都要计算的一个例子，可以看到，3种格式计算的结果非常相似，其差别很小.

图5(Fig.5)

图5 3 种格式对舒-欧舍问题计算结果及其比较 Fig.5 Comparison of numerical results of Shu-Osher problem

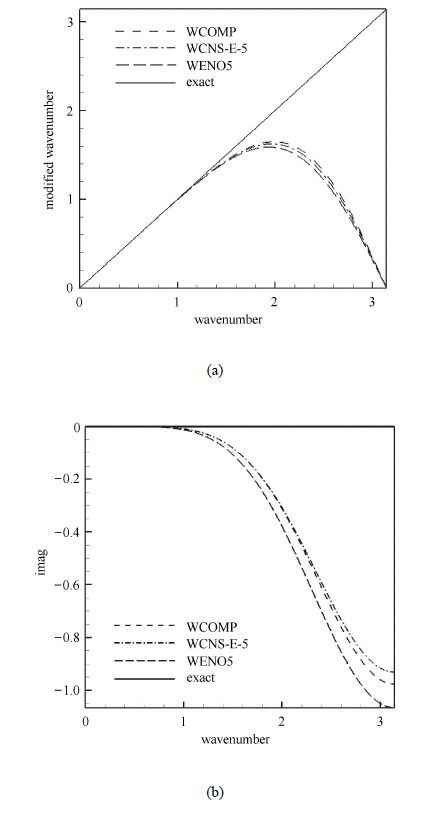
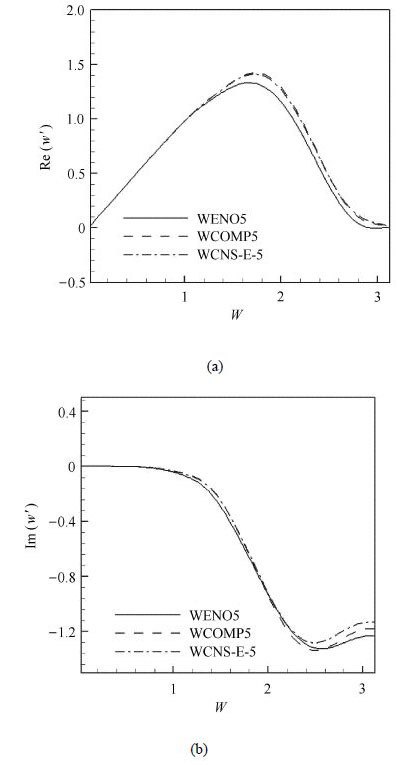
图6给出了3种格式在线性权情况下的修正波数和耗散特性，我们看到，五阶显式加权紧致非线性格式的修正波数比五阶加权本质无波动格式略高，五阶加权紧致格式的修正波数比五阶显式加权紧致非线性格式略高，五阶加权紧致格式的耗散性比五阶加权本质无波动格式略小，五阶显式加权紧致非线性格式的耗散性比五阶加权紧致格式略小，这应该是源于其模板比较宽.采用皮罗佐利(Pirozzoli)发展的方法^[23]，我们计算了3种非线性格式的近似修正波数和耗散特性，并绘于图7，可以看出，3种格式的关系与线性分析一致.涂国华等^[24]也采用相同的方法计算了加权紧致非线性格式与加权本质无波动的近似修正波数和耗散特性并进行了比较.

图6(Fig.6)

图6 3种格式的修正波数 (a)和耗散特性(b)及其比较 Fig.6 (a) dispersion and (b) dissipative properties of three schemes

图7(Fig.7)

图7 3种非线性格式的近似修正波数(a)和耗散特性(b)及其比较 Fig.7 Nonlinear (a) dispersion and (b) dissipative properties of three schemes

对含激波的定常流动不收敛问题是几乎所有捕捉激波格式存在的共同问题，不论是二阶还是高阶精度捕捉激波格式. 造成数值计算不收敛的主要原因是激波下游存在微弱的非物理波动，消除这种非物理波动使格式达到收敛解是计算流体力学面临的一个困难. 在计算流体力学领域，解决好这一问题有两个含义，第一，对于定常问题的计算，通常采用残差作为收敛判据，如果格式不能收敛，会使得此判据失效，人们只能根据经验来判断计算是否停止，会造成计算结果的人为因素. 第二，对多尺度问题的数值模拟，特别是激波噪声的模拟，这种微弱的非物理波动可能会比气动噪声高两个数量级以上，严重影响计算精度. 此外，利用此种格式直接模拟可压缩各向同性湍流，由于小激波串的存在，在小激波串下游的非物理波动，可能会影响湍流的统计规律.

由于加权紧致格式、加权本质无波动格式和加权紧致非线性格式采用不同的分裂技术，加权紧致格式和加权本质无波动格式既可以采用拉克斯-弗里德里希斯(Lax-Friedrichs)分裂，也可以采用罗(Roe)分裂，而加权紧致非线性格式的设计可以采用罗(Roe)分裂、斯特格-瓦明(Steger Warming)分裂或凡雷尔(Van leer)分裂，为方便起见，仅采用罗(Roe)分裂.对于一维欧拉方程，罗(Roe)分裂可以给出精确解，不存在不收敛现象，因此，模拟马赫数为2的二维45$^{\circ}$斜激波^{[25, 26]}问题并对3种格式的收敛特性进行比较.计算区域为[0, 4]×[0,2]，斜激波开始穿过点(3, 0)，采用200×100均匀网格并有 $\Delta x = \Delta y$.起动计算后，我们并不固定斜激波，而允许它在计算区域内漂移，因此，任何微小的扰动都会引起激波的漂移，形成缓慢运动的激波，造成波后严重的数值震荡，这是计算流体力学界的一个难题.

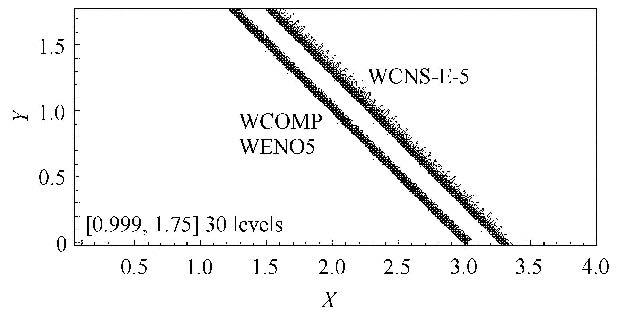
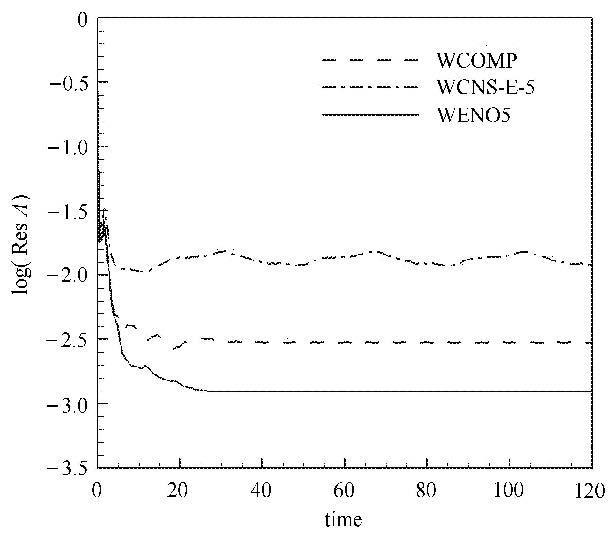
计算到无量纲时间$t=500$终止，图8是计算得到的密度等值线，图9是直线$y=1$上的密度分布和局部放大图，图10是残差收敛历程及其比较，可以看到，尽管3种格式的收敛特性都很不理想，但加权紧致格式和加权本质无波动格式的计算得到的激波基本没有改变其初始位置，加权紧致格式和加权本质无波动的波后非物理波动是个极其微小的量，但是，五阶显式加权紧致非线性格式计算的激波有一个明显漂移，其波后的非物理波动比五阶加权紧致格式和五阶加权本质无波动格式强很多.

图8(Fig.8)

图8 45$^{\circ}$斜激波的计算密度等值线及其比较 Fig.8 Density contours of oblique shock wave problem with angle of 45$^{\circ}$

图9(Fig.9)

图9 45$^{\circ}$斜激波计算得到的密度在以$y=1$上的分布及其比较 Fig.9 Density on $y=1$ of oblique shock wave problem with angle of 45$^{\circ}$

图10(Fig.10)

图10 45$^{\circ}$斜激波计算的收敛历程及其比较 Fig.10 The convergence history of oblique shock wave problem

当然，格式的收敛性与分裂方法有关，本文中，加权本质无波动格式和加权紧致格式采用常用的拉克斯-弗里德里希斯(Lax-Friedrichs)分裂，这种分裂耗散可能比较大，而五阶显式加权紧致非线性格式采用罗(Roe)分裂.

对于复杂多尺度问题，计算常常在并行机或超大规模计算来完成，以此为目的设计的高阶精度格式并行效率是格式设计时需要考虑的一个重要因素，有些格式在单机上计算很好，但难于并行化或者并行效率非常低，也是不可取的.比如，隐式紧致格式的并行化问题就依然是一个难题. 因此，此处我们只考虑五阶加权本质无波动和五阶显式加权紧致非线性格式的计算时间和并行效率.

采用五阶加权本质无波动格式和五阶显式加权紧致非线性格式这两种格式对可压缩各项同性湍流进行直接数值模拟，流动条件与文献^[28]相同，计算网格采用129×129×129，计算时间步长为$d t=0.001$，计算到无量纲时间$t=2$.表3给出了计算所耗时间和并行效率，我们看到，对所有计算，五阶显式加权紧致非线性格式格式比五阶加权本质无波动格式慢近一倍，并行效率也低. 值得说明的是，计算所耗机时问题，与编程技巧有关.

表3(Table 3)

表3 五阶加权本质无波动格式和五阶显式加权紧致非线性格式直接模拟三维各向同性湍流所耗时和并行效率及其比较Table 3 Parallel computing efficiency of DNS on three-dimensional isotropic turbulence Processors (129$^{3}$) WENO5 WCNS-E-5 CPU time/s Parallel computing efficiency CPU time/s Parallel computing efficiency 1×1×1 5.277 8×10$^{4}$ 1.000 9.409 6×10$^{4}$ 1.000 1×1×2 2.489 3×10$^{4}$ 1.060 4.742 7×10$^{4}$ 0.992 1×2×2 1.278 4×10$^{4}$ 1.032 2.438 4×10$^{4}$ 0.965 2×2×2 6.507 2×10$^{3}$ 1.014 1.253 0×10$^{4}$ 0.939 2×2×4 3.430 8×10$^{3}$ 0.961 6.561 3×10$^{3}$ 0.896 2×4×4 1.801 9×10$^{3}$ 0.915 3.588 4×10$^{3}$ 0.819 4×4×4 9.909 1×10$^{2}$ 0.832 2.047 9×10$^{3}$ 0.718 4×4×8 6.656 2×10$^{2}$ 0.619 1.239 5×10$^{3}$ 0.593

表3 五阶加权本质无波动格式和五阶显式加权紧致非线性格式直接模拟三维各向同性湍流所耗时和并行效率及其比较 Table 3 Parallel computing efficiency of DNS on three-dimensional isotropic turbulence

近年来，以莱勒的线性紧致格式^[17]为母格式，采用加权本质无波动格式的插值技术^[4]，发展了一系列高阶精度数值方法，包括加权紧致格式、加权紧致非线性格式和具有谱分辨率的紧致格式，本文对这些格式的设计方法进行了比较系统的综述.特别的，对五阶精度格式，包括五阶加权紧致格式、五阶显式加权紧致非线性格式和五阶加权本质无波动格式的捕捉激波能力、精度、耗散性、所耗计算时间和并行效率进行了较系统比较，主要有如下结论：

(1)加权型紧致格式是以莱勒的线性紧致格式为基础，采用加权本质无波动格式的插值技术而设计的，其捕捉激波能力、对定常激波的收敛特性和格式的精度都保持了加权本质无波动格式的性质.比如，由于波后存在非物理波动，对定常激波计算，残差很难收敛到比较满意的程度.特别地，五阶显式加权紧致非线性格式在斜激波下游会出现较强非物理波动.像加权本质无波动格式一样，加权型紧致格式在极值点附近降阶.当然，不论是提高极值点附近精度，还是降低甚至消除激波下游的非物理波动，针对加权本质无波动格式都有很好的研究，比如，很多学者改善了加权本质无波动格式在极值点附近的精度^{[22, 28, 29, 30]}，张树海等^{[23, 24]}基本解决了加权本质无波动格式对含激波的定常流动不收敛问题.这些方法，对加权类格式是有效的.

(2)五阶显式加权紧致非线性格式比五阶加权本质无波动格式慢近一倍，并行效率也低.

(3) 由于模板宽很多，加权型紧致格式边界处理更为复杂，增加了边界处理的难度，使得复杂问题的工程计算中面临更难问题.

(4)综合考虑格式的捕捉激波能力、分辨率、耗散特性以及并行效率，对于计算气动力等宏观量，现有的加权型紧致格式比五阶加权本质无波动格式没有明显的优势.

Zhang Shuhai